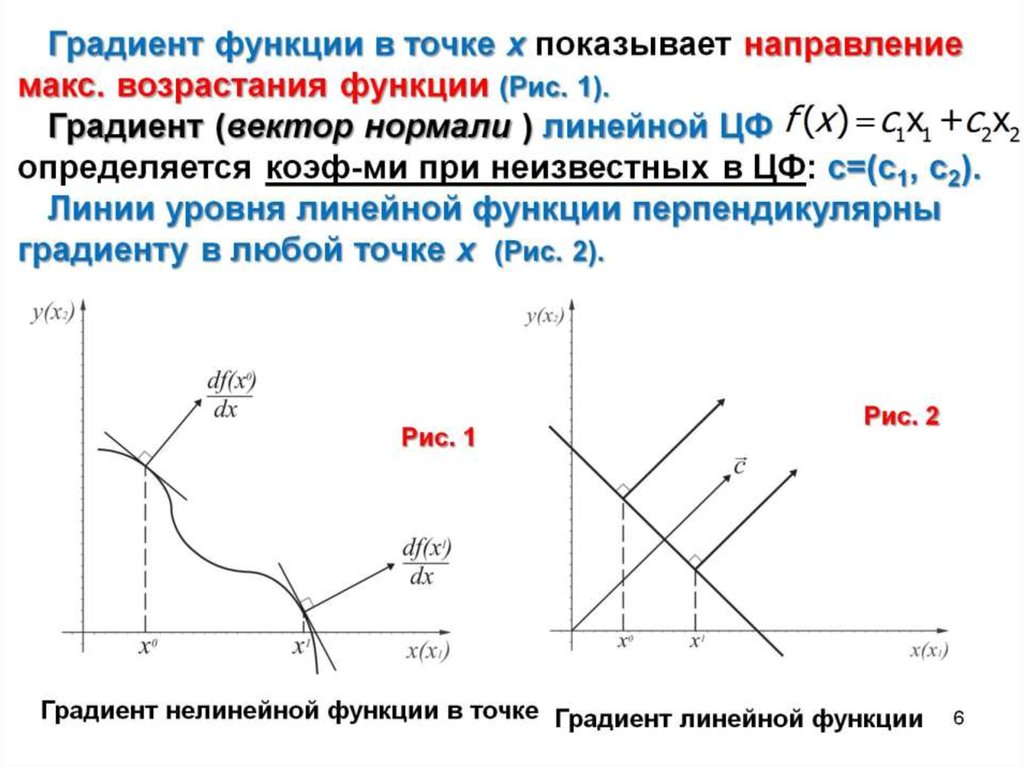
Градиент заданной функции
Используй поиск, чтобы найти научные материалы и собрать список литературы
База статей справочника включает в себя статьи написанные экспертами Автор24, статьи из научных журналов и примеры студенческих работ из различных вузов страны
Определение 1
Если для каждой пары $(x,y)$ значений двух независимых переменных из некоторой области ставится в соответствие определенное значение $z$, то говорят, что $z$ является функцией двух переменных $(x,y)$. Обозначение: $z=f(x,y)$.
Рассмотрим функцию $z=f(x,y)$, которая определена в некоторой области в пространстве $Oxy$.
Для заданной функции определим вектор, для которого проекциями на оси координат являются значения частных производных заданной функции в некоторой точке $\frac{\partial z}{\partial x} ;\frac{\partial z}{\partial y} $.
Определение 2
Градиентом заданной функции $z=f(x,y)$ называется вектор $\overrightarrow{gradz} $ следующего вида:
\[\overrightarrow{gradz} =\frac{\partial z}{\partial x} \cdot \overrightarrow{i} +\frac{\partial z}{\partial y} \cdot \overrightarrow{j} .
{2} =5.\]
Определение 3
Если для каждой тройки $(x,y,z)$ значений трех независимых переменных из некоторой области ставится в соответствие определенное значение $w$, то говорят, что $w$ является функцией трех переменных $(x,y,z)$ в данной области.
Обозначение: $w=f(x,y,z)$.
Рассмотрим функцию $w=f(x,y,z)$, которая определена в некоторой области в пространстве $Oxyz$.
Для заданной функции определим вектор, для которого проекциями на оси координат являются значения частных производных заданной функции в некоторой точке $\frac{\partial z}{\partial x} ;\frac{\partial z}{\partial y} $.
Определение 4
Градиентом заданной функции $w=f(x,y,z)$ называется вектор $\overrightarrow{gradw} $ следующего вида:
\[\overrightarrow{gradw} =\frac{\partial w}{\partial x} \cdot \overrightarrow{i} +\frac{\partial w}{\partial y} \cdot \overrightarrow{j} +\frac{\partial w}{\partial z} \cdot \overrightarrow{k} .\]
Теорема 3
Пусть в некотором скалярном поле $w=f(x,y,z)$ определено поле градиентов
\[\overrightarrow{gradw} =\frac{\partial w}{\partial x} \cdot \overrightarrow{i} +\frac{\partial w}{\partial y} \cdot \overrightarrow{j} +\frac{\partial w}{\partial z} \cdot \overrightarrow{k} .
{2} } =\sqrt{4+64+36} =\sqrt{104} .\]
Перечислим некоторые свойства градиента:
Производная заданной функции в заданной точке по направлению некоторого вектора $\overrightarrow{s} $ имеет наибольшее значение, если направление данного вектора $\overrightarrow{s} $ совпадает с направлением градиента. При этом данное наибольшее значение производной совпадает с длиной вектора градиента, т.е. $|\overrightarrow{gradw} |$.
Производная заданной функции по направлению вектора, который перпендикулярен к вектору градиента, т.е. $\overrightarrow{gradw} $, равна 0. Так как $\varphi =\frac{\pi }{2} $, то $\cos \varphi =0$; следовательно, $\frac{\partial w}{\partial s} =|\overrightarrow{gradw} |\cdot \cos \varphi =0$.
Сообщество экспертов Автор24
Автор этой статьи Дата последнего обновления статьи: 21.04.2022
Выполнение любых типов работ по математике
Решение задач по комбинаторике на заказ Решение задачи Коши онлайн Математика для заочников Контрольная работа на тему числовые неравенства и их свойства Контрольная работа на тему умножение и деление рациональных чисел Контрольная работа на тему действия с рациональными числами Дипломная работа на тему числа Курсовая работа на тему дифференциальные уравнения Контрольная работа на тему приближенные вычисления Решение задач с инвариантами
Подбор готовых материалов по теме
Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы
Градиент — Функции нескольких переменных (Математика)
Градиент
В этом параграфе мы обсудим специально производную числовой функции векторного аргумента, т.
е. функции вида (1) (введение к гл. 2) при .
Из предыдущих рассмотрений ясно, что матрица Якоби такой функции является матрицей-строкой, в каждой точке , в которой функция дифференцируема, имеющую вид:
Введем вектор, имеющий в соответствующем ортонорме пространства вид
Этот вектор называется градиентом функции в точке и обозначается (или ).
Тогда равенство (1) из п. 2.4 (с учетом условия (2) того же параграфа) перепишется в виде:
, (1)
где . Мы можем теперь написать вместо вектора просто бесконечно малую по сравнению с нормой вектора , так как сама функция и ее приращение являются скалярами.
Стоящая в равенстве (1) линейная форма называется первым дифференциалом функции в точке и обозначается .
Итак,
(2)
и
(3)
С использованием вектора градиента мы можем переписать (3) в виде:
(4)
Таким образом, первый дифференциал функции в точке равен скалярному произведению вектора градиента в этой точке на вектор приращения аргумента.
Необходимо подчеркнуть следующее. Как только в точке определены все частные производные функции, так мы можем формально вычислить вектор, компоненты которого равны соответственно частным производным в точке, а затем вычислить и скалярное произведение этого вектора на вектор приращения аргумента. Эти вычисления, однако, будут иметь смысл и дадут градиент функции в точке и первый дифференциал функции в точке, только если функция в этой точке будет дифференцируема, т.е. если разность между приращением функции в точке и значением произведения будет бесконечно малой высшего порядка по сравнению с нормой приращения аргумента.
Так для функции
обе частные производные в точке существуют и равны нулю, но функция в точке не будет даже непрерывна (как мы убедились в п. 2.3). Следовательно, в этой точке данная функция не будет иметь ни градиента, ни первого дифференциала.
Подобное же замечание справедливо и в общем случае векторной функции векторного аргумента: формальная возможность вычислить матрицу частных производных в точке еще не означает, что это будет матрица оператора производной в данной точке.
Обратим внимание на то, что первый дифференциал есть функция точки, т.е. для переменной точки (в которой функция дифференцируема, функция первого дифференциала есть
.
Обсудим теперь связь между понятиями градиента и производной по направлению.
Как известно, в общем случае производная по направлению функции в точке равна результату действия линейного оператора производной в точке на единичный вектор направления :
(5)
(см. формулу (4) п. 2.4).
Для числовой функции выражение (5) примет вид:
(6)
Итак, производная по направлению в точке равна скалярному произведению градиента в данной точке на единичный вектор направления.
Следовательно, если вектор направления коллинеарен вектору градиента, то производная по направлению имеет максимальное значение, равное норме градиента:
Содержательно это означает, что направление градиента есть направление наибыстрейшего возрастания функции.
Точно также направление, задаваемое вектором, противоположным вектору градиента (и называемому вектором антиградиента), есть направление наибыстрейшего убывания функции (в рассматриваемой точке).
В трехмерном пространстве единичный вектор направления задается своими проекциями на оси координат, которые равны косинусам углов, образуемых вектором направления с ортами осей (так называемые направляющие косинусы). В этом случае производная по направлению, задаваемому косинусами , в некоторой точке с координатами будет равна:
В двумерном случае эта формула принимает совсем простой вид:
Опять-таки подчеркнем, что существование частных производных в точке не есть достаточное условие существования в этой точке производной по заданному направлению (отличному от базисного), хотя формально указанное выше скалярное произведение можно вычислить.
Так функция двух переменных, равная нулю на осях координат и единице во всех остальных точках плоскости, не дифференцируема в начале координат ни по одному направлению, кроме базисных, хотя и имеет в этой точке обе частные производные, равные нулю.
Бесплатная лекция: «Лабораторная работа Б» также доступна.
Замечание. Читатель, проработавший п. 1.12, поймет, что оператор производной числовой функции в точке , является линейным функционалом (или ковектором). Но, как следует из теоремы 1.8, для любого линейного функционала , определенного на евклидовом пространстве, однозначно определен вектор , такой, что для любого . Понятно тогда, что вектор градиента функции в точке и есть этот самый вектор для функционала производной в точке. Производная функция числовой функции векторного аргумента есть, очевидно, отображение пространства в сопряженное пространство .
Читатель без труда докажет, что градиент имеет следующие свойства:
1)
2) (для любого вещественного )
3) (градиент константы равен нулю).
Аналогичные свойства имеет и первый дифференциал.
Градиент (наклон) прямой линии
Вычислить
Для расчета градиента:
Разделить изменение высоты на изменение горизонтального расстояния
| Градиент = Изменение по Y Изменение по X |
Поиграйте (перетащите точки):
Примеры:
Градиент = 3 3 = 1 Итак, Градиент равен 1 |
Градиент = 4 2 = 2 | ||
| Линия круче, поэтому градиент больше. | ||
Градиент = 3 5 = 0,6 | ||
Линия менее крутая, поэтому Градиент меньше. | ||
Положительный или отрицательный?
Двигаясь слева направо, велосипедист должен P проехать по положительному склону P Наклон:
При измерении линии:
- Начиная слева и проходя через вправо положительно
(но переходя влево отрицательно). - Верх положительный , нижний отрицательный
Градиент = −4 2 = −2 |
Эта линия идет на вниз на по мере вашего движения, поэтому она имеет отрицательный градиент.
Прямо поперек
Градиент = 0 5 = 0 |
Линия, которая проходит прямо (по горизонтали), имеет нулевой градиент.
Прямо вверх и вниз
Градиент = 3 0 = не определено |
Последнее немного сложно.
.. на ноль делить нельзя,
, поэтому градиент линии «прямо вверх и вниз» (вертикально) «не определен».
Вставай и беги
Иногда изменение по горизонтали называют «бегом», а изменение по вертикали — «подъемом» или «падением»:
Это просто разные слова, расчеты не меняются.
Определение градиента — объяснение и примеры
Следующие свойства градиента помогают понять ориентацию линии.
Для линии, проведенной в n-мерном пространстве, градиент линии относительно определенного измерения называется ее производной по направлению.
Понятие частной производной помогает найти производную по направлению. И это представлено как \(\frac{\delta y}{\delta x} \)
Здесь частная производная по отношению к x дает производную по направлению в направлении оси x. В этом выражении z рассматривается как константа.
\[\begin{align} \frac{\delta y}{\delta x} &= \frac{\delta}{\delta x}(5x + 4z + 3xz + 11) \\ \frac{\delta y}{\delta x} &= \frac{\delta}{\delta x}(5x) + \frac{\delta}{\delta x}(4z) + \frac{\delta}{\delta x} (3xz)
+ \frac{\delta}{\delta x}(11) \\\frac{\delta y}{\delta x} &= 5(1) + 0 + 3(1)z + 0 \\\frac{ \delta y}{\delta x} &=5 + 3z\end{align} \]
\(\следовательно \) 5 + 3z — производная по направлению уравнения прямой относительно оси x.
Think Tank
Уравнение y = mx + c называется формой пересечения наклона. Здесь «m» — это наклон, а «c» — точка пересечения линии по оси Y.
Найдите наклон и точку пересечения по оси Y линии, имеющей уравнение 4x -90 \\ m &=\sqrt3 \end{align} \]
| \(\следовательно \) Градиент лестницы равен \(\sqrt 3 \) |
| Пример 2 |
Альберт отмечает на миллиметровке две точки (4, 3) и (6, 7) и проводит линию, проходящую через эти точки. Найдите градиент линии.
Решение
Даны точки \((x_1, y_1) \) = (4, 3) и \((x_2, y_2) \) = (6, 7)
Градиент — это наклон (м) линии, соединяющей эти точки.
\[\begin{align} m &=\frac{y_2 – y_1}{x_2 – x_1} \\ m &=\frac{(7 – 3)}{(6 – 4)} \\m &= \frac{4}{2} \\ m &= 2 \end{align} \]
| \(\следовательно \) Градиент равен 2 |
| Пример 3 |
Проведена линия, касающаяся кривой \(f(x) = x^3 + 2x^2 -5x + 8 \) в точке (1, 6).
Найдите градиент этой линии. 92 + 4(1) – 5 \\ m &= 3 + 4 – 5 \\ m &= 7 – 5 \\ m &= 2 \end{align} \]
| \(\поэтому \) Градиент касательной равен 2 |
| Пример 4 |
Шерил рисует две параллельные линии, и уравнение одной линии 2x – y + 5 = 0. Найдите градиент другой линии.
Решение
Данное уравнение прямой имеет вид 2x – y = 5
Кроме того, градиент двух параллельных линий равен.
Найдем градиент этой линии.
\[\begin{align} 2x -y + 5 &= 0 \\ -y &= -2x -5 \\ y &= 2x + 5 \end{align} \]
Сравнивая это с наклоном- y = mx + c получаем m = 2
Градиент этой линии равен 2
Следовательно, искомый градиент параллельной линии равен m = 2
| \(\следовательно \) уклон параллельной линии равен 2 |
| Пример 5 |
Учитель просит Сэма нарисовать набор перпендикулярных линий и записать наклон одной линии как 2.
Помогите Сэму найти наклон другой линии.
Решение
Наклон данной прямой равен \(m_1 \) = 2
Произведение наклонов двух перпендикулярных прямых равно -1
\[\begin{align} m_1.m_2 &= -1 \\ 2 \times m_2 &= -1 \\ m_2 &= \frac{-1}{2}\end{align} \]
| \(\следовательно \) Наклон линии равен \(\frac{-1}{2}\) |
Интерактивные вопросы по градиенту
Вот несколько упражнений для практики. Выберите/введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.
0024
Мини-урок был посвящен увлекательной концепции градиента. Математическое путешествие по градиенту началось с основ градиента и продолжилось творческим созданием новой концепции, включающей формулы и уравнения.
Сделано таким образом, что это не только понятно и легко для понимания, но и останется с ними навсегда.
В Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов!
Благодаря интерактивному и увлекательному подходу «обучение-преподавание-обучение» учителя изучают тему со всех сторон.
Будь то рабочие листы, онлайн-классы, сеансы сомнений или любая другая форма отношений, мы в Cuemath верим в логическое мышление и разумный подход к обучению. , Что такое определение градиента?
Градиент — это наклон линии. Он измеряется углом, который линия образует с опорной осью X. Кроме того, две точки на линии или уравнение линии помогают найти градиент.
\[m = tan\theta = \frac{y_2 — y_1}{x_2 — x_1} = \frac{d}{dx}.f(x) \]
2. Что такое градиент матрицы?
Для матрицы, содержащей в качестве элементов различные функции (уравнения), производная этих элементов, представленная в матричной форме, называется градиентом матрицы.