Матрицы и определители. Элементарные преобразования матрицы
ГОСУДАРСТВЕННОЕ ОБЛАСТНОЕ БЮДЖЕТНОЕ
ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«ЛИПЕЦКИЙ ПОЛИТЕХНИЧЕСКИЙ ТЕХНИКУМ»
Методическая разработка урока
по дисциплине «Математика»
по теме
«Матрицы и определители. Элементарные преобразования матрицы»
по программе подготовки специалистов среднего звена
Разработала: преподаватель математики
Клещина Н.В.
Липецк, 2020
Пояснительная записка:
Изучение математики направлено на достижение, в первую очередь, целей интеллектуального развития студентов, формирование качеств мышления, характерных для математической деятельности и необходимых человеку для жизни в современном обществе, для общей социальной ориентации и решения практических проблем.
Все люди на нашей планете погружены в Матрицы . Матрицы как бы пронизывают нашу реальность в каждом ее проявлении. Каждый из нас на протяжении всей своей жизни и в любой ее момент находится в какой-либо из Матриц. С помощью Матриц можно объяснить, почему человек не может достичь успеха в каком-то деле, почему он болеет или почему у него нет шансов добиться успеха вообще, рассчитать количество продукции, месячные и годовые выручки.
В структуре изучаемой дисциплины «Математика» выделяется следующий раздел: «Основы линейной алгебры». Содержание раздела «Основы линейной алгебры » включает тему урока «Матрицы и определители. Элементарные преобразования матрицы» .
В результате изучения данной темы студент должен
Знать:
определение матрицы, виды и свойства матриц;
определение определителя матриц, методы нахождения определителя;
Уметь:
записывать матрицы различных видов;
преобразовывать матрицы;
• определять определитель матрицы;
• решать прикладные задачи с применением матриц;
Тема урока : Матрицы и определители. Элементарные преобразования матрицы.
Элементарные преобразования матрицы.
Цели урока:
Образовательные:
— сформировать умения и навыки понятия матрицы и ее виды, определитель матрицы
— сформировать умения операции сложения, вычитания, умножения матрицы на число и
матрицы на матрицу, возведение в степень, нахождение обратной матрицы;
Развивающие:
— содействовать развитию у учащихся мыслительных операций: умение анализировать,
синтезировать, сравнивать;
— отрабатывать навыки самооценивания знаний и умений, выбора заданий,
соответствующего уровню мыслительной деятельности;
— формировать и развивать умения и навыки: обобщение, поиск способов решения.
Воспитательные:
— воспитание личных качеств, обеспечивающих успешность творческой деятельности;
— воспитание требовательности, принципиальности, самокритичности, благородства,
чувства товарищества.
Тип урока: Урок ознакомления с новым материалом.
Межпредметные связи: физика, информатика, история
Оборудование и наглядные средства обучения: компьютерный класс с ОС Windows 8 и пакетом программ Microsoft Office 2010 (10 ПК), мультимедийный проектор, интерактивная доска SmartBoard, программа Notebook, колонки.
Методическая цель: способы активизации мыслительной деятельности студентов
Ход урока:
I.Организационный момент: Подготовка студентов к уроку (проверка отсутствующих на уроке, наличие тетрадей)
II. Сообщение темы и целей урока.
Сообщение темы и цели урока (понятие матрицы и основанный на нем раздел математики – матричная алгебра – имеют важное значение, так как значительная часть математических моделей экономических объектов и процессов записывается в достаточно простой, а главное – компактной матричной форме).
Итак, цель сегодняшнего урока: рассмотреть понятия матрицы и ее виды, определитель матрицы ,сформировать умения операции сложения, вычитания, умножения матрицы на число и матрицы на матрицу, возведение в степень, нахождение обратной матрицы.
III. Изучение нового материала
3.1 Теоретический материал
1.Определение (в тетрадь) Матрицей размера mn, где m- число строк, n- число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются aij, где i- номер строки, а j- номер столбца.
А =
Основные действия над матрицами.
Матрица может состоять как из одной строки, так и из одного столбца. Вообще говоря, матрица может состоять даже из одного элемента.
Определение (в тетрадь )Если число столбцов матрицы равно числу строк (m=n), то матрица называется квадратной.
Определение (в тетрадь ) Матрица вида:
= E,
называется единичной матрицей.
Определение. Если amn = anm , то матрица называется симметрической.
Пример. — симметрическая матрица
Определение(в тетрадь ) Квадратная матрица вида называется диагональной матрицей.
2.Сложение и вычитание матриц сводится к соответствующим операциям над их элементами. Самым главным свойством этих операций является то, что они определены только для матриц одинакового размера. Таким образом, возможно определить операции сложения и вычитания матриц:
Определение(в тетрадь ) Суммой (разностью) матриц является матрица, элементами которой являются соответственно сумма (разность) элементов исходных матриц.
cij = aij bij
С = А + В = В + А.
Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число.
(А+В) =А В А() = А А
3.Операция умножения матриц.
Определение(в тетрадь ): Произведением матриц называется матрица, элементы которой могут быть вычислены по следующим формулам:
AB = C; .
Из приведенного определения видно, что операция умножения матриц определена только для матриц, число столбцов первой из которых равно числу строк второй.
Свойства операции умножения матриц. (в тетрадь 1-6 )
1)Умножение матриц не коммутативно, т.е. АВ ВА даже если определены оба произведения. Однако, если для каких – либо матриц соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными.
Однако, если для каких – либо матриц соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными.
Самым характерным примером может служить единичная матрица, которая является перестановочной с любой другой матрицей того же размера.
Перестановочными могут быть только квадратные матрицы одного и того же порядка.
АЕ = ЕА = А
Очевидно, что для любых матриц выполняются следующее свойство:
AO = O; OA = O,
где О – нулевая матрица.
2) Операция перемножения матриц ассоциативна, т.е. если определены произведения АВ и (АВ)С, то определены ВС и А(ВС), и выполняется равенство:
(АВ)С=А(ВС).
3) Операция умножения матриц дистрибутивна по отношению к сложению, т.е. если имеют смысл выражения А(В+С) и (А+В)С, то соответственно:
А(В + С) = АВ + АС
(А + В)С = АС + ВС.
4) Если произведение АВ определено, то для любого числа верно соотношение:
(AB) = (A)B = A(B).
5) Если определено произведение АВ , то определено произведение ВТАТ и выполняется равенство:
(АВ)Т = ВТАТ, где
индексом Т обозначается транспонированная матрица.
6) Заметим также, что для любых квадратных матриц det (AB) = detAdetB.
Что такое det будет рассмотрено ниже.
Определение (в тетрадь ). Матрицу В называют транспонированной матрицей А, а переход от А к В транспонированием, если элементы каждой строки матрицы А записать в том же порядке в столбцы матрицы В.
А = ; В = АТ= ;
другими словами, bji = aij.
В качестве следствия из предыдущего свойства (5) можно записать, что:
(ABC)T = CTBTAT,
при условии, что определено произведение матриц АВС.
4.Определители (детерминанты). Определение (в тетрадь ) Определителем квадратной матрицы А= называется число, которое может быть вычислено по элементам матрицы по формуле:
det A = , где (1)
М1к – детерминант матрицы, полученной из исходной вычеркиванием первой строки и k – го столбца. Следует обратить внимание на то, что определители имеют только квадратные матрицы, т.е. матрицы, у которых число строк равно числу столбцов.
Формула (1) позволяет вычислить определитель матрицы по первой строке, также справедлива формула вычисления определителя по первому столбцу:
det A = (2)
Вообще говоря, определитель может вычисляться по любой строке или столбцу матрицы, т.е. справедлива формула:
detA = , i = 1,2,…,n. (3)
Очевидно, что различные матрицы могут иметь одинаковые определители.
Определитель единичной матрицы равен 1.
Для указанной матрицы А число М1к называется дополнительным минором элемента матрицы a1k. Таким образом, можно заключить, что каждый элемент матрицы имеет свой дополнительный минор. Дополнительные миноры существуют только в квадратных матрицах.
Определение (в тетрадь ) Дополнительный минор произвольного элемента квадратной матрицы aij равен определителю матрицы, полученной из исходной вычеркиванием i-ой строки и j-го столбца.
Свойство1. Важным свойством определителей является следующее соотношение:
det A = det AT;
Свойство 2. det ( A B) = det A det B.
Свойство 3. det (AB) = detAdetB
Свойство 4. Если в квадратной матрице поменять местами какие-либо две строки (или столбца), то определитель матрицы изменит знак, не изменившись по абсолютной величине.
Свойство 5. При умножении столбца (или строки) матрицы на число ее определитель умножается на это число.
Свойство 6. Если в матрице А строки или столбцы линейно зависимы, то ее определитель равен нулю.
Определение: Столбцы (строки) матрицы называются линейно зависимыми, если существует их линейная комбинация, равная нулю, имеющая нетривиальные (не равные нулю) решения.
Свойство 7. Если матрица содержит нулевой столбец или нулевую строку, то ее определитель равен нулю. (Данное утверждение очевидно, т.к. считать определитель можно именно по нулевой строке или столбцу.)
Свойство 8. Определитель матрицы не изменится, если к элементам одной из его строк(столбца) прибавить(вычесть) элементы другой строки(столбца), умноженные на какое-либо число, не равное нулю.
Свойство 9. Если для элементов какой- либо строки или столбца матрицы верно соотношение: d = d1 d2 , e = e1 e2 , f = f1 f2 , то верно:
3. 2 Практический материал
2 Практический материал
Задание 1. Даны матрицы А = ; B = , найти 2А + В.
2А = , 2А + В = .
Задание 2. Найти произведение матриц А = и В = .
АВ = = .
ВА = = 21 + 44 + 13 = 2 + 16 + 3 = 21.
Задание 3. Найти произведение матриц А= , В =
АВ = = = .
Задание 4.Даны матрицы А = , В = , С = и число = 2. Найти АТВ+С.
AT = ; ATB = = = ;
C = ; АТВ+С = + = .
Задание5.Вычислить определитель матрицы А =
= -5 + 18 + 6 = 19.
Задание 6. Даны матрицы А = , В = . Найти det (AB).
1-й способ: det A = 4 – 6 = -2; det B = 15 – 2 = 13; det (AB) = det A det B = -26.
2- й способ: AB = , det (AB) = 718 — 819 = 126 –
– 152 = -26.
3.3 Тест по вариантам
Вариант 1.
Задания уровня А:
1. Выберите единичную матрицу из числа предложенных:
1)
2)
3)
4)
2. Укажите матрицу , если матрица A=
1)
2)
3)
4)
3. Выберите вектор – столбец из числа предложенных матриц
1)
2)
3) ;
4)
4. Найдите сумму матриц , если
1)
2)
3);
4) .
5. Найдите сумму матриц , если
;
6. Найдите , если
7. Найдите произведение матриц , если
Найдите произведение матриц , если
произведение не определено;
8. Найдите произведение матриц , если
1) ;
2)
3) произведение не определено;
4)
9. Как изменится определитель при транспонировании матрицы?
1) определитель не изменится;
2 ) знак определителя поменяется на противоположный;
3) значение определителя удвоится;
4) определитель примет значение, обратное исходному.
10. Вычислите определитель 2-го порядка
1) -7;
2 ) -5;
3) 1;
4) 5.
11. Вычислите определитель 3-го порядка
1) 98;
2) -30;
3) 90;
4) 104.
12. Выберите невырожденную матрицу из числа предложенных
13. Найдите минор m12 соответствующего элемента определителя
Найдите минор m12 соответствующего элемента определителя
1) -2;
2) 13;
3) -5;
4) 5.
14. Найдите алгебраическое дополнение соответствующего элемента матрицы
-18;
-19;
18;
19.
15. Найдите значение , решив уравнение =0
1)
2) 0;
3)
4)
Задания уровня В:
1 . Найдите матрицу, обратную данной
2. Решите систему линейных алгебраических уравнений
3. Вычислите определитель 4-го порядка
Вариант 2.
Задания уровня А:
1. Выберите треугольную матрицу из числа предложенных:
1)
2)
3)
4)
2. Укажите матрицу , если матрица
1)
2)
3)
4)
3. Выберите вектор – строку из числа предложенных матриц
4. Найдите разность матриц , если
Найдите разность матриц , если
1) ;
2) ;
3);
4)
5. Найдите сумму матриц , если
2)
3) ;
4)
6. Найдите , если
;
7. Найдите произведение матриц , если
1)
.
произведение не определено;
8. Найдите произведение матриц , если
1) произведение не определено;
2)
3)
4)
9 . Как изменится определитель при перестановке двух его параллельных рядов?
1) определитель не изменится;
2) знак определителя поменяется на противоположный;
3) значение определителя удвоится;
4) определитель примет значение, обратное исходному.
10. Вычислите определитель 2-го порядка
1) -17;
2 ) 13;
3) 3;
4) -13.
11. Вычислите определитель 3-го порядка
1) 92;
2) 72;
3) 56;
4) 54.
12. Выберите вырожденную матрицу из числа предложенных.
13. Найдите минор m21 соответствующего элемента определителя
1) -10;
2) 3;
3) 4;
4) -4.
14. Найдите алгебраическое дополнение А32 соответствующего элемента матрицы .
50;
9 ;
-50;
-9.
15. Найдите значение х, решив уравнение =0
1) 6;
2) 9;
3) 18;
4) -18.
Задания уровень В:
1 . Найдите матрицу, обратную данной
2. Решите систему линейных алгебраических уравнений
3. Вычислите определитель 4-го порядка
Ключи | |
Вариант 1 | Вариант 2 |
А1 2 | А1 1 |
А2 4 | А2 2 |
А3 4 | А3 3 |
А4 2 | А4 1 |
А5 1 | А5 2 |
А6 4 | А6 2 |
А7 3 | А7 4 |
А8 1 | А8 2 |
А9 1 | А9 2 |
А10 4 | А10 4 |
А11 1 | А11 3 |
А12 3 | А12 1 |
А13 4 | А13 3 |
А14 3 | А14 3 |
А15 1 | А15 4 |
В1 . | В1 . |
В2 (1;1;1). | В2 (1; 0; 2). |
В3 — 26 | В3 -20. |
IV. Итоги урока: Проверка теста, выставление оценок
V.Домашняя работа
1.Конспект
2. Даны матрицы . Выполните с заданными матрицами указанные действия .
Решение.
Начинаем с умножения матрицы А на матрицу В:
Теперь умножаем единичную матрицу второго порядка Е на два:
Складываем две полученные матрицы:
Осталось выполнить операцию умножения полученной матрицы на матрицу А:
Интернет-ресурсы:
www.ziimag.narod.ru — персональный сайт автора Мордковича А. Г. «Практика развивающего обучения».
www. math.ru -Интернет
math.ru -Интернет
www.it-n.ru-Сеть творческих учителей. Материалы и ресурсы, касающиеся использования ИКТ в учебном процессе:
– библиотека готовых учебных проектов с применением ИКТ, а также различные проектные идеи, на основе которых можно разработать свой собственный проект;
– библиотека методик проведения уроков использованием разнообразных электронных
ресурсов;
– руководства и полезные советы по использованию программного обеспечения в учебном процессе;
– подборка ссылок на интересные аналитические и тематические статьи для педагогов.
www.exponenta.ru -Образовательный математический сайт. Содержит материалы по работе с математическими пакетами Mathcad, MATLAB, Mathematica, Maple и др. Методические разработки, примеры решения задач, выполненные с использованием математических пакетов. Форум и консультации для студентов и школьников.
http:school-collection.edu -Единая коллекция цифровых образовательных ресурсов. Цифровые образовательные ресурсы (ЦОР) к учебникам.
http://www.intellectcentre.ru – сайт издательства «Интеллект-Центр», -тренировочные материалы, демонстрационные версии, банк тренировочных заданий с ответами, методические рекомендации и образцы решений.
1
Факультативный курс «Матрицы и определители»
Предлагаемый курс преследует цель познакомить учащихся с матричной символикой и основными понятиями алгебры матриц, а также научить их уверенно оперировать с матрицами и определителями как объектами более общего характера по сравнению с числами и функциями. Курс расширяет представления о возможностях математики и легко усваивается данной возрастной группой.
Изучение данного курса способствует
формированию абстрактных представлений,
развитию логического мышления, осуществлению
межпредметных связей.
Курс характеризуется рациональным сочетанием логики и наглядности, увеличивается теоретическая значимость изучаемого материала, учащиеся овладевают приёмами аналитической деятельности при решении задач.
Организация учебно-воспитательного процесса
Изучения курса “Матрицы и определители” в 8-ых классах общеобразовательных учреждений рекомендуется проводить во внеурочное время, 1 раз в неделю в течение учебного года.
Учителю предоставляется право самостоятельно выбирать методические пути и приёмы преподавания данного курса.
При планировании учебных занятий следует ориентироваться не только на теоретическую подготовку учащихся, но и на организацию решения практических задач с учётом дифференциации группы и индивидуальных особенностей детей.
Следует способствовать удовлетворению потребностей школьников, проявляющих склонности и интерес к математики.
Учителю необходимо реализовать
сбалансированное сочетание традиционных и новых
методов обучения, применять иллюстративные и
эвристические методы, рационально сочетать
устные и письменные виды работы.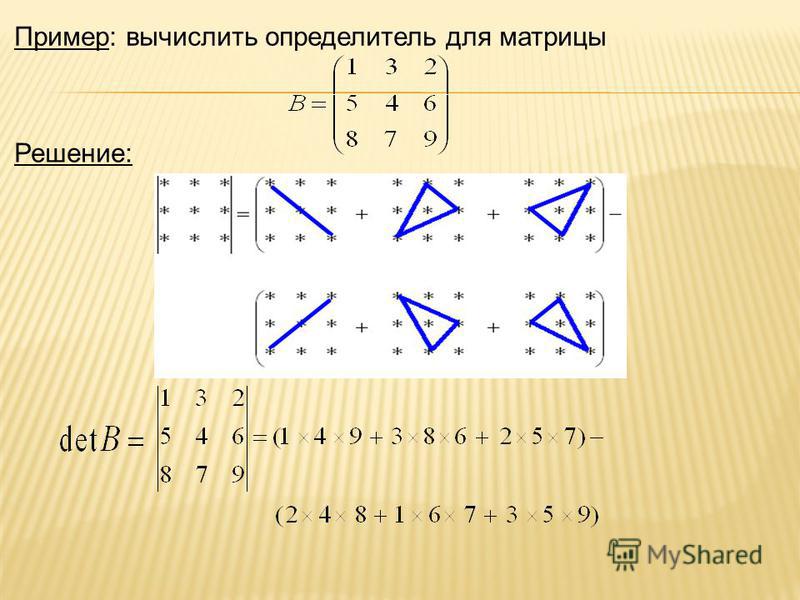
Структура программы
Программа курса “Матрицы и определители” состоит из трёх разделов: “Содержание программы”, “Содержание знаний и умений”, “Список литературы”, “Основные понятия курса”.
Содержание программы
Раздел 1. Основные понятия (4 часа)
- Введение в предмет
- Типы и формы матриц
- Матричная символика
Раздел 2. Операции с матрицами (8 часов)
- Транспонирование матриц
- Сложение матриц
- Умножение матрицы на скаляр
- Умножение матрицы на матрицу
Раздел 3. Определители (10 часов)
- Понятие определителя
- Свойства определителей
- Миноры и алгебраические дополнения
- Разложение определителя по Лапласу
Раздел 4. Вычисление определителей (12 часов)
- Метод элементарных преобразований
- Метод единственного деления
- Метод опорного элемента
Содержание знаний и умений
В результате изучения курса “Матрицы и определители” учащиеся узнают:
- Основные формы и типы матриц.

- Матричную символику.
- Особенности матричных операций.
- Свойства определителей.
- Понятия миноров и алгебраических дополнений.
- Основные методы вычисления определителей.
Умеют:
- Складывать, перемножать, транспонировать и обращать матрицы с вещественными элементами.
- Разлагать определители.
- Вычислять определители и применять их к решению задач.
Основные понятия курса
Произвольная система чисел из некоторого множества, расположенная в виде прямоугольной таблицы, содержащей m строк и n столбцов, называется матрицей.
Две матрицы называются равными, если число строк и столбцов у них соответственно равны.
Если число строк матрицы равно числу её столбцов, то такая матрица называется квадратной, а это число порядком матрицы.
В = - матрица третьего порядка
Пусть даны матрицы
А = и В =
Произведением А на число с называется матрица
С =
Пример
Суммой матриц А и В называется матрица:
С = А + В =
Пример
А = В = А + В =
Для матриц выполняются все свойства действий с
рациональными числами.
Произведением матрицы А на матрицу В называется матрица
С = , где
Пример:
Квадратная матрица, все диагональные элементы которой равны 1, а остальные 0 называется единичной.
Е = .
Матрицы, имеющие вид называют диагональными.
Матрица, которая получается из данной матрицы заменой строк столбцами, называется транспонированной по отношению к данной.
Определителем n порядка матрицы А называется алгебраическая сумма n! Слагаемых, каждое из которых представляет собой произведение n множителей, взятых по одному и только по одному из каждой строки и каждого столбца матрицы А.
А = определитель.
Некоторые способы вычислений определителей:
1) Определитель 2-ого порядка
Пример:
2) Определитель 3-его порядка
Данный способ называется правило элементарных
преобразований или правило Саррюса. Оно
действует и для определителей более высоких
порядков, но является очень громоздким.
Пример:
3) Определители n-ого порядка.
Минором элемента определителя называется определитель, который получается из данного вычёркиванием строки и столбца, проходящих через данный элемент.
Алгебраическим дополнением элемента определителя n-ого порядка называется минор этого элемента, взятый со знаком .
Пример. Пусть .
Найдём
Правило 1. Если в определите n-ого порядка все элементы I-ой строки (j-ого столбца), кроме равны нулю, то такой определитель равен произведению элемента на его алгебраическое дополнение.
Пример.
Вычислить определитель
Преобразуем определитель так, чтобы все элементы четвёртого столбца, кроме первого равнялись нулю. Для этого умножим все элементы первой строчки на –1 и сложим со второй и третьей, затем умножим первую строчку на – 3 и сложим с четвёртой. В результате получим
.
Затем, применяя правило, получим:
.
Прибавляя к третьей строчки вторую, получим
Правило 2. Определитель n-ого порядка равен сумме произведений всех элементов произвольной его строки на их алгебраические дополнения.
Разложение определителя
Пример. Вычислить
Вычислим определитель, разложив его сначала по элементам третьей строки, затем по элементам второго столбца.
Литература
- Энциклопедия “Аванта +”, “Математика”, 2003 год.
- Блох Э. Л. “Основы линейной алгебры” – М., 1979.
- Хедли Л. “Линейная алгебра” — М., 1992.
Детерминанты и матрицы
Матрицы и определители являются важными темами для экзаменов 12-го класса, JEE и различных других конкурсных экзаменов. Наши заметки о матрицах и определителях и решенные примеры помогут вам понять основные идеи, связанные с этой главой, такие как типы матриц и определение определителя. Возникает главный вопрос: что такое матрица? Упорядоченный прямоугольный массив чисел, функций, символов или объектов называется матрицей. Матрица имеет порядок m×n, если в ней m строк и n столбцов.
Возникает главный вопрос: что такое матрица? Упорядоченный прямоугольный массив чисел, функций, символов или объектов называется матрицей. Матрица имеет порядок m×n, если в ней m строк и n столбцов.
Такая матрица размера m×n представлена следующим образом:
\[\begin{bmatrix}a1 & \cdots & an \\\vdots & \ddots & \vdots \\am & \cdots & amn \\ \end{ bmatrix}\]
Типы матриц
Диагональная матрица – Квадратная матрица, все элементы которой, кроме элементов на главной диагонали, равны нулю -\[\begin{bmatrix} 2 & 0 \\ 0 & 3 \\ \end {bmatrix}\], \[\begin{bmatrix} 1 & 0 & 0 \\ 0 & 6 & 0 \\ 0 & 0 & 3 \\ \end{bmatrix}\] 9{-1}\]A = I, где I — единичная матрица.
Определитель квадратной матрицы не должен быть равен нулю.
Операции на матрицах
Следующие операции могут быть выполнены между двумя или более матрицами:
Добавление матрицы
Сборка Matrix
Multiplication MATRIX
- 9
- 2.
 .
.
Решенные примеры матричных операций:
Добавление матрицы
1. Если A=\[\begin{bmatrix} 2 & 5 & -1 \\ 4 & 1 & 3 \\ \end{bmatrix}\] и B =\[\begin{bmatrix } 3 & 2 & 4 \\ -1 & 5 & 2 \\ \end{bmatrix}\],
, тогда A + B = \[\begin{bmatrix} 2 & 5 & -1 \\ -1 & 5 & 2 \\ \end{bmatrix}\] +\[\begin{bmatrix} 3 & 2 & 4 \\ -1 & 5 & 2 \\ \end{bmatrix}\]
=\[\begin{bmatrix } 2+3 и 5+2 и -1+4 \\ 4-1 и 1+5 и 3+2 \\ \end{bmatrix}\]
=\[\begin{bmatrix} 5 & 7 & 3 \\ 3 & 6 & 5 \\ \end{bmatrix}\]
Вычитание матрицы
2. Если A = \[\begin{bmatrix} 1 & 3 & -2 \\ 4 & 7 & 5 \\ \end{bmatrix}\]
и B =\[\begin{bmatrix} -2 & 1 & -1 \\ 3 & 5 & 2 \\ \end{bmatrix}\]
, тогда A-B = A+(-B) =\[\begin{bmatrix} 1 & 3 & -2 \\ 4 & 7 & 5 \\ \end{bmatrix}\] + \[ \begin{bmatrix} 2 & -1 & 1 \\ -3 & -5 & -2 \\ \end{bmatrix}\]
= \[\begin{bmatrix} 1+2 & 3-1 & -2+1 \\ 4-3 & 7-5 & 5-2 \\ \end{bmatrix}\]
= \[\ begin{bmatrix} 3 & 2 & -1 \\ 1 & 2 & 3 \\ \end{bmatrix}\]
Умножение матрицы
3.
 Если A=\[\begin{bmatrix} 1 & 1 \\ 0 & 2 \\ 1 & 1 \\ \end{bmatrix}\] и B = \[\begin{bmatrix} 1 & 2 \\ 2 & 2 \\ \end{bmatrix}\],
Если A=\[\begin{bmatrix} 1 & 1 \\ 0 & 2 \\ 1 & 1 \\ \end{bmatrix}\] и B = \[\begin{bmatrix} 1 & 2 \\ 2 & 2 \\ \end{bmatrix}\], Затем
AB = \[\begin{bmatrix} 1 & 1 \\ 0 & 2 \\ 1 & 1 \\ \end{bmatrix}\] \[\begin{bmatrix} 1 & 2 \\ 2 & 2 \\ \end {bматрица}\]
=\[\begin{bmatrix} 1\times 1+1\times 2 & 1\times 2+1\times 2 \\ 0\times 1+2\times 2 & 0\times 2+2\times 2 \\ 1\times 1+1\times 2 & 1\times 2+1\times 2 \\ \end{bmatrix}\] \[\begin{bmatrix} 3 & 4 \\ 4 & 4 \\ 3 & 4 \\ \end{bmatrix}\]
Определитель матрицы
Далее мы узнаем определение определителя матрицы. Определитель матрицы определяется как скалярное значение, которое может быть вычислено из элементов квадратной матрицы. Он кодирует некоторые свойства линейного преобразования, описываемого матрицей, и обозначается как det A, det (A) или |A|. Поясним это дальше:
Квадратная матрица A определенного порядка имеет связанное с ней число, и это число называется определителем матрицы A.
 Для того чтобы определитель был связан с матрицей, последняя должна быть квадратной матрицей.
Для того чтобы определитель был связан с матрицей, последняя должна быть квадратной матрицей.Таким образом, для квадратной матрицы 2×2
A=\[\begin{bmatrix} a1 & b1 \\ a2 & b2 \\ \end{bmatrix}\]
символ |A|=\[\ begin{bmatrix} a1 & b1 \\ a2 & b2 \\ \end{bmatrix}\]
означает определитель второго порядка.
Его значение определяется как: \[\begin{bmatrix} a1 & b1 \\ a2 & b2 \\ \end{bmatrix}\]= a1b2−a2b1
Аналогично, для квадратной матрицы 3 x 3 A=\ [\begin{bmatrix} a1 & b1 & c1 \\ a2 & b2 & c2 \\ a3 & b3 & c3 \\ \end{bmatrix}\]
символ |A|=\[\begin{bmatrix} a1 & b1 & c1 \\ a2 & b2 & c2 \\ a3 & b3 & c3 \\ \end{bmatrix}\]
означает определитель третьего порядка.
Значение определяется как:
|A|=a1\[\begin{vmatrix} b2 & c2 \\ b3 & c3 \\ \end{vmatrix}\] −b1\[\begin{vmatrix} a2 & c2 \\ b3 & c3 \\ \ end{vmatrix}\] +c1\[\begin{vmatrix} a2 & b2 \\ a3 & b3 \\ \end{vmatrix}\]
Решено Пример:
1.
 Найти определитель матрицы A, если A =\[\begin{bmatrix} 2 и 5 \\ 1 и 3 \\ \end{bmatrix}\]
Найти определитель матрицы A, если A =\[\begin{bmatrix} 2 и 5 \\ 1 и 3 \\ \end{bmatrix}\] Решение: |A|= \[\begin{bmatrix} 2 и 5 \\ 1 и 3 \\ \end{bmatrix}\]
(2 x 3) — (5 x 1) = 6 — 5 = 1
Свойства определителя 9{x+y} N_{x,y}\]
Значение матриц и определителей в математике
Матрицы и определители используются для вычисления линейных уравнений с двумя или тремя переменными. Матрицы и определители также используются, чтобы определить, является ли система стабильной или нет. Определитель можно использовать для решения линейных уравнений, для определения того, как линейные преобразования изменяют площадь или объем, а также для изменения переменных в численных методах. Определитель можно рассматривать как функцию с квадратной матрицей в качестве источника и целым числом в качестве результата. Детерминант — это значащее число, которое присваивается любой квадратной матрице и имеет геометрическое и математическое значение, и, следовательно, они составляют важную тему для изучения математики в реальных приложениях, а также с точки зрения экзамена.

Значение матриц в бизнес-администрировании
Матрица решений может помочь вам не только в вынесении сложных суждений, но и в расстановке приоритетов, решении проблем и обосновании предыдущего решения. Это отличный метод принятия решений, если вы выбираете между несколькими похожими вариантами на основе множества количественных параметров.
Значение определителя матрицы всегда положительно.
Определитель квадратной матрицы можно найти, применяя функции строк для получения треугольной версии матрицы, что означает, что все входные данные выше или ниже оси равны 0. Определитель является результатом элементов на главной оси треугольной формы.
История определителей и матриц
Происхождение матриц и определителей можно проследить вплоть до 2-го века до нашей эры, с намеками на середину 4-го века до нашей эры. Тем не менее, только во второй половине 17 века концепции вновь всплыли на поверхность и начался настоящий прогресс.
 Неудивительно, что исследование процессов линейных уравнений привело к разработке матриц и определителей. Вавилоняне исследовали проблемы, которые привели к параллельным линейным уравнениям, и некоторые из них были записаны на глиняных табличках.
Неудивительно, что исследование процессов линейных уравнений привело к разработке матриц и определителей. Вавилоняне исследовали проблемы, которые привели к параллельным линейным уравнениям, и некоторые из них были записаны на глиняных табличках.Заключение
Здесь мы подробно представили концепции и решения вопросов темы Детерминанты и матрицы. Вы можете найти все, что ищете, в одном месте. В PDF-файлах, которые также можно загрузить бесплатно, учащиеся могут внимательно изучить концепции, определения и вопросы и понять концепции, используемые для решения этих вопросов. Это очень поможет студентам на экзаменах.
Матрицы и определители: формулы, темы, примечания, вопросы
- Дом org/ListItem»> Математика
- Матрицы и определители
Матрица и операции с матрицами
Типы матриц
Транспонирование матрицы, симметричной и кососимметричной матрицы
Сопряжение матрицы, эрмитовой и косоэрмитовой матрицы
Определитель матрицы
Минор и кофактор элемента матрицы/детерминанта
Сопряженная и обратная матрицы
Элементарные операции со строками и их использование для нахождения обратной матрицы
Система линейных уравнений и правило Крамера
Система однородных линейных уравнений
- Матрицы, алгебра матриц, типы матриц [REST_COUNT]+ Еще’> ( АЕЕЕ, JEE Главная, КОМЕДК УГЕТ, КЕАМ ) (112 концепций)
- Сопряжение и вычисление обратной квадратной матрицы с помощью определителей и элементарных преобразований [REST_COUNT]+ Еще’> ( АЕЕЕ, JEE Главная, КОМЕДК УГЕТ, КЕАМ ) (28 концепций)
- Тест на непротиворечивость и решение совместного линейного уравнения с двумя или тремя переменными с использованием определителей и матриц [REST_COUNT]+ Еще’> ( АЕЕЕ, JEE Главная, КОМЕДК УГЕТ, КЕАМ ) (30 концепций)
- Определители и матрицы второго и третьего порядка [REST_COUNT]+ Еще’> ( АЕЕЕ, JEE Главная, КОМЕДК УГЕТ, КЕАМ ) (4 концепции)
- Свойства определителей, вычисление определителей [REST_COUNT]+ Еще’> ( АЕЕЕ, JEE Главная, КОМЕДК УГЕТ, КЕАМ ) (28 концепций)
- Матрицы и типы матриц [REST_COUNT]+ Еще’> ( АЕЕЕ, JEE Главная, КОМЕДК УГЕТ, КЕАМ ) (8 концепций)
- Математическая операция над матрицами [REST_COUNT]+ Еще’> ( АЕЕЕ, JEE Главная, КОМЕДК УГЕТ, КЕАМ ) (10 концепций)
- Специальные матрицы и их свойства [REST_COUNT]+ Еще’> ( АЕЕЕ, JEE Главная, КОМЕДК УГЕТ, КЕАМ ) (22 концепции)
- Элементарные операции со строками и обратная матрица с помощью элементарных операций со строками [REST_COUNT]+ Еще’> ( АЕЕЕ, JEE Главная, КОМЕДК УГЕТ, КЕАМ ) (6 концепций)
- определитель [REST_COUNT]+ Еще’> ( АЕЕЕ, JEE Главная, КОМЕДК УГЕТ, КЕАМ ) (4 концепции)
- Примыкание к матрице [REST_COUNT]+ Еще’> ( АЕЕЕ, JEE Главная, КОМЕДК УГЕТ, КЕАМ ) (8 концепций)
- Обратная матрица (с использованием сопряженной) [REST_COUNT]+ Еще’> ( АЕЕЕ, JEE Главная, КОМЕДК УГЕТ, КЕАМ ) (10 концепций)
- Умножение определителя [REST_COUNT]+ Еще’> ( АЕЕЕ, JEE Главная, КОМЕДК УГЕТ, КЕАМ ) (2 концепции)
- Свойства определителей [REST_COUNT]+ Еще’> ( АЕЕЕ, JEE Главная, КОМЕДК УГЕТ, КЕАМ ) (6 концепций)
- Система одновременных линейных уравнений [REST_COUNT]+ Еще’> ( АЕЕЕ, JEE Главная, КОМЕДК УГЕТ, КЕАМ ) (8 концепций)
Количество действительных значений λ, для которых система линейных уравнений
2x+4y−λz=0
4x+λy+2z=0
λx+2y+2z=0
имеет бесконечно много решений, это:
- Опция 1)
0
- Вариант 2)
1
- Вариант 3)
2
- Вариант 4)
3
- Опция 1)
Пусть A любая обратимая матрица 3×3.

Что такое матрицы и определители
Матрицы и определители:
В математике одна из интересных, простых и важных тем — матрицы и определители. Каждый год вы будете получать по крайней мере 1-3 вопроса на основном экзамене JEE и других экзаменах, прямо или косвенно, концепция этой главы будет задействована во многих других главах, таких как интегральное и дифференциальное исчисление. Концепция этой главы будет использоваться для концепции трансформации осей. Эта глава совершенно новая с точки зрения студента, так как вы увидите эту главу непосредственно в 12-й главе. Таким образом, некоторые учащиеся могут счесть Матрицы и Определитель немного сложными для понимания и решения задач на начальном этапе. Но по мере того, как вы будете решать все больше и больше задач в этой главе, вы будете знакомиться с концепциями и главой в целом, а затем обнаружите, что это одна из самых простых глав.
Матрицы и определители находят широкое применение в реальных задачах, например, в программном обеспечении Adobe Photoshop матрицы используются для обработки линейного преобразования для визуализации изображений. Квадратная матрица используется для представления линейного преобразования геометрического объекта. В компьютерном программировании матрицы и их обратные используются для шифрования сообщений, для хранения данных, выполнения запросов и используются в качестве структуры данных для решения алгоритмических задач и т. д. В робототехнике движение робота программируется с помощью вычислений на основе матриц.
После изучения этой главы:
1. Вам будет легко понять концепцию массива в информатике (если вы изучали информатику в +2).
Вам будет легко понять концепцию массива в информатике (если вы изучали информатику в +2).
2. Это поможет вам решить задачу, связанную с одновременным уравнением с таким же количеством неизвестных переменных, как и уравнений.
3. Определитель поможет вам решить задачи, связанные с площадями и объемами, такие как площадь треугольника и объем тетраэдра.
4. Это поможет вам лучше организовать свою работу в виде матриц и, следовательно, поможет вам сохранять ясность ума в повседневной жизни.
5. И, очевидно, сама глава поможет вам получить некоторые оценки на экзамене, так как она имеет около 7% веса на джи-мейн и примерно такой же вес на других экзаменах.
Обзор матрицы и определителя:
Матрица: Набор чисел или объектов или символов, представленных в виде прямоугольного массива, называется матрицей. Порядок матрицы определяется количеством строк и количеством столбцов, присутствующих в прямоугольном массиве представления. Например
Порядок матрицы определяется количеством строк и количеством столбцов, присутствующих в прямоугольном массиве представления. Например
Матрица имеет 2 строки и 3 столбца, поэтому говорят, что ее порядок равен 2 × 3.
Любой общий элемент матрицы представлен , где представляет элементы i-й строки и j-го столбца.
Операции с матрицами: Алгебраические операции с матрицами, такие как сложение, вычитание, умножение и деление, будут изучаться последовательно в подробной главе, и мы обнаружим, что их очень легко понять.
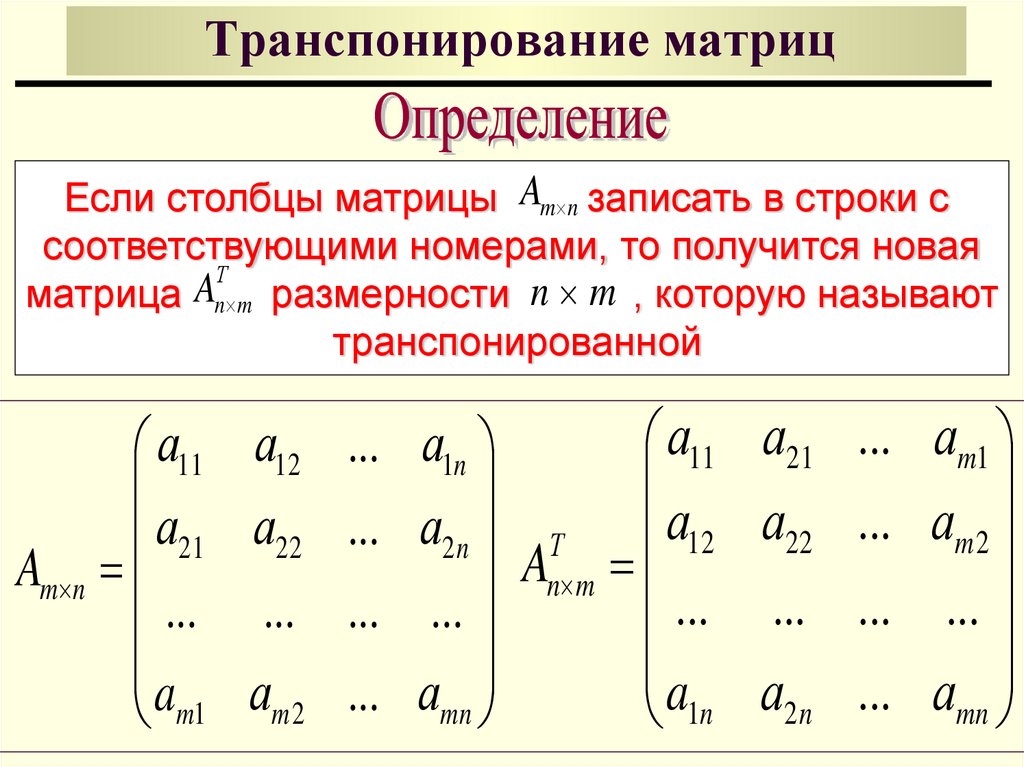
Транспонирование матрицы: Если A является матрицей, то матрица, полученная заменой столбцов матрицы строками или строками столбцов, называется транспонированием матрицы.
Например:
Сопряженная матрица: Если матрица A имеет в качестве элемента комплексное число, то матрица, полученная заменой этих комплексных чисел на сопряженное, называется сопряженной матрицей A, и она обозначается .
Определитель матрицы: число, которое вычисляется из матрицы. Чтобы определитель существовал, матрица A должна быть квадратной матрицей. Определитель матрицы обозначается det A или |A|.
Минор и сомножитель элемента в матрице/детерминанте: Минор любого элемента, где i – количество строк, j – количество столбцов, это det матрицы, оставшийся после удаления i-го строку и j-й столбец.
Сопряжение матрицы: транспонирование кофактора элемента матрицы известно как сопряжение матрицы.
Обратная матрица: неособая квадратная матрица «А» называется обратимой, если существует невырожденная квадратная матрица В такая, что АВ = I=ВА, а матрица В называется обратной матрицей А.
Матрицы и определители — это тема, полезная при преобразовании координат и в некоторых концепциях дифференциальных уравнений, а также в биномиальной теореме. эти понятия, а также это поможет вам получить несколько легких оценок на основных экзаменах.
эти понятия, а также это поможет вам получить несколько легких оценок на основных экзаменах.
1. Начните с понимания основных понятий, таких как определение матрицы, алгебра матрицы, транспонирование матрицы и т. д.
2. Затем переходим к сложному понятию, такому как сопряженная матрица и обратная матрица,
А затем система уравнений, определитель, правила Крамера и однородные уравнения.
3. После изучения этих понятий просмотрите решенные примеры, а затем перейдите к MCQ и попрактикуйтесь в решении задачи, чтобы убедиться, что вы поняли тему.
4. Решите вопросы по книгам, за которыми вы следите, а затем перейдите к работам предыдущего года.
5. Вы можете сначала изучить матрицу, затем определитель или сначала определитель, а затем матрицу. В разных книгах соблюдается разный порядок, вы можете выбрать свой собственный порядок или порядок коучинга или материала, которому вы следуете.
6. При изучении концепции убедитесь, что вы понимаете вывод формул, и попробуйте вывести их самостоятельно, так как часто вам не понадобится точная формула, но некоторые шаги вывода будут очень полезны для решения проблемы, если вы понять вывод, это повысит вашу скорость в решении проблем.
7.Поскольку эта тема требует больших расчетов, потренируйтесь как можно больше и при этом помните об общем весе, который она имеет (7%).
8. В конце главы попробуйте сделать свои собственные краткие заметки для быстрого повторения, составьте список формул для быстрого повторения перед экзаменами или в любое время, когда вам нужно пересмотреть главу, это сэкономит вам много времени.
Лучшие книги для подготовки к этому комплексному числу и квадратным уравнениям:
Во-первых, закончите все концепции, примеры и вопросы, данные в NCERT Maths Book. Вы должны тщательно изучить теорию NCERT. Затем вы можете обратиться к книге «Алгебра, Арихант» доктора С.К. Гояла или Р.Д. Шармы или Cengage Mathematics Algebra, но убедитесь, что вы следуете любой из них, а не всем. Матрица и определитель очень хорошо объясняются в этих книгах, и есть достаточное количество вопросов с кристально ясными понятиями. Выбор справочника зависит от человека к человеку, найдите книгу, которая подходит вам лучше всего, в зависимости от того, насколько хорошо вы разбираетесь в концепциях и сложности вопросов, которые вам нужны.
Затем вы можете обратиться к книге «Алгебра, Арихант» доктора С.К. Гояла или Р.Д. Шармы или Cengage Mathematics Algebra, но убедитесь, что вы следуете любой из них, а не всем. Матрица и определитель очень хорошо объясняются в этих книгах, и есть достаточное количество вопросов с кристально ясными понятиями. Выбор справочника зависит от человека к человеку, найдите книгу, которая подходит вам лучше всего, в зависимости от того, насколько хорошо вы разбираетесь в концепциях и сложности вопросов, которые вам нужны.


 .
. Если A=\[\begin{bmatrix} 1 & 1 \\ 0 & 2 \\ 1 & 1 \\ \end{bmatrix}\] и B = \[\begin{bmatrix} 1 & 2 \\ 2 & 2 \\ \end{bmatrix}\],
Если A=\[\begin{bmatrix} 1 & 1 \\ 0 & 2 \\ 1 & 1 \\ \end{bmatrix}\] и B = \[\begin{bmatrix} 1 & 2 \\ 2 & 2 \\ \end{bmatrix}\],  Для того чтобы определитель был связан с матрицей, последняя должна быть квадратной матрицей.
Для того чтобы определитель был связан с матрицей, последняя должна быть квадратной матрицей. Найти определитель матрицы A, если A =\[\begin{bmatrix} 2 и 5 \\ 1 и 3 \\ \end{bmatrix}\]
Найти определитель матрицы A, если A =\[\begin{bmatrix} 2 и 5 \\ 1 и 3 \\ \end{bmatrix}\] 
 Неудивительно, что исследование процессов линейных уравнений привело к разработке матриц и определителей. Вавилоняне исследовали проблемы, которые привели к параллельным линейным уравнениям, и некоторые из них были записаны на глиняных табличках.
Неудивительно, что исследование процессов линейных уравнений привело к разработке матриц и определителей. Вавилоняне исследовали проблемы, которые привели к параллельным линейным уравнениям, и некоторые из них были записаны на глиняных табличках.