Математика пересечение: Нахождение пересечения и объединения числовых множеств, что такое пересечение множеств

Пересечение множеств — это… Что такое Пересечение множеств?



Пересечение множеств

Категория:

• Теория множеств

Wikimedia Foundation. 2010.

• Объединение множеств
• Пустое множество

Смотреть что такое «Пересечение множеств» в других словарях:

• ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ — понятие теории множеств; пересечение множеств множество, состоящее из всех тех элементов, которые принадлежат одновременно всем данным множествам. Пересечение множеств А и В обозначают А?В или АВ …   Большой Энциклопедический словарь

• пересечение множеств — понятие теории множеств; пересечение множеств  множество, состоящее из всех тех элементов, которые принадлежат одновременно всем данным множествам. Пересечение множеств А и В обозначают А∩В или АВ. * * * ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ …   Энциклопедический словарь

• Пересечение множеств —         множество, состоящее из всех тех элементов, которые принадлежат одновременно всем данным множествам. П. м. A и B обозначают A∩B или AB; П. м. Ak, взятых в конечном или бесконечном числе, обозначают Ak. П. м. может быть пустым, то есть не… …   Большая советская энциклопедия

• ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ — понятие теории множеств; П. м. множество, состоящее из всех тех элементов, к рые принадлежат одноврем. всем данным множествам. П. м …   Естествознание. Энциклопедический словарь

• Пересечение (теория множеств) — Пересечение A и B Пересечение множеств в теории множеств  это множество, состоящее из элементов, которые принадлежат одновременно всем данным множествам. Содержание 1 Определение 2 Замечание …   Википедия

• МНОЖЕСТВ ТЕОРИЯ — раздел математики, в котором изучаются общие свойства множеств, преимущественно бесконечных. понятие множества простейшее математическое понятие, оно не определяется, а лишь поясняется при помощи примеров: множество книг на полке, множество точек …   Большой Энциклопедический словарь

• множеств теория — раздел математики, в котором изучаются общие свойства множеств, преимущественно бесконечных. Понятие множества  простейшее математическое понятие, оно не определяется, а лишь поясняется при помощи примеров: множество книг на полке, множество… …   Энциклопедический словарь

• множеств теория — математическая теория, изучающая точными средствами проблему бесконечности. Предмет М. л. свойства множеств (совокупностей, классов, ансамблей), гл. обр. бесконечных. Множество A есть любое собрание определенных и различимых между собой объектов …   Словарь терминов логики

• Множеств теория — Теория множеств  раздел математики, в котором изучаются общие свойства множеств. Теория множеств лежит в основе большинства математических дисциплин; она оказала глубокое влияние на понимание предмета самой математики. Содержание 1 Теория… …   Википедия

• МНОЖЕСТВ ТЕОРИЯ — раздел математики, в к ром изучаются общие свойства множеств, преим. бесконечных. Понятие множества простейшее матем. понятие, оно не определяется, а лишь поясняется при помощи примеров: множество книг на полке, множество точек на прямой… …   Естествознание. Энциклопедический словарь

Книги

• Игры и задачи. 1-4 классы (CD), Пронина К. Б., Данилов Дмитрий Даимович, Самойлов Евгений Алексеевич. Учебное пособие «1 С:Школа. Русский язык, литература, математика, окружающий мир. Игры и задачи, 1-4 классы» позволит ребенку в игровой форме выучить таблицу умножения, узнать, как пишутся… Подробнее  Купить за 216 руб
• Считаю до 20. Рабочая тетрадь для детей 6 — 7 лет. ФГОС ДО, Шевелев Константин Валерьевич. Рабочая тетрадь предназначена для работы с детьми 6 7 лет. Способствует достижению целей блока Познание путем формирования элементарных математических представлений. Даны методические… Подробнее  Купить за 158 грн (только Украина)

Лекция 3. Пересечение множеств.

Лекция 3.  Пересечение множеств. Свойства пересечения множеств.

       

Определение. Пересечением множеств А и В называется множество, содержащее все элементы, которые принадлежат множеству А и множеству В.

        Пересечение множеств А и В обозначают А∩ В. Таким образом, по определению, А ∩ В = { х | х ∈ А и х ∈ В}.

        Например, если А = { a , c , k , m , n } и В = { 

a , b , c , d , e },  

то А ∩ В = { a , c }.

        Если изобразить множества А и В при помощи кругов Эйлера-Венна, то пересечением данных множеств является заштрихованнаяобласть:

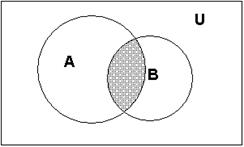
Для пересечения множеств выполняются следующие свойства.

1)    Переместительное или коммутативное свойство: А ∩ В = В ∩ А.

2)    Сочетательное или ассоциативное свойство:(А ∩ В) ∩ С = А ∩ (В ∩ С).

3)    А ∩ ∅ = ∅ (пустое множество является поглощающим элементом).

4)    А ∩ U = А (универсальное множество является нейтральным элементом).

5)   Если В ⊂А, то А∩В = В

Задания для самостоятельной работы по теме:

1. Найдите пересечение множеств А и В, если:

а) А = {26, 39, 5, 58, 17, 81}, В = {17, 26, 58};

б) А = {26, 39, 5, 58, 17, 81}, В = {17, 26, 58, 5, 39, 81}.

2. Из каких элементов состоит пересечение множества букв в слове «математика» и множества букв в слове «геометрия»?

3. М — множество однозначных чисел, Р — множество нечетных натуральных чисел. Из каких чисел состоит пересечение данных множеств? Содержатся ли в нем числа -7 и 9?

4. А- множество точек окружности, В — множество точек прямой l. Из скольких элементов может состоять пересечение данных множеств? Может ли оно быть пустым?

Урок по математике_Пересечение и объединение множеств

Урок по математике

в 6 классе

Тема: «Пересечение и объединение множеств»

Учитель математики

МБОУ «Кабановская СОШ»

Жукова В.В.

ПЛАН-КОНСПЕКТ УРОКА

Тема урока: «Пересечение и объединение множеств».

Тип урока: изучение нового материала.

Цели:

• формирование знаний о пересечении и объединении множеств;

• развитие умений и нахождение числа элементов пересечения и объединения множеств, выявлять закономерность, обобщать и делать выводы, воспитание ответственного отношения к учебе.

Ход урока.

1. Организационный момент.

2. Повторение изученного по теме «Множества».

Вопросы для учащихся:

1. Что такое множество?

2. Что такое элементы множества?

3. Какое множество конечно и бесконечно?

4. Какое множество называется пустым?

3. Изучение нового материала «Пересечение множеств».

Учитель. Рассмотрим следующие два множества: М – множество всех точек круга, N – множество точек прямой, пересекающей круг. Каждый видит, что пересечение круга с прямой – это отрезок; обозначим его концы буквами А и В. Задумаемся: каким свойством обладают точки этого отрезка по отношению к множествам М и N? Ответ ясен: точки отрезка АВ – это в точности те точки, которые принадлежат и множеству М, и множеству N. Так что множество всех точек отрезка АВ естественно назвать пересечением множеств М и N.

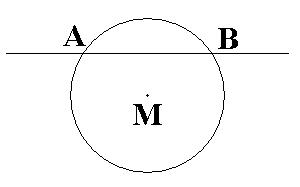
Точно так же можно определить пересечение любых двух множеств М и N. Пересечением множеств М и N называется множество, состоящее из всех элементов, принадлежащих каждому из множеств М и N. Пересечение множеств М и N обозначают МN. Читают: «пересечение М и N» или «М пересечение N». Знак называется знаком пересечения.

Обсудим несколько примеров.

Пример 1. М – множество всех учениц какой-то школы, N – множество всех учащихся данного класса этой школы. Тогда МN – это множество всех девочек из данного класса.

Пример 2. М – множество всех квартир на 1-м этаже в каком-то доме, N – множество всех квартир в данном подъезде этого дома. Тогда

МN – это множество всех квартир на 1-м этаже в данном подъезде.

Пересечение множеств точек двух фигур на плоскости легче представить, если нарисовать эти фигуры. Сделаем это, например, для двух кругов. Множество всех точек первого круга обозначим М, второго – N. Для пересечения МN могут быть три варианта; они изображены на рисунке.

Ø

Если конечные множества записаны при помощи фигурных скобок списками своих элементов, то легко записать их пересечение. Примеры:

=;= ;

=; .

Пересечение можно образовывать не только для двух множеств, но и для любого их числа. Определяется это точно так же, как и для двух множеств: пересечением данных множеств называется множество, состоящее из всех элементов, принадлежащих каждому из этих множеств. Пересечение множеств М, N и Р обозначается МNР.

Вопрос для учащихся:

Что обозначает запись РQRS? Какому множеству равно это пересечение, если Р=; Q=; R=; S=?

4. Первичное закрепление понятия пересечения множеств.

Вопросы:

1. Что такое пересечение двух множеств; нескольких множеств?

2. Что значит, что два множества не пересекаются? Приведите 2-3 примера непересекающихся множеств.

3. Какое множество обозначается знаком ?

Практические задания:

1. Для каждой пары множеств М и N запишите их пересечение:

1. М=, N=;

2. М=, N=;

3. М=, N=;

5. ,N – множество всех неправильных дробей.

2. Для каждой пары множеств М и N укажите их пересечение:

1. М – множество всех нечетных чисел, N – множество всех натуральных чисел, делящихся на 4;

2. М – множество всех правильных дробей, N – множество всех десятичных дробей;

3. М – множество всех натуральных чисел, делящихся на 3, N – множество всех натуральных чисел, делящихся на 5.

3. Дан многоугольник. Каждую его сторону будем рассматривать как множество всех точек, принадлежащих этой стороне. Для каждой пары сторон многоугольника укажите множество, равное пересечению этих двух сторон, если многоугольник – это: а) треугольник АВС; б) прямоугольник KLMN.

4. Рассмотрите три множества , и . Убедитесь, что их пересечение пусто, а пересечение любых двух из этих множеств не пусто.

5. Пусть М – множество всех букв слова СЛОН, N – множество всех букв слова СТОН, Р – множество всех букв слова СТОГ, S – множество всех букв слова СЛОГ.

1. Запишите всевозможные попарные пересечения этих множеств. Имеются ли среди них равные?

2. Запишите всевозможные пересечения троек этих множеств. Имеются ли среди них равные?

3. Запишите пересечение всех этих множеств. Равно ли оно какому-то из множеств, найденных вами в пунктах а) и б)?

5. Изучение нового материала «Объединение множеств».

Учитель. Объединением множеств М и N называется множество всех элементов, принадлежащих хотя бы одному из множеств М и N. Объединение множеств М и N обозначают МN. Читают: «объединение М и N» или «М объединение N». Знак называется знаком объединения.

Разберем несколько примеров. Обдумайте каждый из них.

Пример 1. М – множество всех учеников данного класса, получивших на сегодняшний день пятерку по какому-нибудь предмету, N – множество всех учеников того же класса, получивших в этот день четверку по какому-нибудь предмету. Тогда МN – это множество всех учеников данного класса, получивших за сегодняшний день повышенные отметки.

Пример 2. М – множество всех правильных дробей, N – множество всех неправильных дробей. Тогда МN – это множество всех обыкновенных дробей.

Пример 3. М – множество всех букв слова КОШКА, N – множество всех букв слова МЫШКА. Тогда МN =.

Задание для учащихся:

Приведите сами какой-нибудь пример объединения двух множеств.

Учитель. Как и пересечение, объединение можно образовать не только для двух множеств, но и для любого их числа: объединением данных множеств называется множество, состоящее…

Закончите определение. Догадайтесь, как записать объединение трех множеств М, N и Р.

Если конечные множества записаны при помощи фигурных скобок списками своих элементов, то, как и для пересечения, легко записать их объединения.

=;

=;

=;

=.

Для любых множеств М и N можно образовать их пересечение МN и объединение МN. Это похоже на то, что происходит при действиях над числами: для любых двух чисел m и n можно образовать их произведение m n и сумму m+n. Так получаются действия, которые назвали умножением и сложением. Поэтому образование пересечения и образование объединения можно назвать действиями над множествами.

Выполняются ли те же законы для пересечения и объединения множеств? Давайте рассуждать. Начнем с переместительного закона. Повторим, что такое пересечение двух множеств: множество МN состоит из всех элементов, принадлежащих каждому из множеств М и N, а множество NМ состоит из всех элементов, принадлежащих каждому из множеств N и М. Но сказать «каждому из множеств М и N» или «каждому из множеств N и М» — значит сказать одно и то же: ведь ясно, что неважно, в каком порядке перечислять здесь множества. Значит, множества МN и NМ состоят из одних и тех же элементов, т.е.

МN=NМ

Данное равенство и означает, что переместительный закон для пересечения верен.

Чтобы проверить сочетательный закон, надо убедиться, что для любых трех множеств М, N и Р выполняется равенство

М(NР)= (МN)Р

Легко понять, что в левой и правой частях этого равенства записаны множества, состоящие из всех элементов, принадлежащих каждому из множеств М, N и Р, т.е. состоящие из одних и тех же элементов. Это и означает, что требуемое равенство выполняется.

6. Первичное закрепление изученного понятия объединения множеств.

Вопросы:

1. Что такое объединение двух множеств; нескольких множеств?

2. О выполнении каких законов для действий пересечения и объединения множеств идет речь в объяснительном тексте этого параграфа?

3. Каким множеством – конечным или бесконечным – будет объединение: а) двух конечных множеств; б) двух бесконечных множеств; в) конечного и бесконечного множеств?

Практические задания:

1. Для каждой пары множеств М и N запишите их объединение:

1. М=, N=;

2. М=, N=;

3. М=, N=.

2. Для каждой пары множеств М и N укажите их объединение:

1. М – множество всех нечетных чисел, N – множество всех четных чисел;

2. М – множество всех квадратов на плоскости, N – множество всех прямоугольников на той же плоскости, четырехугольников;

3. М – множество всех натуральных чисел, делящихся на 3, N – множество всех натуральных чисел, делящихся на 15.

3. Пусть М – множество всех букв слова СЛОН, N – множество всех букв слова СТОН, Р – множество всех букв слова СТОГ, S – множество всех букв слова СЛОГ.

1. Запишите всевозможные попарные объединения этих множеств. Имеются ли среди них равные?

2. Запишите всевозможные объединения троек этих множеств. Имеются ли среди них равные?

3. Запишите объединение всех этих множеств. Равно ли оно какому-то из множеств, найденных вами в пунктах а) и б)?

7. Изучение нового – вывод правила подсчета числа элементов объединения и пересечения множеств.

Учитель. Чтобы вывести правило давайте разберем конкретный пример. Пусть М=, т.е. m=4;

N=, т.е. n=3.

Запишем объединение этих множеств:

МN=.

В множестве МN пять элементов, а m+n=4+3=7. Вот мы и видим, что в МN элементов меньше чем 7.

Почему так получилось? Да потому, что в данном примере можно указать учеников, которые в этот день получили и пятерку, и четверку. Другими словами здесь пересечение МN не пусто: МN=. Но в объединении-то МN каждый элемент пересечения МN присутствует (и подсчитывается) только один раз, а не два раза.

Давайте-ка изобразим ситуацию нашего примера на рисунке.

Если бы подсчитали здесь сумму m+n (т.е. 4+3), то каждый элемент пересечения (в данном примере Валя и Игорь, т.е. 2 элемента) оказался бы подсчитанным дважды. Значит, чтобы узнать число элементов объединения, надо из суммы m+n вычесть число лишний раз сосчитанных элементов пересечения. В данном примере получаем 4+3-2=5.

Данная задача была решена с помощью рисунка, этот способ называется «Круги Эйлера». Леонард Эйлер – швейцарский математик, который в 18 веке работал в Российской академии наук и сделал много открытий для нашей науки.

Итак, если мы возьмем сумму m+n, то в ней элементы пересечения МN будут сосчитаны дважды. Значит, чтобы определить число элементов объединения, надо из суммы m+n вычесть число лишний раз сосчитанных элементов из МN, т.е. число р. Получим такую формулу:

q=m+n-p.

Сформулируем правило для нахождения числа элементов объединения множеств:

Чтобы найти число элементов объединения двух множеств, надо сложить числа элементов этих множеств и вычесть из полученной суммы число элементов их пересечения.

Сформулируем правило для нахождения числа элементов пересечения множеств:

Чтобы найти число элементов пересечения двух множеств, надо сложить числа элементов этих множеств и вычесть из полученной суммы число элементов их объединения.

8. Первичное закрепление изученного.

Практические задания (устно):

1. Вычислите число элементов в объединении множеств М и N, если:

1. М содержит 10 элементов, N – 15 элементов, а МN – 7 элементов;

2. М содержит 27 элементов, N – 18 элементов, а МN – 13 элементов;

3. М содержит 45 элементов, N – 57 элементов, а МN – 1 элемент.

2. Вычислите число элементов в пересечении множеств М и N, если:

1. М содержит 10 элементов, N – 15 элементов, а МN – 17 элементов;

2. М содержит 27 элементов, N – 18 элементов, а МN – 45 элементов;

3. М содержит 45 элементов, N – 57 элементов, а МN – 100 элементов.

Решение задач с помощью кругов Эйлера:

№1. В классе 28 учеников. Каждый из них начертил у себя в тетради один из двух четырехугольников – прямоугольник или ромб. При проверке прямоугольников оказалось 17, а ромбов – 15. Как такое могло случиться?

№2. В осенние каникулы 12 учеников класса участвовали в междугородных экскурсиях в Москву и Санкт-Петербург, при этом 8 из них посетили Санкт-Петербург, а 6 – Москву. Сколько из этих учеников побывало и в Москве, и в Санкт-Петербурге?

Задание на дом:

№1. Найдите пересечение множеств учителей, которые вели уроки в вашем классе: а) вчера и сегодня; б) вчера и позавчера. Оказалось ли какое-то из этих двух пересечений пустым?

№2. Вася, рассматривая свой дневник погоды, обнаружил, что в сентябре 17 раз отмечен дождь и 19 раз – сильный ветер. При этом дней, когда одновременно шел дождь и дул сильный ветер, оказалось 7. Был ли хоть один день, когда не было ни дождя, ни сильного ветра?

Пересечение прямых. Точка пересечения двух прямых

Точка пересечения двух прямых на плоскости

Методы решения. Существует два метода решения плоских задач на определение координат точки пересечения прямых:

• графический
• аналитический

Графический метод решения. Используя уравнения, начертить графики прямых и с помощью линейки найти координаты точки пересечения.

Аналитический метод решения. Необходимо объединить уравнения прямых в систему, решение которой, позволит определить точные координаты точки пересечения прямых.

Если система уравнений:

• имеет единственное решение, то прямые пересекаются;
• имеет бесконечное множество решений, то прямые совпадают;
• не имеет решений, то прямые не пересекаются (прямые параллельны между собой)

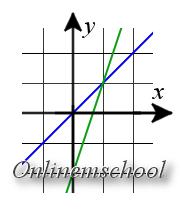
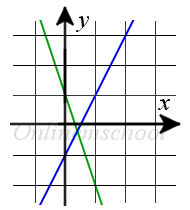Пример 1. Найти точку пересечения прямых y = 2x — 1 и y = -3x + 1.

Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:

y = 2x — 1 y = -3x + 1

Вычтем из первого уравнения второе

y — y = 2x — 1 — (-3x + 1) y = -3x + 1     =>     0 = 5x — 2 y = -3x + 1

Из первого уравнения найдем значение x

5x = 2 y = -3x + 1     =>     x = 25 = 0.4 y = -3x + 1

Подставим значение x во второе уравнение и найдем значение y

x = 0.4 y = -3·(0.4) + 1 = -1.2 + 1 = -0.2

Ответ. Точка пересечения двух прямых имеет координаты (0.4, -0.2)

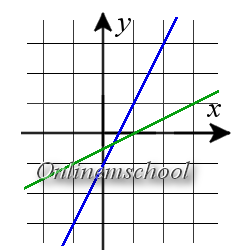Пример 2. Найти точку пересечения прямых y = 2x — 1 и x = 2t + 1y = t.

Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:

y = 2x — 1 x = 2t + 1 y = t

В первое уравнение подставим значения x и y из второго и третьего уравнений.

t = 2·(2t + 1) — 1 x = 2t + 1 y = t     =>     t = 4t + 1 x = 2t + 1 y = t     =>    

-3t = 1 x = 2t + 1 y = t     =>     t = -13 x = 2t + 1 y = t

Подставим значение t во второе и третье уравнение

t = -13 x = 2·(-13) + 1 = -23 + 1 = 13 y = -13

Ответ. Точка пересечения двух прямых имеет координаты (13, -13)

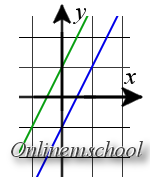
Пример 3 Найти точку пересечения прямых 2x + 3y = 0 и x — 23 = y4.

Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:

2x + 3y = 0 x — 23 = y4

Из второго уравнения выразим y через x

2x + 3y = 0 y = 4·x — 23

Подставим y в первое уравнение

2x + 3·4·x — 23 = 0 y = 4·x — 23     =>     2x + 4·(x — 2) = 0 y = 4·x — 23     =>    

2x + 4x — 8 = 0 y = 4·x — 23     =>     6x = 8 y = 4·x — 23     =>    

x = 86 = 43 y = 4·x — 23     =>     x = 86 = 43 y = 4·4/3 — 23 = 4·-2/3 3 = -89

Ответ. Точка пересечения двух прямых имеет координаты (43, -89)

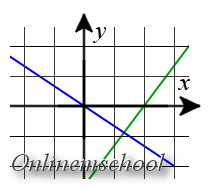
Пример 4. Найти точку пересечения прямых y = 2x — 1 и y = 2x + 1.

Решение: Обе прямые заданы уравнениями с угловым коэффициентом. Так как k₁ = k₂ = 2, то прямые параллельны. Так как эти прямые не совпадают то точек пересечения нет.

Решим также эту задачу используя систему уравнений:

y = 2x — 1 y = 2x + 1

Вычтем из первого уравнения второе

y — y = 2x — 1 — (2x + 1) y = -3x + 1     =>     0 = -2 y = -3x + 1

В первом уравнении получили противоречие (0 ≠ -2), значит система не имеет решений — отсутствуют точки пересечения прямых (прямые параллельны).

Ответ. Прямые не пересекаются (прямые параллельны).

Пример 5. Проверить является ли точка N(1, 1) точкой пересечения прямых y = x и y = 3x — 2.

Решение: Подставим координаты точки N в уравнения прямых.

1 = 1

1 = 3·1 — 2 = 1

Ответ. Так как оба уравнения превратились в тождества, то точка N — точка пересечения этих прямых.

Точка пересечения двух прямых в пространстве

Метод решения. Для определение координат точки пересечения прямых в пространстве, необходимо объединить уравнения прямых в систему, решение которой, позволит определить точные координаты точки пересечения прямых.

Если система уравнений:

• имеет единственное решение, то прямые пересекаются;
• имеет бесконечное множество решений, то прямые совпадают;
• не имеет решений, то прямые не пересекаются (прямые параллельны или скрещиваются между собой)

Пример 6. Найти точку пересечения прямых x — 1 = y — 1 = z — 1 и x — 3-2 = 2 — y = z.

Решение: Составим систему уравнений

x — 1 = a y — 1 = a z — 1 = a x — 3-2 = b 2 — y = b z = b   =>   x = a + 1 y = a + 1 z = a + 1 x — 3-2 = b 2 — y = b z = b   =>  

Подставим значения x, y, z из 1, 2, 3 уравнений в 4, 5, 6 уравнения

x = a + 1 y = a + 1 z = a + 1 a + 1 — 3-2 = b 2 — (a + 1) = b a + 1 = b   =>   x = a + 1 y = a + 1 z = a + 1 a — 2-2 = b 1 — a = b a + 1 = b

К шестому уравнению добавим пятое уравнение

x = a + 1 y = a + 1 z = a + 1 a — 2-2 = b 1 — a = b a + 1 + (1 — a) = b + b   =>   x = a + 1 y = a + 1 z = a + 1 a — 2-2 = b 1 — a = b b = 1

Подставим значение b в четвертое и пятое уравнения

x = a + 1 y = a + 1 z = a + 1 a — 2-2 = 1 1 — a = 1 b = 1   =>   x = a + 1 y = a + 1 z = a + 1 a — 2 = -2 a = 0 b = 1   =>  

x = a + 1 y = a + 1 z = a + 1 a = 0 a = 0 b = 1   =>   x = 0 + 1 = 1 y = 0 + 1 = 1 z = 0 + 1 = 1 a = 0 a = 0 b = 1

Ответ. Прямые пересекаются в точке с координатами (1, 1, 1).

Замечание. Если уравнения прямых заданы параметрически, и в обоих уравнениях параметр задан одной и той же буквой, то при составлении системы в одном из уравнений необходимо заменить букву отвечающую за параметр.

Пример 7. Найти точку пересечения прямых x = 2t — 3 y = t z = -t + 2 и x = t + 1 y = 3t — 2 z = 3 .

Решение: Составим систему уравнений заменив во втором уравнении параметр t на a

x = 2t — 3 y = t z = -t + 2 x = a + 1 y = 3a — 2 z = 3

Подставим значения x, y, z из 1, 2, 3 уравнений в 4, 5, 6 уравнения

x = 2t — 3 y = t z = -t + 2 2t — 3 = a + 1 t = 3a — 2 -t + 2 = 3   =>   x = 2t — 3 y = t z = -t + 2 2t = a + 4 t = 3a — 2 t = -1   =>  

Подставим значение t из шестого уравнения в остальные уравнения

x = 2·(-1) — 3 y = (-1) z = -(-1) + 2 2·(-1) = a + 4 -1 = 3a — 2 t = -1   =>   x = -5 y = -1 z = 3 a = -6 a = 13 t = -1

Ответ. Так как -6 ≠ 13, то прямые не пересекаются.

Пересечение множеств

Пусть даны произвольные множества А и В.

Определение: Пересечением множеств А и В называется множество AB, элементы которого одновременно принадлежат и множеству А и множеству В.

AB={x|xA и xB}

Рассмотрим множества А и В. Покажем на диаграмме пересечение этих множеств. Пусть:

1) множества А и В не вступают в отношение друг с другом.

Очевидно, что в этом случае AB= Ø.

2) множества А и В находятся в отношении равенства.

Тогда AB=A=B.

A=B

3) множества А и В находятся в отношении включения.

Если АВ, то AB=A, если ВА, то AB=В.

A

B

B

A

Штриховкой показано множество элементов, принадлежащих AB.

4) множества А и В находятся в отношении пересечения.

B

A

Двойной штриховкой показано множество элементов, принадлежащих AB.

Пример:

Пусть А = {3; а; b}, B = {1; 3; 7}. Найдем AB.

По определению пересечения двух множеств AB = { 3 }, так как только элемент x = 3 принадлежит и множеству А и множеству В. Изобразим множества А и В и их пересечение на диаграмме:

B

A

Замечание : В речи операции пересечения соответствует союз «И», а операции объединения – союз «ИЛИ».

Таким образом, по определению x AB xA и xB.

В пересечение множеств А и В не войдут те элементы, которые не входят в А, или в В. Таким образом, x AB xA или xB. Другими словами,

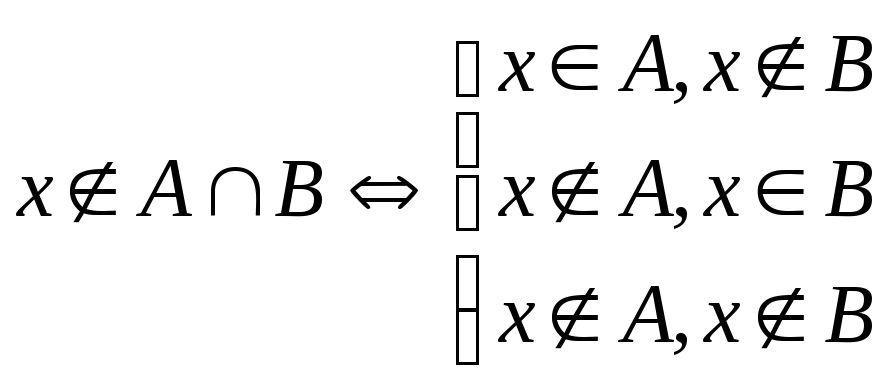
Замечание: Операция отыскания объединения (пересечения) множеств также называется объединением (пересечением).

Вычитание множеств

Пусть даны произвольные множества А и В.

Определение: Разностью двух множеств А и В называется множество А\В, элементы которого принадлежат множеству А, но не принадлежат множеству В.

А\В = {x| xA, xB}

Покажем на диаграмме разность множеств А и В. Пусть:

1) множества А и В не вступают в отношение друг с другом.

Очевидно, что в этом случаеА\В = А, а В\А = В.

A

B

A

B

2) множества А и В находятся в отношении равенства.

Тогда А\В = В\А = Ø.

A=B

3) множества А и В находятся в отношении включения.

Если АВ, то А\В = Ø. Если ВА, то А\В Ø

A

B

B

A

4) множества А и В находятся в отношении пересечения.

A

B

Штриховкой показано множество элементов, принадлежащих А\В.

Примеры:

1) Пусть А = {3; а; b}, B = {1; 3; 7}. Найдем А\В.

По определению разности двух множеств А\В = {a;b}, так как только эти элементы множеству А принадлежат, а множеству В — нет.

2) A = N, B = Z.

Так как NZ, (т.е. AB), то А\В=N\Z= Ø , а Z\N – это множество целых отрицательных чисел или нуль.

Замечание: Если множество В является подмножеством множества А, то разность А\В называется дополнением множества В до множества А и обозначается В.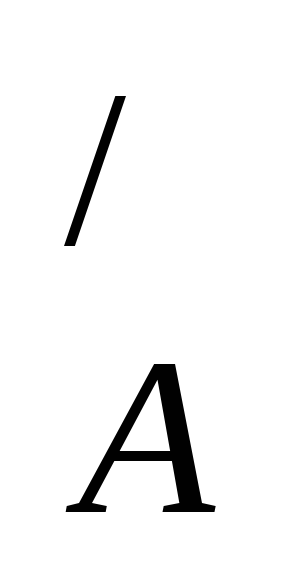

ВА А\В= В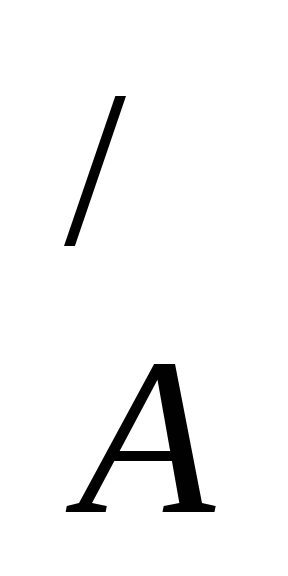

Если А – это универсальное множество (J), то разность J \В= В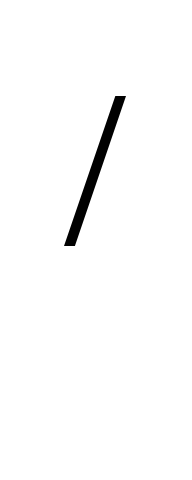. При этом не указывается до какого множества.

Примеры:

1) Пусть А = {3; а; b}, B = {1; 3; 7}. Если возможно, найдите дополнение множества В до А или А до В.

Так как АВ и ВА, то говорить о дополнения одного множества до другого не имеет смысла.

2) A = N, B = Z.

Так как NZ, (т.е. AB), то В\А=Z\N=N – это множество целых отрицательных чисел или нуль.

Замечание: Для задания множества действительных чисел используют специальные обозначения: числовые промежутки. Так, например,

[a; b] = {x|xR, axb}

[a; b) = {x|xR, ax<b}

(a; b] = {x|xR, a<xb}

(a; b) = {x|xR, a<x<b}

Указанные промежутки – это подмножества действительных чисел.

Пересечение множеств

Этот урок объяснит, как найти пересечение множеств. Начнем с определения пересечения двух множеств.

Определение:

Для двух наборов A и B пересечение — это набор, который содержит элементы или объекты, которые принадлежат A и B одновременно.

Мы пишем A B

В основном, мы находим A ∩ B, ища все общие элементы A и B. Далее мы проиллюстрируем это на примерах.

Пример № 1 .

Чтобы упростить задачу, обратите внимание, что общее у них выделено жирным шрифтом.

Пусть A = { 1 апельсин , 1 ананас, 1 банан, 1 яблоко } и B = {1 ложка, 1 апельсин , 1 нож, 1 вилка, 1 яблоко }

A ∩ B = {1 апельсин, 1 яблоко}

Пример № 2 .

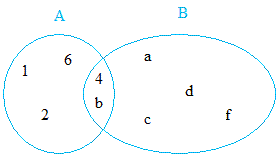
Найдите точку пересечения A и B, а затем составьте диаграммы Венна.

A = { b , 1, 2, 4 , 6} и B = { 4 , a, b , c, d, f}

A ∩ B = {4, б}

Пример № 3 .

A = {x / x — число больше 4 и меньше 8}

B = {x / x — положительное число меньше 7}

A = { 5 , 6 , 7} и B = {1, 2, 3, 4, 5 , 6 }

A ∩ B = {5, 6}

Или A ∩ B = {x / x — число больше 4 и меньше чем 7}

Пример № 4 .

A = {x / x — страна в Азии}

B = {x / x — страна в Африке}

Поскольку нет одинаковых стран в Азии и Африке, перекресток пуст.

A ∩ B = {}

Пример № 5 .

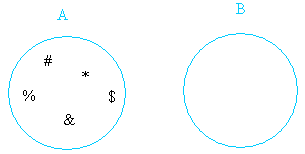A = {#,%, &, *, $}

B = {}

Это тонкий пример! Поскольку пустой набор включен в любой набор, он также включен в A, хотя вы его не видите.

Таким образом, пустое множество — это единственное, что общего между наборами A и B.

A ∩ B = {}

Фактически, поскольку пустой набор включен в любой набор, пересечение пустого набора с любым набором является пустым набором.

Определение объединения трех наборов:

Для трех наборов A, B и C пересечение — это набор, который содержит элементы или объекты, принадлежащие A, B и C одновременно.

Мы пишем A B ∩ C

В основном, мы находим A ∩ B ∩ C, ища все общие элементы A, B и C.

A = { # , 1, 2, 4 , 6}, B = { # , a, b, 4 , c} и C = A = { # ,%, &, * , $, 4 }

A ∩ B ∩ C = {4, #}

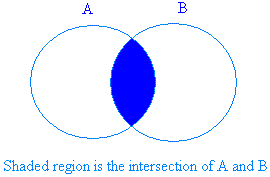
На графике ниже показана заштрихованная область пересечения двух наборов

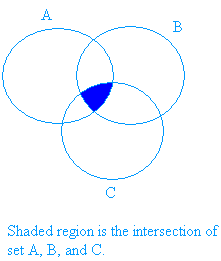
На графике ниже показана заштрихованная область пересечения трех наборов

На этом заканчивается урок о пересечении множеств.Если у вас есть какие-либо вопросы о пересечении множеств, я с радостью отвечу на них.

Воспользуйтесь приведенной ниже викториной, чтобы увидеть, насколько хорошо вы можете найти пересечение множеств.

Новые уроки математики

Ваша электронная почта в безопасности. Мы будем использовать его только для информирования вас о новых уроках математики.

,

пересекающихся линий. (Координатная геометрия) — Math Open Reference

Пересекающиеся линии. (Координатная геометрия) — Открытый справочник по математике Смысл пересечение из двух непараллельный линии можно найти из
уравнения двух линий.

Попробуй это Перетащите любую из 4 точек ниже, чтобы переместить линии. Отметьте, где они пересекаются.

Чтобы найти пересечение двух прямых:

1. Для начала нам нужны уравнения двух линий.Если у вас нет уравнений, см. Уравнение прямой — форма наклона / пересечения и Уравнение прямой — форма точки / наклона (Если одна из линий вертикальная, см. Раздел ниже).
2. Тогда, поскольку в точке пересечения два уравнения будут иметь одинаковые значения x и y, мы полагаем два уравнения равными друг другу. Это дает уравнение, которое мы можем решить относительно x
3. Мы подставляем это значение x в одно из линейных уравнений (не имеет значения, какое именно) и решаем его относительно y.

Это дает нам координаты x и y перекрестка.

Пример

Так, например, если у нас есть две линии, которые имеют следующие уравнения (в форме пересечения наклона):

г = 3х-3

у = 2,3x + 4

В точке пересечения они оба будут иметь одинаковое значение координаты y, поэтому мы приравниваем уравнения друг другу:

3x-3 = 2,3x + 4

Это дает нам уравнение с одним неизвестным ( x ), которое мы можем решить: Измените порядок, чтобы осталось x условий

3х — 2.3х = 4 + 3

Объединение похожих терминов

0,7x = 7

дающий

х = 10

Чтобы найти y, просто установите x равным 10 в уравнении любой строки и решите относительно y: Уравнение для линии (подойдет любая линия)

у = 3х — 3

Установите x равным 10

г = 30 — 3

дающий

г = 27

Теперь у нас есть как x, так и y, поэтому точка пересечения равна (10, 27)

Какую форму уравнения использовать?

Напомним, что линии можно описать форма уклона / пересечения и форма точки / наклона уравнения.Поиск пересечения работает одинаково для обоих. Просто установите уравнения, как указано выше. Например, если у вас есть два уравнения в форме точечного уклона:

у = 3 (х-3) + 9

у = 2,1 (х + 2) — 4

просто установите их равными:

3 (х-3) + 9 = 2,1 (х + 2) — 4

и действуйте, как указано выше, решая для x, а затем подставляя это значение в любое уравнение, чтобы найти y.

Два уравнения не обязательно должны быть в одной и той же форме. Просто установите их равными друг другу и действуйте обычным образом.

Когда одна линия вертикальная

Когда одна из линий вертикальна, у нее нет определенного наклона, поэтому ее уравнение будет выглядеть примерно как x = 12. См. Раздел Вертикальные линии (координатная геометрия). Мы находим перекресток несколько иначе. Предположим, у нас есть прямые, уравнения которых

г = 3х-3	Линия с уклоном вверх и вправо
х = 12	Вертикальная линия

На вертикальной линии все точки на ней имеют координату x 12 (определение вертикальной линии), поэтому мы просто устанавливаем x равным 12 в первом уравнении и решаем его относительно y.
Уравнение для линии:

у = 3х — 3

Установите x равным 12 Используя уравнение второй (вертикальной) линии

г = 36 — 3

дающий

г = 33

Итак, точка пересечения находится в (12,33).

Если обе линии вертикальные, они параллельны и не пересекаются (см. Ниже).

Когда они параллельны

Когда две прямые параллельны, они нигде не пересекаются. Если вы попытаетесь найти пересечение, уравнения будут абсурдными.Например, строки y = 3x + 4 и y = 3x + 8 параллельны, потому что их наклоны (3) равны. См. Параллельные линии (координатная геометрия). Если вы попробуете описанный выше процесс, вы напишете 3х + 4 = 3х + 8. Очевидная невозможность.

Сегменты и лучи могут вообще не пересекаться

Рис 1. Сегменты не пересекаются

В случае двух непараллельных линий пересечение всегда будет где-то на линиях. Но в случае сегменты линии или лучи которые имеют ограниченную длину, они могут не пересекаться.

На рис. 1 мы видим два отрезка, которые не перекрываются и поэтому не имеют точки пересечения. Однако если вы примените к ним описанный выше метод, вы найдете точку, где они пересеклись бы, если бы они были достаточно длинными.

Что попробовать

1. На диаграмме выше нажмите «сброс».
2. Перетащите любую из точек A, B, C, D и обратите внимание на место пересечения линий.
3. Перетащите точку, чтобы получить две параллельные линии, и обратите внимание, что они не пересекаются.
4. Нажмите «скрыть детали» и «показать координаты». Переместите точки в любое новое место, где перекресток еще виден. Вычислите наклоны линий и точки пересечения. Нажмите «Показать подробности», чтобы проверить результат.

Ограничения

Для большей ясности в апплете выше координаты округлены до целых чисел, а длины округлены до одного десятичного знака. Это может привести к небольшому отклонению расчетов.

Подробнее см. Учебные заметки

Прочие темы о координатной геометрии

(C) Открытый справочник по математике, 2011 г.
Все права защищены.

,

math — Java найти пересечение двух линий

Переполнение стека

1. Около
2. Товары
3. Для команд

1. Переполнение стека Общественные вопросы и ответы
2. Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
3. работы Программирование и связанные с ним технические возможности карьерного роста
4. Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
5. реклама Обратитесь к разработчикам и технологам со всего мира
6. О компании

,

Intersection (mathématiques) — Wikipédia

Un article de Wikipédia, l’encyclopédie libre.

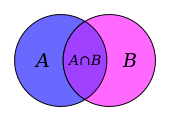Пересечение ансамблей A и B является представителем на диаграмме Венна в центральной фиолетовой зоне.

Dans la théorie des ensembles, l ‘ correction est une opération ensembliste qui porte le même nom que son résultat, à savoir l’ensemble des élements appartenant à la fois aux deux opérandes: l’intersebles de 9000 et deux6 B est l’ensemble, noté A ∩ B , dit « A inter B », qui contient tous les éléments appartenant à la fois à A et à B seulement ceux-là.

A et B sont disjoints si et seulement si A ∩ B est l’ensemble vide ∅.

A , включая B si et seulement si A ∩ B = A .

Проанализируйте правильность, точки пересечения курсов представителей двух функций, которые находятся в описании относительного положения.

Intersection de deux droites [модификатор | модификатор кода файла]

Dans le plan

• Dans le plan, l’intersection de deux droites non parallèles est un point ^[1] : d ∩ d ‘ знак равно { } ,{\ displaystyle d \ cap d ‘= \ {A \}.} On dit qu’elles sont sécantes.
• Si deux droites sont strictement parallèles, elles n’ont pas de point commun; leur crossction est vide: d ∩ d ‘ знак равно ∅ , {\ displaystyle d \ cap d ‘= \ varnothing.}
• Si deux droites sont confondues, tous leurs points sont communs; l’intersection est une droite: d ∩ d ‘ знак равно d знак равно d ‘ ,{\ displaystyle d \ cap d ‘= d = d’.}

Dans l’espace

• Si deux droites ne sont pas coplanaires alors elles n’ont aucun point commun; leur crossction est vide: d ∩ d ‘ знак равно ∅ , {\ displaystyle d \ cap d ‘= \ varnothing.}
• Deux droites parallèles ou sécantes sont coplanaires.

Примеры Autres [модификатор | модификатор кода файла]

Dans l’espace

• Пересечение прямых и прямых участков плана без параллелей является точкой.
• l’intersection de deux planes non parallèles est une droite.

Dans le plan

• Пересечение прав и вершин серка, образовавшееся в центре, несколько точек, расстояние до центра серка, а также право на верхнюю границу, верхняя или нижняя точка округа. Si l’intersection is réduite à un point, la droite est tangente au cercle.
• Intersection de deux cercles is formée de deux points si la distance Entre leurs Centres est (strictement) inférieure à la somme de leurs rayons et supérieure à leur différence, d’un point si cette distance is égale à la somme ou à la différence des rayons (cercles tangent), vide dans les autres cas ^[2] .

Аналитическая геометрия, пересечение двух объектов определяется по системе уравнений, сформированной по объединению ассоциаций с объектами.

En Dimension 2, l’intersection de deux droites est définie par un système de deux équations à 2 inconnues, qui a, en général, une solution unique, sauf si son déterminant est nul, auquel cas il en a soit zéro soit une infinité: на retrouve les trois cas de la géométrie.

Измерение 3, пересечение трех планов — это определенная часть системы трех уравнений, которая представляет собой общее, уникальное решение, однозначно определенное.

En algèbre booléenne, l’intersection est associée à l’opérateur logique et : si A est l’ensemble des éléments de E имеет право собственности P (или удовлетворяет условию P) и ансамбль элементов E , который соответствует условию Q (или соответствует условию Q), alors A ∩ B является ансамблем элементов E, который может принадлежать P и Q (соответствует требованиям Q). fois la условие P и условие Q).

Exemple 1: si E est l’ensemble des entiers naturels inférieurs à 10, A l’ensemble des elements de E impairs, et B l’ensemble des elements de E premiers A ∩ B est l’ensemble des éléments de E ухудшает премьер и :

A = {1, 3, 5, 7, 9}, B = {2, 3, 5, 7}, A ∩ B = {3, 5, 7}.

Пример 2: Пересечение ансамбля прямоугольников (quadrilatères ayant leurs quatre angles droits) и de l’ensemble des losanges (quadrilatères ayant leurs quatre côtés égaux) есть l’ensemble des carrés (quadrilatères quatre angles droits) et leurs quatre côtés égaux).

On définit de même l’intersection d’une classe quelconque d’ensembles (non nécessairement réduite à deux ensembles, ni même finie, ni même indexée par un ensemble: on demande seulement qu’elle soit non vide).

• L’intersection est associative, c’est-à-dire que, pour des ensembles A , B et C quelconques, on a:
  ( A ∩ B ) ∩ C = A ∩ ( B ∩ C ).
• L’intersection est commutative, c’est-à-dire que, pour des ensembles A et B quelconques, на:
  A ∩ B = B ∩ A .
• L’union est distributive sur l’intersection, c’est-à-dire que, pour des ensembles A , B et C quelconques, по адресу:
  A ∪ ( B ∩ C ) = ( A ∪ B ) ∩ ( A ∪ C ).

On généralise ce concept à une famille d’ensembles ( E _i ) _{i ∈ I} (без необходимости удалять ансамбли из двух частей, ni même finie). Пересечение E _и , примечание ∩ _{i ∈ I} E _и , является ансамблем коммуны E

231 и ( есть ансамбль видео, это перекресток и не проходит через определенное место в Абсолю).

Форма выпуска:

∀ Икс , Икс ∈ ⋂ я ∈ я Е я ⇔ ( ∀ я ∈ я , Икс ∈ Е я ) , {\ displaystyle \ forall x, \ quad x \ in \ bigcap _ {i \ in I} E_ {i} \ Leftrightarrow (\ forall i \ in I, \ x \ in E_ {i}).}

1. ↑ Pour être rigoureux, on devrait dire ici: «est un singleton»; l’abus «est un point» считается приемлемым.
2. ↑ Pour le démontrer, il suppit de supposer les cercles, centrés en A et B, sécants en M, et d’écrire les inégalités triangulaires в треугольнике ABM.

,

No related posts.