InScience
Математика и Computer Science
Задачи тысячелетия: гипотеза Римана
Автор: Анастасия Черкесова
Wikimedia Commons
Математический институт Клэя в 2000 году определил семь математических проблем тысячелетия как «важные классические задачи, решение которых не найдено вот уже в течение многих лет». За решение этих задач ученый может получить награду в размере одного миллиона долларов. На данный момент шесть из семи задач остаются нерешенными. Среди них — гипотеза Римана.
Начало математической карьеры
Выдающийся немецкий математик, механик и физик Бернхард Риман родился в 1826 году в городе Бразеленц в Германии. Он рос в небогатой семье священника. Учиться в местную школу мальчик отправился поздно — в 14 лет. Вскоре после этого в семье будущего математика произошла страшная трагедия: мать и две сестры Бернхарда умерли от туберкулеза. Для юноши это стало сильным ударом.
Уже со школьной скамьи Бернхард начал интересоваться не только математикой, но и точными науками в целом. Несмотря на это, в 1846 году под влиянием отца Риман поступил в Геттингенский университет, где должен был изучать филологию и богословие, которые совершенно не были интересны молодому человеку. В университете ему удалось прослушать лекции Карла Фридриха Гаусса — одного из величайших математиков всех времен. После этого Бернхард Риман твердо решил посвятить свою жизнь математике.
В следующем 1847 году будущий ученый поступил в Берлинский университет, который считался главным в Германии. Здесь он посещал лекции таких выдающихся преподавателей, как Дирихле, Якоби и Штейнер. Еще через пару лет Риман возвращается в Геттингенский университет, где знакомится и начинает близкую дружбу с физиком Вильгельмом Вебером, а также математиком Рихардом Дедекиндом.
Наконец, в 1851 году Риман защитил диссертационную работу на тему «Основания теории функций комплексной переменной». Именно в этом труде он впервые вывел понятие, которое позже получит название «риманова поверхность».
Она позволяет геометрически представить функции комплексной переменной. Риман будет и дальше изучать поверхности такого рода и их свойства.
С 1854 года Бернхард работает в Геттингенском университете. В 1857 году Риман, желая получить должность экстраординарного профессора, выступил с докладом перед всем профессорско-преподавательским составом университета на тему «О гипотезах, лежащих в основании геометрии». Именно эта работа положила начало римановой геометрии, а ее публикация (уже после смерти ученого) стала эпохальным событием в истории математики. Но на должность Римана так и не утвердили.
Одна из самых сложных загадок тысячелетия
В 1859 году Бернхард стал ординарным профессором и начал читать лекции по математике. Вскоре он отправился в Берлинский университет вместе с Дедекиндом, где прочитал свою работу «О числе простых чисел, не превышающих заданной величины». Благодаря ей Римана избрали членом Берлинской академии наук.
В этом исследовании ученый сформулировал интегральное представление дзета-функции Римана:
ζ(s) = 1–s + 2–s + 3–s + …
На основе этого исследования Риман представил гипотезу, которую уже более 160 лет никто не может доказать.
Звучит она так: «Все нетривиальные нули дзета-функции имеют вещественную часть, равную ½». Это означает, что дзета-функция равна нулю или в отрицательных четных числах (такие нули называются тривиальными), или в комплексных числах с вещественной частью ½.
Многие математические и физические задачи оказываются связаны с гипотезой Римана. Одна из них — распределение простых чисел на числовой прямой (то есть количество простых чисел меньше какого-либо заданного числа). Если в комплексной плоскости провести линию из точек с вещественной частью ½ и отметить на ней нули дзета-функции (в соответствие с гипотезой они все окажутся на этой линии), то получившийся рисунок должен быть связан с распределением простых чисел на числовой прямой.
Пока что официального доказательства или опровержения этой гипотезы нет, однако британский математик Майкл Атья, лауреат Филдсовской премии (1966) в 2018 году заявил, что нашел доказательство. Оно совсем небольшое: всего 15 строк, а вместе со списком литературы — пять страниц.
Пока что доказательство не подтверждено, однако, если это произойдет, Атья получит награду в размере одного миллиона долларов и впишет свое имя в историю математики.
Подписывайтесь на InScience.News в социальных сетях: ВКонтакте, Telegram
Тэги #ICM2022
Главные математические задачи XX века — некоторые из них до сих пор не решены
В 1900 году прошел II Международный конгресс профессоров математических и физических наук. Профессор Давид Гильберт выдвинул основные задачи математического мира, которые необходимо решить. На рубеже XX и XXI века практически все проблемы были решены, а некоторые автоматически выпали из-за неточной формулировки.
В XXI веке институт Клэя на конгрессе в Париже выдвинули новый список из семи задач, которые требуется решить математикам и физикам нашего времени. К ним относились гипотеза Римана, гипотеза Пуанкаре и другие.
Некоторые задачи так и остаются нерешенными по сей день. Университет обещает выплатить премию $1 млн.
за решение теорий и гипотез. Представляем обзор задач тысячелетия, которые до сих пор остаются крепкими орешками!
Равны ли классы P и NP
Задача относится к области теории алгоритмов, свое начало положила в 1970 году и до сих пор не решена.
Представьте, что начальник сказал вам заказать мебель в школу, компьютеры и спортивное оборудование. Вы заходите на сайт и начинаете изучать цены магазина. По указанию директора в список обязательны 150 парт, 20 компьютеров и 10 мячей, все остальное вы покупаете по желанию. Сколько вариаций? Множество. Конечный вариант проверить легко, но найти его сложно.
В теории алгоритмов задачи такого типа принадлежат классу сложности NP, они проверяются недолго. В класс P включены такие задачи, которые к тому же без труда находятся. Нерешенный вопрос заключается в том, равны или нет классы NP и P (и возможно ли найти легкие алгоритмы для ответа на задачу).
Есть гипотеза, что не все легко проверяемые задачи будут решаться просто.
Профессор Субит Чакрабарти утверждает, что поставленная задача будет решена в срок около пятидесяти лет.
Уравнения Навье – Стокса
Проблема относится к области гидродинамики и не решена уже около века.
Уравнения Навье – Стокса были получены в XIX веке. Они являются, чуть ли не самыми важными в аэродинамике и гидродинамике: с их помощью рассчитывается скорость потока, учитывая давление, плотность, вязкость и др. Проблема стоит в том, что в общем виде уравнения до сих пор никем не были решены.
Поставленную задачу ученые решают с особым энтузиазмом, потому что турбулентность — одна из загадок современности. Свои работы в этой области представили математик из Казахстана Мухтарбай Отелбаев и ученый из Узбекистана Шокир Довлатов (его решение еще поверяют).
Гипотеза Римана
Задача относится к области теории чисел, была выдвинута в 1859 году и до сих пор не решена.
В теории чисел и криптографическом алгоритме неотъемлемую составляющую играют простые числа.
Нарисовав на числовой оси положение простых чисел, можно наблюдать их неравномерность. Изучая данную проблему, математик Бернард Риман показал, что распределение напоминает точки, где дзета-функция равна нулю. Значение нуль функция приобретает при отрицательном четном значении. Также математик выявил, что нули наблюдаются там, где значение – комплексное число, которое содержит одну вторую.
В настоящее время даже с использованием высокотехнологичных компьютеров гипотеза Римана в общем виде до сих пор не решена.
Гипотеза Пуанкаре
Составляет область топологии и решена в 2002 году. Топология изучает свойства геометрических фигур, а также то, как их можно деформировать без порождений.
Если вы смастерите из пластилина пирамиду, то запросто без усилий сможете сделать конус. А если решите слепить бублик, то такую манипуляцию сделать не выйдет. Пуанкаре доказал, что замкнутая двухмерная поверхность гомеоморфна двухмерной сфере.
Гипотеза размерности 5 и 4 была доказана в 60-80-х годах XX века.
Сложнее всего было доказать гипотезу трехмерной фигуры — смог это в 2002 году ученый из Санкт-Петербурга Григорий Перельман.
Гипотеза Ходжа
Гипотеза относится к области алгебраической геометрии, сформулирована в 1941 году.
Математик из Шотландии Ходж выдвинул гипотезу, которая проверяет соответствие алгебраических множеств и уравнений. Но доказать верность его предположений обобщенно до сих пор не выходит, гипотеза подтверждается только для нескольких единичных случаев. Ученый Субит Чакрабати говорит: «Для подтверждения гипотезы нужно более тщательно освоить все составляющие алгебраической геометрии».
Теория Янга – Миллса
Задача входит в область математической физики, разработана в 50-х годах XX века.
Теория Янга – Миллса представляет собой ряд уравнений, предсказывающий поведение частиц. Его предположения – это попытка описать электромагнитное, слабое и сильное природное взаимодействие. К сожалению, доказано это частично.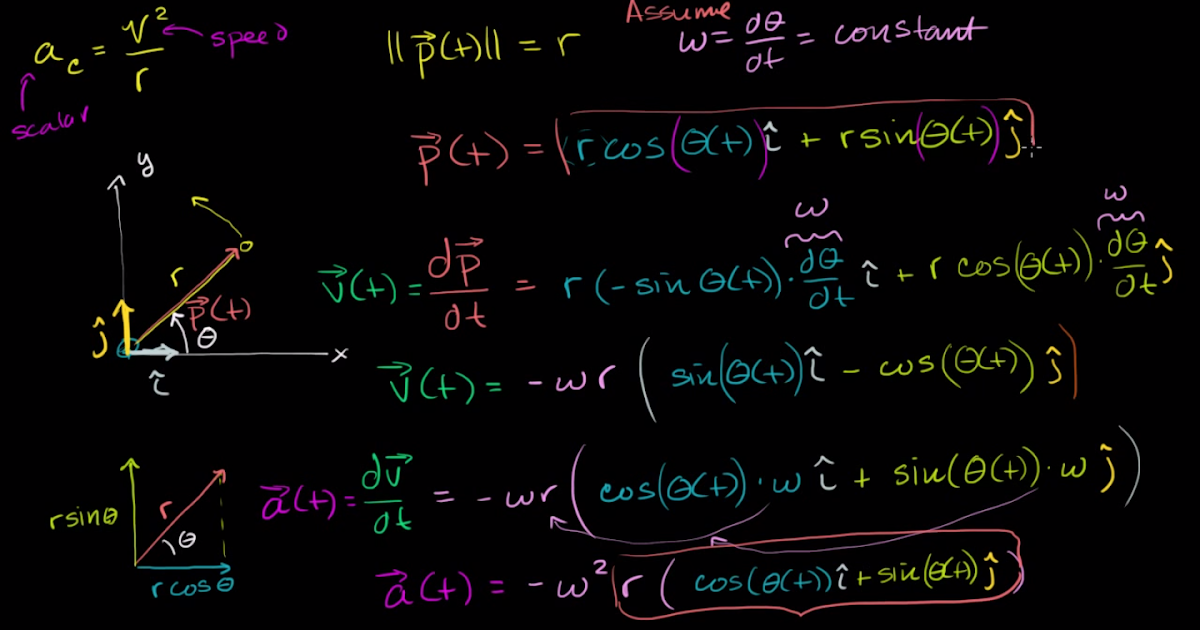
Учеными был создан прибор для описания электрослабого взаимодействия.
Чтобы решить задачу, нужно еще больше века и уникальные ученые-математики.
Гипотеза Бёрча – Свиннертон-Дайера
Относится к области алгебраической геометрии, выдвинута в 60-х годах XX века.
Ученые Питер Свиннертон-Дайер и Брайан Бёрч выдвинули следующую гипотезу: «Поведение L-функции в области 1 определяет множество решений эллиптической кривой». Доказать гипотезу получилось только в одном направлении, когда L(1) ≠ 0, тогда получается конечное количество точек. Смог это ученый Виктор Колывагин. В других направлениях гипотезу доказать не удается по сей день.
проблема существования и единственности Навье-Стокса
СЕРИЯ ПРЕМИИ ТЫСЯЧЕЛЕТИЯ: Проблемы премии тысячелетия — это семь математических задач, изложенных Математическим институтом Клэя в 2000 году. в результате институт присуждает премию в размере 1 000 000 долларов США.
Российский математик Григорий Перельман был удостоен премии 18 марта прошлого года за решение одной из задач — гипотезы Пуанкаре — пока единственной решенной проблемы.
Известно, что он отказался от премии тысячелетия в размере 1 000 000 долларов.
В ближайшие недели каждая из этих проблем будет освещена экспертами из организаций-членов Австралийского института математических наук (AMSI).
Здесь профессор Джим Деньер объясняет проблему существования и единственности Навье-Стокса. Наслаждаться.
Среди семи задач по математике, поставленных Математическим институтом Клэя в 2000 году, есть одна, фундаментальным образом связанная с нашим пониманием физического мира, в котором мы живем.
Это проблема существования и единственности Навье-Стокса, основанная на уравнениях, написанных в 19 веке.
Решение этой призовой задачи оказало бы глубокое влияние на наше понимание поведения жидкостей, которые, конечно же, вездесущи в природе. Воздух и вода — самые узнаваемые жидкости; то, как они двигаются и ведут себя, привлекало ученых и математиков с момента зарождения науки.
Но что такое так называемые уравнения Навье-Стокса? Что они описывают?
Уравнения
Чтобы понять уравнения Навье-Стокса и их вывод, нам нужна значительная математическая подготовка, а также хорошее понимание основ физики.
Без этого мы должны опираться на некоторые очень простые основы и говорить в общих чертах, но этого должно быть достаточно, чтобы дать читателю представление о том, как мы пришли к этим фундаментальным уравнениям, и о важности вопросов.
С этого момента я буду называть уравнения Навье-Стокса «уравнениями».
Уравнения, управляющие движением жидкости, проще всего описать как формулировку второго закона движения Ньютона, поскольку он применим к движению массы жидкости (будь то воздух, вода или более экзотическая жидкость). Второй закон Ньютона гласит:
Масса x Ускорение = Сила, действующая на тело
Для жидкости «масса» — это масса жидкого тела; «ускорение» — это ускорение конкретной частицы жидкости; «силы, действующие на тело» — это суммарные силы, действующие на нашу жидкость.
Не вдаваясь в подробности, здесь можно сказать, что Второй закон Ньютона выводит систему дифференциальных уравнений, связывающих скорость изменения скорости жидкости с силами, действующими на жидкость. Нам нужно, чтобы к нашей жидкости применялось еще одно физическое ограничение, которое проще всего можно сформулировать так:
Масса сохраняется! – т.е. жидкость не появляется и не исчезает из нашей системы.
Решение
Понимание того, что представляют собой уравнения Навье-Стокса, позволяет нам обсудить, почему решение Премии тысячелетия так важно. Задачу о призах можно разбить на две части. Первый фокусируется на существовании решений уравнений. Второй фокусируется на том, ограничены ли эти решения (остаются конечными).
Невозможно дать точное математическое описание этих двух компонентов, поэтому я попытаюсь поместить две части проблемы в физический контекст.
1) Чтобы математическая модель, какой бы сложной она ни была, представляла физический мир, который мы пытаемся понять, модель должна сначала иметь решения.
На первый взгляд это кажется несколько странным утверждением — зачем изучать уравнения, если мы не уверены, что они имеют решения? На практике мы знаем много решений, которые обеспечивают отличное согласование со многими физически значимыми и важными потоками жидкости.
Но эти решения являются аппроксимациями решений полных уравнений Навье-Стокса (аппроксимация возникает потому, что, как правило, нет простых математических формул – приходится прибегать к решению уравнений на компьютере с использованием численных аппроксимаций).
Хотя мы очень уверены, что наши (приблизительные) решения верны, формальное математическое доказательство существования решений отсутствует. Это обеспечивает первую часть задачи Премии Тысячелетия.
2) Вторая часть спрашивает, могут ли решения уравнений Навье-Стокса становиться сингулярными (или неограниченно расти).
Опять же, для объяснения этого требуется много математики. Но мы можем исследовать, почему это важный вопрос.
Есть старая поговорка, что «природа не терпит пустоты». Это имеет современную параллель в утверждении физика Стивена Хокинга о черных дырах, что «природа не терпит голой сингулярности». Сингулярность в данном случае относится к точке, в которой гравитационные силы, притягивающие объекты к черной дыре, становятся (согласно нашим современным теориям) бесконечными.
В контексте уравнений Навье-Стокса и нашей веры в то, что они описывают движение жидкостей в широком диапазоне условий, сингулярность указывает на то, что мы, возможно, упустили какую-то важную, пока еще неизвестную физику. Почему? Потому что математика не имеет дело с бесконечностями.
История гидромеханики изобилует решениями упрощенных версий уравнений Навье-Стокса, которые дают сингулярные решения. В таких случаях сингулярные решения часто намекают на какую-то новую физику, ранее не учитывавшуюся в упрощенных моделях.
Выявление этой новой физики позволило исследователям еще больше усовершенствовать свои математические модели и улучшить соответствие между моделью и реальностью.
Если, как многие считают, уравнения Навье-Стокса действительно имеют сингулярные решения, то, возможно, следующая премия тысячелетия достанется тому, кто обнаружит, какая именно новая физика требуется для устранения сингулярности.
Тогда природа сможет, как это уже делают все механики жидкости, прийти в восторг от уравнений, переданных нам Клодом-Луи Навье и Джорджем Габриэлем Стоксом.
Это первая часть серии наград тысячелетия. Чтобы прочитать другие части, перейдите по ссылкам ниже.
- Часть вторая: Премия тысячелетия: гипотеза Ходжа
- Часть третья: Премия тысячелетия: P vs NP
Задачи на премию тысячелетия. Карьера в математике
Издание 1670 года «Арифметики» Диофанта включает комментарии Ферма, в частности, его «Последнюю теорему».
В школе может показаться, что все математические задачи уже кем-то решены. В конце учебника всегда есть ответ или решение, которое может дать учитель.
Иногда математические проблемы могут оставаться нерешенными сотни лет, и люди задаются вопросом, возможно ли вообще доказательство. Так было в случае с последней теоремой Ферма, теоремой, впервые написанной в 1637 году французским математиком Пьером де Ферма.
Последняя теорема Ферма Теорема утверждает, что если n — целое положительное число больше 2, никакие другие положительные целые числа a, b и c не могут быть найдены так, чтобы a n +b n =c n . (Если n=2, существует множество значений a, b и c, которые работают. На самом деле мы рассматриваем теорему Пифагора!) |
Эндрю Уайлс
В 1995 году математик Эндрю Уайлс опубликовал доказательство последней теоремы Ферма, показав, что даже известные исторические нерешенные теоремы могут быть доказаны в наши дни.
Если вы хотите узнать больше о последней теореме Ферма, прочтите эту статью.
Чем больше вы будете изучать математику, тем больше вы поймете, что математика — обширный предмет, который всегда требует решения новых задач.
Однако есть некоторые особенно известные проблемы, которые все еще нуждаются в решении. Чтобы отпраздновать тысячелетие, Математический институт Клэя собрал семь из них вместе и предложил приз в размере 1 000 000 долларов тому, кто сможет найти решение любой из семи задач.
Проблемы тысячелетия 1. Гипотеза Пуанкаре 2. P по сравнению с NP 3. Гипотеза Ходжа 4. Гипотеза Римана 5. Существование Янга-Миллса и массовый разрыв 6. Существование и гладкость Навье-Стокса 7. Гипотеза Берча и Суиннертона-Дайера |
На данный момент решена только одна из семи задач на премию тысячелетия. В 2010 году российский математик Григорий Перельман доказал гипотезу Пуанкаре, которая является проблемой топологии, типа геометрии.