Matlab inline: (Not recommended) Construct inline object

Содержание

встроенных функций в Matlab | Руководство по встроенным функциям в Matlab

Встроенные функции в Matlab имеют две категории: одна — это встроенные функции, а вторая — используемые определенные функции, созданные пользователем.

Встроенные функции

Matlab имеет множество встроенных функций квадратного корня, sin, cos, tan, exponential, log и т. д. Он также имеет более сложные и специальные математические функции, такие как гамма-функции и функции Бесселя. Он также имеет некоторые встроенные константы pi, I (комплексные числа) и бесконечность.

Пример:

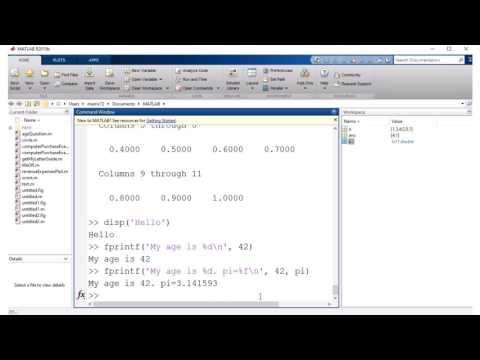
sin (pi / 2)

На выходе получается 1.

В этом примере мы даже не упомянули значение pi, автоматически pi принимает значение 3,14.

sqrt (3)

Выход 1,73.

И если написать оператор программы sqrt ( -1 ), он даст ответ как 0,00 + i

Пользовательские функции

Ключевое слово, используемое для определения нашей собственной функции, — «встроенная», теперь давайте посмотрим, как ее использовать. 92 – 6’, ‘х’) . . . . . . . . . . (1) объявление и определение функции
Fun =
встроенная функция :

Fun= – 6. . . . . . . вывод (1)

Fun (1) (2) дает значение x=1

Ans =

-5. . . .output of(2)

Fun ( 2 ) ....(3) дает значение x=2

Ans =

-2 . . . вывод (3)

Fun ( 3 ) . . . . . . . . . . . . . . . . . . . . (2) дает значение x=3 92 – 5 ’ , ’ x ’ )

Это создаст векторное веселье.

Веселье (1 : 5) И эволюция будет принимать значения x как 1, 2, 3, 4 и 5 первое значение соответствует x = 1 , второе значение соответствует x = 2 , третье значение соответствует x = 3 , четвертое значение соответствует x = 4 и пятое значение соответствует x = 5.

`Синтаксис встроенной функции`

Он состоит из трех частей: 93 + 23 * X - 9 >> z (1: 10)

ANS = столбцы с 1 до 3

15 45 87

Столбцы с 4 по 6

147 231 345

Столбцы с 7 по

495 687 927

Столбец 10

1221

>> Z (1: 0,5: 5)

ANS = столбцы с 1 до 4

15. 0000 28,8750 45.0000 64.1250

Столбцы 5–8

95.0000 64.1250

.0002 87.0000 114.3750 147.0000 185.6250

Столбец 9

231.0000

Заключение. Встроенные функции в Matlab

Встроенные функции являются глобальными, но они никогда не занимают рабочего пространства в Matlab. Он работает как анонимные функции, но это не анонимные функции, потому что анонимные функции занимают место во время создания функции. Встроенные функции возвращают только одно значение через систему, работающую с массивами и матрицами.

Funciones en Linea de Matlab (встроенные функции) — Хулио Эчеверри

Como ya sabemos Matlab Posee Grandes Campacidades en el ámbito científico, Hoy vamos a ver una cualidad más, y es el hecho de que matlab nos de que . creábamos una nueva función, esta debía ser declarada y escrita en un fichero con extensión .m y guardada en disco, esto es útil cuando una función has parte de un programa extenso e incluso la cantidad de código que debe escribirse es значительно, грех эмбарго, сено ocasiones donde necesitamos declarar algunas funciones cortas que se deben ejecutar de forma repetitiva, esto es, por ejemplo una función matemática tipo

f(x)=x*cos(x) , без значения vale la pena (si no es necesario) utilizar переменные simbólicas ya que esto hase que debido a la carga de procesamiento, nuestro programa vaya más lento.
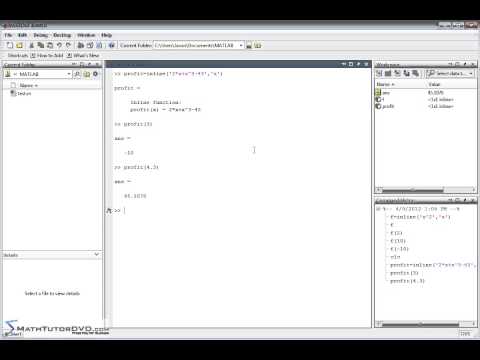
Matlab nos proporciona lo que conocemos como ‘ inline functions’ o en español como ‘ funciones en linea’ o ‘ de linea ‘, esto nos permite crear en la misma ventana de comandos, una corta función que puede ser llamada de forma repetida, supongamos que quiero hacer una función f(x) = sen(x)/x , entonces la sintaxis es la siguiente.

Como Pueden Ver, Solo Basta Con Poner El Nombre LA Función, Seguidamente El Signo Igual (=) y luego el comando inline (), De. De. De. De. De. De, De, De, inline (), De, De, De, dece. debe ser escrito entre comillas simples (‘ ‘ ) como si estuviésemos definiendo una cadena de caracteres. Así cuando ingresemos un valor, este será evaluado en la función y se retornará el valor reportivo al terminar la ejecución de la misma, por ejemplo.

Con Lo Передний nos ahorramos Entnons, Tener Que Reescribir esa expresión cada vez que la necesitemos evaluar o tener que un un ur in discales eviria evitia evitia evitia evitia evitia evitia efitmar2 las cuales para ser evaluadas o manipuladas requieren de una mayor cantidad de procesamiento por parte de Matlab, si tenemos en cuenta que necesitamos hacer muchas operaciones con dicha

Función, Entnonces LAS переменные Simbólicas Generarían Perdidas de Tiempo y Un мэр Esfuerzo Compustacional, LO Contrario Ocurre Si USAMOS Funciones Enea , Funciones en Linea , . () пункт оценки valores en ellas.

Existen unas reglas basicas para el uso efectivo de este typeo de funciones en Matlab y son las siguientes:

Математическое выражение содержит множество независимых переменных, f(x,y,z…,n).
Se puede usar cualquier letra como variable independiente, за исключением i y j (поддержка набора констант Matlab).
La expresión matemática puede contener cualquier función de Matlab или las que sean definidas por el usuario.

La expresión se debe escribir según la Dimensión de los argumentsos de entrada (por ejemplo operaciones elemento a elemento cuando se trabaja con vectores o matrix).
Выражение не включает предварительно определенные переменные в рабочей области (нет доступа к другим).
Una vez que se define la función, ésta puede ser usada tecleando su nombre y pasando sus argumentsos de entrada como en el ejemplo anterior.
Una funciones inline (или de linea ), también se puede usar como argumentso de entrada en otras funciones.

Модуля ejemplo vamos a definir la siguiente función de forma «inline».

Entonces procedemos a crear una función que llamaremos por ejemplo F y la declararemos inline como se ve en la siguiente figura.

Y evaluemos ahora esa función en un valor Arbitrio, esto se haría de la siguiente forma (cómo es de esperarse).

Встроенные функции с независимой переменной.

Se pueden también definir funciones con más de una variable independiente, y esto lo podemos lograr siguiendo el formato de definición de la siguiente figura.

Como podemos ver, lo único que se ha agregado son los nombres de los argumentsos de entrada , estos arguments se usan al interior de la expresión matemática, esto también define el orden en que setradeben ingresar de engreda da cuando la función va a ser invocada, por ejemplo, definamos una función que dependa de dos variable X y Y, entonces una definición posible sería la siguiente.