1.11 Решение систем линейных уравнений
MATLAB позволяет работать с объектами линейной алгебры, т. е. векторами и матрицами, настолько просто, насколько это вообще возможно.
Яркий пример этому – решение систем линейных уравнений.
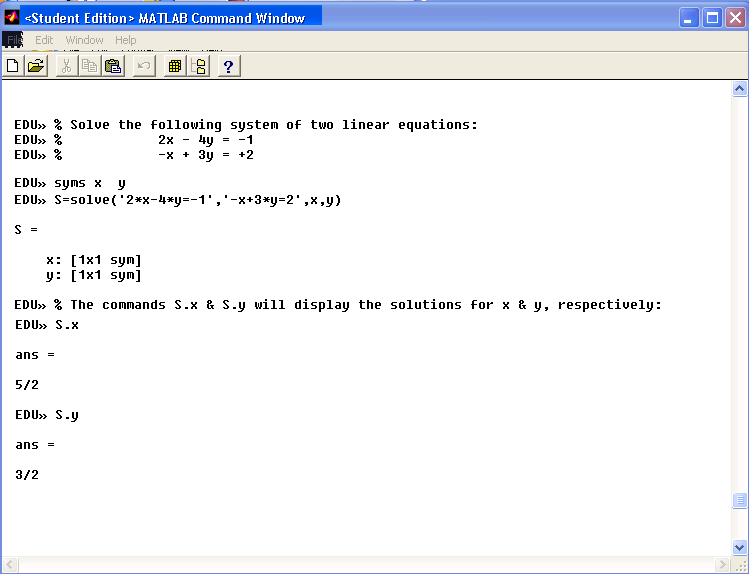
Пример:
Пусть дана система линейных уравнений
Решить систему с применением оператора обратного деления матриц < \ >.
Решение:
В матричной записи система имеет вид Ах = b, где
A = , b = , х =
– соответственно матрица из коэффициентов при незвестных, вектор-столбец из свободных членов и вектор-столбец из неизвестных.
Введем матрицу А и вектор-столбец свободных членов b:
>> А=[1 3 0;-2 -2 5;1 0 -5]
А =
1 3 0
-2 -2 5
1 0 -5
>> b=[-2;10;-9]
b =
-2
10
-9
Известно,
что система имеет единственное решение,
если определитель матрицы А не равен нулю (│A│ = det(A)
≠ 0). Вычислим определитель матрицы А:
Вычислим определитель матрицы А:
>> disp(det(A))
-5
Определитель не равен нулю. Находим решение системы с помощью оператора обратного деления матриц < \ >:
>> x=А\b
x =
1
-1
2
Проверим полученное решение x1 = 1, x2 = -1, x3 = 2 подстановкой в систему уравнений:
>> disp(A*x)
-2.0000
10.0000
-9.0000
В результате проверки получен вектор-столбец свободных членов. Значит, система решена верно.
Найдем теперь решение системы х = A-1b с помощью обратной матрицы. Вначале вычислим обратную матрицу A-1:
>> A1=inv(A)
A1 =
-2.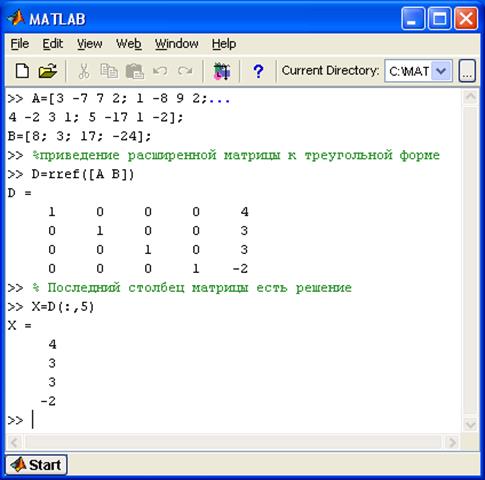 0000 -3.0000 -3.0000
0000 -3.0000 -3.0000
1.0000 1.0000 1.0000
-0.4000 -0.6000 -0.8000
Находим решение системы:
>> A1*b
ans =
-1.0000
2.0000
Отметим, что решение системы с помощью обратной матрицы требует больше времени и памяти, к тому же этот способ может дать большую погрешность решения. Поэтому для решения линейных систем рекомендуется применять оператор обратного деления < \ >.
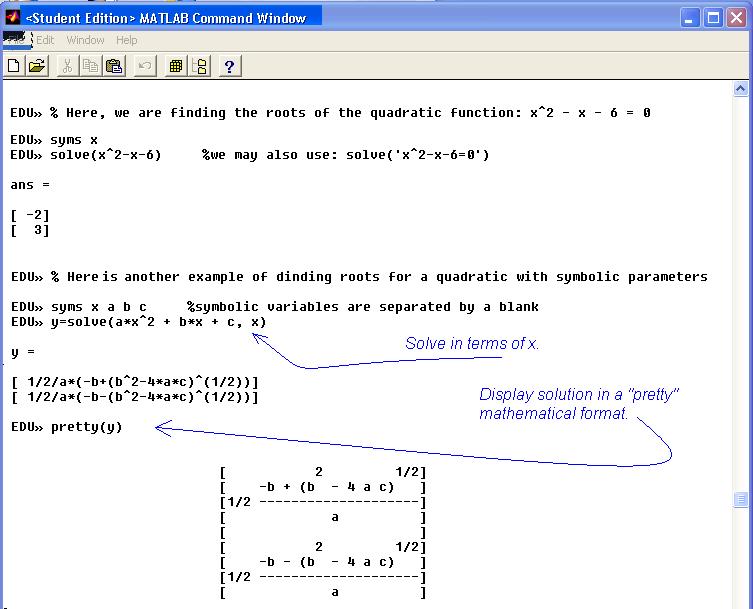
Пример:
Решить систему линейных уравнений
Решение:
>> A=[1 3 0;-2 -2 5;1 0 5]
A =
1 3 0
-2 -2 5
1 0 5
>> b=[-2 10 -9]
b =
-2 10 -9
>> disp(det(A))
35
Находим решение системы:
>> x=A\b’
x = -7.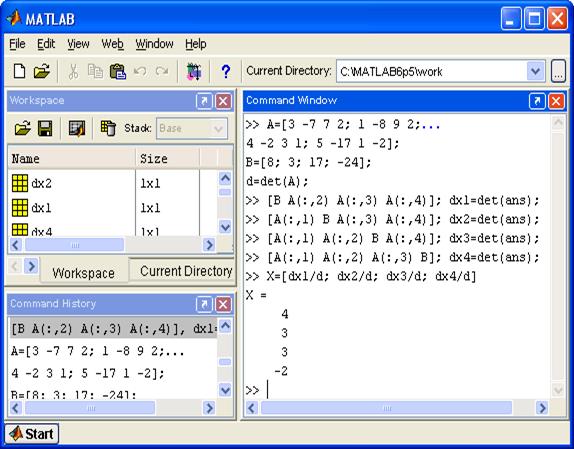 5714
5714
1.8571
-0.2857
Заметим, что обратное деление произведено на вектор-столбец b‘, поскольку вектор b введен как вектор-строка. Получили приближенное решение системы. Вычислим обратную матрицу A-1:
>> disp(inv(A))
-0.2857 -0.4286 0.4286
0.4286 0.1429 -0.1429
0.0571 0.0857 0.1143
Точное решение системы и точная обратная матрица выражаются через рациональные дроби:
>> format rat
>> x=A\b’
x =
-53/7
13/7
-2/7
>> disp(inv(A))
-2/7 -3/7 3/7
3/7 1/7 -1/7
2/35 3/35 4/35
1. Какие окна имеет интерфейс MATLAB и каково
их назначение
Какие окна имеет интерфейс MATLAB и каково
их назначение
2. Какова структура командного окна Command Window
3. Как называется отображение в командном окне сеанса работы с системой На какие зоны подразделяется текстовое поле окна Command Window
4. Для чего служат в MATLAB клавиши <↑> и <↓>
5. Для чего применяется команда disp
6. Как можно ввести слишком длинную команду в окне C ommand Window
7. Какая информация сохраняется в окнах Command History и Workspase после применения команды очистки экрана clc
8. Как получить справку по выбранной команде MATLAB
9. В каких форматах представляются в MATLAB вещественные числа
10. Какие форматы отображения вещественных
чисел используются в MATLAB
Какие форматы отображения вещественных
чисел используются в MATLAB
11. Как в в MATLAB осуществляются операции с комплексными числами
12. В чем измеряются аргументы встроенных тригонометрических функций
13. Какая команда осуществляет векторизацию символьного выражения
14. Как MATLAB реагирует на ошибки ввода
15. Как обнаружить и устранить семантическую ошибку ввода
16. Как в MATLAB создаются векторы и матрицы
17. Как осуществляется просмотр и редактирование переменных в окне Workspase
18. Как в MATLAB осуществляются матричные и поэлементные операции над векторами и матрицами
19. Что вычисляют команды dot и cross
20. Как решается система линейных уравнений с помощью оператора обратного деления < \ >
лаба 5 (Решение уравнений и систем уравнений в Matlab)
МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ»
им.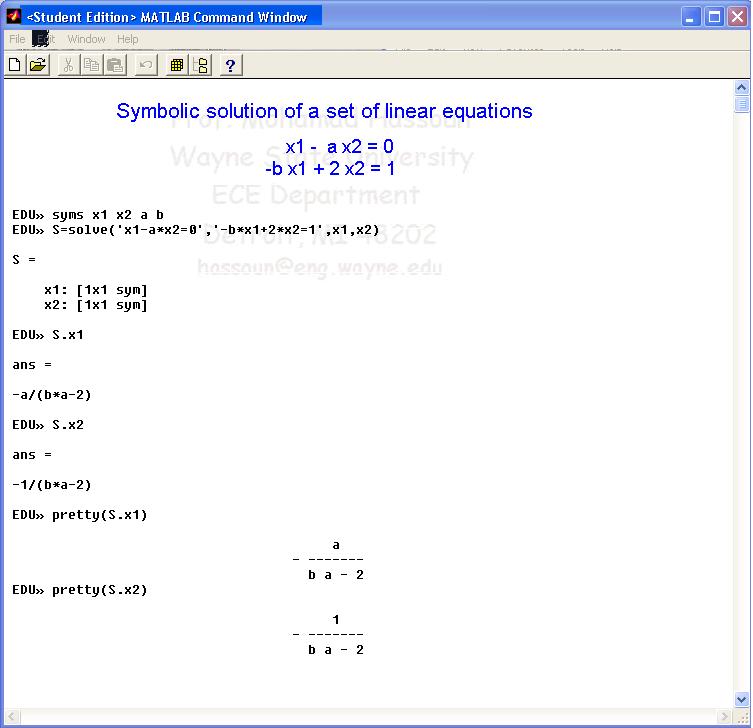 В.И. Ульянова (Ленина)
В.И. Ульянова (Ленина)
Кафедра ВТ
отчет
по лабораторной работе №5
по дисциплине «Информатика»
Тема: Решение уравнений и систем уравнений в Matlab.
Студентка гр. 9494 | Лобазев Н.А. | |
Преподаватель | Гречухин М.Н. |
Санкт-Петербург
2019
Цель работы 2
Основные теоретические положения 3
Вывод 11
Научиться решать уравнения и системы линейных уравнений в Matlab.
Требования и рекомендации к выполнению задания:
Нумерация
вариантов соответствует номеру
студенческого билета. При этом 9-й билет
решает 1 вариант, 10й – 2й вариант, 11й –
3й и так далее.
При этом 9-й билет
решает 1 вариант, 10й – 2й вариант, 11й –
3й и так далее.
Решить уравнение задана в таблице 4.1.
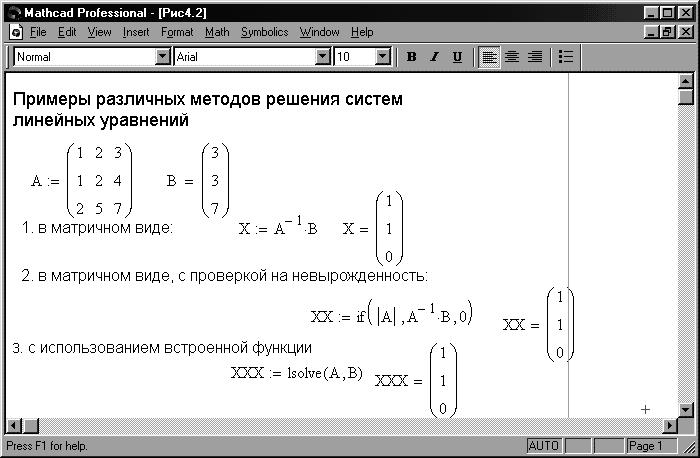
Решить систему уравнений, заданную в таблице 4.2 методом обратной матрицы, Крамера и Гаусса. Вывести на экран все три результата и убедиться, что они совпадают.
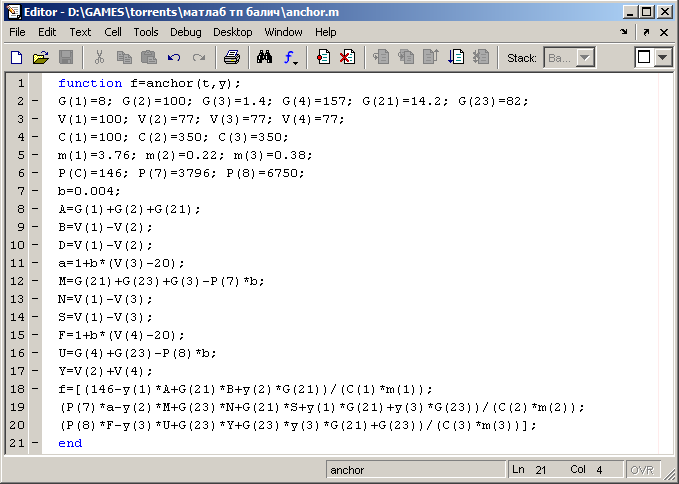
Решение уравнений вида
Для нахождения корней многочлена в Matlab используется функция roots. Полином задаётся в виде вектора коэффициентов при степенях , т. е. имеет вид .
Решение систем линейных уравнений
Система линейных алгебраических уравнений в самом общем случае имеет вид:
Для вычислений в Matlab удобно представлять такую систему в виде матрицы коэффициентов и вектора свободных членов :
Тогда систему (1) можно записать в виде:
где – вектор-столбец неизвестных.
Метод обратной матрицы.
Если , то тогда система (1) имеет единственное решение, которое выражается как
Таким образом, нам необходимо посчитать обратную матрицу для матрицы коэффициентов и перемножить её со столбцом свободных членов.
Метод Крамера.
Суть метода Крамера состоит в следующем. Если для представления системы уравнений (1.1) соблюдается условие , то система имеет единственное решение следующего вида:
и т. д., где
т. е. определитель матрицы А (1.1), в которой столбец заменён столбцом свободных членов .
Метод Гаусса.
Метод
Гаусса предполагает проведение
преобразований с так называемой
расширенной матрицей системы уравнений,
т. е. с матрицей вида с целью приведения её к виду
. Последний столбец будет содержать
значения неизвестных. Система будет
иметь единственное решение, когда
Последний столбец будет содержать
значения неизвестных. Система будет
иметь единственное решение, когда
В Matlab для решения систем уравнений методом Гаусса используется встроенная функция rref.
Ход работы.
Решение уравнений вида
Задание 1
f=[1 -15 78 -178 177 63]
f =
1 -15 78 -178 177 63
>> roots(f)
ans =
6.7223 + 0.0000i
4.9844 + 0.0000i
1.7827 + 1.9317i
1.7827 — 1.9317i
-0.2721 + 0.0000i
>>
Решение систем линейных уравнений
1. Метод обратной матрицы.
A=[3 -3 -1 5 -3; -1 3 4 0 -1; 3 5 3 4 3; 3 -2 -4 1 4; -1 2 4 -4 3]
A =
3 -3 -1 5 -3
-1 3 4 0 -1
3 5 3 4 3
3 -2 -4 1 4
-1 2 4 -4 3
>> b=[-2; 0; -5; -4; -4]
b =
-2
0
-5
-4
-4
>> x=inv(A)*b
x =
15. 4000
4000
8.8000
-5.4000
-11.8000
-10.6000
2.Метод Крамера.
A=[3 -3 -1 5 -3; -1 3 4 0 -1; 3 5 3 4 3; 3 -2 -4 1 4; -1 2 4 -4 3]
A =
3 -3 -1 5 -3
-1 3 4 0 -1
3 5 3 4 3
3 -2 -4 1 4
-1 2 4 -4 3
>> b=[-2; 0; -5; -4; -4]
b =
-2
0
-5
-4
-4
>> rank(A)
ans =
5
>> A1 = A
A1 =
3 -3 -1 5 -3
-1 3 4 0 -1
3 5 3 4 3
3 -2 -4 1 4
-1 2 4 -4 3
>> A2 = A
A2 =
3 -3 -1 5 -3
-1 3 4 0 -1
3 5 3 4 3
3 -2 -4 1 4
-1 2 4 -4 3
>> A3 = A
A3 =
3 -3 -1 5 -3
-1 3 4 0 -1
3 5 3 4 3
3 -2 -4 1 4
-1 2 4 -4 3
>> A4 = A
A4 =
3 -3 -1 5 -3
-1 3 4 0 -1
3 5 3 4 3
3 -2 -4 1 4
-1 2 4 -4 3
>> A5 = A
A5 =
3 -3 -1 5 -3
-1 3 4 0 -1
3 5 3 4 3
3 -2 -4 1 4
-1 2 4 -4 3
>> A1(:,1) = b
A1 =
-2 -3 -1 5 -3
0 3 4 0 -1
-5 5 3 4 3
-4 -2 -4 1 4
-4 2 4 -4 3
>> A2(:,2) = b
A2 =
3 -2 -1 5 -3
-1 0 4 0 -1
3 -5 3 4 3
3 -4 -4 1 4
-1 -4 4 -4 3
>> A3(:,3) = b
A3 =
3 -3 -2 5 -3
-1 3 0 0 -1
3 5 -5 4 3
3 -2 -4 1 4
-1 2 -4 -4 3
>> A4(:,4) = b
A4 =
3 -3 -1 -2 -3
-1 3 4 0 -1
3 5 3 -5 3
3 -2 -4 -4 4
-1 2 4 -4 3
>> A5(:,5) = b
A5 =
3 -3 -1 5 -2
-1 3 4 0 0
3 5 3 4 -5
3 -2 -4 1 -4
-1 2 4 -4 -4
>> x1 = det(A1) / det(A)
x1 =
15. 4000
4000
>> x2 = det(A2) / det(A)
x2 =
8.8000
>> x3 = det(A3) / det(A)
x3 =
-5.4000
>> x4 = det(A4) / det(A)
x4 =
-11.8000
>> x5 = det(A5) / det(A)
x5 =
-10.6000
>> x=[x1;x2;x3;x4;x5]
x =
15.4000
8.8000
-5.4000
-11.8000
-10.6000
3.Метод Гаусса.
A=[3 -3 -1 5 -3; -1 3 4 0 -1; 3 5 3 4 3; 3 -2 -4 1 4; -1 2 4 -4 3]
A =
3 -3 -1 5 -3
-1 3 4 0 -1
3 5 3 4 3
3 -2 -4 1 4
-1 2 4 -4 3
>> b=[-2; 0; -5; -4; -4]
b =
-2
0
-5
-4
-4
>> C = [A b]
C =
3 -3 -1 5 -3 -2
-1 3 4 0 -1 0
3 5 3 4 3 -5
3 -2 -4 1 4 -4
-1 2 4 -4 3 -4
>> D = rref(C)
D =
1. 0000 0 0 0 0 15.4000
0000 0 0 0 0 15.4000
0 1.0000 0 0 0 8.8000
0 0 1.0000 0 0 -5.4000
0 0 0 1.0000 0 -11.8000
0 0 0 0 1.0000 -10.6000
>> x = D(:,6)
x =
15.4000
8.8000
-5.4000
-11.8000
-10.6000
Я научился решать уравнения и системы уравнений в Matlab. По ходу работы у меня получилось так, что всеми 3 способами решения систем уравнений вышли одинаковые ответы, получается, что я все сделал правильно.
MATLAB Tutor, часть 10
MATLAB Tutor, часть 10Репетитор MATLAB
Часть 10.
 Решение линейных задач
Системы
Решение линейных задач
СистемыПредположим, мы хотим решить линейную система
x 2y + z
= 0
2 года
8z = 8
-4x + 5y + 9z = -9
Мы можем решить эту систему за несколько способы в MATLAB; вы узнаете два из них в этой части и еще один в следующей часть.
- Сначала нам нужно сохранить коэффициенты
системы в матрице, а правый вектор в другой матрице.
Введите
A = [1 -2 1
0 2 -8
-4 5 9]
b = [0; 8; -9]и затем введите
X = A\b
Три числа, которые вы видите, являются значениями решения x , y и z .
- Вы можете легко проверить, решение правильное. Матричный продукт A умножить на X должно быть равно правая сторона b . Имеет ли это? Проверьте это.
- Если у вас есть символьная математика MATLAB
Toolkit, вы также можете использовать команду «решить» для решения вышеуказанной системы.
 Введите
Введитеsyms x y z
eq1 = ‘x — 2*y + z = 0’;
eq2 = ‘2*y — 8*z = 8’;
eq3 = ‘-4*x + 5*y + 9*z = -9’;
[x,y,z] = решить(eq1, eq2, eq3) - Если у вас есть система с
меньше уравнений, чем неизвестных, можно найти символьное решение для некоторых
переменных в терминах других, которые мы могли бы назвать «свободными» переменными.
Рассмотрим следующую систему из трех уравнений с четырьмя неизвестными.
x 2 года + г + 2н = 0
Мы можем вычислить x , y и z через w . Последняя запись в команде «решить» сообщает, для каких переменных нужно решить, и следовательно, какая переменная будет свободной. Введите
2 года 8z + w = 8
-4x + 5y + 9z — w = -9syms x y z w
eq1 = ‘x — 2*y + z + 2* w = 0’;
eq2 = ‘2*y — 8*z + w = 8’;
eq3 = ‘-4*x + 5*y + 9*z — w = -9’;
[x,y,z] = решить(eq1, eq2, eq3, ‘x,y,z’) - Попробуйте те же два метода
решение по системе
x + 4y + 3z = 10
2x + y z = -1
3x y 4z = 11О чем говорят результаты? Мы рассмотрим этот пример более внимательно в следующей части.

| модули на math.duke.edu | Copyright CCP и автор(ы), 1999 г. |
Решение системы линейных уравнений в Matlab
Позвольте мне объяснить как решить систему линейных уравнений в Matlab . Видите ли, все дело в матричных и векторных вычислениях.
Позвольте мне привести практический пример для иллюстрации.
Рассмотрим эту систему двух линейных уравнений с двумя неизвестными.
$$ \begin{cases} x+5y-3 = 0 \\ \\ 2x-4y+8=0 \end{cases} $$
Обратите внимание, что система уравнений является линейной, когда наивысшая степень неизвестные равны 1.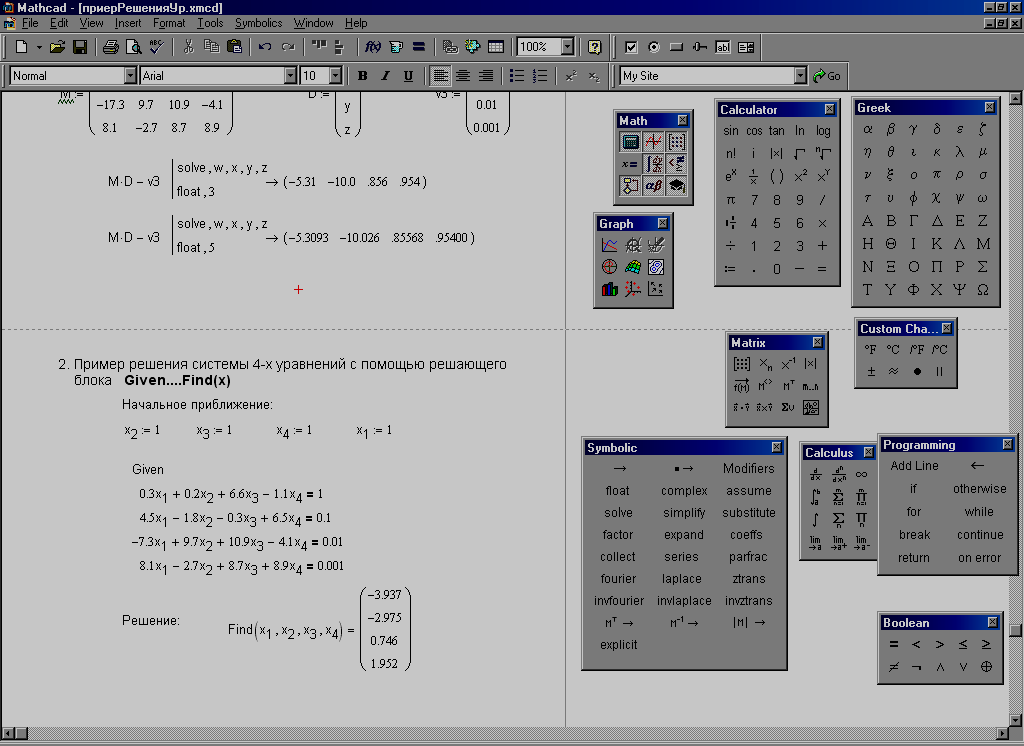
Мы можем переписать систему в стандартной форме ax+by=c, переместив константы в правую часть, а переменные в левую часть каждого уравнения.
$$ \begin{cases} x+5y=3 \\ \\ 2x-4y=-8 \end{cases} $$
Теперь мы можем преобразовать систему уравнений в векторную форму .
$$ \begin{pmatrix} 1 & 2 \\ 2 & -4 \end{pmatrix} \cdot \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 3 \\ -8 \end{pmatrix} $$
Матрица в левой части представляет собой матрицу с коэффициентами для неизвестных x и y.
$$ A = \begin{pmatrix} 1 и 2 \\ 2 & -4 \end{pmatrix} $$
Первый вектор — это вектор неизвестных .
$$ \vec{x} = \begin{pmatrix} x \\ y \end{pmatrix} $$
Последний вектор — это вектор констант из уравнений.
$$ \vec{b} = \begin{pmatrix} 3 \\ -8 \end{pmatrix} $$
Теперь давайте посмотрим, как преобразовать эту информацию в переменные в рабочей среде Matlab.
Чтобы определить матрицу коэффициентов в Matlab, мы создаем двумерный массив, набрав A = [1,2;2,-4] в командной строке.
>> А = [ 1 , 2 ; 5 , -4 ]
А =
1 2
5 -4
Чтобы определить постоянный вектор в Matlab, мы создаем одномерный массив bt, набрав b = [ 3 ; -8 ]
>> б = [ 3 ; -8 ]
б =
3
-8
Система уравнений в векторной форме представляет собой произведение матрицы и вектора.
$$ A \cdot \vec{x} = \vec{b} $$ 9{-1} \cdot \vec{b} $$
Символ A -1 является обратной матрицей матрицы коэффициентов A системы уравнений.
Чтобы решить систему уравнений, нам нужно найти обратную матрицу коэффициентов A, что мы можем сделать в Matlab, набрав inv(A) , а затем умножить ее на вектор констант b.
>> инв(А)*б
ответ =
-2
1
Результатом будет вектор неизвестных x.
$$ \vec{x} = \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} -2 \\ 1 \end{pmatrix} $$
Таким образом, мы имеем найдено решение системы уравнений .
$$ x=-2 $$
$$ y=1 $$
Итак, решением системы уравнений является x=-2 и y=1.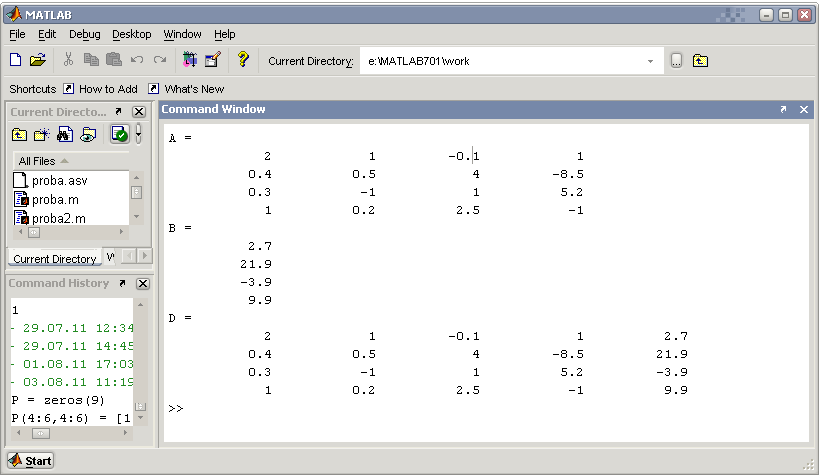

 Введите
Введите