Матриц на вектор умножение: Умножение матрицы на вектор, формула и примеры

НОУ ИНТУИТ | Лекция | Параллельные методы умножения матрицы на вектор

< Лекция 5 || Лекция 6: 1234567 || Лекция 7 >

Аннотация: В лекции рассматривается задача умножения матрицы на вектор. Приводится постановка задачи и последовательный алгоритм ее решения. Описываются методы разделения матрицы между процессорами вычислительной системы, которые необходимы для параллельной реализации матричных операций. Далее излагаются три возможных подхода к параллельной реализации алгоритма умножения матрицы на вектор

Ключевые слова: операции, матричные вычисления, математика, структуры хранения, метод матричных вычислений, перемножение матриц, параллелизм по данным, параллельные алгоритмы матричных вычислений, скалярное умножение, MPI, эффективность, ускорение, операции передачи данных, вычислительный эксперимент, EM64T, computer cluster, частичный результат, каскадная схема, программная реализация

Матрицы и матричные операции широко используются при математическом моделировании самых разнообразных процессов, явлений и систем. Матричные вычисления составляют основу многих научных и инженерных расчетов – среди областей приложений могут быть указаны вычислительная математика, физика, экономика и др.

С учетом значимости эффективного выполнения матричных расчетов многие стандартные библиотеки программ содержат процедуры для различных матричных операций. Объем программного обеспечения для обработки матриц постоянно увеличивается – разрабатываются новые экономные структуры хранения для матриц специального типа (треугольных, ленточных, разреженных и т.п.), создаются различные высокоэффективные машинно-зависимые реализации алгоритмов, проводятся теоретические исследования для поиска более быстрых методов матричных вычислений.

Являясь вычислительно трудоемкими, матричные вычисления представляют собой классическую область применения параллельных вычислений. С одной стороны, использование высокопроизводительных многопроцессорных систем позволяет существенно повысить сложность решаемых задач. С другой стороны, в силу своей достаточно простой формулировки матричные операции предоставляют прекрасную возможность для демонстрации многих приемов и методов параллельного программирования.

В данной лекции обсуждаются методы параллельных вычислений для операции матрично-векторного умножения, в следующей лекции ( «Параллельные методы матричного умножения» ) излагается более общий случай – задача перемножения матриц. Важный вид матричных вычислений – решение систем линейных уравнений – представлен в «Решение систем линейных уравнений» . Общий для всех перечисленных задач вопрос разделения обрабатываемых матриц между параллельно работающими процессорами рассматривается в первом подразделе лекции 6.

При изложении следующего материала будем полагать, что рассматриваемые матрицы являются плотными ( dense ), то есть число нулевых элементов в них незначительно по сравнению с общим количеством элементов матриц.

6.1. Принципы распараллеливания

Для многих методов матричных вычислений характерным является повторение одних и тех же вычислительных действий для разных элементов матриц. Данное свойство свидетельствует о наличии параллелизма по данным при выполнении матричных расчетов, и, как результат, распараллеливание матричных операций сводится в большинстве случаев к разделению обрабатываемых матриц между процессорами используемой вычислительной системы. Выбор способа разделения матриц приводит к определению конкретного метода параллельных вычислений; существование разных схем распределения данных порождает целый ряд параллельных алгоритмов матричных вычислений.

Наиболее общие и широко используемые способы разделения матриц состоят в разбиении данных на полосы (по вертикали или горизонтали) или на прямоугольные фрагменты ( блоки ).

1.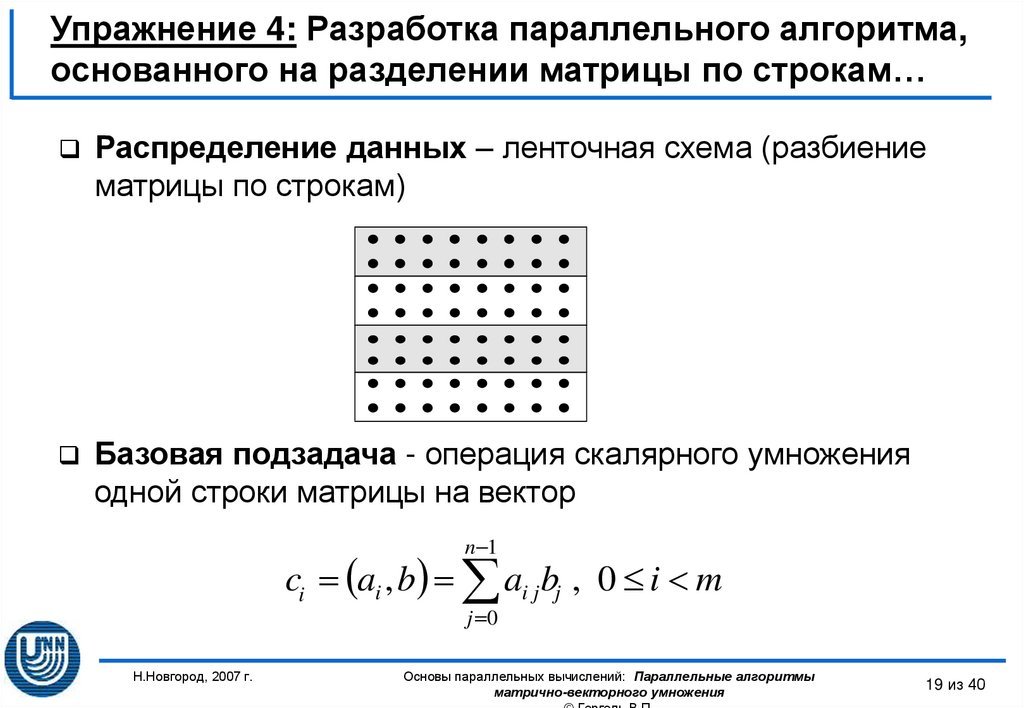 Ленточное разбиение матрицы. При ленточном ( block-striped ) разбиении каждому процессору выделяется то или иное подмножество строк ( rowwise или горизонтальное разбиение ) или столбцов ( columnwise или вертикальное разбиение ) матрицы (рис. 6.1). Разделение строк и столбцов на полосы в большинстве случаев происходит на

непрерывной ( последовательной ) основе. При таком подходе для горизонтального разбиения по строкам, например, матрица A представляется в виде (см. рис. 6.1)

( 6.1)

где a_i=(a_i1,a_i2,…,a_in), 0<=i<m, есть i -я строка матрицы A (предполагается, что количество строк m кратно числу процессоров p, т.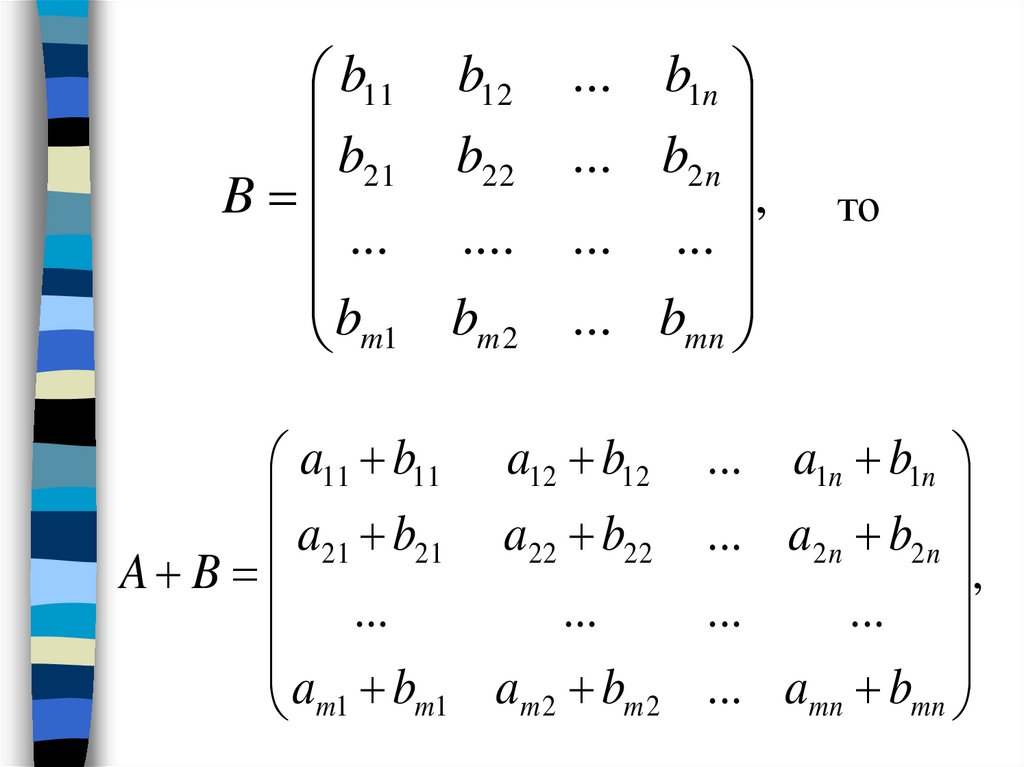 е. m = kxp ). Во всех алгоритмах матричного умножения и умножения матрицы на вектор, которые будут рассмотрены в этой и следующей лекциях, применяется разделение данных на непрерывной основе.

Другой возможный подход к формированию полос состоит в применении той или иной схемы чередования ( цикличности ) строк или столбцов. Как правило, для чередования используется число процессоров p – в этом случае при горизонтальном разбиении матрица A принимает вид

( 6.2)

Циклическая схема формирования полос может оказаться полезной для лучшей балансировки вычислительной нагрузки процессоров (например, при решении системы линейных уравнений с использованием метода Гаусса – см.

«Решение систем линейных уравнений» ).

2. Блочное разбиение матрицы. При блочном ( chessboard block ) разделении матрица делится на прямоугольные наборы элементов – при этом, как правило, используется разделение на непрерывной основе. Пусть количество процессоров составляет p = sxq, количество строк матрицы является кратным s, а количество столбцов – кратным q, то есть m = kxs и n = lxq. Представим исходную матрицу A в виде набора прямоугольных блоков следующим образом:

где A_ij — блок матрицы, состоящий из элементов:

( 6.3)

При таком подходе целесообразно, чтобы вычислительная система имела физическую или, по крайней мере, логическую топологию процессорной решетки из s строк и q столбцов.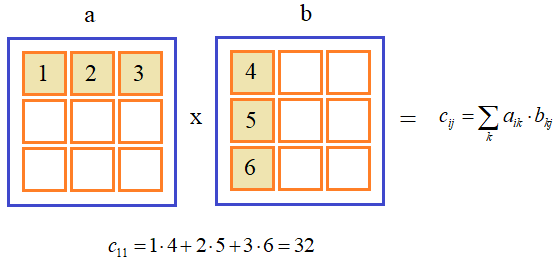

В этом случае при разделении данных на непрерывной основе процессоры, соседние в структуре решетки, обрабатывают смежные блоки исходной матрицы. Следует отметить, однако, что и для блочной схемы может быть применено циклическое чередование строк и столбцов.

В данной лекции рассматриваются три параллельных алгоритма для умножения квадратной матрицы на вектор. Каждый подход основан на разном типе распределения исходных данных (элементов матрицы и вектора) между процессорами. Разделение данных меняет схему взаимодействия процессоров, поэтому каждый из представленных методов существенным образом отличается от двух остальных.

Рис. 6.1. Способы распределения элементов матрицы между процессорами вычислительной системы

Дальше >>

< Лекция 5 || Лекция 6: 1234567 || Лекция 7 >

Векторы и матрицы в инструментарии Numpy

22. 02.2020Рубрика: 14 Инструментарий Numpy на языке PythonАвтор: Андрей Никитенко

Содержание страницы

• 1 Векторы и матрицы
• 2 Создание матриц для работы с ними
• 3 Произведение матриц
• 4 Другие операции с матрицами
• 5 Решение системы линейных уравнений
• 6 Текстовая задача

Векторы и матрицы

Здравствуйте и вновь добро пожаловать на занятия по теме «Инструментарий Numpy на языке Python».

В этой статье мы подробнее рассмотрим векторы, а также поговорим о матрицах.

Вы уже видели, насколько массивы Numpy похож на векторы: мы можем проводить над ними такие операции, как их сложение, умножение на скаляр, выполнять поэлементные операции вроде возведения в квадрат. А что с матрицами? Матрицу можно рассматривать как двухмерный массив. Согласно другому представлению, её также можно рассматривать как список списков. Действительно, можно использовать список списков, чтобы определить матрицу. Попробуем так и сделать.

Итак,первый список будет иметь элементы 1 и 2, второй список – элементы 3 и 4.Обратите внимание, что списки должны иметь одинаковую длину.

M = np.array([ [1,2], [3,4] ])

Считается,что первый индекс – это строка, второй – столбец. Для сравнения создадим такженастоящий список списков:

L = [ [1,2], [3,4] ]

Допустим,мы хотим получить элемент матрицы, скажем, единицу. В списке Python сначала индексируется строка, что даёт нам первыйсписок, содержащий 1 и 2:

L[0]

Итак,теперь у нас есть 1 и 2. Нам нужен первый элемент из этого списка, поэтому

L[0][0]

и получаем 1. Заметьте, то же самое можно сделать ис помощью массива Numpy:

M[0][0]

Этотакже даёт нам 1. Но есть и сокращённая запись, похожая на MATLAB, с использованием запятой:

M[0,0]

Иэто также даёт нам 1. Так несколько удобнее, поскольку нужно набрать на символменьше.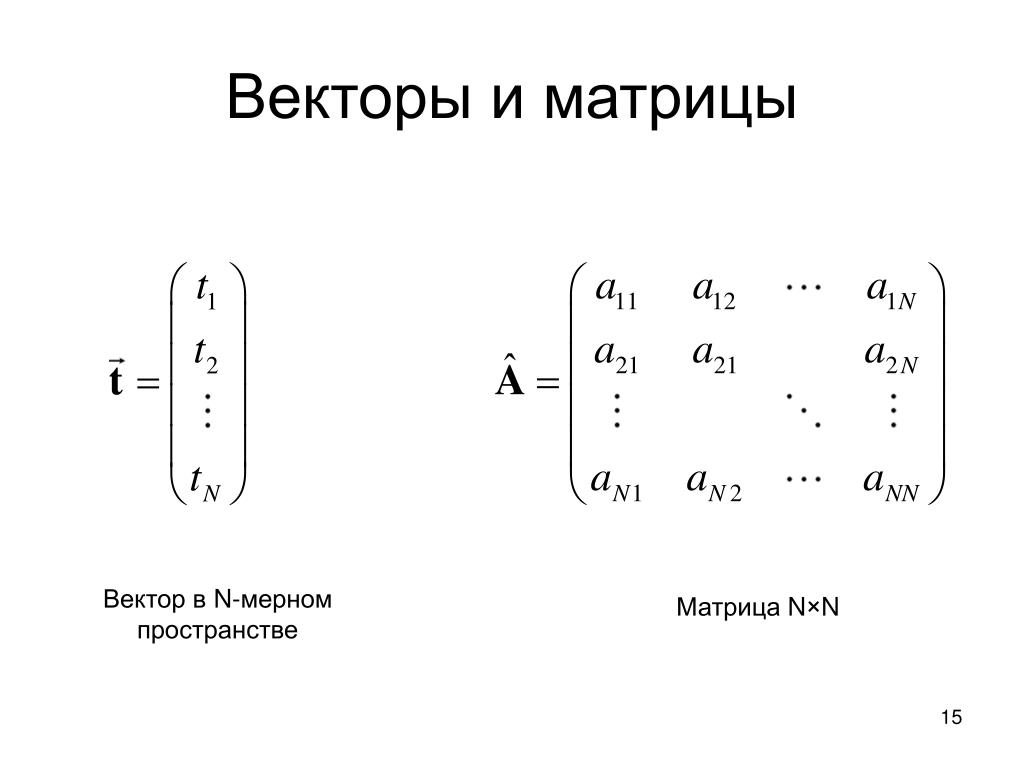

Обратитевнимание, что в Numpy есть типданных, который так и называется – матрица:

M2 = np.matrix([ [1,2], [3,4] ])

Получиласьматрица. Во многом матрица схожа с массивом Numpy,но есть и отличия. В большинстве случаев используются просто массивы Numpy; в действительности даже официальная документацияфактически рекомендует не пользоваться матрицами. Поэтому в данном курсе мы небудем заострять на них своё внимание. Увидев матрицу, имеет смысл преобразоватьеё в массив. Это можно сделать с помощью команды

A = np.array(M2)

Врезультате получим ту же матрицу, но в виде массива. Обратите внимание, что,хоть это и массив, мы можем пользоваться удобными матричными операциями, напримертранспонированием:

A.T

Врезультате получается транспонированная матрица A.

Резюмируем. Мы показали, что матрица на самом деле является лишь двухмерным массивом Numpy, а вектор – одномерным массивом Numpy. Таким образом, матрица на самом деле является двухмерным вектором. Обобщая, можно считать матрицу двухмерным математическим объектом, содержащим числа, а вектор – одномерным математическим объектом, также содержащим числа. Иногда встречается представление вектора в виде двухмерного объекта. Например, в учебниках по математике может указываться вектор-столбец размерности 3×1 и вектор-строка размерности 1×3. Временами мы также будем представлять их в таком виде в Numpy, но наличие двух размерностей делает такой объект более похожим на матрицу, что может сбить с толку. В таком случае просто помните, что обсуждаются лишь две вещи – одномерные и двухмерные массивы.

Создание матриц для работы с ними

Существуют некоторые различные способы генерации массивов данных.

Иногда нужны несколько массивов просто чтобы попрактиковаться – как в этом курсе. Один из способов вы уже видели, когда я воспользовался массивом Numpy для создания списка, например

np.array([1,2,3])

Заметьте,это не очень удобно, поскольку приходится вручную вставлять каждый элемент.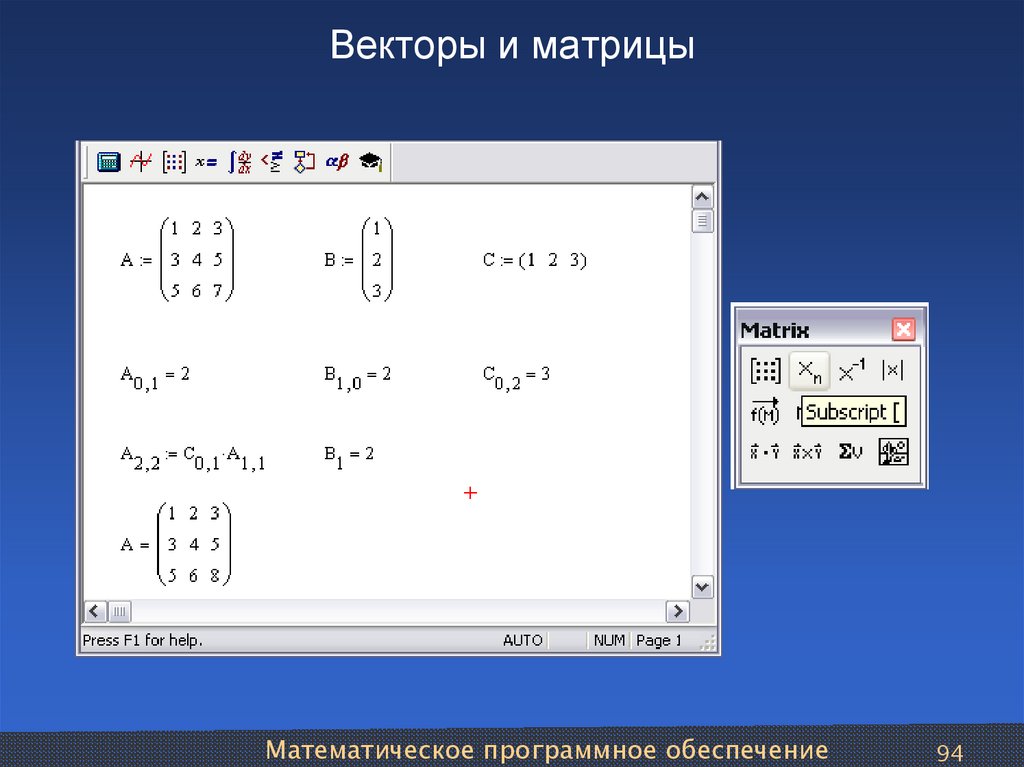 Аесли нужен массив с сотней элементов? А если нужно, чтобы он содержал случайныечисла? Поэтому в данной лекции будет показано, как можно создавать массивы.

Преждевсего я покажу, как создать массив, состоящих из одних нулей. Это делается спомощью функции zeros с указаниемдлины:

Z = np.zeros(10)

Этодаёт вектор с 10 элементами, состоящий из нулей. Можно создать и матрицуразмерности 10×10, состоящую из одних нулей:

Z = np.zeros((10, 10))

Врезультате получаем 100 нулей в матрице размерности 10×10.Обратите внимание, что функция по-прежнему принимает лишь один аргумент – кортеж,содержащий каждую размерность. Есть эквивалентная функция, создающая массив изодних единиц. К примеру,

O = np.ones((10, 10))

Получиласьматрица размерности 10×10, состоящая изодних единиц.

Теперь предположим, что нам нужен ряд случайных числен. Для этого можно воспользоваться функцией np.random.random. Создадим, к примеру, массив случайных чисел размерности 10×10:

R = np.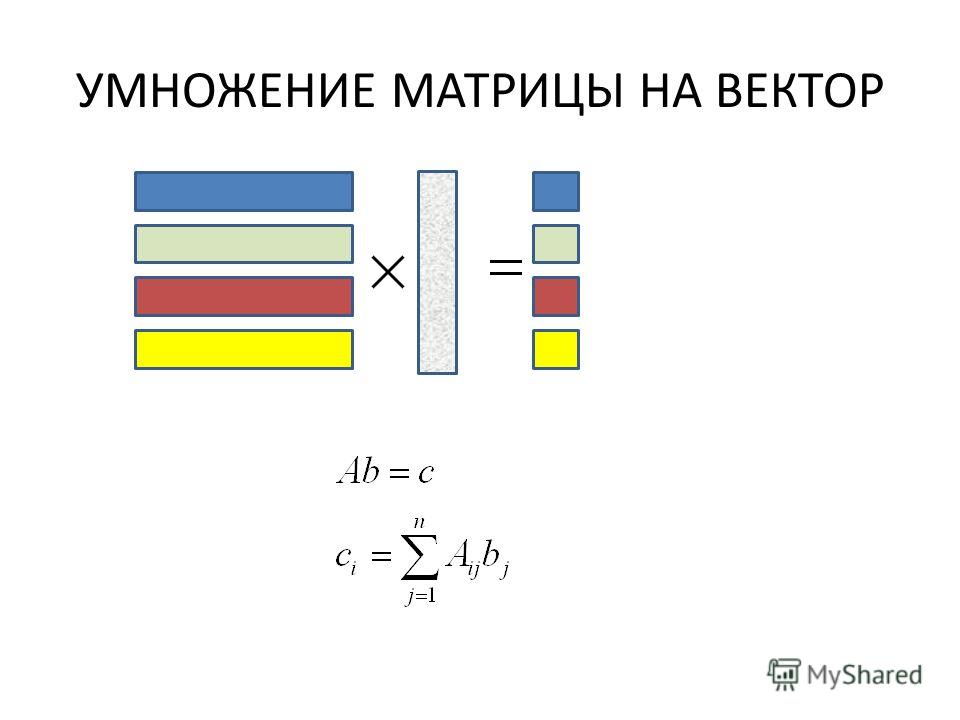 random.random((10,10))

Получилсянабор случайных чисел в матрице размерностью 10×10.Бросается в глаза, что все числа больше 0 и меньше 1. Это связано с тем, чтокогда речь идёт о случайных числах, имеется в виду распределение вероятностей,откуда и возникли случайные числа. Данная конкретная функция случайных чиселдаёт нам равномерно распределённые числа между 0 и 1. А если нам нужны числа сгауссовым распределением? В Numpy есть функция идля этого. Давайте попробуем. Называется она random.randn. Вновь-таки, возьмём размерность 10×10:

G = np.random.randn((10×10))

И у нас ничего не получилось – требуются целые числа. Сама функция правильна, но мы указали неправильный аргумент. Дело в том, что, как ни странно, функция randn библиотеки Numpy воспринимает каждую размерность как отдельный аргумент, в то время как все остальные упоминавшиеся функции принимают кортежи. Поэтому правильно вставлять – только для функции randn! – каждую размерность по отдельности:

G = np. random.randn(10,10)

Теперьвсё работает. Мы имеем числа с гауссовым распределением, средним значением 0 идисперсией 1. Массивы Numpy такжепредоставляют удобные функции для вычисления этих статистических величин. Так,команда

G.mean()

даёт нам среднее значение, а команда

G.var()

позволяет получить дисперсию.

Как видим, полученные числа весьма близки к истинным значениям.

Произведение матриц

Чтоинтересно в произведениях матриц при изучении линейной алгебры, – так это то, чтообычно называется умножением матриц. Умножение матриц имеет специальноетребование: внутренние размерности двух умножаемых матриц должны совпадать.Так, если у нас есть матрица A размерности 2×3и матрица Bразмерности 3×3, то мы можем умножить A на B, поскольку внутренняя размерность равна 3. Однакомы не можем умножить B на A, поскольку внутренняя размерность левого множителяравна 3, а внутренняя размерность правого равна 2.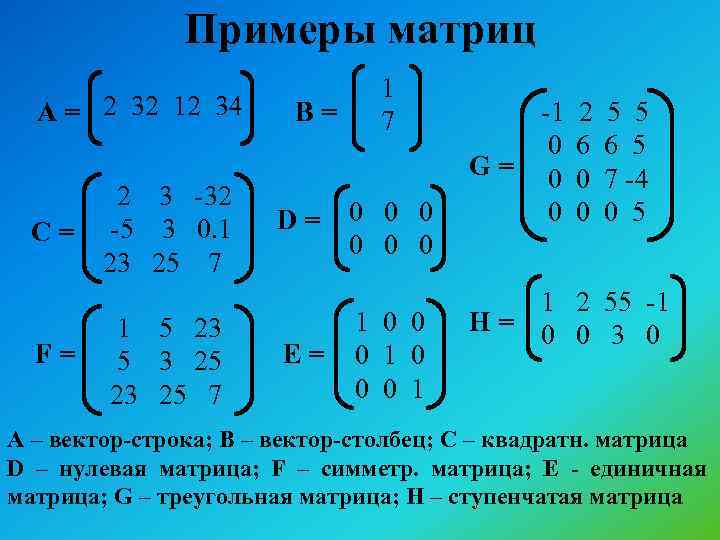

Возникаетвопрос: для чего существует такое требование при умножении матриц? Рассмотримопределение операции умножения матриц:

Тоесть ij-йэлемент матрицы Cравен сумме произведений всех соответствующих элементов из i-й строкиматрицы Aи j-гостолбца матрицы B.Другими словами, ij-йэлемент матрицы Cравен скалярному произведению i-й строки матрицы A и j-го столбца матрицы B. В связи с этим обычно используется функция dot библиотеки Numpy:

C = A.dot(B)

Этои будет умножением матриц.

Как в математике, так и в программировании часто встречается операция поэлементного умножения. В случае векторов мы уже видели, что для этого используется звёздочка (*). Как можно догадаться, в случае двухмерных массивов звёздочка также производит поэлементное умножение. Это означает, что при использовании звёздочки в случае многомерных массивов оба массива должны иметь в точности одинаковую размерность. Это может показаться странным, ведь в других языках звёздочка действительно означает настоящее умножение матриц. Но нужно просто запомнить, что для Numpy звёздочка означает поэлементное умножение, а функция dot – умножение матриц. Также сбивать с толку может то обстоятельство, что при записи математических уравнений нет даже чётко определённого символа для операции поэлементного умножения. Так, некоторые пользуются кружком с точкой внутри, а некоторые – кружком с крестиком внутри. Похоже, в математике просто не существует стандартной записи для данной операции, хотя она часто возникает в машинному обучении в связи с необходимостью использовать градиенты.

Другие операции с матрицами

В данном подразделе, я покажу вам некоторые другие операции с матрицами, которые позволяет библиотека Numpy. При этом предполагается, что вы уже знакомы с ними из курса линейной алгебры, а потому это будет скорее демонстрация того, как их реализовать в Numpy.

Начнёмс нахождения обратной матрицы. Вначале создадим матрицу:

A = np.array([[1,2],[3,4]])

Воспользуемсяфункцией inv модуля linalg:

Ainv = np.linalg.inv(A)

Мыполучили обратную матрицу. Чтобы проверить правильность ответа, умножим матрицу,обратную A,на саму А:

Ainv.dot(A)

Врезультате имеем единичную матрицу. Можем сделать и наоборот, умножив матрицу А на обратную ей:

A.dot(Ainv)

Итоже получаем единичную матрицу.

Следующее– нахождение определителя матрицы. Это можно сделать с помощью команды

np.linalg.det(A)

Каки ожидалось, получаем ответ -2.

Иногданужна диагональ матрицы, для этого используется команда

np.diag(A)

Врезультате имеем диагональные элементы в виде вектора. В других случаях у насесть вектор чисел, представляющий диагональ матрицы, остальные элементы которойсчитаются равными нулю. Чтобы представить такой вектор в виде двухмерногомассива, можно воспользоваться этой же функцией. Например,

np.diag([1,2])

Получим1 и 2 на диагонали, а остальные элементы – нули.

Этонадо запомнить: если подставить двухмерный массив в функцию diag, то получим одномерный массив из диагональныхэлементов; если же подставить одномерный массив, то получится двухмерныймассив, в котором все внедиагональные элементы равны нулю, а первоначальныймассив располагается на главной диагонали матрицы.

Бывает, что у нас есть два вектора, а нам нужно выполнить внешнее произведение. В частности, внешнее произведение возникает, когда мы вычисляем ковариацию ряда векторов-образцов. Мы уже знакомы с поэлементным произведением, для которого используется звёздочка, и скалярным произведением, для чего используется функция dot. Напомню, что скалярное произведение также называется внутренним произведением.

Итак,создадим два вектора:

a = np.array([1,2])

b = np.array([3,4])

Внешнеепроизведение вычисляется по команде

np. outer(a, b)

Можетепроверить правильность ответа. Обратите внимание, что можно выполнить ивнутреннее произведение с помощью команды

np.inner(a, b)

Этодаст тот же ответ, что и при использовании команды

a.dot(b)

Какимиз этих способов пользоваться – сугубо на ваше усмотрение.

Другаяраспространённая операция – нахождение следа матрицы. Это сумма элементовматриц, расположенных на главной диагонали. Заметьте, что мы можем выполнитьэту операцию, используя уже имеющиеся сведения:

np.dialog(A).sum()

Получиможидаемый ответ 5. Но в Numpy для этого естьи соответствующая функция:

np.trace(A)

Имы опять-таки получаем 5.

Ипоследнее, что мы обсудим, – это собственные значения и собственные векторы.Если вы не проходили их в курсе линейной алгебры, то, вероятно, вам следуетуглубить свои знания по этому предмету. Но сейчас я просто покажу, как всё это делаетсяв коде, поэтому если вы не знаете, что такое собственные значения и собственныевекторы, просто пропустите эту часть.

Частовозникает необходимость вычислить собственные значения и собственные векторысимметричной матрицы, такой как ковариационная матрица набора данных. Создадимслучайным образом определённые данные размерности 100×3с гауссовым распределением:

X = np.random.randn(100,3)

Обратитевнимание: считается, что каждый пример – это строка, а каждый признак – этостолбец, поэтому для данного конкретного вымышленного набора данных у насимеется 100 примеров и 3 признака. Разумеется, в Numpyуже есть функция для вычисления ковариации. Опробуем её:

cov = np.cov(X)

Проверимразмерность ковариационной матрицы, чтобы убедиться, что всё правильно.

cov.shape

Получилось,что размерность равна 100×100. Этонеправильная размерность, должно быть 3×3,ведь наши данные имеют размерность 3. Попробуем ещё раз, транспонировав X:

cov = np.cov(X.T)

Теперьразмерность 3×3. Нужно помнить, что при вычислении ковариационнойматрицы данных необходимо её сначала транспонировать.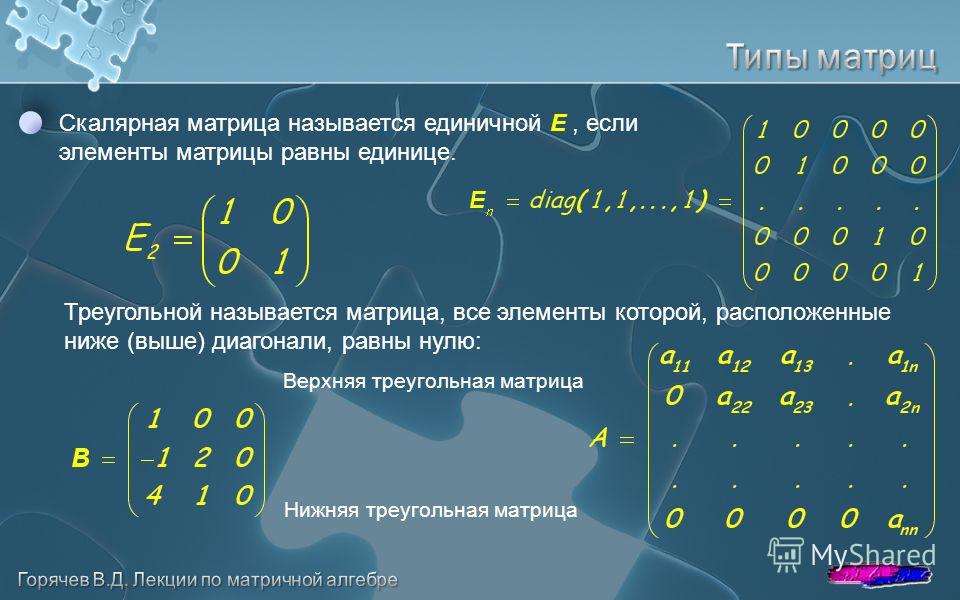

Длявычисления собственных значений и собственных векторов есть две функции – eig и eigh. Eigh предназначена только для симметричных и эрмитовыхматриц. Если вы никогда не изучали линейную алгебру комплексных чисел, небеспокойтесь о том, что такое эрмитова матрица. Симметричной называетсяматрица, которая, будучи транспонированной, остаётся равной сама себе:

Тоесть ij-йэлемент матрицы Cравен сумме произведений всех соответствующих элементов из i-й строкиматрицы Aи j-гостолбца матрицы B.Другими словами, ij-йэлемент матрицы Cравен скалярному произведению i-й строки матрицы A и j-го столбца матрицы B. В связи с этим обычно используется функция dot библиотеки Numpy:

C = A.dot(B)

Этои будет умножением матриц.

Как в математике, так и в программировании часто встречается операция поэлементного умножения. В случае векторов мы уже видели, что для этого используется звёздочка (*).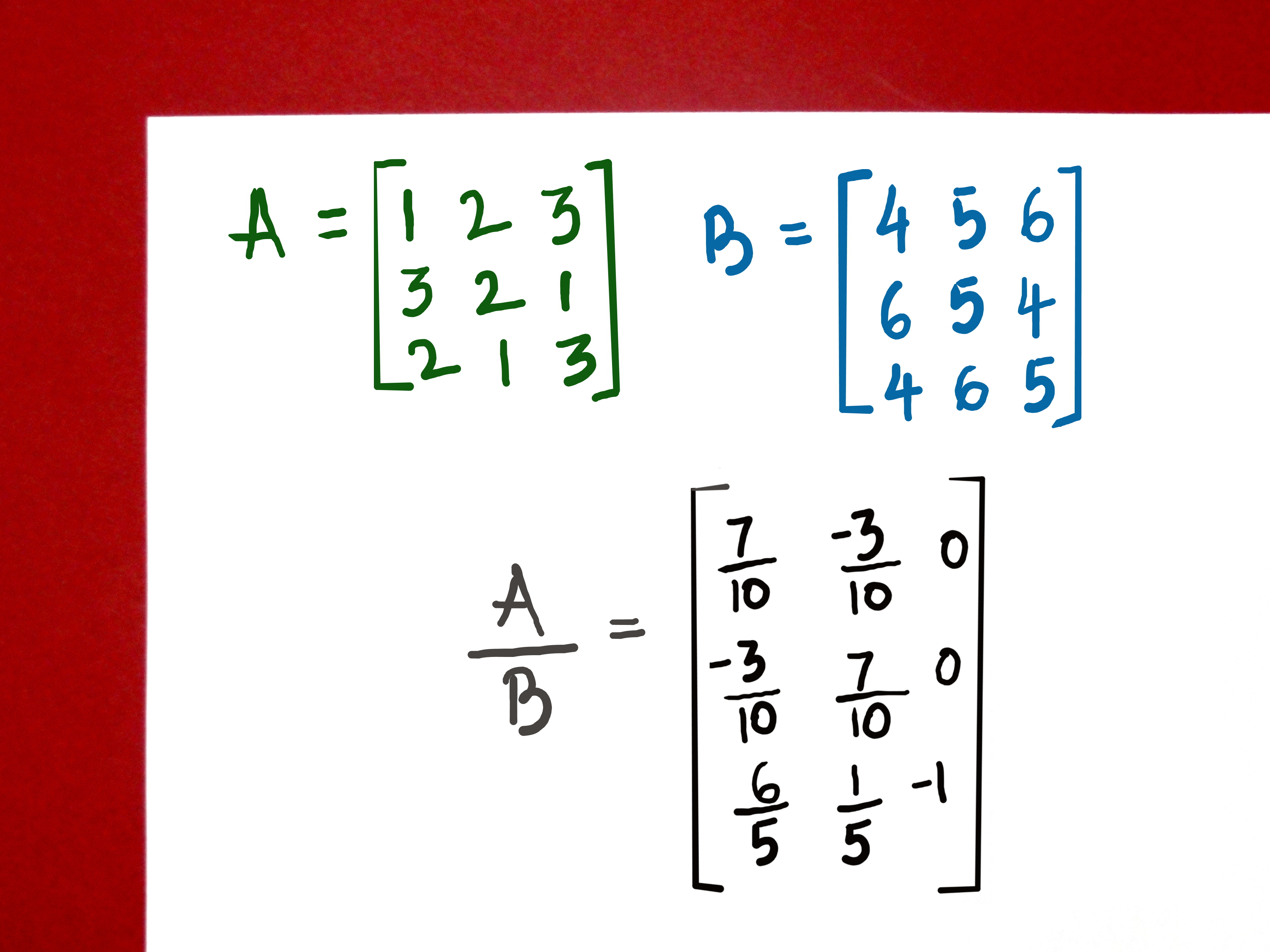 Как можно догадаться, в случае двухмерных массивов звёздочка также производит поэлементное умножение. Это означает, что при использовании звёздочки в случае многомерных массивов оба массива должны иметь в точности одинаковую размерность. Это может показаться странным, ведь в других языках звёздочка действительно означает настоящее умножение матриц. Но нужно просто запомнить, что для Numpy звёздочка означает поэлементное умножение, а функция dot – умножение матриц. Также сбивать с толку может то обстоятельство, что при записи математических уравнений нет даже чётко определённого символа для операции поэлементного умножения. Так, некоторые пользуются кружком с точкой внутри, а некоторые – кружком с крестиком внутри. Похоже, в математике просто не существует стандартной записи для данной операции, хотя она часто возникает в машинному обучении в связи с необходимостью использовать градиенты.

Другие операции с матрицами

В данном подразделе, я покажу вам некоторые другие операции с матрицами, которые позволяет библиотека Numpy. При этом предполагается, что вы уже знакомы с ними из курса линейной алгебры, а потому это будет скорее демонстрация того, как их реализовать в Numpy.

Начнёмс нахождения обратной матрицы. Вначале создадим матрицу:

A = np.array([[1,2],[3,4]])

Воспользуемсяфункцией inv модуля linalg:

Ainv = np.linalg.inv(A)

Мыполучили обратную матрицу. Чтобы проверить правильность ответа, умножим матрицу,обратную A,на саму А:

Ainv.dot(A)

Врезультате имеем единичную матрицу. Можем сделать и наоборот, умножив матрицу А на обратную ей:

A.dot(Ainv)

Итоже получаем единичную матрицу.

Следующее– нахождение определителя матрицы. Это можно сделать с помощью команды

np.linalg.det(A)

Каки ожидалось, получаем ответ -2.

Иногданужна диагональ матрицы, для этого используется команда

np.diag(A)

Врезультате имеем диагональные элементы в виде вектора. В других случаях у насесть вектор чисел, представляющий диагональ матрицы, остальные элементы которойсчитаются равными нулю. Чтобы представить такой вектор в виде двухмерногомассива, можно воспользоваться этой же функцией. Например,

np.diag([1,2])

Получим1 и 2 на диагонали, а остальные элементы – нули.

Этонадо запомнить: если подставить двухмерный массив в функцию diag, то получим одномерный массив из диагональныхэлементов; если же подставить одномерный массив, то получится двухмерныймассив, в котором все внедиагональные элементы равны нулю, а первоначальныймассив располагается на главной диагонали матрицы.

Бывает, что у нас есть два вектора, а нам нужно выполнить внешнее произведение. В частности, внешнее произведение возникает, когда мы вычисляем ковариацию ряда векторов-образцов. Мы уже знакомы с поэлементным произведением, для которого используется звёздочка, и скалярным произведением, для чего используется функция dot. Напомню, что скалярное произведение также называется внутренним произведением.

Итак,создадим два вектора:

a = np.array([1,2])

b = np.array([3,4])

Внешнеепроизведение вычисляется по команде

np.outer(a, b)

Можетепроверить правильность ответа. Обратите внимание, что можно выполнить ивнутреннее произведение с помощью команды

np.inner(a, b)

Этодаст тот же ответ, что и при использовании команды

a.dot(b)

Какимиз этих способов пользоваться – сугубо на ваше усмотрение.

Другаяраспространённая операция – нахождение следа матрицы. Это сумма элементовматриц, расположенных на главной диагонали. Заметьте, что мы можем выполнитьэту операцию, используя уже имеющиеся сведения:

np.dialog(A).sum()

Получиможидаемый ответ 5. Но в Numpy для этого естьи соответствующая функция:

np.trace(A)

Имы опять-таки получаем 5.

Ипоследнее, что мы обсудим, – это собственные значения и собственные векторы. Если вы не проходили их в курсе линейной алгебры, то, вероятно, вам следуетуглубить свои знания по этому предмету. Но сейчас я просто покажу, как всё это делаетсяв коде, поэтому если вы не знаете, что такое собственные значения и собственныевекторы, просто пропустите эту часть.

Частовозникает необходимость вычислить собственные значения и собственные векторысимметричной матрицы, такой как ковариационная матрица набора данных. Создадимслучайным образом определённые данные размерности 100×3с гауссовым распределением:

X = np.random.randn(100,3)

Обратитевнимание: считается, что каждый пример – это строка, а каждый признак – этостолбец, поэтому для данного конкретного вымышленного набора данных у насимеется 100 примеров и 3 признака. Разумеется, в Numpyуже есть функция для вычисления ковариации. Опробуем её:

cov = np.cov(X)

Проверимразмерность ковариационной матрицы, чтобы убедиться, что всё правильно.

cov.shape

Получилось,что размерность равна 100×100. Этонеправильная размерность, должно быть 3×3,ведь наши данные имеют размерность 3. Попробуем ещё раз, транспонировав X:

cov = np.cov(X.T)

Теперьразмерность 3×3. Нужно помнить, что при вычислении ковариационнойматрицы данных необходимо её сначала транспонировать.

Длявычисления собственных значений и собственных векторов есть две функции – eig и eigh. Eigh предназначена только для симметричных и эрмитовыхматриц. Если вы никогда не изучали линейную алгебру комплексных чисел, небеспокойтесь о том, что такое эрмитова матрица. Симметричной называетсяматрица, которая, будучи транспонированной, остаётся равной сама себе:

Эрмитова же матрица – это матрица, которая остаётся равной сама себе, будучи сопряжённой:

Какизвестно, ковариационная матрица является симметричной, поэтому можноиспользовать функцию eigh. Её ипопробуем:

np.linalg.eigh(cov)

Врезультате получаем кортежи. Первый содержит три собственных значения, а второй– собственные векторы, представленные в столбцах. Попробуем теперь с обычнойфункцией eig:

np.linalg.eig(cov)

Получаемтот же ответ. Обратите внимание, что обычная функция eigхоть и даёт тот же ответ, но полученные собственные значения и соответствующиесобственные векторы могут размещаться в другом порядке. В данном конкретномслучае порядок тот же, но есть вероятность, что он может поменяться.

На этом лекция заканчивается. Она довольно короткая, поскольку была создана для тех, кто уже знаком с математическим аппаратом, но ещё не знает, как его реализовать в Numpy.

Решение системы линейных уравнений

В заключение мы рассмотрим последнюю из самых распространённых операций с матрицами – решение системы линейных уравнений.

Напомню, что система линейных уравнений имеет вид

где A – матрица, x – вектор-столбец искомых значений, b – вектор чисел.Решение, конечно же, состоит в умножении обоих частей уравнений на матрицу,обратную A:

Этокорректная операция, поскольку предполагается, что A является квадратной матрицей, что значит, что онаобратима. Тогда xимеет единственное решение. Другими словами, если размерность x равна D, то у нас есть D уравнений с D неизвестными.

Тутне должно возникнуть никаких сложностей, поскольку у нас уже есть весьинструментарий, необходимый для такого рода вычислений. Вы уже видели, какнаходится обратная матрица и как производить умножение матриц, а именно эти двевещи нам и нужны.

Решимпример. Aу нас будет матрицей

Этокорректная операция, поскольку предполагается, что A является квадратной матрицей, что значит, что онаобратима. Тогда xимеет единственное решение. Другими словами, если размерность x равна D, то у нас есть D уравнений с D неизвестными.

Тутне должно возникнуть никаких сложностей, поскольку у нас уже есть весьинструментарий, необходимый для такого рода вычислений. Вы уже видели, какнаходится обратная матрица и как производить умножение матриц, а именно эти двевещи нам и нужны.

Решимпример. Aу нас будет матрицей

bу нас будет вектором [1, 2]:

b = np.array([1, 2])

Решениембудет

x = np.linalg.inv(A).dot(b)

Итак,решением являются числа 0 и 0,5. Для проверки попробуйте решить этот примервручную.

Конечно же, ввиду очень частого проведения такого рода вычислений, есть способ и получше – с помощью функции с соответствующим названием solve. Поэтому можно записать

x = np.linalg.solve(A, b)

Иполучим тот же ответ.

Если вы когда-либо прежде писали код в MATLAB, то могли заметить, что при попытке использовать метод inv MATLAB выдаёт предупреждение и сообщает, что есть и более эффективный способ вычислений. В MATLAB он называется не solve, но по сути это тот же самый алгоритм, и он действительно куда более эффективен и точен. Поэтому если у вас когда-нибудь возникнет необходимость решить подобного рода уравнение, никогда не пользуетесь inv. Всегда используйте solve.

Текстовая задача

Давайте разберём несложный пример, чтобы попрактиковаться в использовании функции solve.

Итак,поставим задачу. На небольшой ярмарке входная плата составляет 1,5 доллара для ребёнкаи 4 доллара для взрослого. Однажды за день ярмарку посетило 2200 человек; приэтом было собрано 5050 долларов входной платы. Сколько детей и сколько взрослыхпосетили ярмарку в этот день?

Итак,обозначим количество детей через X1, а количествовзрослых – через X2. Мы знаем, что

Мытакже знаем, что

Мытакже знаем, что

Обратите внимание, что это линейное уравнение, где A равно:

 а b равно :

 а b равно :

Подставимэти значения в Numpy и найдёмрешение:

A = np.array([[1,1], [1.5,4]])

b = np.array([2200, 5050])

np.linalg.solve(A, b)

Получаемответ: 1500 детей и 700 взрослых. Попробуйте также решить это уравнениевручную, чтобы проверить ответ.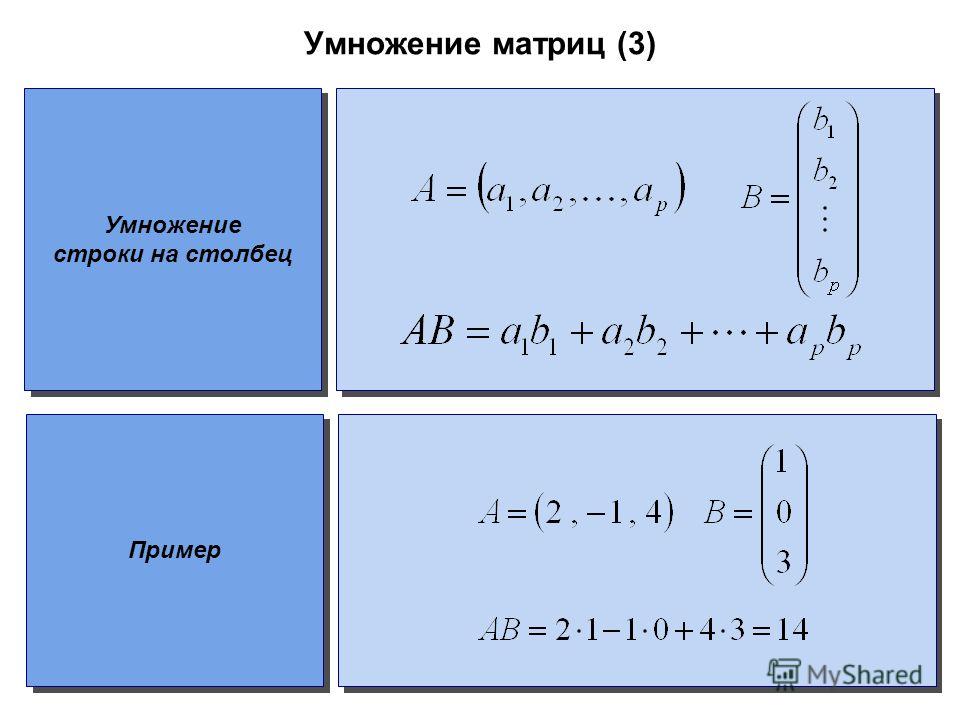

Получаемответ: 1500 детей и 700 взрослых. Попробуйте также решить это уравнениевручную, чтобы проверить ответ.

{T}_{4} & \horzbar \\ \конец{массив} \правильно]

и этот вектор:

 [\
\начать{выравнивать}
    у &= \begin{bmatrix}
           х_{1} \\
           х_{2} \\
           \vdots\\
           х_{м}
         \end{bmatrix}
\end{выравнивание}
\]
 

Но как показать умножение матрицы на вектор?

• матрицы

7

Следуя вероятному определению из Как набирать вертикальные и горизонтальные линии внутри матрицы? 9{T}_{4} & \horzbar \\ \конец{массив}\справа] \begin{bmatrix} х_{1} \\ х_{2} \\ \vdots\\ х_{м} \end{bmatrix} \\ {} &= \begin{bmatrix} б_{1} \\ Би 2} \\ \vdots\\ б_ {м} \end{bmatrix} \конец{выравнивание*} \конец{документ}

1

Вы можете использовать этот код, подставив вместо букв то, что хотите. {T}_{3} & \rule[.2ex]{1em}{0,2pt} \конец{массив} \справа]\cdot \левый[ \начать{массив}{с} х_1\\ х_2\\ \vdots\\ х_n \конец{массив} \правильно] \] \конец{документ}

3

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Матрица, вектор, умножение — Stack Overflow на русском В этом видео показан хороший пример расчета с помощью матриц.

Матрица A = товары, проданные за день (размер 5 x 3)

 c
             о
             о с
             к а р
             я к я
             э э э
             с с с
             
понедельник [ 3 5 3 ]
вторник [ 7 1 2 ]
среда [ 2 5 3 ]
четверг [ 5 4 0 ]
пятница [ 3 4 4 ]
 

Матрица B = Цена за единицу (размер 3 x 1)

 €
печенье [ 4 ]
торты [ 10 ]
пироги [ 8 ]
 

Чтобы иметь возможность умножать 2 матрицы, 2-е измерение 1-й матрицы ДОЛЖНО совпадать с 1-м измерением 2-й матрицы (5 x 3) * (3 x 1) (тройки должны совпадать) и это умножение даст матрицу 5 x 1 .

В этом примере мы умножаем матрицу (дней/товар) на матрицу (товаров/цена) и ожидаем получить матрицу (дни/цена), которая показывает, сколько мы зарабатываем в день.

Здесь сразу видно, почему количество столбцов первой матрицы должно совпадать с количеством строк второй матрицы.

Умножение

Чтобы умножить матрицы, мы сначала расположим их лучше:

 €
                        [ 4 ]
                        [ 10 ]
                        [ 8 ]
понедельник [ 3 5 3 ] [ ]
вторник [ 7 1 2 ] [ ]
среда [ 2 5 3 ] [ ]
четверг [ 5 4 0 ] [ ]
пятница [ 3 4 4 ] [ ]
 

Как показано ниже, каждый элемент результирующей матрицы представляет собой сумму следующих умножений:

 €
                      ---[ 4 ]
                    ╱ --[ 10 ]
                  ╱ ╱ -[ 8 ]
                ╱ ╱ ╱ |
              ╱ ╱ ╱ |
понедельник [ 3 5 3 ] [ ]
вторник [ 7 1 2 ] [ ]
среда [ 2 5 3 ] - [ 82 ]
четверг [ 5 4 0 ] [ ]
пятница [ 3 4 4 ] [ ]
 

Итак, для третьего элемента результат следующий:

 2 печенья * 4 €/печенье + 5 пирожных * 10 €/торт + 3 пирожных * 8 €/пирог = 82 €
 

Расширение примера

Если вы также хотите знать, сколько времени вы тратите на выпечку продуктов, которые вы продаете, вы также можете добавить эти числа во вторую матрицу:

 € мин.
No related posts.