a b матрица
a b матрицаВы искали a b матрица? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и a b найти, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «a b матрица».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как a b матрица,a b найти,i j матрица,reshish matrix,а матрица,все о матрицах,все о матрицах высшая математика,выполните действия над матрицами,выполнить действия над матрицами,выполнить действия над матрицами онлайн с решением,выполнить действия с матрицами,выполнить действия с матрицами онлайн с решением,высшая математика для чайников матрица,высшая математика для чайников матрицы,высшая математика матрица,высшая математика матрица для чайников,высшая математика матрица примеры,высшая математика матрицы,высшая математика матрицы для чайников,вычислить матричный многочлен,вышмат матрица,даны две матрицы а и в найти а в,даны матрицы,даны матрицы а и в найти а в,даны матрицы а и в найти матрицу с,даны матрицы а и в найти матрицу с а в,даны матрицы а и в найти матрицу с онлайн,даны матрицы а и в найти с а в,действие с матрицами,действия над матрицами онлайн,действия с матрицами,действия с матрицами калькулятор онлайн,действия с матрицами онлайн,действия с матрицами онлайн калькулятор,действия с матрицей,деление матрицу на матрицу онлайн,деление матрицы на матрицу онлайн,значение матричного многочлена онлайн,как матрица решается,как найти матрицу,как решается матрица,как решать матрицу,как решать матрицу 2 на 2,как решать матрицы,как решать матрицы для чайников,как решаются матрицы,как решить матрицу,как решить матрицу 2 на 2,как составить матрицу,какие матрицы можно складывать,калькулятор действий с матрицами,калькулятор для решения матриц онлайн,калькулятор матриц онлайн сумма,калькулятор матриц решение матриц онлайн,калькулятор матриц с решением,калькулятор онлайн действия с матрицами,калькулятор онлайн для решения матриц,калькулятор онлайн решение матричных уравнений,калькулятор онлайн решения матриц,калькулятор решение матриц,калькулятор решение матрицы,калькулятор решения матриц,калькулятор решения матриц онлайн,калькулятор решения матриц онлайн калькулятор,калькулятор с решением матрицы,математика все о матрицах,математика для чайников матрицы,математика матрица как решать,математика матрица онлайн,математика матрица примеры,математика матрица решение,математика матрица решение для чайников,математика матрица решение онлайн,математика матрицы,математика матрицы примеры,математика матрицы примеры решения,математика матриця,математическая матрица,математическая матрица решение,математические матрицы,матриц,матриц онлайн решения,матрица 1 на 1,матрица 2 а,матрица 6 на 6,матрица a,матрица a b,матрица a b c b,матрица b a,матрица ba ab,матрица i j,матрица m на n,матрица n на n,матрица а,матрица а 2,матрица а 2 а,матрица в высшей математике для чайников,матрица в математике как решать,матрица высшая математика,матрица высшая математика для чайников,матрица высшая математика примеры,матрица вышмат,матрица для,матрица для чайников высшая математика,матрица как решать,матрица математика,матрица математика для чайников,матрица математика как решать,матрица математика онлайн,матрица математика онлайн решение,матрица математика примеры,матрица математика примеры с решениями,матрица математика решение,матрица математика решение и примеры,матрица математика решение онлайн,матрица математическая решение,матрица онлайн математика,матрица онлайн решать,матрица онлайн решение,матрица онлайн решить,матрица плюс число,матрица по математике,матрица пример,матрица примеры,матрица решать,матрица решать онлайн,матрица решение,матрица решение онлайн,матрица решить,матрица решить онлайн,матрица с нуля,матрица тема,матрица тема математика,матрица тема по математике,матрица формула,матрица формулы,матрица чисел,матрица число,матрица числовая,матрица это в математике,матриці,матрицу,матрицу как решать,матрицы,матрицы a b и b a b,матрицы в математике для чайников,матрицы высшая математика,матрицы высшая математика для чайников,матрицы как решать,матрицы как решаются,матрицы математика,матрицы математика для чайников,матрицы математика как решать,матрицы математика примеры,матрицы математика примеры решения,матрицы нахождение,матрицы онлайн решение,матрицы онлайн решения,матрицы онлайн решить,матрицы операции над матрицами,матрицы по математике,матрицы правила,матрицы пример,матрицы примеры,матрицы примеры математика,матрицы примеры решений,матрицы примеры решения,матрицы решать,матрицы решать онлайн,матрицы решение,матрицы решение калькулятор,матрицы решение математика,матрицы решение онлайн,матрицы решение примеров,матрицы решения,матрицы решения онлайн,матрицы решения примеры,матрицы решить,матрицы решить онлайн,матрицы решить уравнение онлайн,матрицы с,матрицы тема,матрицы теория с примерами,матрицы формула,матрицы формулы,матрицы это,матриця математика,матричное уравнение онлайн калькулятор с решением,матричные уравнения онлайн калькулятор с решением,матричный,найдите матрицу,найти a b,найти a b и b a,найти линейную комбинацию матриц,найти матрицу,найти матрицу 2а,найти матрицу x из уравнения онлайн,найти матрицу с онлайн с решением,найти матрицу х,найти х матрицу,нахождение матрицы,норма матрицы онлайн,онлайн калькулятор действия с матрицами,онлайн калькулятор для решения матриц,онлайн калькулятор решить матричное уравнение,онлайн матриц,онлайн матрица математика,онлайн матрица решать,онлайн матрица решить,онлайн матрицы решения,онлайн операции над матрицами,онлайн операции с матрицами,онлайн программа для решения матриц,онлайн решатель матриц,онлайн решать матрицы,онлайн решение матриц,онлайн решение матриц с комплексными числами,онлайн решение матриц с подробным решением,онлайн решение матриц с решением,онлайн решение матриц уравнений,онлайн решение матрицы,онлайн решения матриц,онлайн решения матрицы,онлайн решить матрицы,онлайн упрощение матрицы,операции над матрицами онлайн,операции с матрицами онлайн,перестановочные матрицы онлайн калькулятор,по математике матрица,по математике матрицы,правила матрицы,пример матрица,пример матрицы,примеры математика матрица,примеры математика матрицы,примеры матриц,примеры матриц для решения,примеры матрица,примеры матрица математика,примеры матрицы,примеры матрицы математика,примеры матрицы решать,примеры матрицы с ответами,примеры матрицы с решением,примеры решение матриц,примеры решения матриц,примеры решения матрицы,примеры решения матрицы в математике,программа для решения матриц,программа для решения матриц онлайн,разность матриц онлайн калькулятор,расчет матриц,решатель матриц онлайн,решатель онлайн матриц,решать матрица,решать матрица онлайн,решать матрицы,решать матрицы онлайн,решать онлайн матрицы,решение математика матрицы,решение матриц,решение матриц онлайн,решение матриц онлайн калькулятор,решение матриц онлайн с комплексными числами,решение матриц онлайн с подробным решением,решение матриц онлайн с решением,решение матриц примеры,решение матриц с решением онлайн,решение матрица онлайн,решение матрица онлайн калькулятор,решение матрицы,решение матрицы 2 на 2,решение матрицы калькулятор,решение матрицы калькулятор онлайн,решение матрицы онлайн,решение матрицы онлайн калькулятор,решение матричного уравнения онлайн калькулятор,решение матричных уравнений калькулятор,решение примеров матрицы,решения матриц,решения матриц калькулятор,решения матриц калькулятор онлайн,решения матриц онлайн,решения матриц онлайн калькулятор,решения матрицы,решения матрицы онлайн,решения онлайн матриц,решения онлайн матрицы,решить матрица,решить матрица онлайн,решить матрицу,решить матрицу 5 на 5,решить матрицу онлайн,решить матрицы,решить матрицы онлайн,решить матричное уравнение калькулятор онлайн,решить матричное уравнение онлайн калькулятор,решить матричное уравнение онлайн калькулятор с подробным решением,решить матричное уравнение онлайн калькулятор с решением,решить онлайн матрица,решить онлайн матрицы,решить онлайн уравнение матрицы онлайн,решить уравнение матрицы онлайн,решить уравнение матрицы онлайн калькулятор,с матрица,с матрицы,сложение матриц онлайн калькулятор,столбец матрица,строка матрица,сумма матриц калькулятор онлайн,сумма матриц онлайн калькулятор,тема матрица,тема матрица по математике,тема матрицы,тема по математике матрица,упрощение матрицы онлайн,уравнения матриц онлайн,формула матрица,формула матрицы,формулы матриц,формулы матрица,формулы матрицы,число матрица,число плюс матрица,числовая матрица,элемент матрицы,элементарные преобразования матриц калькулятор онлайн,элементарные преобразования матриц онлайн,элементарные преобразования матриц онлайн калькулятор.
Решить задачу a b матрица вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Произведение матриц вычисляется следующим образом. Математика для чайников
Сложение матриц:
Вычитание
и сложение матриц сводится к соответствующим операциям
над их элементами. Операция
сложения матриц вводится только для матриц одинакового размера, т.
е. для матриц ,
у которых число строк и столбцов
соответственно равно. Суммой
матриц А и В, называется матрица С, элементы которой равны сумме
соответствующих элементов.
С = А + В
c ij
= a ij
+ b ij
Аналогично
определяется разность
матриц .
Умножение матрицы на число:
Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы
b ij = k × a ij . В = k × A b ij = k × a ij . Матрица — А = (-1) × А называется противоположной матрице А.
Свойства сложения матриц и умножения матрицы на число:
Операции
сложения матриц и умножения матрицы на число обладают следующими свойствами:
1.
А + В = В + А;
2. А + (В + С) = (А + В) + С;
3. А +
0 = А;
4. А — А = 0;
5. 1 × А = А;
6. α × (А + В)
= αА + αВ;
7.
(α + β) × А = αА + βА;
8. α × (βА)
= (αβ) × А;
, где А, В и С — матрицы, α и β —
числа.
Умножение матриц (Произведение матриц):
Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы . Произведением матрицы А m×n на матрицу В n×p , называется матрица С m×p такая, что с ik = a i1 × b 1k + a i2 × b 2k + … + a in × b nk , т. е. находиться сумма произведений элементов i — ой строки матрицы А на соответствующие элементы j — ого столбца матрицы В. Если матрицы А и В квадратные одного размера, то произведения АВ и ВА всегда существуют. Легко показать, что А × Е = Е × А = А, где А квадратная матрица , Е — единичная матрица того же размера.
Свойства умножения матриц:
Умножение
матриц не коммутативно,
т.е. АВ ≠ ВА даже если определены оба
произведения. Однако, если для каких —
либо матриц соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными.
Самым
характерным примером может служить
единичная матрица ,
которая является перестановочной с
любой другой матрицей того же размера. Перестановочными могут
быть только квадратные матрицы одного и того же порядка.
А × Е = Е × А
= А
Умножение матриц обладает следующими свойствами: 1. А × (В × С) = (А × В) × С; 2. А × (В + С) = АВ + АС; 3. (А + В) × С = АС + ВС; 4. α × (АВ) = (αА) × В; 5. А × 0 = 0; 0 × А = 0; 6. (АВ) Т = В Т А Т; 7. (АВС) Т = С Т В Т А Т; 8. (А + В) Т = А Т + В Т;
Определителем матрицы второго порядка, или определителем второго порядка, называется число, которое вычисляется по формуле:
Определителем матрицы третьего порядка, или определителем третьего порядка, называется число, которое вычисляется по формуле:
Это
число представляет алгебраическую
сумму, состоящую из шести слагаемых. В
каждое слагаемое входит ровно по одному
элементу из каждой строки и каждого
столбца матрицы .
Каждое слагаемое состоит из произведения
трех сомножителей.
Знаки, с которыми члены определителя матрицы входят в формулу нахождения определителя матрицы третьего порядка можно определить, пользуясь приведенной схемой, которая называется правилом треугольников или правилом Сарруса. Первые три слагаемые берутся со знаком плюс и определяются из левого рисунка, а последующие три слагаемые берутся со знаком минус и определяются из правого рисунка.
Определить количество слагаемых, для нахождения определителя матрицы , в алгебраической сумме, можно вычислив факториал: 2! = 1 × 2 = 2 3! = 1 × 2 × 3 = 6
Свойства определителей матриц
Свойства определителей матриц:
Свойство № 1:
Определитель матрицы не изменится, если его строки заменить столбцами, причем каждую строку столбцом с тем же номером, и наоборот (Транспонирование). |А| = |А| Т
Следствие:
Столбцы
и строки определителя
матрицы равноправны,
следовательно, свойства присущие строкам
выполняются и для столбцов.
Свойство № 2:
При перестановке 2-х строк или столбцов определитель матрицы изменит знак на противоположный, сохраняя абсолютную величину, т.е.:
Свойство № 3:
Определитель матрицы , имеющий два одинаковых ряда, равен нулю.
Свойство № 4:
Общий множитель элементов какого-либо ряда определителя матрицы можно вынести за знак определителя .
Следствия из свойств № 3 и № 4:
Если все элементы некоторого ряда (строки или столбца) пропорциональны соответствующим элементам параллельного ряда, то такой определитель матрицы равен нулю.
Свойство № 5:
определителя матрицы равны нулю, то сам определитель матрицы равен нулю.
Свойство № 6:
Если все элементы какой–либо строки или столбца определителя представлены в виде суммы 2-х слагаемых, то определитель матрицы можно представить в виде суммы 2-х определителей по формуле:
Свойство № 7:
Если
к какой–либо строке (или столбцу) определителя прибавить соответствующие элементы
другой строки (или столбца), умноженные
на одно и тоже число, то определитель
матрицы не
изменит своей величины.
Пример применения свойств для вычисления определителя матрицы :
Математическая (матричная) запись регрессионной модели с несколькими фиктивными переменными
$\begingroup$
Я потратил на это значительное количество времени, но мои знания в матричной алгебре все еще ограничены. Итак, я не уверен…
У меня есть модель линейной регрессии, основанная на $n$ наблюдениях. Зависимая переменная $y$.
В качестве предикторов используются 10 независимых непрерывных переменных + 9 фиктивных переменных (на основе шкалы из 10 категорий) + 5 фиктивных переменных (на основе ответа по 6 категориям). Модель выглядит так: $$ y = \beta_0+\beta_1 \text{C}_1+\beta_2 \text{C}_2+ …+\beta_{11}\text{dummy}_1+\beta_{12}\text{dummy}_2+ …+ \бета_{19}\text{пустышка}_9+\beta_{20}\text{пустышка}_{10}+…\beta_{24}\text{пустышка}_{14}+\epsilon $$
Будет ли это точной матричной записью приведенной выше модели? $$ \textbf{y} = \textbf{C}{\beta}+\textbf{S} \gamma + \mathbf{R}\lambda + \textbf{e} $$
, где $\textbf{C}$ — это n $\times$ 10+1 матрица плана с единицами в первом столбце и 10 другими столбцами, содержащими непрерывные предикторы, $\textbf{S}$ — это n $\ матрица умножения на 9, содержащая фиктивные переменные для 10-категорийной шкалы, $\textbf{R}$ — матрица n $\times$ 5, содержащая фиктивные переменные для 6-категорийного ответа, ${\beta}$, ${\ gamma}$ и ${\lambda}$ — векторы параметров, $\textbf{e}$ — вектор ошибки.
Достаточно ли точны эти обозначения? Любые ссылки на матричные обозначения для фиктивных переменных также очень ценятся.
С уважением,
Джейкоб
- регрессия
- математико-статистика
- матрица
- нотация
$\endgroup$
1
$\begingroup$
Да, все в порядке. Обратите внимание, что все ваши категориальные векторы будут иметь свой первый уровень, поглощенный в пределах точки пересечения $\beta_0$, поэтому обратите внимание на способ кодирования фиктивных переменных. Я бы сказал, что во всяком случае ваша запись хорошо подходит для групповой регуляризации лассо; стандартное решение лассо будет выбирать только отдельные фиктивные переменные вместо целых факторов. (см. Meier et al. (2007) Групповое лассо для логистической регрессии для получения дополнительной информации об этом аспекте.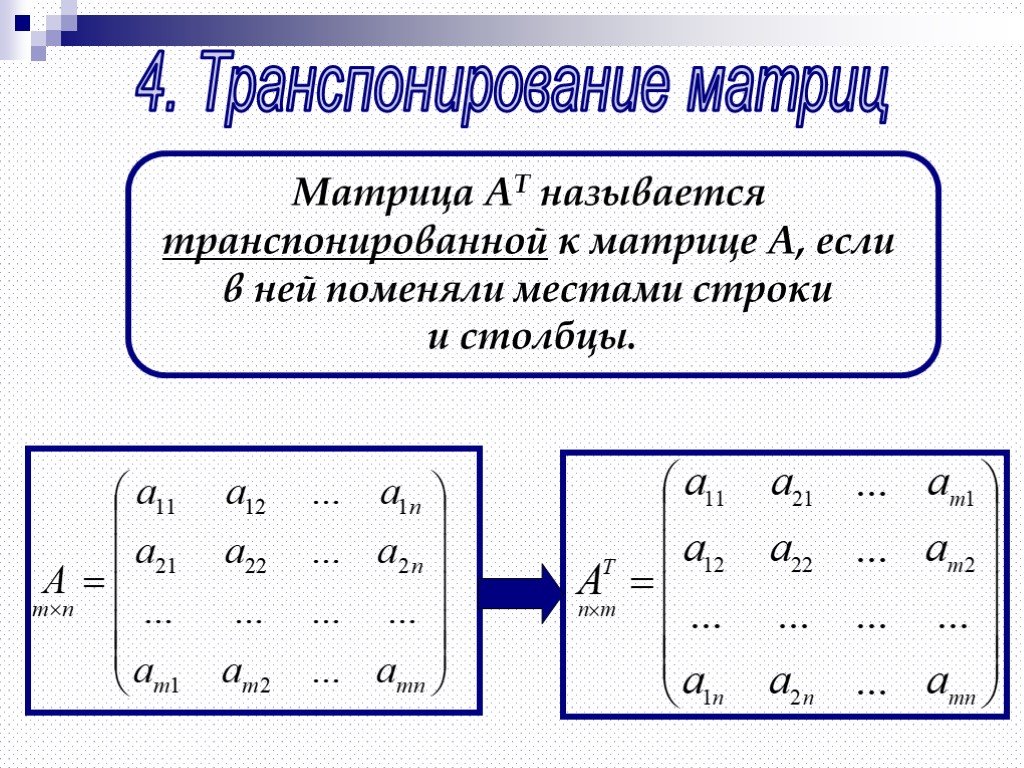
)
Если вы только начинаете и у вас есть вопросы об обозначениях, стандартные учебники по использованию матриц в статистике: Алгебра матриц, полезная для статистики Серла и Алгебра матриц с точки зрения статистика Харвилла. Оба считаются классикой в этом вопросе, и вы можете использовать их как общепринятые ссылки. (Мне также нравится: Матричная алгебра: теория, вычисления и приложения в статистике от Gentle, я много ей пользовался).
$\endgroup$
2
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Операции с матрицами (Алгебра 2, Матрицы) – Mathplanet
Матрицы считаются равными, если они имеют одинаковые размеры и если каждый элемент одной матрицы равен соответствующему элементу другой матрицы. Вы можете умножать матрицу на любую константу, это называется скалярным умножением.
Пример
$$2\begin{bmatrix} 1 & 2\\ 3 & 4 \end{bmatrix}= \begin{bmatrix} {\color{green} 2}\cdot 1 & {\color{ зеленый} 2}\cdot2\\ {\color{green} 2}\cdot3 & {\color{green} 2}\cdot4 \end{bmatrix} = \begin{bmatrix} 2 & 4\\ 6 & 8 \ end {bmatrix}$$
Матрицы одинакового размера можно складывать и вычитать по записи, а матрицы совместимых размеров можно умножать.
Пример
Сложите две матрицы A и B:
$$A=\begin{bmatrix} {\color{green} 2} & {\color{green} -1}\\ {\color {зеленый} 1} & {\color{зеленый} 0} \end{bmatrix}B=\begin{bmatrix} {\color{синий} 1} & {\color{синий} 4} \\ {\color{синий } 2} & \,{\color{blue} 3} \end{bmatrix}$$
Это возможно, так как A и B так как обе матрицы имеют две строки и два столбца.
Складываем каждый элемент матрицы A с соответствующим элементом матрицы B:
$$A+B=\begin{bmatrix} {\color{green} 2}+{\color{blue} 1} & {\color{green} -1}+{\color{blue} 4} \ \ {\color{green} 1}+{\color{blue} 2} & {\color{green} 0}+\,{\color{blue} 3} \end{bmatrix}=\begin{bmatrix} 3 & 3\\ 3 & 3 \end{bmatrix}$$
Точно так же вычитаются матрицы.
Если умножить матрицу A p*q и матрицу B m*n , произведение равно
$$A_{p\times q}+B_{m\times n}=(AB)_{ p\times n}$$
Элемент в g-й строке и h-м столбце матрицы AB является суммой произведения соответствующих элементов g-й строки A и h-го столбца матрицы B. Вы можете умножать две матрицы только в том случае, если количество столбцов в первой матрице и количество строк во второй равно.
Рабочие листы
Если вы хотите попрактиковаться в сложении матриц, у нас есть несколько рабочих листов с ответами ниже.
Рабочий лист 1 Ответы 1
Рабочий лист 2 Ответы 2
Рабочий лист 3 Ответы 3
Рабочий лист 4 Ответы 4
Рабочий лист 5 Ответы 5
Пример
Умножение матрицы A и B:
$ =\begin{bmatrix} {\color{green} 1} & {\color{green} 3}\\ {\color{green} -1} & {\color{green} 0} \end{bmatrix}B= \begin{bmatrix} {\color{blue} 2} & {\color{blue} 1} & {\color{blue} 1}\\ {\color{blue} -1} & {\color{blue} 2 }&{\color{синий} 4} \end{bmatrix}$$ Это возможно, поскольку первая матрица содержит 2 столбца, а вторая — 2 строки.