Математика в библиотеке Numpy | Программирование на Питоне
[185.0, 179.0, 186.0, 195.0, 178.0, 178.0, 196.0, 188.0, 175.0, 185.0, 175.0, 175.0, 182.0, 161.0, 163.0, 174.0, 170.0, 183.0, 171.0, 166.0, 195.0, 178.0, 181.0, 166.0, 175.0, 181.0, 168.0, 184.0, 174.0, 177.0, 174.0, 199.0, 180.0, 169.0, 188.0, 168.0, 182.0, 160.0, 167.0, 182.0, 187.0, 182.0, 179.0, 177.0, 165.0, 173.0, 175.0, 191.0, 183.0, 162.0, 183.0, 176.0, 173.0, 186.0, 190.0, 189.0, 172.0, 177.0, 183.0, 190.0, 175.0, 178.0, 169.0, 168.0, 188.0, 194.0, 179.0, 190.0, 184.0, 174.0, 184.0, 195.0, 180.0, 196.0, 154.0, 188.0, 181.0, 177.0, 181.0, 160.0, 178.0, 184.0, 195.0, 175.0, 172.0, 175.0, 189.0, 183.0, 175.0, 185.0, 181.0, 190.0, 173.0, 177.0, 176.0, 165.0, 183.0, 183.0, 180.0, 178.0, 166.0, 176.0, 177.0, 172.0, 178.0, 184.0, 199.0, 182.0, 183.0, 179.0, 161.0, 180.0, 181.0, 205.0, 178.0, 183.0, 180.0, 168.0, 191.0, 188.0, 188.0, 171.0, 194.0, 166.0, 186. 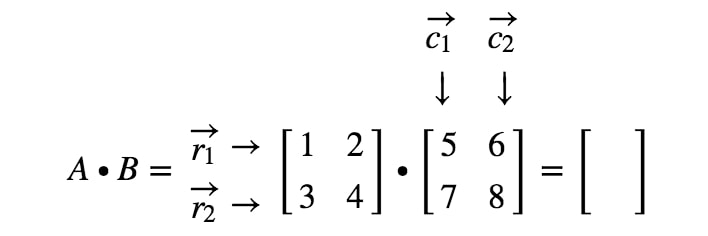  0, 183.0, 176.0, 175.0, 176.0, 184.0, 176.0, 183.0, 201.0, 189.0, 177.0, 192.0, 176.0, 160.0, 170.0, 161.0, 176.0, 180.0, 197.0, 183.0, 178.0, 188.0, 158.0, 182.0, 188.0, 165.0, 191.0, 183.0, 176.0, 186.0, 203.0, 182.0, 182.0, 175.0, 172.0, 188.0, 171.0, 181.0, 175.0, 185.0, 183.0, 190.0, 175.0, 177.0, 170.0, 176.0, 184.0, 188.0, 171.0, 189.0, 194.0, 184.0, 199.0, 172.0, 168.0, 162.0, 195.0, 187.0, 179.0, 183.0, 169.0, 204.0, 181.0, 181.0, 187.0, 185.0, 182.0, 172.0, 185.0, 199.0, 193.0, 196.0, 175.0, 170.0, 179.0, 181.0, 191.0, 163.0, 195.0, 178.0, 176.0, 170.0, 163.0, 188.0, 181.0, 167.0, 167.0, 177.0, 197.0, 177.0, 165.0, 178.0, 177.0, 153.0, 179.0, 178.0, 187.0, 198.0, 191.0, 177.0, 169.0, 206.0, 181.0, 180.0, 180.0, 182.0, 179.0, 174.0, 175.0, 180.0, 175.0, 173.0, 181.0, 177.0, 195.0, 153.0, 191.0, 192.0, 159.0, 177.0, 176.0, 166.0, 172.0, 169.0, 198.0, 189.0, 193.0, 187.0, 169.0, 175.0, 185.0, 168.0, 187.0, 178.0, 176.0, 187.0, 184.0, 176.0, 192.0, 169.0, 186.0, 186.0, 177.0, 183. 0, 183.0, 176.0, 175.0, 176.0, 184.0, 176.0, 183.0, 201.0, 189.0, 177.0, 192.0, 176.0, 160.0, 170.0, 161.0, 176.0, 180.0, 197.0, 183.0, 178.0, 188.0, 158.0, 182.0, 188.0, 165.0, 191.0, 183.0, 176.0, 186.0, 203.0, 182.0, 182.0, 175.0, 172.0, 188.0, 171.0, 181.0, 175.0, 185.0, 183.0, 190.0, 175.0, 177.0, 170.0, 176.0, 184.0, 188.0, 171.0, 189.0, 194.0, 184.0, 199.0, 172.0, 168.0, 162.0, 195.0, 187.0, 179.0, 183.0, 169.0, 204.0, 181.0, 181.0, 187.0, 185.0, 182.0, 172.0, 185.0, 199.0, 193.0, 196.0, 175.0, 170.0, 179.0, 181.0, 191.0, 163.0, 195.0, 178.0, 176.0, 170.0, 163.0, 188.0, 181.0, 167.0, 167.0, 177.0, 197.0, 177.0, 165.0, 178.0, 177.0, 153.0, 179.0, 178.0, 187.0, 198.0, 191.0, 177.0, 169.0, 206.0, 181.0, 180.0, 180.0, 182.0, 179.0, 174.0, 175.0, 180.0, 175.0, 173.0, 181.0, 177.0, 195.0, 153.0, 191.0, 192.0, 159.0, 177.0, 176.0, 166.0, 172.0, 169.0, 198.0, 189.0, 193.0, 187.0, 169.0, 175.0, 185.0, 168.0, 187.0, 178.0, 176.0, 187.0, 184.0, 176.0, 192.0, 169.0, 186.0, 186.0, 177.0, 183.  0, 180.0, 187.0, 169.0, 184.0, 182.0, 185.0, 183.0, 205.0, 174.0, 175.0, 174.0, 174.0, 174.0, 192.0, 194.0, 174.0, 172.0, 185.0, 174.0, 186.0, 182.0, 165.0, 195.0, 198.0, 174.0, 176.0, 183.0, 183.0, 187.0, 200.0, 178.0, 172.0, 166.0, 173.0, 180.0, 198.0, 175.0, 182.0, 180.0, 192.0, 205.0, 175.0, 175.0, 190.0, 187.0, 198.0, 186.0, 176.0, 186.0, 191.0, 188.0, 185.0, 191.0, 192.0, 194.0, 186.0, 178.0, 181.0, 192.0, 172.0, 184.0, 176.0, 180.0, 193.0, 182.0, 180.0, 166.0, 187.0, 186.0, 202.0, 177.0, 182.0, 182.0, 196.0, 179.0, 183.0, 186.0, 182.0, 176.0, 182.0, 191.0, 170.0, 181.0, 173.0, 192.0, 165.0, 174.0, 184.0, 196.0, 179.0, 174.0, 199.0, 166.0, 158.0, 184.0, 175.0, 170.0, 187.0, 182.0, 174.0, 167.0, 189.0, 187.0, 179.0, 198.0, 169.0, 165.0, 173.0, 180.0, 182.0, 178.0, 184.0, 167.0, 194.0, 179.0, 191.0, 183.0, 185.0, 186.0, 184.0, 186.0, 193.0, 182.0, 187.0, 179.0, 194.0, 173.0, 198.0, 180.0, 166.0, 181.0, 173.0, 188.0, 173.0, 176.0, 161.0, 175.0, 156.0, 164.0, 188.0, 188.0, 184.0, 170. 0, 180.0, 187.0, 169.0, 184.0, 182.0, 185.0, 183.0, 205.0, 174.0, 175.0, 174.0, 174.0, 174.0, 192.0, 194.0, 174.0, 172.0, 185.0, 174.0, 186.0, 182.0, 165.0, 195.0, 198.0, 174.0, 176.0, 183.0, 183.0, 187.0, 200.0, 178.0, 172.0, 166.0, 173.0, 180.0, 198.0, 175.0, 182.0, 180.0, 192.0, 205.0, 175.0, 175.0, 190.0, 187.0, 198.0, 186.0, 176.0, 186.0, 191.0, 188.0, 185.0, 191.0, 192.0, 194.0, 186.0, 178.0, 181.0, 192.0, 172.0, 184.0, 176.0, 180.0, 193.0, 182.0, 180.0, 166.0, 187.0, 186.0, 202.0, 177.0, 182.0, 182.0, 196.0, 179.0, 183.0, 186.0, 182.0, 176.0, 182.0, 191.0, 170.0, 181.0, 173.0, 192.0, 165.0, 174.0, 184.0, 196.0, 179.0, 174.0, 199.0, 166.0, 158.0, 184.0, 175.0, 170.0, 187.0, 182.0, 174.0, 167.0, 189.0, 187.0, 179.0, 198.0, 169.0, 165.0, 173.0, 180.0, 182.0, 178.0, 184.0, 167.0, 194.0, 179.0, 191.0, 183.0, 185.0, 186.0, 184.0, 186.0, 193.0, 182.0, 187.0, 179.0, 194.0, 173.0, 198.0, 180.0, 166.0, 181.0, 173.0, 188.0, 173.0, 176.0, 161.0, 175.0, 156.0, 164.0, 188.0, 188.0, 184.0, 170.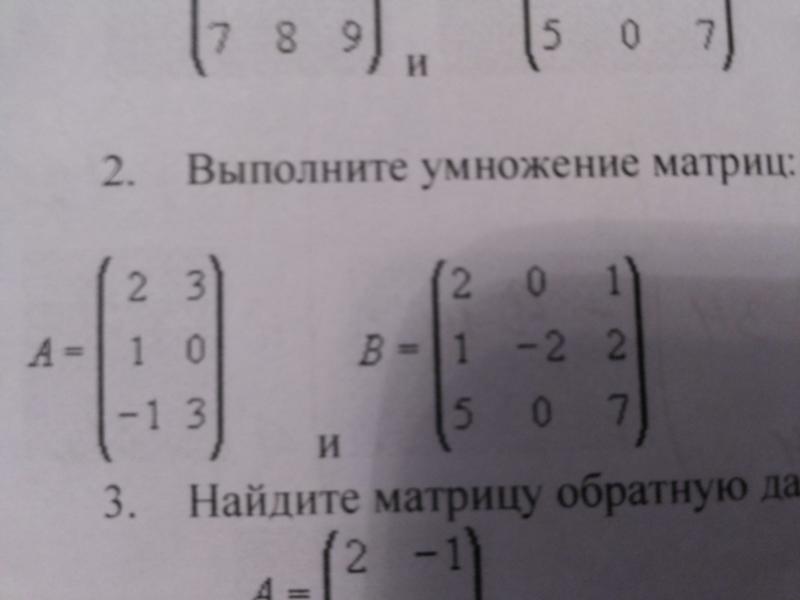 |
algebra
algebraАлгебра
, 141
группа (МФиФМ), осень
2021 г.
Лектор: Прохоров
Юрий Геннадьевич
Экзамен состоится
6 января в 10:00 (ауд. 14-14).
Консультация 5 января 14:00.
Экзаменационные
вопросы
Краткое cодержание прочитанных лекций.
- Матрицы. Операции сложения и умножения на число. Системы линейных уравнений. Метод Гаусса. Следствия. Системы однородных уравнений.
- Умножение матриц. Свойства. Ассоциативность. Матричная
запись систем линейных уравнений.
 Связь однородных и
неоднородных систем линейных уравнений. Понятие кольца. Примеры.
Умножение на диагональные матрицы. Умножение треугольных матриц.
Матричные единицы. Их произведения. Элементарные матрицы.
Умножение произвольной матрицы на элементарную. Подстановки. Их
произведение. Ассоциативность. Транспозиции. Разложение
подстановки в произведение транспозиций.
Связь однородных и
неоднородных систем линейных уравнений. Понятие кольца. Примеры.
Умножение на диагональные матрицы. Умножение треугольных матриц.
Матричные единицы. Их произведения. Элементарные матрицы.
Умножение произвольной матрицы на элементарную. Подстановки. Их
произведение. Ассоциативность. Транспозиции. Разложение
подстановки в произведение транспозиций. - Запись подстановок. Обратная и единичные подстановки. Понятие
группы. Примеры. Число подстановок. Неподвижные элементы.
Независимые подстановки коммутируют. Циклы. Разложение
подстановки в произведение независимых циклов. Применение
подстановки к перестановке. Четность. Корректность определения
четности (как меняется число инверсий при применении
транспозиции).
- Четность произведения подстановок. Четность обратной
подстановки. Число четных и нечетных подстановок. Группа A_n.
Понятие подгруппы.
 Определители. Определитель треугольной
матрицы. Определитель транспонированной матрицы. Вычисление
определителя при помощи элементарных преобразований.
Полилинейные и кососимметрические функции. Полилинейность и
кососимметричность определителя.
Определители. Определитель треугольной
матрицы. Определитель транспонированной матрицы. Вычисление
определителя при помощи элементарных преобразований.
Полилинейные и кососимметрические функции. Полилинейность и
кососимметричность определителя.
- Эквивалентное определение определителя (как полилинейной
кососимметрической формы). Опрелитель с углом нулей. Разложение
определителя по строке (и фальшивое разложение). Определитель
Вандермонда. Теорема Крамера.
- Определитель произведения матриц. Обратная матрица. Единицы и обратные элементы в ассоциативном кольце (единственность). Критерий существования обратной матрицы. Формула для обратной матрицы. Вычисление обратной матрицы при помощи элементарных преобразований. Делители нуля в кольце. Делители нуля в кольце матриц.
- Группы GL_n и SL_n. Векторные пространства. Линейная
зависимость.

- Ранг матрицы. Ранг суммы матриц. Теорема о ранге. Алгоритм
нахождения базиса. Ранг произведения матриц.
Критерий совместности системы линейных уравнений. Решения однородной системы линейных уравнений.
Фундаментальная система решений. Задание подпространства системой линейных уравнений. - Морфизмы алгебраических структур (случай групп, колец,
векторных пространств). Примеры. Понятие алгебры.
Изоморфизмы. Примеры. Изоморфизм векторных пространств одной размерности. Ядро и образ гомоморфизма. - Поля. Определение, свойства, примеры. Конечномерная
ассоциативная алгебра без делителей нуля является телом. Поле
комплексных чисел. Аксиоматическое определение, существование,
единственность. Алгебраическая запись. Вещественная и мнимая
части.
 n=w. Группа _n корней из 1.
Первообразные корни. Циклические группы. Кольца вычетов.
Делители нуля и обратимые элементы. Поля F_p. Конечное
ассоциативное кольцо без делителей 0 является телом. Изоморфизм Z/nZ и _n.
n=w. Группа _n корней из 1.
Первообразные корни. Циклические группы. Кольца вычетов.
Делители нуля и обратимые элементы. Поля F_p. Конечное
ассоциативное кольцо без делителей 0 является телом. Изоморфизм Z/nZ и _n. - Теорема Вилсона. Характеристика поля. Примеры. Умножения целых чисел на элементы аддитивной абелевой группы и элементы кольца. Бином Ньютона. Свойства полей характеристики р. Отображение Фробениуса. Кольцо многочленов. Доказательство единственности.
- Кольцо многочленов. Доказательство существования. Кольцо
формальных степенных рядов. Степень многочлена. Делители нуля в
кольце многочленов. Подстановка элемента в многочлен.
Восстановление многочлена по его значениям. Функциональное
равенство многочленов. Пример для конечных полей. Корни
многочленов. Интерполяционная формула Лагранжа. Схема
Горнера. Теорема Безу.
 AlgI-13.pdf
AlgI-13.pdf - Кратность корня. Деление многочленов над полем с остатком. Делимость в кольцах. Неприводимые многочлены. Наибольший общий делитель. Алгоритм Евклида. Факториальность кольца многочленов над полем. Факториальные и евклидовы кольца. Дифференцирования. Дифференцирования кольца многочленов над полем. AlgI-14.pdf
- Дифференцирования. Понижение кратности при дифференцировании.Формула Тейлора. Основная теорема алгебры(формулировка). Сходимость последовательностей комплексных чисел. Лемма о возрастании модуля многочлена. AlgI-15.pdf
- Лемма Даламбера. Основная теорема алгебры (доказательство). Следствия. Неприводимые многочлены над C и R. Поле частных целостного кольца. Поле рациональных функций. AlgI-16.pdf
- Поле рациональных функций. Простейшие дроби. Разложение дроби
в сумму простейших. Простейшие дроби над C и R.
 Многочлены над факториальным кольцом. Лемма Гаусса.
Факториальность кольца многочленов над факториальным кольцом. AlgI-17.pdf
Многочлены над факториальным кольцом. Лемма Гаусса.
Факториальность кольца многочленов над факториальным кольцом. AlgI-17.pdf - Многочлены от нескольких переменных. Лексикографический порядок. Лемма о старшем члене. AlgI-18.pdf
- Симметрические многочлены. Основная теорема и симметрических многочленах. Формулы Виета. Дискриминант. Результант (определение и свойства).
- Вычисление результанта. Циклические группы. Примеры. Подгруппа циклической группы. Циклические подгруппы. Порядок элемента.
- Порядок элемента. Изоморфизм циклических групп одного порядка. Смежные классы. Теорема Лагранжа. Малая теорема Ферма. Нормальные подгруппы. Свойства. Примеры. Факторгруппа (определение, доказательство не закончено).
- Теорема о гомоморфизме групп. Идеалы. Примеры. Факторкольца.
Теорема о гомоморфизме колец. Присоединение к полю корня
неприводимого многочлена.

Задачи.
Расписание (осень):
- понед. 10-45 — 12-20, ауд. 14-13
- четв. (вторая неделя) 13-15 —14-50, ауд. 14-13
Колоквиум состоялся 27-го октября. Вопросы к коллоквиуму.
Литература.
- Кострикин, А. И. Введение в алгебру. Наука, 1977 (есть новое
издание в 3-х томах)
- Курош, А. Г. Курс высшей алгебры. Наука, 197I
- Винберг, Э. Б. Курс алгебры. Факториал, 2001
- Фаддеев, Д. К. Лекции по алгебре. Наука, 1983
- Ленг, С. Алгебра Мир, 1968
12.1: Базовое умножение матриц — Инженерные тексты LibreText
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 85044
- Кэри Смит
- Oxnard College
Кэри Смит
Матрица, умноженная на вектор (случай 3×3):
\( A*B =
\begin{matrix}
|a & b & c| \\
|p & q & r| \\
|u & v & w|
\end{matrix} * \begin{matrix}
|x|\\
|y|\\
|z|
\end{matrix} = \begin{matrix}
|a*x & b *y & c*z| \\
|p*x & q*y & r*z| \\
|u*x & v*y & w*z|
\end{matrix}
\)
Матрицы не обязательно должны быть квадратными, но количество столбцов в A должно быть равно количеству строк в B.
Умножение матриц обычно не является коммутативным. То есть A*B ≠ B*A, вообще говоря.
.
Посмотрите это видео об умножении матриц:
Видеоруководство Matlab: умножение матриц и векторов, https://www.youtube.com/watch?v=sgzFn42jU6Y
.
Пример \(\PageIndex{1}\) Матрица Умножить 3×3 вектора
A = [3 2 1;
2 1 0
1 0 -1]
В = [4
5
6]
A*B
Раствор
A*B =
28
13
-2
% = [28 %(28 = 3*94 + 1)039 1*5 % 13 %(13 = 2*4 + 1*5 + 0*6)
% -2] %(-2 = 1*4 + 0*5 + -1*6)
.
Упражнение \(\PageIndex{1}\) Умножение матриц Верно/неверно
1. Верно или неверно: Эти две матрицы (с 3 строками и 2 столбцами) можно перемножить вместе:
[ 1 5 ] [ 9 5 ]
А = | 2 9 | В = | 8 9 |
[ 3 4 ] [ 7 5 ]
2. Верно или неверно: эти две матрицы можно перемножить:
Верно или неверно: эти две матрицы можно перемножить:
[ 1 5 ]
A = | 2 9 |; B = [ 1 3 2 ]
[ 3 4 ] [ 4 6 9 ]
- Ответ
1. Нет, поскольку количество столбцов в A (2) не равно количеству строк в B (3).
1. Да, потому что количество столбцов в A (2) равно количеству строк в B (2).
Упражнение \(\PageIndex{2}\) Вычисление умножения матриц
1. Что такое A*B ?
A = [1 4
3 -5]
B = [ 2 12
3 1]
(Умножать матрицу, а не поэлементно)
- Ответ
3
А*В = [14 16
-9 31]
.
Матрица с единицами по диагонали и нулями в других местах называется единичной матрицей:
I = глаз(3) = [1 0 0
0 1 0
0 0 1]
I*A = A
A*I = A
Для получения дополнительной информации см.: https:/ /en.Wikipedia.org/wiki/Matrix_multiplication
.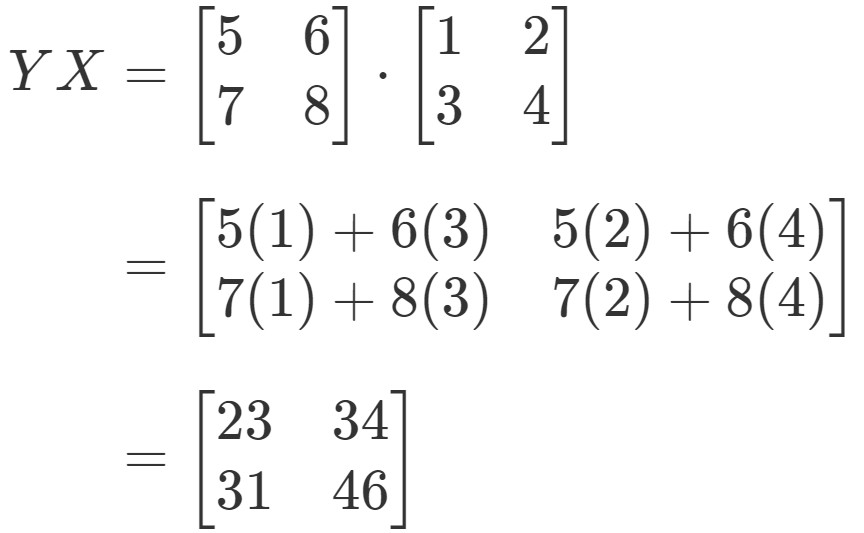
Эта страница под названием 12.1: Базовое умножение матриц распространяется под лицензией CC BY-NC-SA 4.0, ее автор, ремикс и/или куратор — Кэри Смит.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Кэри Смит
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Показать оглавление
- да
- Теги
- Матрица жизненного цикла
- Умножение матриц
- Силы Матрицы
- Матрица вращения
Умножение матриц — Уроки Византа
Умножение матриц на скалярную константу
Матрицы можно умножать на скалярные константы аналогично умножению
любого количества переменных на скалярную константу. Скалярная константа относится к любому числу;
Скалярная константа относится к любому числу;
реальный или мнимый; положительное или отрицательное; целое или дробное, но не переменное.
Когда матрица умножается на скалярную константу, константа одинаково умножает каждые
элементов матрицы, например, при заданной матрице A
найти x A где x скалярная константа
решение:
Как видно из приведенного выше примера, x умножается на всю матрицу A
, влияя на все элементы в A
.
Например: Дана матрица M найти
решение:
Помимо умножения на скалярные константы, матрицы также могут быть умножены на
на другие матрицы. Однако умножение матриц не так прямолинейно, как обычное умножение
Однако умножение матриц не так прямолинейно, как обычное умножение
, необходимо соблюдать определенные правила и выполнять определенные условия.
Свойства умножения матриц
Первое правило, которое вы должны знать, заключается в том, что умножение матриц НЕ коммутативное,
т.е.Для двух матриц A и B
Мы скоро увидим причину этого.
Умножение матриц ассоциативно; например, даны 3 матрицы A , B
и C всегда верно следующее тождествоНо поскольку мы уже сказали, что умножение матриц не является коммутативным, следующее
будет НЕ истинным.или любую другую перестановку в этом роде.
 Матрицы должны сохранять свой порядок.
Матрицы должны сохранять свой порядок.- Матричное умножение является распределительным через сложение
Обратите внимание, однако, что порядок по-прежнему имеет значение, приведенное выше не то же самое, что
Вышесказанное неверно, но верно следующее
- Умножение скалярной константы на матричное умножение является коммутативным в следующей форме
;
Есть еще несколько свойств матричного умножения, и мы увидим эти
через некоторое время.
Правило умножения матриц
Две матрицы А и В могут быть перемножены в виде А В
только тогда и только тогда, когда их размеры принимают следующий вид:
Матрица A имеет размер n x m, а матрица B имеет размер m x x
Другими словами, при умножении матриц количество столбцов в матрице на
слева должно быть равно количеству строк в матрице справа.
Например; учитывая, что матрица A представляет собой матрицу 3 x 3, для того, чтобы умножение матриц
A B было возможным, матрица B должна иметь размер 3 x m, где m может быть
любым количеством столбцов. Это, как мы вскоре увидим, происходит из-за способа умножения
матриц. Это правило является причиной того, что умножение матриц не коммутативно.
Аккуратный способ проверить, можно ли перемножить две матрицы, чтобы увидеть их размеры
рядом. Например, учитывая, что вас попросили перемножить матрицы A
и B , где A имеет размер n x m, а B имеет размер p x q
.
Чтобы A B были возможны, расположите размеры рядом следующим образом и
обратите внимание на
если ты увидишь это m = p , то можно сделать вывод, что A B возможно
и приступить к умножению. Если это не так, то не беспокойте
Если это не так, то не беспокойте
, просто скажите, что это невозможно. Вскоре мы увидим, что результирующая матрица
от умножения A и B имеет размер n x q
.
Чтобы B A были возможны, расположите размеры рядом следующим образом и
обратите внимание на
аналогично, если вы видите, что q = n , то вы можете заключить, что B A
возможно, и продолжить умножение. Если это не так, то
не заморачивайтесь, просто скажите, что это невозможно. Результирующая матрица в этом случае будет
размером p x m.
Алгоритм умножения матриц
Умножение матриц выполняется по тому же алгоритму, что и умножение векторов. Напомним
, что вектор может быть строкой или столбцом, например
где D — вектор-столбец, а E — вектор-строка.
Теперь, когда мы установили это, вы можете думать о D и E как о матрицах
, где D — матрица размера 4 x 1, а E — матрица размера
1 x 4. Итак, если это так, тогда попробуем умножить D на и E на .
D представляет собой матрицу 4 x 1, тогда как E представляет собой матрицу 1 x 4, поэтому по правилу, указанному выше для
, возможны следующие произведения: D равно числу
строк в E
строк в D
Теперь, когда мы увидели, что D E и E D возможны,
давайте перейдем к фактическому выполнению вычислений.
Всегда начинайте с расстановки матриц по мере необходимости, не путайте их порядок.
Тогда возникает вопрос, что делать дальше!
Умножение матриц выполняется путем умножения строк на столбцы. В этом случае у нас только
В этом случае у нас только
есть одна строка, но у нас есть четыре столбца.
Мы делаем это, умножая все строки на все столбцы как таковые:
.
Мы добавляем, потому что каждая запись в результирующей матрице является суммой умножения
записей в строке и столбце для этой позиции. Для приведенного выше примера результирующая матрица
имеет размер 1 x 1.
Теперь вы должны заметить, что это то же самое, что и количество строк в E и
количество столбцов в Д . Таким образом, теперь мы можем, как правило, сказать, что когда вы
умножаете две матрицы, их произведение будет иметь то же количество строк, что и матрица
слева, и то же количество столбцов, что и матрица справа.
Например, если A B = C , где A имеет размер n x m, а
B имеет размер p x q, то C будет иметь размер n x q. Это всегда верно
Это всегда верно
для любого матричного умножения.
Вернемся к перемножению D и E . Мы уже видели E D ,
, так что теперь давайте посмотрим на D E
Итак, теперь у нас есть четыре строки и четыре столбца. Обратите внимание на размеры D
и E
.
мы видим, что результирующая матрица должна иметь размер 4 x 4.
Каждая строка умножает каждый столбец, и это дает одну запись, соответствующую этой позиции
. Увидев результаты D E и E D , вы
должны увидеть причину, по которой умножение матриц не является коммутативным, как указано в первом свойстве
: результат не один и тот же!
Давайте теперь посмотрим на другой пример, иллюстрирующий умножение матриц:
. Даны матрицы А и В , где
Даны матрицы А и В , где
и
Поскольку A и B удовлетворяют правилу умножения матриц, произведение
A B можно найти следующим образом.
Матрица A B представляет собой матрицу 2 x 2.
Из приведенных выше двух примеров мы можем наблюдать следующее для матричного умножения
А В = С
Требуется некоторое время, чтобы привыкнуть ко всему процессу умножения матриц, но трюк
заключается в том, чтобы сделать как можно больше примеров. Ниже приведены несколько проработанных примеров.
Примеры умножения матриц
Пример 1
Найдите C , если A B = C и что
Этап 1
Первым делом нужно посмотреть размеры A и B , чтобы проверить, можно ли их
умножить, а также определить размер C
.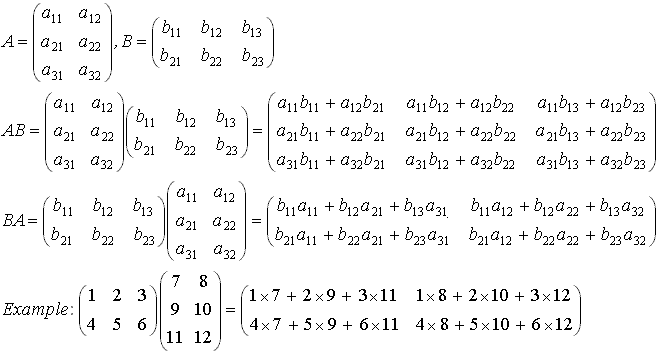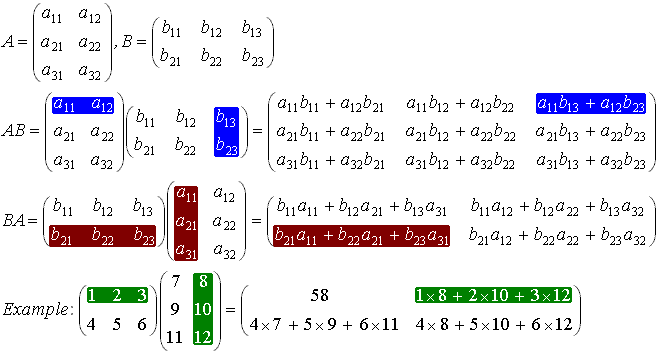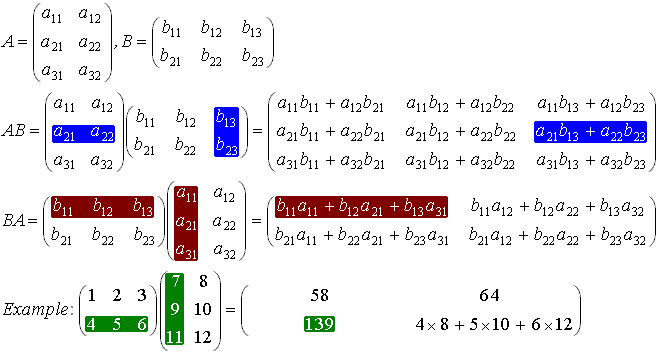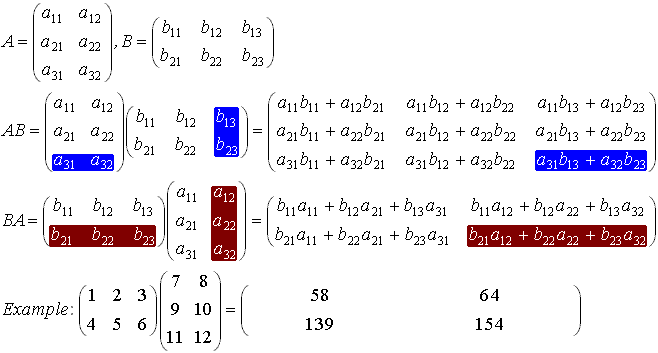
из приведенного выше вы можете видеть, что A B возможен и этот размер C
Далее мы выполняем фактическое умножение
Этап 3
Пример 2
Найдите A 2 , учитывая, что
Этап 1
Поскольку A является матрицей 2 x 2, A A возможно, и результат будет
также может быть 2 x 2
Этап 2
Этап 3
Пример 3
Найдите B A , учитывая, что
.
Шаг 1
Из размеров A и B видно, что результирующая матрица AB
будет иметь размер 3 x 3
Этап 2
Пример 4
Найдите A B C , учитывая, что
Этап 1
Этот конкретный вопрос включает в себя многократное умножение матриц, поэтому нам нужно
, чтобы разбить его на две части, но мы должны сохранить порядок матриц.
Сначала мы умножаем A и B , затем умножаем их произведение AB
на C , чтобы получить ABC
.


 Связь однородных и
неоднородных систем линейных уравнений. Понятие кольца. Примеры.
Умножение на диагональные матрицы. Умножение треугольных матриц.
Матричные единицы. Их произведения. Элементарные матрицы.
Умножение произвольной матрицы на элементарную. Подстановки. Их
произведение. Ассоциативность. Транспозиции. Разложение
подстановки в произведение транспозиций.
Связь однородных и
неоднородных систем линейных уравнений. Понятие кольца. Примеры.
Умножение на диагональные матрицы. Умножение треугольных матриц.
Матричные единицы. Их произведения. Элементарные матрицы.
Умножение произвольной матрицы на элементарную. Подстановки. Их
произведение. Ассоциативность. Транспозиции. Разложение
подстановки в произведение транспозиций.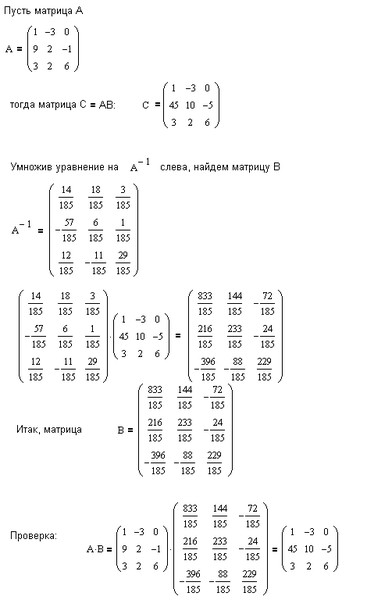 Определители. Определитель треугольной
матрицы. Определитель транспонированной матрицы. Вычисление
определителя при помощи элементарных преобразований.
Полилинейные и кососимметрические функции. Полилинейность и
кососимметричность определителя.
Определители. Определитель треугольной
матрицы. Определитель транспонированной матрицы. Вычисление
определителя при помощи элементарных преобразований.
Полилинейные и кососимметрические функции. Полилинейность и
кососимметричность определителя. 
 n=w. Группа _n корней из 1.
Первообразные корни. Циклические группы. Кольца вычетов.
Делители нуля и обратимые элементы. Поля F_p. Конечное
ассоциативное кольцо без делителей 0 является телом. Изоморфизм Z/nZ и _n.
n=w. Группа _n корней из 1.
Первообразные корни. Циклические группы. Кольца вычетов.
Делители нуля и обратимые элементы. Поля F_p. Конечное
ассоциативное кольцо без делителей 0 является телом. Изоморфизм Z/nZ и _n. AlgI-13.pdf
AlgI-13.pdf Многочлены над факториальным кольцом. Лемма Гаусса.
Факториальность кольца многочленов над факториальным кольцом. AlgI-17.pdf
Многочлены над факториальным кольцом. Лемма Гаусса.
Факториальность кольца многочленов над факториальным кольцом. AlgI-17.pdf
 Матрицы должны сохранять свой порядок.
Матрицы должны сохранять свой порядок.