Метод линейного программирования разработал: HTTP 429 — too many requests, слишком много запросов

Линейное программирование кратко Математическое программирование

Сразу хочу сказать, что здесь никакой воды про линейное программирование, и только нужная информация. Для того чтобы лучше понимать что такое линейное программирование , настоятельно рекомендую прочитать все из категории Математическое программирование.

линейное программирование — математическая дисциплина, посвященная теории и методам решения экстремальных задач на множествах -мерного векторного пространства, задаваемых системами линейных уравнений и неравенств.

Линейное программирование является частным случаем выпуклого программирования, которое в свою очередь является частным случаем математического программирования. Одновременно оно — основа нескольких методов решения задач целочисленного и нелинейного программирования. Одним из обобщений линейного программирования является дробно-линейное программирование.

Многие свойства задач линейного программирования можно интерпретировать также как свойства многогранников и таким образом геометрически формулировать и доказывать их.

История

Математические исследования отдельных экономических проблем, математическая формализация числового материала проводилась еще в XIX веке. Приматематическом анализе процесса расширенного производства использовались алгебраические соотношения, анализ их проводился с помощью дифференциального исчисления. Это давало возможность получить общее представление о проблеме.

Развитие экономики потребовало количественных показателей, и в 1920 годы был создан межотраслевой баланс (МОБ). Он то и послужил толчком в деле создания и исследования математических моделей. Разработка МОБ в 1924—1925 годах в СССР повлияла на работы экономиста и статистика Василия Васильевича Леонтьева. Он разработал межотраслевую модель производства и распределения продукции.

В 1938 году Леонид Витальевич Канторович в порядке научной консультации приступил к изучению чисто практической задачи по составлению наилучшего плана загрузки лущильных станков (фанерный трест). Эта задача не поддавалась обычным методам. Стало ясно, что задача не случайная.

В 1939 году Леонид Витальевич Канторович опубликовал работу «Математические методы организации и планирования производства», в которой сформулировал новый класс экстремальных задач с ограничениями и разработал эффективный метод их решения, таким образом были заложены основы линейного программирования.

Изучение подобных задач привело к созданию новой научной дисциплины линейного программирования и открыло новый этап в развитии экономико-математических методов.

В 1949 году американский математик Джордж Бернард Данциг разработал эффективный метод решения задач линейного программирования (ЗЛП) — симплекс-метод.

Термин «программирование» нужно понимать в смысле «планирования» (один из переводов англ. programming). Он был предложен в середине 1940-х годовДжорджем Данцигом, одним из основателей линейного программирования, еще до того, как компьютеры были использованы для решения линейных задачоптимизации.

Метод внутренних точек был впервые упомянут И. И. Дикиным в 1967 году.

задачи линейного программирования

Задачи

Общей (стандартной) задачей линейного программирования называется задача нахождения минимума линейной целевой функции (линейной формы) вида^:

Задача, в которой фигурируют ограничения в форме неравенств, называется основной задачей линейного программирования (ОЗЛП)

,

.

Задача линейного программирования будет иметь канонический вид, если в основной задаче вместо первой системы неравенств имеет место система уравнений с ограничениями в форме равенства^:

,

Основную задачу можно свести к канонической путем введения дополнительных переменных.

Задачи линейного программирования наиболее общего вида (задачи со смешанными ограничениями: равенствами и неравенствами, наличием переменных, свободных от ограничений) могут быть приведены к эквивалентным (имеющим то же множество решений) заменами переменных и заменой равенств на пару неравенств^.

Легко заметить, что задачу нахождения максимума можно заменить задачей нахождения минимума, взяв коэффициенты с обратным знаком.

Примеры задач

Максимальное паросочетание

Рассмотрим задачу о максимальном паросочетании в двудольном графе: есть несколько юношей и девушек, причем для каждых юноши и девушки известно, симпатичны ли они друг другу . Об этом говорит сайт https://intellect.icu . Нужно поженить максимальное число пар со взаимной симпатией.

Введем переменные , которые соответствуют паре из -того юноши и -той девушки и удовлетворяют ограничениям:

с целевой функцией . Можно показать, что среди оптимальных решений этой задачи найдется целочисленное. Переменные равные 1, будут соответствовать парам, которые следует поженить.

Максимальный поток

Пусть имеется граф (с ориентированными ребрами), в котором для каждого ребра указана его пропускная способность. И заданы две вершины: сток и исток. Нужно указать для каждого ребра, сколько через него будет протекать жидкости (не больше его пропускной способности) так, чтобы максимизировать суммарный поток из истока в сток (жидкость не может появляться или исчезать во всех вершинах, кроме истока и стока, соответственно).

Возьмем в качестве переменных — количество жидкости, протекающей через -тое ребро. Тогда

,

где — пропускная способность -того ребра. Эти неравенства надо дополнить равенством количества втекающей и вытекающей жидкости для каждой вершины, кроме стока и истока. В качестве функции естественно взять разность между количеством вытекающей и втекающей жидкости в истоке.

Обобщение предыдущей задачи — максимальный поток минимальной стоимости. В этой задаче даны стоимости для каждого ребра и нужно среди максимальных потоков выбрать поток с минимальной стоимостью. Эта задача сводится к двум задачам линейного программирования: сначала нужно решить задачу о максимальном потоке, а потом добавить к этой задаче ограничение , где — величина максимального потока, и решить задачу с новой функцией — стоимостью потока.

Эти задачи могут быть решены быстрее, чем общими алгоритмами решения задач линейного программирования, за счет особой структуры уравнений и неравенств.

Транспортная задача

Имеется некий однородный груз, который нужно перевезти с складов на заводов. Для каждого склада известно, сколько в нем находится груза , а для каждого завода известна его потребность в грузе. Стоимость перевозки пропорциональна расстоянию от склада до завода (все расстояния от -го склада до -го завода известны). Требуется составить наиболее дешевый план перевозки.

Решающими переменными в данном случае являются — количества груза, перевезенного из -го склада на -й завод. Они удовлетворяют ограничениям:

Целевая функция имеет вид: , которую надо минимизировать.

Игра с нулевой суммой

Есть матрица размера . Первый игрок выбирает число от 1 до , второй — от 1 до . Затем они сверяют числа и первый игрок получает очков, а второй очков ( — число, выбранное первым игроком, — вторым). Нужно найти оптимальную стратегию первого игрока.

Пусть в оптимальной стратегии, например, первого игрока число нужно выбирать с вероятностью . Тогда оптимальная стратегия является решением следующей задачи линейного программирования:

,

,

(),

в которой нужно максимизировать функцию . Значение в оптимальном решении будет математическим ожиданием выигрыша первого игрока в наихудшем случае.

Алгоритмы решения

Наиболее известным и широко применяемым на практике для решения общей задачи линейного программирования (ЛП) является симплекс-метод. Несмотря на то, что симплекс-метод является достаточно эффективным алгоритмом, показавшим хорошие результаты при решении прикладных задач ЛП, он является алгоритмом сэкспоненциальной сложностью. Причина этого состоит в комбинаторном характере симплекс-метода, последовательно перебирающего вершины многогранникадопустимых решений при поиске оптимального решения.

Первый полиномиальный алгоритм, метод эллипсоидов, был предложен в 1979 году советским математиком Л. Хачияном, разрешив таким образом проблему, долгое время остававшуюся нерешенной. Метод эллипсоидов имеет совершенно другую, некомбинаторную природу, нежели симплекс-метод. Однако в вычислительном плане этот метод оказался неперспективным. Тем не менее, сам факт полиномиальной сложности задач привел к созданию целого класса эффективных алгоритмов ЛП — методов внутренней точки, первым из которых был алгоритм Н. Кармаркара, предложенный в 1984 году. Алгоритмы этого типа используют непрерывную трактовку задачи ЛП, когда вместо перебора вершин многогранника решений задачи ЛП осуществляется поиск вдоль траекторий в пространстве переменных задачи, не проходящих через вершины многогранника. Метод внутренних точек, который, в отличие от симплекс-метода, обходит точки из внутренней части области допустимых значений, использует методы логарифмических барьерных функций нелинейного программирования, разработанные в 1960-х годах Фиако (Fiacco) и МакКормиком (McCormick).

См. также

• дискретное программирование
• Нелинейное программирование
• динамическое программирование ,
• Алгоритм Данцига
• Графический метод решения задачи линейного программирования
• Дробно-линейное программирование
• Модель «затраты — выпуск»

А как ты думаешь, при улучшении линейное программирование, будет лучше нам? Надеюсь, что теперь ты понял что такое линейное программирование и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математическое программирование

ПРИМЕНЕНИЕ ЭЛЕМЕНТОВ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ ПРИ РЕШЕНИИ ПРАКТИЧЕСКИХ ЗАДАЧ И ИХ ЭКОНОМИЧЕСКИЙ АНАЛИЗ

ПРИМЕНЕНИЕ ЭЛЕМЕНТОВ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ ПРИ РЕШЕНИИ ПРАКТИЧЕСКИХ ЗАДАЧ И ИХ ЭКОНОМИЧЕСКИЙ АНАЛИЗ

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Добрыгин О.П. 1

---

1ГБПОУ МО «КРАСНОЗАВОДСКИЙ КОЛЛЕДЖ»

Морозова В.И. 1

---

1ГБПОУ МО «КРАСНОЗАВОДСКИЙ КОЛЛЕДЖ»

Автор работы награжден дипломом победителя III степени

Диплом школьникаСвидетельство руководителя

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение

Линейное программирование – это раздел математики, ориентированный на нахождение экстремума в задачах, которые описываются линейными уравнениями.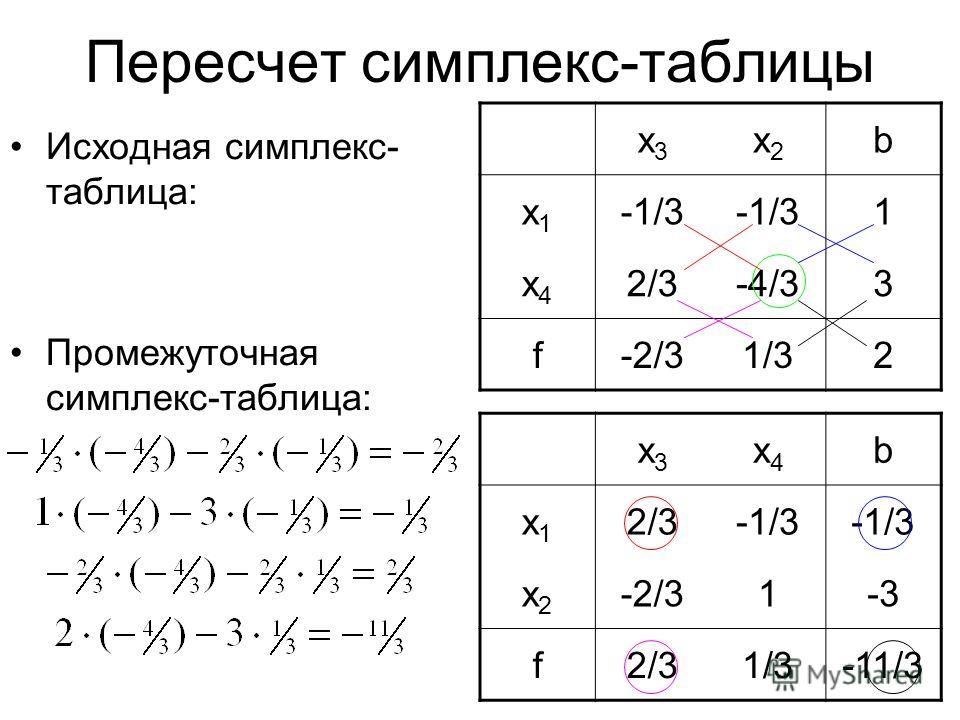

Причем линейными уравнениями описывается как целевая функция, так и входные параметры условия ограничений на входные параметры.

Необходимым условием задач линейного программирования является обязательное наличие ограничений на ресурсы (сырье, материалы, финансы, спрос производственной продукции и т.д.). Другим важным условием решения задачи является выбор критерия останова алгоритма, т.е. целевая функция должна быть оптимальна в некотором смысле. Оптимальность должна быть выражена количественно.

Первое упоминание (1938 г.) о математических методах в эффективном управлении производством принадлежит советскому математику Л.В. Канторовичу. Год спустя, в 1939 г. Л.В. Канторович опубликовал работу «Математические методы организации и планирования производства» и практически применил полученные результаты. Термин «линейное программирование» ввели американские математики Дж. Данциг и Т. Купманс в конце 40-х годов.

Дж. Данциг разработал математический аппарат симплексного метода решения задач линейного программирования (1951 г.). Симплексный метод находит применение для решения широкого круга задач линейного программирования и до настоящего времени является одним из основных методов.

Практическая часть

Для изготовления изделий A и B фабрика расходует в качестве сырья сталь и цветные металлы, имеющиеся в ограниченном количестве. Указанные изделия производят с помощью токарных и фрезерных станков.

Цель: Определить план выпуска продукции, при котором будет достигнута максимальная прибыль.

Исходные данные приведены ниже:

Вид ресурса	Объем ресурса	Нормы расхода на одно изделие
		Изделие A	Изделие B
Сталь, кг	570	10	70
Цветные металлы, кг	420	20	50
Токарные станки, станко-час	5600	300	400
Фрезерные станки, станко-час	3400	200	100
Прибыль, ден. ед.		3	8

Составим математическую модель данной задачи. Для этого необходимо выбрать переменные задачи, задать целевую функцию и составить систему ограничений.

Пусть х₁ – количество изделий А и х₂ – количество изделий В.

Целевая функция будет иметь вид:

Разберемся что здесь к чему:

— Целевая функция, которая образует нашу прибыль — Прибыль компании от x₁ количества выпущенной продукции A— Прибыль компании от x₂ количества выпущенной продукции A

— Функция стремится к максимальному значению, т. к. мы ищем максимальную прибыль нашей компании при искомых значениях аргументов Xn.

Составим ограничения нашей функции, в зависимости условия задачи:

х1 ≥ 0 и х2 ≥ 0 — условие неотрицательности	Ограничение по запасам стали
	Ограничение по запасам цветным металлам
	Ограничение по времени работы на токарных станках
	Ограничение по времени работы на фрезерных станках

Что и откуда?Давайте разбираться:

Как вы уже могли заметить,10 – это норма расхода Стали на изделие A(x1),что видно из нашей таблицы, а 70 – это нормы расхода Стали на изделие B(x2).

570 –это количество ограничения Стали на самой фабрике, что мы и показываем, поставив неравенство (меньше или равно).

Такую операцию мы проделываем с каждым фактором, и получаем исходные ограничения.

Используем графический способ решения задач Линейного программирования.

Для этого, строим прямые линии в системе координат, исходя из ограничений, составленных ранее. Выделяем область допустимых значений, которая удовлетворяет системе ограничений и условиям неотрицательности.

(построение выполнено в программе «Математический конструктор»)

10х1 + 70х2 = 570 (1)			20х1 + 50х2 = 420 (2)
Х1	0	57	Х1	0	21
Х2	8,1	0	Х2	8,4	0
300х1 + 400х2 = 5600 (3)			200х1 +100х2 = 3400 (4)
Х1	0	18,6	Х1	0	17
Х2	14	0	Х2	34	0

Мы нашли область допустимых значений нашей целевой функции (заштрихованная зона). Теперь построим вектор , который будет являться нормальным вектором линии уровня, проведем линию уровня и будем перемещать ее по направлению вектора (для задач на максимум) до тех пор, пока она не будет иметь с областью ограничений только одну общую точку. Проведем через нее опорную прямую. Определим координаты полученной точки максимума. В точке максимума пересекаются прямые (1) и (2). Решим систему из уравнений этих прямых.

Решение:

Теперь находим решение для нашей Целевой функции. В результате мы найдем Максимальную прибыль при данных аргументах (количествах выпускаемой продукции A и B).

Просто подставляем найденные значения в Целевую функцию Z:

Ответ найден: максимальная прибыль компании — 67 ден. ед. который обеспечен выпуском 9 единиц продукции типа A и 6 единиц продукции типа B.

Экономический анализ задачи

Проведем экономический анализ рассмотренной ранее задачи, для этого определим, как влияет на оптимальное решение увеличение или уменьшение запасов исходных продуктов.

Для анализа задачи примем, что неравенства системы ограничений могут быть активными или пассивными. Если прямая проходит через точку, в которой находится оптимальное решение, то будем считать, что она представляет активное ограничение. В противном случае прямая относится к пассивному ограничению.

Если ограничение активное, то будем считать, что соответствующий ресурс является дефицитным, так как он используется полностью. Если ограничение пассивное, то ресурс недефицитный и имеется в фирме в избытке.

Рассмотрим увеличение ресурса правой части ограничения (2) по цветным металлам. При перемещении параллельно самой себе прямой (2) вверх до пересечения с прямыми (1) и (3).

;

Т.к. мы выпускаем целую продукцию, то округляем с недостатком.

Подставляя значения в неравенство (2), получим предельно допустимый суточный запас цветных металлов:

при этом величина дохода составит:

ден.ед.

Вывод: в результате увеличения использования запаса цветных металлов с 420 кг до 480 кг, прибыль компании увеличилась с 67 до 75 ден.ед. (на 8 д.е.)

Заключение

Как показывает практика, линейное программирование очень полезный математический инструмент для изучения прибыли и поиска оптимальных стратегий в экономике и предпринимательстве. Данный инструмент был открыт не так давно (в 1938 г. ) и используется по сегодня.

Для того чтобы продемонстрировать действие этого инструмента мы использовали задачу с реальным условием. Таких условий может быть больше, а изделий (или любых других товаров) в задаче может быть бесконечное множество, но мы рассмотрели самый простой пример, для того чтобы показать основу его действия.

При экономическом анализе задачи, мы выявили, что запас цветных металлов на складе недефицитный, поэтому мы увеличили его и получили увеличение прибыли до возможного максимума.

Список литературы

1. В.П. Агальцов, И.В. Волдайская «Математические методы в программировании» 2014г. ISBN 5-8199-0267-X (ИД «Форум») ISBN 5-16-002652-5 (ИНФРА-М)

2. Под ред. В.И. Ермакова «Сборник задач по высшей математики для экономистов» 2014г. ISBN 5-16-002-395-X

3. М. С. Красс, Б.П. Чупрынов «Математика для экономистов» 2015г.

ISBN 5-94723-672-9

Просмотров работы: 906

Линейное программирование

Линейное программирование
Следующий: Об этом документе

Майкл Л. Овертон

Черновик для Encyclopedia Americana
20 декабря 1997 г.

ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ , особый класс математических задач, в котором линейная функция максимизируется (или минимизируется) при заданных линейных ограничениях. Этот класс задач достаточно широк, чтобы охватить множество интересных и важных задач. приложений, но при этом достаточно специфичных, чтобы с ними можно было работать, даже если количество переменные большие.

История. Линейное программирование как дисциплина было разработано в 1940-х годах, мотивированы изначально необходимостью решения сложных задач планирования в военное время операции. Его развитие быстро ускорилось в послевоенный период, так как многие промышленности нашли ценное применение для линейного программирования. Основателями предмета обычно считаются Джордж Б. Данциг, который разработал симплекс-метод в 1947 году и Джон фон Нейман, создавший в том же году теорию двойственности. Нобелевская премия по экономике была присуждена в 1975 к математик Леонид Канторович (СССР) и экономист Тьяллинг Купманс (США) за вклад в теорию оптимальных распределение ресурсов, в котором линейное программирование играло ключевую роль. Многие отрасли используют линейное программирование в качестве стандартного инструмента. например для оптимального распределения конечного набора ресурсов. Примеры важных областей применения включают расписание экипажей авиакомпаний, судоходные или телекоммуникационные сети, нефтепереработка и смешивание, а также выбор портфеля акций и облигаций.

Обзор. Общая форма линейной программы:

Здесь и даны числа и являются переменными, значения которых должны быть определены, максимизируя заданную цель при заданных ограничениях. Имеется n переменных и m ограничений, в дополнение к ограничениям неотрицательности на переменные. Ограничения называются линейными, потому что они включают только линейные функции переменных. Квадратичные члены, такие как или не разрешены. Если минимизация желательно вместо максимизации, это может быть достигнуто путем обращения признаки .

Пример очень полезен. Рассмотрим линейную программу

где числа и , определяющие цель максимизации , пока не уточняется. В этом примере n , количество переменных равно 2, а m , количество переменных количество ограничений, равно 3 На рисунке 1 каждое ограничение показано прямой линией с одним сторона линии заштрихована, чтобы указать, что точки на этом стороны линии не удовлетворяют соответствующему ограничению. Центральная незаштрихованная область на рисунке 1 представляет собой набор точек которые удовлетворяют все ограничения. Это называется допустимая область . Граница допустимой области представляет собой многоугольник.

Теперь рассмотрим задачу максимизации линейной функции , для заданных чисел , , по точкам лежащие в допустимой области. Количество называется целевая функция . Если , цель состоит в том, чтобы максимизировать , и из рисунка 1 видно, что это достигается за счет . Эта точка называется оптимальным решением . С другой стороны, если , , цель состоит в том, чтобы максимизировать , и оптимальное решение есть. Если , , цель заключается в максимизации , а оптимальное решение — любая точка на прямой отрезок между (2,1) и (2,2). Интуитивно ясно, что независимо от значений , , оптимальное решение находится на границе допустимой области. Для большинства вариантов , оптимальное решение равно уникальный , конкретно в вершине допустимой области, т. е. один из углов границы.

Не каждая линейная программа имеет оптимальное решение. Может случиться так, что решения не существует, либо поскольку допустимая область бесконечно велика, или потому что он пустой. Для n ; SPMgt ;2 допустимая область представляет собой многогранник размерностей n , возможно бесконечно большим или пустым. Если оптимальное решение существует, всегда должен быть один в вершине многогранника, хотя он не всегда уникален.

Наиболее замечательным математическим свойством линейных программ является теория двойственности. двойной линейной программы, приведенной выше, является

Это линейная программа по переменным. это не трудно показать, что если находится в допустимой области для первого линейная программа и находится в допустимой области для двойственной линейной программы, то первая целевая функция меньше или равна двойной целевой функции . Примечателен тот факт, что эти две цели всегда равно для любого и которые являются, соответственно, оптимальными решениями для двух линейных программ. Это имеет большое практическое значение как для интерпретации решений линейных программ и методы их вычисления решения.

Симплексный метод. Симплекс-метод был стандартным методом решения линейной задачи. программа с 1940-х гг. Вкратце, симплекс-метод переходит от вершины к вершина на границе допустимого многогранника, многократно увеличивая целевую функцию пока либо не будет найдено оптимальное решение, либо не будет установлено, что решения не существует. В принципе, время, необходимое может быть экспоненциальной функцией числа переменных, и это может произойти в некоторых надуманных случаях. Однако на практике метод является высокоэффективным, обычно требующим ряда шагов, которые просто мало кратно числу переменных. Линейные программы с тысячами или даже миллионами переменных обычно решается симплекс-методом на современных компьютерах. Эффективные, очень сложные реализации доступны в в виде пакетов компьютерных программ.

Методы внутренних точек. В 1979 году Леонид Хачиян представил метод эллипсоидов, гарантированно решить любую линейную программу за несколько шагов, которая является многочленом функция количества данных, определяющая линейную программу. Следовательно, метод эллипсоидов быстрее, чем симплексный метод в надуманные случаи, когда симплекс-метод работает плохо. На практике, однако симплексный метод намного превосходит эллипсоидный метод. В 1984 году Нарендра Кармаркар представил метод внутренних точек для линейное программирование, сочетание желаемых теоретических свойств метода эллипсоидов и Практические преимущества симплекс-метода. Его успех инициировал взрыв в развитии интерьерной точки. методы. Они не проходят от вершины к вершине, а проходят только через внутренность допустимой области. Хотя это свойство легко сформулировать, анализ методов внутренней точки — тонкий предмет, который гораздо труднее понять, чем поведение симплекс-метода. Методы внутренних точек в настоящее время обычно считаются конкурентоспособными с симплексный метод в большинстве, хотя и не во всех приложениях, и сложные программные пакеты, реализующие их, теперь доступны. Заменят ли они в конечном счете симплексный метод в промышленности? приложений не понятно.

Неотъемлемый компонент как симплексный, так и метод внутренних точек является решением систем линейные уравнения, в которых используются методы, разработанные К.Ф. Гаусс и А. Холецкий в 18-19 вв. (см. ЛИНЕЙНЫЕ УРАВНЕНИЯ и МАТРИЦЫ). Важные обобщения линейного программирования включают целочисленное программирование, квадратичное программирование, нелинейное программирование и стохастическое программирование (См. ИССЛЕДОВАНИЕ ОПЕРАЦИЙ).

ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА

1. Г.Б. Данциг, Линейное программирование и расширения , Издательство Принстонского университета, Принстон, Нью-Джерси, 1963.
2. Р.Дж. Вандербей, Линейное программирование: основы и расширения , Kluwer Academic Publishers, Бостон, 1996.
3. С.Дж. Райт, Первично-двойственные методы внутренней точки , Общество промышленной и прикладной математики, Филадельфия, 1997.
4. Дж.К. Ленстра, А.Х.Г. Ринноой Кан, А. Шривер (ред.), История математического программирования: сборник личных воспоминания , Северная Голландия, Амстердам, 1991 г.

---

• Об этом документе…

---

Далее: Об этом документе

Майкл Овертон
Сб 20 декабря 18:31:43 EST 1997

линейное программирование | Определение и факты

Ключевые люди:

Джордж Данциг Василий Леонтьев Леонид Витальевич Канторович Тьяллинг К. Купманс

Похожие темы:

симплексный метод возможное решение набор ограничений крайняя точка резервная переменная

См. весь соответствующий контент →

линейное программирование , метод математического моделирования, в котором линейная функция максимизируется или минимизируется при различных ограничениях. Этот метод был полезен для принятия количественных решений в бизнес-планировании, в промышленной инженерии и, в меньшей степени, в социальных и физических науках.

Решение задачи линейного программирования сводится к нахождению оптимального значения (наибольшего или наименьшего, в зависимости от задачи) линейного выражения (называемого целевой функцией) с учетом набора ограничений, выраженных в виде неравенств:

Дополнительная информация по этой теме

оптимизация: линейное программирование

Хотя линейное программирование широко используется в настоящее время для решения повседневных задач принятия решений, оно было сравнительно неизвестно до 1947 года. …

a , b и c являются константами, определяемыми возможностями, потребностями, затратами, прибылью и другими требованиями и ограничениями задачи. Основное предположение при применении этого метода состоит в том, что различные отношения между спросом и доступностью являются линейными; то есть ни одно из x _i не возводится в степень, отличную от 1. Чтобы получить решение этой задачи, необходимо найти решение системы линейных неравенств (т.е. набор из n значений переменных x _i , что одновременно удовлетворяет всем неравенствам). Затем целевая функция оценивается путем подстановки значений x _i в уравнение, определяющее f .

Впервые серьезные попытки применения метода линейного программирования были предприняты в конце 1930-х годов советским математиком Леонидом Канторовичем и американским экономистом Василием Леонтьевым в области производственных графиков и экономики соответственно, но их работа игнорировалась на протяжении десятилетий. Во время Второй мировой войны линейное программирование широко использовалось для управления транспортировкой, планированием и распределением ресурсов с учетом определенных ограничений, таких как стоимость и доступность. Эти заявления во многом способствовали признанию приемлемости этого метода, который получил дальнейшее развитие в 1919 г.47 с введением симплекс-метода американского математика Джорджа Данцига, который значительно упростил решение задач линейного программирования.

Однако по мере того, как решались все более сложные задачи с большим количеством переменных, количество необходимых операций увеличивалось экспоненциально и превышало вычислительную мощность даже самых мощных компьютеров. Затем, в 1979 году, русский математик Леонид Хачиян открыл алгоритм с полиномиальным временем, в котором количество вычислительных шагов растет как степень числа переменных, а не экспоненциально, что позволило решить ранее недоступные проблемы. Однако алгоритм Хачияна (называемый методом эллипсоида) на практике работал медленнее, чем симплекс-метод.