Приближенные методы решения дифференциальных уравнений
Рассмотрим задачу Коши (5.2), (5.6) для дифференциального уравнения первого порядка: найти решение уравнения y’=f(x,y), удовлетворяющее условию y(x0)=y0. Пусть y(x)- решение поставленной задачи Коши. Подставив это решение в уравнение (5.2), получим тождество y'(x) ≡ f(x,y(x)). Интегрируя это тождество по x, получаем,
или, что тоже самое,
. (5.15)
Таким образом, мы показали, что всякое решение задачи Коши (5.2), (5.6) есть решение интегрального уравнения (5.15). С другой стороны, если y(x)- решение интегрального уравнения (5.15), то дифференцируя (5.15) по x, получаем, что y(x)- решение задачи Коши (5.2), (5.6).
Решение интегрального уравнения (5.15) будем искать с помощью метода последовательных приближений. Положим
y0(x)=y0, . (5.16)
Если оператор
— (5.17)
сжимающий [12], то последовательные приближения (5.
Пример №1. Найдём с помощью метода последовательных приближений решение уравнения y’ = y, удовлетворяющее условию y(0)=1. Подставляя y(0)=1 в (5.16), получаем
y0=1, …,
С другой стороны, решая исходную задачу Коши, имеем y = ex.
Таким образом, нами получено разложение функции ex в ряд Тейлора в нуле (ряд Маклорена).
Перейдём теперь к изложению численного метода Эйлера решения задачи Коши (5.2), (5.6). Разобьём отрезок [a,b], на котором мы ищем решение, на части точками x0 = a<x1<…<xn = b. Положим yi=y(xi), hi = xi +1 — xi, 0≤i≤n.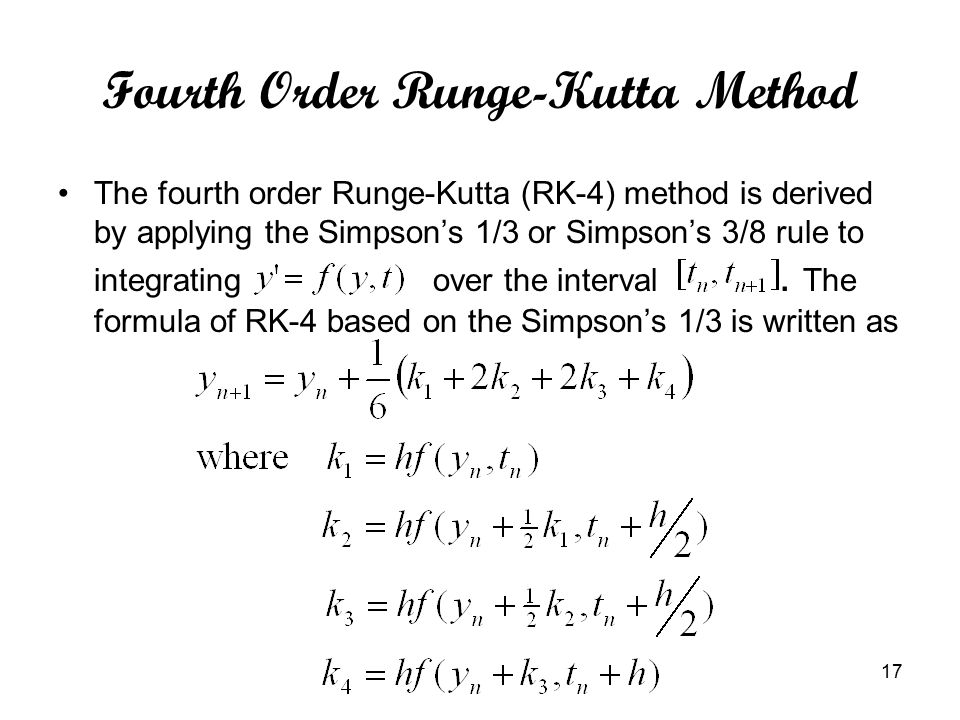
Так как по определению производной то заменяя производную y'(xi) конечной разностью в уравнении (5.2), получаем , или, что то же самое,
yi+1 = yi + h·f(xi, yi), (5.17)
Соотношение (5.17) является расчётной формулой метода Эйлера численного решения задачи Коши (5.2), (5.6). Вычислив yi , i = 0,1,..,n получим таблицу значений решения в точках xi , i = 0,1,..,n Для оценки погрешности на одном шаге сетки в методе Эйлера разложим точное решение y(x) по формуле Тейлора в окрестности точки xi до членов второго порядка малости
y(xi+1)=y(xi+h)=y(xi)+y'(xi)h+o(h2)=yi+hf(xi,yi)+o(h2).
Сравнивая с (5.17) видим, что погрешность формулы (5.17) равна o(h
y=2x
Очевидно, для получения таких интегральных кривых система Wolfram|Alpha использует приближенные (численные) методы интегрирования дифференциальных уравнений.
Чтобы получить само численное решение обыкновенного дифференциального уравнения (Ordinary Differential Equation, ODE, Numerical Differential Equation Solving), в частности, в виде таблицы значений искомой функции, запрос solve нужно уточнить, дополнив его специальными параметрами:
solve {дифференциальное уравнение, начальные условия} (метод интегрирования) [шаг интегрирования] [отрезок интегрирования]
Обязательные параметры — само дифференциальное уравнение, начальные условия и численный метод интегрирования.
Не забудьте, что количество начальных условий должно совпадать с порядком уравнения. Иначе, Wolfram Alpha автоматически подставит в запрос свои начальные или краевые условия.
Рекомендуется указывать явно отрезок интегрирования.
y=2x, y(1)=2} Euler method x=1..4
Если указаны все необходимые параметры, то кроме графика численного решения дифференциального уравнения (интегральной кривой), Wolfram Alpha также выведет само численное решение — таблицу значений искомой функции:
Когда дифференциальное уравнение, которое вы решаете численным методом, допускает также аналитическое решение, тогда по запросу solve система Wolfram Alpha выводит точную и приближенную интегральные кривые уравнения, соответствующие заданным начальным условиям, а также график погрешностей, таблицу значений искомой функции, таблицу погрешностей, и, конечно, само аналитическое решение:
solve {y’+2xy=0, y(1)=2} Euler method x=1..3
Кроме того, здесь Wolfram Alpha выводит таблицу для сравнения погрешностей всех численных методов, которые использует система (в крайней точке интервала интегрирования дифференциального уравнения):
В рассмотренном примере шаг интегрирования, равный 0.
2, был выбран автоматически. Выше было сказано, что можно явно указать нужный шаг интегрирования. Причем, нужно выбирать его так, чтобы на заданном отрезке умещалось не менее, чем 10 шагов интегрирования. Уменьшая шаг интегрирования, можно получать численные решения с желаемой точностью точностью:
solve {y’+2xy=0, y(1)=2} Euler method h=.05 x=1..3
Численные решения дифференциальных уравнений, рассмотренные выше, были получены простейшим методом — методом Эйлера (Euler method). Как мы видели выше, Wolfram Alpha реализует и другие численные методы интегрирования дифференциальных уравнений. Посмотрите примеры (по ссылке):
- Euler method — метод Эйлера;
- midpoint method — метод средних точек, модифицированный метод Эйлера;
- Heun’s method (метод Хойна, вариант модифицированного метода Эйлера)
- third‐order Runge‐Kutta method (метод Рунге-Кутты третьего порядка)
- fourth‐order Runge‐Kutta method (метод Рунге-Кутты четвертого порядка)
- Runge‐Kutta‐Fehlberg method (метод Рунге-Кутты-Фелберга, RKF method )
- Bogacki‐Shampine method
- Dormand‐Prince method(DOPRI method)
- backward Euler method
- implicit midpoint method
С помощью Wolfram Alpha, можно решать не только обыкновенные дифференциальные уравнения 1-го порядка (ОДУ-1), но и обыкновенные дифференциальные уравнения высших порядков.
Например, вот так Wolfram Alpha решает обыкновенное дифференциальное уравнение 3-го порядка:
solve {y«`= -2xy`, y(0) = 0, y`(0) = -1, y«(0) = -2} Runge-Kutta method h =.25 x=0..3
Таким образом, численное решение обыкновенных дифференциальных уравнений в системе Wolfram Alpha является достаточно простой стандартной процедурой, соблюдение которой гарантирует правильный результат.
Следующее Предыдущее Главная страница
Калькулятор метода Рунге-Кутты четвертого порядка
Решение
Метод Рунге-Кутты утверждает, что $$$y_{n+1} = y_{n} + \frac{h}{6} \left(k_{ 1} + 2 k_{2} + 2 k_{3} + k_{4}\right)$$$, где $$$t_{n+1} = t_{n} + h$$$, $$$ k_{1} = f{\left(t_{n},y_{n} \right)}$$$, $$$k_{2} = f{\left(t_{n} + \frac{h} {2},y_{n} + \frac{h k_{1}}{2} \right)}$$$, $$$k_{3} = f{\left(t_{n} + \frac{ h}{2},y_{n} + \frac{h k_{2}}{2} \right)}$$$ и $$$k_{4} = f{\left(t_{n} + h,y_{n} + h k_{3} \right)}$$$.
У нас есть $$$h = \frac{2}{5}$$$, $$$t_{0} = 0$$$, $$$y_{0} = 1$$$ и $ $$f{\left(t,y\right)} = \sin{\left(t y \right)}$$$.
$$$t_{1} = t_{0} + h = 0 + \frac{2}{5} = \frac{2}{5}$$$
$$$ k_{1} = f{\left(t_{0},y_{0} \right)} = f{\left(0,1\right)} = 0$$$
$$$k_{2} = f {\ left (t_ {0} + \ frac {h} {2}, y_ {0} + \ frac {h k_ {1}} {2} \ right)} = f {\ left (0 + \ frac {\ frac {2} {5} {2}, 1 + \ frac {\ left (\ frac {2} {5} \ right) \ cdot \ left (0 \ right)} {2} \ right) } = е {\ влево (\ гидроразрыва {1} {5}, 1 \ вправо)} = 0,198669330795061$$$
$$$k_{3} = f{\left(t_{0} + \frac{h}{2},y_{0} + \frac{h k_{2}}{2} \ right)} = f {\ left (0 + \ frac {\ frac {2} {5}} {2}, 1 + \ frac {\ left (\ frac {2} {5} \ right) \ cdot \ влево (0,198669330795061 \ вправо)} {2} \ вправо)} = f {\ влево (\ гидроразрыва {1} {5}, 1,03973386615901 \ вправо)} = 0,206451342596583$$$
$$$k_{4} = f {\ left (t_ {0} + h, y_ {0} + h k_ {3} \ right)} = f {\ left (0 + \ frac {2} {5}, 1 + \ left (\ frac { 2} {5} \ справа) \ cdot \ слева (0,206451342596583 \ справа) \ справа)} = f {\ слева (\ гидроразрыва {2} {5}, 1,08258053703863 \ справа)} = 0,419625061196877$$$
$$$y_{1} = y{\left(t_{1} \right)} = y{\left(\frac{2}{5} \right)} = y_{0} + \ frac {h} {6} \ left (k_ {1} + 2 k_ {2} + 2 k_ {3} + k_ {4} \ right) = 1 + \ frac {\ frac {2} {5} {6} \left(0 + 2 \cdot 0,198669330795061 + 2 \cdot 0,206451342596583 + 0,419625061196877\right) = 1,08199109386534$$$
1 Шаг 2 9001 _{2} = t_{1} + ч = \frac{2}{5} + \frac{2}{5} = \frac{4}{5}$$$$$$k_{1} = f{\left(t_{1}, у_ {1} \ справа)} = е {\ влево (\ гидроразрыва {2} {5}, 1,08199109386534 \right)} = 0,419411035089935$$$
$$$k_{2} = f{\left(t_{1} + \frac{h}{2},y_{1} + \frac{h k_{ 1}}{2} \right)} = f{\left(\frac{2}{5} + \frac{\frac{2}{5}}{2},1,08199109386534 + \frac{\left(\ frac{2}{5}\right)\cdot\left(0,419411035089935\right)}{2}\right)} = f{\left(\frac{3}{5},1,16587330088333\right)} = 0,6438535344$ $$
$$$k_{3} = f{\left(t_{1} + \frac{h}{2},y_{1} + \frac{h k_{2}}{2} \right )} = е {\ влево (\ гидроразрыва {2} {5} + \ гидроразрыва {2} {5}} {2}, 1,08199109386534 + \ гидроразрыва {\ влево (\ гидроразрыва {2} {5} \ вправо)\cdot\влево(0,6438535344 \ справа) {2} \ справа)} = f {\ слева (\ гидроразрыва {3} {5}, 1,21076180076349 \ справа)} = 0,664225362212255$$$
$$$k_{4} = f{\ влево (t_ {1} + h, y_ {1} + h k_ {3} \ right)} = f {\ left (\ frac {2} {5} + \ frac {2} {5}, 1,08199109386534 + \ влево (\ гидроразрыва {2} {5} \ вправо) \ cdot \ влево (0,664225362212255 \ вправо) \ вправо)} = f {\ влево (\ гидроразрыва {4} {5}, 1,34768123875025 \ вправо)} = 0,881081971595253 $ $ $
$$$y_{2} = y{\left(t_{2} \right)} = y{\left(\frac{4}{5} \right)} = y_{1} + \frac {h}{6} \left(k_{1} + 2k_{2} + 2k_{3} + k_{4}\right) = 1,08199109386534 + \frac{\frac{2}{5}}{6} \left(0,419411035089935 + 2 \cdot 0,6438535344 + 2 \cdot 0,664225362212255 + 0,881081971595253\right) = 1,342104111
Этап 3$ $$t_{3} = t_{2} + h = \frac{4}{5} + \frac{2}{5} = \frac{6}{5}$$$
$$$k_{ 1} = f {\ left (t_ {2}, y_ {2} \ right)} = f {\ left (\ frac {4} {5}, 1,34310114720475 \ right)} = 0,879343087787042 $ $ $
$ $ $ k_ {2} = f {\ left (t_ {2} + \ frac {h} {2}, y_ {2} + \ frac {h k_ {1}} {2} \ right)} = f {\ влево (\ гидроразрыва {4} {5} + \ гидроразрыва {2} {5}} {2}, 1,34310114720475 + \ гидроразрыва {\ влево (\ гидроразрыва {2} {5} \ вправо) \ cdot \ влево (0,879343087787042\справа)}{2}\справа)} = f{\слева(1,1,51896976476216\справа)} = 0,998657304313516$$$
$$$k_{3} = f{\left(t_{2} + \ frac {h} {2}, y_ {2} + \ frac {h k_ {2}} {2} \ right)} = f {\ left (\ frac {4} {5} + \ frac {\ frac {2}{5}}{2},1,34310114720475 + \frac{\left(\frac{2}{5}\right)\cdot \left(0,998657304313516\right)}{2} \right)} = f{ \left(1,1.
54283260806746 \right)} = 0,99960
$$$k_{4} = f{\left(t_{2} + h,y_{2} + h k_{3} \right) } = е {\ влево (\ гидроразрыва {4} {5} + \ гидроразрыва {2} {5}, 1,34310114720475 + \ влево (\ гидроразрыва {2} {5} \ справа) \ cdot \ влево (0,99960
$$$y_{3} = y{\left(t_{ 3} \right)} = y{\left(\frac{6}{5} \right)} = y_{2} + \frac{h}{6} \left(k_{1} + 2 k_{2 } + 2 k_{3} + k_{4}\right) = 1,34310114720475 + \frac{\frac{2}{5}}{6} \left(0,879343087787042 + 2 \cdot 0,998657304313516 + 2 \cdot 0,99960
$$$t_{4} = t_{3} + h = \frac{6}{5} + \frac{2}{5} = \frac {8}{5}$$$
$$$k_{1} = f{\left(t_{3},y_{3}\right)} = f{\left(\frac{6}{5},1,72598970236746\right)} = 0,877394887797677 $$$
$$$k_{2} = f{\left(t_{3} + \frac{h}{2},y_{3} + \frac{h k_{1}}{2} \ справа)} = е {\ влево (\ гидроразрыва {6} {5} + \ гидроразрыва {2} {5} {2}, 1,72598970236746 + \ гидроразрыва {\ влево (\ гидроразрыва {2} {5} \right)\cdot \left(0,877394887797677\right)}{2} \right)} = f{\left(\frac{7}{5},1,
867992699\right)} = 0,461368005308125$$$$$$ k_ {3} = f {\ left (t_ {3} + \ frac {h} {2}, y_ {3} + \ frac {h k_ {2}} {2} \ right)} = f {\ left (\ гидроразрыва {6} {5} + \ гидроразрыва {2} {5} {2}, 1,72598970236746 + \ гидроразрыва {\ влево (\ гидроразрыва {2} {5} \ справа) \ cdot \ влево (0,461368005308125 \ справа)} {2} \ справа)} = f {\ влево (\ гидроразрыва {7} {5} ,1,81826330342908 \right)} = 0,561356508370458$$$
$$$k_{4} = f{\left(t_{3} + h,y_{3} + h k_{3} \right)} = f{ \left(\frac{6}{5} + \frac{2}{5},1.
72598970236746 + \left(\frac{2}{5}\right)\cdot \left(0.561356508370458\right) \right)} = f {\ left (\ frac {8} {5}, 1,95053230571564 \ right)} = 0,020739477392444 $$$
$$$y_{4} = y{\left(t_{4} \right)} = y {\ left (\ frac {8} {5} \ right)} = y_ {3} + \ frac {h} {6} \ left (k_ {1} + 2 k_ {2} + 2 k_ {3} + k_{4}\справа) = 1,72598970236746 + \frac{\frac{2}{5}}{6} \left(0,877394887797677 + 2 \cdot 0,461368005308125 + 2 \cdot 0,561356508370458 + 0,020739477392444\right) = 1,9522238544$
Этап 5$ $$t_{5} = t_{4} + h = \frac{8}{5} + \frac{2}{5} = 2$$$
$$$k_{1} = f{\left (t_{4},y_{4}\right)} = f{\left(\frac{8}{5},1,92222859520394\right)} = 0,06597893710495$$$
$$$k_{2} = f {\ left (t_ {4} + \ frac {h} {2}, y_ {4} + \ frac {h k_ {1}} {2} \ right)} = f {\ left (\ frac {8} {5} + \ frac {\ frac {2} {5} {2}, 1,92222859520394 + \ гидроразрыва {\ влево (\ гидроразрыва {2} {5} \ справа) \ cdot \ влево (0,06597893710495 \ справа)} {2} \ справа)} = f {\ влево (\ гидроразрыва {9} {5} ,1,93542438262493 \right)} = -0,33553324651362$$$
$$$k_{3} = f{\left(t_{4} + \frac{h}{2},y_{4} + \frac{h k_{2}}{2} \right)} = f{\left(\frac{8}{5} + \frac{\frac{2}{5}}{2},1,92222859520394 + \frac{\left (\ frac {2} {5} \ right) \ cdot \ left (-0,33553324651362 \ right)} {2} \ right)} = f {\ left (\ frac {9} {5}, 1,855121945
\ right)} = -0,196342927593455$$$
$$$k_{4} = f{\left(t_{4} + h,y_{4} + h k_{3} \right)} = f{\left(\frac {8}{5} + \фракция{2}{5},1,92222859520394 + \left(\frac{2}{5}\right)\cdot \left(-0,196342927593455\right) \right)} = f{\left(2,1.
84369142416656\right)} = -0,51
$$$y_{5} = y{\left(t_{5} \right)} = y{\left(2 \right)} = y_{4} + \frac{h}{6} \left( k_{1} + 2 k_{2} + 2 k_{3} + k_{4}\right) = 1,92222859520394 + \frac{\frac{2}{5}}{6} \left(0,06597893710495 + 2 \left (-0,33553324651362\справа) + 2 \слева(-0,196342927593455\справа) — 0,5145672128\справа) = 1,82110412475186$$$
12. Численное решение дифференциальных уравнений Рунге-Кутты (RK4)
В последнем разделе метод Эйлера дал нам один из возможных подходов к численному решению дифференциальных уравнений.
Проблема с методом Эйлера заключается в том, что вы должны использовать небольшой размер интервала, чтобы получить достаточно точный результат. То есть это не очень эффективно.
Метод Рунге-Кутты дает лучший результат за меньшее количество шагов.
Метод Рунге-Кутта Порядок 4 Формула
Применение RK4
Механика
- Пружины и амортизаторы на автомобилях (Этот пружинный апплет использует RK4.
)
)Биология
- Модели «хищник-жертва»
- Крах рыболовства
- Доставка лекарств
- Прогноз эпидемии
Физика
- Модели изменения климата
- Защита от озона
Авиация
- Бортовые компьютеры
- Аэродинамика
`y(x+h)` `=y(x)+` `1/6(F_1+2F_2+2F_3+F_4)`
где
`F_1=hf(x,y)`
`F_2=hf(x+h/2,y+F_1/2)` `F_3=hf(x+h/2,y+F_2/2)`
`F_4=hf(x+h,y+F_3)`
Откуда взялась эта формула?
Вот краткое описание формулы.
Вывод формулы
Ранее мы узнали, что ряд Тейлора дает нам достаточно хорошее приближение к функции, особенно если мы находимся достаточно близко к некоторой известной начальной точке и берем достаточно членов.
Однако одним из недостатков метода Тейлора является то, что вам нужно дифференцировать вашу функцию один раз для каждого нового члена, который вы хотите вычислить.
Это может быть проблематично для сложных функций и плохо работает в компьютерном моделировании.
Карл Рунге (произносится как «рунга») и Вильгельм Кутта (произносится как «кута») стремились предоставить метод аппроксимации функции без необходимости дифференцировать исходное уравнение.
Их подход заключался в том, чтобы смоделировать столько же шагов метода ряда Тейлора, но с использованием оценки только исходной функции.
Метод Рунге-Кутты порядка 2
Начнем с двух вычислений функции в форме:
`F_1=hf(x,y)`
`F_2=hf(x+альфа h,y+бета F_1)`
«Альфа» и «бета» неизвестны. Идея заключалась в том, чтобы взять линейную комбинацию терминов «F_1» и «F_2», чтобы получить приближение значения «y» при «x = x_0+h» и найти соответствующие значения «альфа» и «бета». .
Сравнивая значения, полученные с использованием метода ряда Тейлора и приведенных выше условий (здесь я избавлю вас от подробностей), они получили следующее: Метод Рунге-Кутта Заказ 2 :
`y(x+h)=y(x)+1/2(F_1+F_2)`
где
`F_1=hf(x,y)`
`F_2=hf(x+h,y+F_1)`
Рунге-Кутта Метод порядка 3
Как обычно в этой работе, чем больше членов мы берем, тем лучше решение.
Лучший результат дает метод порядка 3:
`у(х+ч)=` `у(х)+1/9(2F_1+3F_2+4F_3)`
где
`F_1=hf(x,y)`
`F_2=hf(x+h/2,y+F_1/2)`
`F_3=hf(x+(3h)/4,y+(3F_2)/4)`
Это было получено аналогично предыдущей формуле путем сравнения результатов ряда Тейлора.
Наиболее часто используемой формулой Рунге-Кутты является формула порядка 4 (RK4), поскольку она обеспечивает наилучшее соотношение между вычислительными требованиями и точностью.
Давайте посмотрим на пример, чтобы увидеть, как это работает. 9(0,1+0,96545654732))` `= -0,03154393258`
Шаг 2
Затем мы берем эти 4 значения и подставляем их в формулу Рунге-Кутты RK4:
`y(x+h)` `=y(x)+1/6(F_1+2F_2+2F_3+F_4)`
`=1+1/6(-0.03678794411` `-\ 2xx0.03454223937` `-\ 2xx0.03454345267` `{:-\ 0.03154393258)`
`=0,9655827899`
Используя это новое значение y, мы начнем заново, найдем новые `F_1`, `F_2`, `F_3` и `F_4` и подставим их в формулу Рунге-Кутты.
Продолжаем этот процесс и создаем следующую таблицу значений Рунге-Кутты. (Я использовал электронную таблицу, чтобы получить таблицу. Использование калькулятора очень утомительно и чревато ошибками.)
| `х` | `у` | `F_1 = h dy/dx` | `х+ч/2` | `у+F_1/2` | `F_2` | `y+F_2/2` | `F_3` | `х+ч` | `у+F_3` | `F_4` | |
| 0 | 1 | −0,0367879441 | 0,05 | 0,9816060279 | −0,0345422394 | 0,9827288803 | −0,0345434527 | 0,1 | 0,9654565473 | −0,0315439326 | |
| 0,1 | 0,9655827899 | −0,0315443 | 0,15 | 0,9498106398 | −0,0278769283 | 0,9516443257 | −0,0278867954 | 0,2 | 0,9376959945 | −0,023647342 | |
| 0,2 | 0,937796275 | −0,023648185 | 0,25 | 0,9259721824 | −0,0189267761 | 0,9283328869 | −0,0189548088 | 0,3 | 0,9188414662 | −0,0138576597 | |
| 0,3 | 0,9189181059 | −0,0138588628 | 0,35 | 0,9119886745 | −0,0084782396 | 0,9146789861 | −0,0085314167 | 0,4 | 0,9103866892 | −0,0029773028 | |
| 0,4 | 0,9104421929 | −0,0029786344 | 0,45 | 0, | 28756 | 0,0026604329 | 0,9117724093 | 0,002580704 | 0,5 | 0,9130228969 | 0,0082022376 |
| 0,5 | 0,913059839 | 0,0082010354 | 0,55 | 0,9171603567 | 0,013727301 | 0,9199234895 | 0,0136258867 | 0,6 | 0,9266857257 | 0,018973147 | |
| 0,6 | 0,9267065986 | 0,0189722976 | 0,65 | 0,9361927474 | 0,0240794197 | 0,9387463085 | 0,0239658709 | 0,7 | 0,9506724696 | 0,0287752146 | |
| 0,7 | 0,9506796142 | 0,0287748718 | 0,75 | 0,9650670501 | 0,0332448616 | 0,967302045 | 0,0331305132 | 0,8 | 0,9838101274 | 0,0372312889 | |
| 0,8 | 0,9838057659 | 0,0372315245 | 0,85 | 1. 0024215282 | 0,0409408747 | 1.0042762033 | 0,0408359751 | 0,9 | 1.024641741 | 0,0441484563 | |
| 0,9 | 1.024628046 | 0,0441492608 | 0,95 | 1.0467026764 | 0,0470593807 | 1.0481577363 | 0,0469712279 | 1 | 1.0715992739 | 0,0494916177 | |
| 1 | 1.0715783953 |
Я не включил значения после `y` в нижнюю строку, так как мы не будем их использовать.
Вот график найденных решений от `x=0` до `x=1`.
Ради интереса я расширил результат до `x=10`, и вот результирующий график:
Упражнение
Решите следующее, используя RK4 (метод Рунге-Кутта порядка 4) для `0 le x le 2`. Используйте размер шага `h=0.2`:
`dy/dx=(x+y)sin xy`
`у(0) = 5`
Ответить
Шаг 1
У нас есть `x_0=0` и `y_0=5`.
`F_1=hf(x,y)` `= 0,2((0+5)sin (0)(5))` `= 0`
Для `F_2` нам нужно знать:
`x+h/2 = 0+0,2/2 = 0,1` и
`y+F_1/2 = 5+0/2=5 `
Подставляем их в выражение `F_2`: `=0.48
4937`Для `F_3` нам нужно знать:
`y+F_2/2` `= 5+0,48
4937/2` `=5,24450702469`
Так
`F_3=hf(x+h/2,y+F_2/2) `
`= 0.2((0.1+5.24450702469)` `{:xxsin (0.1)(5.24450702469))`
`=0.53523913352`
Для `F_4` нам нужно знать:85
`y+F_3` `= 5+0,53523913352` `= 5,53523913352 `
Так
`F_4=hf(x+h,y+F_3)`
`= 0,2((0,2+5,53523913352)` `{:xxsin (0,2)(5,53523913352))` 5=
Шаг 2
Затем мы берем эти 4 значения и подставляем их в формулу Рунге-Кутты RK4:
`y(x+h)=y(x)+1/6(F_1+2F_2+2F_3+F_4) `
`=5+1/6(0+ ` `2xx0.48
4937+ ` `2xx0.53523913352 ` `{:+ 1.025891)` `=5.5124008953`` value и используйте новое значение `x_1=0.
2`, чтобы найти следующее значение, `y_2`, и так далее до `x=2`.
Ниже приведена таблица результирующих значений.
Вот такая таблица значений у нас получается.
Просмотр таблицы
| `х` | `у` | `F_1 = h dy/dx` | `х+ч/2` | `у+F_1/2` | `F_2` | `y+F_2/2` | `F_3` | `х+ч` | `у+F_3` | `F_4` |
| 0 | 5 | 0 | 0,1 | 5 | 0,48494 | 5.2445070247 | 0,5352391335 | 0,2 | 5,5352391335 | 1.02589 |
| 0,2 | 5.5124008953 | 1.0194689011 | 0,3 | 6.0221353458 | 1.229424454 | 6.1271131223 | 1.2397613573 | 0,4 | 6,7521622525 | 0,6102193187 |
| 0,4 | 6.6070775356 | 0,670350862 | 0,5 | 6,9422529666 | -0,4816655538 | 6. 3662447588 | -0,0570142602 | 0,6 | 6.5500632755 | -1,0142481364 |
| 0,6 | 6.3702013853 | -0,8771352065 | 0,7 | 5,931633782 | -1,1235642458 | 5.8084192624 | -1.03691 | 0,8 | 5.3311976162 | -1.1055304726 |
| 0,8 | 5.31804 | -1.0980514561 | 0,9 | 4,7698753724 | -1,0356506358 | 4.8010757825 | -1,0539783626 | 1 | 4,2649227378 | -0,9493143311 |
| 1 | 4.2811304698 | -0,9595184486 | 1,1 | 3.8013712455 | -0,8453508288 | 3,8584550553 | -0,8850171765 | 1,2 | 3,3961132933 | -0,7389191476 |
| 1,2 | 3.421268202 | -0,7592177155 | 1,3 | 3.0416593442 | -0,6304549629 | 3. 1060407205 | -0,6882207337 | 1,4 | 2,7330474682 | -0,5227646767 |
| 1,4 | 2,7680459044 | -0,5581856458 | 1,5 | 2.4889530815 | -0,4450766109 | 2,5455075989 | -0,5066587622 | 1,6 | 2,2613871422 | -0,354308929 |
| 1,6 | 2.2987183509 | -0,3984550218 | 1,7 | 2.09949084 | -0,3150804545 | 2.1411781236 | -0,3672394563 | 1,8 | 1.9314788946 | -0,2454079264 |
| 1,8 | 1,9639678892 | -0,2886730166 | 1,9 | 1.8196313809 | -0,230980612 | 1,8484775833 | -0,2714612259 | 2 | 1,6925066634 | -0,1779964411 |
| 2 | 1.71870 |
Еще раз, я не включил значения после `y` в нижней строке, так как они не требуются.
Вот график найденных решений от `x=0` до `x=2`.
Ради интереса я расширил результат до `x=6`, и вот результирующий график:
Мы наблюдаем, что график не очень гладкий. Если мы используем меньшее значение `h`, кривая обычно будет более гладкой.
На самом деле, эта кривая асимптотична относительно оси `x` (она плавно приближается к оси по мере увеличения `x`). На приведенном выше графике показано, что происходит, когда наши интервалы слишком грубые. (Эти покачивания после `x>4.5` там быть не должно.)
Вот снова график решения, но на этот раз я использовал `h=0.1`. Это лучше, но все еще есть «покачивание» возле `x=5`, которого там быть не должно.
Если бы я взял еще меньшие значения `h`, я бы получил более плавную кривую. Однако это только до определенного момента, потому что ошибки округления со временем становятся значительными. Кроме того, время вычислений увеличивается, что дает небольшую дополнительную выгоду.