Методом лагранжа привести квадратичную форму к каноническому виду: Учебное пособие по линейной алгебре

Учебное пособие по линейной алгебре

Учебное пособие по линейной алгебре

А. П. Громов. Учебное пособие по линейной алгебре. Изд-во «Просвещение». М. 1971 г. Линейные пространства, линейные преобразования, евклидовы пространства, квадратичные формы. Для студентов заочных отделений физико-математических факультетов педагогических институтов по курсу высшей алгебры. Оглавление Глава I. ЛИНЕЙНЫЕ ПРОСТРАНСТВА § 2. ПРОСТЕЙШИЕ СВОЙСТВА ЛИНЕЙНЫХ ПРОСТРАНСТВ § 3. ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЕКТОРОВ § 4. БАЗИС ЛИНЕЙНОГО ПРОСТРАНСТВА. КООРДИНАТЫ ВЕКТОРА ОТНОСИТЕЛЬНО БАЗИСА § 5. РАЗМЕРНОСТЬ ЛИНЕЙНОГО ПРОСТРАНСТВА § 6. ИЗОМОРФИЗМ ЛИНЕЙНЫХ ПРОСТРАНСТВ § 7. ПРЕОБРАЗОВАНИЕ КООРДИНАТ ВЕКТОРА ПРИ ИЗМЕНЕНИИ БАЗИСА § 8. ПОДПРОСТРАНСТВА ЛИНЕЙНОГО ПРОСТРАНСТВА § 9. ЛИНЕЙНАЯ ОБОЛОЧКА ИЛИ ПОДПРОСТРАНСТВО, НАТЯНУТОЕ НА ДАННУЮ СИСТЕМУ ВЕКТОРОВ § 10. ФУНДАМЕНТАЛЬНАЯ СИСТЕМА РЕШЕНИЙ ОДНОРОДНОЙ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ § 11. ЛИНЕЙНОЕ МНОГООБРАЗИЕ. ЛИНЕЙНОЕ МНОГООБРАЗИЕ РЕШЕНИЙ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ Глава II. ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ § 12. ПОНЯТИЕ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ. ПРЕДСТАВЛЕНИЕ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ МАТРИЦЕЙ § 13. ПРИМЕРЫ ЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ § 14. СВЯЗЬ МЕЖДУ МАТРИЦАМИ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ В РАЗЛИЧНЫХ БАЗИСАХ § 15. ДЕЙСТВИЯ НАД ЛИНЕЙНЫМИ ПРЕОБРАЗОВАНИЯМИ И МАТРИЦАМИ. КОЛЬЦО ЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ И КОЛЬЦО МАТРИЦ § 16. ОБРАТНОЕ ПРЕОБРАЗОВАНИЕ. ВЫРОЖДЕННЫЕ И НЕВЫРОЖДЕННЫЕ ПРЕОБРАЗОВАНИЯ. РАНГ И ЯДРО ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ § 17. ОБ ИНВАРИАНТНЫХ ПОДПРОСТРАНСТВАХ И ИНДУЦИРОВАННЫХ ПРЕОБРАЗОВАНИЯХ § 18. СОБСТВЕННЫЕ ВЕКТОРЫ И СОБСТВЕННЫЕ ЗНАЧЕНИЯ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ § 19. ХАРАКТЕРИСТИЧЕСКИЙ МНОГОЧЛЕН МАТРИЦЫ И ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ. СУЩЕСТВОВАНИЕ СОБСТВЕННЫХ ВЕКТОРОВ § 20. О ПРИВЕДЕНИИ МАТРИЦЫ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ К ДИАГОНАЛЬНОЙ ФОРМЕ § 21. О СОБСТВЕННЫХ ВЕКТОРАХ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ С СИММЕТРИЧЕСКОЙ МАТРИЦЕЙ Глава III. ЕВКЛИДОВЫ ПРОСТРАНСТВА § 22. ПОНЯТИЕ ЕВКЛИДОВА ПРОСТРАНСТВА. ПРИМЕРЫ § 23. ДЛИНА ВЕКТОРА. УГОЛ МЕЖДУ ВЕКТОРАМИ. НЕРАВЕНСТВО КОШИ—БУНЯКОВСКОГО § 24. ПОНЯТИЕ МЕТРИЧЕСКОГО ПРОСТРАНСТВА § 25. ОРТОГОНАЛЬНОСТЬ ВЕКТОРОВ. ОРТОНОРМИРОВАННЫЙ БАЗИС. ОРТОГОНАЛЬНО-ДОПОЛНИТЕЛЬНОЕ ПОДПРОСТРАНСТВО § 26. ИЗОМОРФИЗМ ЕВКЛИДОВЫХ ПРОСТРАНСТВ § 27. ОРТОГОНАЛЬНЫЕ МАТРИЦЫ § 28. ОРТОГОНАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ ЕВКЛИДОВА ПРОСТРАНСТВА § 29. СИММЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ ЕВКЛИДОВА ПРОСТРАНСТВА § 30. ПРЕДСТАВЛЕНИЕ НЕВЫРОЖДЕННОГО ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ ЕВКЛИДОВА ПРОСТРАНСТВА В ВИДЕ ПРОИЗВЕДЕНИЯ ОРТОГОНАЛЬНОГО ПРЕОБРАЗОВАНИЯ НА СИММЕТРИЧЕСКОЕ § 31. ТЕОРЕМА О ТРАНСФОРМИРОВАНИИ СИММЕТРИЧЕСКОЙ МАТРИЦЫ В ДИАГОНАЛЬНУЮ МАТРИЦУ С ПОМОЩЬЮ ОРТОГОНАЛЬНОЙ Глава IV. КВАДРАТИЧНЫЕ ФОРМЫ § 32. ПОНЯТИЕ КВАДРАТИЧНОЙ ФОРМЫ § 33. ПРЕОБРАЗОВАНИЕ МАТРИЦЫ КВАДРАТИЧНОЙ ФОРМЫ ПРИ ЛИНЕЙНОЙ ЗАМЕНЕ ПЕРЕМЕННЫХ. КАНОНИЧЕСКИЙ ВИД КВАДРАТИЧНОЙ ФОРМЫ § 34. ОРТОГОНАЛЬНОЕ ПРЕОБРАЗОВАНИЕ КВАДРАТИЧНОЙ ФОРМЫ К КАНОНИЧЕСКОМУ ВИДУ § 35. НАХОЖДЕНИЕ ОРТОГОНАЛЬНОГО ПРЕОБРАЗОВАНИЯ, ПРИВОДЯЩЕГО ВЕЩЕСТВЕННУЮ КВАДРАТИЧНУЮ ФОРМУ К КАНОНИЧЕСКОМУ ВИДУ § 36. МЕТОД ЛАГРАНЖА ПРИВЕДЕНИЯ КВАДРАТИЧНОЙ ФОРМЫ К КАНОНИЧЕСКОМУ ВИДУ § 37. ЗАКОН ИНЕРЦИИ КВАДРАТИЧНЫХ ФОРМ § 38. ЭКВИВАЛЕНТНОСТЬ ВЕЩЕСТВЕННЫХ КВАДРАТИЧНЫХ ФОРМ § 39. ПРИВЕДЕНИЕ ОБЩЕГО УРАВНЕНИЯ ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА К КАНОНИЧЕСКОМУ ВИДУ

112. Приведение квадратичной формы к каноническому виду. Метод Лагранжа. Закон инерции

Теорема 1.

Любую квадратичную форму

F(X1, x2,…, Xn) = F(X)= . (1)

невырожденным линейным преобразованием X=TY, где X = (X1, X2,…, Xn)T, Y = (Y1, Y2,…, Yn)T, можно привести к виду

H(Y1, Y2,…, Yn) = . (2)

Представление квадратичной формы в виде (2) называется Каноническим видом квадратичной формы. Коэффициенты называются Каноническими коэффициентами. Матрица квадратичной формы канонического вида — диагональная матрица.

Доказательство. Докажем теорему методом математической индукции по числу N переменных в квадратичной форме F. Пусть N =1. Тогда квадратичная форма F имеет вид F = B11

X12 и является квадратичной формой канонического вида.

Предположим что теорема доказана для всех квадратичных форм, имеющих меньше чем N переменных, и докажем ее для квадратичной формы F, имеющей N переменных. Рассмотрим два случая.

1. Среди диагональных коэффициентов B11, B22, …, Bnn есть отличный от нуля. Пусть, например, B11 ≠ 0. Рассмотрим квадратичную форму , которая содержит такие же члены с неизвестным, как и наша форма F. Тогда разность

F(X1, X2,…, Xn) —

Будет квадратичной формой, содержащей только неизвестные X2,…, Xn. Отсюда

.

Вводим неизвестные

, (3)

И получим

, (4)

Где G( Y2,…, Yn) — квадратичная форма от не более чем N -1 неизвестной. Преобразование (3) невырожденное, так как матрица этого преобразования равна

,

И определитель равен B11 ≠ 0. Обратное ему преобразование тоже невырожденное и приводит форму F в форму (4). По индуктивному предположению квадратичную форму G( Y2,…, Yn) невырожденным преобразованием переменных Y2,…, Yn можно привести к квадратичной форме канонического вида. Это преобразование можно рассматривать как невырожденное, при котором неизвестная Y1 остается без изменения. Оно приводит квадратичную форму (4) к каноническому виду. Таким образом, невырожденным преобразованием переменных форма F приводится к каноническому виду.

2. Все диагональные коэффициенты B11, B22, …, Bnn равны нулю. Тогда среди коэффициентов формы должен быть отличный от нуля. Так как в противном случае форма тождественно равна нулю и являлась бы канонической. Пусть, например, B12 ≠ 0. Сделаем вспомогательное преобразование переменных так, чтобы в квадратичной форме появился квадрат. Сделаем преобразование переменных:

X1 = Z1 + Z2, X1 = Z1 — Z2, X3 = Z3,…, Xn = Zn.

Оно невырожденное, так как матрица этого преобразования равна

,

И определитель ее равен 2 и не равен нулю. В результате этого преобразования член нашей формы примет вид

2 a12X1X2 = 2 a12( Z1 + z2)(Z1 — z2) = 2 a12Z12 — 2 a12 z22,

И форме появляется ненулевой коэффициенты у квадратов двух переменных. Эти члены не могут сократиться с остальными членами, так как во все остальные члены войдет хотя бы одна из переменных Z3,…, Zn. Полученную квадратичную форму по первой части доказательства можно привести к квадратичной форме канонического вида невырожденным преобразованием переменных.



Пример. Методом Лагранжа привести квадратичную форму к каноническому виду

,

И найти преобразование переменных, приводящую эту форму к каноническому виду.

Решение. Так как в форме нет квадратов переменных, то сделаем преобразование переменных

X1 = Z1 + Z2, X1 = Z1 — Z2, X3 = Z3

Матрица этого преобразования равно

И квадратичная форма преобразуется к виду

.

Выделим полный квадрат из членов, содержащих X1

.

Полагаем Y1 =Z1 +(5/2)Z3, Y2 = Z2+(1/2) Z3, Y3 = Z3 приведем квадратичную форму к каноническому виду

.

Выразим неизвестные Z1 =Y1 — (5/2)Y3, Z2 = Y2-(1/2) Y3, Z3 = Y3. Последнее преобразование имеет матрицу

.

Тогда преобразование, переводящее данную квадратичную форму к форме канонического вида имеет матрицу, равную произведению матриц.

,

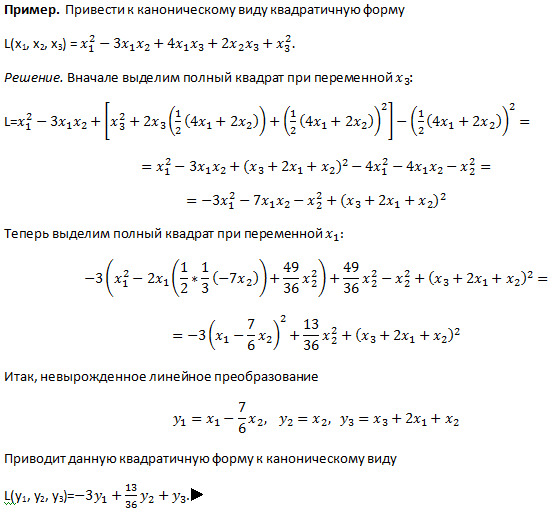
Преобразование переменных имеет вид:

X1 =Y1 + Y2 — 6Y3, X2 =Y1 — Y2 — 4Y3, X3 = Y3.

< Предыдущая		Следующая >

T D P = H, $ требуем, чтобы $P$ было обратимым. Тогда количество положительных элементов на диагонали $D$ равно количеству положительных собственных значений $H,$ количество отрицательных элементов на диагонали $D$ равно количеству собственных значений $H,$ наконец, количество нулевых элементов на диагонали $D$ совпадает с количеством нулевых собственных значений $H.$ Диагональные элементы $D$ равны НЕ собственным значениям $H,$ точно такие же $\ знаки pm$. Итак, новые имена, $$ Д = \левый( \начать{массив}{рррр} 1 и 0 и 0 и 0 \\ 0 и -1 и 0 и 0 \\ 0 и 0 и 1 и 0 \\ 0 и 0 и 0 и 0 \конец{массив} \верно) $$ $$ П = \левый( \начать{массив}{рррр} 1 и 1 и 2 и -1 \\ 0 и 1 и -1 и 1 \\ 0 и -1 и 1 и 1 \\ 0 и -1 и 0 и 1 \конец{массив} \верно), $$ $$ П^Т = \левый( \начать{массив}{рррр} 1 и 0 и 0 и 0 \\ 1 и 1 и -1 и -1 \\ 2 и -1 и 1 и 0 \\ -1 и 1 и 1 и 1 \конец{массив} \верно), $$ затем $$ \det P = 2 $$ $$ P^T D P = H $$

Описание алгоритма симметричной матрицы на http://math. stackexchange.com/questions/1388421/reference-for-linear-алгебра-books-that-teach-reverse-hermite-method-for-symmetr

 parisize = 4000000 , праймлимит = 500509
? ч = [ 1,1,2,-1; 1,1,2,-3; 2,2,4,0; -1,-3,0,1]
%1 =
[1 1 2 -1]
[1 1 2 -3]
[2 2 4 0]
[-1 -3 0 1]
? ht = маттранспонировать (ч)
%2 =
[1 1 2 -1]
[1 1 2 -3]
[2 2 4 0]
[-1 -3 0 1]
? ч - чт
%3 =
[0 0 0 0]
[0 0 0 0]
[0 0 0 0]
[0 0 0 0]
? идентификатор = [ 1,0,0,0; 0,1,0,0; 0,0,1,0; 0,0,0,1]
%4 =
[1 0 0 0]
[0 1 0 0]
[0 0 1 0]
[0 0 0 1]
? г1 = [ 1,-1,-2,1; 0,1,0,0; 0,0,1,0; 0,0,0,1]
%5 =
[1 -1 -2 1]
[0 1 0 0]
[0 0 1 0]
[0 0 0 1]
? r1t = маттранспонировать (r1)
%6 =
[1 0 0 0]
[-1 1 0 0]
[-2 0 1 0]
[1 0 0 1]
? h2 = r1t * h * r1
%7 =
[1 0 0 0]
[0 0 0 -2]
[0 0 0 2]
[0 -2 2 0]
? г2 = [ 1,0,0,0; 0,1,0,0; 0,0,1,0; 0,1,0,1]
%8 =
[1 0 0 0]
[0 1 0 0]
[0 0 1 0]
[0 1 0 1]
? r2t = маттранспонировать (r2)
%9"="
[1 0 0 0]
[0 1 0 1]
[0 0 1 0]
[0 0 0 1]
? h3 = r2t * h2 * r2
%10 =
[1 0 0 0]
[0–4 2–2]
[0 2 0 2]
[0 -2 2 0]
? г3 = [ 1,0,0,0; 0,1,1/2,-1/2; 0,0,1,0; 0,0,0,1]
%11 =
[1 0 0 0]
[0 1 1/2 -1/2]
[0 0 1 0]
[0 0 0 1]
? r3t = маттранспонировать (r3)
%12 =
[1 0 0 0]
[0 1 0 0]
[0 1/2 1 0]
[0 -1/2 0 1]
? h4 = r3t * h3 * r3
%13 =
[1 0 0 0]
[0 -4 0 0]
[0 0 1 1]
[0 0 1 1]
? г4 = [ 1,0,0,0; 0,1,0,0; 0,0,1,-1; 0,0,0,1]
%14 =
[1 0 0 0]
[0 1 0 0]
[0 0 1 -1]
[0 0 0 1]
? r4t = маттранспонировать (r4)
%15 =
[1 0 0 0]
[0 1 0 0]
[0 0 1 0]
[0 0 -1 1]
? h5 = r4t * h4 * r4
%16 =
[1 0 0 0]
[0 -4 0 0]
[0 0 1 0]
[0 0 0 0]
? д = h5
%17 =
[1 0 0 0]
[0 -4 0 0]
[0 0 1 0]
[0 0 0 0]
? г = г1 * г2 * г3 * г4
%18 =
[1 0 -2 3]
[0 1 1/2 -1]
[0 0 1 -1]
[0 1 1/2 0]
? матдет (р)
%19= 1
? q = матадджойнт (r)
%20 =
[1 1 2 -1]
[0 1/2 -1/2 1/2]
[0 -1 1 1]
[0 -1 0 1]
? qt = маттранспонировать (q)
%21 =
[1 0 0 0]
[1 1/2 -1 -1]
[2 -1/2 1 0]
[-1 1/2 1 1]
? час
%22 =
[1 1 2 -1]
[1 1 2 -3]
[2 2 4 0]
[-1 -3 0 1]
? qt * д * q
%23 =
[1 1 2 -1]
[1 1 2 -3]
[2 2 4 0]
[-1 -3 0 1]
? д
%24 =
[1 1 2 -1]
[0 1/2 -1/2 1/2]
[0 -1 1 1]
[0 -1 0 1]
? г
%25 =
[1 0 0 0]
[0 -4 0 0]
[0 0 1 0]
[0 0 0 0]
?
 

линейная алгебра — квадратичная форма с методом Лагранжа

Задавать вопрос

спросил 7 лет, 2 месяца назад

Изменено 6 лет, 2 месяца назад

Просмотрено 3к раз

$\begingroup$

Я пытаюсь понять, как использовать метод Лагранжа в следующей квадратичной форме:

$$q(x_1, x_2, x_3, x_4) = 2x_1x_4 — 6x_2x_3$$ 92\,=\,4ab $$

$\endgroup$

$\begingroup$

Если умножить в первом уравнении, то получится исходное.