Максимум и минимум функции: понятие
Время чтения: 2 минуты
425
Исследование функции в математическом анализе предполагает нахождение экстремумов, которые представляют собой максимальное и минимальное значение на заданном множестве. Для того чтобы определить минимум функции, необходимо произвести несколько простых операций с ее производной. Сначала следует приравнять функцию к нулю и найти значения переменной, а затем, используя их, разбить координатную плоскость и определить, какие отрезки будут положительными или отрицательными.
Определение максимума и минимума функции
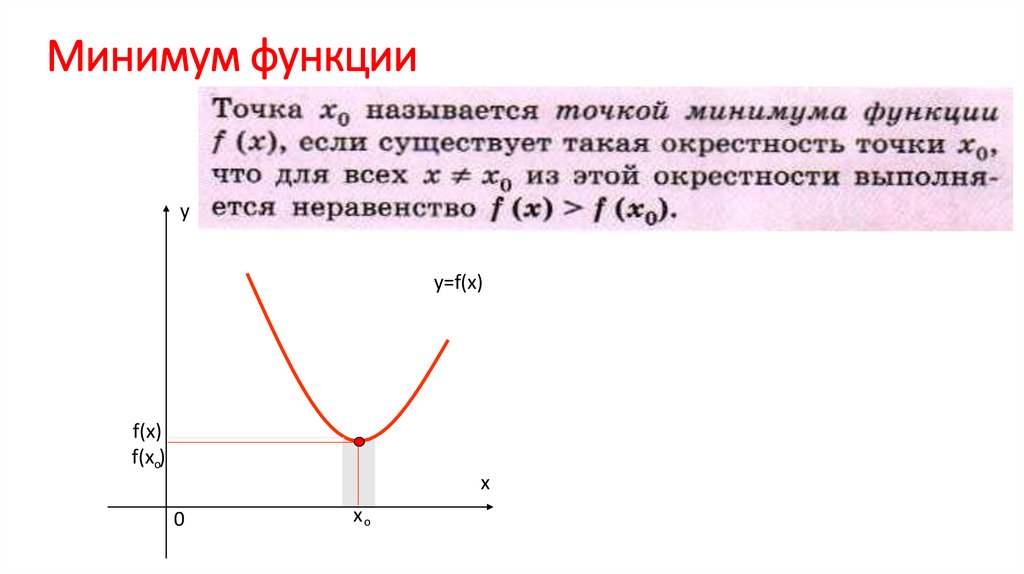
Минимумом заданной функции \[y=f(x)\] принято называть одну некоторую точку, если в ее окрестности соблюдается неравенство \[y=f(x) \geq f\left(x_{0}\right)\].
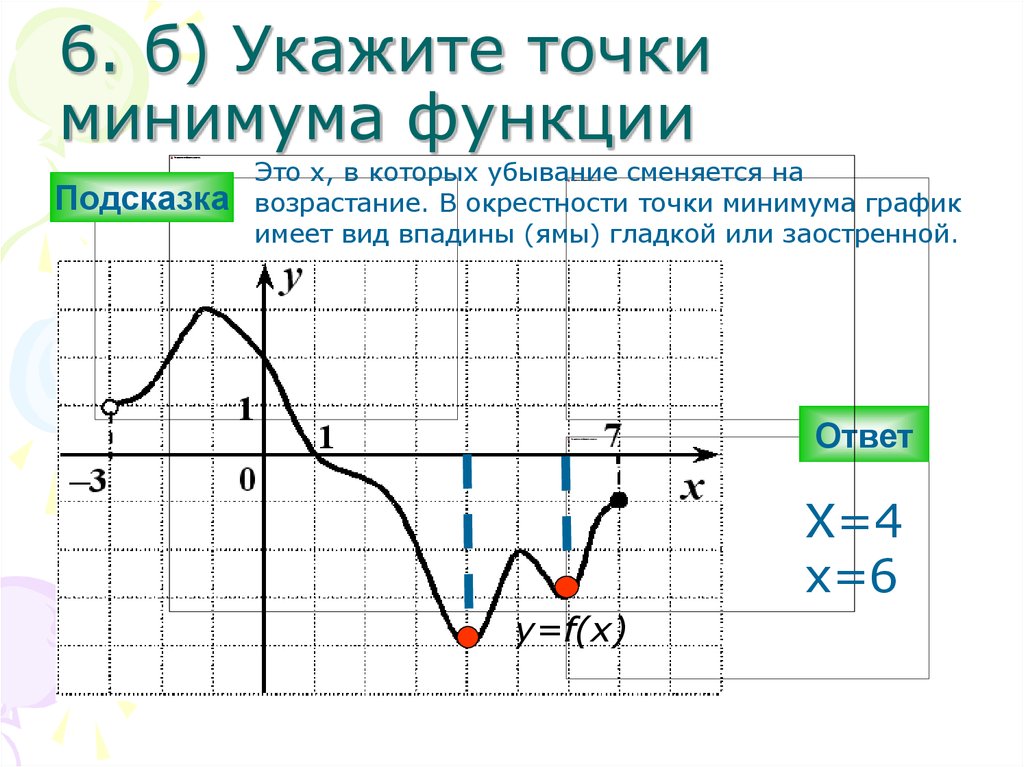
Таким образом \[x_{0}\] – это и есть минимум.
\[x_{0}\] можно назвать максимумом \[y=f(x)\], если в некоторой ее окрестности будет выполняться следующее неравенство \[y=f(x) \leq f\left(x_{0}\right)\].
- максимум, при условии, что \[0>a\];
- минимум, при условии \[a>0\].
Экстремум на всей области определения будет совпадать с вершиной параболы. Это показано на рисунке:
Экстремумы в математическом анализе делятся на два вида:
- глобальный;
- локальный.
К локальному применимо общее определение экстремума. Глобальный вид – это набольшее и наименьшее значение функции на определенном участке.
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Достижение глобальных экстремумов возможно на обоих концах отрезка, а также в местах нахождения локального экстремума. Для определения их необходимого условия используется следующая теорема:
Теорема 1 — 3
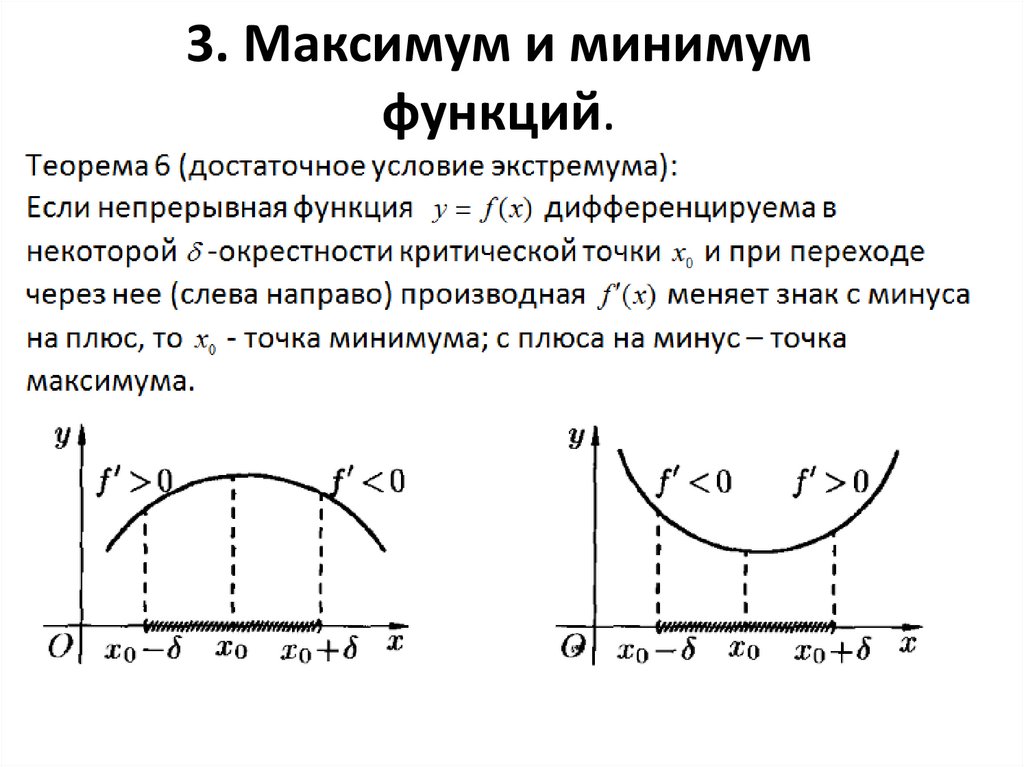
Если экстремум \[y=f(x)\] находится в некоторой точке \[x_{0}\], то производная \[f^{\prime}(x)\] в той же точке будет равна нулю, либо вовсе не будет существовать.
Рассмотренные примеры наглядно показывают, как должно осуществляться исследование функции в математическом анализе. Однако следует учитывать, что в процессе выполнения любого задания нужно также обращать внимание на точки разрыва и интервалы, которые входят в непосредственную область определения. Бывают такие случаи, когда производная находится именно на этих участках.
Оценить статью (79 оценок):
Поделиться
Александр Летов — Магистр физико-математических наук
Популярные статьи
Выполнение любых работ по математике
Максимум, минимум и экстремумы функции. Необходимое условие существования экстремума.
Главная
» Общенаучные дисциплины
» Математика (1 семестр)
»
Максимум, минимум и экстремумы функции. Необходимое условие существования экстремума.
Необходимое условие существования экстремума.
Приведем точные определения точек экстремума.
Определение. Точка x0 называется точкой минимума функции f, если для всех x из некоторой окрестности x0 выполняется неравенство f(x) ≥ f(x0.
Это наглядно показано на рисунке 1:
рисунок 1
Определение. Точка x0 называется точкой максимума функции f, если для всех x из некоторой окрестности x0 выполняется неравенство f(x) ≤ f(x0.
Это наглядно показано на рисунке 2:
рисунок 2
По определению значение функции f в точке x0 является наибольшим среди значений функции в окрестности этой точки, поэтому график функции в окрестности x0 имеет обычно либо вид гладкого холма, либо вид острого пика (рис. 1 а) и б) соответственно).
В окрестности точки минимума графики изображаются в виде загругленной или острой впадины (рис.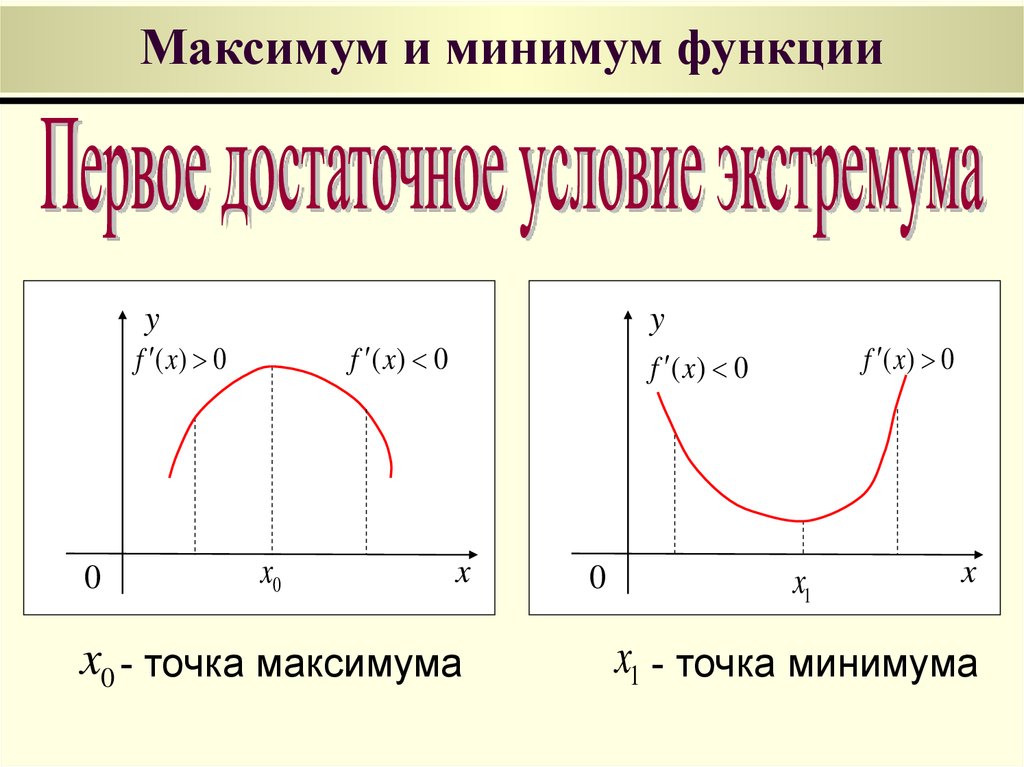 2 а) и б) соответственно).
2 а) и б) соответственно).
Другие примеры поведения графиков функций в точках максимума и минимума приведены на рисунке ниже:
Слева направо: a — точка максимума; a — точка минимума; каждая точка из промежутка [-1; 0] является как точкой максимума, так и точкой минимума.
Для точек минимума и максимума функции есть общее определение — точки экстремума. Значение функции в этих точках соответственно назывется
- Лемма Ферма. Пусть функция дифференцируема в точке экстремума x0. Тогда:
- f‘(x0) = 0.
- Если в точке экстремума существует первая частная производная (по какому-либо аргументу), то она равна нулю.
Друзья! Приглашаем вас к обсуждению.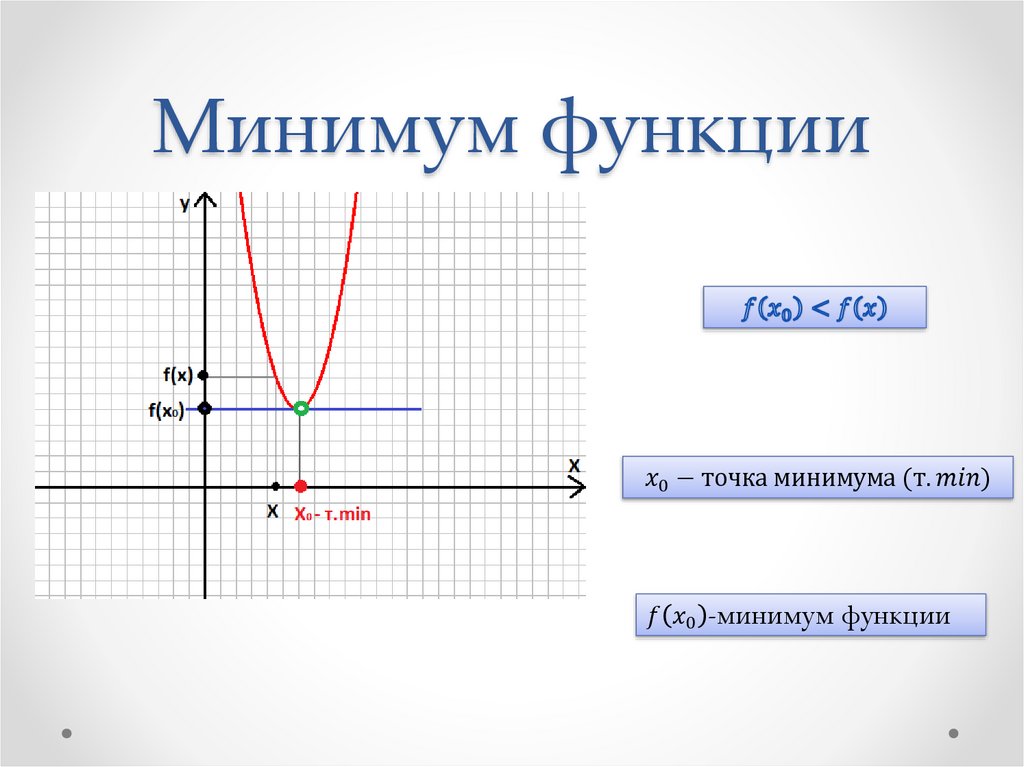 Если у вас есть своё мнение, напишите нам в комментарии.
Если у вас есть своё мнение, напишите нам в комментарии.
Поиск по сайту
Поделиться
Дисциплины
- Информационные системы
- Проектирование ИС
- Интеллектуальные ИС
- Информационная безопасность и защита информации
- Информационные сети
- Моделирование систем
- Администрирование в ИС
- Информационные технологии
- Операционные системы
- Представление знаний в ИС
- Алгоритмизация
- Архитектура ЭВМ
- Технология программирования
- Компьютерная геометрия и графика
- Информатика
- Агрегатор онлайн-курсов
- Самолетостроение
- Конструкция и проектирование самолетов
- Автоматизированное проектирование конструкций
- Основы теории управления
- Теория информационных процессов и систем
- Электротехника
- Физика
- Физика (3 семестр)
- Прикладная механика
- Общенаучные дисциплины
- Экономика
- Метрология
- Философия
- Математика (1 семестр)
- Математика (2 семестр)
- Математика (3 семестр)
- Культурология
- История
- Химия
- Биология
- Английский язык онлайн – быстро и просто
- Что делать, если по учёбе гора долгов?
- Помощь в поступлении в американский ВУЗ от Марии Гурьевой
- Полиграфическая продукция
- Бизнес школа
- Пожарная безопасность: виды инструктажей и требования
- Где записаться на курсы режиссуры монтажа?
- Особенности подготовки к ОГЭ по канадской методике
- Обучение профессии полиграфолога
- ПОИСК ЛУЧШИХ КУРСОВ В СЕТИ в сфере digital
- Курсы подготовки к ЕГЭ 2022 для 10-11 классов в Москве
Поиск минимума и максимума функции в R – КОЛИЧЕСТВЕННАЯ ОЦЕНКА ЗДОРОВЬЯ
Функция оптимизации (также пишется как оптимизация ) в R возвращает минимум или максимум функции f(x) в пределах заданного интервала.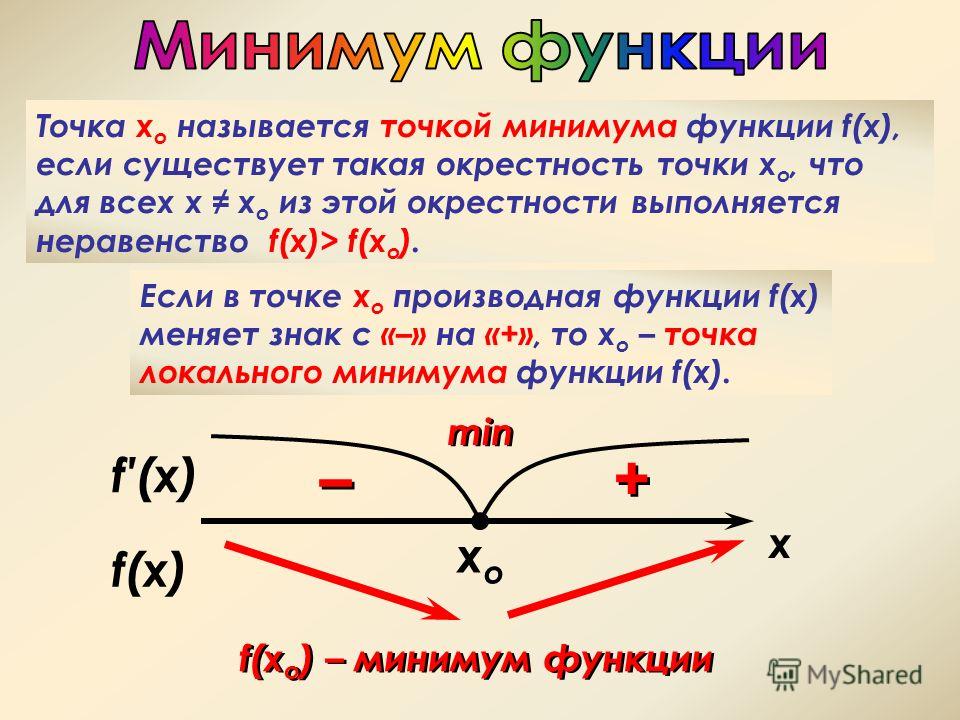
Он принимает в качестве входных данных:
- f: функцию.
- interval:
- максимум: 92 + 1
}
# найти минимум f(x) в интервале [-1, 1]
ответ = оптимизировать (f, интервал = c (-1,1))
# оптимизация возвращает список из 2 значений:
# «минимум» — это значение x, при котором происходит минимум
# и «цель» — это значение y, т.е. f(минимум)
x_min = ответ $минимум
y_min = ответ $ цель
# график f(x)
x = seq(-1, 1, length.out = 100) # генерирует 100 чисел от -1 до 1
график (х, е (х), тип = ‘л’)
# наносим минимальную точку
точки (x_min, y_min, pch = 15)
# аннотация
текст (x = x_min, y = y_min, labels = ‘Минимум’,
pos = 3, col = ‘синий’) 92 — х + 1
}
# найти максимум f(x) в интервале [-1, 1]
ответ = оптимизировать (f, интервал = с (-1,1), максимум = ИСТИНА)
# извлечь координаты максимума
x_max = ответ $максимум
y_max = ответ $ цель
# график f(x)
x = seq(-1, 1, length.
 out = 100)
график (х, е (х), тип = ‘л’)
# построить максимум
точки (x_max, y_max, pch = 15)
текст (x = x_max, y = y_max, labels = ‘Максимум’,
pos = 4, col = ‘синий’)
out = 100)
график (х, е (х), тип = ‘л’)
# построить максимум
точки (x_max, y_max, pch = 15)
текст (x = x_max, y = y_max, labels = ‘Максимум’,
pos = 4, col = ‘синий’) Вывод:
Нахождение максимума: \(f(x) = cos x\)
f = function(x) { потому что (х) } # найти максимум f(x) в интервале [-10, 10] ответ = оптимизировать (f, интервал = с (-10,10), максимум = ИСТИНА) # извлечь координаты максимума x_max = ответ $максимум y_max = ответ $ цель # график f(x) х = последовательность (-10, 10, длина.выход = 100) график (х, е (х), тип = 'л') # построить максимум точки (x_max, y_max, pch = 15) текст (x = x_max, y = y_max, labels = 'Максимум', pos = 4, col = 'синий')Вывод:
Так почему же оптимизировал
Чтобы выяснить, при каких значениях x вычисляется функция, вы можете использовать оператор печати внутри f(x):
f = function(x) { print(x) # печатает значение x всякий раз, когда вызывается f(x) потому что (х) } оптимизировать(f, интервал = c(-10, 10), максимум = ИСТИНА)Вывод:
[1] -2,36068 [1] 2.
 36068
[1] 5.27864
[1] 7.082039
[1] 6.804159[1] 6,2776
[1] 6.25876
[1] 6.283509
[1] 6.283185
[1] 6.283145
[1] 6.283226
[1] 6.283185
$максимум
[1] 6.283185
$цель
[1] 1
36068
[1] 5.27864
[1] 7.082039
[1] 6.804159[1] 6,2776
[1] 6.25876
[1] 6.283509
[1] 6.283185
[1] 6.283145
[1] 6.283226
[1] 6.283185
$максимум
[1] 6.283185
$цель
[1] 1 Далее, давайте нанесем на график эти точки, чтобы увидеть, что происходит:
xs = c(-2,36068, 2.36068, 5.27864, 7.082039, 6.804159, 6.2776, 6.25876, 6.283509, 6.283185, 6.283145, 6.283226, 6.283185) график (х, потому что (х), тип = 'л') точки (xs, cos (xs), col = 'красный', pch = 15) текст (x = xs, y = cos (xs), labels = c (1: 5, '6-12', rep ('', 6)), pos = 4, col = 'красный')Вывод:
Этот график показывает, что оптимизация не обнаружила изменения значения y между точками 1 и 2 и, возможно, подумала, что функция была постоянной между этими двумя точками и пропустила пик в точке x = 0.

Примечание: я попытался изменить интервал с [-10, 10] на [-7, 10], и оптимизировать без проблем обнаружил максимум в (0, 1).
Нахождение минимума \(f(x) = 3\)
f = function(x) { 3 } # найти минимум f(x) в интервале [-1, 1] ответ = оптимизировать (f, интервал = c (-1,1)) x_min = ответ $минимум y_min = ответ $ цель # создать пустой график график (1, тип = "n", xlab = "x", ylab = "f (x)", xlim = c(-1.1, 1.1), ylim = c(0, 5)) # график f(x) аблин (ч = 3) # нанесем точку минимума на f(x) точки (x_min, y_min, pch = 15) текст (x = x_min, y = y_min, labels = 'Минимум', pos = 3, col = 'синий')Вывод:
Несмотря на то, что \(f(x) = 3\) является константой, оптимизировать удалось найти минимум при x = 1!
Дополнительная литература
- Решить полином в R
- Как решить уравнение в R
- Написать функцию, которая возвращает n-е число Фибоначчи в R
- Работа с множествами в R
Задать вопрос 9{2}+1}$ за каждое действительное число для $x$, какое минимальное значение $f$?
Как мне найти минимальное значение этой функции. Я знаю только метод проб и ошибок, но это не обобщенный способ.
Я знаю только метод проб и ошибок, но это не обобщенный способ.Подскажите, пожалуйста, общий способ решения задач такого типа
- алгебра-предварительное исчисление
- функции
$\endgroup$
2
$\begingroup$
Этот случай настолько прост, что его можно решить даже без математических вычислений. Запишите $f(x)$ как $$f(x)= 1- \frac{2}{x²+1} $$ Очевидно, что минимальное значение этой функции имеет место, когда дробь справа наибольшая, что, очевидно, имеет место при наименьшем значении знаменателя, что происходит при $x=0$ Следовательно, минимальное значение функции равно $f(0 )=-1$.
$\endgroup$
2
$\begingroup$ 92}$$
$$f'(x)=0 \Rightarrow x=0$$
$$f'(x)<0,\forall x<0$$
$$f'(x) >0, \forall x>0$$
Следовательно, $f$ убывает на $(-\infty,0]$ и возрастает на $[0,+\infty)$
Итак, $f$ достигает своего минимум в $0$ и минимум равен $f(0)=-1$
$\endgroup$
1
$\begingroup$
Дифференцируя это дает вам ответ: 92+1\ge 1$ тогда очевидно, что минимальное значение имеет место при $x=0$.


 out = 100)
график (х, е (х), тип = ‘л’)
# построить максимум
точки (x_max, y_max, pch = 15)
текст (x = x_max, y = y_max, labels = ‘Максимум’,
pos = 4, col = ‘синий’)
out = 100)
график (х, е (х), тип = ‘л’)
# построить максимум
точки (x_max, y_max, pch = 15)
текст (x = x_max, y = y_max, labels = ‘Максимум’,
pos = 4, col = ‘синий’)  36068
[1] 5.27864
[1] 7.082039
[1] 6.804159[1] 6,2776
[1] 6.25876
[1] 6.283509
[1] 6.283185
[1] 6.283145
[1] 6.283226
[1] 6.283185
$максимум
[1] 6.283185
$цель
[1] 1
36068
[1] 5.27864
[1] 7.082039
[1] 6.804159[1] 6,2776
[1] 6.25876
[1] 6.283509
[1] 6.283185
[1] 6.283145
[1] 6.283226
[1] 6.283185
$максимум
[1] 6.283185
$цель
[1] 1 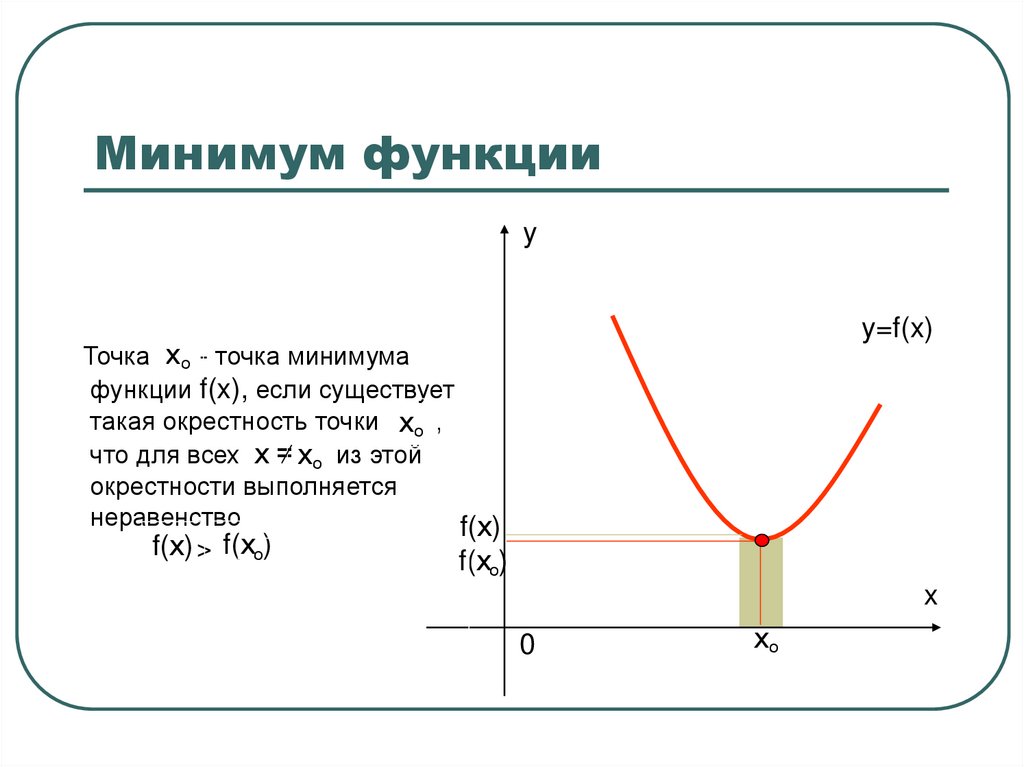
 Я знаю только метод проб и ошибок, но это не обобщенный способ.
Я знаю только метод проб и ошибок, но это не обобщенный способ.