Вычисляем определитель матрицы на Хаскелле / Хабр
Решил выложить код вычисления определителей. Код рабочий, хотя и не претендует на виртуозность. Просто было интересно решить эту задачу именно на Хаскелле. Рассмотрены два подхода к решению задачи: простая рекурсия и метод Гаусса.
Немного теории
Как известно, определитель квадратной матрицы n*n — это сумма n! слагаемых, каждое из которых есть произведение, содержащее ровно по одному элементу матрицы из каждого столбца и ровно по одному из каждой строки. Знак очередного произведения:
определяется чётностью подстановки:
Прямой метод вычисления определителя состоит в разложении его по элементам строки или столбца в сумму произведений элементов какой-либо строки или столбца на их алгебраические дополнения. В свою очередь, алгебраическое дополнение элемента матрицы
есть
при этом
— есть минор элемента (i,j), т. е. определитель, получающийся из исходного определителя вычеркиванием i-й строки и j-го столбца.
е. определитель, получающийся из исходного определителя вычеркиванием i-й строки и j-го столбца.
Такой метод порождает рекурсивный процесс, позволяющий вычислить любой определитель. Но производительность этого алгоритма оставляет желать лучшего — O(n!). Поэтому применяется такое прямое вычисление разве что при символьных выкладках (и с определителями не слишком высокого порядка).
Гораздо производительнее оказывается метод Гаусса. Его суть основывается на следующих положениях:
1. Определитель верхней треугольной матрицы \begin{pmatrix}{a}_{1,1} & {a}_{1,2} &… & {a}_{1,n} \\ 0 & {a}_{2,2} &… & {a}_{2,n} \\ 0 & 0 &… & …\\ 0 & 0 &… & {a}_{n,n} \\\end{pmatrix} равен произведению ее диагональных элементов. Этот факт сразу же следует из разложения определителя по элементам первой строки или первого столбца.
2. Если в матрице к элементам одной строки прибавить элементы другой строки, умноженные на одно и то же число, то значение определителя не изменится.
3. Если в матрице поменять местами две строки (или два столбца), то значение определителя изменит знак на противоположный.
Мы можем, подбирая коэффициенты, складывать первую строку матрицы со всеми остальными и получать в первом столбце нули во всех позициях, кроме первой. Для получения нуля во второй строке, нужно прибавить ко второй строке первую, умноженную на
Для получения нуля в третьей строке, нужно к третьей строке прибавить первую строку, умноженную на
и т.д. В конечном итоге, матрица приведется к виду, в котором все элементы
при n>1 будут равны нулю.
Если же в матрице элемент
оказался равным нулю, то можно найти в первом столбце ненулевой элемент (предположим, он оказался на k-м месте) и обменять местами первую и k-ю строки. При этом преобразовании определитель просто поменяет знак, что можно учесть.
Далее, действуя аналогично, можно получить нули во втором столбце, затем в третьем и т.п. Важно, что при сложении строк полученные ранее нули не изменятся. Если для какой-либо строки не удастся найти ненулевой элемент для знаменателя, то определитель равен нулю и процесс можно остановить. Нормальное завершение процесса Гаусса порождает матрицу, у которой все элементы, расположенные ниже главной диагонали, равны нулю. Как говорилось выше, определитель такой матрицы равен произведению диагональных элементов.
Перейдем к программированию.
Мы работаем с данными с плавающей точкой. Матрицы представляем списками строк. Для начала определим два типа:
type Row = [Double] type Matrix = [Row]
Простая рекурсия
Ничтоже сумняшеся, мы будем раскладывать определитель по элементам первой (т.е. нулевой) строки.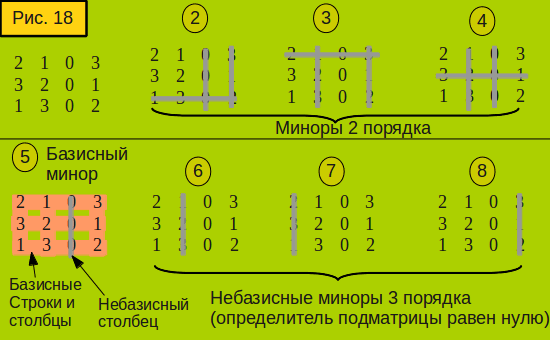 Нам понадобится программа построения минора, получающегося вычеркиванием первой строки и k-го столбца.
Нам понадобится программа построения минора, получающегося вычеркиванием первой строки и k-го столбца.
-- Удаление k-го элемента изо всех строк матрицы deln :: Matrix -> Int -> Matrix deln matrix k = map (\ r -> (take (k) r)++(drop (k+1) r)) matrix
А вот и минор:
-- Минор k-го элемента нулевой строки minor :: Matrix -> Int -> Double minor matrix k = det $ deln (drop 1 matrix) k
Обратите внимание: минор — это определитель. Мы вызываем функцию det, которую еще не реализовали. Для реализации det, нам придется сформировать знакочередующуюся сумму произведений очередного элемента первой строки на определитель очередного минора. Чтобы избежать громоздких выражений, создадим для формирования знака суммы отдельную функцию:
sgn :: Int -> Double sgn n = if n `rem` 2 == 0 then 1.0 else (-1.0)
Теперь можно вычислить определитель:
-- Определитель квадратной матрицы det :: Matrix -> Double det [[a,b],[c,d]] = a*d-b*c det matrix = sum $ map (\c -> ((matrix !! 0)!!c)*(sgn c)*(minor matrix c)) [0..n] where n = length matrix - 1
Код очень прост и не требует особых комментариев. Чтобы проверить работоспособность наших функций, напишем функцию main:
main = print $ det [[1,2,3],[4,5,6],[7,8,(-9)]]
Значение этого определителя равно 54, в чем можно убедиться.
Метод Гаусса
Нам понадобится несколько служебных функций (которые можно будет использовать и в других местах). Первая из них — взаимный обмен двух строк в матрице:
-- Обмен двух строк матрицы
swap :: Matrix -> Int -> Int -> Matrix
swap matrix n1 n2 = map row [0..n]
where n=length matrix - 1
row k | k==n1 = matrix !! n2
| k==n2 = matrix !! n1
| otherwise = matrix !! k
Как можно понять по приведенному выше коду, функция проходит строку за строкой. При этом, если встретилась строка с номером n1, принудительно подставляется строка n2 (и наоборот). Остальные строки остаются на месте.
При этом, если встретилась строка с номером n1, принудительно подставляется строка n2 (и наоборот). Остальные строки остаются на месте.
Следующая функция вычисляет строку r1 сложенную со строкой r2, умноженной поэлементно на число f:
-- Вычислить строку r1+f*r2 comb :: Row -> Row -> Double -> Row comb r1 r2 f = zipWith (\ x y -> x+f*y) r1 r2
Здесь все предельно прозрачно: действия выполняются над строками матрицы (т.е. над списками [Double]). А вот следующая функция выполняет это преобразование над матрицей (и, естественно, получает новую матрицу):
-- прибавить к строке r1 строку r2, умноженную на f
trans :: Matrix -> Int -> Int -> Double -> Matrix
trans matrix n1 n2 f = map row [0..n]
where n=length matrix - 1
row k | k==n1 = comb (matrix !! n1) (matrix !! n2) f
| otherwise = matrix !! k
Функция getNz ищет номер первого ненулевого элемента в списке. Она нужна в случае, когда очередной диагональный элемент оказался равным нулю.
Она нужна в случае, когда очередной диагональный элемент оказался равным нулю.
-- Номер первого ненулевого в списке
getNz :: Row -> Int
getNz xs = if length tmp == 0 then (-1) else snd $ head tmp
where tmp=dropWhile (\ (x,k) -> (abs x) <= 1.0e-10) $ zip xs [0..]
Если все элементы списка равны нулю, функция вернет -1.
Функция search проверяет, подходит ли матрица для очередного преобразования (у нее должен быть ненулевым очередной диагональный элемент). Если это не так, матрица преобразовывается перестановкой строк.
-- Поиск ведущего элемента и перестановка строк при необходимости
search :: Matrix -> Int -> Matrix
search matrix k | (abs ((matrix !! k) !! k)) > 1.0e-10 = matrix
| nz < 0 = matrix -- матрица вырождена
| otherwise = swap matrix k p
where n = length matrix
lst = map (\ r -> r !! k) $ drop k matrix
nz = getNz lst
p = k + nz
Если ведущий (ненулевой) элемент найти невозможно (матрица вырождена), то функция вернет ее без изменений. Функция mkzero формирует нули в очередном столбце матрицы:
Функция mkzero формирует нули в очередном столбце матрицы:
-- получение нулей в нужном столбце
mkzero :: Matrix -> Int -> Int -> Matrix
mkzero matrix k p | p>n-1 = matrix
| otherwise = mkzero (trans matrix p k (-f)) k (p+1)
where n = length matrix
f = ((matrix !! p) !! k)/((matrix !! k) !! k)
Функция triangle формирует верхнюю треугольную форму матрицы:
-- Получение верхней треугольной формы матрицы
triangle :: Matrix -> Int -> Matrix
triangle matrix k | k>=n = matrix
| (abs v) <= 1.0e-10 = [[0.0]] -- матрица вырождена
| otherwise = triangle (mkzero tmp k k1) k1
where n = length matrix
tmp = search matrix k
v = (tmp !! k) !! k -- диагональный элемент
k1 = k+1
Если на очередном этапе не удалось найти ведущий элемент, функция возвращает нулевую матрицу 1-го порядка. Теперь можно составить парадную функцию приведения матрицы к верхней треугольной форме:
Теперь можно составить парадную функцию приведения матрицы к верхней треугольной форме:
-- Парадная функция gauss :: Matrix -> Matrix gauss matrix = triangle matrix 0
Для вычисления определителя нам нужно перемножить диагональные элементы. Для этого составим отдельную функцию:
-- Произведение диагональных элементов proddiag :: Matrix -> Double proddiag matrix = product $ map (\ (r,k) -> r !!k) $ zip matrix [0,1..]
Ну, и «бантик» — собственно вычисление определителя:
-- Вычисление определителя det :: Matrix -> Double det matrix = proddiag $ triangle matrix 0
Проверим, как работает эта функция:
main = print $ det [[1,2,3],[4,5,6],[7,8,-9]] [1 of 1] Compiling Main ( main.hs, main.o ) Linking a.out ... 54.0
Спасибо тем, кто дочитал до конца!
Код можно скачать здесь
| 1 | Множитель | x^2-4 | |
| 2 | Множитель | 4x^2+20x+16 | |
| 3 | График | y=-x^2 | |
| 4 | Вычислить | 2+2 | |
| 5 | Множитель | x^2-25 | |
| 6 | Множитель | x^2+5x+6 | |
| 7 | Множитель | x^2-9 | |
| 8 | Множитель | x^3-8 | |
| 9 | Вычислить | квадратный корень из 12 | |
| 10 | Вычислить | квадратный корень из 20 | |
| 11 | Вычислить | квадратный корень из 50 | |
| 12 | Множитель | x^2-16 | |
| 13 | Вычислить | квадратный корень из 75 | |
| 14 | Множитель | x^2-1 | |
| 15 | Множитель | x^3+8 | |
| 16 | Вычислить | -2^2 | |
| 17 | Вычислить | квадратный корень из (-3)^4 | |
| 18 | Вычислить | квадратный корень из 45 | |
| 19 | Вычислить | квадратный корень из 32 | |
| 20 | Вычислить | квадратный корень из 18 | |
| 21 | Множитель | x^4-16 | |
| 22 | Вычислить | квадратный корень из 48 | |
| 23 | Вычислить | квадратный корень из 72 | |
| 24 | Вычислить | квадратный корень из (-2)^4 | |
| 25 | Множитель | x^3-27 | |
| 26 | Вычислить | -3^2 | |
| 27 | Множитель | x^4-1 | |
| 28 | Множитель | x^2+x-6 | |
| 29 | Множитель | x^3+27 | |
| 30 | Множитель | x^2-5x+6 | |
| 31 | Вычислить | квадратный корень из 24 | |
| 32 | Множитель | x^2-36 | |
| 33 | Множитель | x^2-4x+4 | |
| 34 | Вычислить | -4^2 | |
| 35 | Множитель | x^2-x-6 | |
| 36 | Множитель | x^4-81 | |
| 37 | Множитель | x^3-64 | |
| 38 | Вычислить | 4^3 | |
| 39 | Множитель | x^3-1 | |
| 40 | График | y=x^2 | |
| 41 | Вычислить | 2^3 | |
| 42 | Вычислить | (-12+ квадратный корень из -18)/60 | |
| 43 | Множитель | x^2-6x+9 | |
| 44 | Множитель | x^2-64 | |
| 45 | График | y=2x | |
| 46 | Множитель | x^3+64 | |
| 47 | Вычислить | (-8+ квадратный корень из -12)/40 | |
| 48 | Множитель | x^2-8x+16 | |
| 49 | Вычислить | 3^4 | |
| 50 | Вычислить | -5^2 | |
| 51 | Множитель | x^2-49 | |
| 52 | Вычислить | (-20+ квадратный корень из -75)/40 | |
| 53 | Множитель | x^2+6x+9 | |
| 54 | Множитель | 4x^2-25 | |
| 55 | Вычислить | квадратный корень из 28 | |
| 56 | Множитель | x^2-81 | |
| 57 | Вычислить | 2^5 | |
| 58 | Вычислить | -8^2 | |
| 59 | Вычислить | 2^4 | |
| 60 | Множитель | 4x^2-9 | |
| 61 | Вычислить | (-20+ квадратный корень из -50)/60 | |
| 62 | Вычислить | (-8+ квадратный корень из -20)/24 | |
| 63 | Множитель | x^2+4x+4 | |
| 64 | Множитель | x^2-10x+25 | |
| 65 | Вычислить | квадратный корень из -16 | |
| 66 | Множитель | x^2-2x+1 | |
| 67 | Вычислить | -7^2 | |
| 68 | График | f(x)=2^x | |
| 69 | Вычислить | 2^-2 | |
| 70 | Вычислить | квадратный корень из 27 | |
| 71 | Вычислить | квадратный корень из 80 | |
| 72 | Множитель | x^3+125 | |
| 73 | Вычислить | -9^2 | |
| 74 | Множитель | 2x^2-5x-3 | |
| 75 | Вычислить | квадратный корень из 40 | |
| 76 | Множитель | x^2+2x+1 | |
| 77 | Множитель | x^2+8x+16 | |
| 78 | График | y=3x | |
| 79 | Множитель | x^2+10x+25 | |
| 80 | Вычислить | 3^3 | |
| 81 | Вычислить | 5^-2 | |
| 82 | График | f(x)=x^2 | |
| 83 | Вычислить | квадратный корень из 54 | |
| 84 | Вычислить | (-12+ квадратный корень из -45)/24 | |
| 85 | Множитель | x^2+x-2 | |
| 86 | Вычислить | (-3)^3 | |
| 87 | Множитель | x^2-12x+36 | |
| 88 | Множитель | x^2+4 | |
| 89 | Вычислить | квадратный корень из (-8)^2 | |
| 90 | Множитель | x^2+7x+12 | |
| 91 | Вычислить | квадратный корень из -25 | |
| 92 | Множитель | x^2-x-20 | |
| 93 | Вычислить | 5^3 | |
| 94 | Множитель | x^2+8x+15 | |
| 95 | Множитель | x^2+7x+10 | |
| 96 | Множитель | 2x^2+5x-3 | |
| 97 | Вычислить квадратный корень | квадратный корень из 116 | |
| 98 | Множитель | x^2-x-12 | |
| 99 | Множитель | x^2-x-2 | |
| 100 | Вычислить | 2^2 |
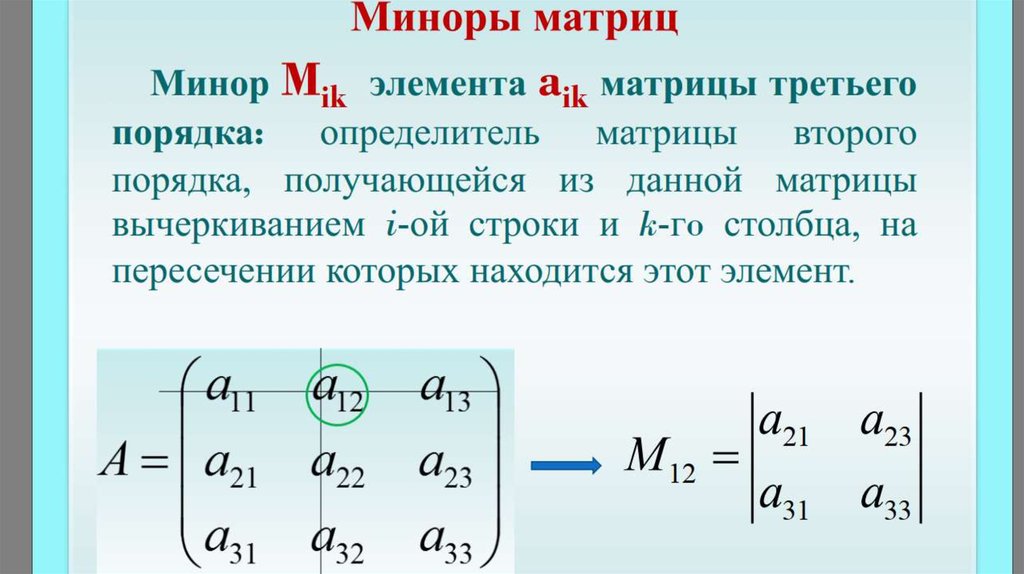
Миноры и сомножители детерминантов
Матрица представляет собой массив действительных чисел (или других подходящих объектов), расположенных в строках и столбцах, где объекты относятся к элементам, присутствующим в матрице. На изображении ниже показана матрица, где элементы, разделенные по горизонтали, называются строками матрицы, а элементы, разделенные по вертикали, называются столбцами матрицы.
На изображении ниже показана матрица, где элементы, разделенные по горизонтали, называются строками матрицы, а элементы, разделенные по вертикали, называются столбцами матрицы.
Как мы знаем, матрица состоит из строк и столбцов, матрица ниже имеет 3 строки и 3 столбца, поэтому Порядок Матрицы равен 3 × 3.
Любые четыре элемента a, b, c и d расположены в две строки и два столбца между двумя вертикальными полосами, как показано ниже, формы, которые называются Определителем определитель второго порядка или определитель второго порядка. Как показано ниже, демонстрирует определитель и расширение определителя.
Определитель матрицы
Определитель полезен для решения линейных уравнений, определения того, как линейное преобразование изменяет площадь или объем, а также для изменения переменных в интегралах. Определитель можно рассматривать как функцию, входом которой является квадратная матрица, а выходом — число. В приведенной ниже статье мы подробно обсуждаем миноры и кофакторы. На простом языке мы можем сказать: каждой малой матрице A можно поставить в соответствие число (действительное или комплексное), которое называется определителем квадратной матрицы A.
На простом языке мы можем сказать: каждой малой матрице A можно поставить в соответствие число (действительное или комплексное), которое называется определителем квадратной матрицы A.
Определитель матрицы может быть легко представлен как det (A) или | А |
Теперь давайте перейдем к нашей теме, а именно к минорным и сопутствующим факторам.
Итак, сначала давайте обсудим несовершеннолетних.
Примечание:
- Вопросы, представленные в этой статье, появлялись в разных опросных листах предыдущего года.
- i представляет строки определителя, тогда как j представляет столбцы определителя.
- Я выделяю термины ij th , чтобы вы могли ясно видеть и не путаться.
- В приведенной ниже статье вы увидите вопросы, решение которых показано на изображении.
Маленькая из матрицы
Маленький элемент A IJ из определителя является определяемой, полученной путем удаления INTER TH ROW и J TH , в котором элемент 9003 A 5 IJ . ложь. Незначительный элемент A IJ обозначен M IJ
ложь. Незначительный элемент A IJ обозначен M IJ
Шаг 1: Скрыть I TH и J столбец матрицы A, где лежит элемент a ij .
Шаг 2: Теперь вычислите определитель матрицы после удаления строки и столбца с помощью шага 1.
Примеры задач на минор матрицы
Задача 1: Если матрица A равна
, то запишите минор числа a 22.
Решение:
Решение: a 22 , элемент, присутствующий в a 22 , равен 0. Как мы узнали из нашего определения минора, мы должны удалить строку i th и столбцы j th , в которых присутствует наш запрошенный элемент. На изображении ниже показано, как удалить i -й -й ряд и j -й -й столбец
После удаления мы записываем наш левый элемент как есть и делаем перекрестное умножение.
Теперь, после удаления i -й -й строки и j -го -го столбца, мы должны расширить определитель, поэтому мы получаем (8 – 15), что при решении дает -7, что и является нашим требуемым ответом.
Примечание: Всегда помните, что после умножения элементов левой диагонали всегда ставьте знак -ve, затем выполните умножение элементов правой диагонали и решите их.
Задача 2: Если матрица A равна
, то найдите минор числа 32.
Решение:
Решение:
Решение:9000 32 элемент, который равен 1. Итак, как мы делали в этой задаче выше, мы будем следовать той же процедуре. Итак, сначала мы должны удалить строку i th и столбец j th , в котором присутствует наш элемент.Итак, мы отменили i -й -й ряд и j -й -й столбец, в котором присутствует наш элемент.
Поэтому напишите элементы, которые остались как есть.
Затем выполните перекрестное умножение и решите:
Следуя той же процедуре, что и в предыдущем вопросе, мы решили и этот вопрос путем расширения определителя, как мы обсуждали во введении.
Кофакторы матрицы
Кофакторы элемента a ij определителя, обозначаемого A IJ или C IJ , определяется как A IJ = (-1) I+J M IJ , где M IJ -Minor An 44444444444444444444. IJ
Формула для поиска кофакторовA IJ = (-1) I+J M IJ
Проблемы выборки на кофакторах MATRIX
Проблемы с фа-факторами MATRIX
9 Если матрица A равна, запишите коэффициент элемента a 32.
Решение:
Как задано в вопросе, мы должны найти коэффициент элемента a32, что означает, что наша строка (i) = 3 и столбец (j) = 2, поэтому у нас есть строка и столбец как мы делаем, чтобы найти минор, удаляя строки и столбец, в которых существует заданный элемент, мы делаем то же самое в этом вопросе, а затем помещаем это в нашу формулу -> A ij = (-1) i+j M ij
Таким образом, после подстановки формулы нахождения сомножителя и выполнения расширения определителя мы получаем (-1) (5 – 16), что при решении дает ответ 11, это наш требуемый ответ.
Задача 2: Если A ij элемента a ij определителя, приведенного ниже, то запишите значение a 32 . A 32
Решение:
В вопросе у нас есть определитель. Итак, у нас есть строка и столбец, указанные в вопросе.
Здесь a 32 = 3+2 = 5
Дано, A ij является кофактором элемента a ij A . Итак, теперь мы можем решить этот вопрос, подставив значения в формулу кофактора, как обсуждалось в предыдущем вопросе.
Итак, 110 — это наш требуемый ответ.
Урок Видео: обратная матрица: метод сопряжения
Стенограмма видео
обратная матрица: сопряженный метод Метод
В этом видео мы собираемся обсудить, как найти обратную любую квадратную матрицу с ненулевым определителем с помощью используя метод сопряжения.
Мы рассмотрим метод в подробно, объясняя, как найти миноры матрицы, как построить кофактор матрица, а затем как построить сопряжения нашей матрицы. Затем мы рассмотрим несколько примеров объясняя, как мы можем применить этот метод, чтобы найти инверсию.
Прежде чем мы обсудим этот новый метод Чтобы найти обратную квадратную матрицу, нам нужно пройти через несколько сначала новые концепции. Мы собираемся начать с определения матричный минор. Если у нас есть матрица 𝐴, имеющая порядок 𝑚 умноженный на 𝑛, тогда минор матрицы, которую мы обозначаем с большой буквы 𝐴 𝑖𝑗, это матрица 𝐴, в которой мы удаляем 𝑖-ю строку и 𝑗-й столбец из матрицы 𝐴. Итак, наш матричный минор 𝐴 𝑖𝑗 равен точно так же, как матрица 𝐴. Однако мы удалили 𝑖-й ряд и 𝑗-й столбец. И мы знаем, если мы удалим одну строку и один столбец из матрицы 𝐴, то наш новый порядок будет 𝑚 минус один на 𝑛 минус один.
И самый простой способ понять это понятие через пример.
Начнем с матрицы 𝐴, которая представляет собой матрицу три на четыре, заданную следующим образом. Теперь посмотрим, как бы мы построить минор матрицы 𝐴 два три. Из нашего определения матрицы второстепенный, мы видим, что нам нужно удалить 𝑖-ю строку и 𝑗-й столбец из нашей матрицы 𝐴. Во-первых, наше значение 𝑖 равно двум. Итак, нам нужно удалить вторую строку из нашей матрицы 𝐴. Далее мы видим, что значение 𝑗 равно равно трем. Итак, нам нужно удалить третий столбец из матрицы 𝐴. Тогда наш матричный минор 𝐴 два три будут все оставшиеся элементы, которые мы не удалили. 𝐴 два три будут следующими матрица.
Однако это, конечно, не единственный минор матрицы, который мы могли построить. Теперь построим матрицу минор 𝐴 три один. На этот раз мы можем увидеть значение 𝑖 равно трем.
Итак, нам нужно удалить третью строку из нашей матрицы 𝐴. И мы видим, что значение 𝑗 равно один. Итак, нам нужно удалить первый столбец из матрицы 𝐴. И тогда мы можем построить нашу матрица 𝐴 три один, используя все оставшиеся элементы, которые мы не удалить из 𝐴. Это дает нам 𝐴 три один следующую матрицу.
Методы, которые мы используем в этом видео поможет нам определить, можем ли мы найти обратную любую матрицу 𝑛-by-𝑛. Однако нам нужно будет найти определитель любой матрицы, к которой мы хотим найти обратную. И мы видели ранее, что это трудно вычислить определитель для больших квадратных матриц. Поэтому мы сосредоточимся в основном на матрицы три на три.
И прежде чем мы это сделаем, мы собираемся чтобы вспомнить, как мы находим определитель матрицы два на два. Пусть 𝐴 равно два на два матрица 𝑎, 𝑏, 𝑐, 𝑑.
Тогда определитель 𝐴 равен в 𝑎𝑑 минус 𝑏𝑐. Теперь мы готовы обсудить ключ часть, которая поможет нам найти обратную любую квадратную матрицу с ненулевым определитель. Нам нужно обсудить, что кофакторная матрица матрицы 𝐴 есть.
Во-первых, потому что мы используем это, чтобы найти обратную матрицу, нам нужно, чтобы наша матрица 𝐴 была квадратной матрицей. Допустим, его порядок 𝑛 на 𝑛. Далее, чтобы построить наш кофактор матрице, нам нужно найти все миноры матрицы 𝐴. Мы будем называть их 𝐴 𝑖𝑗. Теперь мы готовы построить кофакторная матрица 𝐴. Мы назовем эту матрицу 𝐶. И мы определим его элемент с помощью элемент. Запись в строке 𝑖 и столбце 𝑗 нашей матрицы кофакторов будет задана отрицательной единицей, возведенной в степень 𝑖 плюс 𝑗, умноженное на определитель минора матрицы 𝐴 𝑖𝑗. И помните, наша матрица 𝐴 представляет собой квадратная матрица порядка 𝑛 по 𝑛.
Таким образом, наши значения 𝑖 будут работать по строкам нашей матрицы 𝐴. И значения 𝑗 будут пробегая по столбцам нашей матрицы 𝐴. Таким образом, наши значения 𝑖 варьируются от единицы до 𝑛, а наши значения 𝑗 варьируются от единицы до 𝑛. Это означает, что наша кофакторная матрица будет быть квадратной матрицей. Это будет порядка 𝑛 к 𝑛.
Также стоит отметить иногда вы увидите, что это записано во всей матричной форме. И если бы мы это сделали, мы бы получите следующее матричное представление нашей матрицы кофакторов. И стоит отметить все здесь мы создали квадратную матрицу 𝑛 на 𝑛, где в строке 𝑖 и столбце 𝑗 мы использовали нашу формулу для построения записи. Но обычно гораздо проще работать с нашим определением для каждой записи в отдельности. Прежде чем мы обсудим, как мы собираемся чтобы использовать матрицу кофакторов, чтобы найти обратную матрицу, давайте рассмотрим некоторые Примеры.
Учитывая, что 𝐴 равно матрица три на три минус пять, восемь, минус семь, шесть, ноль, один, пять, минус четыре, минус восемь, определить значение минус один к степень одного плюс два, умноженная на определитель минора матрицы 𝐴 один два.
Нам дали три на три квадратная матрица. И нас просят определить значение отрицательной единицы в степени один плюс удвоенный определитель минор матрицы 𝐴 один два. И пока не надо отвечая на этот вопрос, стоит отметить, что это будет запись в строке один и второй столбец нашей матрицы кофакторов.
Первый шаг к ответу этот вопрос состоит в том, чтобы вспомнить, что мы подразумеваем под матрицей 𝐴 один два. Мы называем это матрицей незначительный. Минор матрицы 𝐴 𝑖𝑗 означает мы удаляем строку 𝑖 и столбец 𝑗 из нашей матрицы 𝐴.
В нашем случае мы можем видеть значение 𝑖 равно единице, а 𝑗 равно двум. Затем мы можем записать это в наш определение минора матрицы. Мы видим, что минор матрицы 𝐴 один два означает, что мы удаляем первую строку и второй столбец из матрицы 𝐴.
Итак, чтобы найти минор нашей матрицы 𝐴 раз два, нам нужно начать с нашей матрицы 𝐴, а затем удалить первую строку. Это означает, что мы удаляем следующие три записи. Затем нам также нужно удалить столбец два. Это означает, что нам нужно удалить весь второй столбец матрицы 𝐴. И мы видим, что это оставляет нас всего с четырьмя элементами. Затем мы можем построить нашу минор матрицы 𝐴 один два путем построения матрицы с четырьмя оставшимися элементы. Это дает нам 𝐴 один два матрица два на два шесть, один, пять, минус восемь.
Но вопрос не только просят нас найти минор матрицы 𝐴 один два. Нам также необходимо найти его определитель. А так как 𝐴 один два матрицу два на два, мы можем сделать это, вспомнив формулу для определителя матрицы два на два. Напомним определитель квадратная матрица 𝑎, 𝑏, 𝑐, 𝑑 равна 𝑎𝑑 минус 𝑏𝑐. В нашем случае мы видим, что 𝑎 равно шести, а 𝑑 равно минус восьми. И мы также можем видеть, что наши значение 𝑏 равно единице, а 𝑐 равно пяти. Итак, используя эту формулу, мы иметь определитель 𝐴 один два равно шесть умножить на минус восемь минус один раз пять. И если мы вычислим это выражение, получаем минус 53.
Теперь мы готовы найти значение выражения, данного нам в вопросе. У нас отрицательный степень одного плюс два, умноженная на определитель 𝐴 один два, равна минус один в кубе, так как один плюс два равно трем, и минус 53, так как мы уже нашли значение этого определителя.
И мы можем упростить это до дайте нам 53. Таким образом, мы смогли показать для квадратной матрицы 𝐴, данной нам в вопросе, значение отрицательной единицы в степени один плюс два умножить на определитель минора матрицы 𝐴 один два равно 53,
Давайте теперь рассмотрим пример нахождения кофакторной матрицы квадратной матрицы размером три на три. Мы начнем с квадратная матрица три на три 𝐴 равна трем, нулю, отрицательным трем, минус два, минус три, минус шесть, семь, три, минус пять. А теперь вспомним элемент в строке 𝑖 и столбце 𝑗 нашей матрицы кофакторов будет отрицательна единица в степени 𝑖 плюс 𝑗, умноженное на определитель минора матрицы 𝐴 𝑖𝑗.
Итак, чтобы найти нашу матрицу кофакторов, сначала нам нужно найти все миноры нашей матрицы. Начнем с матрицы минор 𝐴 один один.
Помните, это означает, что мы потребуется удалить первую строку и первый столбец из матрицы 𝐴. Это дает нам следующее матрица два на два. Это дает нам 𝐴 один из них минус три, минус шесть, три, минус пять. Чтобы найти нашу матрицу кофакторов, нам нужно найти все миноры нашей матрицы.
Теперь найдем минор матрицы 𝐴 раз два. Это означает, что нам нужно удалить первая строка и второй столбец из нашей матрицы 𝐴. И это оставляет нас с следующие четыре элемента. Итак, минор матрицы 𝐴 один два минус два, минус шесть, семь, минус пять. Поскольку наша матрица 𝐴 представляет собой матрица три на три, наши значения 𝑖 и 𝑗 будут варьироваться от одного до трех. Таким образом, у нас будет девять полных матриц. несовершеннолетние для расчета. И мы можем найти все девять из этим же методом.
Убираем строку 𝑖 и столбец 𝑗 из нашей матрицы 𝐴. Это дает нам следующее девять матричных миноров.
Теперь мы можем видеть из нашего определение матрицы кофакторов, которое нам теперь понадобится, чтобы найти определитель всех этих матричных миноров. А так как все это матрицы два на два, мы можем сделать это, вспомнив определитель матрица два на два 𝑎, 𝑏, 𝑐, 𝑑 равна 𝑎𝑑 минус 𝑏𝑐. Итак, начнем с поиска определитель минора матрицы 𝐴 один единица. Это равно минус три умножить на минус пять минус минус шесть умножить на три. И если мы вычислим это выражение, оно равно 33,
Мы можем сделать то же самое чтобы найти определитель минора нашей матрицы 𝐴 один два. Это равно минус два умножить на минус пять минус минус шесть умножить на семь. И если мы вычислим это выражение, мы видим, что оно равно 52.
Используя точно такой же метод, мы можно найти определители всех наших матричных миноров. Мы получили бы следующее ценности.
Теперь, когда мы нашли детерминанты всех наших матричных миноров, мы можем найти все элементы нашего кофакторная матрица. Начнем с записи в первая строка и первый столбец нашей матрицы кофакторов. Он будет равен отрицательному один в степени один плюс один, умноженный на определитель нашей матрицы минор 𝐴 один один. Ну, мы знаем, что отрицательный мощность одного плюс один равна единице. И мы это уже показывали определитель 𝐴 единицы равен 33. Таким образом, 𝐶 единица будет равна 33. Итак, мы показали, что 𝐶 один один равно 33. И действительно, мы можем добавить к этому в нашу матрицу кофакторов в первой строке, первом столбце.
Мы можем сделать то же самое, чтобы найти запись в первой строке, во втором столбце. Он равен отрицательной единице степень одного плюс два, умноженная на определитель числа 𝐴 один два. А так как определитель 𝐴 один два равно 52, это упрощает получение отрицательных 52. Затем мы можем добавить это в наша матрица кофакторов в первой строке, во втором столбце. И тогда мы могли бы сделать точно то же самое, чтобы найти все оставшиеся элементы нашей матрицы кофакторов. Это даст нам следующие значения. И так же, как раньше, мы Затем можно добавить их в нашу матрицу кофакторов 𝐶.
Одна вещь стоит указываю здесь. Когда мы вычисляем 𝐶 𝑖𝑗, мы умножить определитель минора нашей матрицы на минус единицу в степени 𝑖 плюс 𝑗. Это означает, что в первой строке столбец единицу, мы всегда будем умножать на положительную единицу.
А затем в первой строке и столбце два, мы всегда будем умножать на минус один. И этот узор будет продолжать. А некоторые люди предпочитают использовать это вместо того, чтобы умножать на минус один в степени 𝑖 плюс 𝑗. Нам просто нужно помнить, чтобы умножить наш определитель на значение.
Теперь, когда мы построили наш матрица кофакторов, мы можем обсудить, как мы можем использовать это, чтобы найти обратную нашу матрица. Во-первых, нам нужен последний определение. Присоединенная матрица матрицы 𝐴, обозначаемый присоединенным 𝐴, равен транспонированию нашей матрицы 𝐶, где 𝐶 есть матрица кофакторов 𝐴. И это тоже стоит помнить когда мы транспонируем матрицу, мы меняем местами строки и столбцы вокруг.
И теперь мы наконец готовы определить, как найти обратную квадратную матрицу.
У нас есть, если 𝐴 является квадратом матрица и определитель 𝐴 не равен нулю, то обратный 𝐴 будет равен единице, деленной на определитель 𝐴, умноженный на сопряженный из 𝐴. Таким образом, чтобы найти обратное любому квадратная матрица состоит из двух частей. Во-первых, нам нужно найти определитель 𝐴, а затем нам нужно найти сопряженный 𝐴. И помните, если определитель 𝐴 равен нулю, то матрица не имеет обратный. Обычно мы проверяем это первый.
Давайте теперь рассмотрим несколько примеров использования сопряженного метода для нахождения обратной некоторых матриц.
Рассмотрим матрицу единица, ноль, три, один, ноль, один, три, один, ноль. Определить, имеет ли матрица обратное, найдя, отличен ли определитель от нуля. Если определитель отличен от нуля, найти обратное, используя формулу обратного, которая включает кофактор матрица.
Нам дают три на три матрица. И первое, что нас просят нужно определить, имеет ли эта матрица обратную, сначала найдя определитель нашей матрицы и проверка, равна ли она нулю. Помните, что если определитель матрица равна нулю, то эта матрица не может быть обратимой. А для квадратной матрицы, если ее определитель не равен нулю, то он обратим. Итак, нам нужно начать с поиска определитель нашей матрицы. Мы назовем эту матрицу 𝐴.
Есть много разных способов нахождение определителя матрицы. Самый простой способ — найти, какой строка или столбец содержит наибольшее количество нулей. Для нашей матрицы 𝐴 мы можем видеть это второй столбец. У него два нуля. Тогда нам нужно вспомнить нашу формулу для определителя матрицы три на три, где мы выбираем столбец 𝑗. Это дает нам следующее выражение, где строчная 𝑎 одна 𝑗, строчная 𝑎 две 𝑗 и строчная 𝑎 три 𝑗 — записи в первой строке столбца 𝑗; вторая строка, столбец 𝑗; и третья строка, столбец 𝑗 нашей матрицы 𝐴.
И заглавная 𝐴 одна 𝑗, заглавная 𝐴 два 𝑗 и заглавные 𝐴 три 𝑗 — наши матричные миноры.
Поскольку мы выбрали второй столбец, мы установим наше значение 𝑗 равным двум. Таким образом, используя 𝑗 равно двум, мы получить следующее выражение. И мы можем упростить это. Во-первых, отрицательная единица в степени один плюс два равно минус один. Отрицательная единица в степени двойки плюс два равно одному. И отрицательный в степени три плюс два равно минус один. Таким образом, мы можем упростить наше выражение дать нам следующее.
Затем мы можем использовать наше определение матрица 𝐴, чтобы найти некоторые из этих значений. Во-первых, строчная 𝑎 из одной двойки запись в строке один, столбец два нашей матрицы. Мы видим, что это ноль. Далее строчная 𝑎 два два — это запись во второй строке, во втором столбце. Мы видим, что это тоже ноль.
Наконец, строчная 𝑎 три два запись в строке три, столбце два. Мы видим, что это равно один. Таким образом, наши первые два термина имеют нулевой множитель и, следовательно, равны нулю. Итак, все это выражение упрощает, чтобы дать нам отрицательное значение, умноженное на определитель минора матрицы 𝑎 три два. И мы можем найти минор нашей матрицы 𝐴 три два из нашего определения 𝐴.
Помните, нам нужно удалить строку три и второй столбец из нашей матрицы 𝐴. И это оставляет нам только четыре элементы: один, три, один, один. Итак, наша присоединенная матрица 𝐴 три два это матрица два на два один, три, один, один. Итак, определитель 𝐴 равен отрицательный, умноженный на определитель матрицы два на два один, три, один, один. И мы знаем, как найти определитель матрицы два на два. Определитель два на два матрица 𝑎, 𝑏, 𝑐, 𝑑 равна 𝑎𝑑 минус 𝑏𝑐.
И, используя это, мы можем показать определитель матрицы два на два один, три, один, один равен единице, умноженной на единицу минус трижды один. И, конечно же, нам еще нужно умножьте это на минус один. А если упростить это выражение, мы видим, что мы получаем два. И поэтому, поскольку определитель нашей квадратной матрицы не равен нулю, мы можем заключить, что он должен иметь инверсия.
Следующая часть нашего вопроса задана нам найти обратную нашу матрицу, используя формулу, которая включает в себя кофакторная матрица. Итак, давайте очистим немного места, а затем вспомните, как мы это сделали бы для нашей матрицы 𝐴. Напомним, что можно найти обратную матрицы, выполнив пять шагов.
Сначала нам нужно рассчитать определитель нашей матрицы 𝐴. Мы делаем это в первую очередь, потому что если это равно нулю, то мы не можем найти обратное.
И мы уже сделали это в первая часть нашего вопроса. Мы обнаружили, что определитель наша матрица 𝐴 была равна двум.
Второе, что нам нужно сделать, это найти все миноры нашей матрицы. Помните, матричный минор 𝐴 𝑖𝑗 это наша матрица 𝐴, в которой мы удаляем строку 𝑖 и столбец 𝑗. Начнем с поиска 𝐴 одного один. Это означает, что нам нужно удалить первая строка и первый столбец нашей матрицы 𝐴. Итак, мы удаляем первую строку и первый столбец из нашей матрицы 𝐴. И, сделав это, мы остаемся с всего четыре элемента. Таким образом, минор матрицы 𝐴 один равен равна матрице два на два ноль, один, один, ноль. Нам нужно найти всю нашу матрицу несовершеннолетние. Теперь нам нужно найти 𝐴 один два. Это означает, что мы удаляем первую строку и второй столбец из нашей матрицы 𝐴. Делая это, мы можем видеть, что мы осталось четыре записи: один, один, три и ноль.
Таким образом, минор матрицы 𝐴 один два равен матрица два на два один, один, три, ноль. И мы можем использовать точно такие же метод, чтобы найти все наши матричные миноры. Получаем следующие девять матрицы.
Третье, что нам нужно сделать, это построить нашу матрицу кофакторов. И помните, запись в строке 𝑖, столбец 𝑗 нашей матрицы кофакторов равен отрицательной единице в степени 𝑖 плюс 𝑗 умножается на определитель минора матрицы 𝐴 𝑖𝑗. Это означает, что нам нужно найти определители всех девяти миноров нашей матрицы. И мы знаем, как найти определитель матрицы два на два. Например, определитель 𝐴 одна единица будет равна нулю, умноженной на ноль, минус единица, умноженная на единицу. И мы можем оценить это выражение. Он равен отрицательной единице.
Точно так же мы можем найти определитель нашей второй матрицы кофакторов.
Получаем, что это равно единице, умноженной на ноль. минус один умножить на три, который мы можем вычислить, равен минус три. И мы можем сделать то же самое найти определитель всех остальных миноров нашей матрицы. Получаем следующие значения. Но помните, нам нужно умножить это минус один в степени 𝑖 плюс 𝑗. Другими словами, мы умножаем определитель 𝐴 один за другим. Затем умножаем определитель 𝐴 один два на отрицательный один, это дает нам положительное три, и умножить определитель 𝐴 один три на один. Умножаем определитель 𝐴 два один минус один. Это дает нам положительную тройку. И мы можем продолжать это для всех наших матричных миноров. Это дает нам следующее ценности.
И помните, каждое из этих значений является записью в нашей матрице кофакторов. Итак, заполнив строку 𝑖, столбец 𝑗 с каждым из этих значений мы получаем нашу матрицу кофакторов 𝐶: матрица три на три.
Итак, давайте очистим нашу работу и перейдем к четвертому шагу. Теперь нам нужно найти наше сопряженное матрица. Это транспонирование нашего кофакторная матрица.
Помните, транспонирование матрицы означает, что нам нужно поменять местами строки со столбцами. Итак, когда мы транспонируем наш кофактор матрица, наша первая строка будет отрицательной один, три, ноль. Так пишем в первой строке минус один, три, ноль. И второго ряда у нас будет три, минус девять, два. И наш третий ряд будет один, отрицательная единица, ноль. А это примыкание к нашему матрица 𝐴. Все, что осталось сделать сейчас, это использовать наша формула, чтобы найти обратную 𝐴.
Используя нашу формулу для обратного 𝐴, мы получаем, что обратное 𝐴 равно следующему выражению. И тогда мы можем упростить это матрица, чтобы найти матрицу три на три, обратную 𝐴.

 .n]
where n = length matrix - 1
.n]
where n = length matrix - 1
 Поэтому напишите элементы, которые остались как есть.
Поэтому напишите элементы, которые остались как есть.
 Мы рассмотрим метод в
подробно, объясняя, как найти миноры матрицы, как построить кофактор
матрица, а затем как построить сопряжения нашей матрицы. Затем мы рассмотрим несколько примеров
объясняя, как мы можем применить этот метод, чтобы найти инверсию.
Мы рассмотрим метод в
подробно, объясняя, как найти миноры матрицы, как построить кофактор
матрица, а затем как построить сопряжения нашей матрицы. Затем мы рассмотрим несколько примеров
объясняя, как мы можем применить этот метод, чтобы найти инверсию. И самый простой способ понять
это понятие через пример.
И самый простой способ понять
это понятие через пример. Итак, нам нужно удалить третью строку
из нашей матрицы 𝐴. И мы видим, что значение 𝑗 равно
один. Итак, нам нужно удалить первый
столбец из матрицы 𝐴. И тогда мы можем построить нашу
матрица 𝐴 три один, используя все оставшиеся элементы, которые мы не
удалить из 𝐴. Это дает нам 𝐴 три один
следующую матрицу.
Итак, нам нужно удалить третью строку
из нашей матрицы 𝐴. И мы видим, что значение 𝑗 равно
один. Итак, нам нужно удалить первый
столбец из матрицы 𝐴. И тогда мы можем построить нашу
матрица 𝐴 три один, используя все оставшиеся элементы, которые мы не
удалить из 𝐴. Это дает нам 𝐴 три один
следующую матрицу. Тогда определитель 𝐴 равен
в 𝑎𝑑 минус 𝑏𝑐. Теперь мы готовы обсудить ключ
часть, которая поможет нам найти обратную любую квадратную матрицу с ненулевым
определитель. Нам нужно обсудить, что
кофакторная матрица матрицы 𝐴 есть.
Тогда определитель 𝐴 равен
в 𝑎𝑑 минус 𝑏𝑐. Теперь мы готовы обсудить ключ
часть, которая поможет нам найти обратную любую квадратную матрицу с ненулевым
определитель. Нам нужно обсудить, что
кофакторная матрица матрицы 𝐴 есть. Таким образом, наши значения 𝑖 будут работать
по строкам нашей матрицы 𝐴. И значения 𝑗 будут
пробегая по столбцам нашей матрицы 𝐴. Таким образом, наши значения 𝑖 варьируются от единицы
до 𝑛, а наши значения 𝑗 варьируются от единицы до 𝑛. Это означает, что наша кофакторная матрица будет
быть квадратной матрицей. Это будет порядка 𝑛 к 𝑛.
Таким образом, наши значения 𝑖 будут работать
по строкам нашей матрицы 𝐴. И значения 𝑗 будут
пробегая по столбцам нашей матрицы 𝐴. Таким образом, наши значения 𝑖 варьируются от единицы
до 𝑛, а наши значения 𝑗 варьируются от единицы до 𝑛. Это означает, что наша кофакторная матрица будет
быть квадратной матрицей. Это будет порядка 𝑛 к 𝑛.
 В нашем случае мы можем видеть
значение 𝑖 равно единице, а 𝑗 равно двум. Затем мы можем записать это в наш
определение минора матрицы. Мы видим, что минор матрицы 𝐴
один два означает, что мы удаляем первую строку и второй столбец из матрицы 𝐴.
В нашем случае мы можем видеть
значение 𝑖 равно единице, а 𝑗 равно двум. Затем мы можем записать это в наш
определение минора матрицы. Мы видим, что минор матрицы 𝐴
один два означает, что мы удаляем первую строку и второй столбец из матрицы 𝐴.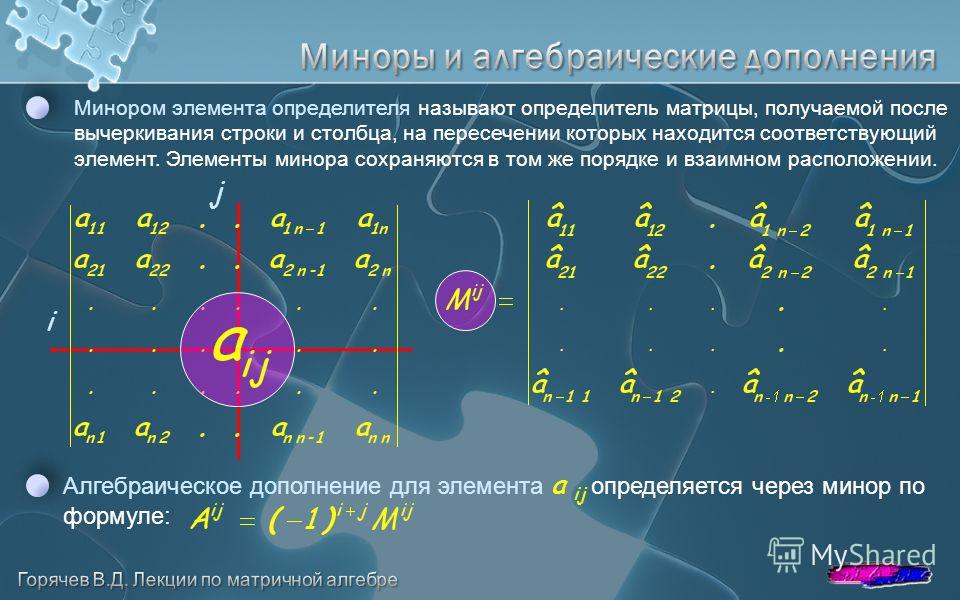
 И мы можем упростить это до
дайте нам 53. Таким образом, мы смогли показать
для квадратной матрицы 𝐴, данной нам в вопросе, значение отрицательной единицы
в степени один плюс два умножить на определитель минора матрицы 𝐴 один
два равно 53,
И мы можем упростить это до
дайте нам 53. Таким образом, мы смогли показать
для квадратной матрицы 𝐴, данной нам в вопросе, значение отрицательной единицы
в степени один плюс два умножить на определитель минора матрицы 𝐴 один
два равно 53, Помните, это означает, что мы
потребуется удалить первую строку и первый столбец из матрицы 𝐴. Это дает нам следующее
матрица два на два. Это дает нам 𝐴 один из них
минус три, минус шесть, три, минус пять. Чтобы найти нашу матрицу кофакторов,
нам нужно найти все миноры нашей матрицы.
Помните, это означает, что мы
потребуется удалить первую строку и первый столбец из матрицы 𝐴. Это дает нам следующее
матрица два на два. Это дает нам 𝐴 один из них
минус три, минус шесть, три, минус пять. Чтобы найти нашу матрицу кофакторов,
нам нужно найти все миноры нашей матрицы. Убираем строку 𝑖 и столбец 𝑗
из нашей матрицы 𝐴. Это дает нам следующее
девять матричных миноров.
Убираем строку 𝑖 и столбец 𝑗
из нашей матрицы 𝐴. Это дает нам следующее
девять матричных миноров. Используя точно такой же метод, мы
можно найти определители всех наших матричных миноров. Мы получили бы следующее
ценности.
Используя точно такой же метод, мы
можно найти определители всех наших матричных миноров. Мы получили бы следующее
ценности.
 А затем в первой строке и столбце
два, мы всегда будем умножать на минус один. И этот узор будет
продолжать. А некоторые люди предпочитают использовать
это вместо того, чтобы умножать на минус один в степени 𝑖 плюс 𝑗. Нам просто нужно помнить, чтобы
умножить наш определитель на значение.
А затем в первой строке и столбце
два, мы всегда будем умножать на минус один. И этот узор будет
продолжать. А некоторые люди предпочитают использовать
это вместо того, чтобы умножать на минус один в степени 𝑖 плюс 𝑗. Нам просто нужно помнить, чтобы
умножить наш определитель на значение. У нас есть, если 𝐴 является квадратом
матрица и определитель 𝐴 не равен нулю, то обратный 𝐴
будет равен единице, деленной на определитель 𝐴, умноженный на сопряженный
из 𝐴. Таким образом, чтобы найти обратное любому
квадратная матрица состоит из двух частей. Во-первых, нам нужно найти
определитель 𝐴, а затем нам нужно найти сопряженный 𝐴. И помните, если
определитель 𝐴 равен нулю, то матрица не имеет
обратный. Обычно мы проверяем это
первый.
У нас есть, если 𝐴 является квадратом
матрица и определитель 𝐴 не равен нулю, то обратный 𝐴
будет равен единице, деленной на определитель 𝐴, умноженный на сопряженный
из 𝐴. Таким образом, чтобы найти обратное любому
квадратная матрица состоит из двух частей. Во-первых, нам нужно найти
определитель 𝐴, а затем нам нужно найти сопряженный 𝐴. И помните, если
определитель 𝐴 равен нулю, то матрица не имеет
обратный. Обычно мы проверяем это
первый.
 И заглавная 𝐴 одна 𝑗, заглавная 𝐴
два 𝑗 и заглавные 𝐴 три 𝑗 — наши матричные миноры.
И заглавная 𝐴 одна 𝑗, заглавная 𝐴
два 𝑗 и заглавные 𝐴 три 𝑗 — наши матричные миноры. Наконец, строчная 𝑎 три два
запись в строке три, столбце два. Мы видим, что это равно
один. Таким образом, наши первые два термина имеют
нулевой множитель и, следовательно, равны нулю. Итак, все это выражение
упрощает, чтобы дать нам отрицательное значение, умноженное на определитель минора матрицы 𝑎
три два. И мы можем найти минор нашей матрицы 𝐴
три два из нашего определения 𝐴.
Наконец, строчная 𝑎 три два
запись в строке три, столбце два. Мы видим, что это равно
один. Таким образом, наши первые два термина имеют
нулевой множитель и, следовательно, равны нулю. Итак, все это выражение
упрощает, чтобы дать нам отрицательное значение, умноженное на определитель минора матрицы 𝑎
три два. И мы можем найти минор нашей матрицы 𝐴
три два из нашего определения 𝐴. И, используя это, мы можем показать
определитель матрицы два на два один, три, один, один равен единице, умноженной на единицу
минус трижды один. И, конечно же, нам еще нужно
умножьте это на минус один. А если упростить это выражение,
мы видим, что мы получаем два. И поэтому, поскольку
определитель нашей квадратной матрицы не равен нулю, мы можем заключить, что он должен иметь
инверсия.
И, используя это, мы можем показать
определитель матрицы два на два один, три, один, один равен единице, умноженной на единицу
минус трижды один. И, конечно же, нам еще нужно
умножьте это на минус один. А если упростить это выражение,
мы видим, что мы получаем два. И поэтому, поскольку
определитель нашей квадратной матрицы не равен нулю, мы можем заключить, что он должен иметь
инверсия. И мы уже сделали это в
первая часть нашего вопроса. Мы обнаружили, что определитель
наша матрица 𝐴 была равна двум.
И мы уже сделали это в
первая часть нашего вопроса. Мы обнаружили, что определитель
наша матрица 𝐴 была равна двум. Таким образом, минор матрицы 𝐴 один два равен
матрица два на два один, один, три, ноль. И мы можем использовать точно такие же
метод, чтобы найти все наши матричные миноры. Получаем следующие девять
матрицы.
Таким образом, минор матрицы 𝐴 один два равен
матрица два на два один, один, три, ноль. И мы можем использовать точно такие же
метод, чтобы найти все наши матричные миноры. Получаем следующие девять
матрицы. Получаем, что это равно единице, умноженной на ноль.
минус один умножить на три, который мы можем вычислить, равен минус три. И мы можем сделать то же самое
найти определитель всех остальных миноров нашей матрицы. Получаем следующие значения. Но помните, нам нужно умножить
это минус один в степени 𝑖 плюс 𝑗. Другими словами, мы умножаем
определитель 𝐴 один за другим. Затем умножаем определитель
𝐴 один два на отрицательный один, это дает нам положительное три, и умножить
определитель 𝐴 один три на один. Умножаем определитель 𝐴
два один минус один. Это дает нам положительную тройку. И мы можем продолжать это для всех
наших матричных миноров. Это дает нам следующее
ценности.
Получаем, что это равно единице, умноженной на ноль.
минус один умножить на три, который мы можем вычислить, равен минус три. И мы можем сделать то же самое
найти определитель всех остальных миноров нашей матрицы. Получаем следующие значения. Но помните, нам нужно умножить
это минус один в степени 𝑖 плюс 𝑗. Другими словами, мы умножаем
определитель 𝐴 один за другим. Затем умножаем определитель
𝐴 один два на отрицательный один, это дает нам положительное три, и умножить
определитель 𝐴 один три на один. Умножаем определитель 𝐴
два один минус один. Это дает нам положительную тройку. И мы можем продолжать это для всех
наших матричных миноров. Это дает нам следующее
ценности. Итак, давайте очистим нашу работу и перейдем
к четвертому шагу. Теперь нам нужно найти наше сопряженное
матрица. Это транспонирование нашего
кофакторная матрица.
Итак, давайте очистим нашу работу и перейдем
к четвертому шагу. Теперь нам нужно найти наше сопряженное
матрица. Это транспонирование нашего
кофакторная матрица.