Чай не водка — он греет: в аномальные холода скорая в Казани спасает пьяных обмороженных, а школьникам продлили каникулы
Пойдут на спад с середины недели аномальные рождественские морозы, когда столбик термометра опустился почти на 20 градусов ниже климатической нормы. За последние три дня скорая в Казани почти 40 раз выезжала на вызовы по поводу переохлаждений и обморожений. Медики отмечают, что от мороза больше всего пострадали подвыпившие граждане, и напоминают, что согреться спиртным в холода невозможно, куда лучше поможет горячий чай.
Как рассказал «Вечерней Казани» профессор кафедры метеорологии, климатологии и экологии атмосферы института экологии и природопользования КФУ Юрий Переведенцев, погода продолжает удивлять нас аномалиями.
— Если декабрь в целом оказался в Татарстане теплее нормы градуса на полтора, и осадков, кстати, выпало в полтора раза больше нормы, то сейчас среднесуточная температура на 18 — 19 градусов ниже нормы, которая для этого периода составляет минус 10 — 11 градусов, — отметил метеоролог.
— Сильное похолодание, которое началось 5 января, обусловлено тем, что в арктическом воздухе, который распространился на всей европейской части России, сформировался антициклон, то есть область очень высокого давления. Арктический воздух и сам по себе холодный, потому что в Арктике сейчас полярная ночь, а антициклон, при котором нет облаков, усиливает эффект, происходит сильное выхолаживание. Последний раз такой холод 9 января был в 1987 году, тогда в Казани было минус 32 градуса.
По словам Переведенцева, со среды благодаря циклону с Северной Атлантики нас ждет небольшое потепление: 11 января днем будет минус 20, к концу недели потеплеет до минус 12 — 13 градусов днем, но среднесуточная температура будет все же на 3 — 4 градуса ниже нормы.
Оттепелей и ледяных дождей, какие были в декабре, в январе не предвидится.
— Все зависит от того, откуда к нам придет воздушная масса. Но, по статистике, вторжения теплых воздушных масс со стороны Атлантики в январе-феврале происходят реже, в это время на нас влияет уже Сибирь, где формируется сибирский антициклон, а мы, как правило, оказываемся в его западной периферии, — объясняет профессор.
Осадки в январе прогнозируются в пределах нормы: 41 мм, из которых 15 мм уже выпало в первые январские дни.
Пока метеорологи фиксируют температурные рекорды, медики в Казани спешат на помощь к пациентам с переохлаждением и обморожениями. С 6 по 8 января городская станция скорой помощи получила 39 таких вызовов, 11 человек попали с обморожениями в больницы. По словам медиков, в основном от холода страдают кисти и пальцы рук, также в мороз нужно беречь и закрывать одеждой нос, щеки и уши.
— При первой степени обморожения пациенты чувствуют боль и жжение на поврежденном участке и изменение цвета кожных покровов, при второй степени на коже появляются пузыри с серозным содержимым, и это уже повод для обращения в больницу, — предупреждает травматолог-ортопед Центра амбулаторной травматологии горбольницы № 18 Эльмир Валеев. — Растирать место обморожения категорически нельзя, тем самым вы еще больше его травмируете. Нужно постепенно увеличивать температуру в месте обморожения — сделать ватно-марлевую повязку, укрыть теплыми вещами.
Также пациенту показано обильное теплое сладкое питье.
— Спиртное на морозе не поможет согреться, это большой обман! — отмечает, в свою очередь, заведующий 1-м стационарным отделением Республиканского клинического наркологического диспансера Дамир Вагапов. — Попадая в организм, алкоголь вызывает расширение мелких периферических сосудов кожи, вызывая ложное ощущение согрева. Однако за счет расширения поверхностных сосудов увеличивается отдача тепла организмом во внешнюю среду, тогда как нормальная реакция на холоде — это, наоборот, сжатие периферических сосудов кожи, чтобы сберечь тепло. Поэтому переохлаждение организма у подвыпившего человека наступает быстрее, чем у трезвого. При этом пьяный человек не способен адекватно оценивать ситуацию. Алкоголь может действовать как наркоз, поэтому пострадавший не чувствует болевых ощущений, он может расслабиться и заснуть, например, в сугробе.
Нарколог отметил, что большинство вызовов скорой помощи на переохлаждения и обморожения в последние дни были как раз к нетрезвым пострадавшим.
Тем временем школьникам в Татарстане из-за сильных морозов на два дня — 9 и 10 января — продлили новогодние каникулы. А вот учителя вышли сегодня на работу и готовы вести уроки, если кто-то из детей все-таки придет в школу.
«Невзирая на показатели термометров, все татарстанские школы и педагогические коллективы работают в обычном режиме и в полном составе. Если вам не с кем оставить несовершеннолетних детей, то школы примут их при любой температуре. С ребенком будут заниматься педагоги, и он будет накормлен горячим питанием», — заверили в пресс-службе Минобрнауки РТ.
В министерстве напомнили, что по регламенту уроки в начальных классах сельских школ могут быть отменены при температуре минус 23 градуса, в средних классах — при минус 25, в старшем звене — при минус 30. В городах «началка» может не учиться при минус 25 градусах, 5 — 9-е классы — при минус 27, 10 — 11-е классы — при минус 32 градусах.
Однако сегодня и завтра мороз на улице такой, что не учиться разрешили всем классам во всех школах.
Как решить кубическое уравнение с помощью схемы Горнера — Гайды на DTF
Гайды
KILLE
Итак, пред вами кубическое уравнение и вы не знаете с чего начать? Тогда этот гайд для вас.
5990 просмотров
Да, это то самое уравнение которое тебе надо решить. Gonna cry?
Выглядит страшно, понимаю, но пугаться не надо. Можно заметить отсутствие икса во второй степени. Хорошо это или плохо? Хуй его знает, блчть.
А с чего начать? А начать надо с начала, то есть с подбора корня. Да, один корень из трех придется подобрать в уме. В данном случае это, очевидно, х=1.
Наша цель привести уравнение к такому виду:
Первая скобка формируется следующим образом: икс минус тот корень, что мы нашли подбором. Во второй скобке стоит некое выражение, которое мы и получим с помощью схемы Горнера.
Делаем табличку 2 на 5. Она всегда будет такой размерности при кубическом уравнении.
Заполняем первую строку. В первую клеточку не пишем ничего. В четыре остальных выписываем коэффициенты при иксах.
Картинка для тупых. Выписываем в таблицу эти коэффициенты. По порядку, а не как захочется. Перед икс в кубе стоит 1. Нет не ноль. Ноль стоит перед икс в квадрате. Икс в квадрате — это та несуществующая хуитень между икс в кубе и 7икс.
Во второй строке в первой клетке пишем наш корень, который мы подобрали. Все, отложи руки в стороны, чтобы ничего не напортачить и смотри на картинку.
Я только что понял, что на картинке для тупых обвел красным 7, а должен был обвести -7. Ну не переделывать же теперь?
А сейчас начнется магия. Во второй клеточке второй строки пишем то же число, что написано клеткой выше. Далее пользуемся формулой, которую не мог запомнить даже Эйнштейн:
(КОРЕНЬ, КОТОРЫЙ МЫ ПОЛУЧИЛИ ПОДБОРОМ)*(ЗНАЧЕНИЕ ИЗ ПРЕДЫДУЩЕЙ КЛЕТКИ В ТОЙ ЖЕ СТРОКЕ) + (ЗНАЧЕНИЕ ИЗ КЛЕТКИ ВЫШЕ)
Это хуйню нужно применить для каждой клетки второй строки, кроме первых двух. Для третьей клетки будет 1*1+0. Если ты ничего не понял, то перечитай еще раз.
Вот та самая схема. Получилось? Эйнштейн тобой гордится!
В самом конце всегда должен получаться 0. Если 0 не получается, то иди пересчитывай, тупица.
Видишь циферки 1, 1, -6? Это коэффициенты квадратного уравнения. Именно это уравнение стоит в скобках вместо многоточия.
Вот так сложная поебень превратилась в произведение хуйни на хуйню.
Как ты знаешь из курса математики детского садика, если произведение равно нулю, то каждая скобочка равна нулю. Первая скобочка зануляется при х=1, а во второй находится квадратное уравнение, которое решается за 5 часов в уме. Его корни х=2 и х=-3.
Таким образом ответ:
Поздравляю! Теперь ты умеешь решать кубические уравнения с помощью схемы Горнера.
Если ты ничего не понял, то ты гуманитарий.
Математическое выражение: закон экспоненты
00:00:01.060
Этот урок является продолжением части 1 Закона Экспоненты.
00:00:07.020
Чтобы подчеркнуть, очень важно понять логику этих законов, прежде чем использовать их.
00:00:13.110
Законы, которые вы собираетесь изучать, могут быть получены из первых трех законов в части 1. Так что они не совсем новые.
00:00:22.050
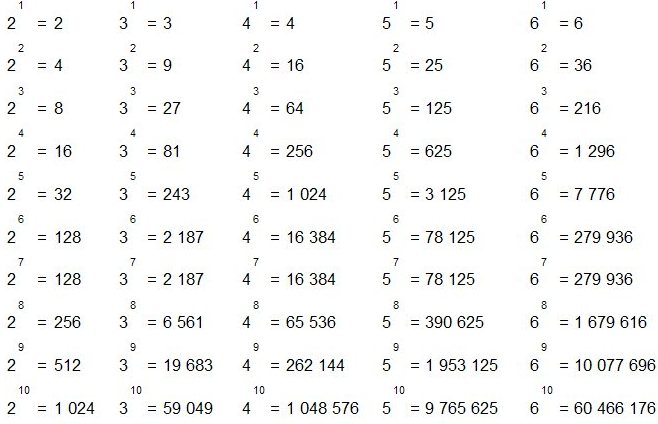
Начнем, рассмотрим этот член, скобка 2 умножить на 3 , в степени 4.
00:00:30,060
Теперь мы можем разбить этот термин на четыре части скобки 2 умножить на 3.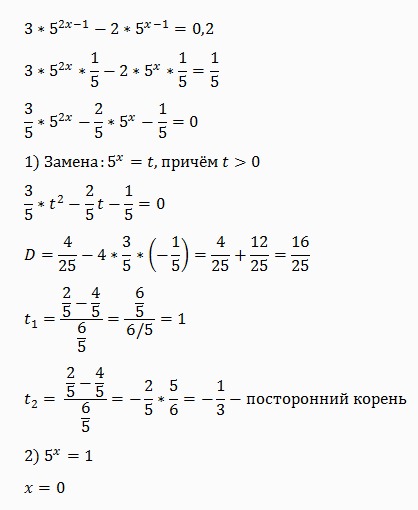
00:00:36,220
Мы можем видеть, что 2 умножить на 2, умножить на 2, умножить на 2, дает 2 в степени 4.
00:00:45,070
Аналогично, 3 умножить на 3, умножить на 3, умножить на 3, дает 3 в степени 4
00:00:54.110
Теперь обратите внимание на эту скобку термина 2 умножить на 3 в степени 4 равно, 2 в степени 4 умножить на 3 в степени 4.
00:01:04.210
С учетом этого наблюдения мы теперь можем сформулировать экспоненциальный закон.
Сначала заменим эти цифры буквами алфавита. Это дает квадратную скобку «а», умноженную на «b» в степени n.
00:01:19.140
Ссылаясь на это, мы также можем увидеть этот термин, скобка ‘a’ умножить на ‘b’ в степени N равно, ‘a’ в степени ‘n’ умножить на ‘b’ в степени n.
00:01:33.100
Итак, у нас есть еще один закон экспоненты. Скобка «а» умножить «b» в степени «n» равно, «а» в степени «n» умножить «b» в степени «n».
00:01:46.060
Давайте посмотрим на следующий закон экспоненты.
Чтобы понять этот закон, давайте рассмотрим деление 2 в степени 3 на 2 в степени 3.
00:01:56.200
Теперь, используя закон второй степени, мы можем увидеть, что этот член равен , 2 в степени 3 минус 3.
00:02:08.090
Три минус три равно 0. Итак, теперь у нас есть 2 в степени 0.
00:02:14.240
Хорошо, давайте посчитаем это термин, используя другой способ. Мы видим, что 2 в степени 3 делится на 2 в степени 3 равно, 8 делится на 8.
00:02:26.200
Теперь 8 делим на 8, получаем 1.
00:02:30.220
Отсюда мы можем увидеть кое-что интересное. Поскольку все эти термины равны друг другу, мы можем сказать, что 2 в нулевой степени равно 1.
00:02:41.230
Теперь мы можем сформулировать экспоненциальный закон.
00:02:46.200
Давайте сначала заменим это число, «2» на «а». Это дает «а» в степени нуля.
00:02:54.160
Ссылаясь на это, мы можем сделать вывод, что «а» в нулевой степени равно 1.
00:03:02.
000
Итак, здесь у нас есть еще один закон показателей. ‘a’ в нулевой степени равно 1.
00:03:02.000
Давайте посмотрим на следующий закон экспоненты. Чтобы понять этот закон, давайте рассмотрим этот термин, 1 делится на 2 в степени 3.
00:03:20.030
Теперь обратите внимание на число 1 в числителе. Используя этот экспоненциальный закон, «а» в степени нуля равно 1, мы можем переписать 1 как, 2 в степени 0.
00:03:36.120
Теперь, используя второй закон экспонент, 2 в степени степень 0 делится на два в степени 3 равно, 2 в степени 0 минус 3.
00:03:50.100
0 минус 3 дает минус 3. Теперь у нас есть 2 в отрицательной степени 3.
00:03:58.150
Опять же, мы можем увидеть кое-что интересное. Если мы внимательно посмотрим, поскольку все эти термины равны, мы увидим, что 2 в отрицательной степени 3 равно 1 делению на 2 в степени 3.
00:04:12.090
Давайте перепишем эти два термина здесь .
00:04:15.240
Теперь мы можем сформулировать экспоненциальный закон.
00:04:20.140
00:04:29.160
Ссылаясь на это, мы можем сделать вывод, что ‘a’ в степени отрицательного ‘n’ равно 1 делится на ‘a’ в степени ‘n’.
00:04:41.080
Наконец, у нас есть еще один закон показателей. «а» в степени отрицательного «n» равно 1 делит «а» в степени «n».
00:04:50.160
На этом уроке все. Следующий урок покажет вам несколько примеров использования того, что вы узнали на этом уроке.
возведение в степень — Правило вычисления степени числа, когда показатель степени отрицателен в Прологе?
Во-первых, следует подумать, как определить 0 0 . Формально говоря, это неопределенное . Это может быть ноль, а может быть 1. Как говорится в статье Wolfram Mathworld о степенях и в статье о нуле:
0 0 (ноль в нулевой степени) само по себе не определено. Отсутствие четкого смысла этой величины вытекает из противоречивых фактов, что a 0 всегда равно 1, поэтому 00 должно равняться 1, но 0 a всегда равно 0 (для a > 0), поэтому 0 a 7 должно равняться 7. выбор определения для 0 0 обычно определяется как неопределенный, хотя определение 0 0 = 1 позволяет выразить некоторые формулы просто (Кнут 1992; Кнут 1997, стр. 57).
выбор определения для 0 0 обычно определяется как неопределенный, хотя определение 0 0 = 1 позволяет выразить некоторые формулы просто (Кнут 1992; Кнут 1997, стр. 57).Итак, вы должны сначала выбрать, как определить особый случай 0 0 : это 0? Это 1? Это не определено?
Я рассматриваю это как неопределенное.
При этом вы можете рассматривать положительный показатель степени как указание на повторное умножение (например, 10 3 равно 10*10*10 или 1000), а отрицательный показатель степени указывает на повторное деление (например, 10 -3 равно (((1/10)/10)/10), или 0,001). Я склоняюсь, отчасти потому, что мне нравится симметричность этого подхода, а отчасти из-за того, что я избегаю сокращений (поскольку разрез часто является сигналом того, что вы неправильно определили решение), будет примерно таким:
% -------------------------------------------- % Внешний/общедоступный предикат % ----------------------------- pow( 0 , 0 , _ ) :- ! , провал .
