Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
1)В воду объемом 1 л ,температура которой 20С°, бросают кусок железа массой 100г, нагретый до 500С°.
Решено
Помогите, пожалуйста!!! Очень важно!!! 1)В коробке вперемешку лежат чайные пакетики с черным и зеленым чаем, одинаковые на вид, причем пакетиков с черным чаем в 9 раз больше, чем с зеленым. Найдите
В соляную кислоту сплав серебра с никелем массой 1,5 г,выделился водород объемом 0,224 л(н.у).Массовая доля никеля(в %)
Пользуйтесь нашим приложением
найдите 4 косинус 2 альфа если Синус альфа равен минус 0,5 — Знания.site
Ответы 1
cos2α = 1 — 2sin²α
cos2α = 1 — (0,5)² = 1 — 0,25 = 0,75
4cos2α = 4*0,75 = 3
Ответ 3
Автор:
hazel
Оценить ответ:
0
Знаешь ответ? Добавь его сюда!
Последние вопросы
Математика
1 минута назад
В магазине за 3 дня было продано 27 коробок сока. Сколько коробок продали за 1 день,если ежедневно продавали равное количество сока?
Сколько коробок продали за 1 день,если ежедневно продавали равное количество сока?Химия
1 минута назад
Какая мерная посуда применяется в методе титрования? Укажите ее назначение. На нейтрализацию 10 мл раствора гидроксида натрия потребовалось 17 мл 0,1 н раствора азотной кислоты. Вычислите титр раствора NaOH- История
6 минут назад
Помогите мне сделать доклад по истории, называется «Литература и Живопись». Қазақ тiлi
6 минут назад
6-тапсырма. Өлеңді оқып, әр ой белiгiне такырып кой. Негізгі идеясын аныкта. Әр ой бөлiгiндегi тiрек сездi теріп жаз. Абзацтар Тақырыбы Негізгі идеясы Тірек сөздер помогите
Абзацтар Тақырыбы Негізгі идеясы Тірек сөздер помогитеМатематика
6 минут назад
В коробке 8 кубиков, что в 2 раза больше,чем конусов.Сколько конусов в коробке? По-вашему, кто из детей прав?- Математика
6 минут назад
2. Упростите выражение: Химия
6 минут назад
h3O2 + K2Cr2O7 + h3SO4 → O2 + Cr2(SO4)3 + K2SO4 + h3O AgNO3 → Ag + NO2 + O2Математика
16 минут назад
виконайте завдання на фотоАнглийский язык
21 минут назад
в Выберите правильный вариант ответа. 1 Have you been to France? A yet When A have you finished 2 3 5 6 your project? B already B did you finish He hasn’t been to school a week. A since B for You’re late. The maths lesson has A already B yet started. The teacher us any homework for tonight. A haven’t given B gave Two days, Rob started guitar lessons. A since 8 ago C ever C you finished C before C since C hasn’t given C before
1 Have you been to France? A yet When A have you finished 2 3 5 6 your project? B already B did you finish He hasn’t been to school a week. A since B for You’re late. The maths lesson has A already B yet started. The teacher us any homework for tonight. A haven’t given B gave Two days, Rob started guitar lessons. A since 8 ago C ever C you finished C before C since C hasn’t given C beforeАлгебра
21 минут назад
Здравствуйте, помогите пожалуйста:Найдите значение аргумента, при котором функция (у=4х+3) принимает значение равное 12Математика
21 минут назад
В первый день было отправлено в школы 13%, во второй день 24% и в третий день 18% всего запаса угля. На складе 165 тонн угля. Сколько угля было?
Сколько угля было?Алгебра
21 минут назад
1) f(x) = 5sin8x — 6;найти экстримумБиология
26 минут назад
Допоможіть варіант на вибір даю 25 балівМатематика
26 минут назад
«n!» и «In» в калькуляторе значение клавишҚазақ тiлi
26 минут назад
2. Әңгімеде кездескен географиялык атауларға түсінік беріндер.
How much to ban the user?
1 hour 1 day 100 years
2(альфа-бета) + 2ab cos(альфа-бета)Ответ
Пошаговое решение от экспертов, которое поможет вам в сомнениях и получить отличные оценки на экзаменах.
Стенограмма
когда возникает вопрос, если cos тета минус альфа равно a и Cos тета минус бета равно b, то значение sin квадрат альфа минус b + cos альфа минус бета здесь у нас есть причина тета минус альфа равен а, учитывая, что квадрат греха х + квадрат квадрата х равен 1, так что грех х можно записать как под корнем из 1 — потому что квадрат х, используя это, мы можем написать знак мы можем написать грех тета минус альфа будет под корень 1 минус квадрат, аналогично у нас есть причина тета минус бета как
знак тета минус бета будет равен под корнем 1 минус b квадрат мы можем написать так теперь мы должны найти значение этого выражения сначала мы должны знать значение sin alpha минус beta поэтому здесь мы можем написать sin alpha минус бета равен греху тета минус альфа минус тета минус B квадрат минус бета и здесь будет минус альфа читать и писать вот так альфа минус бета может быть записано так помогает это будет аннулировано и станет Альфа минус бета теперь это Sin A минус b Sin A минус b равно
sin a cos b минус cos a sin b Pradesh становится равным знаку a, т. е. тета минус тета в cos тета минус альфа минус Cos тета минус тета в Sin минус альфа теперь у нас есть значения sin тета минус бета отсюда корень из 1 минус b в квадрате и Cos тета минус альфа это минус потому что тета минус бета это b а грех тета минус альфа находится под корнем 1 минус A квадрат теперь в вопросе у нас есть cos альфа минус бета так же как мы будем вычислять значение из Cos
е. тета минус тета в cos тета минус альфа минус Cos тета минус тета в Sin минус альфа теперь у нас есть значения sin тета минус бета отсюда корень из 1 минус b в квадрате и Cos тета минус альфа это минус потому что тета минус бета это b а грех тета минус альфа находится под корнем 1 минус A квадрат теперь в вопросе у нас есть cos альфа минус бета так же как мы будем вычислять значение из Cos
минус b, потому что альфа, минус бета, можно записать как стоимость тета минус тета, минус тета, минус альфа так же, как мы написали грех альфа минус тета, потому что альфа, минус бета, можно записать так, теперь это cos A минус Cos A минус b который равен cos a cos b + sin a в Sin B этот результат мы скажем, что он становится причинным a то есть cos theta минус theta в cos theta минус alpha + sin of theta минус B в Sin of theta минус Alpha потому что тета минус бета у нас есть равный b и потому что тета минус альфа это
поезд, чтобы быть + синус тета минус бета отсюда корень 1 минус б квадрат и грех тета минус альфа и корень из 1 минус Квадрат должен найти выражение син квадрат синус квадрат от Альфа минус тета + 2 AV стоимость Альфа минус тета sin квадрат A минус тета + 2 AV потому что альфа минус бета мы должны найти значение выражения теперь это значение sin alpha минус бета поэтому мы должны найти это в 1 минус b квадрат и корень минус b в под корнем 1 минус b квадрат целый квадрат минус квадрат синуса альфа минус бета
в a b cos a минус b в быть замкнутым под корнем из 1 минус b в квадрате под корнем из 1 — это мы должны упростить квадрат несправедливость превращается в квадрат в 1 минус b квадрат + b квадрат в 1 минус b квадрат минус 2 AV под Tok 1 — x квадрат в 1 минус 2 x из a-b целого квадрата + b квадратный корень из 1 — x квадрат в меньше корня из 1 минус b в квадрате, теперь вы можете ясно видеть, что этот член сокращается
, поэтому мы осталось с квадратом минус A в квадрат B + квадрат b минус A в квадрат B + 2 x квадрат от 1 до 20 квадрат квадрат в b квадрат также аннулируется мы остаемся с квадратом + b квадрат Садашив значение выражения спасибо ты
Формула дублирования, двойная, архи-ассоциированная и простая
Тригонометрические функции с числовым значением свойств, специально предназначенных для алгебраического представления. Quando siamo di fronte ad una espressione che contiene Queste funzioni, Infatti, è spesso possibile manipolarla utilizzando le cosiddette Formule Trigomonometriche , O Anche 66777676767676767676767676767676767676767676767676767676767676767676767676.
Quando siamo di fronte ad una espressione che contiene Queste funzioni, Infatti, è spesso possibile manipolarla utilizzando le cosiddette Formule Trigomonometriche , O Anche 66777676767676767676767676767676767676767676767676767676767676767676767676.
L’obiettivo che si vuole ottenere ogni volta che si prova a lavorare con queste formule è, mainmente, quello di semplificare l’espressione che ci si trova di fronte. Più generalmente, le identità trigonometriche vengono utilizzate per tentare di ricondurre l’esercizio che si vuole risolvere a una forma che possiamo gestire con metodi conosciuti. 92 \альфа}$$
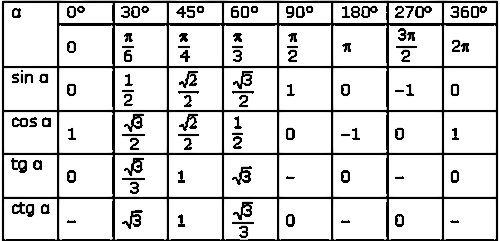
Сопоставление и несоответствие $\sin x,\ \cos x,\ \tan x,\ \cot x$
Valgono le seguenti uguaglianze:
##KATEX##\begin{aligned}\sin (-\alpha) & = — \sin \alpha \\\cos (-\alpha) & = \cos \alpha \\\tan (-\alpha) & = — \tan \alpha \\\cot (-\alpha) & = — \cot \alpha\end{aligned}##KATEX##
Possiamo quindi vedere come il segno meno “esca fuori” dall’argomento delle funzioni trigonometriche $\sin x, \tan x, \cot x$.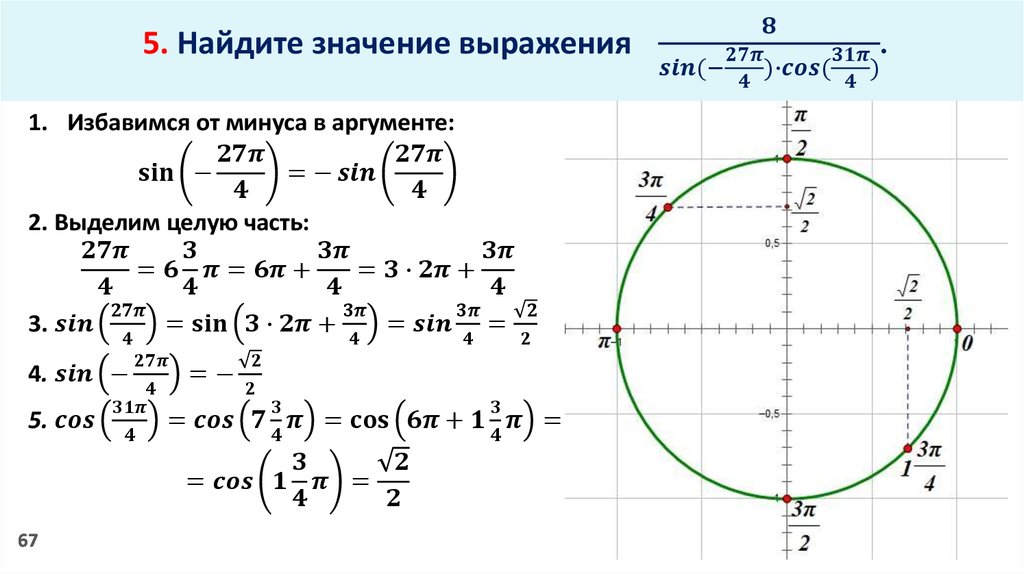 Questa caratteristica, cioè il fatto che $f(-x) = -f(x)$, viene di solito indicata dicendo che le funzioni seno, tangente e cotangente sono funzioni dispari.
Questa caratteristica, cioè il fatto che $f(-x) = -f(x)$, viene di solito indicata dicendo che le funzioni seno, tangente e cotangente sono funzioni dispari.
Invece vediamo che il segno meno viene “assorbito” dalla funzione $\cos x$. Le funzioni con questa caratteristica, cioè il fatto che $f(-x) = f(x)$, vengono dette funzioni pari : quindi il coseno è l’unica funzione trigonometrica elementare ad essere pari.
Formule degli archi (o angoli) associati
Формула ассоциаций архивов позволяет определить значение тригонометрических функций тригонометрического расчета для негли анголи дель типо $\alpha \pm \frac{\pi}{2}, \alpha \pm \pi, \alpha \pm \frac{3\ pi}{2}, \alpha \pm 2\pi$, рикондуцированные значения функций, вычисленные в $\alpha$.
- Angoli $\mathbf{\alpha \pm \frac{\pi}{2}}$:
##KATEX##\begin{aligned}\sin \left ( \alpha + \frac{\pi}{2 } \right ) & = \cos \alpha & \qquad \sin \left ( \alpha — \frac{\pi}{2} \right ) & = — \cos \alpha \\\cos \left ( \alpha + \frac{\pi}{2} \right ) & = — \sin \alpha & \qquad \cos \left ( \alpha — \frac{\pi}{2} \right ) & = \sin \alpha \\ \tan \left ( \alpha + \frac{\pi}{2} \right ) & = — \cot \alpha & \qquad \tan \left ( \alpha — \frac{\pi}{2} \right ) & = — \cot \alpha \\\cot \left ( \alpha + \frac{\pi}{2} \right ) & = — \tan \alpha & \qquad \cot \left ( \alpha — \frac{ \pi}{2} \right ) & = — \tan \alpha \end{aligned}##KATEX## - Angoli $\mathbf{\alpha \pm \pi}$:
##KATEX##\begin{align}\sin \left ( \alpha + \pi \right ) & = -\sin \alpha & \qquad \ sin \left ( \alpha — \pi \right ) & = — \sin \alpha \\\cos \left ( \alpha + \pi \right ) & = — \cos \alpha & \qquad \cos \left (\ alpha — \pi \right ) & = — \cos \alpha \\\tan \left ( \alpha + \pi \right ) & = \tan \alpha & \qquad \tan \left ( \alpha — \pi \right ) & = \tan \alpha \\\cot \left ( \alpha + \pi \right ) & = \cot \alpha & \qquad \cot \left ( \alpha — \pi \right ) & = \cot \alpha \end{выровнено}##KATEX##
Эта формула не имеет значения, в частности, тригонометрических функций $\tan x$ e $\cot x$ с периодическим периодом $\pi$.
- Анголи $\mathbf{\alpha \pm \frac{3\pi}{2}}$ :
##KATEX##\begin{align}\sin \left ( \alpha + \frac{3\pi {2} \right ) & = -\cos \alpha & \qquad \sin \left ( \alpha — \frac{3\pi}{2} \right ) & = \cos \alpha \\\cos \left ( \alpha + \frac{3\pi}{2} \right ) & = \sin \alpha & \qquad \cos \left ( \alpha — \frac{3\pi}{2} \right ) & = — \sin \alpha \\\tan \left ( \alpha + \frac{3\pi}{2} \right ) & = -\cot \alpha & \qquad \tan \left ( \alpha — \frac{3\ pi}{2} \right ) & = -\cot \alpha \\\cot \left ( \alpha + \frac{3\pi}{2} \right ) & = — \tan \alpha & \qquad \cot \left ( \alpha — \frac{3\pi}{2} \right ) & = — \tan \alpha \end{aligned}##KATEX## - Анголо $\mathbf{\alpha \pm 2\pi}$:
##KATEX##\begin{aligned}\sin \left ( \alpha + 2\pi \right ) & = \sin \alpha & \qquad \sin \left ( \alpha — 2\pi \right ) & = \sin \alpha \\\cos \left ( \alpha + 2\pi \right ) & = \cos \alpha & \qquad \cos \left ( \alpha — 2\pi \right ) & = \cos \alpha \\\tan \left ( \alpha + 2\pi \right ) & = \tan \alpha & \qquad \tan \left ( \alpha — 2\ pi \right ) & = \tan \alpha \\\cot \left ( \alpha + 2\pi \right ) & = \cot \alpha & \qquad \cot \left ( \alpha — 2\pi \right ) & = \cot \alpha \end{выровнено}##KATEX##
В этой формуле заметна, в частности, тригонометрическая функция $\sin x$ e $\cos x$ с периодическим периодом $2\pi$.
Sfruttando ле proprietà ди parità e disparità del seno e del coseno, possiamo determinare il valore di espressioni Analoghe a quelle che abbiamo appena visto. Например: $$\sin \left ( \frac{\pi}{2} — \alpha \right ) = \sin \left ( — \left ( \alpha — \frac{\pi}{2} \right ) \right ) = — \sin \left ( \alpha — \frac{\pi}{2} \right ) = — (- \cos \alpha ) = \cos \alpha$$oppure: $$\cos ( — \ альфа — \pi ) = \cos ( — (\alpha + \pi) ) = \cos ( \alpha + \pi ) = -\cos \alpha.$$
Формула добавления и дополнения
Формула добавления и сопоставления позволяет определить значение тригонометрических функций тригонометрического расчета в $\alpha + \beta$ o $\alpha — \beta$, sapendo il valore che esse separatamente in $\alpha$ e $\beta $.
##KATEX##\begin{aligned}\sin(\alpha + \beta) & = \sin \alpha \cdot \cos \beta + \cos \alpha \cdot \sin \beta \\\sin(\alpha — \beta) & = \sin \alpha \cdot \cos \beta — \cos \alpha \cdot \sin \beta \\\cos(\alpha + \beta) & = \cos \alpha \cdot \cos \beta — \sin \alpha \cdot \sin \beta \\\cos(\alpha — \beta) & = \cos \alpha \cdot \cos \beta + \sin \alpha \cdot \sin \beta \\\tan( \ alpha + \ beta) & = \ frac {\ tan \ alpha + \ tan \ beta} {1- \ tan \ alpha \ tan \ beta} \\\ tan (\ alpha — \ beta) & = \ frac {\ tan \alpha — \tan\beta}{1+ \tan \alpha \tan \beta} \\\cot(\alpha + \beta) & = \frac{1- \tan \alpha \tan \beta}{\ tan \alpha + \tan\beta} \\\cot(\alpha — \beta) & = \frac{1+ \tan \alpha \tan \beta}{\tan \alpha — \tan\beta}\end{ выровнено}##KATEX##
Факсиамо из-за важности сохранения:
- Queste identità possono essere lette anche «al contrario».
 Capita infatti, in alcuni esercizi, di trovare delle espressioni in cui si possa riconoscere un termine uguale a quello presente nella parte destra di una delle precentti uguaglianze: spesso, è utile applicare la формула di addizione o di sottrazione per poterlo riscrivere come il membro a Синистра.
Capita infatti, in alcuni esercizi, di trovare delle espressioni in cui si possa riconoscere un termine uguale a quello presente nella parte destra di una delle precentti uguaglianze: spesso, è utile applicare la формула di addizione o di sottrazione per poterlo riscrivere come il membro a Синистра. - Формула архивов, ассоциированная с некоторыми частными формулами дополнений и дополнений: basta porre $\beta$ (oppure $\alpha$) uguale a $\frac{\pi}{2}, \pi, \frac{3\ pi}{2}$ заткнуть $2\pi$. 92 \alpha}\end{align}##KATEX##
Chiaramente l’ultima Formula può essere utilizzata solo se $\alpha \neq \frac{\pi}{2} + k\pi, k \in \mathbb{ Z}$.Vale la pena di fare le seguenti osservazioni.
- Присоединяйтесь к формуле добавления и сотрации, и эта формула может быть использована «al contrario», для упрощения всех эспрессий.
- Формула Ciascuna di duplicazione può essere ottenuta a partire dalle формула di addizione, ponendo $\beta = \alpha$.

- Использование комбинированной формулы добавления и дублирования позволяет получить формулу тройного, четырехкратного и повторного использования.
Формула двойного назначения
Формула бисезона позволяет вычислить тригонометрическое значение тригонометрических функций в $\frac{\alpha}{2}$, используя значение, которое принимается в $\alpha$.
##KATEX##\begin{align}\sin \left ( \frac{\alpha}{2} \right ) & = \pm \sqrt{ \frac{1-\cos \alpha}{2}} \ \\cos \left ( \frac{\alpha}{2} \right ) & = \pm \sqrt{ \frac{1+\cos \alpha}{2}} \\\tan \left ( \frac{\ alpha}{2} \right ) & = \frac{\sin \alpha}{1 + \cos \alpha} = \frac{1 — \cos \alpha}{\sin \alpha} \\\cot \left ( \ frac {\ alpha} {2} \ right ) & = \ frac {\ sin \ alpha} {1 — \ cos \ alpha} = \ frac {1 + \ cos \ alpha} {\ sin \ alpha} \ end { выровнено}##KATEX##
Il segno di $\sin \left ( \frac{\alpha}{2} \right )$ e di $\cos \left ( \frac{\alpha}{2} \right )$ определяется по основанию a dove si trova l’angolo $\alpha$, in modo che i segni nell’uguaglianza siano bilanciati. Facciamo alcuni esempi:
Facciamo alcuni esempi:- Se volessimo calcolare $\sin \left ( \frac{\alpha}{2} \right )$ con $\alpha = \frac{\pi}{6}$, но не более $\frac{\alpha}{ 2} = \frac{\pi}{12}$, che si trova nel primo quadrante, dove la funzione seno ha valori positivi. Di conseguenza al secondo membro, davanti alla radice quadrata, scegliamo il segno $+$: $$\sin \left (\frac{\pi}{12} \right ) = + \sqrt{\frac{1-\cos \ frac{\pi}{6}}{2}} = \ldots = \frac{\sqrt{6} — \sqrt{2}}{4}.$$
- По вычислению $\cos \left ( \frac{\alpha}{2} \right )$ с $\alpha = \frac{7 \pi}{6}$, но точно так же, как $\frac{\alpha}{ 2} = \frac{7\pi}{12}$ è nel terzo quadrante, dove il coseno accept valori negativi. Di conseguenza al secondo membro, davanti alla radice quadrata, scegliamo il segno $-$: $$\cos \left ( \frac{7\pi}{12} \right ) = — \sqrt{\frac{1+\cos \frac{7\pi}{6}}{2}} = \ldots = \frac{\sqrt{2} — \sqrt{6}}{4}.$$
Formule di Werner (prodotto $\to$ somma)
Формула Вернера позволяет преобразовать prodotto di due funzioni trigonometriche in una somma di altre funzioni trigonometriche (ovviamente, a patto di modificare adeguatamente gli argomenti delle funzioni).

##KATEX##\begin{aligned}\cos \alpha \cdot \cos \beta & = \frac{1}{2}\cos(\alpha — \beta) + \frac{1}{2} \ cos (\alpha + \beta) \\\sin \alpha \cdot \sin \beta & = \frac{1}{2}\cos(\alpha — \beta) — \frac{1}{2} \cos (\alpha + \beta) \\\sin \alpha \cdot \cos \beta & = \frac{1}{2}\sin(\alpha — \beta) + \frac{1}{2} \sin ( \alpha + \beta)\end{выровнено}##KATEX##
A partire da queste formule possibile ottenere altre formule Analoghe. Например:
##KATEX##\begin{aligned}\tan\alpha\cdot\tan\beta & = \frac{\sin\alpha\cdot\sin\beta}{\cos\alpha\cdot\cos\ бета} = \\& = \frac{cos(\alpha — \beta) — \cos (\alpha + \beta)}{\cos(\alpha — \beta) + \cos (\alpha + \beta)} \end{выровнено}##KATEX##Формула линеаризации
Формула линеаризации разрешает преобразование и квадратные тригонометрические функции в линейных выражениях тригонометрических функций. 9n \alpha$ за единицу $n \in \mathbb{N}$ универсально. Non spieghiamo in questa lezione il procedimento che dobbiamo seguire; Объявленная идея является продолжением применения формулы Вернера для преодоления потенциала $n$ в $1$.
Формула простаты (сумма $\to$ prodotto)
Формула простаты стоимостная, своего рода «обратная» формула Вернера. Infatti, con queste formule possiamo trasformare la somma di due funzioni trigonometriche in un prodotto di altre funzioni trigonometriche.
##KATEX##\begin{align}\sin \alpha + \sin \beta & = 2 \sin \left ( \frac{\alpha + \beta}{2} \right ) \cos \left ( \frac {\ alpha — \beta}{2} \right ) \\\sin \alpha — \sin \beta & = 2 \sin \left ( \frac{\alpha — \beta}{2} \right ) \cos\ влево ( \frac{\alpha + \beta}{2} \right ) \\\cos \alpha + \cos \beta & = 2 \cos \left ( \frac{\alpha + \beta}{2} \right ) \cos \left ( \frac{\alpha — \beta}{2} \right ) \\\cos \alpha — \cos \beta & = -2 \sin \left ( \frac{\alpha + \beta} {2} \right ) \sin \left ( \frac{\alpha — \beta}{2} \right ) \\\end{align}##KATEX## 92}{2t}\end{align}##KATEX##
Queste sono particolarmente utili quando si vuole risolvere un Inintegrale Che Contiene Trigonometriche funzioni, ma anche quando si vuole risolvere alcune tipologie di equazioni e disequazioni trigonometriche.

 02.19
02.19 Сколько коробок продали за 1 день,если ежедневно продавали равное количество сока?
Сколько коробок продали за 1 день,если ежедневно продавали равное количество сока? Абзацтар Тақырыбы Негізгі идеясы Тірек сөздер помогите
Абзацтар Тақырыбы Негізгі идеясы Тірек сөздер помогите 1 Have you been to France? A yet When A have you finished 2 3 5 6 your project? B already B did you finish He hasn’t been to school a week. A since B for You’re late. The maths lesson has A already B yet started. The teacher us any homework for tonight. A haven’t given B gave Two days, Rob started guitar lessons. A since 8 ago C ever C you finished C before C since C hasn’t given C before
1 Have you been to France? A yet When A have you finished 2 3 5 6 your project? B already B did you finish He hasn’t been to school a week. A since B for You’re late. The maths lesson has A already B yet started. The teacher us any homework for tonight. A haven’t given B gave Two days, Rob started guitar lessons. A since 8 ago C ever C you finished C before C since C hasn’t given C before Сколько угля было?
Сколько угля было?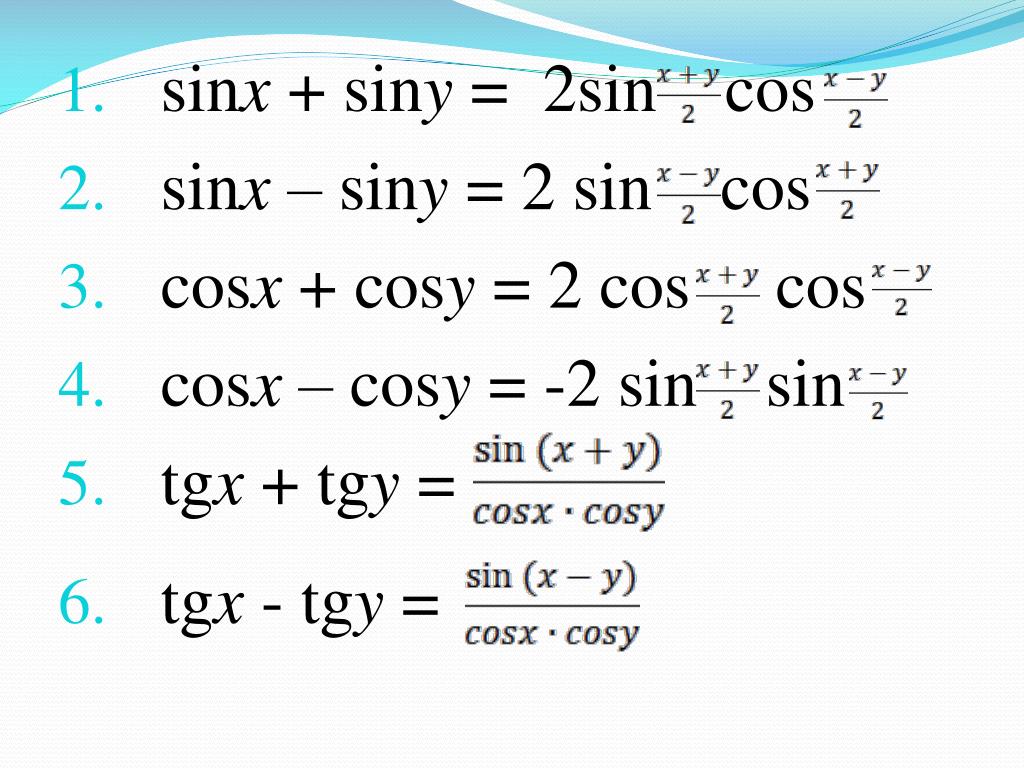

 Capita infatti, in alcuni esercizi, di trovare delle espressioni in cui si possa riconoscere un termine uguale a quello presente nella parte destra di una delle precentti uguaglianze: spesso, è utile applicare la формула di addizione o di sottrazione per poterlo riscrivere come il membro a Синистра.
Capita infatti, in alcuni esercizi, di trovare delle espressioni in cui si possa riconoscere un termine uguale a quello presente nella parte destra di una delle precentti uguaglianze: spesso, è utile applicare la формула di addizione o di sottrazione per poterlo riscrivere come il membro a Синистра.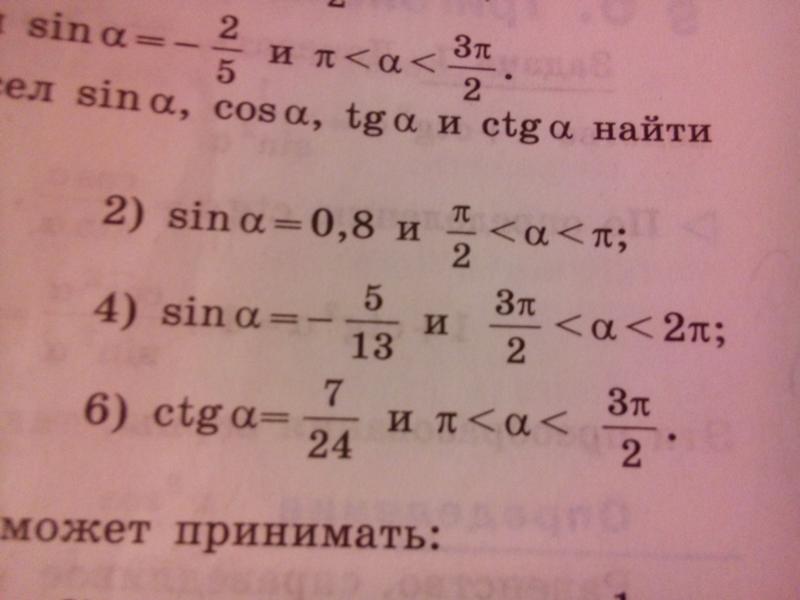
 Facciamo alcuni esempi:
Facciamo alcuni esempi:

