Мкнф и мднф: Недопустимое название — Циклопедия

12.Понятие мднф и мкнф переключающей функции

Метод Квайна — способ представления функции в ДНФ или КНФ с минимальным количеством членов и минимальным набором переменных

Преобразование функции можно разделить на два этапа:

-на первом этапе осуществляется переход от канонической формы (СДНФ или СКНФ) к так называемой сокращённой форме;

-на втором этапе — переход от сокращённой формы к минимальной форме.

 

Триггерами или, точнее, триггерными системами называют большой класс электронных устройств, обладающих способностью длительно находиться в одном из двух или более устойчивых состояний и чередовать их под воздействием внешних сигналов. Каждое состояние триггера легко распознаётся по значению выходного напряжения. По характеру действия триггеры относятся к импульсным устройствам — их активные элементы (транзисторы, лампы) работают в ключевом режиме, а смена состояний длится очень короткое время.

Отличительной особенностью триггера как функционального устройства является свойство запоминания двоичной информации.

Под памятью триггера подразумевают способность оставаться в одном из двух состояний и после прекращения действия переключающего сигнала. Приняв одно из состояний за «1», а другое за «0», можно считать, что триггер хранит (помнит) один разряд числа, записанного в двоичном коде.

Асинхронный триггер изменяет своё состояние непосредственно в момент появления соответствующего информационного сигнала(ов), с некоторой задержкой равной сумме задержек на элементах составляющих данный триггер.

Синхронные триггеры реагируют на информационные сигналы только при наличии соответствующего сигнала на так называемом входе синхронизации С (от англ. clock). Этот вход также обозначают термином «такт». Такие информационные сигналы называют синхронными. Синхронные триггеры в свою очередь подразделяют на триггеры со статическим (статические) и динамическим (динамические) управлением по входу синхронизации С.

Одноступенчатые триггеры состоят из одной ступени представляющей собой элемент памяти и схему управления, делятся на триггеры со статическим управлением и триггеры с динамическим управлением.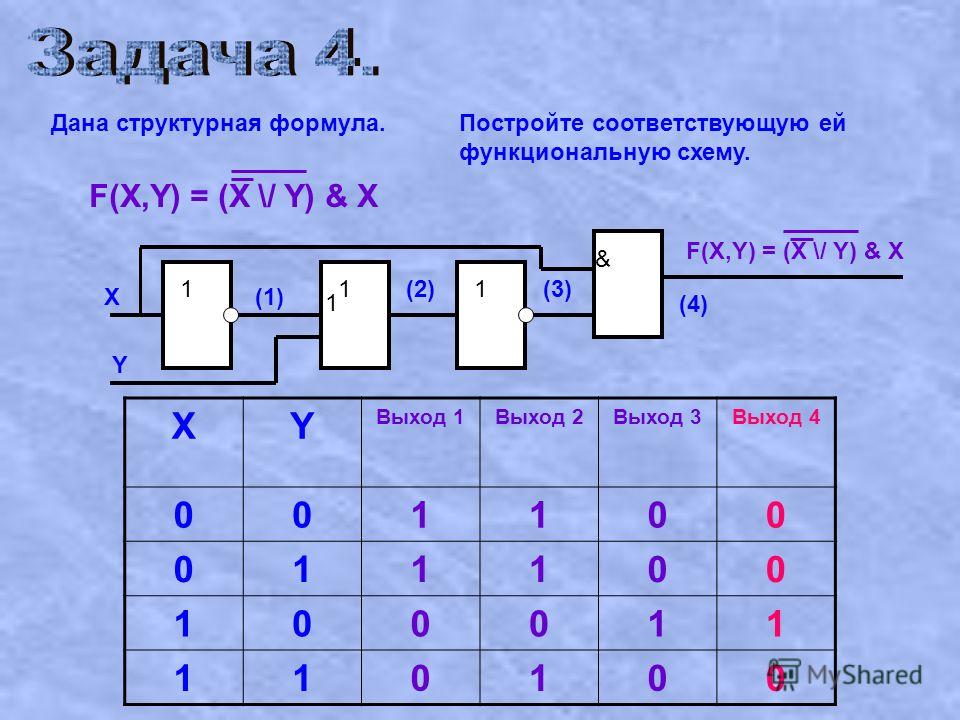

Триггеры со статическим управлением воспринимают информационные сигналы при подаче на вход С логической единицы (прямой вход) или логического нуля (инверсный вход).

Триггеры с динамическим управлением воспринимают информационные сигналы при изменении (перепаде) сигнала на входе С от 0 к 1 (прямой динамический С-вход) или от 1 к 0 (инверсный динамический С-вход). Также встречается название «триггер управляемый фронтом».

Двухступенчатые триггеры бывают, как правило, со статическим управлением. При одном уровне сигнала на входе С запись информации, в соответствии с логикой работы триггера, записывается в первую ступень (вторая ступень заблокирована для записи). При другом уровне этого сигнала происходит копирование состояния первой ступени во вторую (первая ступень заблокирована для записи), выходной сигнал появляется в этот момент времени с задержкой равной задержке срабатывания ступени. Обычно двухступенчатые триггеры применяются в схемах, где логические функции входов триггера зависят от его выходов, во избежание временных гонок.

Двухступенчатые триггеры с динамическим управлением встречаются крайне редко. Двухступенчатый триггер обозначают ТТ.

 

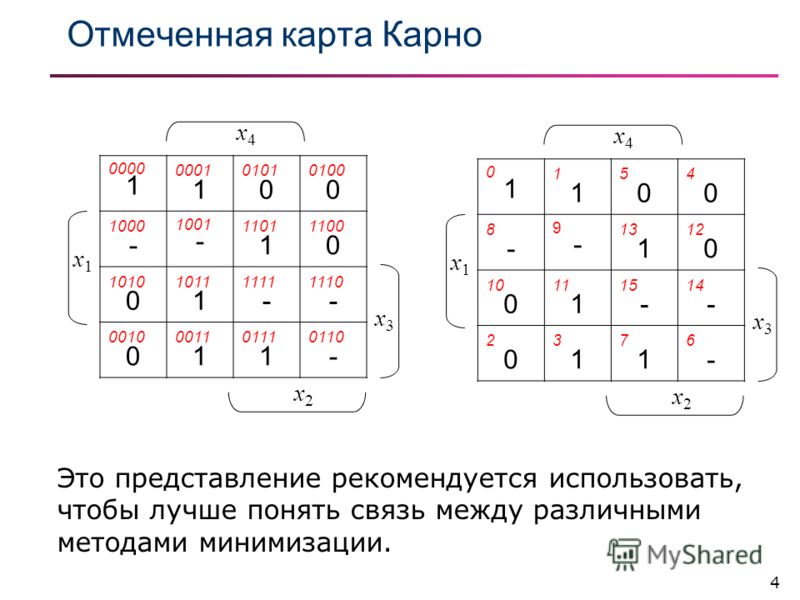
Минимизация функций с помощью карт Карно

Занятие 17. Тема «Минимизация функций с помощью карт Карно»

План лекции:

1. Понятие карты Карно

2. Виды карт Карно и метод их заполнение

3. Принципы склейки

4. Правило нахождения МДНФ и МКНФ

Понятие карты Карно

МДНФ – минимальная дизъюнктивная нормальная форма

МКНФ — минимальная конъюнктивная нормальная форма

Метод карт Карно позволяет быстро получить минимальные ДНФ и КНФ.

Карта Карно – это таблица, каждая клетка в ней соответствует набору переменных булевой функции в её таблице истинности. Строки и столбцы карты обозначаются таким образом, чтобы любые соседние клетки по строкам или по столбцам отличались бы между собой значением только одной переменной. Это сделано для того, чтобы было бы возможно применить закон склеивания.

Виды карт Карно и метод их заполнение

Карта Карно для 2-х переменных – квадратная таблица размером (4 ячейки)

х1 х2	0	1
0
1

Ячейки заполняются 0 или 1, полученные в последнем столбце таблицы истинности, соответствующие наборам 00, 01, 10, 11.

Карта Карно для 3-х переменных – прямоугольная таблица размером (8ячеек). Каждая ячейка соответствует наборам 000, 001, 010, 011, 100, 101, 110, 111.

х2х3 х1	00	01	11	10
0
1

Любые две рядом расположенные клетки являются соседними. Клетки, находящиеся на границах одной строки или столбца, так же считаются соседними, то есть, клетки, которые будут соседними при скручивании карты в вертикальный и горизонтальный цилиндры.

Карта Карно для 4-х переменных – квадратная таблица размером (16 ячеек). Каждая ячейка соответствует наборам 0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111.

Карта Карно для 5-х переменных – прямоугольная таблица размером (32 ячейки).

Минимизация функций с помощью карт Карно или нахождение МДНФ (МКНФ) – это процесс склеивания одинаковых значений, стоящих в соседних ячейках.

Принципы склейки

• Склейку клеток карты Карно можно осуществлять по единицам (если необходимо получить  МДНФ) или по нулям (если требуется МКНФ).

• Склеивать можно только прямоугольные области с числом единиц (нулей) 2ⁿ, где n — целое число.

• Область, которая подвергается склейке, должна содержать только единицы (нули).

• Крайние клетки каждой горизонтали и каждой вертикали также граничат между собой и могут объединяться в прямоугольники. Следствием этого правила является смежность всех четырёх угловых ячеек карты Карно для N=4. Если во всех четырёх угловых ячейках стоят единицы (нули), они могут быть объединены в квадрат.

• Все единицы (нули) должны попасть в какую-либо область.

• С точки зрения МДНФ (МКНФ), число областей должно быть как можно меньше (каждая область представляет собой терм), а число клеток в области должно быть как можно больше (чем больше клеток в области, тем меньше переменных содержит терм).

• Области могут пересекаться.

• Область должна располагаться симметрично оси (оси располагаются через каждые четыре клетки) Несмежные области, расположенные симметрично оси, могут объединяться в одну.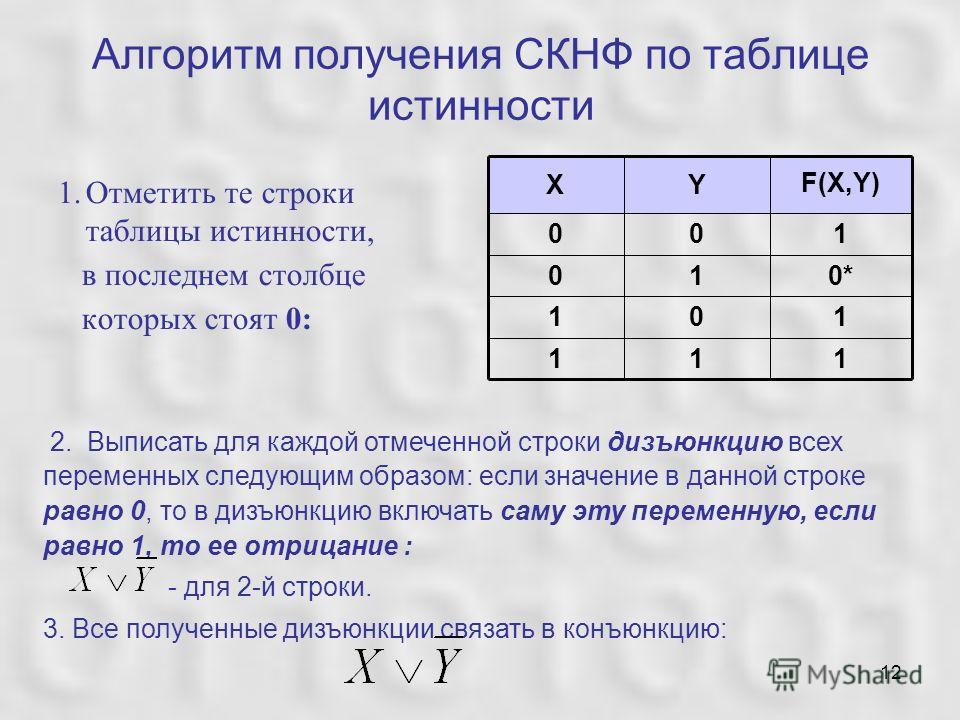

Правило нахождения МДНФ (МКНФ).

Берём первую полученную область и смотрим, какие переменные не меняются в пределах этой области, выписываем конъюнкцию для МДНФ (дизъюнкцию для МКНФ) этих переменных; если неменяющаяся переменная нулевая, проставляем над ней инверсию для МДНФ (для МКНФ не ставим инверсию). Если переменная единичная, то не ставим инверсию для МДНФ (ставим инверсию для МКНФ). Берём следующую область, выполняем то же самое, что и для первой, и т. д. для всех областей. Конъюнкции областей объединяем дизъюнкцией для МДНФ (дизъюнкции областей объединяем конъюнкцию для МКНФ).

Функции могут быть записаны не формулой, а аналитическим путем, то есть содержать номера наборов из таблицы истинности дизъюнктивно ( работает с 1) или конъюнктивно (& работает с 0). Например, Y= (1,4,8,10,12,14,15). Это означает, что карта Карно из 4-х переменных заполняется единицами в ячейках с номерами 1,4,8,10,12,14,15, а остальные ячейки заполняются нулями.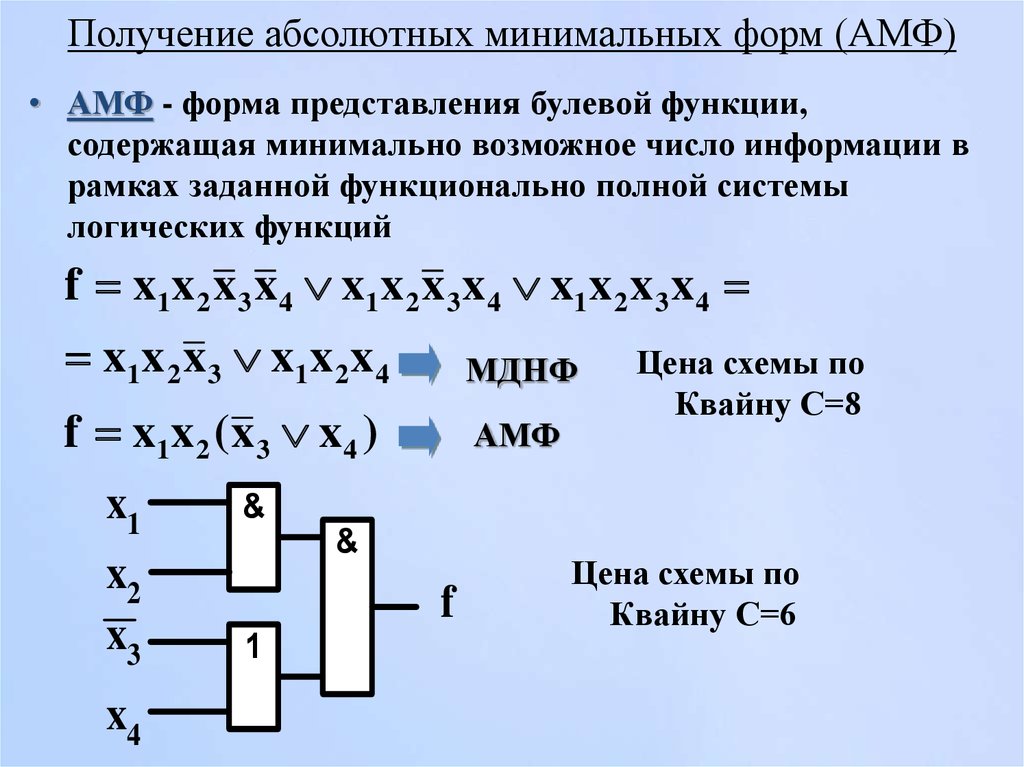

Пример.

x	y	z							B
0	0	0	1	1	1	1	1	0	1
0	0	1	1	1	0	1	1	0	1
0	1	0	1	0	1	1	1	0	1
0	1	1	1	0	0	0	0	0	0
1	0	0	0	1	1	1	0	0	0
1	0	1	0	1	0	1	0	1	1
1	1	0	0	0	1	1	0	0	0
1	1	1	0	0	0	0	0	1	1

Для нахождения МДНФ

— Составим карту для 3-х переменных и заполним ее 1 из последнего столбца таблицы истинности.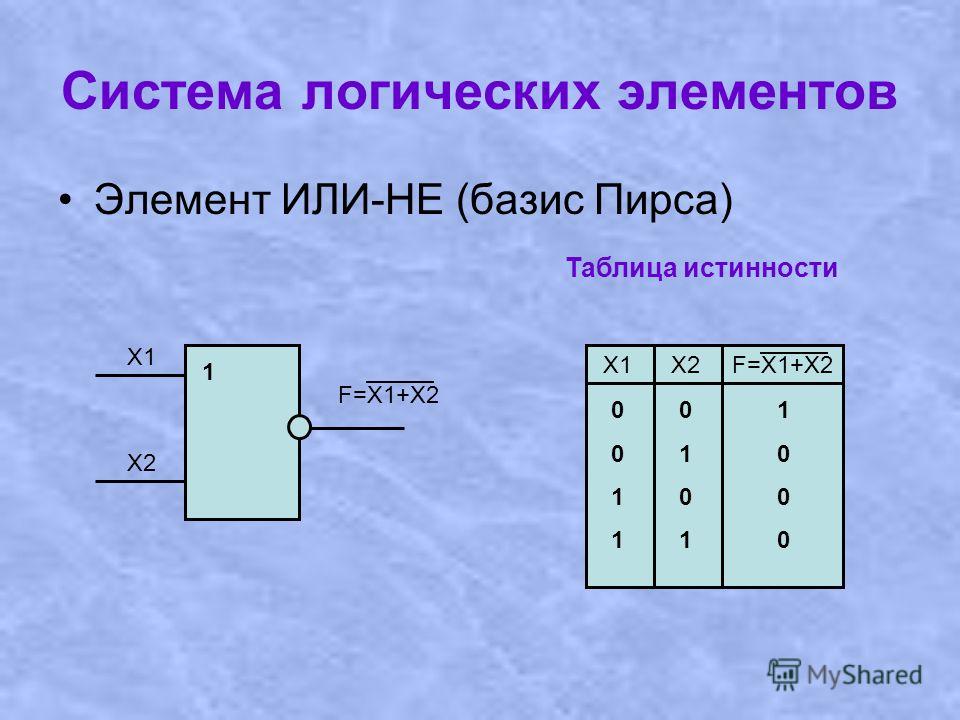

уz х	00	01	11	10
0	1	1		1
1		1	1

— Выделим покрытия по принципам склейки

— Для каждого покрытия составляем элементарную конъюнкцию, зачеркивая столбец с разными значениями и записывая оставшие переменные с инверсией, если все 0 и без инверсии, если все 1.

x y z x y z x y z

0 0 0 0 0 1 1 0 1

0 1 0 1 0 1 1 1 1

МДНФ: у=

Для нахождения МКНФ

— Составим карту для 3-х переменных и заполним ее 0 из последнего столбца таблицы истинности.

уz х	00	01	11	10
0			0
1	0			0

— Выделим покрытия по принципам склейки

— Для каждого покрытия составляем элементарную дизъюнкцию, зачеркивая столбец с разными значениями и записывая оставшие переменные с инверсией, если все 1 и без инверсии, если все 0.

x y z x y z

1 0 0 0 1 1

1 1 0

МКНФ: у=

Задание для самостоятельного выполнения

1. составить карту Карно и найти МДНФ и МКНФ для следующих функций

а)

б)

1. Ответить на контрольные вопросы:

1. Что называется картой Карно?

2. Какие разновидности карт Карно есть?

3. Как заполняются карты Карно?

4. Для чего нужны принципы склейки?.

5. Чем отличается правило нахождения МДНФ от правила нахождения МКНФ?

6. Пользуясь этим и теоретическим материалом учебника М.С. Спирина «Дискретная математика» глава 4 п.4,6,3 стр.180, выполнить 1 задание.

Выполненное задание отправить на адрес электронной почты преподавателя. Имя файла – фамилия студента и номер занятия. (например Петров-17)

Булева функция, какова цель DNF и CNF?

спросил 10 лет, 4 месяца назад

Изменено 7 лет назад

Просмотрено 6к раз

Булевы функции могут быть выражены в дизъюнктивной нормальной форме (DNF) или конъюнктивной нормальной форме (CNF). Может ли кто-нибудь объяснить, почему эти формы полезны?

• логическая логика
• логическое выражение
• конъюнктивная нормальная форма

2

CNF полезен, потому что эта форма непосредственно описывает логическую задачу SAT, которая, хотя и является NP-полной, имеет много неполных и эвристических экспоненциальных решателей времени. CNF был дополнительно стандартизирован в формат файла, называемый «формат файла DIMACS CNF», с которым может работать большинство решателей. Так, например, производители чипов могут проверить свои схемы, преобразовав их в DIMACS CNF и используя любой из доступных решателей. Преобразование Цейтина может преобразовать схемы в

равновыполнимый CNF.

ДНФ не так полезен с практической точки зрения, но преобразование формулы в ДНФ означает, что можно увидеть список возможных присвоений, которые удовлетворяют формуле. К сожалению, преобразование формулы в ДНФ в общем случае сложно и может привести к экспоненциальному взрыву (очень большой ДНФ), что очевидно, потому что может быть экспоненциально число удовлетворяющих присваиваний формуле.

Хотя CNF может быть кратким по сравнению с DNF, иногда с ним трудно рассуждать, потому что он может потерять структуру, например, при преобразовании из схемы, и поэтому была бы полезна другая краткая форма. Для этой цели была разработана структура данных графа and-inverter; он может более точно моделировать структуру схем, и поэтому с ним намного легче рассуждать в некоторых типах формул. Однако существует не так много решателей, которые работают с ним.

Другие формы включают:

• Двоичная диаграмма решений
• Пропозициональный ориентированный ациклический граф
• Нормальная форма отрицания
• Другие (википедия)

Помогает выразить функции некоторым стандартным способом. При этом проще автоматически проходить многие алгоритмы.

Обе формы можно использовать, например, при автоматизированном решении теорем, а именно КНФ в методе разрешения.

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя адрес электронной почты и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Конъюнктивная нормальная форма (CNF) и дизъюнктивная нормальная форма (DNF) из таблицы истинности, объяснение! – Hackrly

Поиск DNF (дизъюнктивной нормальной формы) и CNF (конъюнктивной нормальной формы) по заданной таблице истинности – очень простая задача. Если вы не знаете, просто погуглите, вы найдете множество веб-страниц, объясняющих этот метод. Но задумывались ли вы когда-нибудь о причинах выполнения этих шагов.

Когда я узнавал об этих формах, это было для меня проблемой. Я мог понять причины. Я дам вам абстрактное представление о том, что происходит.

Этот метод предназначен для нахождения логического (или логического в булевой алгебре) выражения с использованием таблицы истинности. Я объясню метод на примере отсюда.

Это таблица истинности.

Сначала рассмотрим ДНФ.

В этом случае обычно вам нужно посмотреть строки, которые заканчиваются на T, и когда вы найдете эти строки, взять x и y из каждого соответствующего столбца. Таким образом, вы получаете

Вот объяснение. На самом деле вы здесь пишете логическое выражение, которое становится истинным для 1, 4, 6 и 7 строк и ложным для других строк. Если вы рассмотрите первое элементарное произведение ответа (ДНФ — это сумма элементарных произведений), вы увидите, что оно становится истинным, когда x, y, z берут строку по значениям, и эти значения x, y, z не могут составить никаких других значений. elementary product Истинно, так как каждая строка имеет дискретные значения x, y, z. (Поскольку мы берем произведение значений x, y, z, только значения в первой строке делают это элементарное произведение истинным).

То же самое происходит и со вторым элементарным произведением. Теперь x остается как x, так как он получает значение True. Но значения y и z не должны сталкиваться с операцией, так как вы хотите, чтобы значения True для элементарного произведения стали истинными. Точно так же вы пишете элементарные продукты, которые получают значение True только для связанных с ними строк в таблице. Но если вы внимательно проверите, то увидите, что ни одна из других строк не может сделать хотя бы одно из этих элементарных произведений истинным. С тех пор, когда вы получите сумму этих элементарных произведений, вы получите результат, который станет истинным только для 1, 4, 6 и 7 строк; что означает, что у вас есть логическое выражение для данной таблицы истинности, но в дизъюнктивной нормальной форме.

Теперь давайте перейдем к CNF,

В этом случае я собираюсь написать логическое выражение, которое становится False только для значений 2, 3, 5 и 8 строк таблицы истинности. Поскольку вы должны сделать выражение False, соедините некоторые составные предлоги, например. (~x∨~y∨z), вы должны использовать союз (∧), чтобы соединить их, поскольку, если вы используете дизъюнкт (∨) , все выражение станет истинным, когда один составной предлог станет истинным.

При построении составных предлогов для выражения можно выбрать либо дизъюнкцию, либо союз. Посмотрите на абзац выше еще раз, я выделил слово «только». Я хотел подчеркнуть, что выражение должно стать True для 1,4,6,7 строк. Для этого следует использовать дизъюнкцию для соединения предлогов в составном предлоге. (Если вы посмотрите внимательно, я увижу, что по крайней мере один предлог из всех составных предлогов становится истинным для значений 1, 4, 6 и 7 строк. Наконец, вы получите это для приведенной выше таблицы истинности.

Существует еще один способ записи CNF. Сделайте это как упражнение.

• Замените все значения True на значения False и все значения False на значения True в последнем столбце.
• Напишите ДНФ для модерируемой таблицы истинности.

Теперь у вас есть логическое выражение, которое дает противоположное значение для каждой строки. (Пожалуйста, помните, что это выражение не равно выражению, которое вы получили из DNF выше, так как вы выбрали 1,4,6 и 7 строки)

• Поскольку вы получаете противоположное значение для каждой отдельной строки, возьмите отрицание (~, не) всего выражения.
• Упростите выражение, используя законы Де Моргана.
• Вы получите CNF таблицы истинности.

Вот кое-что интересное, что вы можете доказать, используя ту же концепцию (не ту, которую мы использовали в упражнении), которую мы использовали для формирования CNF.

Докажите, что любое комплексное число можно записать как следующий член последовательности 2,4,6,8.

No related posts.