Числовые множества
Главная / i / t
- Что такое множество
- N – Натуральные числа
- Z – Целые числа
- Q – Рациональные числа
- I – Иррациональные числа
- R – Действительные (вещественные) числа
Для дальнейшего изучения математики нам необходимо познакомиться с некоторыми терминами.
Что такое множество
Множеством называется набор каких-либо объектов. Например, множеством может быть совокупность всех книг в библиотеке, множество всех библиотек в городе, множество всех слонов в каком-нибудь зоопарке или множество всех селедок в мире.
Чтобы легче понять всю структуру и иерархию числовых множеств, разберем точно такую же структуру и иерархию множеств животного мира. Отличаются множества чисел от этих множеств животных только тем, что они состоят не из чисел и тем, что они конечны, их структура и буквенное обозначение абсолютно такое же.
Объекты, из которых состоит множество, называются элементами этого множества. Чтобы отличить одно множество от другого их обозначают разными латинскими буквами. Для примера назовем множество всех селедок в мире буквой N, а какую-нибудь конкретную селедку буквой a, значит, элемент a будет являться одним из элементов множества N, тогда говорят, что элемент a принадлежит множеству N. Принадлежность элемента a множеству N обозначают символом ∈:
a ∈ N
Читается эта запись так: «a принадлежит N».
Изобразим множество N в виде фигуры, внутрь которой мысленно поместим все селедки в мире.
Назовем множество всех рыб в мире буквой Z, так как каждая селедка является рыбой, то элемент a принадлежит и множеству Z:
a ∈ Z
Нарисуем множество всех рыб Z так, чтобы каждая селедка из множества N оказалась еще и внутри множества рыб Z. Тогда будет видно, что любая селедка принадлежит множествам N и Z.
Тогда будет видно, что любая селедка принадлежит множествам N и Z.
Если каждый элемент из множества селедок N является еще и элементом множества рыб Z, то N называют подмножеством Z и обозначают символом ⊂. Следующая запись означает, что множество N является подмножеством множества Z:
N ⊂ Z
Обозначим множество всех морских животных буквой Q, тогда наша селедка a будет принадлежать и этому множеству:
a ∈ Q
А так как любая рыба – это морское животное, то множество всех рыб Z будет еще и подмножеством всех морских животных Q:
Z ⊂ Q
Значит, нарисуем множество Q так, чтобы его частью было множество Z.
Множество сухопутных животных назовем заглавной латинской буквой I. Это множество стоит совершенно отдельно от множества морских животных и не имеет с ним ни одного общего элемента.
Осталось только объединить всех морских и сухопутных животных в одно множество, которое мы обозначим буквой R. Теперь точно можно сказать, что любое животное будет принадлежать этому множеству R.
По этому рисунку легко определить, что селедка принадлежит сразу четырем множествам N, Z, Q, и R, т. е. она является селедкой, рыбой, морским животным и вообще животным из множества R. Акула принадлежит множествам Z, Q, R, значит она – рыба морское животное и просто животное одновременно. Морская звезда – элемент множеств Q и R, потому что она не селедка, не рыба, а морское животное и вообще животное. Кот принадлежит множествам сухопутных животных I и просто животных R.
Каждое из множеств животных N, Z, Q, I, R состоит из огромного, но конечного количества элементов, но множества могут содержать и бесконечное количество элементов, к таковым относятся всевозможные числовые множества, элементами которого являются числа.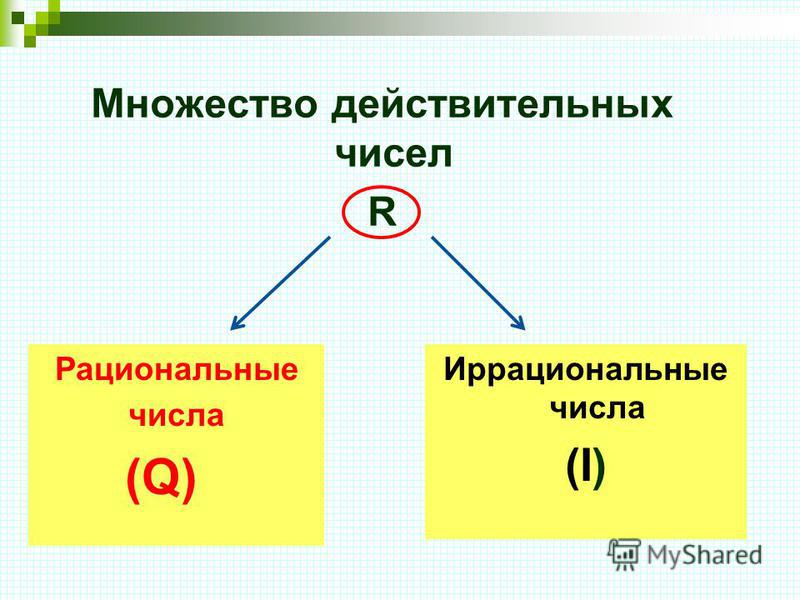 Далее подробно разберем каждое из числовых множеств, после тренировки на селедках это будет гораздо проще.
Далее подробно разберем каждое из числовых множеств, после тренировки на селедках это будет гораздо проще.
N – Натуральные числа
Это самое легкое для понимания множество чисел, которое всем известно еще с детства. Элементами этого множества являются такие числа как:
1; 2; 3; 4; 5 …
Такими числами обозначают количество неделимых объектов, например, количество людей в городе или стране, количество сортов колбасы, количество квартир в доме. Еще натуральными числами нумеруют всевозможные объекты: квартиры, дома, страницы в книге. Не существует квартир с номером 1.5 или минус третьей страницы в книге.
Количество натуральных чисел бесконечно и все они положительные. Один – наименьшее натуральное число, наибольшего натурального числа не существует – всегда найдется число еще больше: миллион больше тысячи, а миллиард больше миллиона и т. д:
1; 2; 3; 4; 5; …; 100; …; 1000; …; 1000000; …; 1000000000; …; 9563615827; …
Множество натуральных чисел обозначается заглавной латинской буквой N. Когда хотят сказать, что число a является натуральным, пишут так:
Когда хотят сказать, что число a является натуральным, пишут так:
a ∈ N
Такая запись означает, что число a принадлежит множеству N, в котором находятся только натуральные числа, а значит, и само a является натуральным.
Z – Целые числа
Если к множеству натуральных чисел присовокупить число ноль и все целые отрицательные числа, то получится множество целых чисел, которое принято обозначать буквой Z. К целым относятся такие числа как:
… −5; −4; −3; −2; −1; 0; 1; 2; 3; 4; 5; …
Получается, что множество натуральных чисел N является подмножеством целых чисел Z:
N ⊂ Z
Значит, любое натуральное число будет еще и целым, но не каждое целое будет натуральным, подобно тому, как каждая селедка является рыбой, но не каждая рыба является селедкой. Число 4 будет являться как натуральным, так и целым, а число −4 является целым, но не является натуральным.
4 ∈ N, 4 ∈ Z, −4 ∈ Z
Целые числа не будут иметь не только самого большого числа, но и самого маленького, потому что они бесконечны как в положительную сторону, так и в отрицательную:
…; −1937499345; …; −1000000000; …; −1000000; …; −1000; …; −5; −4; −3; −2; −1; 0; 1; 2; …
Q – Рациональные числа
Число x называется рациональным, если его можно представить в виде дроби, где числителем является целое число, а знаменателем – натуральное:
Попробуем выяснить, является ли число −2.5 рациональным числом. Для этого представим его в виде дроби. Очевидно, что −5 деленое на 2 будет равно −2.5:
В получившейся дроби числитель −5 – целое число, а знаменатель 2 – натуральное, значит, −2.5 – рациональное число.
Число 0.25 также можно представить в виде дроби с целым числителем и натуральным знаменателем:
Каждое целое (а значит, и натуральное) число является еще и рациональным, потому что целое число всегда можно представить в виде дроби, у которой целый числитель и натуральный знаменатель. Таким дробям равны числа 2 и −2, поэтому они рациональные:
Таким дробям равны числа 2 и −2, поэтому они рациональные:
Не обязательно знаменатель должен быть равен единице, числа 2 и −2 можно представить и в виде других дробей:
Следовательно, число 2 является сразу и натуральным, и целым, и рациональным; число −2 – целым и рациональным; а число 0.25 – рациональным. Подобно тому как селедка – это с одной стороны – рыба, с другой – морское животное, а морская звезда – только морское животное.
Сразу не удастся понять какой дроби равно число 12.96875, тогда умножим и разделим его на 100000, оно от этого не изменится:
Числитель 1296875 – целое число, Знаменатель 100000 – натуральное, значит, 12.96875 ∈ Q.
Хотя любое число в виде десятичной дроби с конечным количеством цифр после десятичной запятой (или точки) всегда является рациональным, потому что его всегда можно представить в виде дроби. В числе 12.96875 после десятичной точки стоит пять цифр, а пять – конечное число, значит, число 12.96875 – точно рациональное.
В числе 12.96875 после десятичной точки стоит пять цифр, а пять – конечное число, значит, число 12.96875 – точно рациональное.
Если все-таки число в виде десятичной дроби имеет бесконечное количество цифр после десятичной точки или запятой, но при этом с некоторой очередной цифры начинает повторяться один и тот же набор цифр, то такое число тоже рациональное. Например, это число рациональное, потому что в нем бесконечно повторяется сочетание цифр 2, 7 и 0:
1.4270270270270270270…
Его можно представить в виде дроби с целым числителем и натуральным знаменателем:
Разделим в столбик 264 на 185, чтобы убедиться, что цифры 2, 7, 0 будут постоянно повторяться до бесконечности.
Вот еще примеры рациональных чисел с повторяющимся набором цифр 3, 15, 123, 2376, 142857:
На самом деле повторяющиеся цифры есть в любом рациональном числе, просто если эта повторяющаяся цифра – ноль, то ее обычно не пишут. Например, в числе 12.96875 после цифры пять можно написать любое количество нулей, но значение этого числа от того не изменится:
Например, в числе 12.96875 после цифры пять можно написать любое количество нулей, но значение этого числа от того не изменится:
12.96875= 12.96875000000000000…
В любом целом числе, которое тоже считается рациональным, идет бесконечное количество нулей, но писать их как правило нет нужды:
8=8.00000000000…
Среди целых чисел можно найти два таких, между которыми других целых чисел нет. Например, на числовой прямой между числами 3 и 6 есть два других целых числа 4 и 5, а между числами 8 и 9 ни одного другого целого числа нет.
А среди рациональных найти такую пару разных чисел не получится: между любыми двумя разными рациональными числами всегда есть бесконечное количество других рациональных чисел: например, между числом 0.1 и 0.2 есть числа 0.15, 0.16, 0.17, и найти их там можно сколько угодно.
I – Иррациональные числа
Иррациональными называются числа, которые не являются рациональными. Такие числа невозможно представить в виде дроби, у которой целый числитель и натуральный знаменатель. Иррациональные числа, представленные в виде десятичной дроби, имеют бесконечный набор цифр после десятичной запятой или точки, только в отличие от рациональных, там никогда не будет повторяющегося одинакового набора цифр. Например, число π и число e – оба иррациональные:
Такие числа невозможно представить в виде дроби, у которой целый числитель и натуральный знаменатель. Иррациональные числа, представленные в виде десятичной дроби, имеют бесконечный набор цифр после десятичной запятой или точки, только в отличие от рациональных, там никогда не будет повторяющегося одинакового набора цифр. Например, число π и число e – оба иррациональные:
Значит, эти числа принадлежат множеству иррациональных чисел, которое обозначают буквой I:
Через несколько разделов этого сайта мы обязательно познакомимся с числами π и e значительно ближе, оба они играют очень важную роль в мире математики.
Попробуем подобрать число, которое при умножении на себя будет равно 7. Число 2 при умножении на само себя меньше семи, а 3 – больше семи:
2∙2=4
3∙3=9
Значит, чтобы получить 7, нужно подобрать число больше двух и меньше трех, попробуем 2. 6:
6:
2.6∙2.6=6.76
Уже ближе к семи, попробуем число 2.64:
2.64∙2.64=6.9696
Можно подобраться еще ближе:
2.645∙2.645= 6.996025
И еще:
2.6457∙2.6457= 6.99972849
2.64575∙2.64575= 6.9999930625
2.645751∙2.645751= 6.999998354001
И сколько бы мы не добавляли еще цифр к числу 2.64575, мы никогда не получим ровно 7, а будем только приближаться к семи, и никогда не встретим повторяющегося набора цифр, как это было в рациональном числе.
Поэтому число, которое при умножении на само себя равно 7, является иррациональным. Представить точное значение этого числа (как и любого другого иррационального) в виде десятичной дроби невозможно, потому что для этого понадобится написать бесконечное количество цифр. Вот близкое, но все же только приближенное значение этого числа:
2.6457513110645905905016…
И если умножить его на само себя, то получится хоть и очень близкое к семи число, но все-таки не семь.
R – Действительные (вещественные) числа
Если объединить рациональные и иррациональные числа в одно большое множество, то получится множество действительных чисел, которое также называют множеством вещественных чисел и обозначают буквой R. Любое число из множества натуральных, целых, рациональных и иррациональных чисел неизбежно является еще и действительным числом. Например, все эти числа действительные:
Хотя каждое из этих чисел также принадлежит и другим множествам:
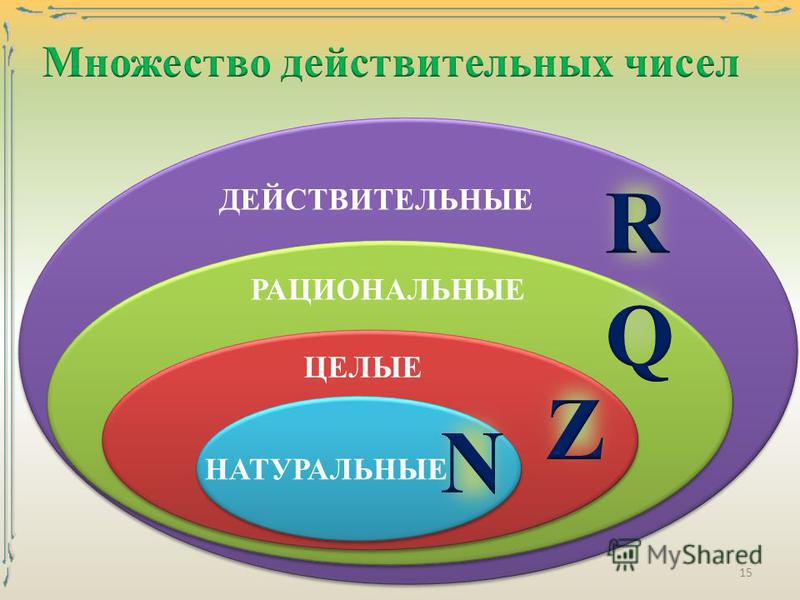
Сориентироваться во всем этом многообразии поможет следующий рисунок, на котором изображено множество R со всеми подмножествами.
На множестве R числа не заканчиваются, существуют и другие множества чисел, для которых R – это лишь их подмножество, но это уже выходит за пределы школьной математики.
Числа можно разбить на множества, в следующем порядке возрастания мощности — 1. 5. Множество — подмножество действительных чисел, которые представимы в виде радикалов над полем действительных чисел. Сюда включаются все рациональные (Q), а также некоторые иррациональные, например, . Более точно — в этом множестве числа, которые можно представить в виде записи с возведением в степень, где в степени будет рациональное число, а любое число которое возводится в степень — рациональное положительное. 6. Множество — подмножество действительных чисел, которые представимы в виде радикалов над полем комплексных чисел. Отличие множества 6 от множества 5. Например, корни уравнения, Вопрос. У меня предположение, что части этой записи — будут комплексными числами, т.е. там не обойтись без . Будут корни из отрицательных чисел обязательно. Верно ли предположение? Если предположение верно, то всегда действительные корни кубических уравнений — принадлежат множеству , но они могут не принадлежать множеству . А вот корни квадратного уравнения всегда принадлежат маломощному множеству . Вопрос. Всегда ли синус от аргумента (в градусах) представленного в виде рационального числа — принадлежит множеству (или даже ), т.е. всегда ли его можно выразить в радикалах? Но перейдем к еще более мощному множеству чисел. Действительные корни уравнения 5-й степени, вообще не всегда могут быть выражены в радикалах, т.е. они могут не входить даже в , но есть такое множество, куда они входят — 7. Множество — множество алгебраических чисел, (подмножество действительных чисел) . В это множество входят все возможные действительные корни всех возможных алгебраических уравнений, любых степеней, и с любыми рациональными коэффициентами. Какие более мощные множества, чем , рассматриваются в математике (не считая самых широких множеств — действительных и комплексных)? Я более мощных не встречал, обычно, если число не входит в то его просто называют трансцендентным. А я бы ввел еще одно множество — 8. Множество — множество чисел, которые могут быть корнями любого математического уравнения (не обязательно алгебраического), с любыми известными функциями (типа синус, дзета-функция, интегральный логарифм и т. До сих пор все рассматриваемые множества были подмножествами следующего, т.е. подмножество , и т.д. — подмножество . Следующее множество, — отдельное ( в него не входит), но самое мощное. 9. Множество — множество хаотических чисел. (хаотических — мое определение). Это множество всех действительных чисел, которые не входят в . Если число входит в , то никакими математическими описаниями конечных размеров (не важно — рядами, или функциями и т.п.), это число невозможно представить, т.е. если мы зададим описание конечных размеров, то мы не сможем по этому описанию найти любую цифру после запятой данного числа — до бесконечности. 10. Множество — множество ВСЕХ действительных чисел. Это объединение непересекающихся множеств и . 11. Множество — множество всех комплексных чисел. Можно было разбить и его на аналогичные подмножества (алгебраические комплексные, аналитические, хаотические и др.) но уже думаю, необязательно. Правильна моя классификация? Какие еще у математиков есть множества, являющиеся подмножествами трансцендентных, но не являющиеся алгебраическими числами? |
IB Studies 1:1 – Наборы чисел (N/Z/Q/R) | IDEA IB Math
IB, как и многие математики, группирует числа в «числовые наборы». Группируя числа, мы можем делать выводы о том, как будут вести себя похожие числа, и даже о том, имеют ли смысл наши ответы.
Вот таблица, чтобы вы могли попытаться запомнить различные наборы чисел:
Обратите внимание, что каждая отдельная группа чисел на этой странице также является действительными числами.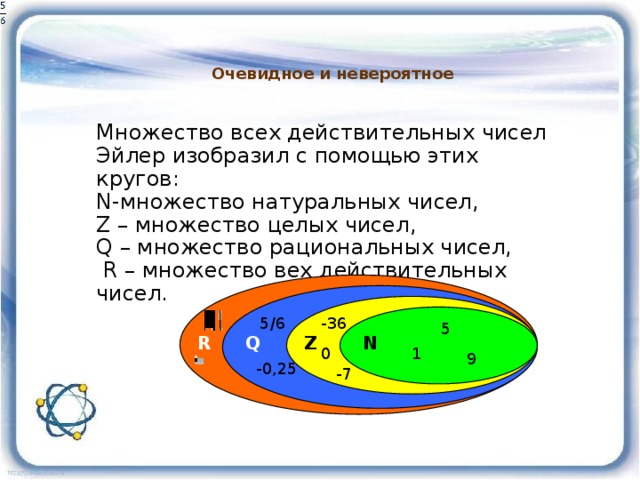 Эта диаграмма читается как диаграмма Венна. Это означает, что натуральные числа также являются целыми, рациональными числами и действительными числами.
Эта диаграмма читается как диаграмма Венна. Это означает, что натуральные числа также являются целыми, рациональными числами и действительными числами.
Вот несколько кратких описаний каждого типа чисел:
Вещественные числа: Каждое число, которое мы встретим в этом курсе, является действительным числом.
Рациональные числа: Слово «рациональный» содержит слово «отношение». Это подсказка. Все числа, которые можно описать как отношения (дроби, целые числа, конечные десятичные дроби, повторяющиеся десятичные дроби), являются рациональными числами. Другие числа, такие как десятичные дроби, которые не заканчиваются и нигде не повторяются (например, квадратный корень из 5, π и натуральное число e), являются иррациональными.
Целые числа: Это положительные целые числа, отрицательные целые числа и ноль. В основном это только дроби больше 1. (Например, -12 можно записать как -12/1)
Натуральные числа: Это числа, которые вы можете сосчитать пальцами рук, ног или палочками (если у вас есть достаточно!). По сути, это все числа, которые можно использовать для подсчета целых чисел — не отрицательных, не нулевых, просто так, как мы считаем окружающие предметы. (Например, я вижу два дерева, трех человек…)
По сути, это все числа, которые можно использовать для подсчета целых чисел — не отрицательных, не нулевых, просто так, как мы считаем окружающие предметы. (Например, я вижу два дерева, трех человек…)
Пример вопроса IB:
Рассмотрим квадратный корень чисел из 3, 72, -5, 6,4 и 7, а также множества N, Z, Q и R. Заполните следующую таблицу, поставив галочку в соответствующее поле, если число является элементом множества.
Пустой ящик для вопросов:
| Н | З | В | Р | |
| корень 3 | ||||
| 72 | ||||
| -5 | ||||
| 6,4 | ||||
| 7 |
Поле для ответов на вопросы:
| Н | З | В | Р | |
| корень 3 | ✗ | ✗ | ✗ | ✓ |
| 72 | ✓ | ✓ | ✓ | ✓ |
| -5 | ✗ | ✓ | ✓ | ✓ |
| 6,4 | ✗ | ✗ | ✓ | ✓ |
| 7 | ✓ | ✓ | ✓ | ✓ |
Нравится:
Нравится Загрузка. ..
..
В: Существует ли числовой набор, который выше комплексных чисел?
Физик : Да, но они не решают проблемы так, как комплексные числа.
Хорошая вещь о действительных числах (которые включают практически все числа, о которых вы можете подумать: 0, 1, π, -5/2, …) заключается в том, что независимо от того, как вы складываете, вычитаете, умножаете или делите (кроме 0 ) их вместе, вы всегда получите другое действительное число. Это свойство называется «закрытым». Математик сказал бы: «Настоящие числа — это , закрытые при сложении, потому что любые действительные числа, сложенные вместе, всегда дают другое действительное число».
Закрытость утешительна, потому что это означает, что когда вы занимаетесь элементарной математикой, независимо от того, как вы прыгаете, вам всегда будет куда приземлиться. Математически говоря.
Однако! Когда вы извлекаете квадратные корни, действительные числа не являются закрытыми. Когда вы спрашиваете «», вы имеете в виду «».
Каждое комплексное число можно записать как «A+Bi», где A и B — обычные числа. Обратите внимание, что когда B=0, у вас есть обычное действительное число, поэтому комплексные числа включают в себя действительные числа.
Вот где возникает вопрос. может исправить проблему с помощью , но не порождает ли это новую проблему, когда вы пытаетесь выяснить, что это такое? Выходит: нет!
Вы можете проверить это, возведя его в квадрат:
Как ни странно, нет абсолютно никакой комбинации корней/возведения в степень или умножения/деления или сложения/вычитания, которая могла бы выйти из комплексных чисел. Там, где закрытость действительных чисел терпит неудачу, комплексные числа остаются в силе.

 Множество — множество простых чисел (не имеет простых делителей, кроме самого себя).
Множество — множество простых чисел (не имеет простых делителей, кроме самого себя).  Сюда включаются все рациональные (Q), а также некоторые иррациональные, например, , которое окажется действительным в итоге. Более точно — в этом множестве числа, которые можно представить в виде записи с возведением в степень, где в степени будет рациональное число, а число которое возводится в степень — рациональное, и может быть отрицательным.
Сюда включаются все рациональные (Q), а также некоторые иррациональные, например, , которое окажется действительным в итоге. Более точно — в этом множестве числа, которые можно представить в виде записи с возведением в степень, где в степени будет рациональное число, а число которое возводится в степень — рациональное, и может быть отрицательным.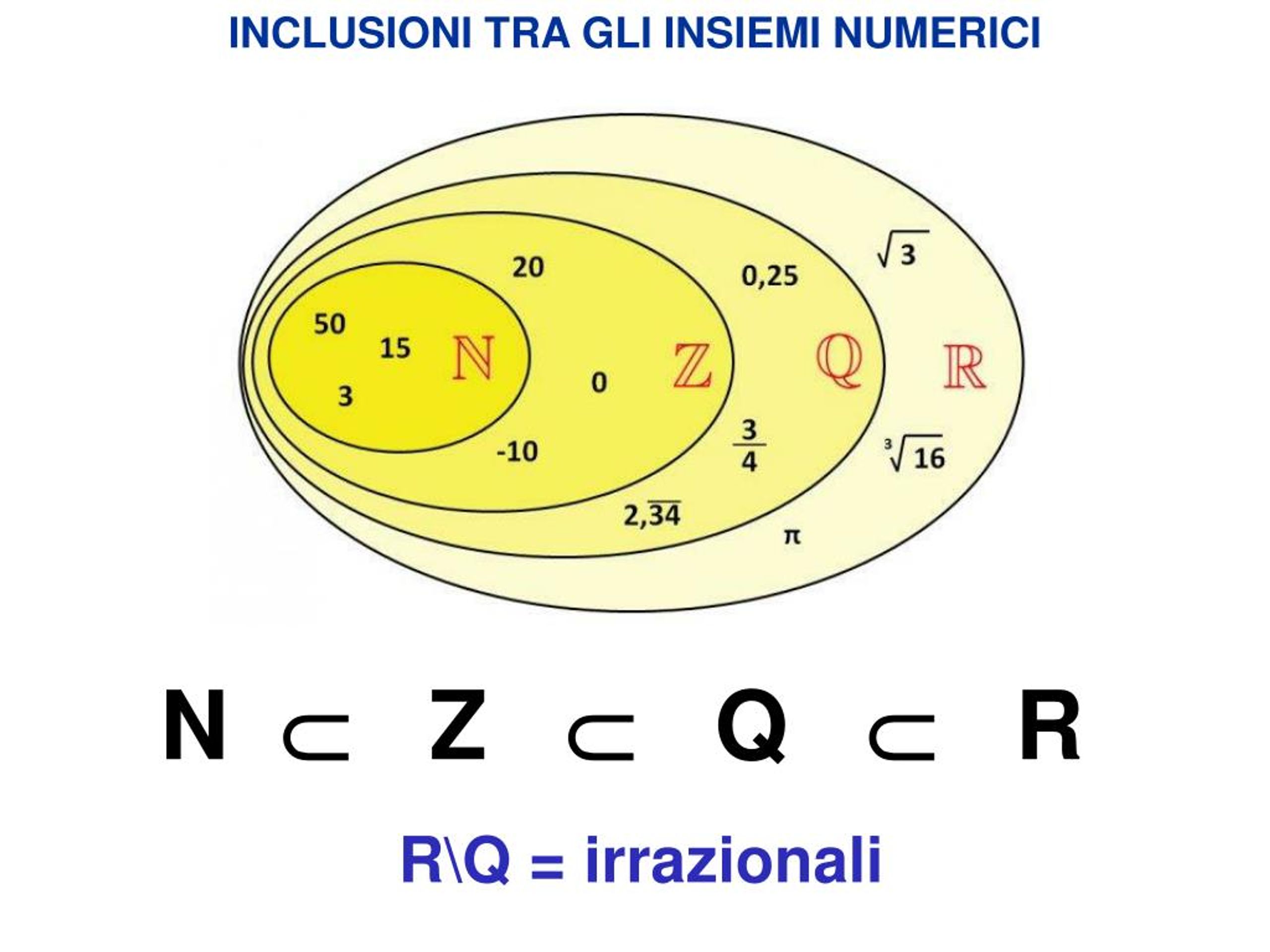
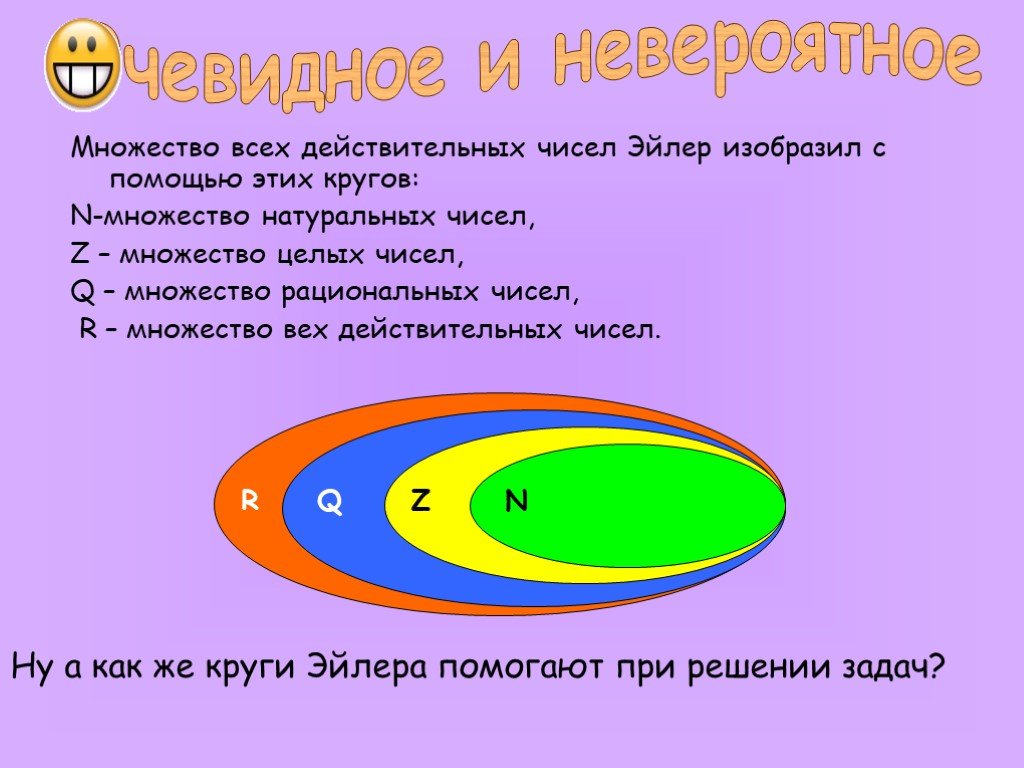
 Причем множество в множестве — имеет меру нуль. Т.е. в множестве действительных чисел — большинство чисел — хаотические, и меньшинство — аналитические.
Причем множество в множестве — имеет меру нуль. Т.е. в множестве действительных чисел — большинство чисел — хаотические, и меньшинство — аналитические.