Множество и операции над ними: 04. Множества и операции над ними. Числовые множества. Некоторые обозначения

04. Множества и операции над ними. Числовые множества. Некоторые обозначения

Множество – первичное неопределяемое понятие. Обозначают множества прописными латинскими буквами A, B, C, X, …. Под множеством понимают совокупность (группу, набор и т. д.) элементов, которые характеризуются одинаковыми свойствами.

Множества изображают Диаграммами (кругами) Эйлера-Венна (рис. 1.2).

 

Рис. 1.2

Если элемент А принадлежит множеству А, то пишут A Î A; если элемент А не принадлежит множеству А, то пишут A Ï A.

Множество может задаваться с указанием его характеристического свойства. Например, если A состоит из элементов X, для которых выполняется свойство P(X), то пишут

Если каждый элемент множества A есть элемент множества B, то множество A называется Подмножеством множества

B (или говорят, что A Включено в B), пишут A Ì B (или B É A) (рис. 1.3). Два множества A, B называются Равными (A = B), если они состоят из одних и тех же элементов: A = B тогда и только тогда, когда A Ì B и B Ì A. Множество, которое не имеет элементов, называется Пустым И обозначается символом Æ.

К основным операциям над множествами относят пересечение, объединение, разность, дополнение.

Пересечением множеств A, B называется множество A Ç B, состоящее из всех тех элементов, которые принадлежат и множеству A, и множеству B (рис. 1.4).

Объединением множеств A, B называется множество A È B, состоящее из всех тех элементов, которые принадлежат или множеству A, или множеству

B (хотя бы одному из множеств A, B) (рис. 1.5).

Разностью множеств A\B называется множество, состоящее из всех тех элементов, которые принадлежат множеству A и не принадлежат множеству B (рис. 1.6).

Дополнением множества A до конкретного (универсального) множества U называется множество , которое определяется равенством (рис. 1.7).

 

A Ì B A Ç B A È B

Рис. 1.3 Рис. 1.4 Рис. 1.5

 

А\В

Рис. 1.6 Рис. 1.7

Для произвольных множеств A, B, C справедливы свойства:

1) Коммутативность объединения;

2) коммутативность пересечения;

3) Ассоциативность объединения;

4) Ассоциативность пересечения;

5) , дистрибутивность;

6) ;

7) ;

8) ;

9) .

Пусть – количество элементов множеств А и В соответственно, тогда справедлива формула

(1.8)

Рассматривают следующие числовые множества:

1) Множество натуральных чисел;

2) Множество целых чисел;

3) Q – Множество рациональных чисел: это множество всех обыкновенных дробей, т.  е. чисел вида где

Множество Q определяется также, как множество всех бесконечных десятичных периодических дробей;

4) I – Множество иррациональных чисел: это множество всех бесконечных десятичных непериодических дробей;

5) R – Множество действительных чисел: .

Верны соотношения:

, , .

Произведение первых N натуральных чисел называется Факториалом, для него введен специальный символ:

.

По определению принимают 0! = 1.

Для всякого определены следующие понятия:

Целая часть (антье) числа X, определяется как целое число такое, что

;

Дробная часть (мантисса), определяется равенством

;

– Знак числа (сигнум), определяется следующим образом:

Если некоторые действительные числа, то Сумму Этих величин обозначают с использованием Знака суммы:

,

Где K – Индекс суммирования.

Свойства суммы:

1) – сумма не зависит от того, какой буквой обозначен индекс суммирования;

2)

3)

4) – свойство сдвига индекса суммирования.

Пример 1. Доказать равенство

(1.9)

Доказательство. Пусть Согласно определению разности, получаем и Поскольку выполняются оба эти условия, то это возможно только в случае Получаем, что и т. е. Этим мы доказали, что

(1.10)

Допустим, что Тогда и но это означает, что

Два условия и которые имеют место, означают, что т. е.

(1.11)

Равенство (1.9) доказано, поскольку установлена справедливость включений (1.10) и (1.11).

Пример 2. На первом курсе учатся 200 студентов. Из них своевременно сдали зачет по математике 175 человек, а по физике – 185 человек. Не сдали зачет ни по математике, ни по физике 10 человек. Сколько студентов сдали оба зачета?

Решение. Пусть A – множество всех студентов курса; B – множество студентов, которые сдали зачет по математике, C – по физике (рис.

1.8).

Согласно условию задачи, , , , и надо найти .

Рис. 1.8

Находим, сколько человек сдали хотя бы один зачет:

Используем далее формулу (1.8), из которой выражаем

Получаем

Пример 3. Сократить дробь

Решение. Выделим общий множитель в числителе и знаменателе. Очевидно, что

Поэтому

Пример 4. Вычислить сумму

Решение. Получим последовательно слагаемые, придавая значения 1, 2, …, 7:

Вычисляя, приходим к ответу

< Предыдущая		Следующая >

Новости — Костромской автотранспортный колледж

Новости

Форма входа

Пароль

Запомнить меня

• Регистрация
• Забыли логин?
• Забыли пароль?

Версия для слабовидящих

Подробности

Опубликовано 24 Январь 2023

Важно! Важно помнить и знать свою историю! Оставаться благодарными за возможность жить!
С 23 января по 3 февраля 2023 года в России пройдёт ежегодная «Неделя памяти», посвящённая двум датам.

Подробнее…

Подробности

Опубликовано 30 Сентябрь 2022

ОГБПОУ «Костромской автотранспортный колледж» продлевает прием документов на 2022-2023 учебный год по следующим образовательным программам:

Подробнее…

Подробности

Опубликовано 26 Сентябрь 2022

«С Днем среднего профессионального образования!» — такими теплыми словами впервые начнется праздничный концерт во Дворце творчества 01.10.2022 года. День среднего профессионального образования, объявленный Президентом страны 2 октября, должен коснуться каждого студента, преподавателя колледжа, мастера производственного обучения.

Подробнее…

Подробности

Опубликовано 29 Август 2022

График проведения 1 сентября 2022 г.

1 курс
11.30-12.00 — линейка
12.00-12.45 — классный час

2, 3, 4, 5 курс
8.40-9.40 — 1 пара
9.50-10.50 — 2 пара, согласно расписания
11.00-11.30 — классный час
11.30-12.00 — линейка

 

Подробности

Опубликовано 16 Август 2022

ОГБПОУ «Костромской автотранспортный колледж» продлевает прием документов на 2022-2023 учебный год по следующим образовательным программам:

Подробнее…

1. Кострома отмечает 78-ю годовщину образования Костромской области
2. Окончание учебного года в КАТК
3. Награждения участников IV Всероссийской летней Спартакиады «Юность России»
4. Свидетельства «Слесарь по ремонту автомобилей 1 разряда» вручены учащимся 8 и 9 классов
5. Фестиваль культур народов Костромской области

Операции над множествами — формулы, свойства, примеры

Операции над множествами — это концепция, аналогичная основным операциям над числами. Множества в математике имеют дело с конечным набором объектов, будь то числа, алфавиты или любые объекты реального мира. Иногда возникает необходимость установить связь между двумя или более множествами. Возникает понятие операций над множествами.

Существует четыре основных операции над множествами, включая объединение множеств, пересечение множеств, дополнение множеств и разность множеств. В этой статье мы изучим различные операции с множествами, обозначения представления множеств, способы работы с множествами и их использование в реальной жизни.

1.	Что такое операции над множествами?
2.	Базовый набор операций
3.	Свойства операций над множествами
4.	Часто задаваемые вопросы по работе с наборами

Что такое операции над множествами?

Набор определяется как набор объектов. Каждый объект внутри набора называется «Элемент». Множество может быть представлено в трех формах. Это форма заявления, форма списка и нотация построителя наборов. Операции над множествами — это операции, которые применяются к двум или более множествам для установления связи между ними. Существует четыре основных типа операций над множествами, которые заключаются в следующем.

• Объединение наборов
• Пересечение множеств
• Дополнение к набору
• Различие между наборами/относительное дополнение

Прежде чем мы перейдем к обсуждению различных операций над множествами, давайте вспомним концепцию диаграмм Венна, поскольку она важна для понимания операций над множествами. Диаграмма Венна — это логическая диаграмма, показывающая возможную связь между различными конечными множествами. Диаграмму Венна можно представить следующим образом.

Базовый набор операций

Теперь, когда мы знаем концепцию множества и диаграммы Венна, давайте подробно обсудим каждую операцию над множеством. Различные операции с множествами:

Объединение множеств

Для двух заданных множеств A и B, A∪B (читается как объединение B) представляет собой множество различных элементов, принадлежащих множеству A и множеству B или обоим. Количество элементов в A ∪ B определяется выражением n(A∪B) = n(A) + n(B) − n(A∩B), где n(X) — количество элементов в множестве X. Чтобы Чтобы лучше понять эту операцию объединения множеств, давайте рассмотрим пример: если A = {1, 2, 3, 4} и B = {4, 5, 6, 7}, то объединение A и B равно определяется как A ∪ B = {1, 2, 3, 4, 5, 6, 7}.

Пересечение множеств

Для двух заданных множеств A и B, A ∩ B (читается как пересечение A B) — это множество общих элементов, принадлежащих множествам A и B. Количество элементов в A ∩ B определяется выражением n(A∩B) = n(A)+n(B)−n(A∪B), где n(X) — количество элементов в множестве X. Чтобы лучше понять эту операцию пересечения множеств, рассмотрим пример: если A = {1, 2, 3, 4} и B = {3, 4, 5, 7}, то пересечение A и B задается A ∩ B = {3, 4} .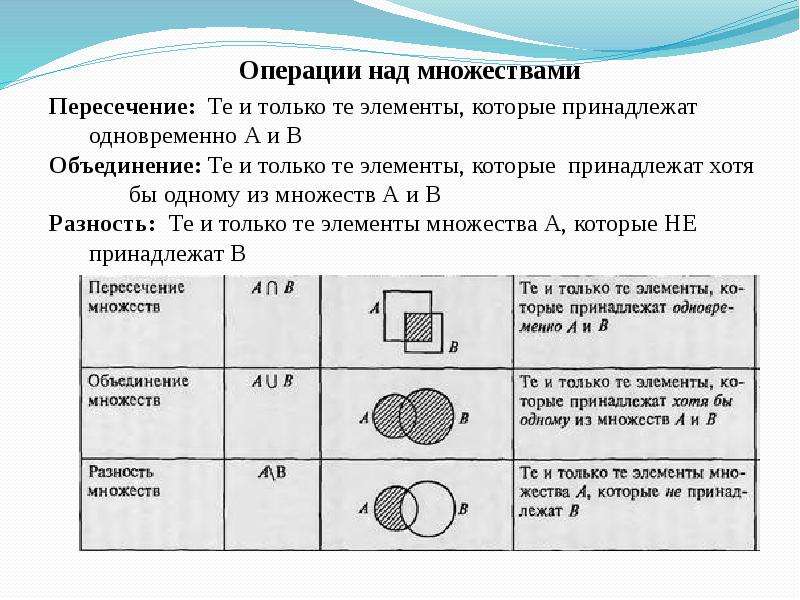

Установить разницу

Операция над множествами разница между множествами подразумевает вычитание элементов из множества, что аналогично понятию разности между числами. Разница между наборами A и набором B, обозначенная как A − B, перечисляет все элементы, которые находятся в наборе A, но не в наборе B. Чтобы лучше понять эту операцию над набором разности наборов, рассмотрим пример: если A = {1, 2, 3, 4} и B = {3, 4, 5, 7}, то разница между множествами A и B определяется соотношением A — B = {1, 2}.

Дополнение к наборам

Дополнение множества A, обозначаемое как A′ или A ^c (читается как дополнение A), определяется как множество всех элементов данного универсального множества (U), которые не присутствуют в множестве A. Чтобы понять эту операцию дополнения множеств лучше, рассмотрим пример: если U = {1, 2, 3, 4, 5, 6, 7, 8, 9} и A = {1, 2, 3, 4}, тогда дополнение множества A задается как A’ = {5, 6, 7, 8, 9}.

На изображении выше показаны различные операции над наборами с помощью диаграмм Венна. Когда элементы одного множества B полностью лежат в другом множестве A, то B называется собственным подмножеством A. Когда два множества не имеют общих элементов, они называются непересекающимися множествами. Теперь давайте рассмотрим свойства операций над множествами.

Свойства операций над множествами

Свойства операций над множествами аналогичны свойствам основных операций над числами. Важные свойства операций над множествами указаны ниже:

• Закон перестановочности . Для любых двух заданных множеств A и B свойство перестановочности определяется как
  A ∪ B = B ∪ A
  Это означает, что множественная операция объединения двух множеств коммутативна.
  А ∩ В = В ∩ А
  Это означает, что множественная операция пересечения двух множеств коммутативна.
• Ассоциативный закон — Для любых трех заданных наборов A, B и C свойство ассоциативности определяется как
  (A ∪ B) ∪ C = A ∪ (B ∪ C)
  Это означает, что операция объединения множеств ассоциативна.
  (А ∩ В) ∩ С = А ∩ (В ∩ С)
  Это означает, что операция пересечения множеств ассоциативна.
• Закон Де-Моргана — Закон Де Моргана гласит, что для любых двух множеств A и B мы имеем (A ∪ B)’ = A’ ∩ B’ и (A ∩ B)’ = A’ ∪ B’
.
• А ∪ А = А
• А ∩ А = А
• А ∩ ∅ = ∅
• А ∪ ∅ = А
• А ∩ В ⊆ А
• А ⊆ А ∪ В

Важные замечания по операциям над множествами

• Формула операции над множествами для объединения множеств: n(A∪B) = n(A) + n(B) − n(A∩B) множества есть n(A∩B) = n(A)+n(B)−n(A∪B).
• Объединение любого множества с универсальным множеством дает универсальное множество, а пересечение любого множества A с универсальным множеством дает множество A.
• Объединение, пересечение, разность и дополнение — это различные операции над множествами.
• Дополнением универсального множества является пустое множество U′ = ϕ. Дополнением пустого множества является универсальное множество ϕ′ = U.

Темы, связанные с операциями над множествами

• Надмножество
• Блок питания
• Конечные и бесконечные множества

Часто задаваемые вопросы по операциям набора

Что такое

Операции над множествами в теории множеств?

Операции над множествами — это операции, применяемые к двум или более множествам для установления связи между ними. Существует четыре основных вида операций над множествами.

Каковы различные операции над наборами?

Существует четыре основных вида операций над множествами:

• Объединение наборов
• Пересечение множеств
• Дополнение к набору
• Различие между наборами/относительное дополнение

Как мы используем операции над множествами в реальной жизни?

Набор — это набор элементов. Некоторые примеры наборов из реальной жизни — это список всех штатов в стране, список всех фигур в геометрии, список всех целых чисел от 1 до 100. Мы можем определить общие области, используя операцию пересечения множества.

Как вы решаете проблемы с работой набора?

Для решения задач с операциями над множествами мы используем диаграмму Венна для представления отношений между множествами и применяем формулу операций над множествами для объединения, пересечения, разности или дополнения множества.

Какие из операций над множествами являются коммутативными и некоммутативными?

Объединение и пересечение множеств являются коммутативными операциями над множествами, в то время как разность множеств не является коммутативной.

Что такое набор символов операций?

Существуют разные символы, используемые для различных операций над множествами, которые называются обозначениями множеств. Для объединения множеств мы используем ‘ ∪ ‘, для пересечения множеств используем ‘∩’, для разности множеств используем ‘-‘, а для дополнения множества A мы пишем как A’ или A ^c .

Как найти разницу между двумя наборами?

Для любых двух наборов A и B разность A-B перечисляет все элементы набора A, которых нет в наборе B.

Как найти дополнение к набору?

Для универсального множества U и множества A дополнение множества A определяется как множество всех элементов универсального множества, отсутствующих в множестве A.

Что такое операции объединения и пересечения множеств ?

Для любых двух наборов A и B объединение определяется как комбинация элементов как в наборе A, так и в наборе B. Пересечение наборов дает общие элементы в наборе A и наборе B.

Операции над наборами

Горячая математика

Напомним, что набор представляет собой набор элементов.

Данные наборы А и Б , мы можем определить следующие операции:

Операция	Обозначение	Значение
Перекресток	А ∩ Б	все элементы, которые есть в обоих А и Б
Союз	А ∪ Б	все элементы, которые находятся в любом А или Б (или оба)
Разница	А − Б	все элементы, находящиеся в А но не в Б
Дополнение	А ¯ (или А С )	все элементы, которых нет в А

Пример 1:

Позволять А «=» { 1 , 2 , 3 , 4 } и разреши Б «=» { 3 , 4 , 5 , 6 } .

Затем:

А ∩ Б «=» { 3 , 4 }

А ∪ Б «=» { 1 , 2 , 3 , 4 , 5 , 6 }

А − Б «=» { 1 , 2 }

А С «=» { все действительные числа, кроме 1 , 2 , 3 и 4 }

Пример 2:

Позволять А «=» { у , г } и разреши Б «=» { Икс , у , г } .