Тема 4
В первой части экзаменационной работы чаще всего предоставлены задания проверяющие:
а) умения «считывать» свойства функции по ее графику;
б) умение анализировать графики, которые описывают зависимость между величинами, например, между расстоянием и временем, между объемом выполненной работы и временем и т.д., умение установить соответствие между графиком функции ее аналитическим заданием.
Во второй части работы практически во всех заданиях по этой теме требуется сначала построить график функции, а затем его использовать и ответить на дополнительные вопросы.
Чаще всего в заданиях встречаются квадратичные, линейные или кусочно-заданные функции.
Теоретическая часть
D(y) (область определения функции у) множество на котором задается функция.
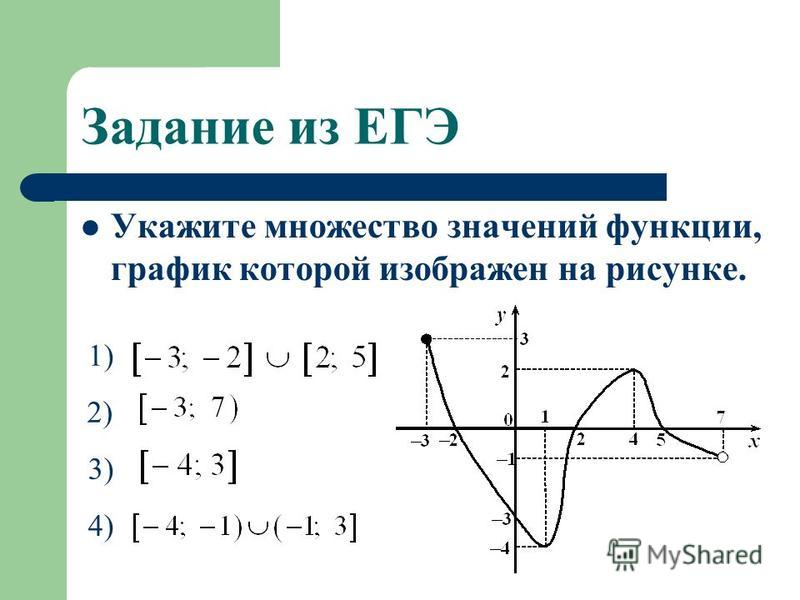
Е(у) (область значений функции у), которые она принимает при всех значениях аргумента из ее области определения. Проще находить область значений функции, если задан график. В этом случае надо спроецировать все точки графика функции на ось 0у.
Получившееся множество точек будет областью значений функции.
Нули функции. Для функции f(x), заданной графически,- это абсциссы точек, в которых график функции пересекает ось абсцисс или касается ее. Чтобы найти нули функции, заданной аналитически, надо решить уравнение f(x)=0.
Функция называется возрастающей на множестве Х, если большему значению аргумента из этого множества Х, соответствует большее значение функции.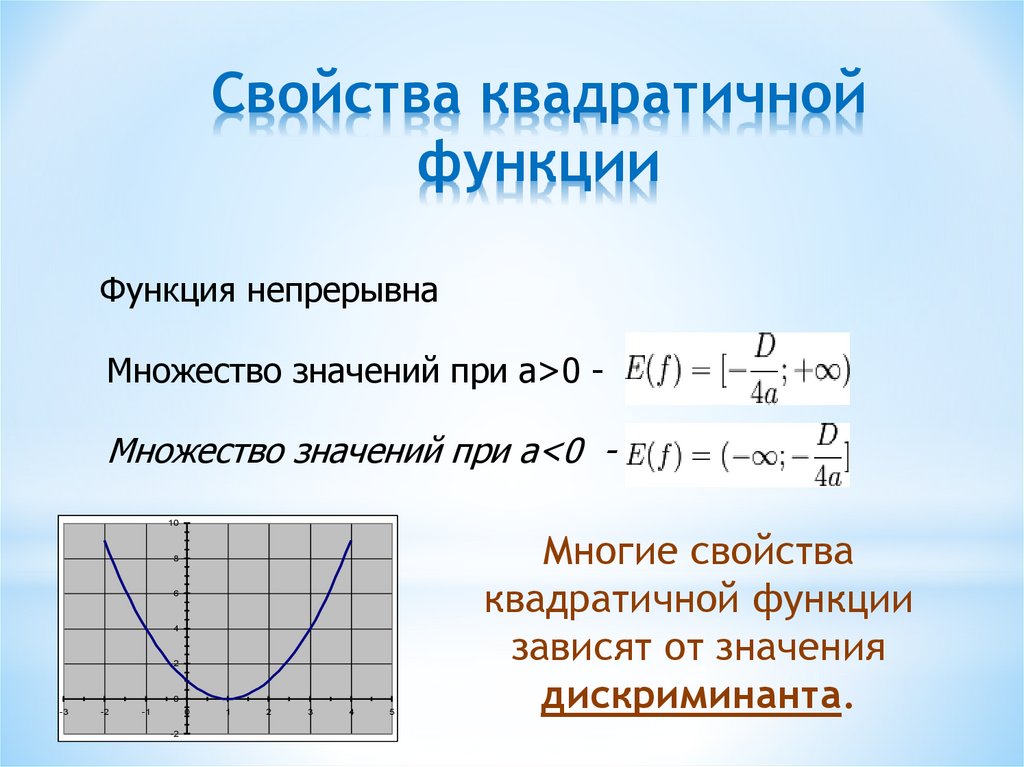
Функция называется убывающей на множестве Х, если большему значению аргумента из этого множества Х, соответствует меньшее значение функции.
Функция у f(x) называется четной, если выполняется два условия:
1)
2)
График четной функции симметричен относительно оси ординат.
Функция у f(x) называется нечетной, если выполняется два условия:
1)
2)
График нечетной функции симметричен относительно начала координат.
Свойства линейной функции
1) .
2) , если .
E(y)={b}, если k=0.
3) монотонность:
если k>0, то функция возрастает на всей области определения;
если k<0,то функция убывает на всей области определения.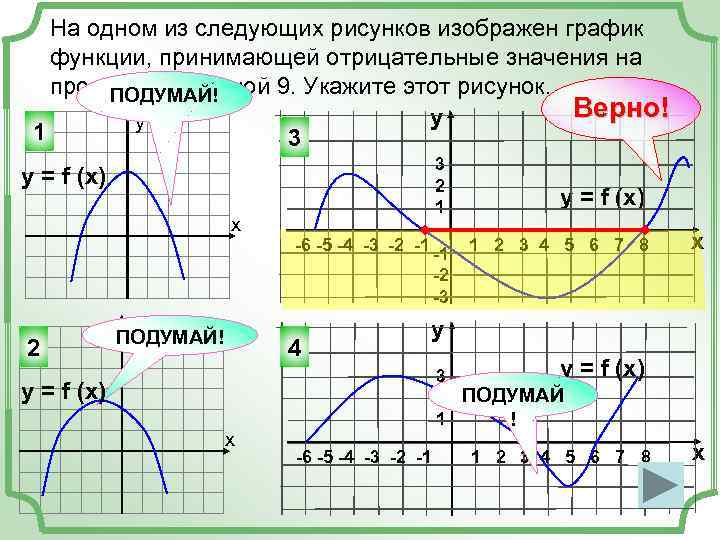
Свойства обратной пропорциональности
1) .
2) .
3) монотонность:
если k>0, то функция убывает на всей области определения;
если k<0,то функция возрастает на всей области определения.
4) функция является нечетной.
где P(x) и Q(x) — многочлены от х.
1) Область определения D(y) — любые действительные х, не обращающие знаменатель Q(x) в нуль.
2) Множество значений Е(у) зависит от конкретной функции.
Свойства квадратичной функции у=ax2+bx+c
— коэффициенты, .
1) .
2) График квадратного трехчлена — парабола с вершиной в точке с абсциссой , направленная ветвями вверх, если а>0; направленная ветвями вниз, если a<0.
3) Множество значений зависит от координат вершины параболы и направления ветвей.
Свойства функции
1) .
2) .
3) Монотонность: функция возрастает на всей области определения.
Примеры решения заданий контрольной работы
Задание 1
График описывает движение парусной яхты, которая первую часть пути прошла под парусом. Спустив парус, она продолжала движение.
1) Найдите скорость яхты «под парусом» и «без паруса» (выразив ее в км/ч).
2) На каком расстоянии от начала движения находилась яхта через 50 минут, через 2 часа?
3) Сколько времени потребуется яхте на обратный путь, если она будет двигаться с той же скоростью, что и на первом участке «под парусом»?
Решение 1: Под парусом яхта прошла 30 км за 60 минут, т.е. за 1 час, значит, ее скорость была . Без паруса яхта прошла 5 км за 60 минут, значит ее скорость была 5 км/ч.
Ответ: 30 км/ч; 5 км/ч.
Решение 2: На графике найдем точку с абсциссой, равной 50.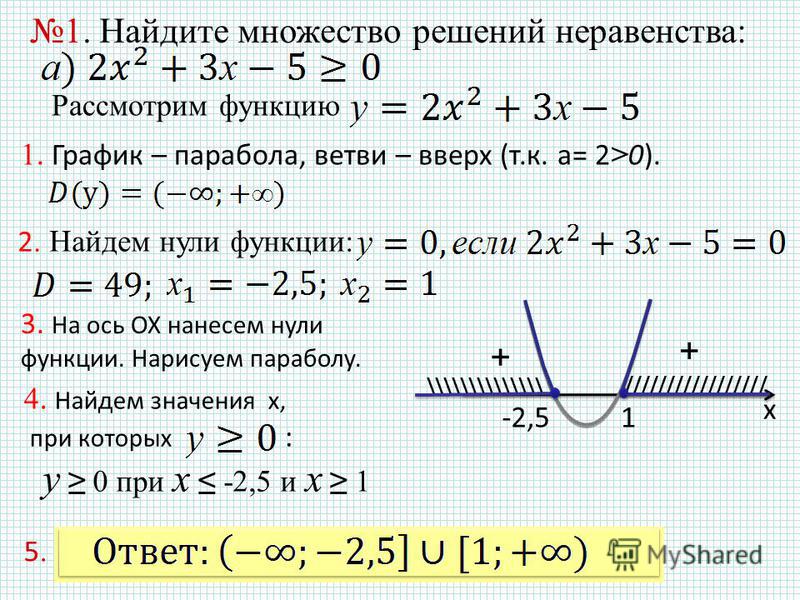
Найдем ординату этой точки. Она равна 25. Получили, что за 50 минут яхта пройдет 25 км. Аналогично, за 120 минут — 35 км.
Ответ: 25 км, 35 км.
Решение 3: Обратный путь составляет 35 км. Скорость яхты 30 км/ч. Найдем время обратного пути: , что составляет 1 час 10 минут.
Ответ: 1 час 10 минут.
Задание 2
Используя график функции y=f(x), определите, какое утверждение верно.
А) Нулями функции являются числа -7; -2; 4.
Б) Функция убывает на промежутке .
В) f(x)<0 при -7<x<0.
Г) f(0)=6.
Решение: Нулями функции являются числа -7; 4. , поэтому х=-2 не является нулями функции. f(0)=5.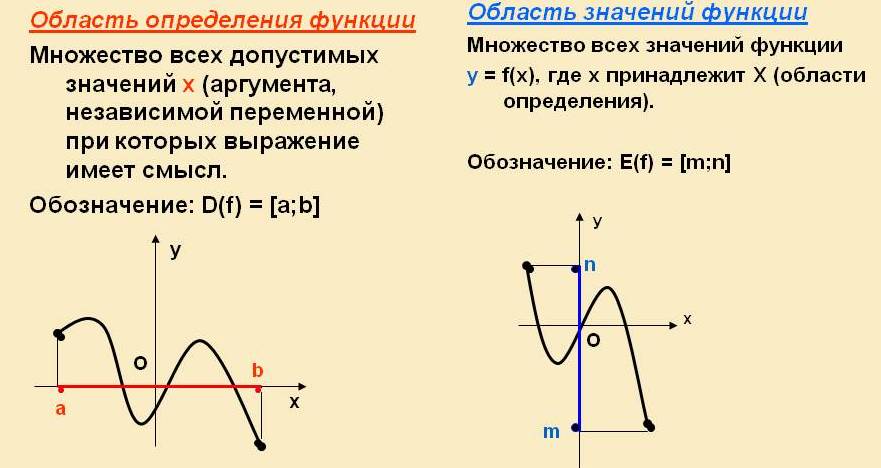
Ответ: Б.
Задание 3
Постойте график функции .
А) При каких значениях аргумента функция принимает положительные значения?
Б) Какова область ее значений?
В) Какие значения принимает функция, если ?
Г) Найдите координаты точки пересечения графика функции с осями.
Решение: Построим график функции и с помощью его ответим на вопросы.
Графиком линейной функции является прямая. Найдем координаты двух точек, принадлежащих этой прямой (-3; 0) и
(3; 4).
Ответим на вопросы:
А) функция принимает положительные значения там, где график расположен выше оси 0х, т.
е. на промежутке .
Ответ: .
Б) функция модет принимать любые значения, поэтому область ее значений .
Ответ: .
В) y(-3)=0, y(1,5)=3. Если , то .
Ответ: [0; 3].
Г) точка пересечения с осью абсцисс уже найдена: (-3; 0). Точку пересечения с осью ординат найдем по графику: (0; 2).
Ответ: (-3; 0); (0; 2).
Задание 4
Постойте график функции y=x2-6x+5.
А) При каких значениях аргумента функция принимает положительные значения?
Б) Укажите наименьшее значение функции.
В) Какова область ее значений?
Г) Найдите координаты точки пересечения графика функции с осью 0х.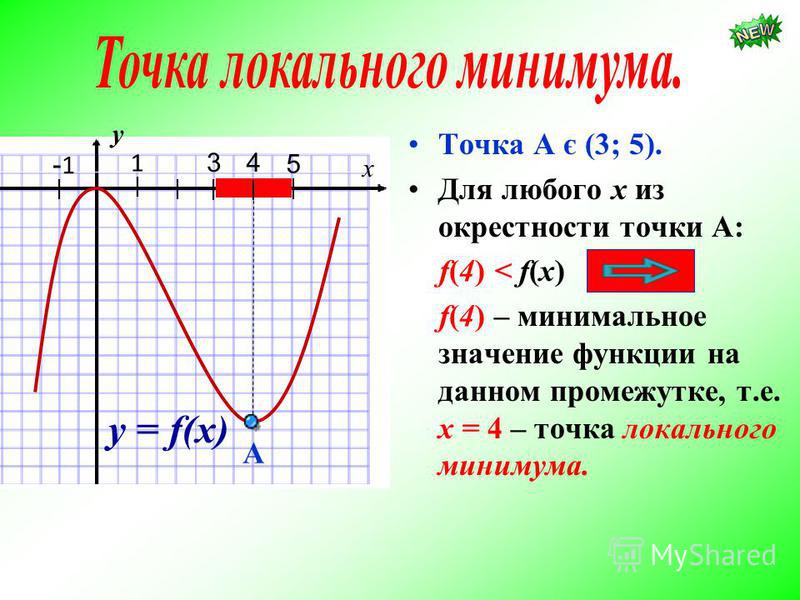
Д) Укажите промежутки возрастания и убывания функции.
Е) Какие значения принимает функция, если ?
Решение: Построим график функции y=x2-6x+5. Графиком квадратичной функции является парабола. Для ее построения найдем координаты вершины параболы и точки пересечения с осями координат ,
|
х |
0 |
1 |
5 |
|
у |
5 |
0 |
0 |
А) выше оси абсцисс (y>0) находится точка графика с абсциссами больше 5 или меньше 1.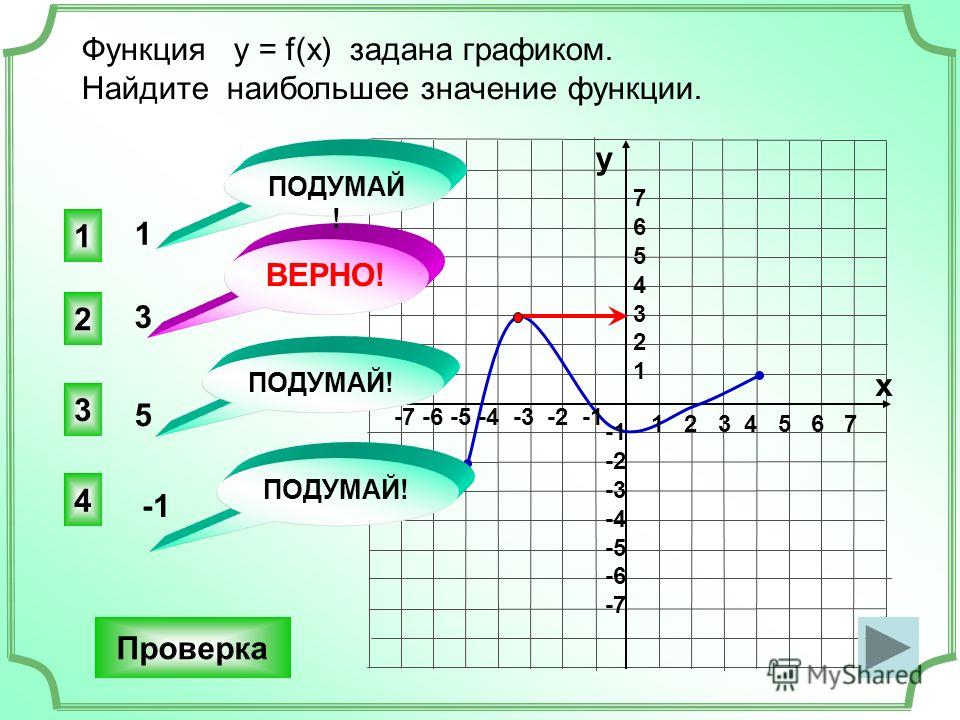
Ответ: ;
Б) наименьшее значение функции у=-4 функция принимает в своей вершине.
Ответ: -4 — наименьшее значение функции;
В) функция может принимать все значения, больше, чем значения в своей вершине.
Ответ: .
Г) точек пересечения с осью 0х две. Их координаты (1; 0) и (5; 0).
Ответ: (1; 0) и (5; 0).
Д) Правее абсциссы вершины функция возрастает, а левее — убывает.
Ответ: промежуток возрастания функции , промежуток убывания функции .
Е) изобразим график функции y=x2-6x+5, если . Для того чтобы найти значение функции, можно найти ординаты всех точек получившегося графика. Спроектируем точки графика на ось ординат, получим отрезок
[-4;5].
Ответ: [-4;5].
Замечание: Обратите внимание на то, что нахождение области значений недостаточно было найти значения функции на концах промежутка [0; 4]: y(0)=5, у(4)=-3. Функция убывает на промежутке [0; 3] и возрастает на промежутке [3; 4], поэтому на промежутке [2;4] принимает значения, меньшие -3.
Задание 5
Постройте график функции . Сколько общих точек может иметь с этим графиком прямая y=m?
Решение: Для построения графика функции «раскроем» модуль. Преобразуем выражение под знаком модуля .
х(х=4)>0, если x<-4 или x>0;
, если .
Построим каждую из парабол на заданной области определения.
Прямая y=m может иметь с графиком этой функции две, три или четыре общих точки, но может их не иметь. Все будет зависеть от расположения прямой.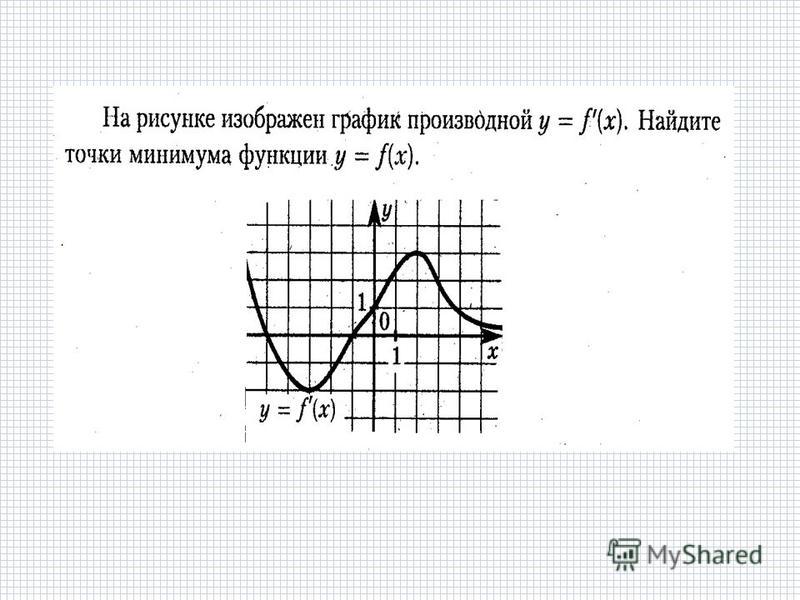
Для того чтобы определить значения параметра m в каждом случае, надо «перемешать» прямую y=m вдоль оси 0y и замечать количество пересечений графика функции и прямой.
Ответ: при m=0 и m>4 прямая y=m может иметь с графиком функции две общие точки. При m=4<4 прямая y=m может иметь с графиком функции четыре общие точки. При m<0 прямая y=m не имеет с графиком функции общих точек.
Задание 6
Задайте аналитическую функцию, график которой иображен на рисунке.
Решение: График заданной кусочной функции состоит из трех прямых, заданных на своих интервалах. Зададим аналитически каждую из прямых.
1) На интервале -4х0 прямая проходит через точки с координатами
(-4;4) и (-2;0). Уравнение прямой y=kx+b.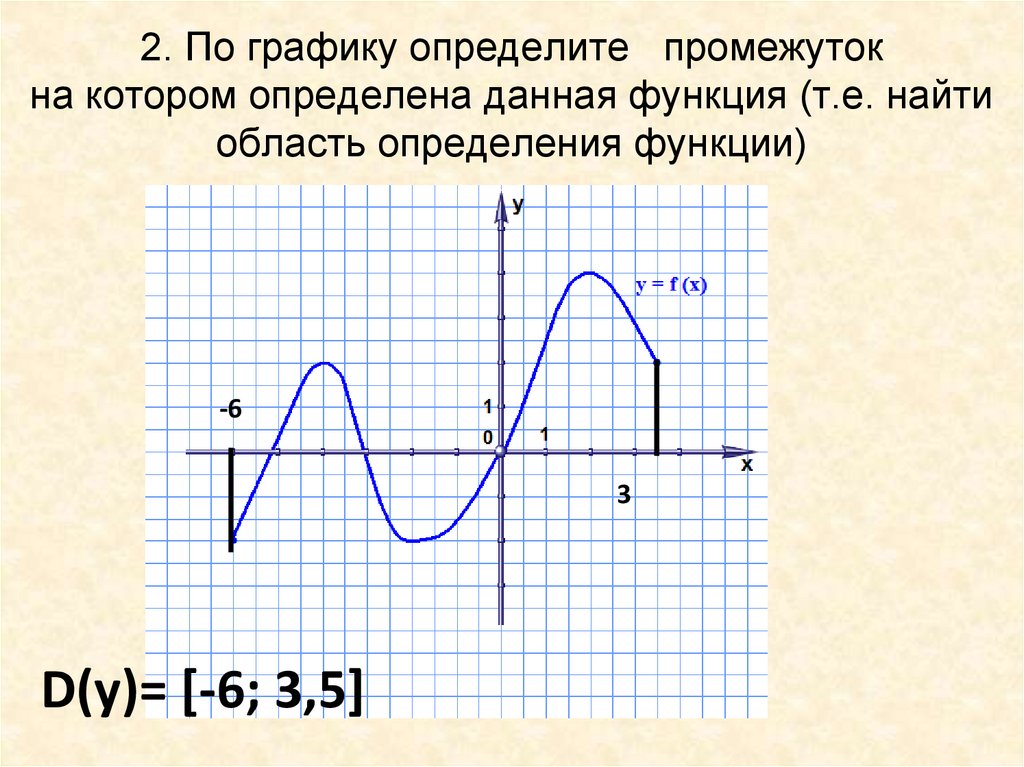
Найдем коэффициенты k и b, решив систему уравнений
Уравнение прямой на этой интервале имеет вид y=-2x-4.
2) На интервале прямая проходит через точки с координатами (0;-4) и (4;-1). Аналогично первому интервалу, получим y=0,75x-4.
3) На интервале прямая проходит через точки с координатами (8;2) и (9;2). Уравнение прямой имеет вид у=2.
4) Зададим функцию изображенную на рисунке:
Замечание: Если задана кусочная функция, то концы областей определения включаются только в один из интервалов, причем не имеет значения в какой.
Задание 7
Найдите область определения следующих функций, заданных аналитически:
А) ;
Б) .
Решение:
А) Областью определения функции является промежуток , поэтому область определения функции можно найти из неравенства .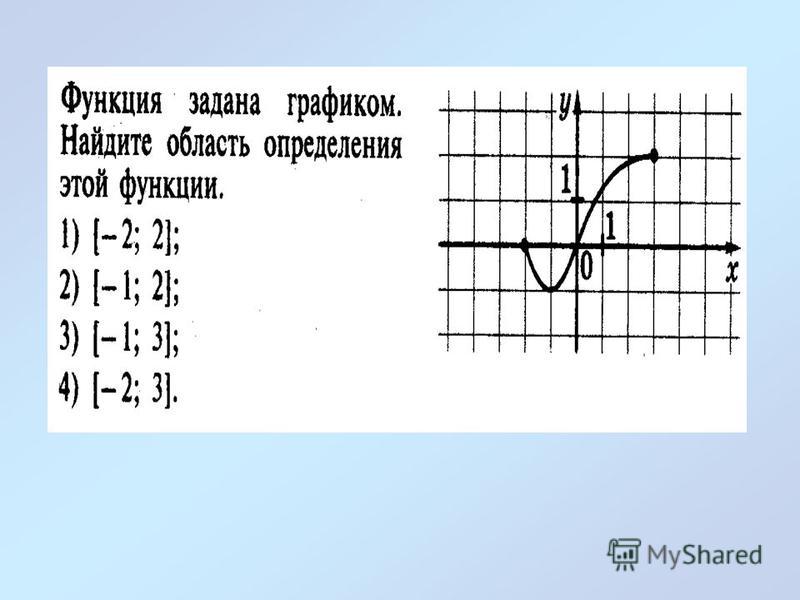
Ответ: [2;4].
Б) Областью определения дробно-рациональной функции являются любые действительные х, не обращающие знаменатель Q(x) в нуль. Поэтому областью определения функции являются все действительные числа, кроме корней уравнения х2-9=0: х=3 или х=-3.
Обратите внимание на то, что сокращение дроби на общий множитель привело бы к неверному ответу.
Ответ:
Скачать задания контрольной работы № 4
Желаю успехов!
Нина Васильевна
Найдите область определения функции Глава 7 §1 B05 ГДЗ Алгебра 9 класс Шестаков С.А. – Рамблер/класс
Найдите область определения функции Глава 7 §1 B05 ГДЗ Алгебра 9 класс Шестаков С.А. – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
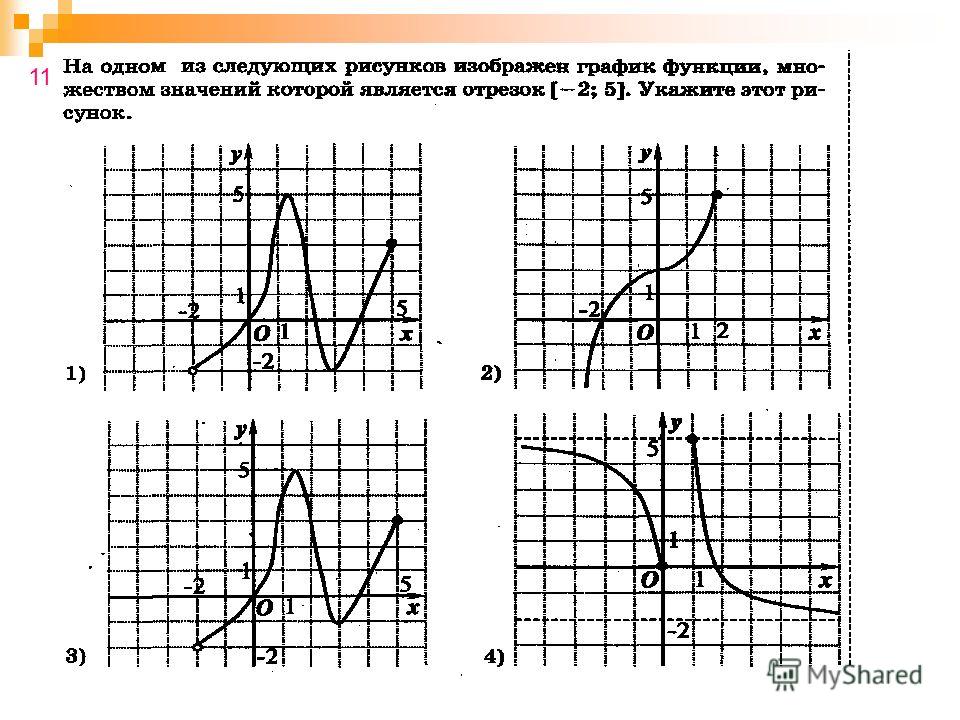
а) По графику функции у =ƒ(х), изображенному на рисунке 29, найдите:
1) область определения функции;
2) множество значений функции;
3) значения ж, при которых значение у равно —3;
4) промежутки возрастания и убывания ƒ(х).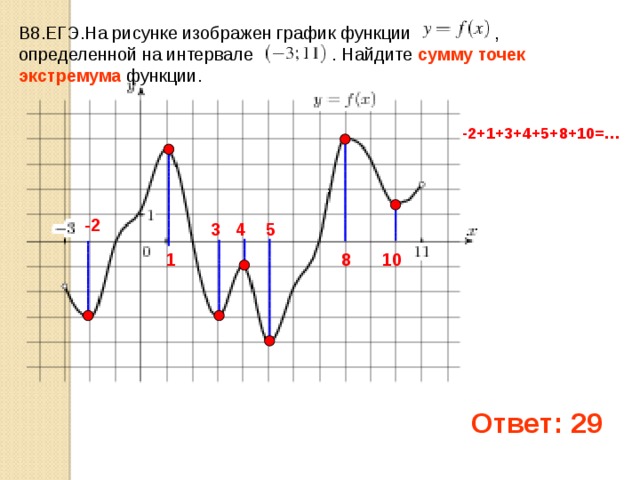
б) По графику функции у = f(x),изображенному на рисунке 30, найдите:
1) область определения функции;
2) множество значений функции;
3) значения х, при которых значение у равно 3;
4) промежутки возрастания и убывания f(x).
ответы
а) 1) D(f) = [-4; 6]
2) E(f) = [-3; 4]
3) х = -1
4) f(x) возрастает на [-1; 6], убывает на [-4; -1]
б) l)D(f) = [-4; 6]
2) E(f) = [0; 4]
3) у = 3 при х = -1, х = 5
4) f(x) возрастает на [-4; -1] и на [2; 6] убывает на [-1; 2].
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
ЕГЭ
10 класс
11 класс
Химия
похожие вопросы 5
2.
Найдите стороны и углы треугольника АВС, если угол В=45°, угол С=60°, ВС=см. 3. Найдите косинус угла М треугольника КСМ, если К (3;9), С(0;6), М(4;2).
9 класс
Кто поможет Глава 6 §1 B08 ГДЗ Алгебра 9 класс Шестаков С.А.
Решите систему неравенств: (Подробнее…)
ГДЗАлгебра9 классШестаков С.А.
Решите , пожалуйста🙏🏻 С чертежом и подробно, прошу…
УчебникиГДЗЭкзамены
Определите, какие изобразительно выразительные средства языка использованы в приведенных ниже отрывках
Березы желтою резьбой
Блестят в лазури голубой,
Как вышки, елочки темнеют (Подробнее…)
ГДЗДосугУчителя
Решите двойное неравенство Глава 6 §3 D01 ГДЗ Алгебра 9 класс Шестаков С.А.
Решите двойное неравенство: (Подробнее…)
ГДЗАлгебра9 классШестаков С.А.
График уравнения
Пример графика функции
Как нарисовать график функции
Во-первых, начните с пустой диаграммы, подобной этой.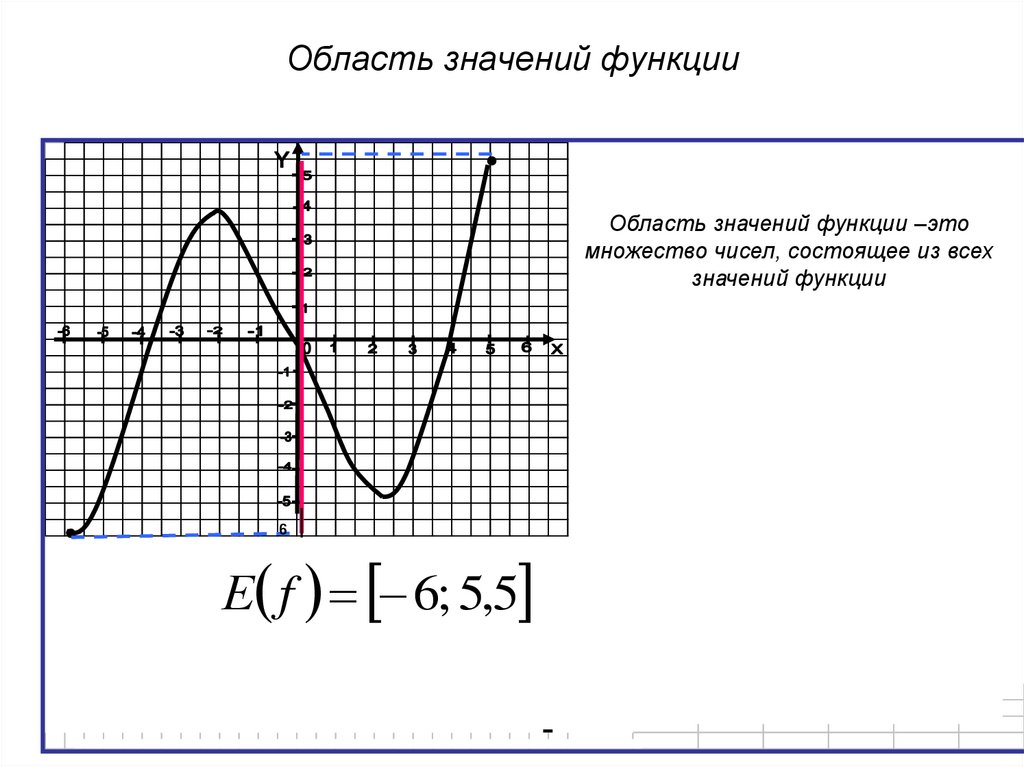
У него значения x идут слева направо, а значения y идут снизу вверх:
Оси x и y пересекаются с
, где x и y равны нулю.
Точки построения
Простой (но не идеальный) подход состоит в том, чтобы вычислить функцию в некоторых точках и затем построить их.
График функции представляет собой набор точек значений, принимаемых функцией.
Пример: y = x
2 − 5Вычислим несколько точек :
| x | у = х 2 −5 |
|---|---|
| −2 | −1 |
| 0 | −5 |
| 1 | −4 |
| 3 | 4 |
И начертите их так:
Пока не очень полезно. Добавим еще точек :
Выглядит лучше!
Теперь мы можем предположить, что построение всех точек будет выглядеть так:
Красивая парабола.
Мы должны попытаться нанести достаточно точек, чтобы быть уверенными в том, что происходит!
Пример: у = х
3 — 5хС этими рассчитанными точками:
| x | у = х 3 -5х |
|---|---|
| −2 | 2 |
| 0 | 0 |
| 2 | −2 |
Мы можем подумать, что это график:
Но это реальный график:
Таким образом, «нанесение некоторых точек» полезно, но может привести к ошибкам .Полный график
Чтобы график был «полным», нам нужно показать все важные функции:
- Пункты пересечения
- Пики
- Долины
- Плоские участки
- Асимптоты
- Любые другие особенности
Это часто означает тщательное обдумывание функции.
Пример: (x−1)/(x
2 −9)На странице Rational Expressions мы делаем некоторую работу, чтобы обнаружить, что функция:
- пересекает ось x в точке 1,
- пересекает ось Y в точке 1/9,
- имеет вертикальные асимптоты (где оно направлено к минус/плюс бесконечности) при −3 и +3
В результате мы можем сделать этот эскиз:
Эскиз (x−1)/(x 2 − 9) из Рациональных выражений.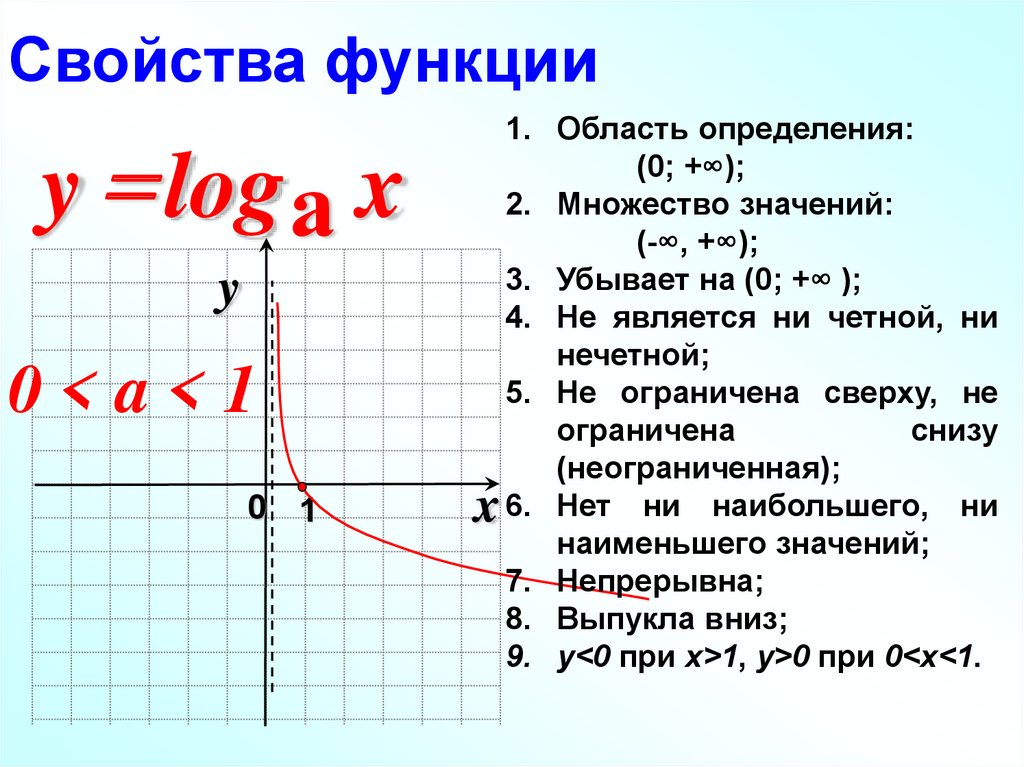
2 \to \R$ (перепутали?),
то его график является поверхностью
образован множеством всех точек $(x,y,z)$
где $z=f(x,y)$, т. е. множество точек $(x,y,f(x,y))$.
Построив график этой поверхности, мы можем визуализировать поведение функции. 92$ над областью $-2 \le x \le 2$ и $-2 \le y \le 2$.
Дополнительная информация об апплете.
Трехмерные графики, такие как на рисунке выше, сложнее рисовать и визуализировать, чем двумерные графики. Более того, графиком функции $f(x,y,z)$ трех переменных будет множество точек $(x,y,z,f(x,y,z))$ в четырех измерениях, и было бы трудно представить, как будет выглядеть такой график.
Другой способ визуализации функции — через 9Уровень 0221 устанавливает , т. е. множество точек в области определения функции, где функция постоянна.
Хорошая часть наборов уровней заключается в том, что они живут в тех же измерениях, что и область определения функции.
Множеством уровня функции двух переменных $f(x,y)$ называется кривая в двумерной $xy$-плоскости, называемая линией уровня.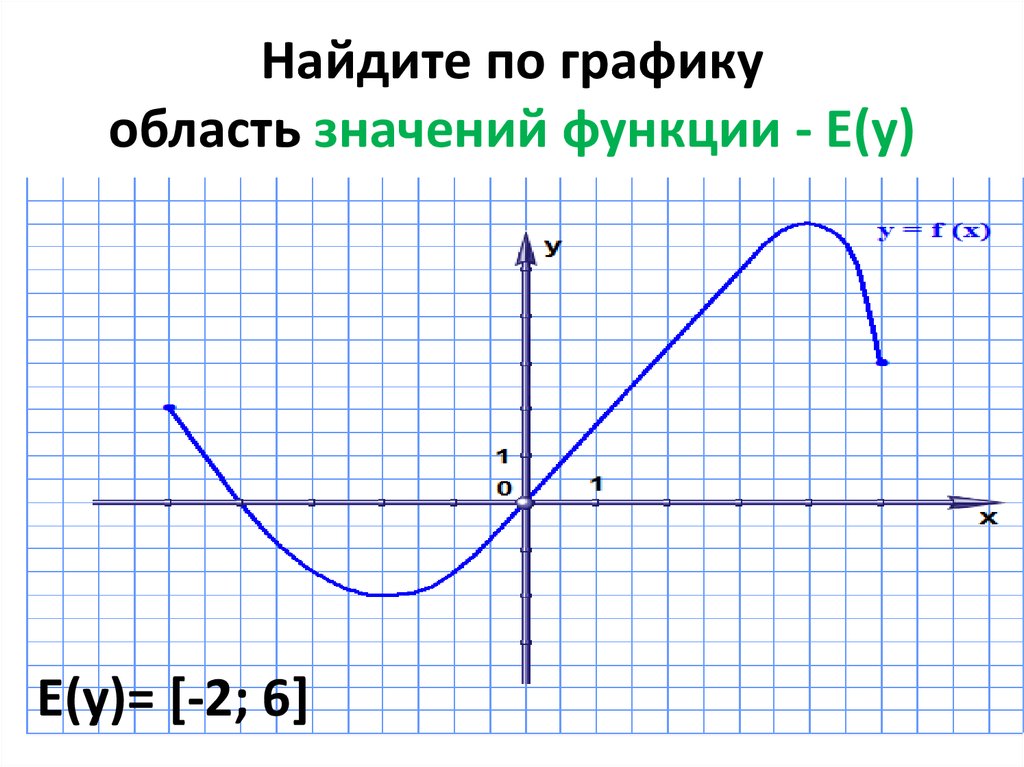
Множеством уровня функции трех переменных $f(x,y,z)$ называется поверхность в трехмерном пространстве, называемая поверхностью уровня.
Кривые уровня
Один из способов свернуть график скалярнозначной функции двух переменных в двумерный график через уровень кривых . Линия уровня функции $f(x,y)$ — это кривая точек $(x,y)$ где $f(x,y)$ — некоторая постоянная величина. Кривая уровня — это просто сечение графика $z=f(x,y)$, взятое при постоянном значении, скажем $z=c$. Функция имеет много кривых уровня, так как получается разные кривые уровня для каждого значения $c$ в диапазоне $f(x,y)$. Мы можем построить кривые уровня для набора различных констант $c$ вместе на графике кривой уровня, который иногда называют контуром участок. 92$. Пока $c
На приведенном ниже графике показано соотношение между кривыми уровня и графиком функции.
Ключевым моментом является то, что кривую уровня $f(x,y)=c$ можно рассматривать как горизонтальный срез графика на высоте $z=c$.
2$ показан на первой панели вместе с графиком кривой уровня на второй панели. Кривая уровня $f(x,y)=c$ показана красным цветом на графике кривой уровня, который совпадает со срезом графика $z=f(x,y)$ плоскостью $z=c $. Вы можете изменить $c$, перетащив мышью плоскость, разрезающую график, вверх или вниз. Вы также можете изменить $c$, перетащив красную кривую уровня.
Дополнительная информация об апплете.
Топографические карты — это просто кривые уровня высоты земли (или воды).
Например, на стандартных картах Геологической службы США каждая контурная линия представляет собой 10 футов высоты над уровнем моря.
как на этой топографической карте Орлиной горы, самой высокой горы (ну… холма) в Миннесоте.
Чем ближе контурные линии друг к другу, тем круче склон земли.
Неудивительно, что самые крутые склоны кажутся очень близкими к вершинам Орлиной горы и Лосиной горы. 93 \к \R$,
нам потребуются четыре измерения, чтобы нарисовать его график.
Граф представляет собой множество точек $(x,y,z,f(x,y,z))$.
Вам следует ознакомиться с
векторы в более высоких измерениях
привыкнуть к идее четырех измерений.
Однако, если только ваш ум не лучше справляется с абстрактной визуализацией, чем
В большинстве случаев вам может быть трудно представить себе, что представляет собой этот график из четырех
размеры бы выглядели.
Вместо этого мы можем посмотреть на наборы уровней , где функция постоянный. Для функции двух переменных выше мы видели, что уровень множество представляло собой кривую в двух измерениях, которую мы назвали кривой уровня. Для функцией трех переменных, множество уровня представляет собой поверхность в трехмерное пространство, которое мы будем называть ровная поверхность . При постоянном значении $c$ в диапазоне $f(x,y,z)$ поверхность уровня $f$ неявная поверхность дается графиком $c=f(x,y,z)$.
Приведенная ниже версия апплета кривой уровня поможет вам увидеть, что кривые уровня и поверхности уровня похожи
концепции, поскольку эта версия помещается в
формат, который мы будем использовать для ровных поверхностей.
В этом случае единовременно отображается только одна кривая уровня $f(x,y)=c$.
Кривая уровня эллиптического параболоида. 92}$. Даже хотя мы не можем построить график $f(x,y,z)$ (без использования четырех размеры), мы все еще можем визуализировать поведение функции с помощью построение его поверхностей уровня. Мы просто строим $f(x,y,z)=c$ для $c$ между 0 и 10. (Обратите внимание, что $f(x,y,z)$ всегда лежит от $0$ до $10$. Аргумент экспоненты всегда отрицательное или нулевое, поэтому значение экспоненты всегда находится между ноль и единица.) Поведение этих поверхностей уровня показано на следующий апплет. 92}=c$ отображается. Вы можете перетащить синюю точку на ползунке с помощью мыши, чтобы изменить $c$ и, следовательно, отображаемую поверхность уровня.
Дополнительная информация об апплете.
Значение поверхностей уровня может стать яснее, если вы подумаете
$f(x,y,z)$ как задающий температуру в точке $(x,y,z)$. Затем,
поверхность уровня $f(x,y,z)=2$ — это поверхность точек, где
температура равна 2.