Модуль икс равен 5: Решите уравнение |x|=-5 — ответ на Uchi.ru

Ответы на все модули (для контрольного теста) по предмету математика.

Автор admin На чтение 11 мин. Просмотров 2.2k. Опубликовано 14.05.2013

Ответы на все модули (для контрольного теста) по предмету математика.

Ответы на модуль 1 (ЧИСЛА) по предмету математика.

1) Найдите значение выражения

2) Упростите иррациональное выражение

22

3) Сколько целых чисел удовлетворяют неравенству -8 <x< 4?

11

4) Укажите натуральный ряд чисел

1, 2, 3, 4, 5, 6, 7, 8, 9, …

5) Выполните действия

10000

6) Какое из перечисленных чисел является иррациональным?

3,141592…

7) Вычислите

6*5/21

8) Какая из перечисленных дробей является смешанной периодической дробью?

2,75(12)

9) Вычислите с точностью до десятых

0,3

10) Найдите значение выражения при a= 2

2/3

11) Упростите

12) Найдите

-2

13) Какие числа называются целыми?

натуральные числа, числа противоположные натуральным, и число 0

Ответы на модуль 2 (ВЕКТОРНАЯ АЛГЕБРА) по предмету математика.

1) Дано: Найдите a*b

32

2) Дано: Вычислите

13

3)  Найдите l, если

3 или -3

4) Что называется скалярным произведением двух векторов?

число, определяемое по формуле

5) Найдите l, если

2,5 или -2,5

6) Даны векторы и Найдите — проекцию вектора на ось вектора

7) Даны точки M(-5; 7; -6), N(7; -9; 9). Вычислите проекцию вектора на вектор MN

3

8) При каком значении l векторы MP и KD коллинеарны, если M(-3; 2), P(-1; -2), K(2; 1), D(5;l)?

-5

9) Какие векторы называются коллинеарными?

лежащие на одной прямой или параллельных прямых

10) Векторы называются компланарными, если

они лежат в одной плоскости или параллельных плоскостях

11) Какой из перечисленных векторов коллинеарен вектору

12) Векторы a и b взаимно перпендикулярны (ортогональны), причем |a|=5 и |b|=12 . Определите

13

13) Векторы AC=a и BD=d служат диагоналями параллелограмма ABCD. Выразите вектор DA через векторы a и b

Ответы на модуль 3 (АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ) по предмету математика.

1) Найдите координаты точки K пересечения прямой с плоскостью 2x+ 5y- 3z= 0

2) Найдите уравнение прямой, проходящей через точку пересечения прямых 2x + 3y — 8 = 0 и x — 4y + 5 = 0 и через точку M₁(-2; 3)

5x+ 13y— 29 = 0

3) Укажите канонические уравнения прямой, проходящей через точки M₁(3; 2; 5) и M₂(-1; 3; -2)

 

4) Даны прямые  и  При каком значении a они перпендикулярны?

a= 2

5) Установите взаимное расположение прямых  и 

прямые перпендикулярны

6) Укажите канонические уравнения прямой 

 

7) Найдите острый угол между прямыми  и  

60°

8) Составьте уравнение плоскости, проходящей через параллельные прямые  и 

6x— 20y— 11z+ 1 = 0

9) Даны вершины треугольника ABC: A(3; -1),B(4; 2) и C(-2; 0).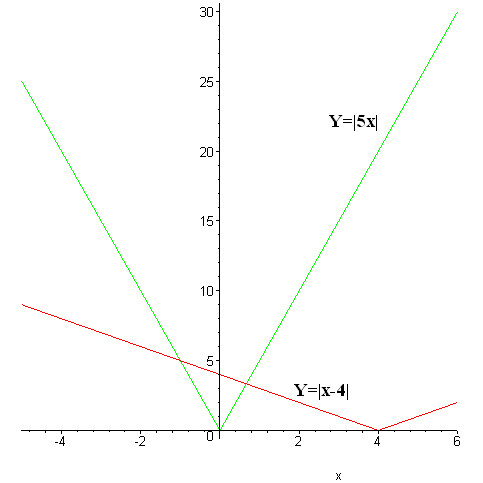 Напишите уравнения его сторон

3x—y— 10 = 0,   x— 3y+ 2 = 0,   x+ 5y+ 2 = 0

10) Уравнение 3x— 4y+ 12 = 0 преобразуйте к уравнению в отрезках

 

11) Определите уравнение прямой, отсекающей на оси Oy отрезок b = 2 и составляющей с осью Ox угол j= 45°

y=x+ 2

12) Найдите координаты точки пересечения прямых  2x—y— 3 = 0 и 4x+ 3y— 11 = 0

(2; 1)

13) Найдите уравнение прямой, проходящей через точки M₁(3; 2), M₂(4;-1)

3x+y— 11 = 0

Ответы на модуль 4 (КРИВАЯ 2-ГО ПОРЯДКА) по предмету математика.

1) Определите эксцентриситет равносторонней гиперболы

2) Укажите уравнение окружности, которая проходит через точки А(3;1) и В(-1; 3), а ее центр лежит на прямой 3x—y— 2 = 0

(x— 2)²+ (y— 4)²= 10

3) Укажите уравнение окружности радиуса R= 8 с центром в точке C(2;-5)

(x— 2)²+ (y+ 5)²= 8²

4) Определите полуоси гиперболы 

a= 4, b= 1

5) Укажите уравнение окружности, центр которой совпадает с началом координат, а прямая 3x— 4y+ 20 = 0 является касательной к окружности

x²+y²= 16

6) Укажите уравнение окружности, которая проходит через точку А(2;6) и ее центр совпадает с точкой C(-1; 2)

(x+ 1)²+ (y— 2)²= 25

7) Укажите каноническое уравнение эллипса, расстояние между фокусами которого равно 8, а малая полуось b= 3

 

8) Напишите уравнение эллипса, если даны его полуоси a= 5 и b= 4

 

9) Укажите уравнение окружности, проходящей через точку (4; 5) с центром в точке (1; -3)

(x— 1)²+ (y+ 3)²= 73

10) Определите полуоси гиперболы 25x²— 16y²=1

 

11) Напишите уравнение гиперболы, фокусы которой лежат на оси Ox, если даны a= 6 и b= 2

 

12) Укажите уравнение параболы, с вершиной в точке O и фокусом F(4; 0)

y²=16x

13) Укажите уравнение окружности, для которой точки А(3; 2) и В(-1; 6) являются концами одного из диаметров

(x— 1)²+ (y— 4)²= 8

Ответы на модуль 5 (КРИВАЯ 2-ГО ПОРЯДКА) по предмету математика.

1) Найдите общее решение системы

или

 

2) Вычислите определитель 

-89

3) Найдите ранг и базисные строки матрицы 

2. 1-я строка, 2-я строка

4) Вычислите определитель 

0

5) Найдите А × В, где ; 

6) Решите систему уравнений методом Крамера  

{(-1; 0; 1)}

7) Найдите обратную матрицу для матрицы 

 

8)  Найдите ранг матрицы 

4

9) Определитель системы трех линейных уравнений с тремя неизвестными равен 5. Это означает, что

система имеет единственное решений

10) Найдите АВ — АС, где ; ;

 

11) Метод Гаусса решения системы линейных уравнений предполагает использование

последовательного исключения неизвестных

12) Система линейных уравнений называется совместной, если

она имеет хотя бы одно решение

13) Решите матричное уравнение AX + AXA = B, где ; 

Ответы на модуль 6 (МАТЕМАТИЧЕСКИЙ АНАЛИЗ) по предмету математика.

1) Найдите предел 

3

2) Найдите предел 

5

3) Найдите предел 

5

4) Найдите предел 

1/e

5) Найдите предел 

0

6) Найдите предел 

0

7) Найдите предел 

 

8) Найдите предел 

1/2

9) Найдите предел 

e^—5

10) Найдите предел 

1

11) Найдите предел 

0

12) Найдите предел 

5/3

13) Найдите предел 

3/5

Ответы на модуль 7 (ДИФФЕРЕНЦИРОВАНИЕ) по предмету математика.

1) Вычислите предел по правилу Лопиталя

0

2) Найдите производную функции f(x)=(1+ cos x)sin x

cos x+ cos 2x

3) Вычислите предел по правилу Лопиталя  

1/18

4) Вычислите предел по правилу Лопиталя 

-4/3

5) Найдите производную функции  y= sin(2x²+ 3)

4xcos(2x²+ 3)

6) Найдите производную функции y=(3e^x+x)× cos x

(3e^x+ 1) × cos x— (3e^x+x) × sin x

7) Для функции   найдите y(49)

1/14

8) Найдите производную функции  

 

9) Найдите производную функции y=2^tgx

 

10) Найдите производную функции 

 

11) Найдите скорость тела, движущего по закону S=3t-5

3

12)  Дана функция  Решите уравнение 

 

13) Найдите производную функции y=xe^x—e^x

xe^x

Ответы на модуль 8 (ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНОЙ) по предмету математика.

1) Число f(x₀) называется наибольшим значением функции на отрезке [a;b], если

для всех x из этого отрезка выполняется неравенство f(x) <= f(x0)

2) Найдите промежутки возрастания или убывания функции y=x²— 3x+ 1

убывает при x<3/2, возрастает при x>3/2

3) Найдите точки максимума (минимума) функции y=- 5x²— 2x+ 2

(-0,2;2,2) — точка максимума

4) Каково необходимое условие возрастания функции?

если функция y=f(x) дифференцируема и возрастает на интервале (a;b), то f(x)>=0 для всех xиз этого интервала

5) Определите поведение функции y= 2x² при x= 1

возрастает

6) В каких точках выпукла или вогнута кривая y=x²— 3x+ 6

вогнута во всех точках

7) Найдите промежутки возрастания или убывания функции y=- 2x²+ 8x— 1

убывает при x> 2, возрастает x< 2

8) Найдите точку перегиба кривой 

(0; 0)

9) Найдите точки перегиба кривой y=x⁴— 12x³+ 48x²— 50

(2; 62) и (4; 206)

10) Найдите точки максимума (минимума) функции y=x²— 2x

(1;-1) — точка минимума

11) Вертикальные асимптоты к графику функции  имеют вид

x= 4, x= 0

12) Найдите наибольшее и наименьшее значения функции y=x² на промежутке [-1; 3]

y_наиб= 9, y_наим= 0

13) В каких точках выпукла или вогнута кривая y= 2 — 3x—x²

выпукла во всех точках

Ответы на модуль 9 (ФУНКЦИЯ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ) по предмету математика.

1) Найдите частные производные функции двух переменных 

2) Найдите частные производные второго порядка функции z=x³y⁴+ycos x

 

3) Найдите предел функции  при x->0, y->0

0

4) На каком из рисунков изображена область определения функции 

 

5) Найдите частные производные функции двух переменных z=xe^y+ye^x

 

6) Найдите частные производные функции z=x²× ln y

 

7) Найдите полный дифференциал функции z=x²y+xy²

dz=(2xy+y²)dx+(x²+2xy)dy

8) Какая поверхность называется графиком функции n переменных?

n-мерная гиперповерхность в пространстве R^{n+ 1}, точки которой имеют вид (х₁, х₂, …, х_n, f(x₁, х₂, …, x_n))

9) Укажите полное приращение функции f(x;y)

f(x +Dx; y +Dy)- f(x; y)   D-треугольничек.

10) Найдите 

4

11) Укажите частное приращение функции f(x;y)по переменной у

f(x;y +Dy)- f(x;y)

12) На каком из рисунков изображена область определения функции 

 

13) Найдите область определения функции 

xy<=1,  x²не =y²

Ответы на модуль 10 (НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ) по предмету математика.

1) Найдите 

x²+С

2) Найдите 

 

3) Найдите 

 

4) Найдите 

 

5) Найдите 

 

6) Найдите 

 

7) Найдите 

 

8) Найдите 

 

9) Найдите 

 

10) Найдите  если при x= 2 первообразная функция равна 9

 

11) Найдите 

 

12) Найдите  если при x=0 первообразная функция равна 0

arctg x+x

13) Найдите 

 

Ответы на модуль 11 (ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ) по предмету математика.

1) Скорость точки, движущейся прямолинейно, задана уравнением v=9t²-2t-8. Вычислите путь, пройденный точкой за 3 с от начала движения

48 м

2) Вычислите определенный интеграл 

9

3) Сила в 6 кГ растягивает пружину на 8 см. Какую работу она производит?

0,24 кГм

4) Вычислите определенный интеграл 

 

5) Вычислите определенный интеграл 

e^p-1

6) Найдите площадь фигуры, заключенной между прямыми y=4x— 5, x=-3, x=-2 и осью Ox

15

7) Скорость падающего в пустоте тела определяется по формуле v= 9,8t м/сек. Какой путь пройдет тело за первые 10 секунд падения?

490 м

8) Найдите площадь фигуры, ограниченной прямыми y=5x, x=2 и осью Ox

10

9) Вычислите определенный интеграл 

2

10) Вычислите определенный интеграл 

4*2/3

11) Вычислите определенный интеграл 

2/3

12) Вычислите определенный интеграл 

0,24

13) Вычислите определенный интеграл 

0,25

Ответы на модуль 12 (ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ) по предмету математика.

1) Как называется решение, полученное из общего при конкретных значениях произвольных постоянных?

частным решением

2) Найдите общее решение уравнения (x+y)dx+xdy=0

 

3) При решении каких уравнений используют подстановку 

при решении однородных уравнений

4) Найдите общее решение уравнения xy²dy=(x³+y³)dx

y³=3x³ln| Cx |

5) Среди перечисленных дифференциальных уравнений укажите уравнение Бернулли

 

6) Найдите общее решение уравнения y — 9y = e^2x

 

7) Найдите общее решение уравнения 

y=-2lnx+ Cx+ C_1\

8) Найдите частное решение уравнения ds=(4t-3)dt, если при t= 0  s= 0

s=2t²-3t

9) Найдите общее решение уравнения y—y= 0

y= C₁e^x+ C₂e^—x

10) Найдите общее решение уравнения 

y=x²+ Cx

11) Среди перечисленных дифференциальных уравнений укажите однородное уравнение

x²y=xy+y²

12) Найдите общее решение уравнения y— 4y+ 3y= 0

y= C₁e^x+ C₂e^3x

13) Найдите общее решение уравнения y = cos x

y=-cos x+ Cx+ C₁

Ответы на модуль 13 (РЯДЫ) по предмету математика.

1) Исследуйте сходимость ряда

 

сходится

2) Найдите интервал сходимости ряда x+2x²+3x³+4x⁴+…+nxⁿ+…, не исследуя концов интервала

(-1; 1)

3) Найдите радиус сходимости ряда 

R=1

4) Разложите в степенной ряд f(x)= arctg 3x

 

5) Исследуйте сходимость ряда 

расходится

6) Исследуйте сходимость ряда 

сходится

7) Найдите интервал сходимости ряда 

(-; +)

8) Исследуйте сходимость ряда 

расходится

9) Исследуйте сходимость ряда 

расходится

10) Исследуйте сходимость ряда 

сходится

11) Разложите в степенной ряд f(x)= sin 2x

 

12) Исследуйте сходимость ряда 

расходится

13) Исследуйте сходимость ряда 

сходится

Ответы на задачник по предмету математика.

1) Составьте уравнение плоскости, зная, что точка А(1, -1,3) служит основанием перпендикуляра, проведенного из начала координат к этой плоскости.

x — y + 3z — 11 = 0 

2) Вычислить определитель D, разложив его по элементам второго столбца.

D=

 

-20 

3) Вычислить J= ∫cos(lnx) dx/x

sin(lnx)+ C 

4) Найти lim _x—>0 (5^x — cos x)

0 

5) Вычислить площадь фигуры, ограниченной линиями 4y = x² , y² = 4x.

16/3 

6) Найти производную функции  y =ln sinx

ctg x 

7) Найдите угол между векторами a = 2m+4n и b = m-n, где m и n — единичные векторы и угол между m и n равен 120^о

120 

8) Найти наименьшее значение функции y = x² – 6x + 5 на отрезке (1,2).

-3 

9)

Решить систему уравнений:
2x₁ + 3x₂ + 2x₃ = 9
x₁ + 2x₂ – 3x₃ =14
3x₁ + 4x₂ + x₃ = 16

X1=2, X2=3, X3=-2.

10) При каком положительном значении параметра t прямые, заданные уравнениями
3tx — 8y + 1 = 0 и (1+t)x — 2ty = 0, параллельны?

2

Прокачивайте математику – вот как это поможет при программировании / Хабр

Пол Орланд исследует, как можно прокачать навыки программирования, развивая математическую подготовку и всё лучше разбираясь в том, как сохраняется связь между математикой и программированием.

Эта статья адресована всем, кто хочет улучшить математические навыки, но в особенности программистам, желающим применять математические навыки в повседневной работе.

К счастью, если вы уже умеете писать код, это значит, что серьёзными математическими навыками вы уже обладаете, и математические идеи должны прийти вам на ум сами собой. Я считаю, что лучше всего изучать математику на основе высокоуровневого языка программирования. Спрогнозирую, что в недалёком будущем такой подход станет нормой на уроках математики.

Есть несколько конкретных идей, которые перелицовываются непосредственно из программирования в математику. Эти идеи напомнят вам о тех навыках, на которые вам уже доводилось опираться при изучении математики.

Использование формального языка

Один из первых уроков, который крепко усваиваешь при обучении программированию – что нельзя писать код так же, как пишешь текст на естественном языке. Например, если вы пишете электронное сообщение и слегка ошибаетесь в орфографии, то адресат, вероятно, всё равно поймёт, о чём вы пишете. Но при программировании любая синтаксическая ошибка или неправильно записанный идентификатор могут привести к обрушению программы. В некоторых языках программа не заработает, даже если просто не поставить точку с запятой в конце инструкции, которая в остальном написана совершенно верно.

Простой пример – присваивание переменной. Непрограммисту покажется, что две следующие строки на Python означают одно и то же:

x = 5
5 = x

Я мог бы прочитать обе эти строки так: «пятёрка обозначена через x». Но на самом деле всё не совсем так, и лишь первый вариант корректен. Код Python x = 5 – это инструкция, обязывающая привязать значение 5 к символу x. С другой стороны, нельзя привязать символ к значению литерала 5. Может показаться, что это излишне педантично, но вы же должны знать, как правильно пишутся программы.

Другой пример, на котором прокалываются программисты-новички (равно как и опытные) – это ссылочная эквивалентность.

>>> class A(): pass
...
>>> A() == A()
False

Если определить новый класс Python и создать два идентичных экземпляра этого класса, то они будут неэквивалентны. Логично ожидать, что два одинаковых выражения эквивалентны, но в Python такое правило, очевидно, не работает. Поскольку это разные экземпляры класса A, они одинаковыми не считаются.

Следите за новыми математическими объектами, которые выглядят, казалось бы, знакомо, а на практике проявляют неожиданные свойства. Например, если буквы A и B представляют числа, то A x B = B x A.

Но так может и не быть, если A и B – не числа. Так, если A и B – это матрицы, то произведения A x B и B x A обычно будут отличаться. Может быть и так, что лишь одно из этих произведений является возможным, либо ни одно не является.

При написании кода мало просто обеспечить синтаксическую корректность инструкций. Чтобы идеи, выраженные в ваших инструкциях, были действительными, сами эти инструкции должны иметь смысл. Если писать инструкции в коде с той же тщательностью, что и математические выражения, то любые ошибки будут отлавливаться быстрее. Ещё лучше, если прямо в коде вы будете писать математические выражения – тогда с проверкой вашей работы вам поможет компьютер.

Пишем собственный калькулятор

Калькулятор — не редкость на уроках математики, ведь с его помощью удобно проверять работу. Вы должны уметь умножить в уме шесть на семь, но чтобы убедиться, что ответ действительно равен 42 – можно проверить его на калькуляторе. Также калькулятор помогает экономить время, когда концептуально предмет уже усвоен.

Если вы занимаетесь тригонометрией и хотите узнать, сколько будет 3,14159 / 6, то калькулятор вам очень поможет, а вы сможете задуматься о смысле этого ответа. Теоретически, чем больше функций в калькуляторе реализовано «из коробки», тем полезнее он должен быть.

Калькулятор для учеников, которые учатся считать

Но иногда калькуляторы чрезмерно усложняются, что не идёт им на пользу. В старших классах мне потребовалось обзавестись графическим калькулятором, и я раздобыл TI-84. На нём было примерно 40 кнопок, и для каждой было предусмотрено два-три режима работы. Я умел работать примерно с 20 из них, так что освоить этот инструмент стоило большого труда. Такая же история была и в первом классе, где даже на простейшем калькуляторе были такие клавиши, которых я на тот момент не понимал. Если бы потребовалось изобрести калькулятор для студентов, то он выглядел бы примерно как на рисунке выше.

На этом калькуляторе всего две кнопки. Одна сбрасывает значение в 1, а другая делает переход к следующему числу. Подобный инструмент как раз «не парил» бы детей, которые учатся считать. Мой пример кажется слегка глупым, но вы, в самом деле, можете купить калькулятор, устроенный именно так. Обычно он механический и называется «ручной счётчик».

Калькулятор, на котором можно записывать и складывать целые числа

Итак, вы освоили счёт, и теперь хотите научиться писать числа и складывать их. Идеальный калькулятор, который понадобится вам на данном этапе обучения, может иметь уже побольше кнопок, на рисунке выше.

Нам пока не требуется кнопок для вычитания, умножения и деления, чтобы справиться с нашими задачами. Если у вас будет пример на вычитание, скажем, «5 — 2», то всё равно можно убедиться в правильности ответа 3 и на таком калькуляторе, убедившись, что «3 + 2 = 5.» Аналогично, можно решать и примеры на умножение, последовательно складывая множители. Далее можно усовершенствовать калькулятор так, чтобы на нём выполнялись все арифметические действия, после того, как напрактикуетесь с показанным выше.

Теоретически, было бы отлично добавлять на наш калькулятор новые кнопки по мере того, как мы будем готовы пользоваться ими, но в таком случае понадобился бы целый ворох запчастей под рукой. Также возникла бы и другая проблема: наш калькулятор должен был бы поддерживать не только числа, но и другие типы данных. В алгебре некоторые выражения содержат только нечисловые символы, а в тригонометрии и дифференциальном исчислении часто приходится оперировать функциями, чтобы получать новые функции.

Расширяемые калькуляторы, поддерживающие множество типов данных – пример слегка натянутый, но именно таким инструментом вы и пользуетесь, когда пишете на высокоуровневом языке программирования. В Python зашита арифметика, предусмотрен математический модуль, а ещё можно подтянуть множество сторонних математических библиотек, чтобы ваше рабочее окружение стало мощнее (если захотите). Поскольку язык Python является Тьюринг-полным, на нём (в принципе) вычислимо всё, что может быть вычислено. Для этого потребуется лишь достаточно мощный компьютер, достаточно умная реализация, либо и то, и другое.

Наилучший способ изучить, как Python может помочь вам с математикой – закопаться в язык и начать его использовать. Самостоятельная проработка различных реализаций – отличный способ закрепить представления о новой концепции – и вот, у вас в арсенале появляется новый инструмент. Опробовав инструмент самостоятельно, вы всегда можете заменить его на вылизанную мейнстримовую библиотеку (если захотите). В любом случае, новые инструменты, которые вы исследуете или импортируете, подготовят вам почву для исследования ещё более масштабных идей.

Построение абстракций из функций

В программировании вышеописанный процесс называется «абстрагированием». Когда вы устаёте раз за разом складывать числа, вы создаёте абстракцию умножения – и так далее.
Важнейший из всех способов создания абстракций в программировании, который применим и в математике – это создание функции. Функция в Python – это способ многократно выполнять некую задачу, которая может принимать на вход одно или несколько значений, а потом давать вывод. Например:

def greet(name):
  print("Hello %s!" % name)

Так можно выдать множество приветствий при помощи краткого выразительного кода:

>>> for name in ["John","Paul","George","Ringo"]:
...   greet(name)
...
Hello John!
Hello Paul!
Hello George!
Hello Ringo!

Эта функция может быть полезна, но это не математическая функция. Математические функции всегда принимают входные значения и возвращают выходные, без побочных эффектов. В программировании те функции, которые обладают такими «математическими» свойствами, называются «чистыми функциями». Например, квадратная функция принимает число и возвращает произведение числа на эту функцию. Получаем 9. Это не значит, что тройка теперь изменилась и превратилась в девятку. Такую квадратную функцию можно изобразить как машину, во входную ячейку которой забрасывается число, а из выходной ячейки появляется результирующее число.

Это простая и удобная воображаемая модель. Что мне в ней особенно нравится – что функция изображается как вещь в себе. В математике, как и в Python, функции являются данными, и этими данными можно как манипулировать независимо, так и передавать их другим функциям.

Иногда математика кажется страшноватой именно из-за своей абстрактности. Помните, что в любой качественной программе абстракция вводится не просто так: она помогает сообщить более масштабные и сильные идеи. Если вам удалось ухватить эти идеи и выразить их в коде, то перед вами откроются захватывающие возможности.

С книгой, послужившей источником вдохновения, вы можете ознакомиться здесь.

Что такое 5 мод 5? (5 по модулю 5)

Вам нужно знать, что означает 5 по модулю 5? Может надо посчитать? В этом небольшом руководстве мы покажем вам, как точно вычислить мод числа. Вы также можете увидеть, что это называется модулем или модулем.

Хотите быстро научиться или показать учащимся, как считать 5 по модулю 5? Включи это очень быстрое и веселое видео прямо сейчас!

Так что же такое модуль или модуль? Проще говоря, по модулю — это математическая операция нахождения остатка при делении двух чисел. Если вы спрашиваете «что такое 5 мод 5?» тогда вам действительно нужно знать: «Каков остаток при делении 5 на 5?».

Существует множество причин, по которым вы хотели бы использовать модуль по модулю, в том числе проверка того, является ли число четным или нечетным, подсчет чего-либо определенное количество раз, и даже обычные часы в вашем доме будут использовать модуль для определения времени. .

Давайте рассмотрим два метода вычисления 5 по модулю 5. Мы назовем их методом по модулю и методом по модулю.

Примечание: первое число (5) называется Дивидендом, а второе число (5) называется Делителем. Когда вы делите дивиденд на делитель, ответ, который у вас остается, это частное. Это частное имеет целую числовую часть (называемую целым) и десятичную часть, которая называется дробной.

Метод по модулю

Сначала нужно разделить дивиденд на делитель:

5 / 5 =  1,00

Затем мы берем целую часть частного (1) и умножаем ее на делитель (5):

1 x 5 = 5

И, наконец, мы берем ответ на втором шаге и вычитаем его из Дивиденд для получения ответа на 5 по модулю 5:

5 — 5 = 0

Как видите, ответ на 5 по модулю 5 равен 0 .

Модульный метод

Модульный метод требует, чтобы мы сначала выяснили, каково наибольшее общее кратное Делителя (5), которое меньше или равно Делимому (5).

Мы видим, что числа, кратные 5, равны 0, 5, 10, 15 и т. д. Наибольшее кратное, меньшее или равное 5, равно 5. наибольшего кратного из Дивиденда и ответьте на вопрос «чему равно 5 по модулю 5?»:

5 — 5 = 0

Как мы видим, это тот же ответ, что и метод по модулю, и ответ равен 0 .

Надеюсь, вы поняли это краткое, но увлекательное путешествие по модулю и модульному методу вычислений. Если вам интересно, возьмите ручку и бумагу и сделайте пару таких упражнений сами, чтобы посмотреть, действительно ли вы чему-то научились.

Процитируйте, дайте ссылку или ссылку на эту страницу

Если вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большую услугу и используйте приведенный ниже инструмент, чтобы убедиться, что вы правильно ссылаетесь на нас, где бы вы его ни использовали. Мы очень ценим вашу поддержку!

• Что такое 5 mod 5?

• «Что такое 5 мод 5?». VisualFractions.com . По состоянию на 17 февраля 2023 г. http://visualfractions.com/calculator/modulo/what-is-5-mod-5/.

• «Что такое 5 мод 5?».

  VisualFractions.com , http://visualfractions.com/calculator/modulo/what-is-5-mod-5/. По состоянию на 17 февраля 2023 г.

• Что такое 5 mod 5?. VisualFractions.com. Получено с http://visualfractions.com/calculator/modulo/what-is-5-mod-5/.

Калькулятор модуля

Хотите решать больше задач на модуль? Введите свои числа ниже и нажмите рассчитать.

Введите задачу по модулю

Следующий расчет по модулю

• Что такое 6 mod 5?

Как найти наименьшее значение x в функции Mod

Вопрос 1:

Найдите наименьшее положительное значение x, такое что

(i) 71  ≡  x (mod 8)

Решение

71 — x = 8n

71 — x кратно 8

если x = 1, 71 — x = 70 не кратно 8,

Число, ближайшее к 71, равно 64 (кратно 8 ). Чтобы сделать 71 равным 64, мы должны вычесть 7,9.0003

Итак, значение x равно 7.

Следовательно, 7 — наименьшее число.

(ii) 78 + x ≡ 3 (mod 5)

Решение:

78 + x = 3 (мод 5)

78 + x — 3 = 5n

75 + x = 5n

Если x = 5, тогда 75 + 5 = 80 (которое кратно 5)

Следовательно, 5 — наименьшее число.

(iii) 89 ≡ (x + 3) (mod 4)

Решение:

89  =  (x + 3) (mod 4)

89 — x — 3  =  4n

86 — x = 4n

Если x = 2, то 86 — 2 =  84 (кратное 4)

Следовательно, 2 — наименьшее число.

(iv)  96 ≡ (x/7) (mod 5)

Решение:

96 ≡ (x/7) (mod 5)

Разделив 96 на 5, мы получим 1 как остаток

3 1 = x/7

x = 7

Следовательно, наименьшее значение x равно 7.

(v)  5x ≡  4 (mod 6)

Решение :

7 9 0 0 06 4

5x — 4  =  6n

Если x = 2, то 10 — 4  = 6 (которое кратно 6)

Следовательно, 2 — наименьшее число.

Вопрос 2 :

Если x сравнимо с 13 по модулю 17, то 7x -3 сравнимо с каким числом по модулю 17?

Решение:

Вопрос 3:

Решение 5x ≡ 4 (мод 6)

Решение:

5x — 4 =

n = (5x — 4)/6

N. =  [(6–1)x–(6–2)]/6 

n = 6(-1x + 2)/6

n = (-1x + 2)

Если x = 2, то n = -2 + 2  = 0

Если x = 8, то n = — 8 + 2 = -6

Если x = 14, то n = -14 + 2  = -12

Следовательно, значения x равны 2, 8, 14,…….

Вопрос 4 :

Решить 3x −2 ≡ 0 (mod 11)

Решение :

3x — 2 = 11n

n = (3x — 2)/11

, тогда -n = 8 00023 90 2)/11 = 2

(8 + 11) = 19

Если x = 19, то n = (57 — 2)/11  =  5

Следовательно, значения x равны 8, 19, 30 ……

Вопрос 5 :

Что такое время 100 часов после 7 утра?

Решение:

День состоит из 24 часов, разделив 100 на 24, мы получим 96 в частном и 4 в остатке.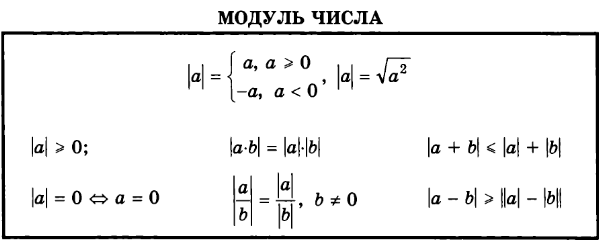

7 + 4  =  11:00

Вопрос 6:

Сколько времени за 15 часов до 23:00?

Решение:

11 — 15  =  -4

Не является делителем 12.

Найдите следующее целое число после  4, которое точно делится на 12. Это 12.  Теперь -4 можно записать как -4 = -12 + 8 

Следовательно, ответ 8 утра.

Вопрос 7:

Сегодня вторник. Мой дядя придет через 45 дней. В какой день придет мой дядя?

Решение:

Разделив 45 на 7, мы получим 6 в частном и 3 в остатке.

«0» соответствует «воскресенью»

«1» соответствует «понедельнику»

«2» соответствует «вторнику»

«3» соответствует «среде»

«4» соответствует «четвергу»

«5» соответствует «пятнице»

«6» соответствует «субботе»

2(вторник) + 45  =  47

Разделив 47 на 7, мы получим 5 в остатке.

5 — Пятница.

Следовательно, ответ пятница.

Вопрос 8 :

Докажите, что 2 ⁿ + 6×9 ⁿ всегда делится на 7 для любого натурального числа n.

Решение:

Если n = 1

= 2 ¹ + 6 × 9 ¹

= 2 + 54

= 56

56 делится на 7.

для n = 10003

56. , это правда. Пусть n = k

Предположим, что при n = k данное утверждение верно.

  =  2 ^k  + 6×9 ^k  делится на 7.

2 ^k  + 6×9 ^k    = 7m                   

Доказать для n = k + 1

  =  2 ^k+1 3 901 + 901 + 901 + 6 901 903

= 2 ^K ⋅ 2+ 6 × (9 ^K ⋅ 9)

= 2 ^K ⋅ 2+ 6 × ^K (9)

, применив значение 6 × ^K из (1)

  =  2 ^к  ⋅ 2 + (7m — 2 ^к )  (9)

  =  2 ^к  ⋅ 9 0 1 + (63m  — 2 9 0)⋅0003

= 2 ^K (2 — 9) + 63M

= 2 ^K (-7) + 63M

= 63M — 7 ⋅ 2 ^K

= 7 (9 — 2 9030 K )

Следовательно, он делится на 7.

Вопрос 9:

Найти остаток, когда 2 ⁸¹ делится на 17.

Решение:

2⁸

= 2⁸⁰ ac 2

2⁸

= 2⁸⁰ 2

=

=

=

2⁸⁸

= 2⁸⁰ 2

2⁸⁸

= 2⁸⁰ 2

. 2⁴ˣ²° ⋅ 2

= (2⁴)²⁰ ⋅ 2

= (16)²⁰ ⋅ 2

2⁸⁸/17 напоминание

= (-1) ²⁰ ⋅ 2

= 1 ⋅ 2

= 2

Вопрос 10:

Продолжительность полета из Ченная в Лондон-британские авиабилеты составляет приблизительно 110003

. часы. Самолет начинает свое путешествие в воскресенье в 23:30. Если время в Ченнаи на четыре с половиной часа опережает время в Лондоне, то найдите время в Лондоне, когда рейс приземлится в лондонском аэропорту.

Решение:

Поскольку время в пути составляет 11 часов, рейс прибудет в аэропорт Лондона в 23:30 + 11 часов = 10:30 по времени Ченнаи.

Но мы знаем, что время в Ченнаи опережает лондонское на 4:30, поэтому время посадки будет 10:30 — 4:30 = 6:30 по лондонскому времени.