Монету подбросили 3 раза какова вероятность того что орел выпадет 1 раз: Монету подбросили 3 раза. Какова вероятность того, что “орел” выпадет 3 раза. Ответы: а)…

Содержание

Файл: 2800 задач по теории вероятностей.pdf — Страницы №№156-160

Наши сайты:

Fizmathim.ru

reshaem-zadachi.ucoz.ru

Группа ВКонтакте

https://vk.com/fizmathim_resh

Перейти на

Решения заданий по теории вероятностей

2145. Производится 10 выстрелов по мишеням. Вероятность попадания при одном выстреле 0,9. Найти
вероятность того, что будет не менее 9 попаданий.

Решенная задача по теории вероятностей

2146. Производятся 7 выстрелов по мишени с вероятностью попадания при одном выстреле 2/10. Какова
вероятность, что будет ровно 4 попадания? Какое наиболее вероятное количество попаданий?

Решенная

задача по теории вероятностей

2147. Вероятность попадания стрелка в мишень при одном выстреле 0,8. Стрелок производит 6
выстрелов по мишени. Определить вероятность 4-х попаданий.

Решенная задача по теории вероятностей

2148. Вероятность попадания в мишень при 1 выстреле равна 0,9. Найти вероятность того, что при 10
выстрелах, попаданий будет: а) ровно 4; б) не менее 8.

Решенная задача по теории вероятностей

2149. Вероятность попадания стрелка в мишень при одном выстреле равна 9/11. Производится 9
выстрела. Найти вероятность того, что он промахнется не более двух раз.

Решенная задача по теории

вероятностей

2150. Вероятность попадания стрелка в мишень при одном выстреле равна 7/9. Производится 8
выстрелов. Найти вероятность того, что он промахнется не более 2 раз.

Решенная задача по теории

вероятностей

2151. Вероятность попадания стрелком в мишень при одном выстреле равна 0,81. Найти вероятность
того, что при 9 выстрелах будет от 3 до 8 попаданий.

Решенная задача по теории вероятностей

2152. Вероятность попаданием стрелков в мишень при одном выстреле равна 0,52. Найти вероятность
того, что при 12 выстрелах будет от 5 до 9 попаданий.

Решенная задача по теории вероятностей

2153. Вероятность попадания стрелком в мишень при одном выстреле 0,6. Найти вероятность того, что
мишень будет поражена хотя бы один раз при трех выстрелах.

Решенная задача по теории вероятностей

2154. Вероятность попадания стрелка в мишень при 1-м выстреле равна 0,5. Производится 5 выстрелов.
Найти вероятность того, что стрелок промахнется не более двух раз.

Решенная задача по теории

вероятностей

2155. Вероятность попадания стрелка в мишень при одном выстреле равна 4/6 = 2/3. Производится 7
выстрелов. Найти вероятность того, что стрелок промахнется не более двух раз.

Решенная задача по

теории вероятностей

2156. Вероятность попадания стрелка в мишень при одном выстреле равна 3/5. Производится 6
выстрелов. Найти вероятность того, что он промахнется не более двух раз.

Решенная задача по теории

вероятностей

2157. Вероятность попадания стрелка в мишень при одном выстреле равна 3/4. Производится 9
выстрелов. Найти вероятность того, что он промахнется не более двух раз

Решенная задача по теории

вероятностей

2158. Вероятность попадания стрелка в мишень при одном выстреле равна 11/13. Производится 9
выстрела. Найти вероятность того, что он промахнется не более двух раз?

Решенная задача по теории

вероятностей

2159. Производится 5 выстрелов в мишень. Вероятность попадания при каждом выстреле равна 3/4.
Найти вероятность того, что в мишени будет не менее трёх, но и не более четырёх пробоин. Найти
наивероятнейшее число попаданий и соответствующую ему вероятность.

Решенная задача по теории

вероятностей

Наши сайты:

Fizmathim.ru

reshaem-zadachi.ucoz.ru

Группа ВКонтакте

https://vk.com/fizmathim_resh

Перейти на

Решения заданий по теории вероятностей

2160.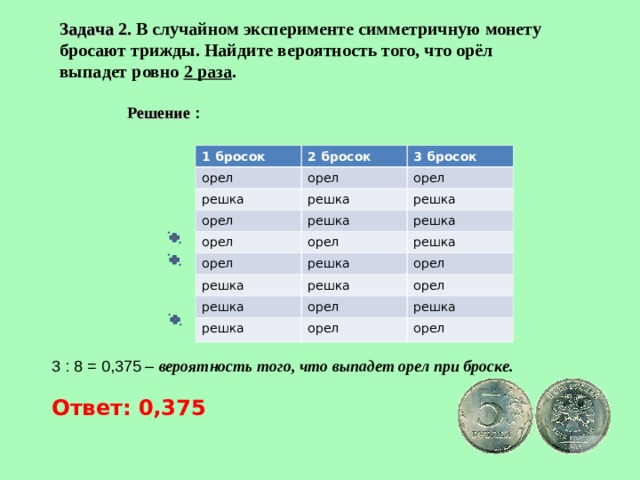 Вероятность попадания в цель при одном выстреле равна 0,7. Производится 4 выстрела. Найти
вероятность того, что цель будет поражена три раза.

Решенная задача по теории вероятностей

2161. Вероятность хотя бы одного попадания в цель при двух выстрелах равна 0,96. Найти а)
вероятность двух попаданий при трех выстрелах; б) вероятность не менее двух попаданий при трех
выстрелах.

Решенная задача по теории вероятностей

2162. Вероятность хотя бы одного попадания при двух выстрелах равна 0,84. Найти: а) наивероятнейшее
число попаданий в серии из семи выстрелов и модальную вероятность; б) что вероятнее: три попадания
при четырех выстрелах или шесть попаданий при восьми?

Решенная задача по теории вероятностей

2163. Вероятность хотя бы одного попадания в цель при 2 выстрелах равна 0,96. Найти: а) вероятность
попадания при одном выстреле, б) вероятность двух попаданий при 4 выстрелах.

Решенная задача по

теории вероятностей

2164. Вероятность хотя бы одного попадания при 4-х выстрелах составляет 0,59. Какова вероятность
попадания при одном выстреле?

Решенная задача по теории вероятностей

2165. Вероятность хотя бы одного попадания в мишень равна 0,81 при 9 выстрелах. Найдите
вероятность Р попадания при одном выстреле.

Решенная задача по теории вероятностей

2166. Вероятность хотя бы одного попадания при двух выстрелах равна 0,91. Найти вероятность
четырех попаданий при пяти выстрелах.

Решенная задача по теории вероятностей

2167. Найти вероятность того, что из шести выстрелов по мишени попаданий будет: а) пять, б) не менее
пяти, в) не более пяти, если в среднем поражение мишени составляет 80%.

Решенная задача по теории

вероятностей

2168. Производится 5 независимых выстрелов по некоторой цели. Вероятность попадания при одном
выстреле равна 0,8. Найти вероятность того, что будет хотя бы одно попадание.

Решенная задача по

теории вероятностей

2169. Производится 10 независимых выстрелов по цели, вероятность попадания в которую при одном
выстреле равна 0,2. Найти а) наиболее вероятное число попаданий; б) вероятность того, что число
попаданий будет не меньше 2 и не больше 4.

Решенная задача по теории вероятностей

2170. Производится 4 независимых выстрела по цели. Вероятность попадания при одном выстреле р =
0,25. Найти вероятности: а) двух попаданий; б) не менее двух попаданий.

Решенная задача по теории

вероятностей

2171. Стрелок производит 7 независимых выстрелов. Вероятность попадания в цель при одном выстреле
равна 0,8. Найдите вероятность того, что он попал 4 раза.

Решенная задача по теории вероятностей

2172. Вероятность попадания в цель при одном выстреле равна 0,18. Сделано 7 выстрелов. Найдите
вероятность того, что в цель попали менее трех раз.

Решенная задача по теории вероятностей

2173. Стрелок производит 5 независимых выстрелов, по мишени. Вероятность попадания в цель при
каждом выстреле p=0,3. Найдите вероятность того, что при пяти выстрелах произойдёт: 1) два
попадания; 2) хотя бы одно попадание.

Решенная задача по теории вероятностей

2174. Вероятность того, что стрелок попадёт в цель при одном выстреле, равна 0,7. Он производит 5
выстрелов. Какова вероятность, что в мишени окажется хотя бы одна пробоина?

Решенная задача по

теории вероятностей

Наши сайты:

Fizmathim.ru

reshaem-zadachi.ucoz.ru

Группа ВКонтакте

https://vk.com/fizmathim_resh

Перейти на

Решения заданий по теории вероятностей

2175. Вероятность хотя бы одного попадания в мишень при n=4 выстрелах равна р=18/25. Найдите Р
попаданий при одном выстреле.

Решенная задача по теории вероятностей

2176. Вероятность попадания в цель при одном выстреле равна р=47/50. Сделано n=7 выстрелов.
Найдите вероятность Р того, что в цель попали менее трех раз.

Решенная задача по теории вероятностей

2177. Вероятность попадания стрелком в цель равна р=1/17. Сделано n=170 выстрелов. Определите
наивероятнейшее число М попаданий в цель.

Решенная задача по теории вероятностей

2178. Вероятность попадания стрелком в цель равна 0,85. Сделано 7 выстрелов. Определить вероятность
наивероятнейшего числа промахов.

Решенная задача по теории вероятностей

2179. Вероятность хотя бы одного попадания в мишень при n = 13 выстрелах равна p = 0,71. Найдите
вероятность попадания при одном выстреле.

Решенная задача по теории вероятностей

2180. Вероятность хотя бы одного попадания в цель при трех выстрелах равна 0,992. Вычислите
вероятность попадания в цель при одном выстреле.

Решенная задача по теории вероятностей

2181. Вероятность попадания в цель хотя бы один раз при трёх выстрелах равна 0,992. Найти
вероятность одного попадания в цель при двух выстрелах.

Решенная задача по теории вероятностей

2182. Вероятность хотя бы одного попадания в цель при трех выстрелах равна 0,992. Найти вероятность
четырех попаданий при пяти выстрелах.

Решенная задача по теории вероятностей

2183. Вероятность попадания в цель при одном выстреле равна 0,97. Сделано 6 выстрелов. Найдите
вероятность того, что в цель попали менее трех раз.

Решенная задача по теории вероятностей

2184. Монету бросают 10 раз. Найти вероятность того, что герб выпадет: а) меньше 3-х раз; б) не менее
8 раз.

Решенная задача по теории вероятностей

2185. Монету бросают 10 раз. Найдите вероятность, что герб выпадет: 1) 4 раза; 2) не менее 4 раз.

Решенная задача по теории вероятностей

2186. Монета бросается 10 раз. Какова вероятность того, что орел выпадает 3 раза?

Решенная задача по

теории вероятностей

2187. Найти вероятность того, что герб выпадет не менее трех раз при десятикратном подбрасывании
монеты.

Решенная задача по теории вероятностей

2188. Монету подбрасывают 10 раз. Какова вероятность того, что при десятикратном подбрасывании
монеты герб выпадет 3 раза?

Решенная задача по теории вероятностей

2189. Монета брошена 10 раз. Найти вероятность того, что герб выпадет: а) от 4-х до 6-ти раз; б) хотя бы
один раз.

Решенная задача по теории вероятностей

2190. Найти вероятность того, что при 10-кратном бросании монеты герб выпадет ровно 5 раз.

Решенная

задача по теории вероятностей

2191. Монета подбрасывается 10 раз. Какова вероятность того, что герб выпадет 4 раза? Найти наиболее
вероятное число выпадений герба при 15 подбрасываниях монеты.

Решенная задача по теории

вероятностей

2192. Монету подбросили 10 раз. Какая вероятность того, что герб выпадет ровно 4 раза?

Решенная

Наши сайты:

Fizmathim.ru

reshaem-zadachi.ucoz.ru

Группа ВКонтакте

https://vk.com/fizmathim_resh

Перейти на

Решения заданий по теории вероятностей

задача по теории вероятностей

2193. Монета подбрасывается 5 раз. Найти вероятность того, что герб появится не менее 3-х раз.

Решенная задача по теории вероятностей

2194. Вычислить вероятность того, что при 5 подбрасываниях монеты герб выпадет: а) не менее трех
раз; б) ни одного раза.

Решенная задача по теории вероятностей

2195. Монета подбрасывается 5 раз. Найти вероятность того, что герб появится: а) все 5 раз, б) только 3
раза, в) хотя бы 3 раза.

Решенная задача по теории вероятностей

2196. Какова вероятность появления «решки» при пяти подбрасываниях правильной монеты: а) один
раз; б) хотя бы один раз; в) хотя бы три раза; г) ровно три раза?

Решенная задача по теории вероятностей

2197. Монета слегка изогнута, из-за чего вероятность выпадения герба равна 0,4. Какова вероятность
того, что при трех бросаниях герб выпадает два раза?

Решенная задача по теории вероятностей

2198. Какова вероятность того, что при пяти бросаниях монеты она три раза упадет гербом к верху?

Решенная задача по теории вероятностей

2199. Монета слегка изогнута, из-за чего вероятность выпадения герба равна 0,6. Найти вероятность
того, что при трёх бросаниях герб выпадет два раза.

Решенная задача по теории вероятностей

2200. Правильная монета подбрасывается 9 раз. Какова вероятность того, что герб выпадет хотя бы один
раз.

Решенная задача по теории вероятностей

2201. Монету подбрасывают 9 раз. Какова вероятность того, что при этом герб выпадет 2 раза?

Решенная задача по теории вероятностей

2202. Монету подбрасывают 9 раз. Какова вероятность, что при этом герб выпадет ровно 3 раза?

Решенная задача по теории вероятностей

2203. Монету подбрасывают 9 раз. Какова вероятность того, что герб выпадет а) 3 раза; б) не менее 3
раз; в) более 6 раз.

Решенная задача по теории вероятностей

2204. Монета подбрасывается 9 раз. Какова вероятность того, что «решка» выпадет а) 5 раз; б) не более 4
раз; в) нечетное число раз; г) хотя бы один раз?

Решенная задача по теории вероятностей

2205. Монету подбрасывают 12 раз. Какова вероятность того, что выпадет герб ровно 3 раза?

Решенная

задача по теории вероятностей

2206. Монету подбрасывают 12 раз. Найти вероятность того что герб выпадет. а) 5 раз б) ни разу в) хотя
бы один раз

Решенная задача по теории вероятностей

2207. Монету подбросили 8 раз. Какова вероятность того, что число выпавших гербов будет не меньше
двух, но не больше четырех?

Решенная задача по теории вероятностей

2208. Монету подбрасывают 10 раз подряд. Какова вероятность того, что выпадет 5 орлов?

Решенная

задача по теории вероятностей

2209. Монету подбросили 10 раз. Какова вероятность того, что число выпавших гербов будет не меньше
7, но не больше 9-и?

Решенная задача по теории вероятностей

2210. Монету подбросили 10 раз. Какова вероятность того, что выпало не менее 9 орлов?

Решенная

Наши сайты:

Fizmathim.ru

reshaem-zadachi.ucoz.ru

Группа ВКонтакте

https://vk.com/fizmathim_resh

Перейти на

Решения заданий по теории вероятностей

задача по теории вероятностей

2211. Монету подбрасывают 8 раз. Какова вероятность того, что 6 раз она упадет гербом вверх?

Решенная задача по теории вероятностей

2212. Монету подбрасывают 8 раз. Какова вероятность того, что она ни разу не упадет гербом вверх.

Решенная задача по теории вероятностей

2213. Монету подбрасывают восемь раз. Какова вероятность того, что она четыре раза упадет гербом
вверх?

Решенная задача по теории вероятностей

2214. Какова вероятность того, что при 8 бросаниях монеты герб выпадет 5 раз?

Решенная задача по

теории вероятностей

2215. Монету подбрасывают 8 раз. Какова вероятность того, что число выпавших гербов будет не
меньше 2-х, но не больше 4-х?

Решенная задача по теории вероятностей

2216. Монету бросают 8 раз. Какова вероятность того, что орел выпадет 5 раз?

Решенная задача по

теории вероятностей

2217. Монета подброшена 8 раз. Какова вероятность что «орел» выпадет не менее 5 раз?

Решенная

задача по теории вероятностей

2218. Монета бросается 8 раз. Найти вероятность того, что орел выпадет 7 раз.

Решенная задача по

теории вероятностей

2219. Монету бросают 8 раз. Какова вероятность того, что орел и решка выпадут поровну?

Решенная

задача по теории вероятностей

2220. Вероятность попадания в цель при каждом выстреле равна 0,005. Найти вероятность попадания в
цель не менее трех раз, если число выстрелов равно 800.

Решенная задача по теории вероятностей

2221. Вероятность попадания в цель при каждом выстреле равна 0,001. Найти вероятность попадания в
цель двух и более пуль, если число выстрелов ровно 5000.

Решенная задача по теории вероятностей

2222. Вероятность попадания в цель при одном выстреле равна 0,01. Какова вероятность того, что число
попаданий при 200 выстрелах составит не менее 5 и не более 10?

Решенная задача по теории

вероятностей

2223. Вероятность попадания в цель при каждом выстреле равна 0,002. Найти вероятность попадания в
цель двух и более пуль, если число выстрелов равно 3000.

Решенная задача по теории вероятностей

2224. Вероятность попадания в цель при каждом выстреле равна 0,03. Найти вероятность попадания в
цель двух и более пуль, если число выстрелов равно 100.

Решенная задача по теории вероятностей

2225. По цели производится 100 независимых выстрелов. Вероятность попадания в цель при одном
выстреле равна 0,04. Найти вероятность того, что в цель не попадет ни один снаряд.

Решенная задача по

теории вероятностей

2226. По некоторой цели производится 50 независимых выстрелов. Вероятность попадания в цель при
одном выстреле равна 0,04. Найти вероятность того, что в цель попадет: один снаряд, два снаряда, не
попадает ни одного снаряда.

Решенная задача по теории вероятностей

2227. Вероятность попадания стрелком в мишень при одном выстреле равна 0,41. Найти вероятность

математика — Вероятность выпадения минимум 2 орлов подряд из 4 попыток

Как правильно считать вероятности?

Подбрасываем монету, например, какова вероятность выпадения 2х орлов подряд из 4 попыток?

Когда задаешь подобный вопрос, то специалисты в комбинаторике, почему, начинают прикидывать, что всего успешных комбинаций 3: выпадение на позициях 1-2 2-3 3-4…. оорр роор рроо

Вроде как логично, но… почему они не учитывают, что при выпадении комбинация типа ооро тоже входит в множество, ибо и в этом случае мы достигли результата? А ведь учитывая все варианты расстановки, мы получим не 3 варианта, а 8!

Что не так в логике? Или что-то не так в постановке задачи?

Как получить эти 8 вариантов используя формулу?

Кроме оорр роор рроо подпадают под условие и варианты типа ооро ороо оооо и т.д.

подскажите логику и формулу расчета любого минимального количества подряд орла (k) из n попыток

математика
комбинаторика
теория-вероятностей

Предложу вариант решения задачи «вероятность выпадения минимум 2 орлов подряд из n попыток».

Будем обозначать орла и решку o и p, последовательность выпадений орла и решки за n попыток словом длины n (например, opoop — подходящее слово длины 5).

Рассмотрим:

a_n — количество слов длины n, в которых нет 2 подряд орлов И которые оканчиваются на o (для n = 3 имеем a_n = 2: opo, ppo)
b_n — количество слов длины n, в которых нет 2 подряд орлов И которые оканчиваются на
p (для n = 3 имеем b_n = 3: opp, pop, ppp)

Тогда заметим:

a_n+1 = b_n, потому что получить количество слов длины n+1, в которых нет 2 подряд орлов И которые оканчиваются на o, можно только добавлением o к словам длины n. Добавить o, не получив 2 подряд o, можно только к словам, оканчивающимся на p
b_n+1 = a_n + b_n, потому что получить количество слов длины n+1, в которых нет 2 подряд орлов И которые оканчиваются на p, можно только добавлением p к словам длины n. Добавить p
, не получив 2 подряд o, можно как к оканчивающимся на o словам, так и к оканчивающимся на p словам

Рассмотрим сумму:

a_n + b_n = <используем 1> = b_n-1 + b_n = <используем 2> = b_n-1 + a_n-1 + b_n-1 = <ещё раз используем 2> = (a_n-2 + b_n-2) + (a_n-1 + b_n-1)

Внезапно, получили, что последовательность сумм является последовательностью Фибоначчи. Рассмотрев базовые случаи (F_1 и F_2), по индукции получаем, что a_n + b_n = F_n+2. n, где phi = (1 + sqrt(5)) / 2

Примеры:

Для k орлов можно использовать последовательности Фибоначчи k-ого порядка, как указал участник @MBo в своём ответе. На Википедии как раз сказано, что «Последователь количеств строк из 0 и 1 длины m, содержащих не более n последовательных нулей, также является последовательностью Фибоначчи порядка n.»

и приводятся аналитические формулы для подсчёта членов таких последовательностей.

Забавно, что именно это можно решать, как блондинка из анекдота — «1/2, или получим, или нет!» 🙂 А если всерьез…

Решаем вашу задачу — 2 орла подряд из 4 выпадений. Проще всего просто расписать все варианты — их всего 16 — и посчитать:

oooo  ooop  oopo  oopp
opoo  opop  oppo  oppp
pooo  poop  popo  popp
ppoo  ppop  pppo  pppp

Как видите, нужных вариантов — 8. Итого — вероятность получить 2 орла подряд — 1/2.

Так просто и понятно, или вы хотите какое-то иное решение?…

Update

«По формуле»…

Для данного случая рассматриваем 2 орла начиная с 1, 2 и 3 выпадения. Вероятность такого выпадения — 1/4.

Для первого выпадения вероятность — 1/4.
Для второго выпадения вероятность 1/4, умноженная на вероятность, что первое выпадение решка (1/2) = 1/4*1/2 = 1/8.
Для третьего выпадения вероятность 1/4, умноженная на вероятность, что второе выпадение решка (1/2) = 1/4*1/2 = 1/8.
Итого общая вероятность = 1/4+1/8+1/8 = 1/2.

Так сойдет?

От противного: посчитаем, сколько вариантов длиной N не содержат двух орлов подряд.

Назовём эту функцию F(N)

Количество вариантов с последней решкой равно F(N-1) (решку можно добавить к любому хорошему варианту меньшей длины)

Количество вариантов с последним орлом равно F(N-2), т.

N — Fib(N) N O(N) 1 0 2 1 3 3 4 8 5 19

Для большего количества k орлов подобная (но более сложная) логика приведёт к использованию последовательностей Фибоначчи порядка k.

Например, для трёх орлов будет последовательность «трибоначчи»

1, 1, 2, 4, 7, 13, 24,

Например, для n=5 будет 32-24=8 вариантов с минимум тремя орлами, для n=4: 16-13=3 варианта

Для n=6,k=4 с использованием «тетраначчи» 64-56=8 вариантов

Зарегистрируйтесь или войдите

Регистрация через Google

Регистрация через Facebook

Регистрация через почту

Отправить без регистрации

Почта

Необходима, но никому не показывается

Отправить без регистрации

Почта

Необходима, но никому не показывается

Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки

ACT Math Help

Учащиеся, нуждающиеся в помощи ACT Math, получат большую пользу от нашей интерактивной программы. Мы разбираем все ключевые элементы, чтобы вы могли получить адекватную помощь по ACT Math. Имея под рукой обязательные концепции обучения и соответствующие практические вопросы, вы мгновенно получите много помощи по ACT Math. Получите помощь сегодня с нашей обширной коллекцией необходимой информации ACT Math.

По мере того, как колледжи становятся все более избирательными, вступительные тесты, такие как ACT, становятся все более важными. Математическая часть ACT, проверенная в нескольких разделах, направлена на то, чтобы понять, как учащиеся старших классов справляются с различными навыками алгебры, геометрии и предварительного исчисления. При надлежащем изучении математический раздел ACT становится более простым. Кроме того, поскольку у большинства учащихся первоначальные проблемы с выполнением разделов в указанные сроки, свободное владение материалом полезно для повышения эффективности. Нужны ли вам лучшие репетиторы по математике ACT в Атланте, репетиторы английского языка ACT в Хьюстоне или лучшие репетиторы по математике ACT в Сан-Франциско, работа с профессионалом может вывести ваше обучение на новый уровень.

Учащиеся, сдающие ACT, должны понимать большое количество тем, в том числе:

Предварительная алгебра: темы в этом разделе включают числовые ряды, десятичные дроби, дроби, квадратные корни, экспоненты, научное представление, пропорции, абсолютное значение и начальное значение. вероятность. Эти навыки имеют решающее значение для понимания, поскольку они составляют основу знаний, необходимых в дальнейшем.

Алгебра: вычисление алгебраических выражений посредством подстановки, выражения факториальных отношений и решения квадратных уравнений.

Координатная геометрия: распознавание и определение линий, плоскостей, сегментов, многочленов, окружностей и других кривых; неравенства; определение уклона; и нахождение середины параллельных и перпендикулярных прямых и отрезков.

Плоская геометрия: Параллельные и перпендикулярные линии составляют основу плоской геометрии. Учащихся просят понять взаимосвязь между различными углами, определяемыми пересечением параллельных прямых. Кроме того, учащиеся узнают, как изображать треугольники, прямоугольники и другие геометрические фигуры в системе координат и использовать такие процессы, как перенос, вращение и отражение, для перемещения этих фигур. Наконец, учащиеся изучают основы корректуры двух столбцов и абзацев. Доказательство конгруэнтности и сходства между треугольниками является основной конечной точкой планиметрии, поскольку аспекты системы координат, параллельных линий и пересекающихся линий требуют объединения в одну задачу.

Тригонометрия: Понимание прямых углов и тригонометрических функций, таких как синус, косинус и тангенс, проверяется в разделе тригонометрии. Студентов часто просят найти значение неизвестной переменной, для чего требуются базовые знания функций тригонометрии.

Успех в математическом разделе ACT часто требует визуализации проблемы. Для учащихся, начинающих подготовку к ACT, это часто сложные наборы навыков, на формирование которых требуется время. Начиная с практических моделей, таких как деревянные блоки различной формы, или используя цветную плотную бумагу для обозначения частей формы или линии, вы можете создать визуальное представление, на основе которого можно построить необходимую информацию. Вы также можете воспользоваться репетиторством по математике ACT или бесплатной цифровой книгой для подготовки к ACT, предлагаемой репетиторами Varsity Tutors.

Тем не менее, основным средством достижения успеха в математическом разделе ACT является свободное время для изучения и решения практических задач. Студенты должны планировать просмотр заблаговременно и просматривать содержание, прежде чем пытаться решить большое количество практических задач. Репетиторы ACT по математике, которые работают со студентами, часто могут предоставить наилучшие возможности для обучения, поскольку у них есть обширные стратегии сдачи тестов, которые оказались полезными в прошлом, и многочисленные практические задачи и отрывки. Когда вы будете готовы приступить к решению задач ACT Math, вы можете воспользоваться бесплатными ресурсами ACT Math от Varsity Tutors, в том числе карточками ACT Math, организованными по принципу . Эта организация позволяет вам сосредоточиться только на концепциях, которые вы считаете наиболее сложными, и наиболее эффективно использовать свое время при изучении раздела ACT Math. Каждая задача ACT Math поставляется с полным и подробным объяснением ответа, поэтому, если вы пропустите какой-либо из них, вы сможете выяснить, в какой части ответа на задачу вы допустили ошибку. Ознакомившись с тем, какие виды математики рассматриваются в разделе ACT Math, и используя бесплатные практические задачи ACT Math от Varsity Tutors для повторения этих понятий, вы сможете подготовиться к контрольному дню в кратчайшие сроки!

Биномиальное распределение

Автор(ы)

Дэвид М. Лейн

Предпосылки

Распределения, Базовая вероятность, вариативность

Цели обучения

Определение биномиальных результатов
Вычислить вероятность получения X успешных попыток в N испытаниях
Вычисление кумулятивных биномиальных вероятностей
Найдите среднее значение и стандартное отклонение биномиального распределения

При подбрасывании монеты возможны два исхода: головы и хвосты. Каждый исход имеет фиксированную вероятность, одинаковую от суда к суду. В случае с монетами орел и решка каждый имеют одинаковую вероятность 1/2. В общем, бывают ситуации в котором монета смещена, так что орел и решка имеют разные вероятности. В настоящем разделе мы рассматриваем вероятность распределения, для которых есть только два возможных исхода с фиксированные вероятности, суммирующиеся с единицей. Эти распределения называются биномиальными дистрибутивы.

Простой пример

Четыре возможных исхода, которые могут произойти, если вы дважды подбросил монету, перечислены ниже в Таблице 1. Обратите внимание, что четыре исхода равновероятны: каждый имеет вероятность 1/4. К см. это, обратите внимание, что броски монеты независимы (ни влияет на другое). Следовательно, вероятность выпадения орла на Flip 1 а голова на флипе 2 есть произведение P(H) и P(H), т. е. 1/2 х 1/2 = 1/4. Тот же расчет применим к вероятности головы на перевороте 1 и хвоста на перевороте 2. Каждый из них равен 1/2 x 1/2. = 1/4.

Таблица 1. Четыре возможных исхода.

Исход	Первый флип	Второй флип
1	Головы	Головы
2	Головы	хвосты
3	хвосты	Головы
4	хвосты	хвосты

Можно классифицировать четыре возможных исхода по количеству выпавших голов. Номер может быть два (Исход 1), один (Исход 2 и 3) или 0 (Исход 4). Вероятности этих возможностей показаны в таблице 2 и на рис. 1. Поскольку два исхода представляют случай в котором при двух бросках выпадает только одна голова, вероятность этого события равно 1/4 + 1/4 = 1/2. Таблица 2 резюмирует ситуация.

Таблица 2. Вероятность выпадения 0, 1 или 2 решек.

Количество головок	Вероятность
0	1/4
1	1/2
2	1/4

Рисунок 1. Вероятности 0, 1 и 2 головы.

Рисунок 1 представляет собой дискретное распределение вероятностей: Он показывает вероятность для каждого из значений на оси X. Определив голову как «успех», на рис. 1 показана вероятность из 0, 1 и 2 успехов для двух испытаний (флипов) для события, которое имеет вероятность 0,5 успеха в каждом испытании. Этот делает рис. 1 примером биномиального распределения.

Формула биномиальных вероятностей

Биномиальное распределение состоит из вероятностей каждого из возможных чисел успехов в N испытаниях для независимых событий, каждое из которых имеет вероятность π (греческая буква пи) происходящего. Для примера подбрасывания монеты N = 2 и π = 0,5. Формула для биномиальное распределение показано ниже:

, где P(x) — вероятность x успехов. N испытаний, N — количество испытаний, а π — вероятность успеха в данном испытании. Применяя это к примеру с подбрасыванием монеты,

Если дважды подбросить монету, какова вероятность получения одной или нескольких голов? Поскольку вероятность получения ровно одна голова равна 0,50, а вероятность получить ровно две решки 0,25, вероятность выпадения одной и более решек 0,50 + 0,25 = 0,75.

Теперь предположим, что монета смещена. Вероятность головок всего 0,4. Какова вероятность выпадения головы хотя бы один раз за два броска? Подставляя в общую формулу выше, вы должны получить ответ 0,64.

Кумулятивные вероятности

Подбрасываем монету 12 раз. Какова вероятность что мы получаем от 0 до 3 голов? Ответ находится путем вычисления вероятность выпадения ровно 0 орлов, ровно 1 орла, ровно 2 головы, а ровно 3 головы. Вероятность получения от 0 до 3 голов — это сумма этих вероятностей. Вероятности составляют: 0,0002, 0,0029, 0,0161 и 0,0537. Сумма вероятностей составляет 0,073. Расчет кумулятивных биномиальных вероятностей может быть довольно утомительным. Поэтому мы предоставили биномиальный калькулятор для облегчения расчета этих вероятностей.

Биномиальный Калькулятор

Среднее и стандартное отклонение биномиальных распределений

Рассмотрим эксперимент с подбрасыванием монеты, в котором вы подбросил монету 12 раз и записал количество выпавших орлов. Если вы проводил этот эксперимент снова и снова, что бы среднее количество голов быть? В среднем вы ожидаете половину подбрасывает монету, чтобы выпал орел. Поэтому среднее количество голов будет 6. В общем, среднее значение биномиального распределения с параметры N (количество испытаний) и π (вероятность успеха в каждом испытании):

мк = Nπ

, где μ — среднее значение биномиального распределения.

Файл: 2800 задач по теории вероятностей.pdf — Страницы №№156-160

математика — Вероятность выпадения минимум 2 орлов подряд из 4 попыток

Зарегистрируйтесь или войдите

Отправить без регистрации

Отправить без регистрации

ACT Math Help

Биномиальное распределение

Добавить комментарий Отменить ответ