N 2 180: Сумма углов выпуклого n-угольника вычисляется по формуле 180°(n-2). Найдите n-число углов ,если сумма всех углов…

alexxlab / / Разное

Содержание

Правильный многоугольник. Формулы, признаки и свойства правильного многоугольника

Навигация по странице: Определение правильного многоугольника Признаки правильного многоугольника Основные свойства правильного многоугольника Правильный n-угольник — формулы       — длина стороны       — радиус вписанной окружности       — радиус описанной окружности       — площадь       — периметр       — угол между сторонами Правильный треугольник Правильный четырехугольник Правильный шестиугольник Правильный восьмиугольник

Определение. Правильный многоугольник — это многоугольник, у которого все стороны и углы одинаковые.

Многоугольником называется часть площади, которая ограничена замкнутой ломаной линией, не пересекающей сама себя.

Многоугольники отличаются между собой количеством сторон и углов.

Рис. 1		 Рис.2

Признаки правильного многоугольника

Многоугольник будет правильным, если выполняется следующее условие:

Все стороны и углы одинаковы:

a1 = a2 = a3 = … = an-1 = an

α1 = α2 = α3 = … = αn-1 = αn


Основные свойства правильного многоугольника

1. Все стороны равны:

a1 = a2 = a3 = … = an-1 = an

2. Все углы равны:

α1 = α2 = α3 = … = αn-1 = αn

3. Центр вписанной окружности Oв совпадает з центром описанной окружности Oо, что и образуют центр многоугольника O

4. Сумма всех углов n-угольника равна:

180° · (n — 2)

5. Сумма всех внешних углов n-угольника равна 360°:

β1 + β2 + β3 + … + βn-1 + βn = 360°

6. Количество диагоналей (Dn) n-угольника равна половине произведения количества вершин на количество диагоналей, выходящих из каждой вершины:

Dn = n · (n — 3)
2

7. В любой многоугольник можно вписать окружность и описать круг при этом площадь кольца, образованная этими окружностями, зависит только от длины стороны многоугольника:

S = πa2
4

8. Все биссектрисы углов между сторонами равны и проходят через центр правильного многоугольника O


Правильный n-угольник — формулы

Формулы длины стороны правильного n-угольника

1. Формула стороны правильного n-угольника через радиус вписанной окружности:

a = 2r · tg180°
n
a = 2r · tgπ
n

2. Формула стороны правильного n-угольника через радиус описанной окружности:

a = 2 R · sin180°
n
a = 2 R · sinπ
n

Формула радиуса вписанной окружности правильного n-угольника

Формула радиуса вписанной окружности n-угольника через длину стороны:

r = a : (2tg180°)
n
r = a : (2tgπ)
n

Формула радиуса описанной окружности правильного n-угольника

Формула радиуса описанной окружности n-угольника через длину стороны:

R = a : (2sin180°)
n
R = a : (2sinπ)
n

Формулы площади правильного n-угольника

1. Формула площади n-угольника через длину стороны:

S = na2 · ctg180°
4n

2. Формула площади n-угольника через радиус вписанной окружности:

S = nr2 · tg180°
n

3. Формула площади n-угольника через радиус описанной окружности:

S = nR2 · sin360°
2n

Формула периметра правильного многоугольника:

Формула периметра правильного n-угольника:

P = na

Формула определения угла между сторонами правильного многоугольника:

Формула угла между сторонами правильного n-угольника:

αn = n — 2 · 180°
n


Рис. 3

Правильный треугольник

Формулы правильного треугольника:

1. Формула стороны правильного треугольника через радиус вписанной окружности:

a = 2r √3

2. Формула стороны правильного треугольника через радиус описанной окружности:

a = R√3

3. Формула радиуса вписанной окружности правильного треугольника через длину стороны:

r = a√3
6

4. Формула радиуса описанной окружности правильного треугольника через длину стороны:

R = a√3
3

5. Формула площади правильного треугольника через длину стороны:

S = a2√3
4

6. Формула площади правильного треугольника через радиус вписанной окружности:

S = r2 3√3

7. Формула площади правильного треугольника через радиус описанной окружности:

S = R2 3√3
4

8. Угол между сторонами правильного треугольника:

α = 60°


Рис.4

Правильный четырехугольник

Правильный четырехугольнику — квадрат.

Формулы правильного четырехугольника:

1. Формула стороны правильного четырехугольника через радиус вписанной окружности:

a = 2r

2. Формула стороны правильного четырехугольника через радиус описанной окружности:

a = R√2

3. Формула радиуса вписанной окружности правильного четырехугольника через длину стороны:

r = a
2

4. Формула радиуса описанной окружности правильного четырехугольника через длину стороны:

R = a√2
2

5. Формула площади правильного четырехугольника через длину стороны:

S = a2

6. Формула площади правильного четырехугольника через радиус вписанной окружности:

S = 4 r2

7. Формула площади правильного четырехугольника через радиус описанной окружности:

S =  2 R2

8. Угол между сторонами правильного четырехугольника:

α = 90°

Смотрите также формулы и свойства квадрата


Правильный шестиугольник

Формулы правильного шестиугольника:

1. Формула стороны правильного шестиугольника через радиус вписанной окружности:

a = 2√3r
3

2. Формула стороны правильного шестиугольника через радиус описанной окружности:

a = R

3. Формула радиуса вписанной окружности правильного шестиугольника через длину стороны:

r = a√3
2

4. Формула радиуса описанной окружности правильного шестиугольника через длину стороны:

R = a

5. Формула площади правильного шестиугольника через длину стороны:

S = a2 3√3
2

6. Формула площади правильного шестиугольника через радиус вписанной окружности:

S = r2 2√3

7. Формула площади правильного шестиугольника через радиус описанной окружности:

S = R2 3√3
2

8. Угол между сторонами правильного шестиугольника:

α = 120°


Правильный восьмиугольник

Формулы правильного восьмиугольника:

1. Формула стороны правильного восьмиугольника через радиус вписанной окружности:

a = 2r · (√2 — 1)

2. Формула стороны правильного восьмиугольника через радиус описанной окружности:

a = R√2 — √2

3. Формула радиуса вписанной окружности правильного восьмиугольника через длину стороны:

r = a(√2 + 1)
2

4. Формула радиуса описанной окружности правильного восьмиугольника через длину стороны:

R = a√4 + 2√2
2

5. Формула площади правильного восьмиугольника через длину стороны:

S = a2 2(√2 + 1)

6. Формула площади правильного восьмиугольника через радиус вписанной окружности:

S = r2 8(√2 — 1)

7. Формула площади правильного восьмиугольника через радиус описанной окружности:

S = R2 2√2

8. Угол между сторонами правильного восьмиугольника:

α = 135°

Все таблицы и формулы

Углы треугольника равны 180? – Обзоры Вики

Сумма углов треугольника равна 180°доказательство.

Отсюда, почему треугольник равен 180? Сумма углов треугольника равна 180 градусов, потому что один внешний угол равен сумме двух других углов в треугольнике. Другими словами, два других угла в треугольнике (те, которые в сумме образуют внешний угол) должны объединиться с третьим углом, чтобы получился угол 180.

Сумма треугольников равна 180 или 360? Сумма углов треугольника всегда будет равна 180°. Сумма углов четырехугольника равна 360°, а треугольник можно получить, разрезав четырехугольник пополам от угла к углу. Поскольку треугольник по существу является половиной четырехугольника, его угловая мера также должна быть равна половине. Половина 360° составляет 180°.

Кроме того, все ли углы в сумме составляют 180? Знаете ли вы, что если сложить количество градусов в трех углах любого треугольника, то в сумме всегда получится одно и то же число? Это верно!

Какие углы в сумме дают 90? Два угла называются дополнительный когда их меры складываются в 90 градусов.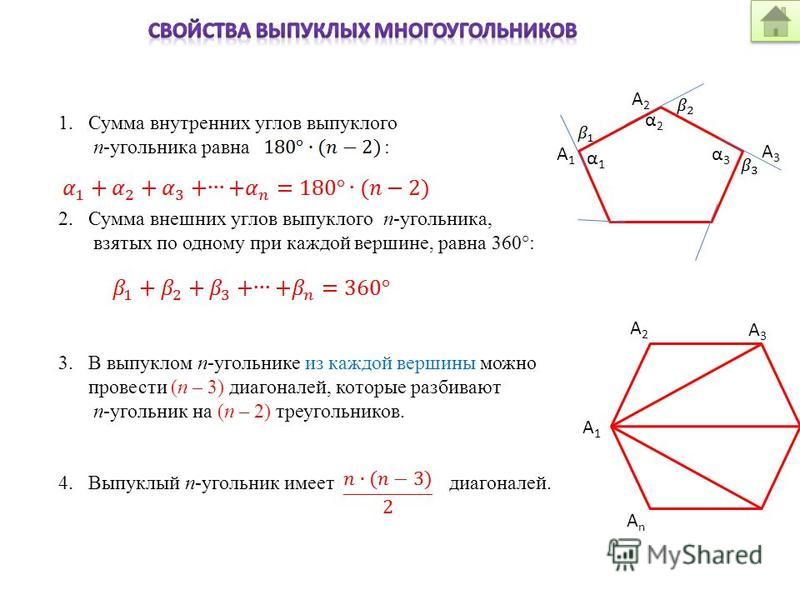

Как найти гипотенузу?

Как найти гипотенузу равнобедренного прямоугольного треугольника?

  1. Найдите длину одной из сторон без гипотенузы.
  2. Возведите в квадрат длину стороны.
  3. Удвойте результат предыдущего шага.
  4. Корень квадратный из результата шага 3. Это длина гипотенузы.

Какой угол равен 180 градусам? Прямой угол есть угол, равный 180 градусам.

треугольник равен 90? Сумма внутренних углов треугольника всегда равна 180 градусам. Нам дан угол, и, поскольку он указан как прямоугольный треугольник мы знаем, что угол равен 90 градусов.

треугольник равен 160?

Сумма углов в треугольнике. Почему треугольник всегда равен 180 градусам? … У этого прямоугольника четыре угла по 90 градусов в сумме дают 360 градусов. Так как треугольники конгруэнтный каждый треугольник имеет вдвое меньше градусов, а именно 180.

Также прямоугольник 180? В общем случае сумма внутренних углов любого многоугольника (окружности не являются многоугольниками) будет равна 180°(n-2), где n — количество сторон многоугольника.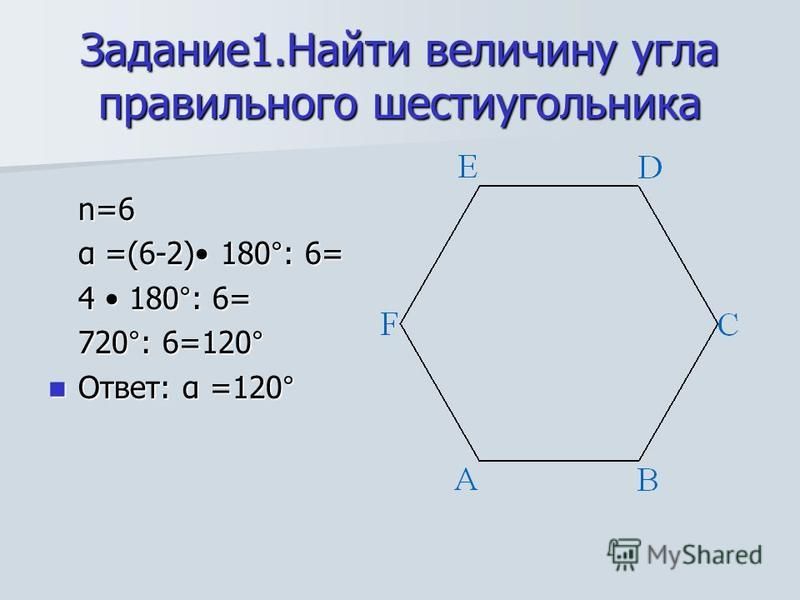 Таким образом, для треугольника n = 3 треугольник имеет сумму 180 ° (3–2) = 180 °. Прямоугольный: 180°(4–2) = 360 °. Шестиугольник 180°(6–2) = 720°.

Какой угол равен 180 градусам?

Углы, составляющие 180 градусов (θ = 180 °), известны как прямые углы. Углы между 180 и 360 градусами (180° < θ < 360°) называются рефлекторными углами.

Могут ли углы быть больше 180? Тупой угол – угол больше 90 градусов и меньше 180 градусов. Прямой угол – угол, равный ровно 180 градусам. Угол рефлекса – Угол больше 180 градусов и меньше 360 градусов.

Какой угол 470?

Угол находится в третий квадрант.

Что такое дополнительный угол 22?

Дополнение 22° — это угол, который при сложении со 22° образует прямой угол (180° ).

Как решить прямоугольный треугольник?

Ключевые моменты

  1. Теорема Пифагора, a2 + b2 = c2, a 2 + b 2 = c 2, используется для определения длины любой стороны прямоугольного треугольника. 2 а2+b2=с2.

    Является ли этот треугольник прямоугольным? Определить, есть ли в треугольнике прямой угол, можно с помощью теоремы Пифагора. Если квадраты двух более коротких сторон в сумме составляют квадрат гипотенузы, треугольник содержит прямой угол.

    Как найти угол 90 градусов?

    геометрия — Почему сумма внутренних углов в выпуклом многоугольнике равна $(n-2)\cdot 180$

    спросил

    Изменено 9 месяцев назад

    Просмотрено 8к раз

    $\begingroup$

    пару дней назад на уроках математики в средней школе я узнал, что сумма внутренних углов выпуклого многоугольника равна:

    $Z$ = сумма углов, $n$ = количество сторон в многоугольнике

    $Z=(n-2)\cdot 180$

    Может ли кто-нибудь помочь мне понять эту формулу и почему она такая ?

    • геометрия

    $\endgroup$

    3

    $\begingroup$

    Вот полезная диаграмма:

    Сумма всех углов во всех треугольниках равна сумме внутренних углов многоугольника. Обратите внимание, что у фигуры $7$ сторон, и мы можем разместить внутри $5$ треугольников, сумма углов каждого из которых равна $180$ градусам. Это обобщается до $n$-стороннего многоугольника, который может вместить в себя $n-2$ треугольников, как показано выше. Тогда сумма углов должна = $(n-2)*180$ градусов

    $\endgroup$

    1

    $\begingroup$

    Один из способов понять это — посмотреть на внешние углы при обходе многоугольника в одну сторону — внешний угол — это угол, повернутый при прохождении каждой вершины. (Например, в правильном десятиугольнике внешний угол в каждой вершине равен $36°$.) Ясно, что сумма таких углов $\{\epsilon_i\}$ равна $360°$, так как вы возвращаетесь на исходное ребро, повернув полностью вокруг полигона. Каждый внутренний угол $\{\theta_i\}$ равен $\theta_k=180°-\epsilon_k$, так что у вас есть $$\sum^n \theta_i = \sum^n (180°-\epsilon_i) = n\cdot180° — \sum^n \epsilon_i = n \cdot 180°-360° = (n-2)180°$ $ 9{\circ} $ из треугольника, образованного исходным ребром и двумя новыми.

    0$, что соответствует формуле. 9{\circ}$.

    $\endgroup$

    почему в формуле (n-2)180 нужно вычесть 2 (это формула суммы внутренних углов многоугольников).

    Полигоны геометрии

    Брук С.

    спросил 13.11.17

     Я пытаюсь объяснить формулу (n-2)180, используемую для нахождения суммы внутренних углов многоугольников, я понимаю формулу, но мне просто интересно, почему она минус 2? Я знаю, что вы также можете разделить многоугольник на 3 треугольника и сложить суммы, чтобы получить 540, но почему 3 треугольника? Почему не 5 треугольников?

    Подписаться І 2

    Подробнее

    Отчет

    1 ответ эксперта

    Лучший Новейшие Самый старый

    Автор: ЛучшиеНовыеСамыеСтарые

    Мэтью С. ответил 13.11.17

    Репетитор

    5,0 (65)

    Репетитор по математике и естественным наукам — выпускник Массачусетского технологического института, Google — доступен в кратчайшие сроки!

    Об этом репетиторе ›

    Об этом репетиторе ›

    Это правда, что это сбивает с толку. Если вы рисуете все треугольники, исходящие из центра, нужно понимать, что (n-2) не потому, что существует n-2 треугольников. Если вы нарисуете это таким образом, очевидно, что треугольников будет n. Вместо этого -2 выходит из математики.

     

    Давайте рассмотрим, что происходит, когда вы рисуете эти треугольники. Все они выходят из одной точки в центре, всего n. Сумма углов во всех этих треугольниках равна 180*n. Мы знаем, что это не может быть правильным значением суммы внутренних углов, потому что мы видим, что каждый треугольник имеет один из углов в центре. Мы бы явно пересчитали, включив эти центральные углы.

     

    Но заметим кое-что. Поскольку все эти треугольники встречаются в центре, мы можем нарисовать полный круг из углов, где они встречаются. Это означает, что все эти углы в центре в сумме составляют 360 градусов, поэтому, если мы вычтем 360, у нас останутся только углы по краям. Это означает, что наша сумма будет n*180 — 360 = n*180 — 2*180 = (n-2)*180

     

     

    Стоит отметить, что есть еще один способ рисования треугольников, который создает только n -2 треугольника, все углы которых лежат в вершинах многоугольника. Возьмите сторону вашего многоугольника и проведите линию от одной из вершин этой стороны к соседней другой. (Например, если у вас есть пентаграмма ABCDE, возьмите сторону AB и добавьте линию AC.) Теперь из этой новой вершины проведите линию к соседу вершины, с которой вы ее только что соединили. (Соедините C с E) Повторяйте, пока не соедините вершину с ее собственным соседом (конечно, с которым она уже соединена).

    No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *