На рисунке 3 буквы а имеют одинаковую форму: помогите пжна рисунке у буквы (а) имеют одинаковую форму.1)Во сколько раз третья буква больше первой2) Во сколько раз вторая буква меньше третьей?

Содержание

Векторы, графическое изображение векторов, величина вектора, направление вектора

Векторы могут быть графически представлены направленными отрезками. Длина выбирается по определенной шкале, чтобы обозначить величину вектора, а направление отрезка представляетнаправление вектора. Например, если мы примем, что 1 см представляет 5 км/час, тогда северо-восточный ветер со скоростью 15 км/час будет представлен направленным отрезком длиной 3 cм, как показано на рисунке.

Вектор на плоскости это направленный отрезок. Два вектора равны если они имеют одинаковуювеличину и направление.

Рассмотрим вектор, нарисованный из точки A к точке B. Точка называется начальной точкой вектора, а точка B называется конечной точкой. Символическим обозначением для этого вектора есть (читается как “вектора AB”). Векторы также обозначается жирными буквами, такими как U, V и W. Четыре вектора на рисунке слева имеют одинаковую длину и направление. Поэтому они представляют

равные веторы; то есть,

В контексте векторов мы применяем = чтобы обозначить их равность.

Длина, или величина выражается как ||. Для того, чтобы определить, равны ли векторы, мы находим их величины и направления.

Пример 1 Векторы u, , w показаны на рисунке внизу. Докажите, что u = = w.

Решение Сначала мы находим длину каждого вектора с использованием формулы расстояния:
|u| = √[2 — (-1)]² + (4 — 3)² = √9 + 1 = √10,
|| = √[0 — (-3)]² + [0 — (-1)]² = √9 + 1 = √10,
|w| = √(4 — 1)² + [-1 — (-2)]² = √9 + 1 = √10.
Отсюда
|u| = | = |w|.
Векторы u, , и w, как видно из рисунка, вроде бы имеют одно и то же направление, но мы проверим их наклон. Если прямые, на которых они находятся, имеют одинаковые наклоны, то векторы имеют одно и то же направление. Рассчитываем наклоны:
Так как u, , и w имеют равные величины и одно и то же напраывление,

u = = w.

Имейте в виду, что равность векторов требует только одинаковой величины и одинакового направления, а не расположения в одном месте. На самом верхнем рисунке — пример равности векторов.

Предположим, что человек делает 4 шага на восток, а затем 3 шага на север. Тогда человек будет в 5 шагах от начальной точки в направлении, показанном слева. Вектор в 4 единицы длиной и с направление направо представляет 4 шага на восток и вектор 3 единицы длиной направление вверх представляет 3 шага на север. Сумма двух этих векторов есть вектор 5-ти шагов величины и в показанном направлении. Сумма также называется результирующим двух векторов.

В общем, два ненулевых вектора u и v могут быть сложены геометрически расположением начальной точки вектора v в конечную точку вектора u, и затем нахождением ветора, который имеет ту же самую начальную точку, что и вектор u и ту же самую конечную точку что и вектор v, как показано на рисунке внизу.

Суммой есть вектор, представленный направленным отрезком из точки A вектора u в конечную точку C вектора v.

Таким образом, если u = и v = , тогда
u + v = + =

Мы также можем описать сложение векторов как совместное размещение начальных точек векторов, построением параллелограмма и нахождением диагонали параллелограмма. (на рисунке внизу.) Это сложение иногда называется как правило параллелограмма сложения векторов. Векторное сложение коммутативно. Как показано на рисунке, оба вектора u + v и v + u представлены одним и тем же направленным отрезком.

Если две силы F₁ и F₂ действуют на один объект, результирующая сила есть сумма F₁ + F₂ этих двух отдельных сил.

Пример Две силы в 15 ньютонов и 25 ньютонов действуют на один объект перпендикулярно друг другу. Найдите их сумму, или результирующую силу и угол, которая она образовывает с большей силой.

Решение Нарисуем условие задачи, в этом случае — прямоугольник, используя v или для представления результирующей. Чтобы найти ее величину, используем теорему Пифагора:
|v|² = 15² + 25² Здесь |v| обозначает длину или величину v.
|v| = √15² + 25²
|v| ≈ 29,2.
Чтобы найти направление, отметим, что так как OAB есть прямым углом,
tanθ = 15/25 = 0,6.
Используя калькулятор, мы находим θ, угол, который большая сила образует с результирующей силой:
θ = tan^{— 1}(0,6) ≈ 31°
Результирующая имеет величину 29,2 и угол 31° с большей силой.

Пилоты могут корректировать направление их полёта, если есть боковой ветер. Ветер и скорость самолёта могут быть изображены как веторы.

Пример 3. Скорость самолёта и направление. Самолёт движется по азимуту 100° со скоростью 190 км/час, в то время как скорость ветра 48 км/ч, а его азимут — 220°. Найдите абсолютную скорость самолета и направление его движения с учетом ветра.

Решение Сначала сделаем рисунок. Ветер представлен и вектор скорости самолета есть . Результирующий вектор скорости есть v, сумма двух векторов. Угол θ между v и называется угол сноса.

Обратите внимание, что величина COA = 100° — 40° = 60°. Тогда величина CBA также равна 60° (противоположные углы параллклограмма равны). Так как сумма всех углов параллелограмма равна 360° и COB и OAB имеют одну и ту же величину, каждый должен быть 120°. По

правилу косинусов в OAB, мы имеем
|v|² = 48² + 190² — 2.48.190.cos120°
|v|² = 47,524
|v| = 218
Тогда, |v| равно 218 км/ч. Согласно правилу синусов, в том же самом треуголнике,
48/sinθ = 218/sin120°,
или
sinθ = 48.sin120°/218 ≈ 0,1907
θ ≈ 11°
Тогда, θ = 11°, к ближайшему целому углу. Абсолютная скорость равна 218 км/ч, и направление его движения с учетом ветра: 100° — 11°, или 89°.

Если нам задан вектор w, мы можем найти два других вектора u и v, сумма которых есть w. Векторы u и v называются компонентами w и процесс их нахождения называется разложением, или представлением вектора его векторными компонентами.

Когда мы раскладываем вектор, обычно мы ищем перпендикулярные компоненты.

Очень часто, однако, одна компонента будет параллельной оси x, и другая будет параллельна оси y. Поэтому, они часто называются горизонтальными и вертикальными компонентами вектора. На рисунке внизу вектор w = разложен как сумма u = и v = .

Горизонтальная компонента w есть u и вертикальная компонента — v.

Пример 4 Вектор w имеет величину 130 и наклон 40° относительно горизонтали. Разложите вектор на горизонтальные и вертикальные компоненты.

Решение Сначала мы нарисуем рисунок с горизонтальными и вертикальными векторами u и v, чья сумма есть w.

Из ABC, мы находим |u| и |v|, используя определения косинуса и синуса:
cos40° = |u|/130, или |u| = 130.cos40° ≈ 100,
sin40° = |v|/130, или |v| = 130.sin40° ≈ 84.
Тогда, горизонтальная компонента w есть 100 направо и вертикальная компонента w есть 84 вверх.

Белорусский государственный университет транспорта — БелГУТ (БИИЖТ)

Регистрация на конференцию «Феноменология транспорта

в литературе и искусстве: прошлое, настоящее, будущее»

Как поступить в БелГУТ

Как получить место

в общежитии БелГУТа

ГОРЯЧАЯ ЛИНИЯ
по вопросам приемной кампании

События

Все события

Пн	Вт	Ср	Чт	Пт	Сб	Вс
	1	2
3	4	5	6 Дата : 2023-04-06	7 Дата : 2023-04-07	8	9
10 Дата : 2023-04-10	11	12	13 Дата : 2023-04-13	14	15	16
17 Дата : 2023-04-17	18	19 Дата : 2023-04-19	20 Дата : 2023-04-20	21 Дата : 2023-04-21	22	23
24	25	26 Дата : 2023-04-26	27 Дата : 2023-04-27	28	29	30

Все анонсы

Смотр-кастинг конкурса «Мисс и Мистер БелГУТа». ..
ФИНАЛ весенней серии игр «ЧТО? ГДЕ? КОГДА?» среди …
Билеты на концерт Дианы Анкудиновой…
Дни доноров 26 и 27 апреля 2023
Музыкальный квартирник
Программа. V Международная научно-практическая кон…
Программа. I Международная научно-практическая кон…

ЕДИ «Ключевые аспекты послания Президента Республ…
Игра между сборными командами БелГУТа и БГЭУ…
Поздравление Высокопреосвященнейшего Стефана с Вос…

Анонсы

Университет

Абитуриентам

Студентам

Конференции

Приглашения

Смотр-кастинг конкурса «Мисс и Мистер БелГУТа»…

ФИНАЛ весенней серии игр «ЧТО? ГДЕ? КОГДА?» среди …

Билеты на концерт Дианы Анкудиновой…

Дни доноров 26 и 27 апреля 2023

Новости

Университет

Международные связи

Спорт

ИВР

Жизнь студентов

Новости подразделений

Университет

Лекторский потенциал – достояние университета!.

..
21 апреля 2023

Воспитательная работа

Послание Президента обсудили с молодежью Жлобинщины…
21 апреля 2023

Университет

На форуме ТИБО-2023 «Цифровое развитие Беларуси»…
21 апреля 2023

Спорт

Спартакиада вузов по гиревому спорту
21 апреля 2023

Воспитательная работа

Дорогами мира и созидания. Мемориал в д. Бацунь…
21 апреля 2023

Воспитательная работа

Встреча с председателем ЦИК Беларуси
21 апреля 2023

Университет

С юбилеем! Борис Валерьевич Рябцев
21 апреля 2023

Университет

Образование на всю жизнь
20 апреля 2023

Воспитательная работа

Неделя леса — БелГУТ посадил дубовую рощу. ..
20 апреля 2023

Другие новости

«Праздник Светлой Пасхи» в БелГУТе
Эстафета «Живая память благодарных поколений» передана дальше…
Победа БелГУТа в матче Республиканской студенческий футбольной лиги…
Диалоговая площадка, посвященная обсуждению послания президента Респуб…
Победа в соревнованиях по плаванию в рамках Республиканской Универсиад…
Лидер РОО «Белая Русь» Олег Романов на встрече со студентами вузов в Б…
Третий тур весенней серии «Что? Где? Когда?» для студентов…
Материалы I конференции «Архитектура и строительство: традиции и иннов…
Встреча студентов с военнослужащими Гомельской пограничной группы…
70-я спартакиада студентов. Шахматы
Курсы повышения квалификации «Применение табличного процессора для обр…

БелГУТ на Доске почета

Достижения университета

КУДА ПОСТУПАТЬ

Все факультеты

Предложения

Все предложения

Видеотека

Все видео

Фотогалерея

Все фото

Q3 На каждом рисунке рядом с буквой алфавита показана вертикальная черта.

Возьмите ми…

Перейти к

Упражнение 13.1
Упражнение 13.2
Упражнение 13.3

Зная наши цифры
Целые числа
Игра с числами
Основные геометрические идеи
Понимание элементарных форм
Целые числа
Фракции
Десятичные
Обработка данных
Измерение
Алгебра
Соотношение и пропорция
Симметрия
Практическая геометрия

Главная > Решения НЦЭРТ Класс 6 Математика > Глава 13 — Симметрия > Упражнение 13.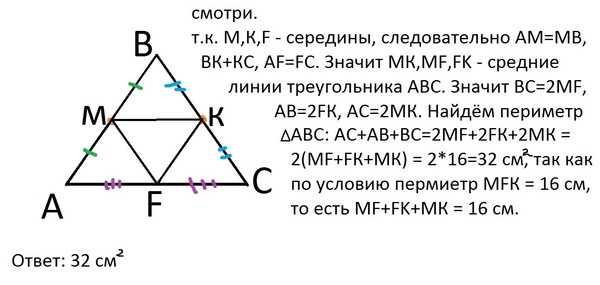 3 > Вопрос 3

Вопрос 3 Упражнение 13.3

Q3) На каждом рисунке рядом буква

алфавита показана вдоль

вертикальной чертой. Возьмите

зеркальное отражение буквы в

данная строка. Найдите, какие буквы выглядят

одинаково после отражения (т. е.

какие буквы выглядят одинаково на изображении

), а какие нет. Может

догадаетесь почему?

Попробуйте

Ответ:

РЕШЕНИЕ:

9000 003

Стенограмма видео

привет всем меня зовут нито Джейкоб, я репетитор в Лидо и приветствую всех вас на лидерском обучении здесь, у нас есть вопрос из главы Система кровообращения, поэтому вопрос состоит в том, дайте любые три различия между артерией и грузом, хорошо, мы должны выяснить, какие три различия между артерия и вес, так что это вопрос, поэтому мы увидим первое различие между артерией и крылом, хорошо, так в чем же первое различие, что вы можете сказать об артерии, главное, в чем основное различие между артерией и веной, да, артерия она переносит кровь от сердца к различным частям тела, а как насчет вены, как раз наоборот, то есть она переносит кровь из разных частей тела к сердцу, так что это первое различие, теперь переходим ко второму различию. кровь переносится артериями, несущими кровь от сердца к различным частям тела, поэтому мы можем сказать, что она переносит насыщенную кислородом кровь, поэтому насыщенная кислородом кровь распределяется по различным частям тела, но в этом случае есть исключение, которое легочная артерия легочная артерия несет насыщенную кислородом кровь, что является исключительным случаем, аналогично вене, мы можем сказать, что она несет насыщенную кислородом кровь, и снова есть исключение, за исключением легочной вены, которая несет насыщенную кислородом кровь, так что это второе отличие теперь переходим к третьему в артерии кровь течет с высокой скоростью она течет с высокой скоростью и также под высоким давлением хорошо да но как насчет вены кровь течет с точностью до наоборот поэтому кровь течет с низкой скоростью под низким давлением, хорошо, так что это основные три различия между артерией и весом, хорошо, поэтому я надеюсь, что вы поняли этот вопрос, решение для этого очень просто, если у вас есть какие-либо сомнения относительно этого, пожалуйста, прокомментируйте ниже и подпишитесь на этот канал для получения регулярные обновления увидимся в следующий раз с новым видео следите за обновлениями до тех пор берегите себя и до свидания

Связанные вопросы

В1) Найдите количество осей симметрии в каждой из следующих фигур. Как вы проверите свой ответ…

Q2) Скопируйте следующий рисунок на бумаге в клетку. Завершите каждое из них так, чтобы в результате…

Найдите количество осей симметрии в каждой из следующих фигур. Как вы проверите свой ответ…

Скопируйте следующий рисунок на бумагу в клетку. Дополните каждую из них так, чтобы получившаяся фигура…

На каждом рисунке рядом с вертикальной линией показана буква алфавита. Возьми мир…

Фейсбук WhatsApp

Копировать ссылку

Было ли это полезно?

Упражнения

Упражнение 13. 1

Упражнение 13.2

Упражнение 13.3

Главы

Знание наших чисел

Целые числа9 Игра с числами 002303

Основные геометрические идеи

Понимание элементарных фигур

Целые числа

Дроби

Десятичные числа

Обработка данных

Измерение

Алгебра

Отношение и пропорция

Симметрия

Практическая геометрия

Курсы

Быстрые ссылки

Условия и политика

2022 © Quality Tutorials Pvt Ltd Все права защищены (или «зеркальной симметрии»). В результате в школьных материалах слово «симметрия» используется так, как если бы оно имело только одно значение. Эта статья сосредоточится на этом одном значении, но также проиллюстрирует и другие.

На этой фотографии показано простое изображение с зеркалом, расположенным вдоль линии симметрии. Результат, который вы видите — половина оригинала и зеркальное отражение этой половины — точно соответствует исходной фигуре. Мы говорим, что исходная фигура «симметрична» относительно зеркала; имеет отражательную симметрию.

Отражающая симметрия и «линия симметрии»

Зеркально-симметричные объекты имеют по крайней мере одну линию симметрии , линию, по которой фигуру можно сложить на две точно совпадающие части, части, являющиеся зеркальным отображением каждой другой.

Эта фигура имеет две линии симметрии: горизонтальная линия симметрии делит фигуру на верх и низ, которые являются зеркальными отражениями друг друга; вертикальная линия симметрии разрезает фигуру на левую и правую части, которые являются зеркальными отражениями друг друга. Звезда внизу имеет 5 линий симметрии, пять линий, по которым ее можно сложить так, чтобы обе стороны идеально совпадали.

Распространенное заблуждение , встречающееся даже во многих глоссариях и текстах: не все линии, делящие фигуру на две конгруэнтные части, являются линиями симметрии. Например, диагональ (неквадратного) прямоугольника не является линией симметрии.

Когда зеркало помещается по диагонали прямоугольника, результат не выглядит так же, как исходный прямоугольник, поэтому диагональ не является линией симметрии. Эта новая форма — комбинация треугольной половины исходного прямоугольника и его отражения в зеркале — называется воздушным змеем.

Игра с зеркалом

Задолго до того, как дети начнут какое-либо формальное изучение симметрии, играя с зеркалами — возможно, с рисунками, которые они строят, — они развивают опыт и интуицию, которые могут служить как их геометрическому мышлению, так и их художественным идеям. Красочный дизайн выше имеет только вертикальные и горизонтальные линии симметрии, но размещение зеркала под другим углом может создать новый красивый дизайн.

На первом рисунке ниже видно, что буква А имеет вертикальную линию симметрии, но это скорее «ручная» игра. Более смелые эксперименты дают другие интересные результаты.

То же самое и с буквой M.

Буквы типа B и D имеют горизонтальную линию симметрии: их верхняя и нижняя части совпадают.

Некоторые буквы, например X, H и O, имеют как вертикальные, так и горизонтальные линии симметрии.

А некоторые, например P, R и N, не имеют линий симметрии.

Вращательная симметрия

Еще одна симметрия, которую дети иногда используют в своих рисунках из блоков узоров, называется «вращательная симметрия». Фигура обладает вращательной симметрией, если при некотором вращении (кроме полного поворота на 360 °) получается та же фигура. Например, эти фигуры при правильном вращении — 360°/3 для изображения «имя» и 360°/5 для звезды — выглядят точно так же, как и до поворота.

Буквы N, Z и S также обладают этим свойством.

Обратите внимание, что некоторые фигуры, такие как звезда и красочное пятно в верхней части страницы, но не буквы N, Z или S, имеют как отражающую, так и вращательную симметрию.

Самая симметричная фигура

Круг имеет бесконечно много линий симметрии: любой диаметр лежит на линии симметрии, проходящей через центр круга.