Медиана треугольника abc: определение, основание, свойства, задачи
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Геометрия Определение и свойства медианы треугольника
В данной статье мы рассмотрим определение медианы треугольника, перечислим ее свойства, а также разберем примеры решения задач для закрепления теоретического материала.
- Определение медианы треугольника
- Свойства медианы
- Свойство 1 (основное)
- Свойство 2
- Свойство 3
- Свойство 4
- Свойство 5
- Примеры задач
Определение медианы треугольника
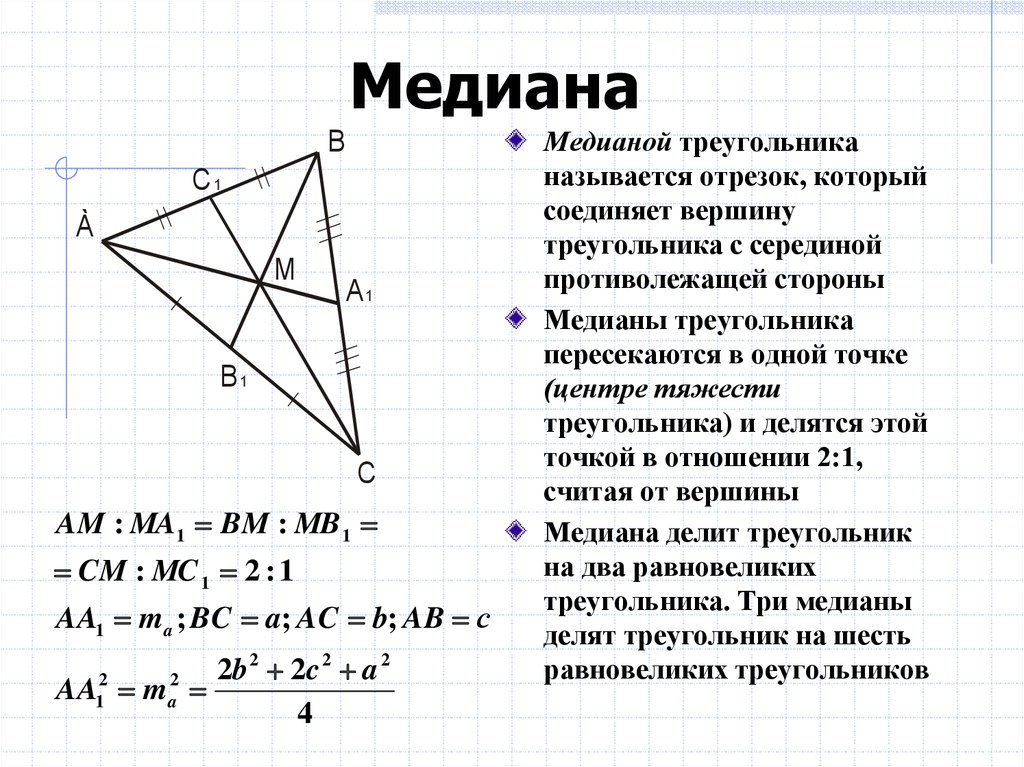
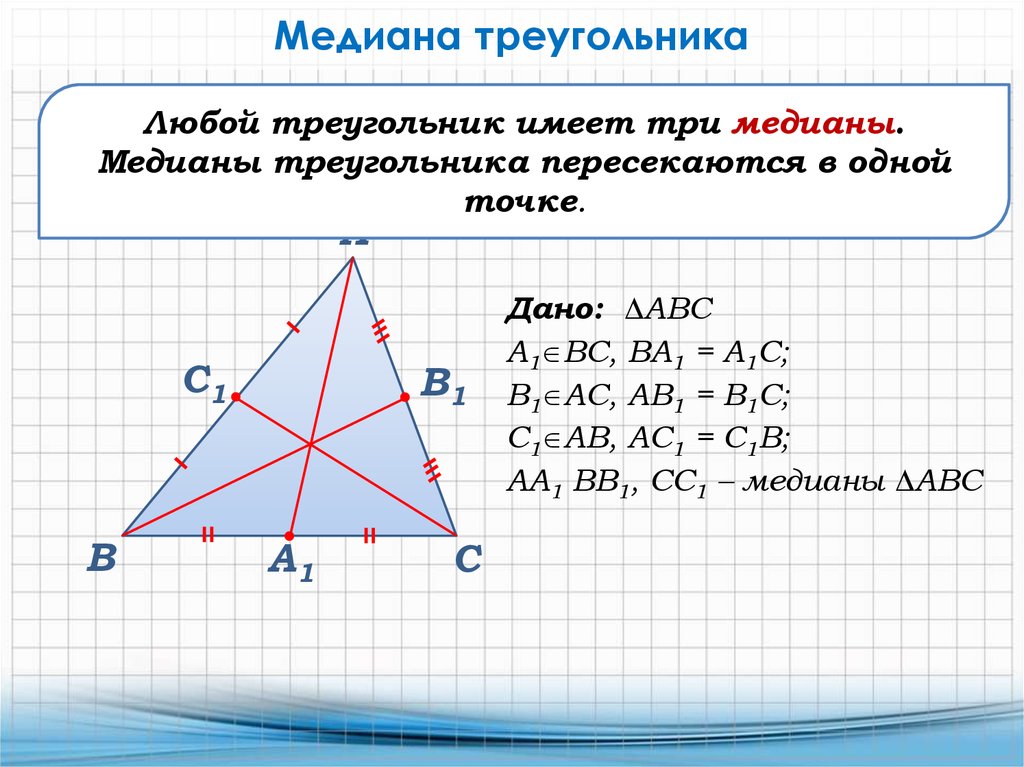
Медиана – это отрезок, соединяющий вершину треугольника с серединой стороны, расположенной напротив данной вершины.
- BF – медиана, проведенная к стороне AC.
- AF = FC
Основание медианы – точка пересечения медианы со стороной треугольника, другими словами, середина этой стороны (точка F).
Свойства медианы
Свойство 1 (основное)
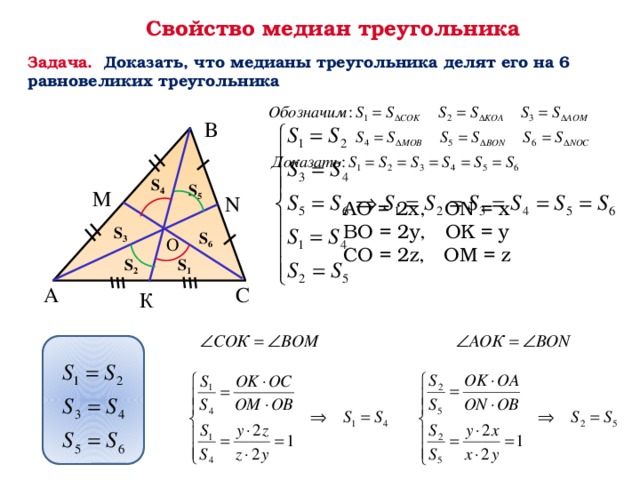
Т.к. в треугольнике три вершины и три стороны, то и медиан, соответственно, тоже три. Все они пересекаются в одной точке (O), которая называется центроидом или центром тяжести треугольника.
В точке пересечения медиан каждая из них делится в отношении 2:1, считая от вершины. Т.е.:
- AO = 2OE
- BO = 2OF
- CO = 2OD
Свойство 2
Медиана делит треугольник на 2 равновеликих (равных по площади) треугольника.
S1 = S2
Свойство 3
Три медианы делят треугольник на 6 равновеликих треугольников.
S1 = S2 = S3 = S4 = S5 = S6
Свойство 4
Наименьшая медиана соответствует большей стороне треугольника, и наоборот.
- AC – самая длинная сторона, следовательно, медиана BF – самая короткая.

- AB – самая короткая сторона, следовательно, медиана CD – самая длинная.
Свойство 5
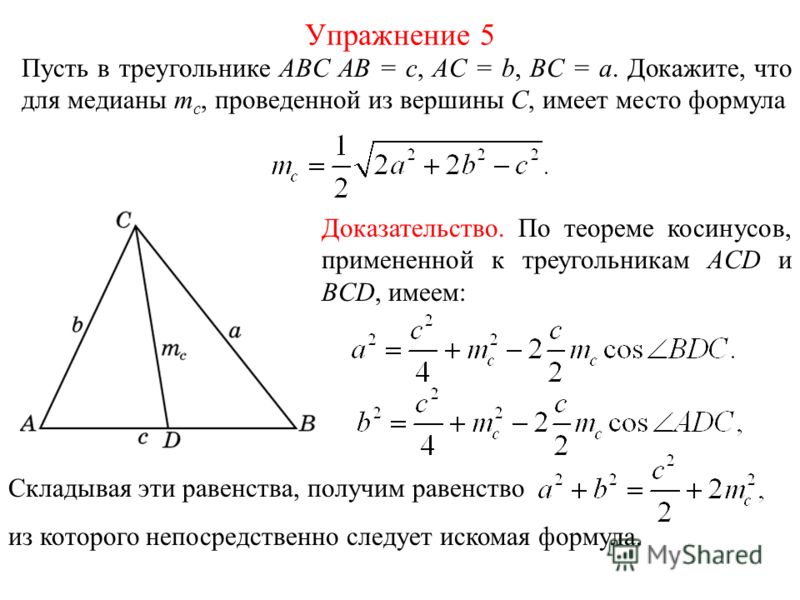
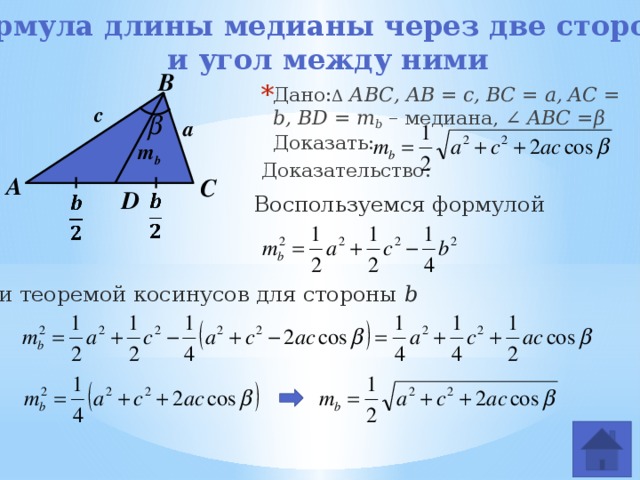
Допустим, известны все стороны треугольника (примем их за a, b и c).
Длину медианы ma, проведенную к стороне a, можно найти по формуле:
Примеры задач
Задание 1
Площадь одной из фигур, образованной в результате пересечения трех медиан в треугольнике, равняется 5 см2. Найдите площадь треугольника.
Решение
Согласно свойству 3, рассмотренному выше, в результате пересечения трех медиан образуются 6 треугольников, равных по площади. Следовательно:
S△ = 5 см2 ⋅ 6 = 30 см2.
Задание 2
Стороны треугольника равны 6, 8 и 10 см. Найдите медиану, проведенную к стороне с длиной 6 см.
Решение
Воспользуемся формулой, приведенной в свойстве 5:
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Длина медианы правильного треугольника – формула, примеры
3. 9
9
Средняя оценка: 3.9
Всего получено оценок: 108.
3.9
Средняя оценка: 3.9
Всего получено оценок: 108.
Медиана – это один из характеризующих отрезков треугольника, наравне с биссектрисой и высотой. Особую сложность у учеников часто вызывают задачи на нахождение медианы. В обычном случае приходится применять формулу, но для правильного треугольника можно вывести упрощенную версию нахождения медианы.
Необходимые данные
Для вывода формул потребуется вспомнить несколько теоретических выкладок:
- Медиана это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Три медианы треугольника пересекаются в одной точке.
- В равнобедренном треугольнике, медиана, проведенная к основанию, является биссектрисой и высотой. А правильный треугольник это частный случай равнобедренного треугольника, у которого основанием может выступать любая из сторон. Значит каждая медиана равностороннего треугольника будет совпадать с соответствующей биссектрисой и высотой.

Получилась та же формула длины медианы правильного треугольника. Значит, вывод первым способом был осуществлен верно и можно использовать любой из двух способов, если вы вдруг забыли формулу нахождения медианы правильного треугольника.
Рис. 3. Точка пересечения медиан правильного треугольника.Последний метод очень часто используется не только для вывода формул правильного треугольника, но и для решения задач.
Что мы узнали?
Мы несколькими методами вывели формулу длины медианы правильного треугольника. Указали на метод решения простых задач на нахождение характеристик правильного треугольника, а так же вспомнили основные свойства медианы.
Тест по теме
Доска почётаЧтобы попасть сюда — пройдите тест.
Оксана Шмидт
3/5
Оценка статьи
3.9
Средняя оценка: 3.9
Всего получено оценок: 108.

А какая ваша оценка?
Уравнение медианы треугольника
В треугольнике медиана — это отрезок, соединяющий вершину с серединой соответствующей противоположной стороны. У треугольника три медианы.
В ΔABC, показанном ниже, D — это середина стороны BC, а AD — медиана, проходящая через вершину A.
Мы можем найти уравнение медианы, как описано ниже.
Шаг 1 :
Используя формулу средней точки, найдите середину BC, то есть D.
Шаг 2 :
Найдите наклон медианы AD, используя точки A и D.
Шаг 3:
Используя уравнение формы точка-наклон y — y 1 = m(x — x 1 ), найдите уравнение медианы ОБЪЯВЛЕНИЕ.
Примечание:
Когда для нахождения уравнения медианы используется форма точка-наклон, обычно берется точка в вершине.
Пример 1 :
Найдите уравнения трех медиан ΔABC с вершинами A(1, -3), B(-2, 5) и C(-3, 4).
Решение:
Пусть D, E и F — середины сторон AB, BC и AC соответственно.

Уравнение среднего интерфейса AD:
Средняя точка BC:
= (x 1 + x 2 )/2, (x 1 + x 2 )/2)
Заместитель ( х 1 , у 1 ) = В(-2, 5) и (х 2 , у 2 ) = С(-3, 4).
= D((-2 — 3)/2, (5 + 4)/2)
= D(-5/2, 9/2)
Наклон AD :
= (y 2 — y 1 )/(x 2 — x 1 )
Замена (x 1 , y 1 = 2 (1, -3) A и х 2 , у 2 ) = D(-5/2, 9/2).
= (9/2 + 3)/(-5/2 — 1)
= (15/2)/(-7/2)
= -15/7
Уравнение медианы AD :
y — y 1 = m(x — x 1 )
Замена (x 1 , y 1 ) = A(1, -3) и m = -15/7.
у + 3 = (-15/7)(х — 1)
7(y + 3) = -15(x — 1)
7y + 21 = -15x + 15
15x + 7y + 6 = 0 = ((x 1 + x 2 )/2, (x 1 + x 2 )/2)
Замена (x 1 , ( 1 , 0 ) 900 3) и (х 2 , у 2 ) = С(-3, 4).

= E((1 — 3)/2, (-3 + 4)/2)
= E(-1, 1/2)
Наклон BE :
= (y 2 — y 1 )/(x 2 — x 1 )
Замена (x 1 , y 1 ) = 1 B(0 2 х 90) и 2 ) = E(-1, 1/2).
= (1/2 — 5)/(-1 + 2)
= (-9/2)/1
= -9/2
Уравнение медианы BE :
y — y 1 = m(x — x 1 )
Замена (x 1 , y 1 ) = B(-2, 5) и m = -9/2.
у — 5 = (-9/2)(х + 2)
2(y — 5) = -9(x + 2)
2y — 10 = -9x — 18
9x + 2y + 8 = 0 ((x 1 + x 2 )/2, (x 1 + x 2 )/2)
Замена (x 1 , (y 1) ) и (х 2 , у 2 ) = В (-2, 5).
= F((1 — 2)/2, (-3 + 5)/2)
= E(-1/2, 1)
Наклон CF :
= (y 2 — y 1 )/(x 2 — x 1 )
Заместитель (x 1 , Y 1 ) = C (-3, 4) и (x 2 , Y 2 ) = F(-1/2, 1).

= (1 — 4)/(-1/2 + 3)
= -3/(5/2)
= -6/5
Уравнение медианы CF :
y — y 1 = m(x — x 1 )
Замена (x 1 , y 1 ) = C(-3, 4) и m = -6/5.
у — 4 = (-6/5)(х + 3)
5(у — 4) = -6(х + 3)
5y — 20 = -6x — 18
6x + 5y — 2 = 0
Пример 2:
С(8, 10). Найдите уравнение прямой по медиане из вершины A.
Решение:
Пусть D — середина стороны BC.
Середина BC :
= ((x 1 + x 2 )/2, (x 1 + x 2 )/2)
0002 Замена (x 1 , y 1 ) = B(8, 4) и (x 2 , y 2 ) = C(8, 10).= D((8 + 8)/2, (4 + 10)/2)
= D(8, 7)
Наклон AD :
= (y 2 — y 1 ) /(x 2 — x 1 )
Замена (x 1 , y 1 ) = A(-4, 4) и (x 2 , y
0 ) , 7).

= (7 — 4)/(8 + 4)
= 3/12
= 1/4
Уравнение прямой вдоль медианы из вершины A :
y — y 1 = m(x — x 1 )
Замена (x 1 , y 1 ) = A() , 4) и m = 1/4.
y — 4 = (1/4)(x + 4)
4(y — 4) = 1(x + 4)
4y — 16 = x + 4
x — 4y + 20 = 0
Помимо всего вышеперечисленного, если вам нужны какие-либо другие материалы по математике, воспользуйтесь нашим пользовательским поиском Google здесь.
Пожалуйста, присылайте свои отзывы на [email protected]
Мы всегда ценим ваши отзывы.
©Все права защищены. onlinemath5all.com
Как построить (начертить) медианы треугольника
На этой странице показано, как построить медианы треугольника с циркулем и линейкой или линейкой. У треугольника три медианы. Это линии, соединяющие вершина к середина противоположной стороны. Сначала находим середину, затем проводим медиану.
Печатные пошаговые инструкции
Вышеупомянутая анимация доступна как распечатанная пошаговая инструкция, которую можно использовать для изготовления раздаточных материалов или когда компьютер недоступен.

Доказательство
Аргумент Причина 1 S является средней точкой PQ .По конструкции. См. Биссектриса отрезка с компасом и линейкой. для метода и доказательства. 2 RS — медиана треугольника PQR А Медиана треугольника — это отрезок, соединяющий вершину с серединой противоположной стороны. Две другие медианы из Q,P доказываются аналогичным образом — Q.E.D
Попробуйте сами
Нажмите здесь, чтобы распечатать рабочий лист, содержащий задачи построения медианы. Когда вы попадете на страницу, используйте команду печати браузера, чтобы распечатать столько, сколько хотите. Распечатанный результат не защищен авторским правом.

Другие страницы по конструкциям на этом сайте
- Список рабочих листов по конструкциям для печати
Линии
- Введение в конструкции
- Скопируйте сегмент линии
- Сумма n отрезков
- Разница двух сегментов линии
- Биссектриса отрезка
- Перпендикуляр в точке на прямой
- Перпендикуляр от прямой через точку
- Перпендикулярно от конечной точки луча
- Разделить отрезок на n равных частей
- Параллельная линия через точку (угловая копия)
- Параллельная линия через точку (ромб)
- Параллельная линия через точку (перемещение)
Углы
- Разделение угла пополам
- Скопируйте угол
- Построить угол 30°
- Построить угол 45°
- Построение угла 60°
- Построить угол 90° (прямой угол)
- Сумма n углов
- Разность двух углов
- Дополнительный уголок
- Дополнительный уголок
- Построение углов 75° 105° 120° 135° 150° и более
Треугольники
- Скопируйте треугольник
- Равнобедренный треугольник по основанию и стороне
- Равнобедренный треугольник с основанием и высотой
- Равнобедренный треугольник по катету и углу при вершине
- Равносторонний треугольник
- 30-60-90 треугольник, учитывая гипотенузу
- Треугольник с 3 сторонами (sss)
- Треугольник по одной стороне и прилежащим углам (asa)
- Треугольник с двумя углами и не включенной стороной (aas)
- Треугольник по двум сторонам и углу между ними (sas)
- Медианы треугольника
- Средняя часть треугольника
- Высота треугольника
- Высота треугольника (вне корпуса)
Прямоугольные треугольники
- Прямоугольный треугольник с одним катетом и гипотенузой (HL)
- Прямоугольный треугольник с учетом обеих сторон (LL)
- Прямоугольный треугольник по гипотенузе и одному углу (HA)
- Прямоугольный треугольник по одному катету и одному углу (LA)
Центры треугольников
- Центры треугольников
- Центр окружности треугольника
- Ортоцентр треугольника
- Центр тяжести треугольника
Окружности, дуги и эллипсы
- Нахождение центра окружности
- Круг дан 3 очка
- Касательная в точке окружности
- Касательные через внешнюю точку
- Касательные к двум окружностям (внешние)
- Касательные к двум окружностям (внутренние)
- Вписанная окружность треугольника
- Точки фокусировки данного эллипса
- Окружность треугольника
Полигоны
- Квадрат с одной стороной
- Квадрат, вписанный в круг
- Шестиугольник с одной стороной
- Шестиугольник, вписанный в данную окружность
- Пятиугольник вписан в заданный круг
Неевклидовы конструкции
- Построение эллипса с помощью нити и булавок
- Найдите центр круга с любым прямоугольным объектом
(C) 2011 Copyright Math Open Reference.