Нахождение медианы в треугольнике: Как найти длину медианы треугольника

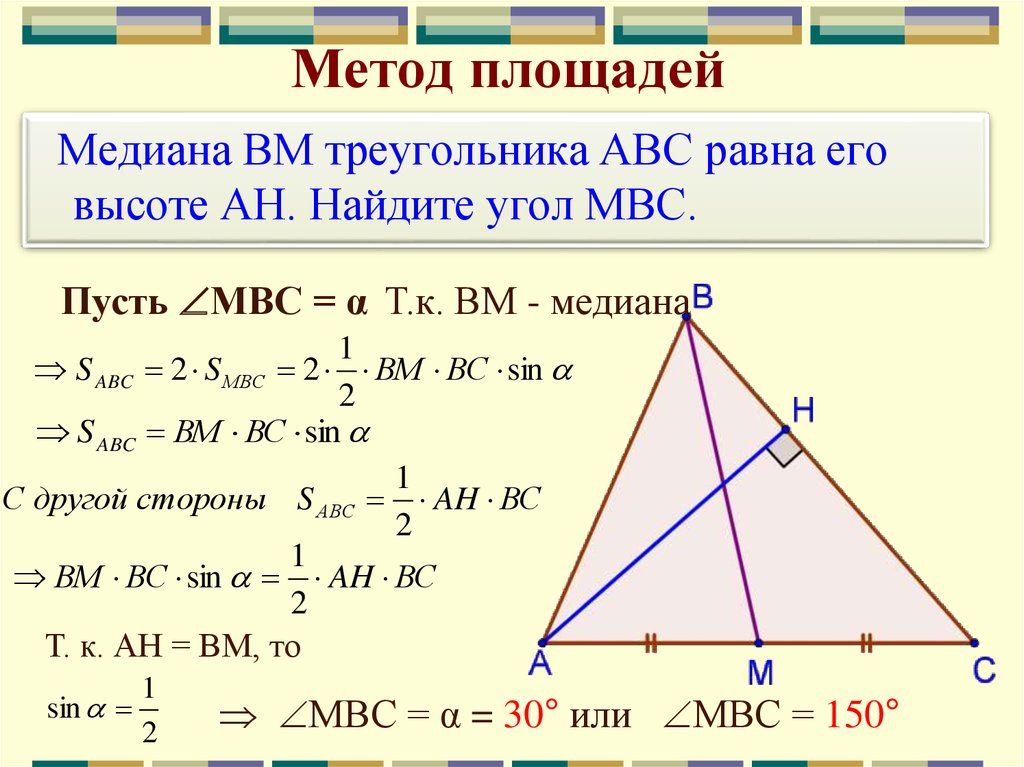
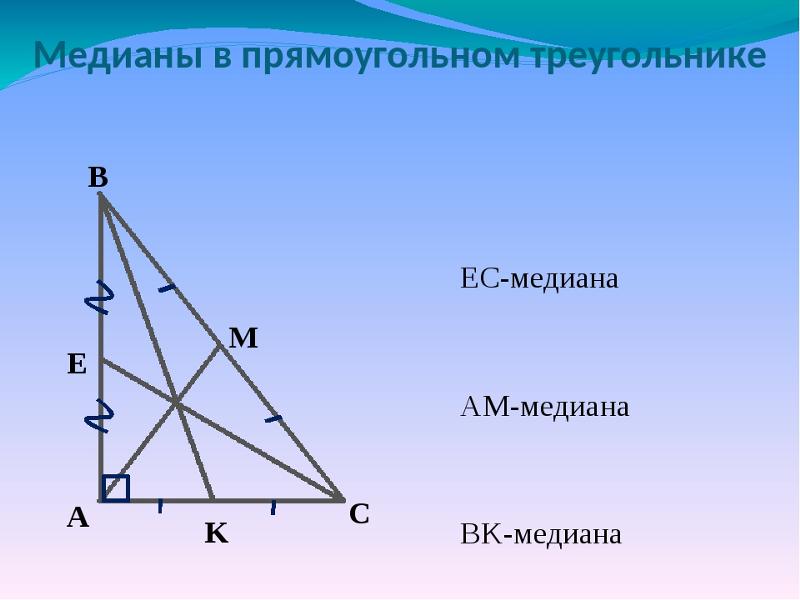
Медиана к гипотенузе прямоугольного треугольника: свойства, задача

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Определение и свойства медианы прямоугольного треугольника

В данной статье мы рассмотрим определение и свойства медианы прямоугольного треугольника, проведенной к гипотенузе. Также разберем пример решения задачи для закрепления теоретического материала.

• Определение медианы прямоугольного треугольника
• Свойства медианы прямоугольного треугольника
  • Свойство 1
  • Свойство 2
  • Свойство 3
• Пример задачи

Определение медианы прямоугольного треугольника

Медиана – это отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.

Прямоугольный треугольник – это треугольник, в котором один из углов является прямым (90°), а два остальных – острыми (<90°).

Свойства медианы прямоугольного треугольника

Свойство 1

Медиана (AD) в прямоугольном треугольнике, проведенная из вершины прямого угла (∠

BAC) к гипотенузе (BC), равна половине гипотенузы.

• BC = 2AD
• AD = BD = DC

Следствие: Если медиана равняется половине стороны, к которой она проведена, то данная сторона является гипотенузой, а треугольник – прямоугольным.

Свойство 2

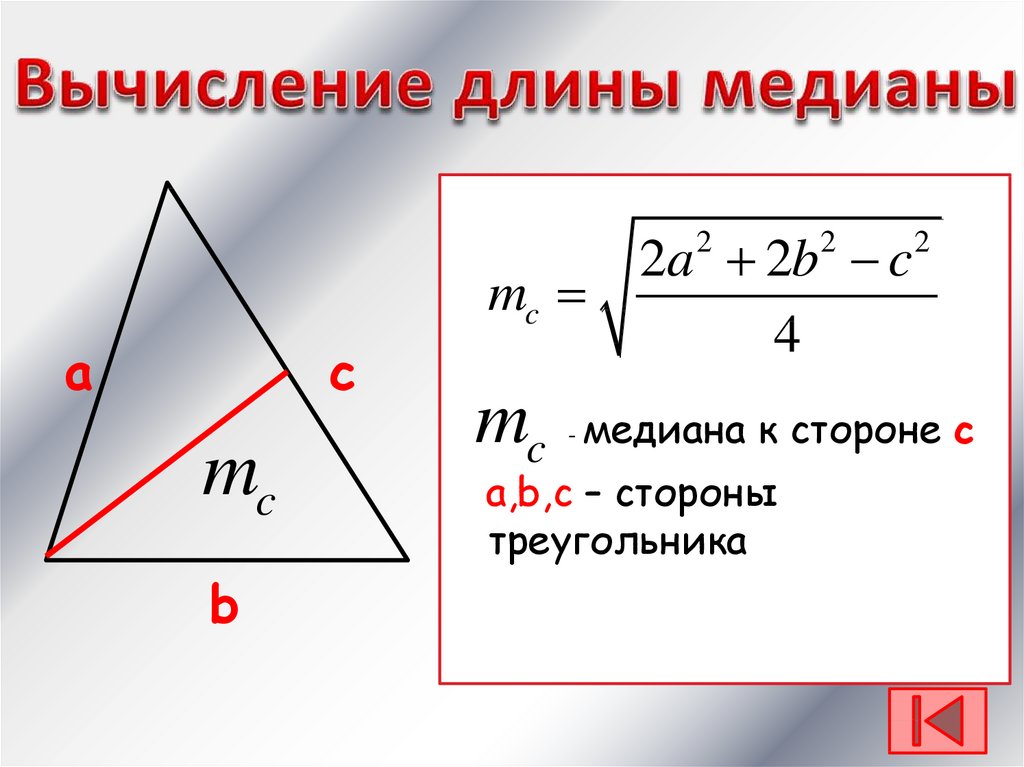
Медиана, проведенная к гипотенузе прямоугольного треугольника, равняется половине квадратного корня из суммы квадратов катетов.

Для нашего треугольника (см. рисунок выше):

Это следует из теоремы Пифагора и Свойства 1.

Свойство 3

Медиана, опущенная на гипотенузу прямоугольного треугольника, равна радиусу описанной вокруг треугольника окружности.

Т.е. BO – это одновременно и медиана, и радиус.

Примечание: К прямоугольному треугольнику также применимы общие свойства медианы, независимо от вида треугольника.

Пример задачи

Длина медианы, проведенной в гипотенузе прямоугольного треугольника, составляет 10 см. А один из катетов равен 12 см. Найдите периметр треугольника.

Решение
Гипотенуза треугольника, как следует из Свойства 1, в два раза больше медианы. Т.е. она равняется: 10 см ⋅ 2 = 20 см.

Воспользовавшись теоремой Пифагора находим длину второго катета (примем его за “b”, известный катет – за “a”, гипотенузу – за “с”):
b² = с² – a² = 20² – 12² = 256.
Следовательно, b = 16 см.

Теперь мы знаем длины всех сторон и можем посчитать периметр фигуры:

P_△ = 12 см + 16 см + 20 см = 48 см.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Медиана треугольника abc: определение, основание, свойства, задачи

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel. ru Математика Геометрия Определение и свойства медианы треугольника

В данной статье мы рассмотрим определение медианы треугольника, перечислим ее свойства, а также разберем примеры решения задач для закрепления теоретического материала.

• Определение медианы треугольника
• Свойства медианы
  • Свойство 1 (основное)
  • Свойство 2
  • Свойство 3
  • Свойство 4
  • Свойство 5
• Примеры задач

Определение медианы треугольника

Медиана – это отрезок, соединяющий вершину треугольника с серединой стороны, расположенной напротив данной вершины.

• BF – медиана, проведенная к стороне AC.
• AF = FC

Основание медианы – точка пересечения медианы со стороной треугольника, другими словами, середина этой стороны (точка F).

Свойства медианы

Свойство 1 (основное)

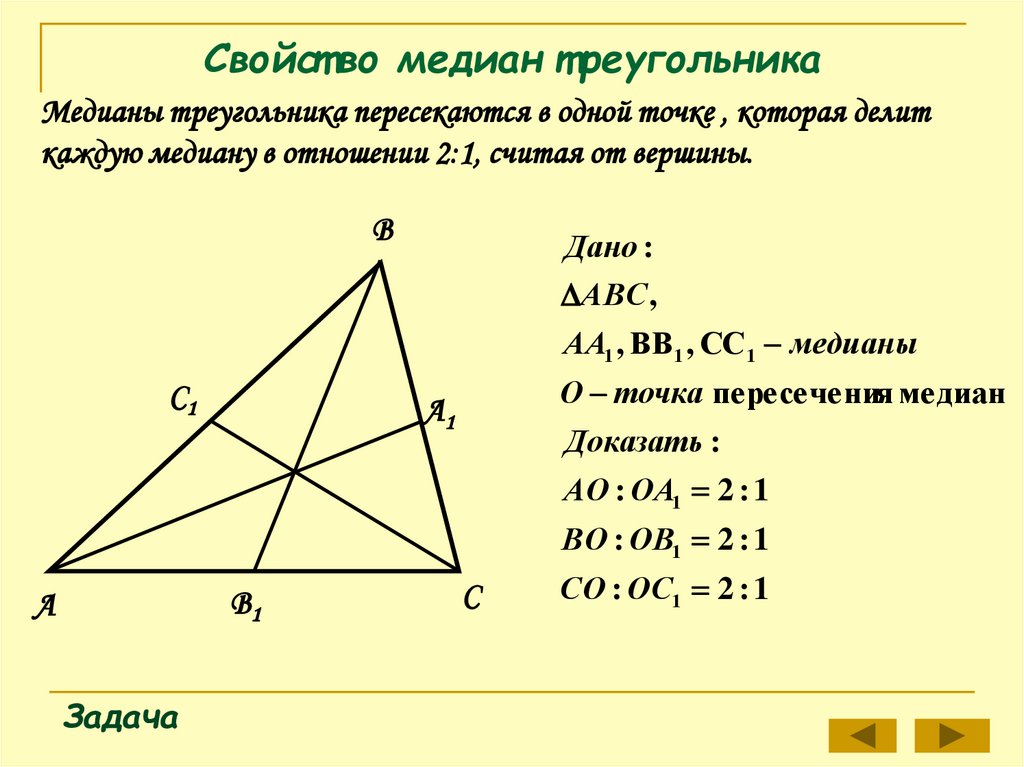
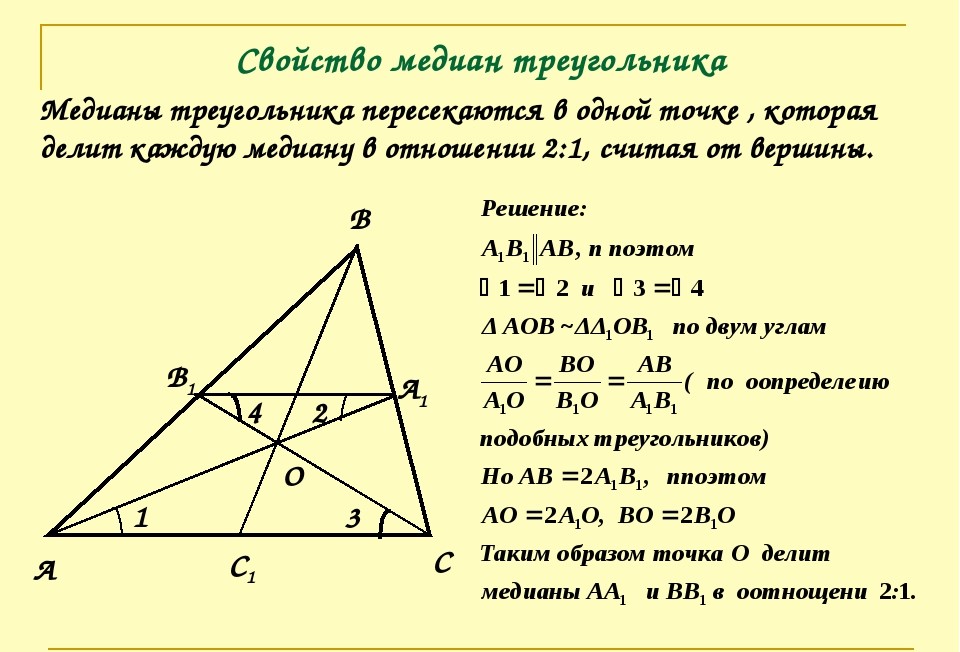
Т.к. в треугольнике три вершины и три стороны, то и медиан, соответственно, тоже три. Все они пересекаются в одной точке (O), которая называется центроидом или центром тяжести треугольника.

В точке пересечения медиан каждая из них делится в отношении 2:1, считая от вершины. Т.е.:

• AO = 2OE
• BO = 2OF
• CO = 2OD

Свойство 2

Медиана делит треугольник на 2 равновеликих (равных по площади) треугольника.

S₁ = S₂

Свойство 3

Три медианы делят треугольник на 6 равновеликих треугольников.

S₁ = S₂ = S₃ = S₄ = S₅ = S₆

Свойство 4

Наименьшая медиана соответствует большей стороне треугольника, и наоборот.

• AC – самая длинная сторона, следовательно, медиана BF – самая короткая.
• AB – самая короткая сторона, следовательно, медиана CD – самая длинная.

Свойство 5

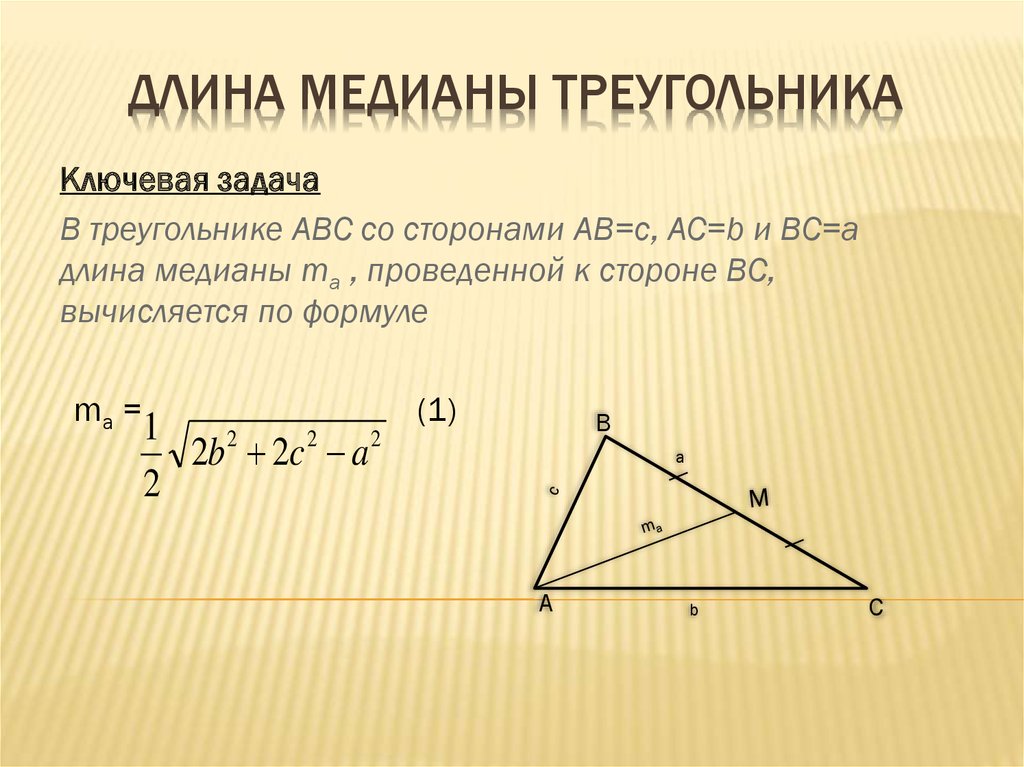
Допустим, известны все стороны треугольника (примем их за a, b и c).

Длину медианы m_a, проведенную к стороне a, можно найти по формуле:

Примеры задач

Задание 1
Площадь одной из фигур, образованной в результате пересечения трех медиан в треугольнике, равняется 5 см². Найдите площадь треугольника.

Решение
Согласно свойству 3, рассмотренному выше, в результате пересечения трех медиан образуются 6 треугольников, равных по площади. Следовательно:
S_△ = 5 см² ⋅ 6 = 30 см².

Задание 2
Стороны треугольника равны 6, 8 и 10 см. Найдите медиану, проведенную к стороне с длиной 6 см.

Решение
Воспользуемся формулой, приведенной в свойстве 5:

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Значение, примеры, формула и расчет

Предположим, вам нужно разделить последний кусок торта со своим братом. И ни один из вас не хочет получить меньший кусок. Чтобы избежать драки между вами и вашим братом из-за торта, ваша мать отрезает треугольный кусок торта от его медианы , чтобы вы оба получили одинаковый размер торта. Но что это за медиана? Как твоя мама решила, где разрезать торт?

Определим медиану треугольника как отрезок, соединяющий вершину с серединой противоположной стороны. В этой статье мы рассмотрим определение медиана , ее различные свойства, математическая формула и, наконец, работа с несколькими примерами.

В конце этой статьи вы сможете:

• Определить медиану и связать ее с площадью треугольника.

• Определите и начертите медианы в треугольнике.

• Вычислить длину медианы по сторонам и координатам треугольника.

Значение медианы

Итак, что именно означает медиана? Представьте, что у вас есть кусок пиццы, который вам нужно разделить между собой и вашим другом. Для простоты назовем эту пиццу \(\bigtriangleup ABC\). Теперь имейте в виду, что вам нужно разделить пиццу поровну между своими друзьями. Здесь может помочь медиана .

Медиана куска пиццы, pexels.com

Выберите сторону пиццы, скажем, сторону \(a\) (то есть сторону \(BC\)), и разрежьте пиццу по отрезку, соединяющему среднюю точку линии и противоположный внутренний угол, как показано на рисунке ниже. Ура! Теперь вы и ваш друг можете наслаждаться пиццей поровну. Воображаемая линия, разрезающая пиццу на две равные части, — это медиана . Поскольку все треугольники имеют \(3\) сторон и \(3\) внутренних углов. У него всегда будут \(3\) медианы.

Медиана — построенная линия, соединяющая середину одной стороны с противоположным внутренним углом.

Интересно отметить, что периметр треугольника всегда больше суммы трех его медиан.

Что такое центроид?

Теперь, когда мы знаем, что такое медиана, давайте рассмотрим, что такое центроид. Точка пересечения трех медиан называется центроидом . Центроид представляет собой точки параллелизма. Точка параллелизма — это точка, в которой пересекаются две или более линий. Например, точка пересечения медиан, серединных перпендикуляров и высот. Центроид всегда будет лежать внутри треугольника, в отличие от других точек параллелизма.

Точка пересечения трех медиан называется центроидом .

Рис. 1. Три медианы с центром тяжести в качестве точки пересечения.

Центроид имеет несколько интересных свойств. Он всегда будет делить медиану на соотношение \(2:1\). Центроид всегда расположен на расстоянии двух третей медианы от внутреннего угла.

Представим себе, как медиана делится на соотношение \(2:1\). Возьмите \(\bigtriangleup ABC\) и проведите \(3\) медианы из каждой вершины. Пусть теперь \(O\) будет центром тяжести треугольника. Если \(AM\) — медиана треугольника из вершины \(A\), то \(2OM = OA\).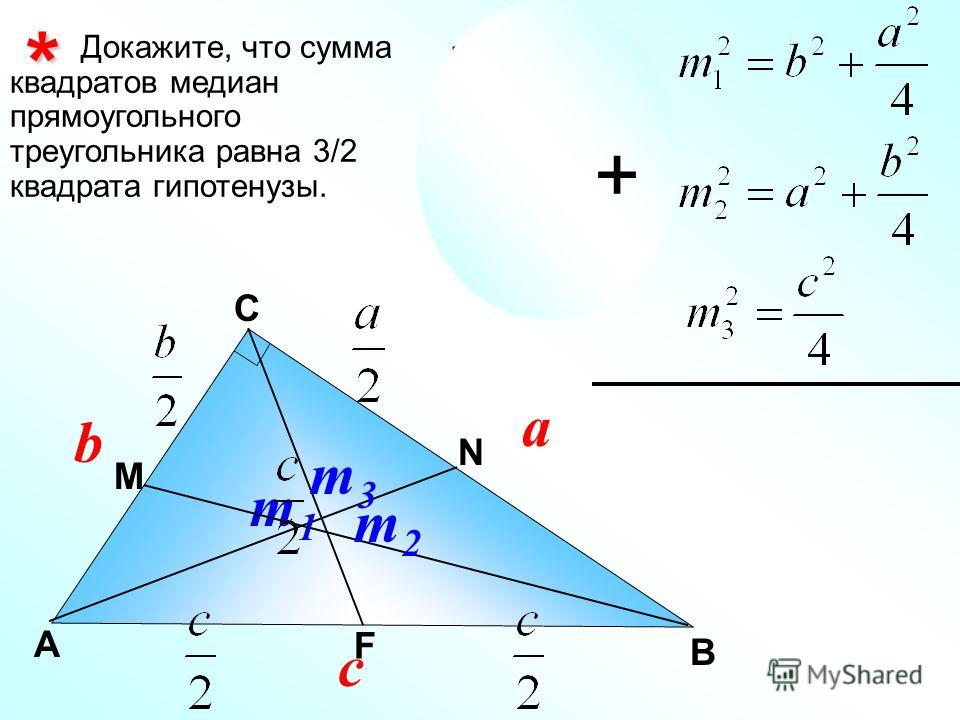

Рис. 2. Центроид делит медиану на части \(2:1\).

В прямоугольном треугольнике медиана, проведенная из вершины прямого угла, равна половине длины гипотенузы треугольника. Медиана из прямого угла треугольника делит гипотенузу на две равные части и каждая часть гипотенузы равна длине медианы.

Рис. 3. Медиана, равная половине гипотенузы.

На приведенном выше рисунке медиана \(AD\) делит гипотенузу на две равные части \(CD\) и \(BD\) таким образом, что \(AD=CD; AD=BD\).

Свойства медианы

Свойства медианы можно описать следующим образом:

• Любой треугольник содержит 3 медианы с точкой пересечения, называемой центром тяжести.

• Соединительная сторона медианы разделена на две равные части.

• Два треугольника одинакового размера и площади образуются путем построения медианы из любой из вершин треугольника.

• На самом деле любой треугольник делится на 6 меньших треугольников с одинаковой площадью 3 медианами треугольника.

Медиана и высота треугольника

Различие между медианой и высотой треугольника может немного сбить с толку, но легко принять их за одно и то же. Но медиана и высота треугольника — это два разных элемента треугольника. Медиана треугольника — это отрезок прямой от одной вершины до середины его противоположной стороны. Принимая во внимание, что высота треугольника — это перпендикулярный отрезок прямой от вершины до его противоположной стороны.

Рис. 4. Медиана и высота треугольников.

На приведенном выше рисунке \(AD, BE,\) и \(CF\) — медианы треугольника \(\bigtriangleup ABC\), а \(XM, YN,\) и \(ZO\) — высоты треугольника \(\bigtriangleup XYZ\).

Разница между медианой и высотой

Посмотрим разницу между медианой и высотой треугольника.

Медиана	Высота
Медиана — это отрезок прямой от середины одной стороны до ее противоположной вершины.	Высота – это отрезок перпендикулярной линии, образованный от одной стороны к противоположной точке вершины.
Треугольник имеет 3 медианы с точкой пересечения, называемой центром тяжести.	Треугольник имеет 3 высоты с точкой пересечения, называемой ортоцентром.
Все 3 медианы находятся внутри треугольника любой формы.	Высота может быть или не быть внутри треугольника в зависимости от формы.
Медиана делит треугольник на два меньших треугольника равной площади.	Высота делит треугольник на два меньших треугольника, но их площади могут быть разными. 9{2}}{4}}\] где медиана треугольника равна \(m_c\), стороны треугольника равны \(a, b,\) и \(c\), а медиана образована на стороне \ (‘с’\). Но как тогда вычислить длину, используя только координаты треугольника? Сначала мы оцениваем середины стороны с медианой, используя приведенную ниже формулу. Рис. 6. Треугольник с серединой и медианой. \[M(x_m, y_m)=\frac{(x_2+x_3)}{2}, \frac{(y_2+y_3)}{2}\] где \(M(x_m,y_m)\ ) является одним из концов медианы. Используя эти координаты и оставшуюся точку, мы можем вычислить длину медианы. Координаты нужно подставить в следующую формулу. Это формула расстояния, и она дает расстояние между любыми двумя координатами на двумерной плоскости. 92}\] где \(M(x_m, y_m)=\frac{(x_1+x_2)}{2}, \frac{(y_1+y_2)}{2}\). Примеры медиан Давайте посмотрим на некоторые примеры медиан и поймем их. Найдите длину медианы данного треугольника \(ABC\), стороны которого заданы следующим образом: \(AB = 10\, единицы\), \(BC = 6\, единицы\) и \(AC = 8\, ед.\) соответственно, в котором АМ — медиана, образованная на стороне \(ВС\). Рис. 7. Треугольник с длинами сторон. Решение: 92}{4}} = 8,54\] Следовательно, длина медианы \(AM\) равна \(8,54 \; единиц\). Найдите длину медианы \(AM\), если координаты треугольника \(ABC\) заданы как \(A (2,5), B (6,3), C (-3,0 )\). Рис. 8. Треугольник с координатами. Решение: Шаг 1: Вычислить координаты средней точки \(BC\) \begin{align}M(x,y)&=\frac{(x_1+x_2)}{ 2}, \frac{(y_1+y_2)}{2} \\&=\frac{(6+(-3))}{2}, \frac{3+0}{2} \\&=( 1.5, 1.5)\end{выравнивание} 92} \\&=\sqrt{12.5} \\&=3.53\end{align} Это дает нам длину \(3.53\) единиц. Это подводит нас к концу статьи. Вот основные выводы, которые помогут освежить в памяти то, что мы уже узнали. Медиана — ключевые выводы Медиана — это отрезок, соединяющий вершину и середину противоположной стороны. Он делит противоположную сторону на две равные части, деля ее пополам. Медиана делит треугольник на два равновеликих треугольника. \(3\) медианы разделят треугольник на \(6\) равных треугольников. 92}\), где \(D\) — расстояние. Узнать определение, факты и примеры Введение в медиану треугольника Дата последнего обновления: 23 апреля 2023 г. • Всего просмотров: 68 .7k • Просмотров сегодня: 0.37k Отрезок, соединяющий вершину треугольника с серединой другой стороны и делящий эту сторону пополам, в геометрии называется медианой треугольника. В каждом треугольнике три медианы, по одной из каждой вершины. В центре треугольника эти медианы пересекаются. Медиана треугольника — это отрезок, соединяющий вершину с серединой стороны, противоположной этой вершине. Медиана (AD) в приведенном ниже примере делит BC на две равные части, в результате чего BD = DC. Это отвечает на вопрос, что такое медиана в геометрии? Медиана треугольника Свойства медианы треугольника Ниже перечислены некоторые свойства медианы треугольника: Отрезок от вершины треугольника до середины его противоположной стороны называется медианой треугольника. Он делит противоположную сторону на две равные части, разрезая ее пополам. Треугольник делится на два треугольника с одинаковой площадью по медиане. Три медианы любого треугольника сходятся в одной точке, независимо от его размера или формы. Для каждого треугольника существуют три медианы, по одной из каждой вершины. Центроид треугольника образован пересечением трех медиан. Центроид — это точка совпадения медиан треугольника. Высота треугольника Отрезок, образующий прямой угол (90°) от вершины треугольника к противоположной стороне, считается высотой треугольника. В зависимости от типа треугольника высота может быть внутри или снаружи треугольника. Каждый треугольник имеет три высоты, по одной из каждой вершины, которые сходятся в ортоцентре треугольника. Как найти медиану треугольника 9{2}}{4}}$ , где $P Q=3, P R=4, Q R=5$ $PM=\sqrt{\dfrac{18+32-25}{4}}=\sqrt{ \dfrac{50-25}{4}}=\sqrt{\dfrac{25}{4}}=\dfrac{5}{2}=2,5 \text { ед. }$ Q2. Определите длину медианы треугольника ABC, стороны которого равны AB = 10, BC = 8 и AC = 13 единиц соответственно. Медиана, созданная на стороне BC, задается как AD, где D — медиана. Ответ: Здесь мы должны найти AD. Итак, мы должны использовать медиану формулы треугольника, т.е. 9{2}}{4}}$ , где $A B=10, B C=8, A C=13$ $A D=\sqrt{\dfrac{200+338-64}{4}}=\sqrt{ \dfrac{474}{4}}=10,88$ единиц. Q3. Треугольники имеют медианы 28 см, 45 см и 53 см. Чему равна площадь треугольника? Ответ: Мы получили тройку Пифагора, то есть 28 см, 45 см, 53 см. Таким образом, площадь треугольника равна $\dfrac{4}{3}$, умноженной на площадь треугольника, образованного медианой. {2}$. 9{2}=100-36=64$ $\Rightarrow B D=8$ $\Rightarrow B C=2 B D=2 \times 8=16$ Площадь $\Delta \mathrm{BGD}=\ dfrac{1}{2} \times \mathrm{GD} \times \mathrm{BD}$ $=\dfrac{1}{2} \times 8 \times 6=24$ кв.ед. Q5. Два равносторонних треугольника со стороной 4 см каждый, но обозначенные как △ABC и △LHN, не равны. Правда или ложь? Ответ: Два равносторонних треугольника с равными сторонами всегда равны, независимо от того, как они обозначены. Итак, утверждение Ложное. 9{2}}{4}}$ Q2. Найдите длину медианы AD, если координаты треугольника ABC равны A(1,0), B(0,1), C(1,1) Ответ: $\dfrac{\sqrt{5}}{ 2}$ Q3. Данное утверждение истинно или ложно, то есть точка, где медиана встречается с противоположными сторонами, является серединой этой линии. Ответ: Правда Q4. Для любого треугольника центр тяжести является точкой совпадения __________ треугольника Ответ: медианы Q5. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт