Как найти производную по определению?
Составить отношение 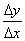 и вычислить предел
и вычислить предел 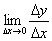 .
.
Откуда появилась таблица производных и правила дифференцирования? Благодаря единственному пределу 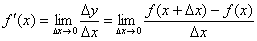 . Кажется волшебством, но в действительности – ловкость рук и никакого мошенничества. На уроке Что такое производная? я начал рассматривать конкретные примеры, где с помощью определения нашёл производные линейной и квадратичной функции. В целях познавательной разминки продолжим тревожить таблицу производных, оттачивая алгоритм и технические приёмы решения:
. Кажется волшебством, но в действительности – ловкость рук и никакого мошенничества. На уроке Что такое производная? я начал рассматривать конкретные примеры, где с помощью определения нашёл производные линейной и квадратичной функции. В целях познавательной разминки продолжим тревожить таблицу производных, оттачивая алгоритм и технические приёмы решения:
Пример 1
Найти производную функции 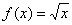
По сути, требуется доказать частный случай производной степенной функции, который обычно фигурирует в таблице: 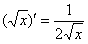 .
.
Решение технически оформляется двумя способами. Начнём с первого, уже знакомого подхода: лесенка начинается с дощечки, а производная функция – с производной в точке.
Рассмотрим некоторую (конкретную) точку 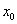 , принадлежащую области определения функции
, принадлежащую области определения функции 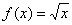 , в которой существует производная. Зададим в данной точке приращение
, в которой существует производная. Зададим в данной точке приращение  (разумеется, не выходящее за рамки
(разумеется, не выходящее за рамки
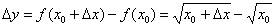
Вычислим предел: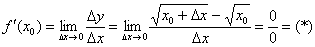
Неопределённость 0:0 устраняется стандартным приёмом, рассмотренным ещё в первом веке до нашей эры. Домножим числитель и знаменатель на сопряженное выражение 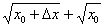 :
:
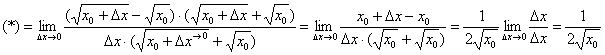
Техника решения такого предела подробно рассмотрена на вводном уроке о пределах функций.
Итак, 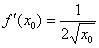 .
.
Поскольку в качестве 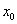
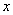 интервала
интервала 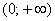 , то, осуществив замену
, то, осуществив замену 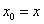 , получаем:
, получаем:
Ответ: по определению производной: 
Готово.
В который раз порадуемся логарифмам:
Пример 2
Найти производную функции 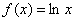 , пользуясь определением производной
, пользуясь определением производной
Решение: рассмотрим другой подход к раскрутке той же задачи. Он точно такой же, но более рационален с точки зрения оформления. Идея состоит в том, чтобы в начале решения избавиться от подстрочного индекса и вместо буквы 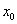
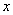 .
.
Рассмотрим произвольную точку 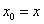 , принадлежащую области определения функции
, принадлежащую области определения функции 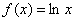 (интервалу
(интервалу 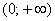 ), и зададим в ней приращение
), и зададим в ней приращение  . А вот здесь, кстати, как и в большинстве случаев, можно обойтись без всяких оговорок, поскольку логарифмическая функция дифференцируема в любой точке области определения.
. А вот здесь, кстати, как и в большинстве случаев, можно обойтись без всяких оговорок, поскольку логарифмическая функция дифференцируема в любой точке области определения.
Тогда соответствующее приращение функции:
Найдём производную: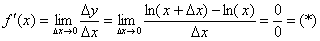
Простота оформления уравновешивается путаницей, которая может возникнуть у начинающих (да и не только). Ведь мы привыкли, что в пределе изменяется буква «икс»! Но тут всё по-другому: 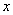 – античная статуя, а
– античная статуя, а  – живой посетитель, бодро шагающий по коридору музея. То есть «икс» – это «как бы константа».
– живой посетитель, бодро шагающий по коридору музея. То есть «икс» – это «как бы константа».
Устранение неопределённости 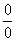 закомментирую пошагово:
закомментирую пошагово:
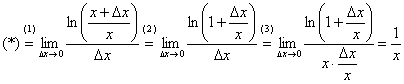
(1) Используем свойство логарифма 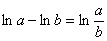 .
.
(2) В скобках почленно делим числитель на знаменатель.
(3) В знаменателе искусственно домножаем и делим на «икс» чтобы воспользоваться замечательным пределом 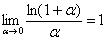 , при этом в качестве бесконечно малой величины выступает
, при этом в качестве бесконечно малой величины выступает 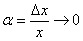 .
.
Ответ: по определению производной: 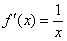
Или сокращённо: 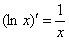
Пример 3
Найти производную 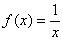 по определению
по определению
В данном случае составленное приращение 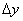 сразу же удобно привести к общему знаменателю. Примерный образец оформления задания в конце урока (первый способ).
сразу же удобно привести к общему знаменателю. Примерный образец оформления задания в конце урока (первый способ).
Пример 3:Решение: рассмотрим некоторую точку 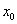 , принадлежащую области определения функции
, принадлежащую области определения функции 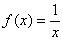 . Зададим в данной точке приращение
. Зададим в данной точке приращение  и составим соответствующее приращение функции:
и составим соответствующее приращение функции:
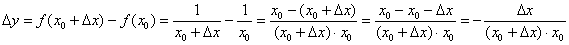
Найдём производную в точке
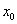 :
: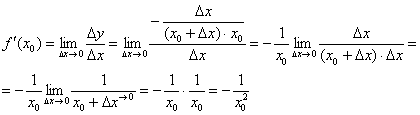
Так как в качестве
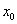 можно выбрать любую точку
можно выбрать любую точку 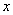 области определения функции
области определения функции 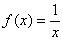 , то
, то 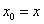 и
и 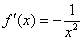
Ответ:
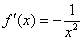 по определению производной
по определению производной
Пример 4
Найти производную 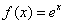 по определению
по определению
А тут всё необходимо свести к замечательному пределу 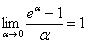 . Решение оформлено вторым способом.
. Решение оформлено вторым способом.
Аналогично выводится ряд других табличных производных. Полный список можно найти в школьном учебнике, или, например, 1-м томе Фихтенгольца. Не вижу особого смысла переписывать из книг и доказательства правил дифференцирования – они тоже порождены формулой 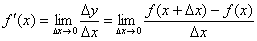 .
.
Пример 4:
Решение: рассмотрим произвольную точку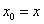 , принадлежащую
, принадлежащую  , и зададим в ней приращение
, и зададим в ней приращение  . Тогда соответствующее приращение функции:
. Тогда соответствующее приращение функции: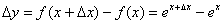
Найдём производную:
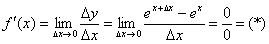
Используем замечательный предел
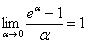
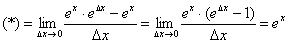
Ответ
 по определению
по определению
Пример 5
Найти производную функции  , используя определение производной
, используя определение производной
Решение: используем первый стиль оформления. Рассмотрим некоторую точку 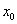 , принадлежащую
, принадлежащую  , изададим в ней приращение аргумента
, изададим в ней приращение аргумента  . Тогда соответствующее приращение функции:
. Тогда соответствующее приращение функции: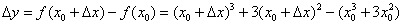
Возможно, некоторые читатели ещё не до конца поняли принцип, по которому нужно составлять приращение 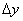 . Берём точку
. Берём точку 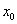 (число) и находим в ней значение функции:
(число) и находим в ней значение функции: 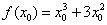 , то есть в функцию
, то есть в функцию  вместо «икса» следует подставить
вместо «икса» следует подставить 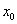 . Теперь берём тоже вполне конкретное число
. Теперь берём тоже вполне конкретное число 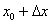 и так же подставляем его в функцию
и так же подставляем его в функцию  вместо «икса»:
вместо «икса»: 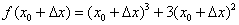 . Записываем разность
. Записываем разность 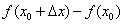 , при этом
, при этом 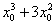 необходимо полностью взять в скобки.
необходимо полностью взять в скобки.
Составленное приращение функции 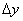 бывает выгодно сразу же упростить. Зачем? Облегчить и укоротить решение дальнейшего предела.
бывает выгодно сразу же упростить. Зачем? Облегчить и укоротить решение дальнейшего предела.
Используем формулы 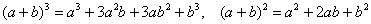 , раскрываем скобки и сокращаем всё, что можно сократить:
, раскрываем скобки и сокращаем всё, что можно сократить: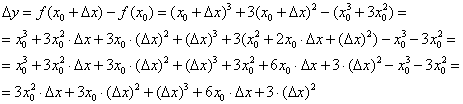
Индейка выпотрошена, с жаркое никаких проблем: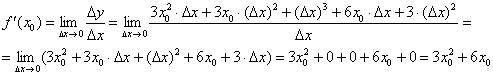
В итоге: 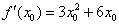
Поскольку в качестве 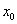 можно выбрать любое действительное число, то проведём замену
можно выбрать любое действительное число, то проведём замену 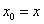 и получим
и получим 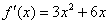 .
.
Ответ: 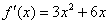 по определению.
по определению.
В целях проверки найдём производную с помощью правил дифференцирования и таблицы: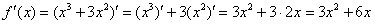
Всегда полезно и приятно знать правильный ответ заранее, поэтому лучше мысленно либо на черновике продифференцировать предложенную функцию «быстрым» способом в самом начале решения.
Пример 6
Найти производную функции 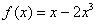 по определению производной
по определению производной
Это пример для самостоятельного решения. Результат лежит на поверхности: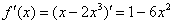
Пример 6:Решение: рассмотрим некоторую точку 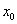 , принадлежащую
, принадлежащую  , и зададим в ней приращение аргумента
, и зададим в ней приращение аргумента  . Тогда соответствующее приращение функции:
. Тогда соответствующее приращение функции:
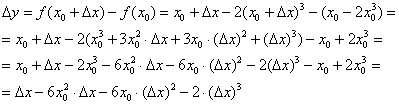
Вычислим производную:
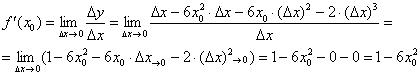
Таким образом: 
Поскольку в качестве 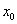 можно выбрать любое действительное число, то
можно выбрать любое действительное число, то 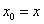 и
и 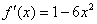
Ответ: 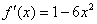 по определению.
по определению.
Вернёмся к стилю №2:
Пример 7
Пользуясь определением, найти производную функции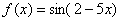
Давайте немедленно узнаем, что должно получиться. По правилу дифференцирования сложной функции: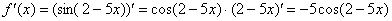
Решение: рассмотрим произвольную точку 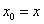 , принадлежащую
, принадлежащую  , зададим в ней приращение аргумента
, зададим в ней приращение аргумента  и составим приращение функции:
и составим приращение функции: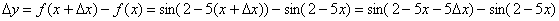
Найдём производную: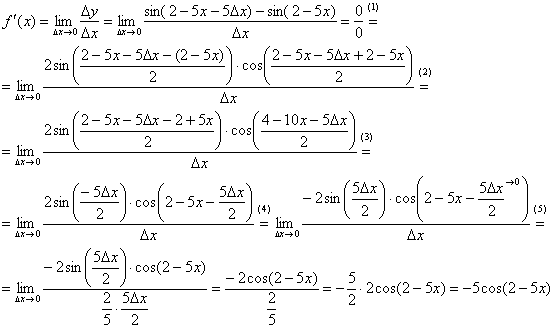
(1) Используем тригонометрическую формулу 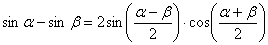 .
.
(2) Под синусом раскрываем скобки, под косинусом приводим подобные слагаемые.
(3) Под синусом сокращаем слагаемые, под косинусом почленно делим числитель на знаменатель.
(4) В силу нечётности синуса выносим «минус». Под косинусом указываем, что слагаемое 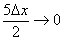 .
.
(5) В знаменателе проводим искусственное домножение, чтобы использовать первый замечательный предел 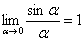 . Таким образом, неопределённость устранена, причёсываем результат.
. Таким образом, неопределённость устранена, причёсываем результат.
Ответ: 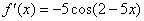 по определению
по определению
Как видите, основная трудность рассматриваемой задачи упирается в сложность самого предела + небольшое своеобразие упаковки. На практике встречаются и тот и другой способ оформления, поэтому я максимально подробно расписываю оба подхода. Они равноценны, но всё-таки, по моему субъективному впечатлению, чайникам целесообразнее придерживаться 1-го варианта с «икс нулевым».
Пример 8
Пользуясь определением, найти производную функции
Пример 8:Решение: рассмотрим произвольную точку 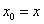 , принадлежащую
, принадлежащую  , зададим в ней приращение
, зададим в ней приращение  и составим приращение функции:
и составим приращение функции:
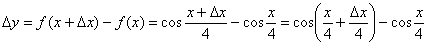
Найдём производную:
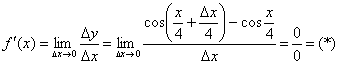
Используем тригонометрическую формулу 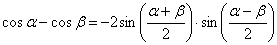 и первый замечательный предел:
и первый замечательный предел:
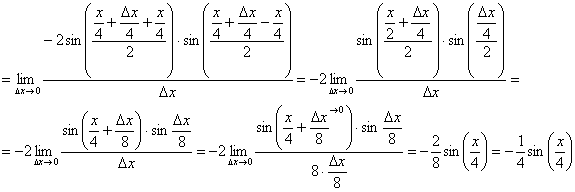
Ответ: 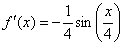 по определению
по определению
Разберём более редкую версию задачи:
Пример 9
Найти производную функции 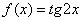 в точке
в точке  , пользуясь определением производной.
, пользуясь определением производной.
Во-первых, что должно получиться в сухом остатке? Число
Вычислим ответ стандартным способом: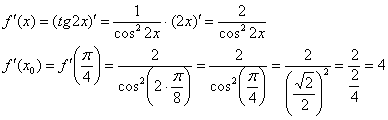
Решение: с точки зрения наглядности это задание значительно проще, так как в формуле 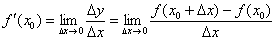 вместо
вместо 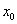 рассматривается конкретное значение.
рассматривается конкретное значение.
Зададим в точке  приращение
приращение  и составим соответствующее приращение функции:
и составим соответствующее приращение функции: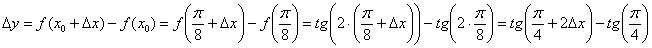
Вычислим производную в точке:
Используем весьма редкую формулу разности тангенсов 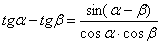 и в который раз сведём решение к первому замечательному пределу:
и в который раз сведём решение к первому замечательному пределу:
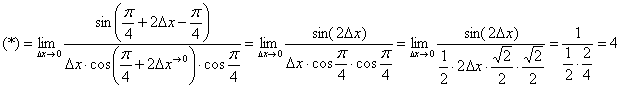
Ответ: 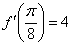 по определению производной в точке.
по определению производной в точке.
Задачу не так трудно решить и «в общем виде» – достаточно заменить 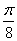 на
на 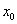 или просто
или просто 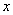 в зависимости от способа оформления. В этом случае, понятно, получится не число, а производная функция.
в зависимости от способа оформления. В этом случае, понятно, получится не число, а производная функция.
Пример 10
Используя определение, найти производную функции 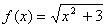 в точке
в точке 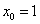
Пример 10:Решение: Зададим приращение  в точке
в точке 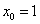 . Тогда приращение функции:
. Тогда приращение функции:
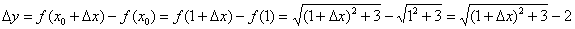
Вычислим производную в точке:
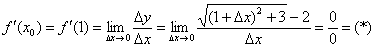
Умножим числитель и знаменатель на сопряженное выражение:
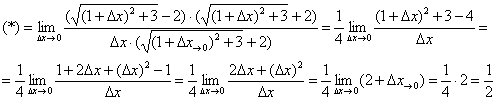
Ответ: 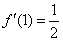 по определению производной в точкеЗаключительная бонус-задача предназначена, прежде всего, для студентов с углубленным изучением математического анализа, но и всем остальным тоже не помешает:
по определению производной в точкеЗаключительная бонус-задача предназначена, прежде всего, для студентов с углубленным изучением математического анализа, но и всем остальным тоже не помешает:
Пример 11
Будет ли дифференцируема функция  в точке
в точке 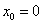 ?
?
Решение: очевидно, что кусочно-заданная функция непрерывна в точке 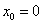 , но будет ли она там дифференцируема?
, но будет ли она там дифференцируема?
Алгоритм решения, причём не только для кусочных функций, таков:
1) Находим левостороннюю производную в данной точке: 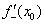 .
.
2) Находим правостороннюю производную в данной точке:  .
.
3) Если односторонние производные конечны и совпадают: 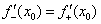 , то функция
, то функция 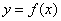 дифференцируема в точке
дифференцируема в точке 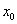 и геометрически здесь существует общая касательная (см. теоретическую часть урока Определение и смысл производной). Если получены два разных значения:
и геометрически здесь существует общая касательная (см. теоретическую часть урока Определение и смысл производной). Если получены два разных значения:  (одно из которых может оказаться и бесконечным), то функция не дифференцируема в точке
(одно из которых может оказаться и бесконечным), то функция не дифференцируема в точке 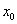 .
.
Если же обе односторонние производные равны бесконечности (пусть даже разных знаков), то функция 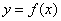 не дифференцируема в точке
не дифференцируема в точке 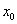 , но там существует бесконечная производная и общая вертикальная касательная к графику (см. Пример 5 урока Уравнение нормали).
, но там существует бесконечная производная и общая вертикальная касательная к графику (см. Пример 5 урока Уравнение нормали).
! Примечание: таким образом, между вопросами «Будет ли дифференцируема функция в точке?» и «Существует ли производная в точке?» есть разница!
Всё очень просто!
1) При нахождении левосторонней производной приращение аргумента отрицательно: 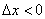 , а слева от точки
, а слева от точки 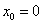 расположена парабола
расположена парабола 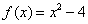 , поэтому приращение функции равно:
, поэтому приращение функции равно: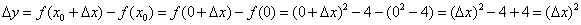
И соответствующий левосторонний предел численно равен левосторонней производной в рассматриваемой точке: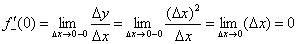
2) Справа от точки 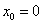 находится график прямой
находится график прямой 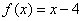 и приращение аргумента положительно:
и приращение аргумента положительно: 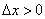 . Таким образом, приращение функции:
. Таким образом, приращение функции: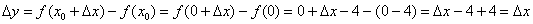
Правосторонний предел и правосторонняя производная в точке: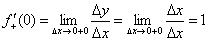
3) Односторонние производные конечны и различны: 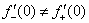
Ответ: функция не дифференцируема в точке 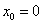 .
.
Ещё легче доказывается книжный случай недифференцируемости модуля 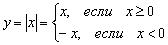 в точке
в точке 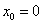 , о котором я в общих чертах уже рассказал на теоретическом уроке о производной.
, о котором я в общих чертах уже рассказал на теоретическом уроке о производной.
Некоторые кусочно-заданные функции дифференцируемы и в точках «стыка» графика, например, котопёс  обладает общей производной и общей касательной (ось абсцисс) в точке
обладает общей производной и общей касательной (ось абсцисс) в точке 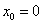 . Кривой, да дифференцируемый на
. Кривой, да дифференцируемый на  ! Желающие могут убедиться в этом самостоятельно по образцу только что решённого примера.
! Желающие могут убедиться в этом самостоятельно по образцу только что решённого примера.
Читайте также:
Рекомендуемые страницы:
Поиск по сайту
Конспект занятия на тему «Приращение аргумента и функции. Определение производной. Алгоритм вычисления производной по определению. Таблица производных. Правила вычисления производной»














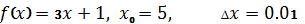 Конспект занятия на тему «Приращение аргумента и функции. Определение производной. Алгоритм вычисления производной по определению. Таблица производных. Правила вычисления производной»
Конспект занятия на тему «Приращение аргумента и функции. Определение производной. Алгоритм вычисления производной по определению. Таблица производных. Правила вычисления производной»
Цели:
ввести понятия приращение аргумента и приращение функции;
научить находить приращение аргумента и приращение функции;
ввести понятие производной;
способствовать выработке навыка нахождения производной по определению;
Учить находить производную по таблице;
Учить использовать правила дифференцирования;
Дидактический материал: опорный конспект, карточки-задания для индивидуальной работы, памятки, учебник Колмогорова А.Н. «Алгебра и начала анализа. 10-11классы», обучающий видеокурс «Математика 7-11», Математика – учебное электронное издание 5-11. Математический дневник .
План урока
Организационный момент.
Актуализация знаний:
Фронтальный опрос;
Работа с карточками.
Изучение нового материала:
Приращение аргумента и приращение функции;
Понятие «Производная»;
Схема вычисления производной по определению;
Таблица производных;
Правила дифференцирования.
Закрепление изученного.
Подведение итогов.
Домашнее задание.
Рефлексия.
Ход урока
Организационный момент
доброжелательный настрой учителя и учащихся;
быстрое включение класса в деловой ритм;
организация внимания всех учащихся;
сообщение темы и целей урока.
Актуализация знаний
(выявление факта выполнения (не выполнения) домашнего задания у всего класса, устранение типичных ошибок; работа организована параллельно: учащимся на выбор предлагается письменно ответить на вопросы или участвовать в фронтальном опросе. Учащиеся, работающие письменно, садятся на первые парты. Двое учащихся вызывается к доске для написания домашней работы.)
2.1. Фронтальный опрос
— Что такое последовательность?
— Какие виды последовательностей вы знаете?
— Как задаётся числовая последовательность?
— Что мы называем пределом последовательности?
— Как найти предел последовательности, при  ?
?
— Как найти предел при  к конкретному числу?
к конкретному числу?
2.2. Индивидуальные задания для учащихся
Карточка 1
Дайте определение понятию «Предел последовательности»
Вычислите
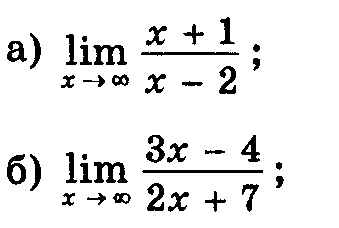
Как найти предел последовательности, при 
Если Вы не справились с заданием укажите причину вызвавшую у Вас затруднение.
Карточка 2
Дайте определение понятию «Предел последовательности»
Вычислите
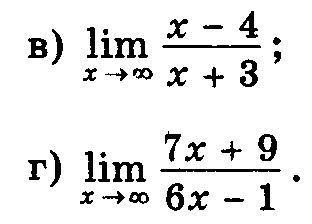
Как найти предел, при 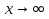 ? При
? При 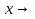 к конкретному числу
к конкретному числу
Если Вы не справились с заданием укажите причину вызвавшую у Вас затруднение.
Изучение нового материала
Приращение аргумента и приращение функции
Часто нас интересует не значение какой либо величины, а ее изменение. Например, сила упругости пружины пропорциональна удлинению пружины; работа есть изменение энергии; средняя скорость это отношение перемещения к промежутку времени, за который было совершено это перемещение, и т. д.
При сравнении значения функции f в некоторой фиксированной точке х0 со значениями этой функции в различных точках х, лежащих в окрестности х0, удобно выражать разность f (х )- f (х0) через разность (х-х0), пользуясь понятиями «приращение аргумента» и «приращение функции». Объясним их смысл. (Просмотр видеокурса «Математика 7-11» — Определение производной (приращение аргумента и приращение функции)).
Пусть х- произвольная точка, лежащая в некоторой окрестности фиксированной точки х0. Разность (х-х0 ) называется приращением независимой переменной х (или приращением аргумента) в точке х0 и обозначается 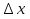 .
. 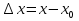
Приращение функции f в точке х0, соответствующее приращению 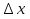 , обозначается
, обозначается 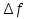 , и находится по формуле
, и находится по формуле 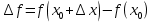
Графически это можно изобразить так: x, х0 — это точки, f(x), f(x0)-значения функции в этих точек. Тогда ∆f – это разность (f(x) – f(x0) — (отрезок ∆f), а ∆х- разность (х-х0 ) — отрезок ∆х. На графике хорошо видно, что приращение функции ∆f зависит от приращения аргумента ∆х. Если мы уменьшим значение ∆х , то значение ∆f тоже уменьшится.( в процессе обсуждения преподаватель чертит график на доске)
f(x)
∆f
f(x0)
∆х
х
х0
Составьте опорный конспект.
Для лучшего понимания давайте рассмотрим несколько примеров по данной формуле
№ 178 –Найдите приращение функции f в точке х0
а) решает учитель с объяснением у доски
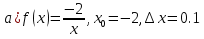
Решение: 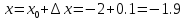
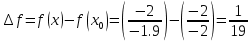
Ученик у доски. 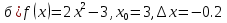
Самостоятельно: Найдите приращение функции f в точке х0
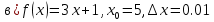
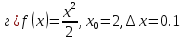
Выполнить на компьютерах «Математика – учебное электронное издание 5-11» задания «Приращение аргумента и приращение функции — № 1-4». Результаты выполнения заносятся в журнал программы. Правильность решения проверяется всей группой сверяя свои результаты с результатом программы.
3.2. Понятие «Производная»
— Мы усвоили понятие приращение функции и приращение аргумента, что позволяет нам перейти к рассмотрению понятия «Производная». Формулировка определения производной основано на понятии предела.
Производной функции f в точке х0 называется число, к которому стремится разностное отношение 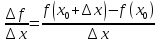 при
при 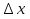 , стремящемся к нулю.
, стремящемся к нулю.
Производная функции f в точке хо обозначается f‘ (х0) (читается: «эф штрих от х0»).
3.3.Схема вычисления производной по определению
1. С помощью формулы, задающей функцию f , находим ее приращение в точке х0: 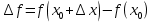
2. Находим выражение для разностного отношения 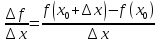 , которое затем преобразуем – упрощаем, сокращаем на
, которое затем преобразуем – упрощаем, сокращаем на 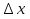 и т.д.
и т.д.
3. Выясняем, к какому числу стремится 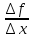 , если считать что
, если считать что 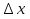 стремится к нулю.
стремится к нулю.
(дежурный раздает памятки «Вычисление производной по пределению»)
— Рассмотрим вычисление производной по данной схеме на конкретном примере:
Пример 1. Найдем производную функции f(x)=x3 в точке х0.
Будем действовать используя памятку.


Заметим, что
 постоянно, а при
постоянно, а при  очевидно, что
очевидно, что  , а значит
, а значит . Получаем
. Получаем  .
.Следовательно f’(x0)=3x02.
Пример 2. Найдем производную функции f(x)=kx+b (k, b — постоянны) в точке х0.
∆f=(k(x0+∆x)+b)-(kx0+b)=k∆x

Поскольку k— постоянная,
 — постоянное число при любом ∆ х, и, значит,
— постоянное число при любом ∆ х, и, значит,  при
при  .
.Итак, (kx+b)’=k
— Для закрепления решим у доски №194
(задания решаются параллельно: слабых учащихся вызывают к доске, а более сильные пробуют решить самостоятельно в тетрадях. После решения обязательно сверить результаты с доской)
Учащиеся получают карточки-консультанты.
194. Пользуясь карточкой-консультантом, найдите значения производной функции f, если:
а) f (х) = х 2— 3х в точках -1; 2;
б) f (х) = 2х 3 в точках 0; 1;
в) f (х) =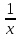 в точках -2; 1;
в точках -2; 1;
г) f (х) = 4- х 2в точках 3; о.
3.4.Таблица производных
— Часто встречаются задания, в которых неудобно, долго вычислять производную по определению. Поэтому существует таблица производных, которая помогает и облегчает работу по нахождению производной. Данной таблицей пользоваться очень просто. В ней представлена функция и найдена ее производная. Вам нужно найти необходимую функцию и посмотреть, чему равна ее производная. Давайте вместе прочитаем данную таблицу (дежурный раздает всем учащимся таблицы производных).
Функция
Производная
y=C
y´=0
y=x
y´=1
y=kx
y´=k
y=kx+m
y´=k
y=x ͫ
y´=mx ͫ¯¹
y=k x ͫ
y´=kmx ͫ¯¹
y =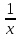
y´=-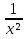
y=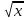
y´=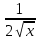
y=sin x
y´=cos x
y=cos x
y´= — sin x
y=tg x
y´=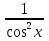
y=ctg x
y´=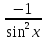
— Давайте вычислим производную функции используя таблицу:
(При работе с заданием учащиеся по цепочке выходят к доске, называют функцию, показывают в таблице соответствующую формулу, при необходимости называют постоянный множитель и под руководством преподавателя записывают решение на доске)
а) y=2.5
и) y=2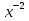
б) y=-3.2
к) y=3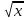
в) y=7.5x
л) y= sin x
г) y=-10x
м) y=2cos x
д) y=x²
н) y=3sin x
е) y=2x⁵
о) y=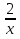
ж) y=2.4x⁴
п) y=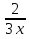
з) y=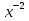
р) y= — 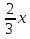
3.5.Правила дифференцирования
Мы рассматривали с вами простые задания, в которых дана одна функция и с этой функцией не выполняют ни каких операций. Но если мы рассмотрим такой пример : 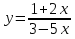 . Как найти производную?
. Как найти производную?
Для вычисления производных используют правила дифференцирования
Пр 1. Если функции u и v дифференцируемы в точке хо, то их сумма дифференцируема в этой точке и (u + v )’ = и’+ v ‘
Пример:
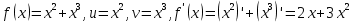
Лемма. Если функция f дифференцируема в точке х0, то она непрерывна в этой точке: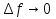 при x
при x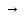 x0, т.е.
x0, т.е. 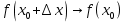 при
при 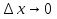 .
.
Пр 2. Если функции и и v дифференцируемы в точке хо, то их произведение дифференцируемо в этой точке и (uv)’ = u’v + uv’
Пример: 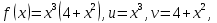
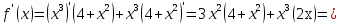
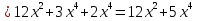
Следствие. Если функция и дифференцируема в хо, а С постоянная, то функция Си дифференцируема в этой точке и (Си)’ = Си’.
Пр 3. Если функции и и v дифференцируемы в точке хо и функция v не равна нулю в этой точке, то частное 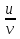 также дифференцируемо в хо и
также дифференцируемо в хо и 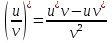
Пример: 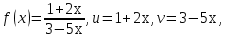
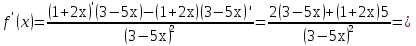
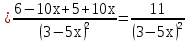
Для закрепления правил дифференцирования просмотр видеокурса «Математика 7- 11» (правила дифференцирования).
Составьте математическую карту темы.
4. Закрепление изученного
— На конкретных примерах рассмотрим, как пользоваться данными правилами (задания решаются под руководством учителя. Задания стоящие под буквой а) учитель решает на доске с четким объяснением. При работе с заданиями следует постоянно обращаться к правилам дифференцирования. Учащимся предлагается, по желанию, решить задания самостоятельно или у доски. Учащиеся, которые выполняли задания самостоятельно, могут пользоваться карточкой-консультантом, обязательно сверяют свои решения с доской. Первые учащиеся, справившиеся с заданиями, подносят тетради на проверку преподавателю.)
4.
3.
2.
1.

5. Подведение итогов
— С какими новыми понятиями вы познакомились на сегодняшнем занятии
— что такое приращение функции и приращение аргумента и как они вычисляются
— дайте определение производной
— как вычислить производную с помощью определения?
-как еще можно вычислить производную?
-какие правила дифференцирования мы узнали?
-какие новые правила необходимо занести в математический дневник?
6. Задание на дом
— занести необходимые правила в математический дневник (из учебника «Алгебра и начала анализа 10-11 кл» Колмогоров А.Н.)
— подготовить доклады на тему «Из истории «Производной»»
— выучить основные понятия, правила, и таблицу производных
— начать выполнение домашней самостоятельной работы
7. Рефлексия
Откройте и заполните свои математические дневники.
Заполните колонку «Рекомендации себе» ответами на следующие вопросы:
Что Вам понравилось на уроке?
Довольны ли Вы своей работай на уроке?
Устали ли Вы за урок?
Был ли материал урока, для Вас, понятен, полезен, интересен?
Какой материал необходимо повторить?
Производная функции по определению
Пример 1. Исходя из определения производной (не пользуясь формулами дифференцирования), найти производную функции
Решение. Дадим х приращение , тогда у получит приращение :
Найдем приращение функции:
Находим отношение приращения функции к приращению аргумента:
Найдем предел этого отношения при
Следовательно, по определению производной
Пример 2. Исходя из определения производной (не пользуясь формулами дифференцирования), найти производную функции
Решение. Находим приращение функции: . Отсюда и
Таким образом,
Итак, .
Пример 3. Найти производную (добавлено по просьбам)
Решение. Исходную функцию желательно сразу сократить Находим приращение функции: . Отсюда и
Таким образом,
Производная функции. Геометрический и физический смысл
Категория: Справочные материалы
Елена Репина 2013-08-06 2014-01-11Определение производной

Производной функции  в точке
в точке  называется предел отношения приращения функции
называется предел отношения приращения функции  к приращению аргумента
к приращению аргумента  при
при  , если этот предел существует.
, если этот предел существует.

Пример:


Но нет необходимости каждый раз пользоваться этим определением для нахождения производной…
Работу нам упростит таблица производных и правила дифференцирования.
Геометрический смысл производной

Если мы рассмотрим прямоугольный треугольник  , то заметим, что
, то заметим, что  есть
есть  .
.
А при стремлении  к нулю, точка
к нулю, точка  будет приближаться к точке
будет приближаться к точке  и секущая
и секущая  «превратится» в касательную к графику функции
«превратится» в касательную к графику функции  в точке
в точке  .
.
Поэтому геометрический смысл производной таков:
Производная в точке  (
( ) равна тангенсу угла наклона касательной к графику функции
) равна тангенсу угла наклона касательной к графику функции  в этой точке:
в этой точке:
 ,
,
где  – угол наклона касательной (проведенной к
– угол наклона касательной (проведенной к  в т.
в т.  )
)

Физический смысл производной
Если точка движется вдоль оси  и ее координаты изменяются по закону
и ее координаты изменяются по закону  , то мгновенная скорость точки:
, то мгновенная скорость точки:
 ,
,
а ускорение:

Пример:
Материальная точка движется прямолинейно по закону  , где
, где  — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах,  — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени
— время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени  .
.
Решение:

 м/с
м/с
Ответ: 60.
Уравнение касательной
Уравнение касательной к графику  в точке
в точке  :
:

Пример:
Составить уравнение касательной к графику функции  в точке
в точке  .
.
Решение:
1. 

2. 
3. 

Ответ: 
Смотрите также «Производная функции в точке. Знак производной и монотонность функции»
Автор: egeMax | Нет комментариев
Вторая производная — Студопедия
Всё очень просто. Вторая производная – это производная от первой производной: 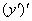
Стандартные обозначения второй производной: 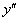 ,
, 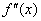 или
или 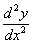 (дробь читается так: «дэ два игрек по дэ икс квадрат»). Чаще всего вторую производную обозначают первыми двумя вариантами. Но третий вариант тоже встречается, причем, его очень любят включать в условия контрольных заданий, например: «Найдите
(дробь читается так: «дэ два игрек по дэ икс квадрат»). Чаще всего вторую производную обозначают первыми двумя вариантами. Но третий вариант тоже встречается, причем, его очень любят включать в условия контрольных заданий, например: «Найдите 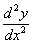 функции…». А студент сидит и битый час чешет репу, что это вообще такое.
функции…». А студент сидит и битый час чешет репу, что это вообще такое.
Рассмотрим простейший пример. Найдем вторую производную от функции 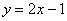 .
.
Для того чтобы найти вторую производную, как многие догадались, нужно сначала найти первую производную:
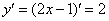
Теперь находим вторую производную:
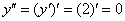
Готово.
Рассмотрим более содержательные примеры.
Пример 11
Найти вторую производную функции 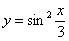
Найдем первую производную: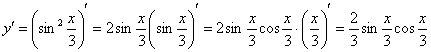
На каждом шаге всегда смотрим, нельзя ли что-нибудь упростить? Сейчас нам предстоит дифференцировать произведение двух функций, и мы избавимся от этой неприятности, применив известную тригонометрическую формулу 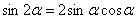 . Точнее говоря, использовать формулу будем в обратном направлении:
. Точнее говоря, использовать формулу будем в обратном направлении: 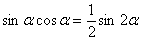 :
:
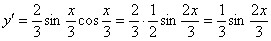
Находим вторую производную: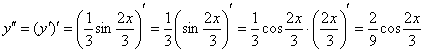
Готово.
Можно было пойти другим путём – понизить степень функции еще перед дифференцированием, используя формулу 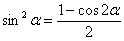 :
:
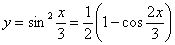
Если интересно, возьмите первую и вторую производные снова. Результаты, естественно, совпадут.
Отмечу, что понижение степени бывает очень выгодно при нахождении частных производных функции. Здесь же оба способа решения будут примерно одинаковой длины и сложности.
Как и для первой производной, можно рассмотреть задачу нахождения второй производной в точке.
Например: Вычислим значение найденной второй производной в точке 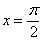 :
:
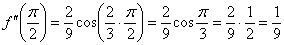
Необходимость находить вторую производную и вторую производную в точке возникает при исследовании графика функции на выпуклость/вогнутость и перегибы.
Пример 12
Найти вторую производную функции 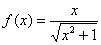 . Найти
. Найти 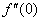
Это пример для самостоятельного решения.
Аналогично можно найти третью производную, а также производные более высоких порядков. Такие задания встречаются, но встречаются значительно реже. Можно рассказать о специфических приемах, формуле Лагранжа, и по мере наличия времени я обязательно напишу отдельный методический материал.
Желаю успехов!
Решения и ответы:
Пример 2: Найдем производную: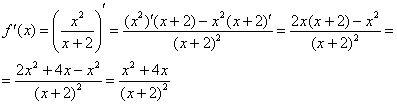
Вычислим значение функции в точке 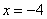 :
:
Пример 4: Найдем производную: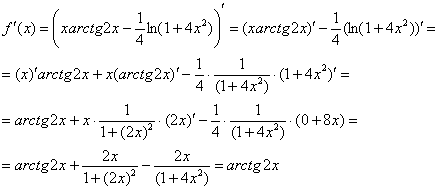
Вычислим производную в заданной точке:
Пример 6: Уравнение касательной составим по формуле 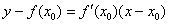
1) Вычислим значение функции в точке  :
: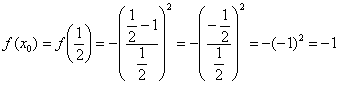
2) Найдем производную. Перед дифференцированием функцию выгодно упростить: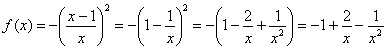

3) Вычислим значение производной в точке  :
: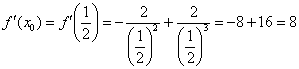
4) Подставим значения 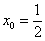 ,
, 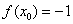 и
и 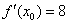 в формулу
в формулу 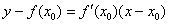 :
:
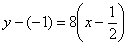
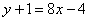
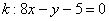
Пример 8: Преобразуем функцию: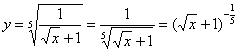
Найдем производную:
Запишем дифференциал: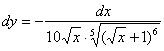
Пример 10: Найдем производную: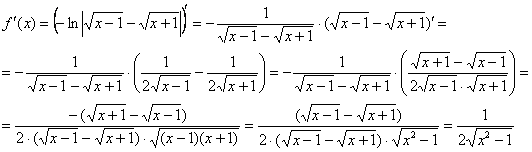
Запишем дифференциал: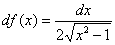
Вычислим дифференциал в точке 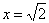 :
: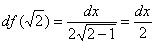
Пример 12: Найдем первую производную:
Найдем вторую производную: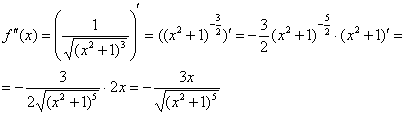
Вычислим: 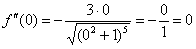
Автор: Емелин Александр
Производная по определению (через предел). Примеры решений
Когда человек сделал первые самостоятельные шаги в изучении математического анализа и начинает задавать неудобные вопросы, то уже не так-то просто отделаться фразой, что «дифференциальное исчисление найдено в капусте». Поэтому настало время набраться решимости и раскрыть тайну появления на свет таблицы производных и правил дифференцирования. Начало положено в статье о смысле производной, которую я настоятельно рекомендую к изучению, поскольку там мы как раз рассмотрели понятие производной и начали щёлкать задачи по теме.
Этот же урок носит ярко выраженную практическую направленность, более того, рассматриваемые ниже примеры, в принципе, можно освоить и чисто формально (например, когда нет времени/желания вникать в суть производной). Также крайне желательно (однако опять не обязательно) уметь находить производные «обычным» методом – хотя бы на уровне двух базовых занятий: Как найти производную? и Производная сложной функции.
Но без чего-чего сейчас точно не обойтись, так это без пределов функций. Вы должны ПОНИМАТЬ, что такое предел и уметь решать их, как минимум, на среднем уровне. А всё потому, что производная функции в точке
в точке  задаётся формулой:
задаётся формулой: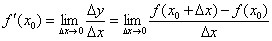
Напоминаю обозначения и термины: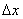 называют приращением аргумента;
называют приращением аргумента; 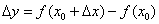 – приращением функции;
– приращением функции; – это ЕДИНЫЕ символы («дельту» нельзя «отрывать» от «икса» или «игрека»).
– это ЕДИНЫЕ символы («дельту» нельзя «отрывать» от «икса» или «игрека»).
Очевидно, что 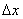 является «динамической» переменной,
является «динамической» переменной,  – константой и результат вычисления предела
– константой и результат вычисления предела 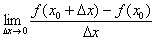 – ЧИСЛОМ. И в самом деле, ведь производная в точке
– ЧИСЛОМ. И в самом деле, ведь производная в точке 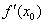 – это число (см. практикум Простейшие задачи дифференцирования).
– это число (см. практикум Простейшие задачи дифференцирования).
В качестве точки  можно рассмотреть ЛЮБОЕ значение
можно рассмотреть ЛЮБОЕ значение 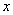 , принадлежащее области определения функции
, принадлежащее области определения функции 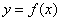 , в котором существует производная.
, в котором существует производная.
! Примечание: оговорка «в котором существует производная» – в общем случае существенна! Так, например, точка 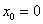 хоть и входит в область определения функции
хоть и входит в область определения функции 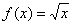 , но производной
, но производной 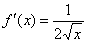 там не существует. Поэтому формула
там не существует. Поэтому формула 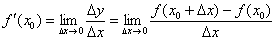 не применима в точке
не применима в точке 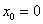 , и укороченная формулировка без оговорки будет некорректна. Это же замечание следует делать для некоторых других функций с «обрывами» графика, в частности, для арксинуса, арккосинуса, а также у функций, графики которых содержат «плохие» остриё и изломы. Данные моменты подробнее разъясняются в статье Интервалы монотонности и экстремумы функции.
, и укороченная формулировка без оговорки будет некорректна. Это же замечание следует делать для некоторых других функций с «обрывами» графика, в частности, для арксинуса, арккосинуса, а также у функций, графики которых содержат «плохие» остриё и изломы. Данные моменты подробнее разъясняются в статье Интервалы монотонности и экстремумы функции.
Таким образом, после замены 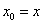 , получаем вторую рабочую формулу:
, получаем вторую рабочую формулу: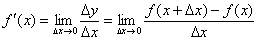
Обратите внимание на коварное обстоятельство, которое может запутать чайника: в данном пределе «икс», будучи сам независимой переменной, исполняет роль статиста, а «динамику» задаёт опять же приращение 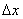 . Результатом вычисления предела
. Результатом вычисления предела 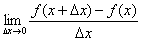 является производная функция
является производная функция  .
.
Исходя из вышесказанного, сформулируем условия двух типовых задач:
– Найти производную в точке, используя определение производной.
– Найти производную функцию, используя определение производной. Эта версия, по моим наблюдениям, встречается заметно чаще и ей будет уделено основное внимание.
Принципиальное отличие заданий состоит в том, что в первом случае требуется найти число, а во втором – функцию.
лесенка начинается с дощечки, а производная функция – с производной в точке. — Студопедия
Рассмотрим некоторую (конкретную) точку  , принадлежащую области определенияфункции
, принадлежащую области определенияфункции 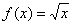 , в которой существует производная. Зададим в данной точке приращение
, в которой существует производная. Зададим в данной точке приращение 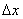 и составим соответствующее приращение функции:
и составим соответствующее приращение функции: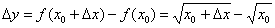
Вычислим предел: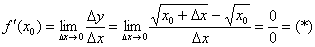
Неопределённость 0:0 устраняется стандартным приёмом, рассмотренным ещё в 1-ом веке до нашей эры. Домножим числитель и знаменатель на сопряженное выражение 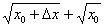 :
:
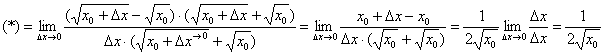
Техника решения такого предела подробно рассмотрена на вводном уроке о пределах функций.
Итак, 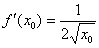 .
.
Поскольку в качестве  можно выбрать ЛЮБУЮ точку
можно выбрать ЛЮБУЮ точку 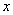 интервала
интервала  , то, осуществив замену
, то, осуществив замену 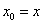 , получаем:
, получаем: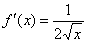
Ответ: по определению производной: 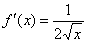
Готово.
В который раз порадуемся логарифмам:
Пример 2
Найти производную функции 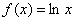 , пользуясь определением производной
, пользуясь определением производной
Решение: рассмотрим другой подход к раскрутке той же задачи. Он точно такой же, но более рационален с точки зрения оформления. Идея состоит в том, чтобы в начале решения избавиться от подстрочного индекса и вместо буквы  использовать букву
использовать букву 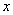 .
.
Рассмотрим произвольную точку 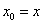 , принадлежащую области определения функции
, принадлежащую области определения функции 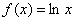 (интервалу
(интервалу  ), и зададим в ней приращение
), и зададим в ней приращение 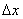 . А вот здесь, кстати, как и в большинстве случаев, можно обойтись без всяких оговорок, поскольку логарифмическая функция дифференцируема в любой точке области определения.
. А вот здесь, кстати, как и в большинстве случаев, можно обойтись без всяких оговорок, поскольку логарифмическая функция дифференцируема в любой точке области определения.
Тогда соответствующее приращение функции:
Найдём производную: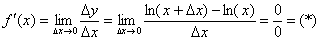
Простота оформления уравновешивается путаницей, которая может возникнуть у начинающих (да и не только). Ведь мы привыкли, что в пределе изменяется буква «икс»! Но тут всё по-другому: 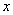 – античная статуя, а
– античная статуя, а 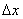 – живой посетитель, бодро шагающий по коридору музея. То есть «икс» – это «как бы константа».
– живой посетитель, бодро шагающий по коридору музея. То есть «икс» – это «как бы константа».
Устранение неопределённости 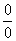 закомментирую пошагово:
закомментирую пошагово:
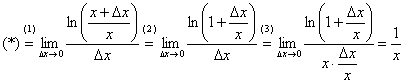
(1) Используем свойство логарифма 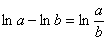 .
.
(2) В скобках почленно делим числитель на знаменатель.
(3) В знаменателе искусственно домножаем и делим на «икс» чтобы воспользоватьсязамечательным пределом 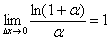 , при этом в качестве бесконечно малой величины выступает
, при этом в качестве бесконечно малой величины выступает 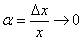 .
.
Ответ: по определению производной: 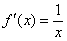
Или сокращённо: 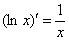
Предлагаю самостоятельно сконструировать ещё две табличные формулы:
Пример 3
Найти производную 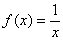 по определению
по определению
В данном случае составленное приращение  сразу же удобно привести к общему знаменателю. Примерный образец оформления задания в конце урока (первый способ).
сразу же удобно привести к общему знаменателю. Примерный образец оформления задания в конце урока (первый способ).
Пример 4
Найти производную 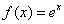 по определению
по определению
А тут всё необходимо свести к замечательному пределу 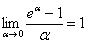 . Решение оформлено вторым способом.
. Решение оформлено вторым способом.
Аналогично выводится ряд других табличных производных. Полный список можно найти в школьном учебнике, или, например, 1-ом томе Фихтенгольца. Не вижу особого смысла переписывать из книг и доказательства правил дифференцирования – они тоже порождены формулой 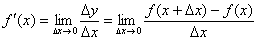 .
.
Переходим к реально встречающимся заданиям:
Пример 5
Найти производную функции  , используя определение производной
, используя определение производной
Решение: используем первый стиль оформления. Рассмотрим некоторую точку  , принадлежащую
, принадлежащую  , и зададим в ней приращение аргумента
, и зададим в ней приращение аргумента 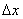 . Тогда соответствующее приращение функции:
. Тогда соответствующее приращение функции:
Возможно, некоторые читатели ещё не до конца поняли принцип, по которому нужно составлять приращение  . Берём точку
. Берём точку  (число) и находим в ней значение функции:
(число) и находим в ней значение функции: 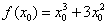 , то есть в функцию
, то есть в функцию  вместо «икса» следует подставить
вместо «икса» следует подставить  . Теперь берём тоже вполне конкретное число
. Теперь берём тоже вполне конкретное число 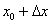 и так же подставляем его в функцию
и так же подставляем его в функцию  вместо «икса»:
вместо «икса»: 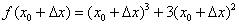 . Записываем разность
. Записываем разность 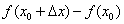 , при этом
, при этом 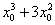 необходимо полностью взять в скобки.
необходимо полностью взять в скобки.
Составленное приращение функции  бывает выгодно сразу же упростить. Зачем? Облегчить и укоротить решение дальнейшего предела.
бывает выгодно сразу же упростить. Зачем? Облегчить и укоротить решение дальнейшего предела.
Используем формулы 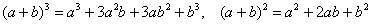 , раскрываем скобки и сокращаем всё, что можно сократить:
, раскрываем скобки и сокращаем всё, что можно сократить: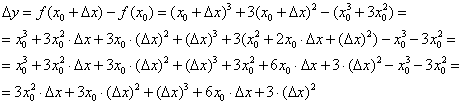
Индейка выпотрошена, с жаркое никаких проблем: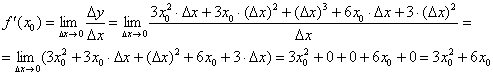
В итоге: 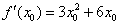
Поскольку в качестве  можно выбрать любое действительное число, то проведём замену
можно выбрать любое действительное число, то проведём замену 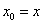 и получим
и получим 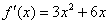 .
.
Ответ: 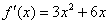 по определению.
по определению.
В целях проверки найдём производную с помощью правил дифференцирования и таблицы: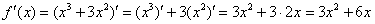
Всегда полезно и приятно знать правильный ответ заранее, поэтому лучше мысленно либо на черновике продифференцировать предложенную функцию «быстрым» способом в самом начале решения.
Пример 6
Найти производную функции 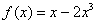 по определению производной
по определению производной
Это пример для самостоятельного решения. Результат лежит на поверхности: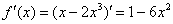
Вернёмся к стилю №2:
Пример 7
Пользуясь определением, найти производную функции
Давайте немедленно узнаем, что должно получиться. По правилу дифференцирования сложной функции: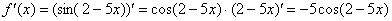
Решение: рассмотрим произвольную точку 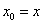 , принадлежащую
, принадлежащую 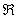 , зададим в ней приращение аргумента
, зададим в ней приращение аргумента 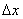 и составим приращение функции:
и составим приращение функции: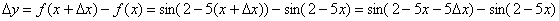
Найдём производную: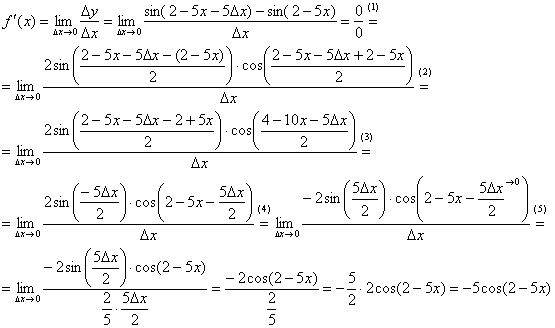
(1) Используем тригонометрическую формулу 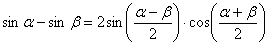 .
.
(2) Под синусом раскрываем скобки, под косинусом приводим подобные слагаемые.
(3) Под синусом сокращаем слагаемые, под косинусом почленно делим числитель на знаменатель.
(4) В силу нечётности синуса выносим «минус». Под косинусом указываем, что слагаемое 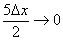 .
.
(5) В знаменателе проводим искусственное домножение, чтобы использовать первый замечательный предел 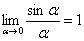 . Таким образом, неопределённость устранена, причёсываем результат.
. Таким образом, неопределённость устранена, причёсываем результат.
Ответ:  по определению
по определению
Как видите, основная трудность рассматриваемой задачи упирается в сложность самого предела + небольшое своеобразие упаковки. На практике встречаются и тот и другой способ оформления, поэтому я максимально подробно расписываю оба подхода. Они равноценны, но всё-таки, по моему субъективному впечатлению, чайникам целесообразнее придерживаться 1-го варианта с «икс нулевым».
Пример 8
Пользуясь определением, найти производную функции
Это задание для самостоятельного решения. Образец оформлен в том же духе, что предыдущий пример.
Разберём более редкую версию задачи:
Пример 9
Найти производную функции  в точке
в точке  , пользуясь определением производной.
, пользуясь определением производной.
Во-первых, что должно получиться в сухом остатке? Число
Вычислим ответ стандартным способом: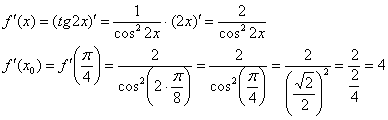
Решение: с точки зрения наглядности это задание значительно проще, так как в формуле 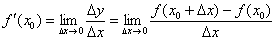 вместо
вместо  рассматривается конкретное значение.
рассматривается конкретное значение.
Зададим в точке  приращение
приращение 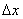 и составим соответствующее приращение функции:
и составим соответствующее приращение функции:
Вычислим производную в точке: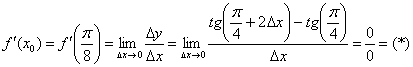
Используем весьма редкую формулу разности тангенсов 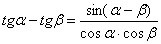 и в который раз сведём решение к первому замечательному пределу:
и в который раз сведём решение к первому замечательному пределу:
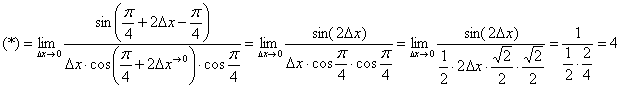
Ответ: 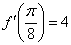 по определению производной в точке.
по определению производной в точке.
Задачу не так трудно решить и «в общем виде» – достаточно заменить 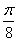 на
на  или просто
или просто 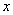 в зависимости от способа оформления. В этом случае, понятно, получится не число, а производная функция.
в зависимости от способа оформления. В этом случае, понятно, получится не число, а производная функция.
Пример 10
Используя определение, найти производную функции 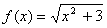 в точке
в точке 
Это пример для самостоятельного решения.
Заключительная бонус-задача предназначена, прежде всего, для студентов с углубленным изучением математического анализа, но и всем остальным тоже не помешает:
Пример 11
Будет ли дифференцируема функция 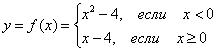 в точке
в точке 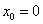 ?
?
Решение: очевидно, что кусочно-заданная функция непрерывна в точке 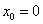 , но будет ли она там дифференцируема? Алгоритм решения данной задачи таков:
, но будет ли она там дифференцируема? Алгоритм решения данной задачи таков:
1) Находим левостороннюю производную в данной точке: 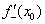 .
.
2) Находим правостороннюю производную в данной точке: 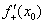 .
.
3) Если односторонние производные совпадают: 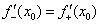 , то в точке
, то в точке  существуетобщая производная, то есть функция
существуетобщая производная, то есть функция 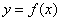 дифференцируема в данной точке и геометрически здесь существует общая касательная (см. теоретическую часть урокаОпределение и смысл производной). Если же получены два разных значения:
дифференцируема в данной точке и геометрически здесь существует общая касательная (см. теоретическую часть урокаОпределение и смысл производной). Если же получены два разных значения: 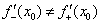 , то функция не дифференцируема в точке
, то функция не дифференцируема в точке  .
.
Всё очень просто!
1) При нахождении левосторонней производной приращение аргумента отрицательно: 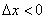 , а слева от точки
, а слева от точки  расположена парабола
расположена парабола 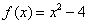 , поэтому приращение функции равно:
, поэтому приращение функции равно: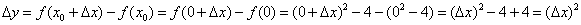
И соответствующий левосторонний предел численно равен левосторонней производной в рассматриваемой точке: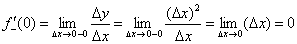
2) Справа от точки 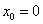 находится график прямой
находится график прямой 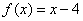 и приращение аргумента положительно:
и приращение аргумента положительно: 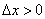 . Таким образом, приращение функции:
. Таким образом, приращение функции:
Правосторонний предел и правосторонняя производная в точке: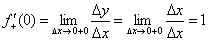
3) Односторонние производные различны: 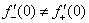
Ответ: функция не дифференцируема в точке 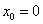 .
.
Ещё легче доказывается книжный случай недифференцируемости модуля 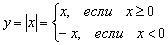 в точке
в точке 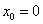 , о котором я в общих чертах уже рассказал натеоретическом уроке о производной.
, о котором я в общих чертах уже рассказал натеоретическом уроке о производной.
Некоторые кусочно-заданные функции дифференцируемы и в точках «стыка» графика, например, котопёс  обладает общей производной и общей касательной (ось абсцисс) в точке
обладает общей производной и общей касательной (ось абсцисс) в точке 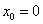 . Кривой, да дифференцируемый на
. Кривой, да дифференцируемый на  ! Желающие могут убедиться в этом самостоятельно по образцу только что решённого примера.
! Желающие могут убедиться в этом самостоятельно по образцу только что решённого примера.
На этом забавном гибриде и закончим повествование =)
Решения и ответы:
Пример 3: Решение: рассмотрим некоторую точку  , принадлежащую области определения функции
, принадлежащую области определения функции 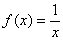 . Зададим в данной точке приращение
. Зададим в данной точке приращение 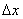 и составим соответствующее приращение функции:
и составим соответствующее приращение функции: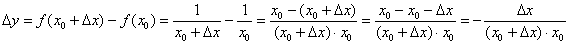
Найдём производную в точке  :
: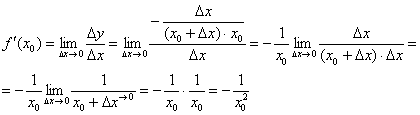
Так как в качестве  можно выбрать любую точку
можно выбрать любую точку 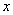 области определения функции
области определения функции 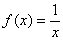 , то
, то 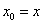 и
и 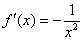
Ответ: 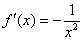 по определению производной
по определению производной
Пример 4: Решение: рассмотрим произвольную точку 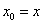 , принадлежащую
, принадлежащую 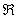 , и зададим в ней приращение
, и зададим в ней приращение 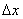 . Тогда соответствующее приращение функции:
. Тогда соответствующее приращение функции: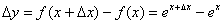
Найдём производную:
Используем замечательный предел 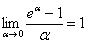
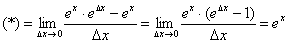
Ответ:  по определению
по определению
Пример 6: Решение: рассмотрим некоторую точку  , принадлежащую
, принадлежащую 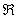 , и зададим в ней приращение аргумента
, и зададим в ней приращение аргумента 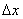 . Тогда соответствующее приращение функции:
. Тогда соответствующее приращение функции: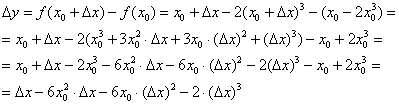
Вычислим производную: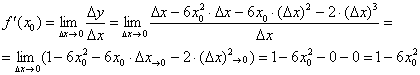
Таким образом: 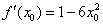
Поскольку в качестве  можно выбрать любое действительное число, то
можно выбрать любое действительное число, то 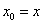 и
и 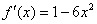
Ответ: 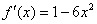 по определению.
по определению.
Пример 8: Решение: рассмотрим произвольную точку 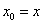 , принадлежащую
, принадлежащую 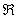 , зададим в ней приращение
, зададим в ней приращение 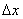 и составим приращение функции:
и составим приращение функции: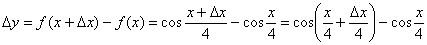
Найдём производную:
Используем тригонометрическую формулу 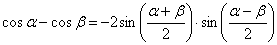 и первый замечательный предел:
и первый замечательный предел:
Ответ:  по определению
по определению
Пример 10: Решение: Зададим приращение 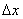 в точке
в точке  . Тогда приращение функции:
. Тогда приращение функции: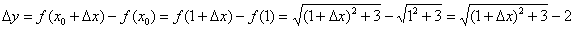
Вычислим производную в точке: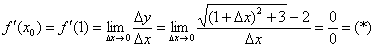
Умножим числитель и знаменатель на сопряженное выражение: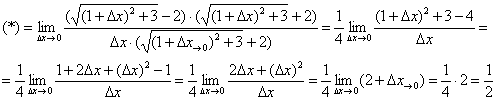
Ответ: 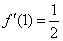 по определению производной в точке
по определению производной в точке
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)
Как можно отблагодарить автора?
Приближенные вычисления с помощью дифференциала
На данном уроке мы рассмотрим широко распространенную задачу о приближенном вычислении значения функции с помощью дифференциала. Здесь и далее речь пойдёт о дифференциалах первого порядка, для краткости я часто буду говорить просто «дифференциал». Задача о приближенных вычислениях с помощью дифференциала обладает жёстким алгоритмом решения, и, следовательно, особых трудностей возникнуть не должно. Единственное, есть небольшие подводные камни, которые тоже будут подчищены. Так что смело ныряйте головой вниз.
Кроме того, на странице присутствуют формулы нахождения абсолютной и относительной погрешность вычислений. Материал очень полезный, поскольку погрешности приходится рассчитывать и в других задачах. Физики, где ваши аплодисменты? =)
Для успешного освоения примеров необходимо уметь находить производные функций хотя бы на среднем уровне, поэтому если с дифференцированием совсем нелады, пожалуйста, начните с урока Как найти производную? Также рекомендую прочитать статьюПростейшие задачи с производной, а именно параграфы о нахождении производной в точке и нахождении дифференциала в точке. Из технических средств потребуется микрокалькулятор с различными математическими функциями. Можно использовать Эксель, но в данном случае он менее удобен.
Урок состоит из двух частей:
– Приближенные вычисления с помощью дифференциала функции одной переменной.
– Приближенные вычисления с помощью полного дифференциала функции двух переменных.
Кому что нужно. На самом деле можно было разделить богатство на две кучи, по той причине, что второй пункт относится к приложениям функции нескольких переменных. Но что поделать, вот люблю я длинные статьи.
Рассматриваемое задание тесно связано с понятием дифференциала, и его геометрический смысл можно узнать на уроке Что такое производная? А сейчас ограничимся формальным рассмотрением примеров, чего вполне достаточно, чтобы научиться их решать.
Приближенные вычисления
с помощью дифференциала функции одной переменной
В первом параграфе рулит функция одной переменной. Как все знают, она обозначается через  или через
или через 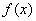 . Для данной задачи намного удобнее использовать второе обозначение. Сразу перейдем к популярному примеру, который часто встречается на практике:
. Для данной задачи намного удобнее использовать второе обозначение. Сразу перейдем к популярному примеру, который часто встречается на практике:
Пример 1
Вычислить приближенно 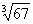 , заменяя приращения функции ее дифференциалом.
, заменяя приращения функции ее дифференциалом.
Решение: Пожалуйста, перепишите в тетрадь рабочую формулу для приближенного вычисления с помощью дифференциала:
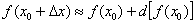
Начинаем разбираться, здесь всё просто!
На первом этапе необходимо составить функцию 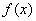 . По условию предложено вычислить кубический корень из числа:
. По условию предложено вычислить кубический корень из числа: 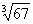 , поэтому соответствующая функция имеет вид:
, поэтому соответствующая функция имеет вид: 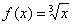 . Нам нужно с помощью формулы найти приближенное значение
. Нам нужно с помощью формулы найти приближенное значение 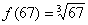 .
.
Смотрим на левую часть формулы 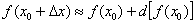 , и в голову приходит мысль, что число 67 необходимо представить в виде
, и в голову приходит мысль, что число 67 необходимо представить в виде 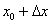 . Как проще всего это сделать? Рекомендую следующий алгоритм: вычислим данное значение на калькуляторе:
. Как проще всего это сделать? Рекомендую следующий алгоритм: вычислим данное значение на калькуляторе: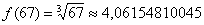 – получилось 4 с хвостиком, это важный ориентир для решения.
– получилось 4 с хвостиком, это важный ориентир для решения.
В качестве  подбираем «хорошее» значение, чтобы корень извлекался нацело. Естественно, это значение
подбираем «хорошее» значение, чтобы корень извлекался нацело. Естественно, это значение  должно быть как можно ближе к 67. В данном случае:
должно быть как можно ближе к 67. В данном случае: 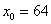 . Действительно:
. Действительно: 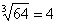 .
.
Примечание: Когда с подбором  всё равно возникает затруднение, просто посмотрите на скалькулированное значение (в данном случае
всё равно возникает затруднение, просто посмотрите на скалькулированное значение (в данном случае  ), возьмите ближайшую целую часть (в данном случае 4) и возведите её нужную в степень (в данном случае
), возьмите ближайшую целую часть (в данном случае 4) и возведите её нужную в степень (в данном случае 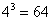 ). В результате и будет выполнен нужный подбор:
). В результате и будет выполнен нужный подбор: 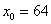 .
.
Если 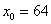 , то приращение аргумента:
, то приращение аргумента: 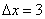 .
.
Итак, число 67 представлено в виде суммы 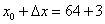
Далее работаем с правой частью формулы 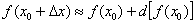 .
.
Сначала вычислим значение функции в точке 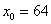 . Собственно, это уже сделано ранее:
. Собственно, это уже сделано ранее: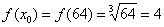
Дифференциал в точке находится по формуле: 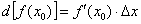 – тоже можете переписать к себе в тетрадь.
– тоже можете переписать к себе в тетрадь.
Из формулы следует, что нужно взять первую производную: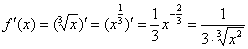
И найти её значение в точке  :
:
Таким образом: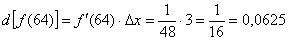
Всё готово! Согласно формуле 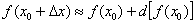 :
: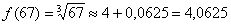
Найденное приближенное значение достаточно близко к значению  , вычисленному с помощью микрокалькулятора.
, вычисленному с помощью микрокалькулятора.
Ответ: 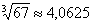
Пример 2
Вычислить приближенно  , заменяя приращения функции ее дифференциалом.
, заменяя приращения функции ее дифференциалом.
Это пример для самостоятельного решения. Примерный образец чистового оформления и ответ в конце урока. Начинающим сначала рекомендую вычислить точное значение  на микрокалькуляторе, чтобы выяснить, какое число принять за
на микрокалькуляторе, чтобы выяснить, какое число принять за  , а какое – за
, а какое – за  . Следует отметить, что
. Следует отметить, что  в данном примере будет отрицательным.
в данном примере будет отрицательным.
У некоторых, возможно, возник вопрос, зачем нужна эта задача, если можно всё спокойно и более точно подсчитать на калькуляторе? Согласен, задача глупая и наивная. Но попытаюсь немного её оправдать. Во-первых, задание иллюстрирует смысл дифференциала функции. Во-вторых, в древние времена, калькулятор был чем-то вроде личного вертолета в наше время. Сам видел, как из местного политехнического института году где-то в 1985-86 выбросили компьютер размером с комнату (со всего города сбежались радиолюбители с отвертками, и через пару часов от агрегата остался только корпус). Антиквариат водился и у нас на физмате, правда, размером поменьше – где-то с парту. Вот так вот и мучились наши предки с методами приближенных вычислений. Конная повозка – тоже транспорт.
Так или иначе, задача осталась в стандартном курсе высшей математики, и решать её придётся. Это основной ответ на ваш вопрос =)
Пример 3
Вычислить приближенно с помощью дифференциала значение функции  в точке
в точке 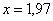 . Вычислить более точное значение функции в точке
. Вычислить более точное значение функции в точке 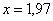 с помощью микрокалькулятора, оценить абсолютную и относительную погрешность вычислений.
с помощью микрокалькулятора, оценить абсолютную и относительную погрешность вычислений.
Фактически то же самое задание, его запросто можно переформулировать так: «Вычислить приближенное значение 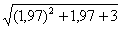 с помощью дифференциала»
с помощью дифференциала»
Решение: Используем знакомую формулу: 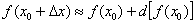
В данном случае уже дана готовая функция:  . Ещё раз обращаю внимание, что для обозначения функции вместо «игрека» удобнее использовать
. Ещё раз обращаю внимание, что для обозначения функции вместо «игрека» удобнее использовать 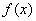 .
.
Значение 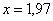 необходимо представить в виде
необходимо представить в виде 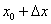 . Ну, тут легче, мы видим, что число 1,97 очень близко к «двойке», поэтому напрашивается
. Ну, тут легче, мы видим, что число 1,97 очень близко к «двойке», поэтому напрашивается 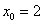 . И, следовательно:
. И, следовательно: 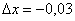 .
.
Вычислим значение функции в точке 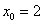 :
: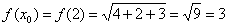
Используя формулу 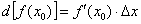 , вычислим дифференциал в этой же точке.
, вычислим дифференциал в этой же точке.
Находим первую производную: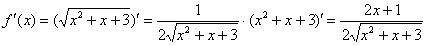
И её значение в точке 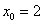 :
: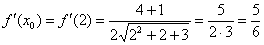
Таким образом, дифференциал в точке: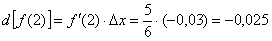
В результате, по формуле 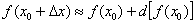 :
: 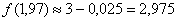
Вторая часть задания состоит в том, чтобы найти абсолютную и относительную погрешность вычислений.
Исчисление I — Определение производной
Онлайн-заметки ПавлаНоты Быстрая навигация Скачать
- Перейти к
- Ноты
- Проблемы с практикой
- Проблемы с назначением
- Показать / Скрыть
- Показать все решения / шаги / и т. Д.
- Скрыть все решения / шаги / и т. Д.
- Разделы
- Деривативы Введение
- Интерпретация производного инструмента
- Разделы
- Пределы
- Применение производных инструментов
- Классы
- Алгебра
- Исчисление I
- Исчисление II
- Исчисление III
- Дифференциальные уравнения
- Дополнительно
- Алгебра и триггерный обзор
- Распространенные математические ошибки
- Праймер комплексных чисел
- Как изучать математику
- Шпаргалки и таблицы
- Разное
- Свяжитесь со мной
- Справка и настройка MathJax
- Мои студенты
- Notes Загрузки
- Полная книга
- Текущая глава
- Текущий раздел
- Practice Problems Загрузок
- Полная книга — Только проблемы
- Полная книга — Решения
- Текущая глава — Только проблемы
- Текущая глава — Решения
- Текущий раздел — Только проблемы
- Текущий раздел — Решения
- Проблемы с назначением Загрузок
- Полная книга
- Текущая глава
- Текущий раздел
- Прочие товары
- Получить URL для загружаемых элементов
- Распечатать страницу в текущем виде (по умолчанию)
- Показать все решения / шаги и распечатать страницу
- Скрыть все решения / шаги и распечатать страницу
- Дом
- Классы
- Алгебра
- Отборочные
- Целочисленные экспоненты
- Рациональные экспоненты
- Радикалы
- Полиномы
- Факторинговые многочлены
- Рациональные выражения
- Комплексные числа
- Решение уравнений и неравенств
- Решения и наборы решений
- Линейные уравнения
- Приложения линейных уравнений
- Уравнения с более чем одной переменной
- Квадратные уравнения — Часть I
- Квадратные уравнения — Часть II
- Квадратные уравнения: сводка
- Приложения квадратных уравнений
- Уравнения, сводимые к квадратичным в форме
- Уравнения с радикалами
- Линейные неравенства
- Полиномиальные неравенства
- Рациональные неравенства
- Уравнения абсолютных значений
- Неравенства абсолютных значений
- Графики и функции
- График
- Строки
- Круги
- Определение функции
- Графические функции
- Комбинирование функций
- Обратные функции
- Общие графы
- Прямые, окружности и кусочные функции
- Параболы
- Эллипсы
- Гиперболы
- Разные функции
- Преобразования
- Симметрия
- Рациональные функции
- Полиномиальные функции
- Делительные многочлены
- Нули / корни многочленов
- Графические полиномы
- Нахождение нулей многочленов
- Частичные дроби
- Экспоненциальные и логарифмические функции
- Экспоненциальные функции
- Логарифм функций
- Отборочные
IV. Найдите предел $$ \ frac {{\ Delta y}} {{\ Delta x}} $$, где $$ \ Delta x \ to 0 $$
\ [\ begin {gather} \ mathop {\ lim} \ limits _ {\ Delta x \ to 0} \ frac {{\ Delta y}} {{\ Delta x}} \ mathop {= \ lim} \ limits _ {\ Delta x \ to 0} (2x + \ Delta x) \\ \ Rightarrow \ frac {{dy}} {{dx}} = (2x + 0) \\ \ Rightarrow \ frac {{dy}} {{dx}} = 2x \\ \ end {собрано} \]
Это производная от $$ y = {x ^ 2} — 1 $$ w.r.t $$ x $$.
Пример:
Найдите по определению производную функции $$ \ frac {1} {{x + a}} $$ по $$ x $$.
Решение :
Пусть \ [y = \ frac {1} {{x + a}} \]
I. Измените $$ x $$ на $$ x + \ Delta x $$ и $$ y $$ на $$ y + \ Delta y $$
\ [y + \ Delta y = \ frac {1 } {{x + \ Delta x + a}} \]
II. Найдите $$ \ Delta y $$ вычитанием
\ [\ begin {gather} \ Delta y = \ frac {1} {{x + \ Delta x + a}} — y \\ \ Delta y = \ frac { 1} {{x + \ Delta x + a}} — \ frac {1} {{x + a}} \\ \ Delta y = \ frac {{x + a — (x + \ Delta x + a)} } {{(x + \ Delta x + a) (x + a)}} \\ \ Delta y = \ frac {{x + a — x — \ Delta x — a}} {(x + \ Delta x + a) (x + a)}} \\ \ Delta y = \ frac {{- \ Delta x}} {{(x + \ Delta x + a) (x + a)}} \\ \ end {собрано } \]
III. Разделите обе стороны на $$ \ Delta x $$
\ [\ begin {gather} \ frac {{\ Delta y}} {{\ Delta x}} = \ frac {{- \ Delta x}} {{\ Дельта x (x + \ Delta x + a) (x + a)}} \\ \ frac {{\ Delta y}} {{\ Delta x}} = \ frac {{- 1}} {{(x + \ Delta x + a) (x + a)}} \\ \ end {gather} \]
IV. Найдите предел $$ \ frac {{\ Delta y}} {{\ Delta x}} $$, где $$ \ Delta x \ to 0 $$
\ [\ begin {gather} \ mathop {\ lim} \ limits _ {\ Delta x \ to 0} \ frac {{\ Delta y}} {{\ Delta x}} = \ mathop {\ lim} \ limits _ {\ Delta x \ to 0} \ frac {{- 1} } {{(x + \ Delta x + a) (x + a)}} \\ \ Rightarrow \ frac {{dy}} {{dx}} = \ frac {{- 1}} {{(x + 0 + a) (x + a)}} \\ \ Rightarrow \ frac {{dy}} {{dx}} = \ frac {{- 1}} {{(x + a) (x + a)}} \ \ \ Rightarrow \ frac {{dy}} {{dx}} = \ frac {{- 1}} {{{{{(x + a)} ^ 2}}} \\ \ end {gather} \]
Это производная от $$ y = \ frac {1} {{x + a}} $$ w.r.t $$ x $$.
.
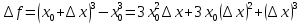
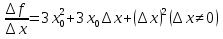
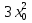 постоянно, а при
постоянно, а при 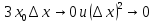 , а значит
, а значит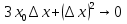 . Получаем
. Получаем 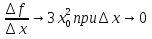 .
.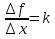
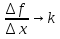 при
при