Что такое производная сложной функции?
Оглавление
Время чтения: 3 минуты
410
Перед тем как говорить о производной сложной функции давайте сначала определимся, что собой представляет сложная функция. Как вы увидите чуть позже, не всякую функцию кажущуюся сложной можно действительно так назвать.
Определение + примеры
Сложной функцией называют функцию, аргумент которой тоже является функцией.
Обозначается сложная функция как f(g(x)). Иногда наружные скобки являются квадратными f[g(x)]. g(x) – аргумент f(g(x)), иногда его называют внутренней функцией.
Уровень вложенности может быть абсолютно любым
y = f (g1 (g2 (g3 (. . . (g n (x)))))).
y=sin (x+1) есть сложная функция т. к. её можно представить в виде двух функций, вложенных одна в другую y = sin(u) и u = x + 1.
y=cos (7x³ -4x²) тоже сложная. Внутренней в ней является: u = 7x³ — 4x².
y = 7x³ — 4x² является простой. Аргументом здесь будет только x.
\end{aligned}\]
Отсюда легко вывести алгоритм или правило нахождения производной сложной функции
Сначала в сложной функции нужно выделить простые. Затем найти их производные, после этого составить произведение из найденных производных. Оно и будет тем, что нам нужно.
Задачи 1 — 5
Найдите производную y = sin3x.
Решение: Запишем в выражение в виде y = (sinx)3. Отсюда ясно, что g = sin(x). Эту производную найти очень легко. Она следующая (sin(x))’ = cos(x).
Производная внутреннего выражения будет (g3)’ = 3u3-1= 3u2.
Из всего этого получаем
y’ = (sinx3)’ = (u3)’
Далее нужно лишь воспользоваться приведённой выше формулой, показывающей, как найти производную сложной функции
В результате получим
y’= (u3)’*u’ = 3u3-1(sinx)’= 3u2cosx = 3sin2xcosx
Ответ:
y’ = 3sin2xcosxНайти производную y = ln(ax2 + c)
Решение: Находим внутреннюю функцию.
Очевидно, что здесь она g = ax2 + c
Производная y’ = (ln(g))’ = 1/g
Производная g’ = a*2x
Из этого по формулам, приведённым выше мы будем иметь
y’ = (1/(ax2 + c))*u’ = 2ax/(ax2 + c)
Ответ: y’ = (1/(ax2 + c))*u’ = 2ax/(ax2 + c).
Найти y’ = exp(-x2)
Решение: Внутренней здесь будет g = -x2
y’ = (exp(u))’ = exp(-x2)
Производная –x2 = -2x
Из этого имеем
y’ = (exp(-x2))’= exp(-x2)*(-2x) = -2x*exp(-x2)
Ответ: y’ = -2x*exp(-x2).
Как видите, ничего трудного здесь нет, но требуется быть очень внимательным.
Теперь рассмотрим задачу, где вложено не одно, а несколько выражений.
Найти y’=cos³(3x-12)
Решение: Главное правильно выделить все внутренние составляющие указанного выражения.
Первым очевидно будет g1 = 3x – 12
Вторым будет g2 = cos(g1) = cos(3x – 12)
Сначала найдём производную g1.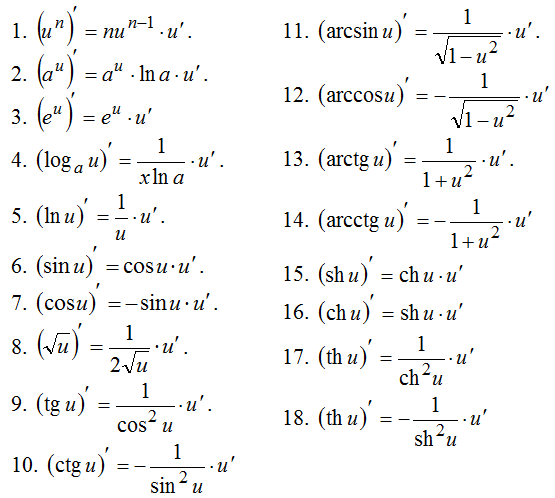
Она равняется (g1)’ = (3x-12)’ = 3
Затем находим (g2)’ = (cos(u1))’ = — sin(3x-12)
Далее ищем производную внешней функции. Она равна
(cos(3x — 12)3)’ = 3cos2(3x -12)
В результате вычислений получаем
y’ = (3cos2(3x -12))*( — sin(3x-12))*3 = -9cos2(3x -12))*(sin(3x-12))
Не всегда следует сразу выделять вложенные составляющие выражения, производных которого нам нужно найти.
Чему равна y’ = (3/sin2x) + (cos2x/3)
Решение: Выражение представляет собой сумму двух производных, которые следует найти по отдельности и после этого сложить.
Сначала находим (3/sin2x)’, затем (cos2x/3)’. Решением нашей задачи будет их сумма.
В выражении (3/sin2x) вынесем общий множитель за скобки и уже после этого станем искать производную
3*(sin-2x)’ = 3*(-2)sin-3x * (sinx)’ = -6sin-3x * cosx = -(6cosx)/(sin3x)
Далее находим тоже самое делаем со вторым слагаемым.
{\prime}\]
Не забывайте также, что иногда перед поиском производных выражение можно упростить с помощью различных тригонометрических либо логарифмических преобразований. На сложных функциях это часто приводит к нужному результату, а иногда и вовсе позволяет сразу привести их к простому виду.
Оценить статью (77 оценок):
Поделиться
Нахождение производных
На прошлой лекции и семинаре мы нашли производные нескольких функций, пользуясь определением. Однако, как и в случае пределов, доказательства по определению — довольно трудоёмкое занятие. На этой лекции мы докажем несколько теорем, позволяющих вычислять производные функций, заданных формулами, с помощью достаточно простого алгоритма.
16.1Арифметика производных
16.1.1Производная суммы
Начнём с простого: производной суммы.
Теорема 1. Пусть функции f и g дифференцируемы в точке x0.
Тогда функция
h(x):=f(x)+g(x) дифференцируема в точке x0 и
h′(x0)=f′(x0)+g′(x0)
Доказательство. Воспользуемся определением производной:
h′(x0)=limΔx→0h(x0+Δx)−h(x0)Δx==limΔx→0(f(x0+Δx)+g(x0+Δ))−(f(x0)+g(x0))Δx=…
h′(x0)=limΔx→0h(x0+Δx)−h(x0)Δx==limΔx→01Δx((f(x0+Δx)+g(x0+Δ))−−(f(x0)+g(x0)))=…
Перегруппируем слагаемые в числителе и разобъём дробь на две:
…=limΔx→0(f(x0+Δx)−f(x0)Δx+g(x0+Δx)−g(x0)Δx)=…
…=limΔx→0(f(x0+Δx)−f(x0)Δx++g(x0+Δx)−g(x0)Δx)=…
По теореме о пределе суммы:
…=limΔx→0f(x0+Δx)−f(x0)Δx+limΔx→0g(x0+Δx)−g(x0)Δx==f′(x0)+g′(x0).
…=limΔx→0f(x0+Δx)−f(x0)Δx++limΔx→0g(x0+Δx)−g(x0)Δx==f′(x0)+g′(x0).
Пределы в левой части равенства существуют, поскольку f и g
дифференцируемы в точке x0, и следовательно теорему о пределе суммы
применять можно. Теорема доказана.
∎
16.1.2Производная произведения
Тут получится немножко сложнее, но не сильно.
Теорема 2. Пусть функции f и g дифференцируемы в точке x0. Тогда функция h(x):=f(x)g(x) дифференцируема в точке x0 и
h′(x0)=f′(x0)g(x0)+f(x0)g′(x0).
Доказательство. Снова запишем определение производной:
h′(x0)=limΔx→0h(x0+Δx)−h(x0)Δx==limΔx→0f(x0+Δx)g(x0+Δx)−f(x0)g(x0)Δx=…(16.1)
h′(x0)==limΔx→0h(x0+Δx)−h(x0)Δx==limΔx→0(f(x0+Δx)g(x0+Δx)−−f(x0)g(x0))1Δx=…(16.1)
Аналогично теореме о пределе произведения, полезно нарисовать картинку 16.1 и представить разность произведений в виде суммы площадей двух прямоугольников.
Рис. 16.1: Разбиваем разность произведений в сумму двух произведений
f(x0+Δx)g(x0+Δx)−f(x0)g(x0)==(f(x0+Δx)−f(x0))g(x0+Δx)+f(x0)(g(x0+Δx)−g(x0)).
f(x0+Δx)g(x0+Δx)−f(x0)g(x0)==(f(x0+Δx)−f(x0))g(x0+Δx)++f(x0)(g(x0+Δx)−g(x0)).
Подставляя это в (16.1) и разбивая дробь в сумму двух дробей, получаем:
…=limΔx→0(g(x0+Δx)f(x0+Δx)−f(x0)Δx+f(x0)g(x0+Δx)−g(x0)Δx).
…=limΔx→0(g(x0+Δx)f(x0+Δx)−f(x0)Δx++f(x0)g(x0+Δx)−g(x0)Δx).
Каждая из двух дробей стремится к соответствующей производной, сомножитель f(x0) не зависит от Δx и стремится сам к себе, g(x0+Δx) стремится к g(x0), поскольку функция g непрерывна в точке x0, т.к. она дифференцируема в этой точке (см. теорему 1 из предыдущей главы). Пользуясь теоремами о пределах суммы и произведения, получаем искомое.∎
Пример 1. Найдём производную функции f(x)=x2sinx:
f′(x)=(x2sinx)′=(x2)′sinx+x2(sinx)′=2xsinx+x2cosx.
f′(x)=(x2sinx)′=(x2)′sinx+x2(sinx)′==2xsinx+x2cosx.
16.2Производная частного
Теорема 3. Пусть функция g дифференцируема в точке x0 и g(x0)≠0. Тогда функция h(x):=1/g(x) дифференцируема в точке x0 и
h′(x0)=−g′(x0)g(x0)2.
Доказательство этой теоремы несложно провести пользуясь определением, аналогично двум предыдущим теоремам. Оставляем это в качестве полезного упражнения.
Теорема 4. Пусть функции f и g дифференцируемы в точке x0 и g(x0)≠0. Тогда функция h(x):=f(x)/g(x) дифференцируема в точке x0 и
h′(x0)=f′(x0)g(x0)−g′(x0)f(x0)g(x0)2.
Эту теорему легко вывести из теоремы о производной произведения и теоремы 3. Тоже оставляем в качестве упражнения.
16.3Производная сложной функции
16.3.1Картинка и формулировка
Чтобы сформулировать теорему о производной сложной функции полезно нарисовать
картинку и обсудить ещё один способ думать о производной.
Пусть функция f дифференцируема в точке x0, а функция g
дифференцируема в точке f(x0). Рассмотрим их композицию — функцию
h(x):=g(f(x)). Будем использовать переменные x, y и z: функция f
отображает x в y, функция g отображает y в z, а функция h — x в
z, см.
Рис. 16.2: Действие композиции на маленький отрезок
Проследим за тем, что происходит с отрезком I под действием отображения h. Сначала на I действует отображение f и он превращается в f(I), растягиваясь примерно в f′(x0) раз. Затем на отрезок f(I) действует отображения g и он превращается в отрезок g(f(I)). Во сколько раз отрезок g(f(I)) больше отрезка f(I)? Во столько, во сколько раз отображение g растягивает маленькие отрезки, один конец которых совпадает с точкой f(x0). Чтобы найти это число нам нужно вычислить значение производной функции g в точке f(x0), то есть g′(f(x0)).
Во сколько раз отрезок g(f(I)) больше отрезка I? Мы сначала растянули
отрезок I в f′(x0) раз, а потом ещё в g′(f(x0)).
Значит, в итоге он
растянулся в f′(x0)g′(f(x0)) раз. Это и есть значение прозводной функции
h в точке x0.
Эти рассуждения не претендуют на аккуратность — аккуратное доказательство будет ниже. Но теперь мы можем сформулировать теорему о производной сложной функции, и получающаяся в ней формула не будет казаться взявшейся с потолка.
Теорема 5. Пусть функция f дифференцируема в точке x0, а функция g дифференцируема в точке f(x0). Тогда функция h(x):=g(f(x)) дифференцируема в точке x0 и
h′(x0)=g′(f(x0))f′(x0).
16.3.2Аккуратные оценки
Доказательство. Обозначим y0:=f(x0). Определим следующие функции: Δf(Δx):=f(x0+Δx)−f(x0),Δg(Δy):=g(y0+Δy)−g(y0). Тогда
f′(x0)=limΔx→0Δf(Δx)Δx,g′(y0)=limΔy→0Δg(Δy)Δy,
f′(x0)=limΔx→0Δf(Δx)Δx,g′(y0)=limΔy→0Δg(Δy)Δy,
и
h′(x0)=limΔx→0Δg(Δf(Δx))Δx.(16.2)
Последнее равенство мгновенно следует из картинки (см.
рис. 16.3), но формально доказывается так. Заметим, что
y0+Δf(Δx)=y0+f(x0+Δx)−f(x0)=f(x0+Δx).
y0+Δf(Δx)=y0+f(x0+Δx)−f(x0)==f(x0+Δx).
Таким образом,
Δg(Δf(Δx))=g(y0+Δf(Δx))−g(y0)=g(f(x0+Δx))−g(f(x0)).
Δg(Δf(Δx))=g(y0+Δf(Δx))−g(y0)==g(f(x0+Δx))−g(f(x0)).
и правая часть (16.2) превращается в определение производной h′(x0).
Рис. 16.3: Функции Δf и Δg
Первая попытка. Естественный первый шаг состоит в том, чтобы представить отношение
Δg(Δf(Δx))Δx
в виде произведения двух отношений:
Δg(Δf(Δx))Δf(Δx)⋅Δf(Δx)Δx(16.3)
Дальше мы могли бы перейти к
пределу при Δx→0 и получить искомое произведение производных.
Однако, тут нас поджидает проблема: значение выражения (16.3)
определено не всегда. Может так случиться, что отображение f переведёт
x0+Δx в ту же точку, что и x0, то есть отрезок I схлопнется в
точку.
В этом случае Δf(Δx)=0 и делить на него нельзя. Что
же делать?
Новые функции. Давайте рассмотрим такую функцию:
G(Δy):=Δg(Δy)Δy.(16.4)
Она определена в некоторой проколотой окрестности нуля. По определению производной функции g,
limΔy→0G(Δy)=g′(y0).
Теперь рассмотрим новую функцию:
~G(Δy)={G(Δy),Δy≠0,g′(y0),Δy=0.
Иными словами, мы доопределили функцию G(Δy) в нуле значением g′(y0). Функция ~G непрерывна в точке 0 — мы её ровно так доопредили, чтобы предел функции в этой точке был равен её значению.
Докажем, что для всех Δx из некоторой проколотой окрестности нуля выполняется равенство
Δg(Δf(Δx))Δx=~G(Δf(Δx))Δf(Δx)Δx.(16.5)
Δg(Δf(Δx))Δx==~G(Δf(Δx))Δf(Δx)Δx.(16.5)
Рассмотрим два случая:
- Пусть Δf(Δx)≠0. Тогда
~G(Δf(Δx))=G(Δf(Δx))=Δg(Δf(Δx))Δf(Δx).
~G(Δf(Δx))=G(Δf(Δx))==Δg(Δf(Δx))Δf(Δx).
В этом случае правая часть (16.5) совпадает с (16.3) и в нём можно сократить на Δf(Δx) и равенство выполняется.
- Пусть теперь Δf(Δx)=0. Тогда левая часть (16.5) равна нулю (поскольку функцию Δg в нуле принимает значение 0), равно как и правая часть, и значит равенство снова выполняется.
Предел сложной функции. Перейдём теперь в равенстве (16.5) к пределу при Δx→0. Имеем:
limΔx→0Δg(Δf(Δx))Δx=limΔx→0~G(Δf(Δx))⋅Δf(Δx)Δx.
limΔx→0Δg(Δf(Δx))Δx==limΔx→0~G(Δf(Δx))⋅Δf(Δx)Δx.
Второй сомножитель стремится к f′(x0). Для нахождения предела первого сомножителя воспользуемся теоремой о пределе сложной функции. Предел внутренней функции Δf при Δx→0 равен нулю. (Действительно, функция f непрерывна в точке x0, поскольку дифференцируема в этой точке, и значит limΔx→0f(x0+Δx)−f(x0)=0.) Внешняя функция ~G непрерывна в нуле по построению. Значит,
limΔx→0~G(Δf(Δx))=~G(limΔx→0Δf(Δx))=~G(0)=g′(y0)=g′(f(x0)).
limΔx→0~G(Δf(Δx))=~G(limΔx→0Δf(Δx))==~G(0)=g′(y0)==g′(f(x0)).
Таким образом, по теореме о пределе произведения,
h′(x0)=limΔx→0Δg(Δf(Δx))Δx=g′(f(x0))f′(x0)
и теорема доказана.∎
Пример 2. Найдём производную функции h(x)=sin(x3). Внутренняя функция f(x)=x3. Внешняя функция g(y)=siny. Их производные: f′(x)=3×2, g′(y)=cosy. Тогда
(sin(x3))′=g′(f(x))f′(x)=g′(x3)3×2=cos(x3)⋅3×2=3x2cosx3.
(sin(x3))′=g′(f(x))f′(x)=g′(x3)3×2==cos(x3)⋅3×2=3x2cosx3.
16.4Заключение
Мы доказали основные теоремы, позволяющие находить производные любых функций,
заданных формулами, если известны производные их элементарных составных частей.
Например, сколь бы сложной ни была формула, если в ней участвуют только
арифметические операции, экспоненты и тригонометрические функции, мы можем
посчитать её производную. Когда производная найдена, она позволяет ответить на
множество вопросов про поведение функции — в частности, найти её экстремумы и
промежутки монотонности.
Подробнее о связи свойств производной со свойствами
самой функции — на следующей лекции.
← Предыдущая глава Следующая глава →
производных — Понимание сложной дифференциации
Задавать вопрос
спросил
Изменено 3 года, 8 месяцев назад
Просмотрено 851 раз
$\begingroup$
Я пытаюсь понять сложное дифференцирование и не понимаю, как соотносятся частные производные. Во-первых, функция $f:V\rightarrow \mathbb{C}$ на открытом множестве $V$ сложного плана комплексно дифференцируема, если предел
$$\underset{h\rightarrow 0}{\lim}\ frac{f(z+h)-f(z)}{h}$$
существует для каждой точки в $V$.
$f$ можно записать в виде $f(x+iy)=u(x,y)+iv(x,y)$, где $u$ и $v$ — действительная и мнимая части $f$ соответственно. . Если функция комплексно дифференцируема, то она должна удовлетворять знаменитым уравнениям Коши-Римана: $u_x=v_y$ и $u_y=-v_x$, где
$$ u_x(x,y)=\underset{h\rightarrow 0}{\lim}\frac{u(x+h,y)-u(x,y)}{h}$$
В моем учебнике (в приложении) говорится, что, используя уравнения CR, мы видим, что
$$f’=u_x+iv_x$$
Я не понимаю, как обосновать приведенное выше уравнение. $f’$ является производной от $f$ через $z$, но правая часть уравнения выражена через частные производные. Как вывести эту формулу? Я знаю, что комплексная функция комплексно дифференцируема тогда и только тогда, когда она действительно дифференцируема и удовлетворяет уравнениям CR, и что если комплексная функция имеет непрерывные частные производные и удовлетворяет уравнениям CR в точке, то она комплексно дифференцируема в этой точке.
- комплексный анализ
- производные
- частные производные
$\endgroup$
2
$\begingroup$
Запись пределов с помощью $h$ делает оба уравнения похожими на одну и ту же процедуру ограничения.
Но есть небольшая разница: в вашем первом уравнении $h \in \mathbb{C}$, тогда как второе уравнение действительное и, следовательно, $h \in \mathbb{R}$.
Следовательно, первое уравнение намного сильнее , чем второе. Вместо того, чтобы приближаться к $0$ только слева или справа, $h$ может делать все что угодно на комплексной плоскости. Существование предела в вашем первом уравнении означает, что имеет значение , а не , какое приближение к нулю мы выбираем.
В частности, мы можем быть скучными и идти к нулю по действительной (или комплексной) оси. Это сводится к ограничению $h$ вещественным числом в первом уравнении. В формулах получаем для комплексной дифференцируемой функции
\начать{выравнивать}
f'(z) &=
\lim_{\mathbb{C} \ni h \to 0} \frac{f(z+h)-f(z)}{h} \\
&= \lim_{\mathbb{R} \ni h \to 0} \frac{f(z+h)-f(z)}{h} \\
&= \lim_{\mathbb{R} \ni h \to 0} \frac{\big(u(z+h)+iv(z+h)\big)-\big(u(z)+iv( г)\большой)}{ч} \\
&= \lim_{\mathbb{R} \ni h \to 0} \frac{u(z+h)-u(z)}{h}
+ я \ lim _ {\ mathbb {R} \ ni h \ to 0} \ frac {v (z + h) -v (z)} {h} \\
&= u_x(z) + iv_x(z).
\end{выравнивание}
Здесь мы использовали, что определение пределов линейно, комплексные числа непосредственно разлагаются на действительную и мнимую части и что $f$ непрерывно дифференцируема, т.е. е. ограничения, которые мы взяли, все существуют.
$\endgroup$
1
$\begingroup$
Я думаю, вы можете найти все ингредиенты в книге Ульриха на страницах 4-6.
Ульрих объясняет, что $f$ комплексно дифференцируема в $z$ тогда и только тогда, когда существует $a \in \mathbb C$ такое, что $f(z+h) = f(z) +a \cdot h + o(h) $. Тогда $f'(z) = а$.
Отображение $L : \mathbb C \to \mathbb C, L(h) = a \cdot h = f'(z)\cdot h,$ является $\mathbb C$-линейным и, следовательно, тривиально также $\ mathbb R$-линейный.
Рассматривая $L$ как $\mathbb R$-линейное отображение, мы можем выразить его как вещественную матрицу относительно базиса $\{1, i\}$ $\mathbb C$.
Если $a = \alpha + i\beta$, то эта матрица
$$M(L) = \left(\begin{массив}{rrr}
\альфа & -\бета \\
\бета и \альфа\\
\конец{массив}\справа) . $$
Это хорошо известный факт из линейной алгебры, и его легко проверить, написав $h = \mu + i\nu$ и сравнив $M(L) \cdot \left( \begin{array}{rrr}
\мю\\
\nu \end{array}\right)$ и $a \cdot h = (\alpha + i\beta)\cdot (\mu + i\nu)$.
Ульрих также показывает, что $f = u + iv$ действительно дифференцируемо, а это означает, что существует $\mathbb R$-линейное отображение $L’$ такое, что $f(z+h) = f(z) + L ‘(ч) + о(ч)$. Выражение $L’$ в виде вещественной матрицы дает $$M(L’) = \left(\begin{массив}{rrr} u_x(z) и u_y(z) \\ v_x(z) и v_y(z) \\ \end{массив}\right) = \left( \begin{массив}{rrr} u_x(z) & -v_x(z) \\ v_x(z) и u_x(z) \\ \end{массив}\right)$$ благодаря уравнениям CR.
Очевидно, что $L’ = L$. Сравнивая матрицы, мы видим, что $\alpha = u_x(z), \beta = v_x(z)$, откуда $$f'(z) = a = \alpha + i\beta = u_x(z) + iv_x(z).$$
PS. Я думаю, что прямое доказательство, данное Майклом Хайнсом, проще.
Ульрих, кажется, сосредотачивается на отношениях между комплексной и действительной дифференцируемостью.
$\endgroup$
$\begingroup$
Вы знаете, что $f'(z)=$ $\left[\begin{массив}{cc} u_x & -v_x \\ v_x & u_x \конец{массив}\справа] $, то $f'(a,b)$ равно
$\left[\begin{массив}{cc} u_x & -v_x \\ v_x & u_x \end{массив}\right] \left[\begin{массив}{c} a\\ b \end{массив}\right]=\left[\begin{массив}{c} au_x -bv_x\\ av_x+ bu_x \end{массив}\right]$ В книге рассматривается $a+ib = \left[\begin{array}{c} a\\ b \end{array}\right]$ И $f'(a,b)$ будет, как я писал ранее, умножением матриц, где верхняя запись является реальной частью, а нижняя — мнимой частью, и если вы вычислите $(a+ib)(u_x+iv_x )$ и напишите, что в качестве матрицы 2×1 вы увидите, что это то же самое
$\endgroup$
исчисление — Почему бы нам не приблизиться к точке под углом, чтобы найти производную сложных функций?
В случае вещественных функций мы приближаемся к точке слева и справа и проверяем, равны ли обе производные.
Но в случае Комплексных функций к точке можно подойти с бесконечно многих направлений. Тогда как мы можем проверить, что производные по всем направлениям равны?
Я думаю, что в случае Комплексных функций мы должны подходить к точке под углом. Например, чтобы найти производную в точке $z$, мы можем повернуть на угол $d\theta$ вокруг начала координат по часовой стрелке или против часовой стрелки, найти разницу в значении функции, затем разделить на угол измените и примените ограничение $d\theta\rightarrow0$. В этом случае у нас будут производные по часовой и против часовой стрелки, и мы сможем увидеть, равны ли они. Итак, если аргумент $z$ равен $\arg{(z)}$, то производная будет:
$$\lim_{d\theta \rightarrow0}\frac{f(|z|(\cos{(\arg{(z)}+d\theta})+i\sin{(\arg{(z )}+d\theta})))-f(z)}{d\theta}$$
Думаю, приближаться к точке под углом должно быть удобнее, чем подходить к ней со всех сторон. Итак, почему мы приближаемся к точке линейно даже в случае Комплексных функций?
РЕДАКТИРОВАТЬ: У меня есть еще одна идея, мы можем даже приблизиться к точке с внешнего и внутреннего направлений по линии, соединяющей точку с началом координат.
Итак, у нас есть внешняя производная и внутренняя производная.
В этом случае угол остается постоянным, но модуль изменяется на бесконечно малую величину. Это будет:
$$\lim_{dz\rightarrow 0}\frac{f((|z|+dz)(\cos{(\arg{(z)})}+i\sin{(\arg {(z)})})-f(z)}{dz}$$
Таким образом, если комплексная функция задана как функция модуля ($|z|$) и аргумента ($\theta$) вместо как функция координат, то моя «угловая» производная есть частная производная функции по $\theta$, а моя «модульная» производная есть частная производная функции по $|z|$.{|z_2|}m({|z|, \arg{(z_2)}})d|z|$$
Кроме того, что, если определение комплексной производной $$f'(z) = \lim_ {w\to z} \frac{f(w)-f(z)}{w-z}$$
Это не имеет значения. Проблема в том, как мы оцениваем этот предел? Если подставить $w=z+h$, то это то же самое, что подойти к $z$ справа по прямой, параллельной вещественной оси, проходящей через $z$. Если подставить $w=z+ih$, то это то же самое, что приблизиться к $z$ сверху по прямой, параллельной воображаемой оси, проходящей через $z$.