Молекулярная физика и термодинамика
В этом разделе приводятся некоторые следствия, вытекающие из формул (3.29) и (3.30). В качестве примера на рис. 3.3 изображены две кривые, соответствующие распределениям f(v) молекул кислорода O2 по абсолютным величинам скоростей при температурах Т1 = 300 К и Т2 = 1 300 К.
Рис. 3.3. Распределение молекул кислорода по скоростям при разных температурах T1 = 300 К и T2 = 1 300 К
Наиболее вероятная скорость. При бесконечно малых и неограниченно больших значениях скоростей функция распределения стремится к нулю
то есть такие предельные значения скоростей маловероятны в системе. Следовательно, при каком-то значении скорости функция f(v) достигает своего максимума.
|
Наиболее вероятная скорость 
|
Ее можно найти, решая уравнение
откуда следует, что
|
|
(3.31) |
Иными словами, наиболее вероятной называется скорость, вблизи которой на единичный интервал приходится наибольшее число молекул. В этой точке f(v) принимает максимальное значение:
|
|
(3.32) |
Соотношения (3.31), (3.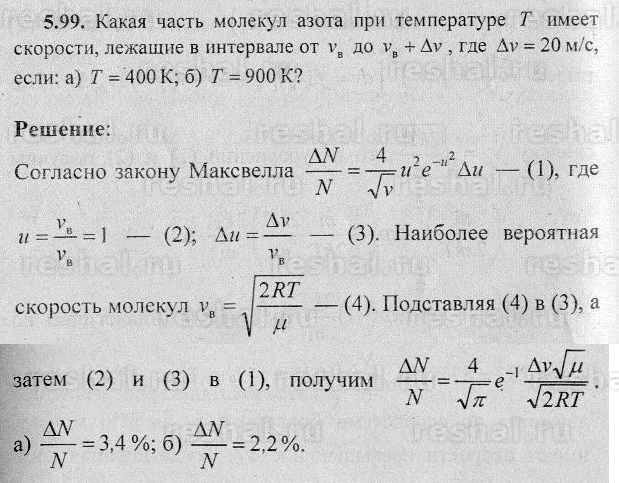 32) могут быть полезны для анализа изменения функции распределения при изменении температуры газа или при изменении рода газа, то есть массы молекул. Отметим, что как следует из (3.26) – (3.29), распределение Максвелла зависит не отдельно от массы молекул и отдельно от температуры газа, а от их отношения . Поэтому распределение не только «буквенно» но и численно одно и тоже, например, для молекулярного водорода при температуре и для гелия при температуре .
32) могут быть полезны для анализа изменения функции распределения при изменении температуры газа или при изменении рода газа, то есть массы молекул. Отметим, что как следует из (3.26) – (3.29), распределение Максвелла зависит не отдельно от массы молекул и отдельно от температуры газа, а от их отношения . Поэтому распределение не только «буквенно» но и численно одно и тоже, например, для молекулярного водорода при температуре и для гелия при температуре .
С ростом температуры наиболее вероятная скорость vВЕР (3.31) увеличивается, то есть максимум функции f(v) сдвигается вправо (см. рис. 3.3), Т2 > Т1. При этом f(vВЕР) уменьшается, то есть кривая становится более пологой. Так же деформируется кривая, если температура постоянна, но масса молекул уменьшается. Напомним, что при любых деформациях функции распределения 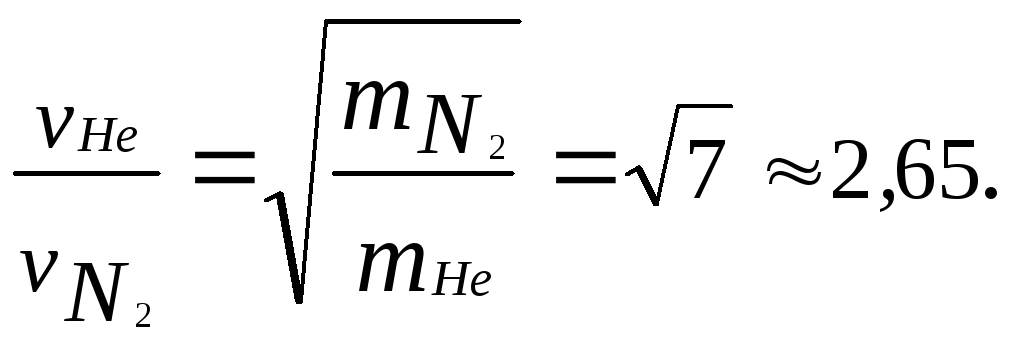 30).
30).
Относительное количество молекул, скорость которых превышает некоторое значение v0, определяется выражением
|
|
(3.33) |
На графике (см. рис. 3.3) этому интегралу соответствует лежащая справа от v0часть площади (отмечена штриховкой), ограниченная кривой f(v) и осью скоростей. Как видно из рис. 3.3, относительное количество молекул, имеющих скорости, превышающие v0, растет с повышением температуры.
В заключение этого раздела заметим, что во всех формулах для функции распределения и характерных скоростей входит отношение массы молекулы к постоянной Больцмана
Умножая числитель и знаменатель на число Авогадро NAи учитывая, что
— молярная масса газа, a
— универсальная газовая постоянная, мы всюду можем использовать это отношение в наиболее удобной для конкретной задачи форме
Распределение молекул по величинам безразмерной скорости.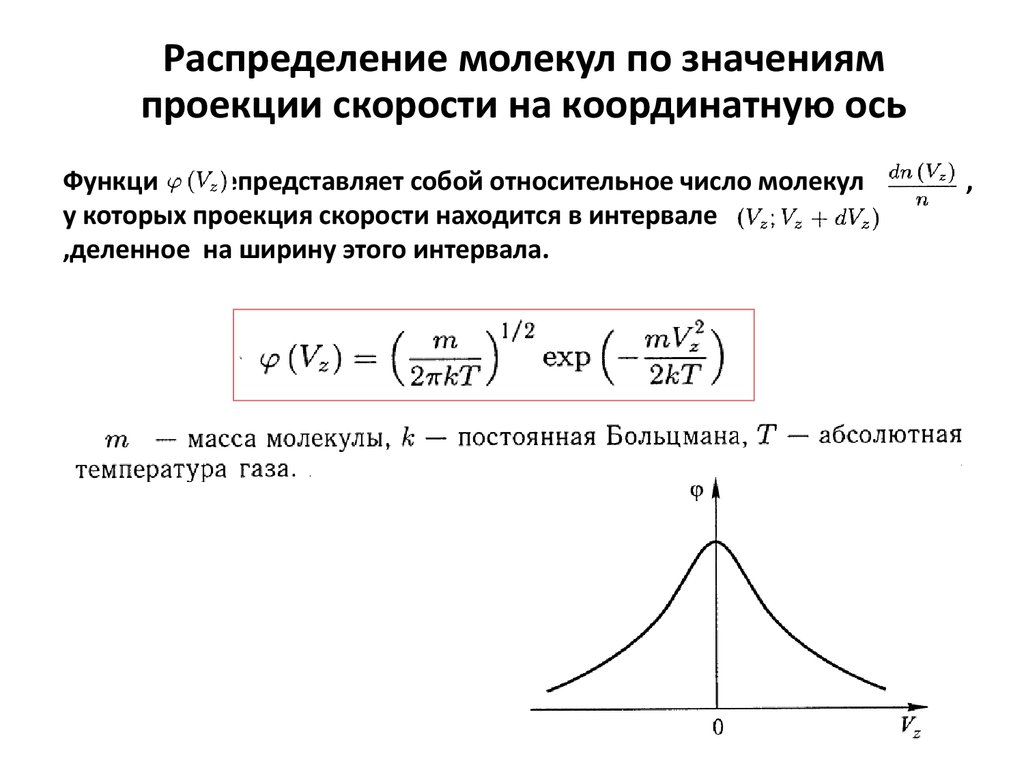 Если при графическом изображении функции распределения Максвелла (3.29) по оси абсцисс откладывать скорости молекул
Если при графическом изображении функции распределения Максвелла (3.29) по оси абсцисс откладывать скорости молекул
то для всех температур и любых масс молекул (любых газов) получится одна и та же кривая (рис. 3.4).
Рис. 3.4. Распределение Максвелла по величинам безразмерной скорости
Сделав замену переменной
в (3.29) и учитывая, что
получим распределение Максвелла в форме
|
|
(3. |
Эта формула и соответствующий ей график (см. рис. 3.4) удобны для решения многих задач.
Пример. Найдем, какая часть общего числа молекул кислорода имеет при температуре 27 °С скорости, отличающиеся от наиболее вероятной не более, чем на 1 %; а также скорости в интервале 562–572 м/с.
Произведем необходимые вычисления. Чтобы ответить на первый вопрос задачи, учтем, что u = 1 при v = vВЕР. Величина интервала du = 0,02. Следовательно,
Вычислим наиболее вероятную скорость:
Найдем отношение v = 562 м/с к vВЕР = 395 м/с
Определим по кривой (см. рис. 3.4) значение функции f(u) при u = 1,42. Получаем f(u) = Следовательно, доля молекул в этом интервале
Следовательно, доля молекул в этом интервале
Интересно отметить, что молекула кислорода проходит за секунду путь, равный в среднем 0,4 км. Но не нужно забывать о соударениях молекул. Из-за них молекула по прямой движется очень недолго, и ее путь представляет собой ломаную линию. Поэтому молекула, двигаясь с огромной скоростью по отдельным звеньям ломаной траектории, передвигается от слоя к слою газа со сравнительно небольшой скоростью.
Средняя арифметическая скорость. Знание функции распределения молекул по скоростям f(v) дает возможность найти среднее значение скорости, а также любой величины, являющейся функцией скорости, например квадрата скорости v2или кинетической энергии молекулы mv 2/2.
|
Средняя арифметическая скорость <v> — это отношение суммы абсолютных величин скоростей всех молекул в системе к числу этих молекул. |
Разобьем интервал всех возможных значений скорости от 0 до бесконечности на малые интервалы Dvi. Каждому интервалу соответствует количество молекул
|
|
(3.35) |
Так как интервалы Dv
|
|
(3. |
Сумма значений скоростей всех молекул
|
|
(3.37) |
Разделив эту сумму на число молекул, получим выражение для средней арифметической скорости
|
|
(3.38) |
Переходя от суммы к интегралу, получаем
|
|
(3. |
Вычисляя интеграл, получаем среднюю арифметическую скорость молекул
|
|
(3.40) |
Среднеквадратичная скорость. Чтобы найти среднее значение произвольной функции L(v) скорости, нужно эту функцию умножить на функцию распределения и проинтегрировать по всем возможным значениям скорости:
|
|
(3.41) |
В частности, при L(v) = v отсюда находится <v>.
Среднее значение квадрата скорости равно отношению суммы квадратов скоростей всех молекул системы к общему числу молекул. Таким образом,
|
|
(3.41) |
|
Среднеквадратичная скорость — это корень квадратный из среднего значения квадрата скорости молекул
|
Следует отметить, что характерные скорости отличаются друг от друга лишь численными множителями, причем
|
|
(3. |
а зависимость от Т и m0(или m) у них одинаковая.
Через среднеквадратичную скорость выражается средняя кинетическая энергия поступательного движения молекул
|
|
(3.44) |
Этот результат находится в согласии с формулой (1.14) кинетической теории идеальных газов и с законом о равнораспределении энергии, который гласит, что на каждую степень свободы молекулы приходится энергия kBТ/2. Три степени свободы поступательного движения молекулы как раз соответствуют полученному здесь результату (3.44). В сущности, именно для того, чтобы получить такое соответствие, мы выбрали должным образом коэффициент α в (3.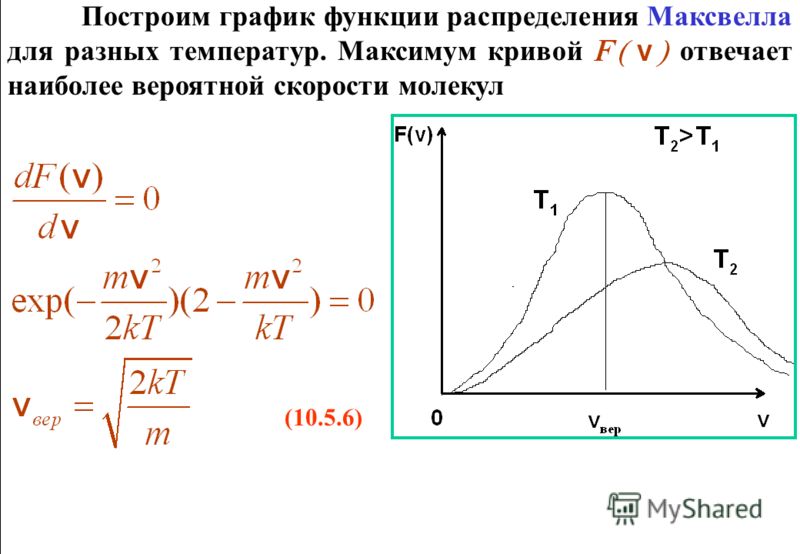 26).
26).
Эксперимент по проверке распределения Максвелла. Необходимо еще раз подчеркнуть, что установленный Максвеллом закон распределения молекул по скоростям и все вытекающие из него следствия справедливы только для газа, находящегося в равновесии.
Закон справедлив для любого числа молекул N, если только это число достаточно велико. Закон Максвелла — статистический, а законы статистики выполняются тем точнее, чем к большему числу одинаковых объектов они применяются. При малом числе объектов могут наблюдаться значительные отклонения от предсказанной статистики — флуктуации.
Экспериментальное определение распределения скоростей молекул было осуществлено впервые О. Штерном в 1920 г. Исследовалось распределение по скоростям одноатомных молекул паров металлов (Ag или Pt), из которых была изготовлена нить, расположенная на оси двух цилиндров. Нить нагревалась электрическим током, и металл испарялся (см. рис 3.5).
рис 3.5).
Рис. 3.5 Схема опыта Штерна: 1 — вид установки сбоку; 2 — вид установки сверху
Молекулы, прошедшие через щель во внутреннем цилиндре, летели по прямой и оседали на стенке холодного внешнего цилиндра. Если привести всю установку во вращение (щель все время против точки В0), то молекулы, обладающие большой скоростью v, попадут в некоторую точку вблизи В0, а более медленные затратят на путь больше времени и попадут в точки, отстоящие дальше от В0. Следует обратить внимание, что вылетающие молекулы движутся по прямой, они не участвуют во вращательном движении. Поскольку молекулы в зависимости от скорости попадают в разные точки внешнего цилиндра, то исследуя толщину слоя металла, осевшего на его стенку, можно составить представление о распределении молекул по скоростям.
Найдем распределение молекул по расстояниям S от точки В0 до места их попадания на стенку цилиндра. Если R и r — радиусы большого и малого цилиндров, соответственно (см. рис.), то время полета от щели до стенки цилиндра
Если R и r — радиусы большого и малого цилиндров, соответственно (см. рис.), то время полета от щели до стенки цилиндра
За это время цилиндр повернется на угол
где ω — угловая скорость вращения установки. Соответственно, точка попадания будет смещена относительно В0 на расстояние
Подставляя сюда время полета, получаем связь скорости молекулы с расстоянием S:
Подставляя, в свою очередь, полученное выражение в распределение Максвелла и учитывая, что
находим распределение молекул по расстояниям S:
(мы опускаем выражение для нормировочной постоянной С).
Опыты Штерна подтвердили справедливость закона, установленного Максвеллом.
Наиболее вероятная, среднеквадратичная и средняя арифметическая скорости молекул газа
Рассмотрим, как изменяется с абсолютной
величиной скорости число частиц,
приходящихся на единичный интервал
скоростей, при единичной концентрации
частиц.
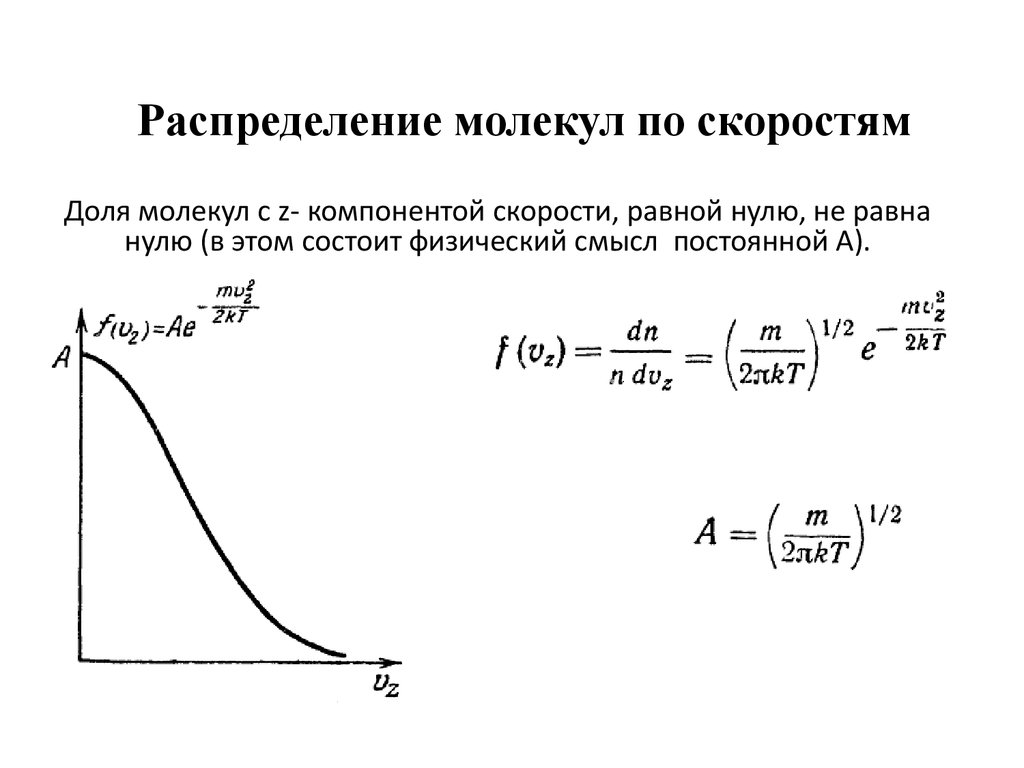
График функции распределения Максвелла
,
приведен на рисунке 2.6.
Рис. 2.6
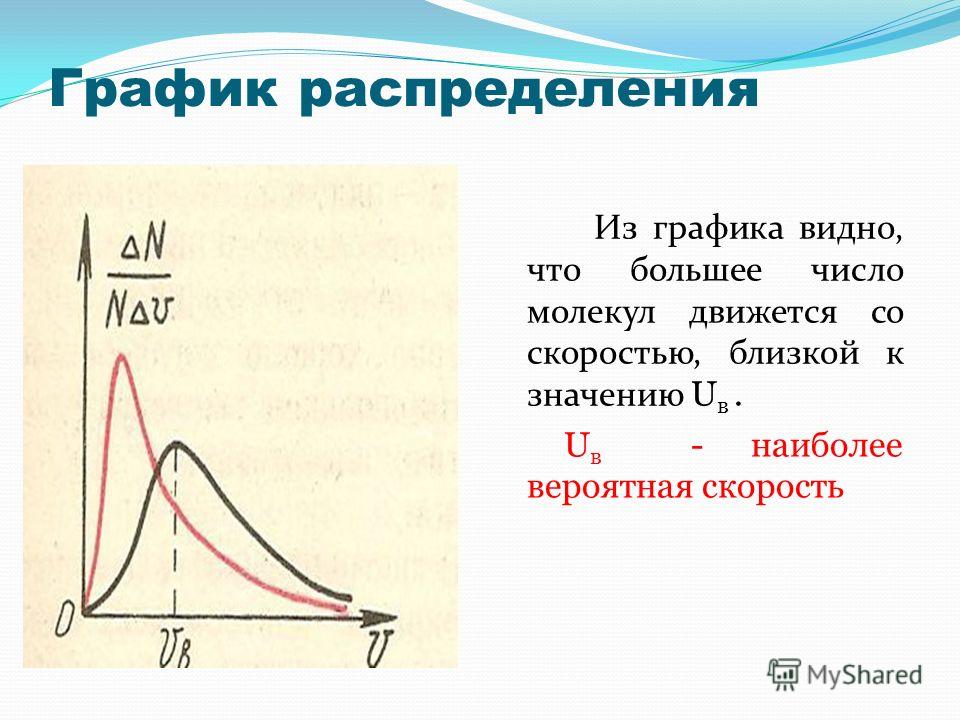
Из графика видно, что при «малых» υ, т.е. при , имеем ; затем достигает максимума А и далее экспоненциально спадает .
Величину скорости, на которую приходится максимум зависимости , называют наиболее вероятной скоростью.
Найдем эту скорость из условия равенства производной .
, (2.3.6)
– наиболее вероятная скорость одной молекулы.
Для одного моля газа:
. (2.3.7)
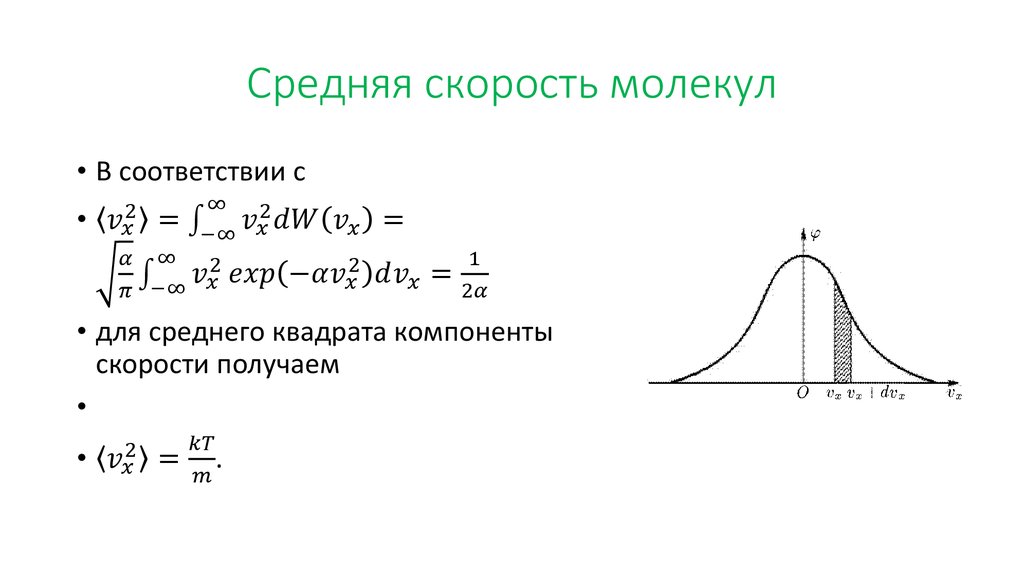
Среднюю квадратичную скорость найдем, используя соотношение :
– для одной молекулы. (2.3.8)
– для одного моля газа. (2.3.9)
Средняя арифметическая скорость:
где – число молекул со скоростью от υ
до
. Если подставить сюда f(υ)
и вычислить, то получим:
Если подставить сюда f(υ)
и вычислить, то получим:
– для одной молекулы. (2.3.10)
– для одного моля газа. (2.3.11)
Все три скорости незначительно отличаются друг от друга множителем порядка единицы, причем
Формула Максвелла для относительных скоростей
Для решения многих задач удобно использовать формулу Максвелла, где скорость выражена в относительных единицах.
Относительную скорость обозначим через u:
(2.3.13)
где . Тогда из (2.3.3), получим
. (2.3.14)
Это уравнение универсальное. В таком виде функция распределения не зависит ни от рода газа, ни от температуры.
На рисунке 2.7 показано максвелловское распределение частиц f(υ), имеющих скорости от υ до За единицу скорости здесь взята наиболее вероятная скорость.
Полезно
знать, что .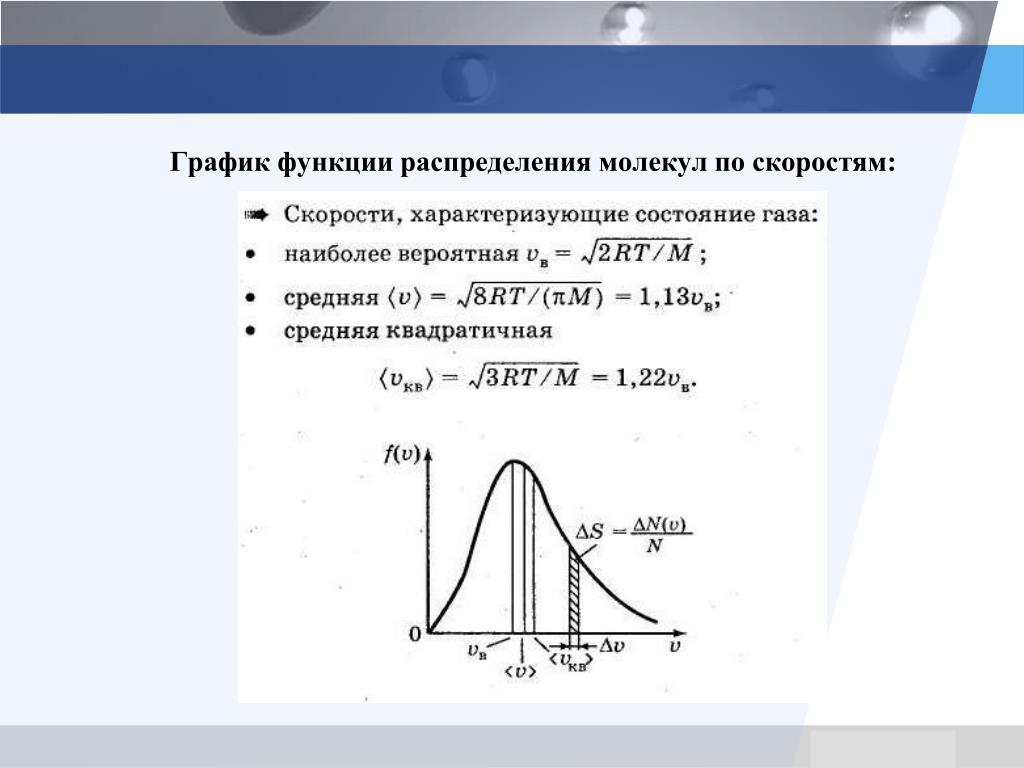
Рис. 2.7
Зависимость функции распределения Максвелла от массы молекул и температуры газа
На рисунке 2.8 показана зависимость при различных температурах и массах молекул газа.
Рис. 2.8
Из рисунка 2.8 можно проследить за изменением при изменении m и T. В данном случае (при ) или (при ). Площадь под кривой величина постоянная, равная единице ( ), поэтому важно знать как будет изменяться положение максимума кривой:
кроме того
Максвелловский закон распределения по скоростям и все вытекающие следствия справедливы только для газа в равновесной системе. Закон статистический, и выполняется тем лучше, чем больше число молекул.
Барометрическая формула
Рассмотрим ещё один очень важный закон.
Атмосферное
давление на какой-либо высоте h обусловлено весом слоёв газа, лежащих
выше. Пусть P – давление на высоте h,
а –
на высоте (рис. 2.9).
Пусть P – давление на высоте h,
а –
на высоте (рис. 2.9).
Рис. 2.9
Причём , а dР < 0, так как на большей высоте давление меньше. Разность давления равна весу газа, заключённого в объёме цилиндра с площадью основания равного единице и высотой dh.
Т.к. где плотность газа на высоте h, медленно убывающая с высотой, то можно записать:
.
или .
Проинтегрировав это выражение, получим:
,
где С – произвольная постоянная.
В силу произвольности, примем, что С = Р0 – давление на высоте . Отсюда, после потенцирования, получаем барометрическую формулу:
(2.4.1)
Из
формулы (2.4.1) следует, что P убывает с высотой тем быстрее, чем
тяжелее газ (чем больше μ) и чем ниже
температура (например, на больших высотах
концентрация легких газов Не и Н2 гораздо больше, чем у поверхности Земли).
На рисунке 2.10 изображены две кривые, которые можно трактовать, либо как соответствующие разным μ (при одинаковой Т), либо как отвечающие разным Т, при одинаковых μ.
Таким образом, чем тяжелее газ (больше μ) и чем ниже температура, тем быстрее убывает давление.
Рис. 2.10
Пусть идеальный газ находится в поле консервативных сил в условиях теплового равновесия. При этом концентрация газа будет различной в точках с различной потенциальной энергией, что необходимо для соблюдения условий механического равновесия. Так, число молекул в единичном объеме n убывает с удалением от поверхности Земли, и давление, в силу соотношения , падает.
Если известно число молекул в единичном
объеме, то известно и давление, и наоборот.
Давление и плотность пропорциональны
друг другу, поскольку температура в
нашем случае постоянна. Давление с
уменьшением высоты должно возрастать,
потому что нижнему слою приходится
выдерживать вес всех расположенных
сверху атомов.
Исходя из основного уравнения молекулярно-кинетической теории: , заменим P и P0 в барометрической формуле (2.4.1) на n и n0 и получим распределение Больцмана для молярной массы газа:
(2.5.1)
где n0 и n число молекул в единичном объёме на высоте h = 0 и h.
Так как а , то (2.5.1) можно представить в виде
(2.5.2)
С уменьшением температуры число молекул на высотах, отличных от нуля, убывает. При тепловое движение прекращается, все молекулы расположились бы на земной поверхности. При высоких температурах, наоборот, молекулы оказываются распределёнными по высоте почти равномерно, а плотность молекул медленно убывает с высотой. Так как – это потенциальная энергия U, то на разных высотах – различна. Следовательно, (2.5.2) характеризует распределение частиц по значениям потенциальной энергии:
, (2. 5.3)
5.3)
– это закон распределения частиц по потенциальным энергиям – распределение Больцмана. Здесь n0 – число молекул в единице объёма там, где .
На рисунке 2.11 показана зависимость концентрации различных газов от высоты. Видно, что число более тяжелых молекул с высотой убывает быстрее, чем легких.
Рис. 2.11
Из (2.5.3) можно получить, что отношение концентраций молекул в точках с U1 и U2 равно:
. (2.5.4)
Больцман доказал, что соотношение (2.5.3) справедливо не только в потенциальном поле сил гравитации, но и в любом потенциальном поле, для совокупности любых одинаковых частиц, находящихся в состоянии хаотического теплового движения.
В п. 2.3 мы получили выражение для распределения молекул по скоростям (распределение Максвелла):
Из
этого выражения легко найти
распределение молекул газа по значениям
кинетической энергии K. Для этого перейдём от переменной υ
к переменной :
Для этого перейдём от переменной υ
к переменной :
где dn(K) – число молекул, имеющих кинетическую энергию поступательного движения, заключённую в интервале от K до Отсюда получим функцию распределения молекул по энергиям теплового движения:
(2.6.1)
Средняя кинетическая энергия молекулы идеального газа:
то есть получаем результат, совпадающий с прежним результатом, полученным в п. 1.3.
Итак, закон Максвелла даёт распределение частиц по значениям кинетической энергии, а закон Больцмана – распределение частиц по значениям потенциальной энергии. Оба распределения можно объединить в единый закон Максвелла – Больцмана:
. (2.6.2)
Здесь n0 – число молекул в единице объёма в той
точке, где
, – полная энергия.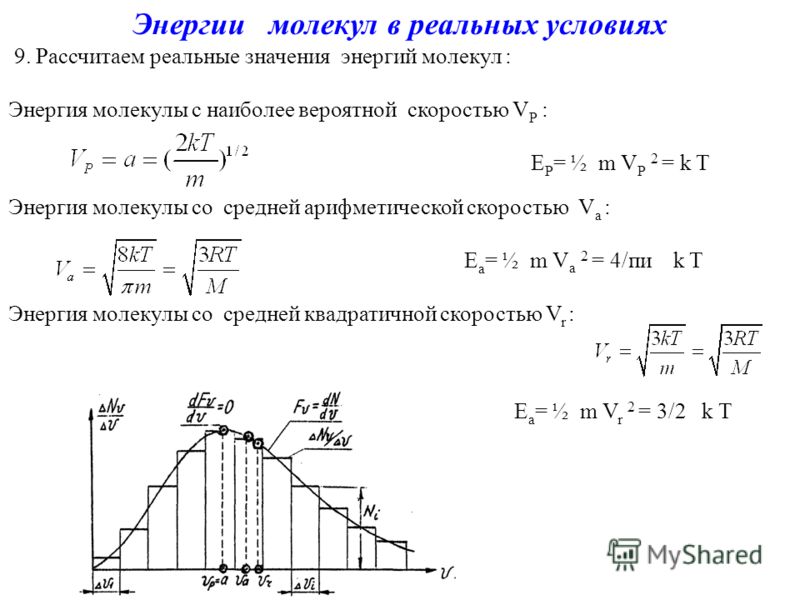
В последнем выражении, потенциальная и кинетическая энергии, а следовательно и полная энергия Е, могут принимать непрерывный ряд значений. Если же энергия частицы может принимать лишь дискретный ряд значений Е1, Е2…, (как это имеет место, например, для внутренней энергии атома), то в этом случае распределение Больцмана имеет вид:
, (2.6.3)
где Ni – число частиц, находящихся в состоянии с энергией Еi, а А – коэффициент пропорциональности, который должен удовлетворять условию
где N – полное число частиц в рассматриваемой системе.
Тогда окончательное выражение распределения Максвелла – Больцмана для случая дискретных значений энергий будет иметь вид:
(2.6.4)
5.9: Молекулярное распределение скоростей — Химия LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 169982
Распределения значения молекулярной скорости
В середине 19В -м -м веке Джеймс Максвелл и Людвиг Больцман вывели уравнение для распределения молекулярных скоростей в газе. График этого уравнения дает нам распределений скоростей Максвелла-Больцмана. Кривая распределения скорости Максвелла-Больцмана для N 2 при 25ºC показана ниже.
График этого уравнения дает нам распределений скоростей Максвелла-Больцмана. Кривая распределения скорости Максвелла-Больцмана для N 2 при 25ºC показана ниже.
Например, при скорости 500 м/с значение y равно 0,00185. Это говорит нам о том, что доля молекул, имеющих скорость около 500 м/с, равна 0,00185. Примечание: если вы затрудняетесь с понятием доли, переведите ее в проценты (умножьте на 100): 0,185% молекул имеют скорости в этом диапазоне. Чем выше кривая при данной скорости, тем больше молекул перемещается с этой скоростью. Например, многие молекулы имеют скорость около 500 м/с, тогда как немногие молекулы имеют скорость около 1000 м/с.
Скорость, которая соответствует пику кривой, называется наиболее вероятной скоростью . С этой скоростью (или близкой к ней) движется больше молекул, чем с любой другой. Для N 2 при 25°С наиболее вероятная скорость составляет 421 м/с. Средняя скорость немного больше, чем наиболее вероятная скорость. Для N 2 при 25ºC средняя скорость составляет 475 м/с. Среднеквадратическая скорость — это скорость, которая соответствует средней кинетической энергии молекул. Для № 2 при 25ºC, среднеквадратическая скорость 515 м/сек.
Для N 2 при 25ºC средняя скорость составляет 475 м/с. Среднеквадратическая скорость — это скорость, которая соответствует средней кинетической энергии молекул. Для № 2 при 25ºC, среднеквадратическая скорость 515 м/сек.
Для любого газа эти скорости можно рассчитать по следующим формулам:
наиболее вероятная скорость, \(v_{mp}\):
\[v_{mp} = \sqrt{\dfrac{2RT}{M }},\]
средняя скорость, \(v_{ave}\):
\[v_{ave} = \sqrt{\dfrac{8RT}{\pi M}},\]
среднее значение -квадратичная скорость, \(v_{rms}\):
\[v_{rms} = \sqrt{\dfrac{3RT}{M}},\]
, где \(T\) — температура по Кельвину, \(R\) — газовая постоянная, выраженная в единицах Дж/моль-К (8,314 Дж/моль-К), а \(М\) — молярная масса газа, выраженная в единицах кг/моль.
Доля молекул в широком диапазоне скоростей
Предположим, мы хотим узнать долю молекул, имеющих скорости в широком диапазоне, скажем, от 500 до 1000 м/сек. В принципе, мы могли бы сложить дроби для каждой отдельной скорости в этом диапазоне точно так же, как мы сложили размеры столбцов на нашей гистограмме. Однако на практике это нецелесообразно, потому что нужно будет сложить слишком много «столбцов» (для этого конкретного диапазона нам нужно добавить 500 «столбцов»!!) Гораздо лучший способ определить долю молекул в широком диапазоне скоростей заключается в измерении площади области под кривой Максвелла-Больцмана.
Однако на практике это нецелесообразно, потому что нужно будет сложить слишком много «столбцов» (для этого конкретного диапазона нам нужно добавить 500 «столбцов»!!) Гораздо лучший способ определить долю молекул в широком диапазоне скоростей заключается в измерении площади области под кривой Максвелла-Больцмана.
Площадь под всей кривой Максвелла-Больцмана равна ровно 1. Следовательно, площадь под любой частью кривой равна доле молекул в соответствующем диапазоне скоростей.
Например, если мы хотим определить долю молекул со скоростью от 500 до 1000 м/с, нам нужно измерить площадь заштрихованной области ниже.
Существует несколько способов оценки этой площади. Самое простое, что вы будете делать в лаборатории, это вырезать и взвесить график. В принципе, мы могли бы использовать исчисление для определения точной площади под кривой, поскольку известно уравнение, порождающее кривую Максвелла-Больцмана. К сожалению, это уравнение не может быть проинтегрировано аналитически.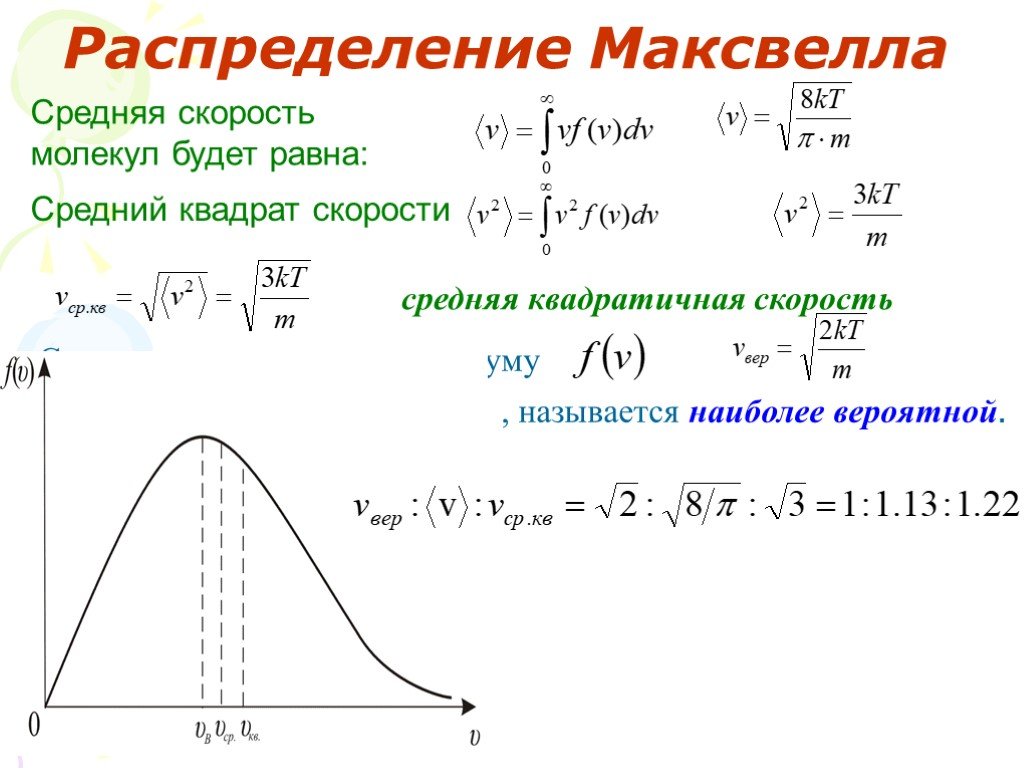 Однако, если вам интересно, площадь заштрихованной области равна 0,39.2, поэтому доля молекул, имеющих скорость от 500 до 1000 м/с, равна 0,392. (Как всегда, мы можем думать об этом в процентах: 39,2%.)
Однако, если вам интересно, площадь заштрихованной области равна 0,39.2, поэтому доля молекул, имеющих скорость от 500 до 1000 м/с, равна 0,392. (Как всегда, мы можем думать об этом в процентах: 39,2%.)
Форма кривой распределения скорости
Большой объем информации о газе можно получить, рассматривая общую форму кривой распределения скорости. Форма кривой распределения скорости зависит как от температуры, так и от молярной массы газа.
Когда мы рассматриваем газ при повышении температуры:
- Кривая Максвелла-Больцмана расширяется и выравнивается.
- Наиболее вероятная скорость увеличивается (пик смещается вправо).
- Увеличивается доля быстродвижущихся молекул.
- Уменьшается доля медленно движущихся молекул.
Распределение скоростей Максвелла-Больцмана для азота при четырех различных температурах
Обратите внимание, что при повышении температуры частицы в газе стремятся двигаться быстрее . В результате все распределение смещается вправо, в сторону более высоких скоростей. Когда мы повышаем температуру, наиболее вероятная скорость увеличивается (самая высокая точка на кривой смещается вправо). Кроме того, вся кривая становится шире и ниже: у нас шире диапазон скоростей, но меньше молекул на наиболее вероятной скорости.
В результате все распределение смещается вправо, в сторону более высоких скоростей. Когда мы повышаем температуру, наиболее вероятная скорость увеличивается (самая высокая точка на кривой смещается вправо). Кроме того, вся кривая становится шире и ниже: у нас шире диапазон скоростей, но меньше молекул на наиболее вероятной скорости.
Кроме того, когда мы повышаем температуру, доля молекул, движущихся с высокими скоростями i nувеличивает . Например, когда мы повышаем температуру с 25°С до 300°С, увеличивается доля молекул, движущихся быстрее 800 м/сек.
Аналогичным образом, когда мы повышаем температуру, доля молекул, движущихся с низкими скоростями , уменьшается . Например, когда мы повышаем температуру с 25ºC до 300ºC, доля молекул, движущихся медленнее 800 м/сек, становится меньше.
Когда мы рассматриваем газы с увеличивающейся молекулярной массой:
- Кривая Максвелла-Больцмана становится выше и уже.

- Наиболее вероятная скорость снижается (пик смещается влево).
- Уменьшается доля быстродвижущихся молекул.
- Увеличивается доля медленно движущихся молекул.
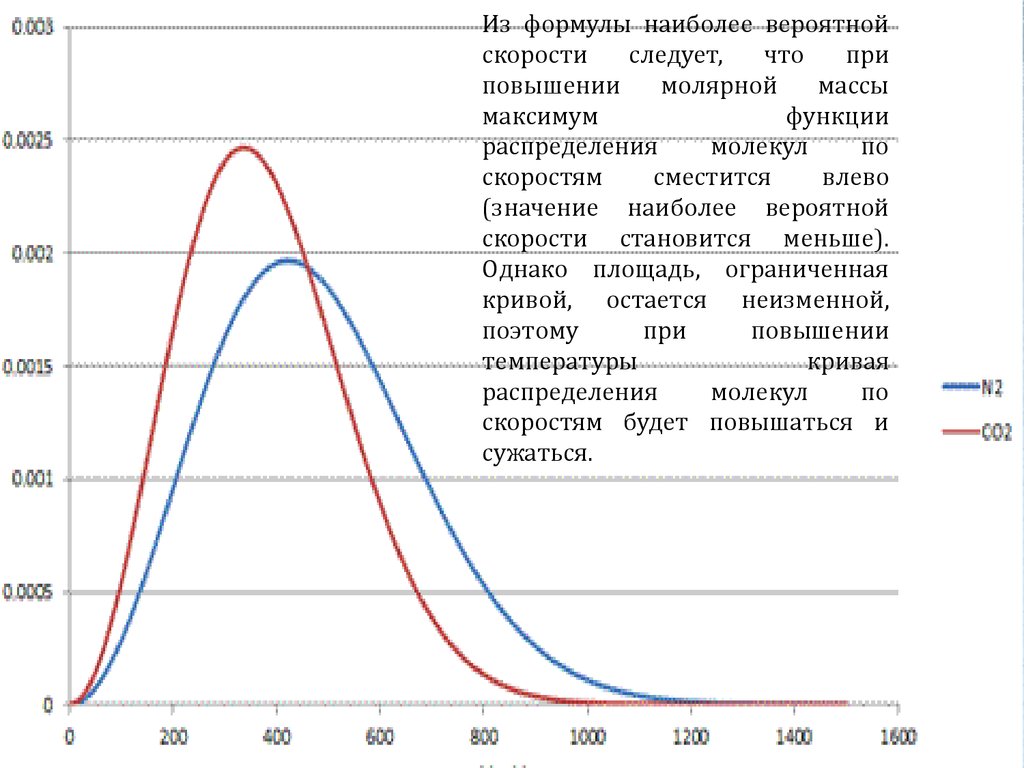
Кривые распределения скоростей Максвелла-Больцмана для трех различных газов
Обратите внимание, что газ с наименьшей молекулярной массой (гелий) имеет самые высокие молекулярные скорости, а газ с наибольшей молекулярной массой (ксенон) имеет самую низкую молекулярные скорости. При увеличении молярной массы наиболее вероятная скорость уменьшается (самая высокая точка кривой смещается влево). Кроме того, вся кривая становится уже и выше: у нас меньший диапазон скоростей, но больше молекул на наиболее вероятной скорости.
Пример \(\PageIndex{1}\): что больше?
Для каждой из следующих пар величин укажите, какая из них больше, и объясните свой ответ. Если они равны, скажите об этом и объясните, как вы можете это определить. («КЭ» означает кинетическую энергию)
(«КЭ» означает кинетическую энергию)
а) Среднеквадратичная скорость азота при 25ºC или среднеквадратичная скорость кислорода при 75ºC.
б) Средняя скорость водорода или средняя скорость гелия при той же температуре.
c) Доля молекул \(CH_4\) со скоростями более 500 м/с или доля молекул \(NH_3\) со скоростями более 500 м/с при той же температуре.
Решения:
а) O кислород при 75ºC больше. Среднеквадратическая скорость зависит как от молярной массы, так и от температуры, поэтому проще всего просто рассчитать среднеквадратичную скорость для каждого газа, v rms для N 2 составляет 515 м/с, а для O 2 составляет 521 м/с. /с.
б) Водород больше. Если температура постоянна, распределение скорости обратно пропорционально молекулярной массе; чем меньше молярная масса, тем быстрее молекулы.
c) Доля молекул CH 4 со скоростями более 500 м/сек больше. Это похоже на часть c. Газ с меньшей молекулярной массой будет иметь большую долю «быстрых молекул» и меньшую долю «медленных молекул», независимо от того, где мы выбираем границу между «быстрым» и «медленным».
Это похоже на часть c. Газ с меньшей молекулярной массой будет иметь большую долю «быстрых молекул» и меньшую долю «медленных молекул», независимо от того, где мы выбираем границу между «быстрым» и «медленным».
5.9: Molecular Speed Distribution распространяется по незадекларированной лицензии, автором, ремиксом и/или куратором является LibreTexts.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Показать страницу TOC
- да на странице
- Теги
- Распространение измерений
- источник-хим-169606
Почему наиболее вероятная скорость соответствует вершине кривой распределения Максвелла-Больцмана, хотя среднеквадратическая скорость самая высокая? Почему среднее и среднеквадратичное вправо?
Потому что наиболее вероятная скорость наиболее вероятна, т. е. большая часть молекул будет иметь эту скорость. Это НЕ указывает на то, что это самая высокая величина — только вероятность.
е. большая часть молекул будет иметь эту скорость. Это НЕ указывает на то, что это самая высокая величина — только вероятность.
Пусть #upsilon_»mp»#, #<< upsilon >># и #upsilon_»rms»# будут наиболее вероятными , средними и среднеквадратичными скоростями соответственно.
- #upsilon_»mp» = sqrt((2k_BT)/m)#
- #<< ипсилон >> = sqrt((8k_BT)/(pim))#
- #upsilon_»rms» = sqrt((3k_BT)/m)#
Выбрасывая все, что не является #sqrt((k_BT)/m)#, вы получаете порядок #sqrt3 > 2sqrt(2/pi) > sqrt2#. Что соответствует горизонтальному расположению каждого вида скорости на графике. То есть #upsilon_»rms» > << upsilon >> > upsilon_»mp»#, так как молекулярная скорость равна увеличивается слева направо по оси x.
Высота по оси Y означает, что , а не , указывает на более высокую скорость.
Я вывожу эти уравнения ниже, используя распределение Максвелла-Больцмана (вам нужно знать, как вычислять производные, но используемые интегралы приведены в таблице).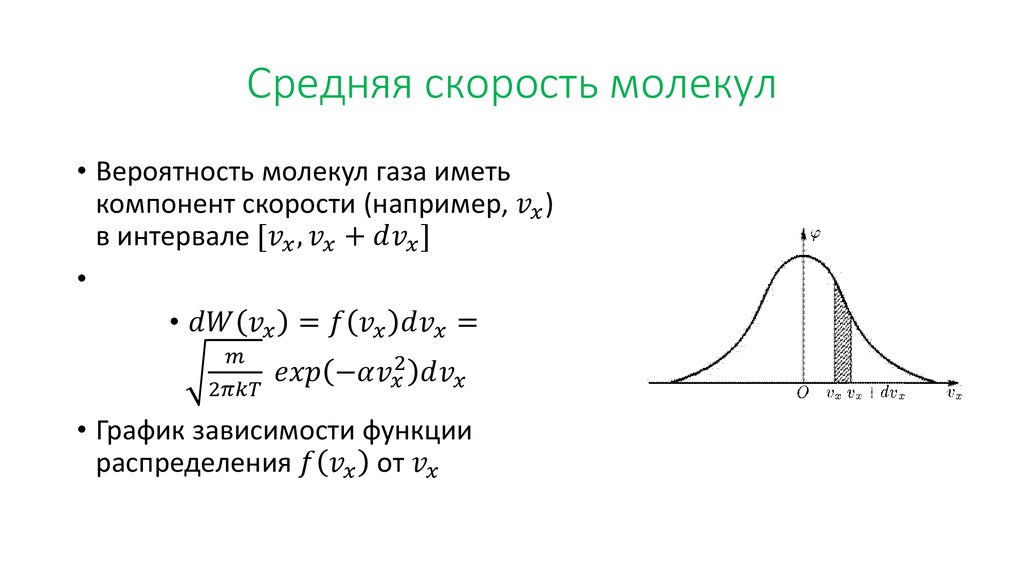


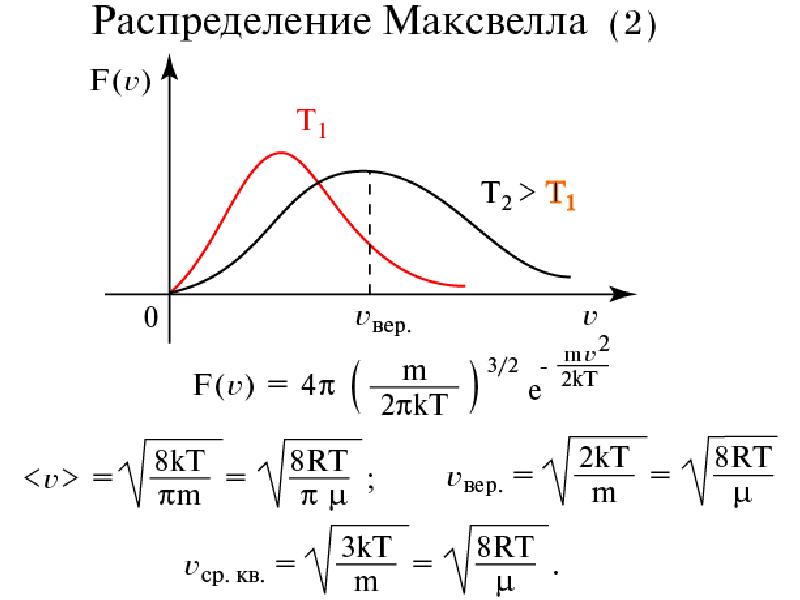 36)
36) 39)
39) 43)
43)