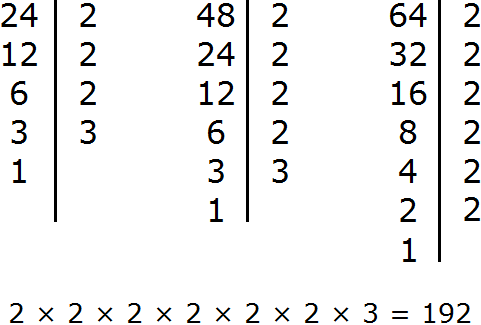Число 288
Свойства и характеристики одного числа
Все делители числа, сумма и произведение цифр, двоичный вид, разложение на простые множители…
Свойства пары чисел
Наименьшее общее кратное, наибольший общий делитель, сумма, разность и произведение чисел…
Сейчас изучают числа:
12 и 24 6740 1189000 256 и 64 4155191586 143327 85085 35000 147 29308 8796093022208 350000 32 358 11 10606879 1391 126 3328 135 и 75 120212021202 0 709399 63252 и 335
Двести восемьдесят восемь
Описание числа 288
Неотрицательное действительное
трёхзначное
число 288
– составное число.
Произведение цифр: 128.
18 — количество делителей числа.
819 — сумма делителей.
0.003472222222222222 является обратным числом к 288.
Другие представления числа 288: двоичная система: 100100000, троичная система: 101200, восьмеричная система: 440, шестнадцатеричная система: 120. Перевод из числа байтов — 288 байтов .
Число 288 азбукой Морзе: ..— —.. —..
Число не является числом Фибоначчи.
Косинус: 0.5178, синус: -0.8555, тангенс: -1.6522.
Число 288 имеет натуральный логарифм: 5.6630.
У числа 288 есть десятичный логарифм: 2.4594.
16.9706 — корень квадратный из числа 288, 6.6039 — корень кубический.
Число 288 в квадрате: 82944.
4 минуты 48 секунд представляет из себя число секунд 288. Цифра 9 — это нумерологическое значение числа 288.
- ← 287
- 289 →
Каково наименьшее общее кратное чисел 12 и 24? – Обзоры Вики
Ответ: LCM 12 и 24 — это 24.
Точно так же, каково наименьшее общее кратное 18 и 24? Ответ: LCM 18 и 24 72.
Что такое НОК 12 и 18? Ответ: LCM 12 и 18 — это 36.
Как найти наименьшее общее кратное 12? НОК – это наименьшее общее кратное. Мы можем найти LCM, перечислив кратные двух чисел и указав наименьшее общее кратное. 12: 12,24,36,48,60,72,84… LCM 60 .
Во-вторых, каково наименьшее кратное 12? 12:12,24,36_,48,60,72,… 36 — первое число, встречающееся в обоих списках. Итак, 36 — это LCM.
Каково наименьшее число, кратное 12 и 18?
НОК 12 и 18 — это 36. Чтобы найти НОК (наименьшее общее кратное) 12 и 18, нам нужно найти кратные 12 и 18 (кратные 12 = 12, 24, 36, 48; кратные 18 = 18, 36, 54, 72) и выберите наименьшее кратное, которое точно делится на 12 и 18, т.
е. на 36.
тогда каково наибольшее общее кратное чисел 18 и 24? Правильный ответ:
18 и 24 имеют общие 2 и 3. Мы умножаем их, чтобы получить GCF, поэтому 2 * 3 = 6 это GCF 18 и 24.
У какой пары чисел НОК равен 24? Это наименьшее число среди общих кратных. Поскольку наименьшее число среди 24, 48 и 72 равно «24», LCM 8 и 6 это 24.
Чему равно общее кратное чисел 12 и 18?
12, 24, 36, 48, 60, 72, 84, 96, 108, 12….. 18, 36, 54, 72, 90, 108, 126, 144, 162, 180…. Следовательно, первые два общих кратных 12 и 18 равны 36 и 72.
Чему равно наименьшее общее кратное чисел 12, 18 и 3? Наименьшее общее кратное чисел 3, 12 и 18 равно 36.
Чему равно третье общее кратное чисел 3 и 12?
Ответ: Первые три общих кратных 6 и 8 равны 24, 48 и 72. И первые три общих кратных 12 и 18 равны 36, 72 и 108.
Каковы общие кратные чисел 12 и 18? 12, 24, 36, 48, 60, 72, 84, 96, 108, 12….. 18, 36, 54, 72, 90, 108, 126, 144, 162, 180….
Следовательно, первые два общих кратных 12 и 18 равны 36 и 72.
Какое наименьшее общее кратное числам 12, 18 и 36?
НОК 12,18,36 12, 18, 36 является 2⋅2⋅3⋅3=36 2 ⋅ 2 ⋅ 3 ⋅ 3 знак равно 36 .
Какое наименьшее общее кратное числам 12, 15 и 18?
НОК 12, 15 и 18 — это 180.
Каковы общие кратные чисел 12 и 18? 12, 24, 36, 48, 60, 72, 84, 96, 108, 12….. 18, 36, 54, 72, 90, 108, 126, 144, 162, 180…. Следовательно, первые два общих кратных 12 и 18 равны 36 и 72.
Какое из этих кратных является НОК 12, 16 и 24? Ответ: LCM 12, 16 и 24 48.
Какое общее кратное 12 и 18?
12, 24, 36, 48, 60, 72, 84, 96, 108, 12….. 18, 36, 54, 72, 90, 108, 126, 144, 162, 180…. Следовательно, первые два общих кратных 12 и 18 равны 36 и 72.
Чему равно наименьшее общее кратное числа 12? 12:12,24,36_,48,60,72,… 36 — первое число, встречающееся в обоих списках. Итак, 36 — это LCM. Метод перечисления нецелесообразен для больших чисел.
Какой самый большой общий делитель для 12 и 24?
Ответ: ЗКФ 12 и 24 — 12.
Каков наибольший общий мономный множитель чисел 12, 18 и 24? Наибольшее число, которое точно делит 12, 18 и 24, является их наибольшим общим делителем. HCF 12, 18 и 24 составляет 6.
Как найти наименьшее общее кратное?
Найдите наименьшее общее кратное (НОК) двух чисел, перечислив кратные
- Назовите первые несколько кратных каждого числа.
- Найдите несколько общих для обоих списков. …
- Найдите наименьшее число, общее для обоих списков.
- Это номер LCM.
У какой пары чисел НОК равен 18? Когда мы накладываем эти два ограничения, мы видим, что единственными общими для обоих наборов значениями являются 6 и 18. Итак, наши возможные пары: (6,6), (6,18) или (18,18). Но подождите — только одна из этих пар имеет НОК, равный 18, и GCF, равный 6. Это пара (6,18) .
Что такое общее кратное 24?
Кратные 24 24, 48, 72, 96,120, 144, 168, 192, И так далее.
У какой пары чисел НОК равен 12? Здесь мы знаем, что общие кратные 12, 24 и 36. НОК этих двух чисел равен 12. Это наименьшее общее число, которое они оба имеют.
| 1 | Найдите количество возможностей | 7 выбрать 3 | |
| 2 | Найдите количество возможностей | 8 выбрать 3 | |
| 3 | Найдите количество возможностей | 5 выбрать 2 | |
| 4 | Найдите количество возможностей | 4 выбрать 2 | |
| 5 | Найдите количество возможностей | 8 выбрать 4 | |
| 6 | Найдите количество возможностей | 10 выбрать 3 | |
| 7 | Найдите количество возможностей | 7 выбрать 4 | |
| 8 | Найдите количество возможностей | 6 выбрать 3 | |
| 9 | Найдите количество возможностей | 9 выбрать 3 | |
| 10 | Найдите количество возможностей | 3 выбрать 2 | |
| 11 | Найдите количество возможностей | 6 выбрать 4 | |
| 12 | Найдите количество возможностей | 5 выбрать 4 | |
| 13 | Найдите количество возможностей | 7 переставить 3 | |
| 14 | Найдите количество возможностей | 7 выбрать 2 | |
| 15 | Найдите количество возможностей | 10 выбрать 5 | |
| 16 | Найдите количество возможностей | 10 выбрать 6 | |
| 17 | Найдите количество возможностей | 13 выбрать 5 | |
| 18 | Найдите количество возможностей | 3 выбрать 3 | |
| 19 | Найдите количество возможностей | 4 выбрать 1 | |
| 20 | Найдите количество возможностей | 4 выбрать 4 | |
| 21 | Найдите количество возможностей | 5 выбрать 1 | |
| 22 | Найдите количество возможностей | 6 переставить 3 | |
| 23 | Найдите количество возможностей | 8 выбрать 5 | |
| 24 | Найдите количество возможностей | 9переставить 4 | |
| 25 | Найдите количество возможностей | 13 выбрать 3 | |
| 26 | Найдите количество возможностей | 12 выбрать 2 | |
| 27 | Найдите количество возможностей | 12 выбрать 4 | |
| 28 | Найдите количество возможностей | 12 выбрать 3 | |
| 29 | Найдите количество возможностей | 9 выбрать 5 | |
| 30 | Найдите количество возможностей | 9 выбрать 2 | |
| 31 | Найдите количество возможностей | 7 выбрать 5 | |
| 32 | Найдите количество возможностей | 6 переставить 6 | |
| 33 | Найдите количество возможностей | 8 переставить 5 | |
| 34 | Найдите количество возможностей | 8 переставить 3 | |
| 35 | Найдите количество возможностей | 7 переставить 5 | |
| Найдите количество возможностей | 52 выбрать 5 | ||
| 37 | Найдите количество возможностей | 5 переставить 3 | |
| 38 | Найдите количество возможностей | 12 выбрать 5 | |
| 39 | Найдите количество возможностей | 3 выбрать 1 | |
| 40 | Найдите количество возможностей | 11 выбрать 5 | |
| 41 | Найдите количество возможностей | 10 выбрать 2 | |
| 42 | Найдите количество возможностей | 15 выбрать 3 | |
| 43 | Найдите количество возможностей | 52 выбрать 4 | |
| 44 | Найдите количество возможностей | 9 выбрать 4 | |
| 45 | Найдите количество возможностей | 9 переставить 3 | |
| 46 | Найдите количество возможностей | 7 переставить 4 | |
| 47 | Найдите количество возможностей | 7 переставить 2 | |
| 48 | Найдите количество возможностей | 11 выбрать 4 | |
| 49 | Найдите количество возможностей | 11 выбрать 2 | |
| 50 | Найдите количество возможностей | 11 выбрать 3 | |
| 51 | Найдите количество возможностей | 10 переставить 5 | |
| 52 | Найдите количество возможностей | 5 выбрать 5 | |
| 53 | Найдите количество возможностей | 6 выбрать 1 | |
| 54 | Найдите количество возможностей | 8 переставить 4 | |
| 55 | Найдите количество возможностей | 8 выбрать 6 | |
| 56 | Найдите количество возможностей | 13 выбрать 4 | |
| 57 | Оценить | и | |
| 58 | Найти любое уравнение, перпендикулярное прямой | -7x-5y=7 | |
| 59 | Найдите количество возможностей | 13 выбрать 2 | |
| 60 | Найдите количество возможностей | 10 переставить 2 | |
| 61 | Найдите количество возможностей | 10 переставить 3 | |
| 62 | Найдите количество возможностей | 10 выбрать 7 | |
| 63 | Найдите количество возможностей | 20 выбрать 4 | |
| 64 | Найдите количество возможностей | 6 переставить 4 | |
| 65 | Найдите количество возможностей | 5 переставить 4 | |
| 66 | Найдите количество возможностей | 6 выбрать 5 | |
| 67 | Найдите количество возможностей | 52 выбрать 3 | |
| 68 | Найдите количество возможностей | 4 выбрать 0 | |
| 69 | Найдите количество возможностей | 9переставить 7 | |
| 70 | Найдите количество возможностей | 6 выбрать 2 | |
| 71 | Найдите количество возможностей | 5 переставить 5 | |
| 72 | Найдите количество возможностей | 5 переставить 2 | |
| 73 | Найдите количество возможностей | 6 выбрать 6 | |
| 74 | Найдите количество возможностей | 7 выбрать 6 | |
| 75 | Найдите количество возможностей | 8 переставить 6 | |
| 76 | Найдите количество возможностей | 7 переставить 7 | |
| 77 | Найдите количество возможностей | 9 переставить 5 | |
| 78 | Найдите количество возможностей | 2 переставить 2 | |
| 79 | Найдите количество возможностей | 10 выбрать 8 | |
| 80 | Найдите количество возможностей | 12 выбрать 7 | |
| 81 | Найдите количество возможностей | 15 выбрать 5 | |
| 82 | Найдите обратное | [[1,0,1],[2,-2,-1],[3,0,0]] | |
| 83 | Найти диапазон | 1/4x-7 | |
| 84 | Найдите количество возможностей | 10 переставить 7 | |
| 85 | Найдите количество возможностей | 12 выбрать 6 | |
| 86 | Найдите количество возможностей | 2 выбрать 1 | |
| 87 | Найдите количество возможностей | 30 выбрать 3 | |
| 88 | Найдите количество возможностей | 9 выбрать 6 | |
| 89 | Найдите количество возможностей | 8 переставить 2 | |
| 90 | Найдите количество возможностей | 7 выбрать 1 | |
| 91 | Найдите количество возможностей | 6 перестановка 2 | |
| 92 | Найдите количество возможностей | 4 переставить 2 | |
| 93 | Найдите количество возможностей | 4 переставить 3 | |
| 94 | Найдите количество возможностей | 3 переставить 3 | |
| 95 | Найдите количество возможностей | 46 выбрать 6 | |
| 96 | Найдите количество возможностей | 5 переставить 1 | |
| 97 | Найдите количество возможностей | 52 выбрать 7 | |
| 98 | Найдите количество возможностей | 52 переставить 5 | |
| 99 | Найдите количество возможностей | 9выбрать 1 | |
| 100 | Найдите количество возможностей | 9 переставить 6 |
LCM 8, 12 и 24
Калькуляторы Учебные ресурсы по математике
- Главная страница
- Математические функции
- Калькулятор LCM
- LCM 8, 12 и 24
LCM 8, 12 и 24 равно 24.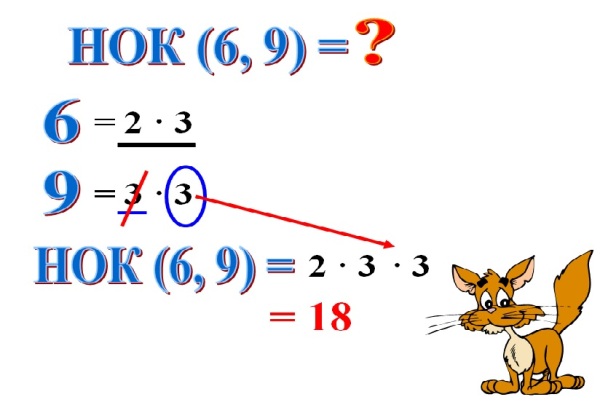
Подробная работа дает больше информации о том, что можно найти. это lcm 8, 12 и 24 с использованием простых множителей и специальных методов деления, а также пример использования математики и реальных задач.
что такое lcm 8, 12 и 24?
lcm (8 12 24) = (?)
8 => 2 x 2 x 2
12 => 2 x 2 x 3
24 => 2 x 2 x 2 x 3
= 2 x 2 x 2 x 3
= 24
lcm (8, 12 и 24) = 24
24 – lcm 8, 12 и 24. 24 — это lcm чисел 8, 12 и 24,
{2, 2, 2, 3} в {2 x 2 x 2, 2 x 2 x 3, 2 x 2 x 2 x 3} — наиболее повторяющиеся множители числа 8. , 12 и 24,
: В {2 x 2 x 2, 2 x 2 x 3, 2 x 2 x 2 x 3} нет неповторяющихся множителей 8, 12 и 24.
Использование в математике: НОК 8, 12 и 24
Ниже приведены некоторые математические приложения, в которых можно использовать МОК 8, 12 и 24:
- найти наименьшее число, которое точно делится на 8, 12 и 24.
- , чтобы найти общие знаменатели дробей, имеющих 8, 12 и 24 в знаменателях при сложении или вычитании разнородных дробей.
Использование в реальных задачах: 8, 12 и 24 lcm
разное расписание происходит вместе в одно и то же время. Например, задачи реального мира включают lcm в ситуациях, когда нужно определить, в какое время все колокола A, B и C звонят вместе, если колокол A звонит через 8 секунд, B звонит через 12 секунд и C звонит через 24 секунды неоднократно. Ответ заключается в том, что все колокола A, B и C звонят вместе через 24 секунды в первый раз, через 48 секунд во второй раз, через 72 секунды в третий раз и так далее.
Важные примечания: 8, 12 и 24 lcm
Ниже приведены важные примечания, которые следует помнить при решении lcm из 8, 12 и 24:
- Повторяющиеся и неповторяющиеся простые множители 8, 12 и 24 следует умножить, чтобы найти наименьшее общее кратное 8, 12 и 24, при решении lcm с использованием метода простых множителей.
- Результаты lcm 8, 12 и 24 идентичны, даже если мы изменим порядок заданных чисел в вычислении lcm, это означает, что порядок заданных чисел в вычислении lcm не повлияет на результаты.
Для значений, отличных от 8, 12 и 24, используйте этот инструмент ниже:
В приведенном ниже решенном примере с пошаговой работой показано, как найти lcm числа 8, 12 и 24, используя либо метод простых множителей, либо специальный метод деления. .
Пример решения с использованием метода простых множителей:
Чему равно НОК 8, 12 и 24?
шаг 1
Обратитесь к входным параметрам, значениям и посмотрите, что будет найдено:
Входные параметры и значения:
A = 8
B = 12
C = 24
Что нужно найти:
найти lcm чисел 8, 12 и 24
Шаг 2 Найти простые делители 8
Простые множители числа 8 = 2 x 2 x 2
Простые множители числа 12 = 2 x 2 x 3
Простые множители числа 24 = 2 x 2 x 2 x 3
шаг 3 Определите повторяющиеся и неповторяющиеся простые делители числа 8 , 12 и 24:
{2, 2, 2, 3} являются наиболее повторяющимися факторами, и нет неповторяющихся факторов 8, 12 и 24.
шаг 4 Найдите произведение повторяющихся и неповторяющихся простых множителей чисел 8, 12 и 24:
= 2 x 2 x 2 x 3
= 24
lcm(20 и 30) = 24
Следовательно,
lcm 8, 12 и 24 равно 24
Пример решения с использованием специального метода деления:
Этот специальный метод деления является самым простым способом понять весь расчет того, что такое lcm для 8, 12 и 24.
шаг 1 Обратитесь к входным параметрам, значениям и посмотрите, что нужно найти:
Входные параметры и значения:
Целые числа: 8, 12 и 24
Что нужно найти:
lcm (8, 12, 24) = ?
шаг 2 Расположите заданные целые числа по горизонтали, разделяя их пробелами или запятыми. Формат:
8, 12 и 24
шаг 3 Выберите делитель, который делит каждое или большинство заданных целых чисел (8, 12 и 24), разделите каждое целое число отдельно и запишите частное в следующей строке прямо под соответствующими целыми числами.