Найдите наклонные асимптоты графика функции: Найти наклонные асимптоты функции онлайн

5.2.2.3. Асимптоты графика функции

Пример 1
Найдите вертикальные асимптоты графика функции .
Решение
,  и . Из этого следует, что прямые ,  и  являются вертикальными асимптотами графика функции. Чтобы выяснить поведение функции вблизи вертикальных асимптот, исследуем заданную функцию на знак. Рис. 22. Из рисунка 22 можно определить знаки бесконечных пределов.  и .  и .  и . Легко выяснить, что. Эскиз графика функции можно построить, не проводя исследования функции на экстремум и не выясняя характер ее выпуклости (рис. 23). Рис. 23.
Теорема
Прямая  является наклонной асимптотой графика функции  тогда и только тогда, когда существуют и конечны пределы: .
Доказательство
1) Пусть прямая  является наклонной асимптотой графика функции . Тогда по определению наклонной асимптоты справедливо . Разделив выражение под знаком предела на , получим , или . Так как , то 2) Пусть , где . Тогда функция  является бесконечно малой при . Из этого следует, что , а это означает, что прямая  является наклонной асимптотой графика функции .
Замечание 1
Если , то уравнение наклонной асимптоты принимает вид . Такая асимптота называется горизонтальной.
Замечание 2
Функция может вести себя по-разному вблизи наклонной асимптоты. —   Функция может иметь одну и ту же наклонную асимптоту при  (рис.24 a). —   Функция может иметь разные наклонные асимптоты при  и  (рис.24 b). —   Функция может иметь наклонную асимптоту только при  или при  (рис. 24 c). Рис. 24 a.             Рис. 24 b.                   Рис. 24 c.
Пример 2
Найдите асимптоты графика функции .
Решение
Заданная функция определена и непрерывна на всей числовой оси, следовательно, ее график не имеет вертикальных асимптот. Выясним, имеет ли график функции наклонные асимптоты вида . . Поскольку , то асимптоты разные при  и . Поэтому . . При  график функции имеет горизонтальную асимптоту . . . При  график функции имеет горизонтальную асимптоту . График функции показан на рисунке 25. Рис. 25.
Пример 3
Проведите полное исследование функции  и постройте ее график.
Решение
Проведем исследование заданной функции по следующей схеме. 1.   Область определения функции (ООФ) и вертикальные асимптоты. О.О.Ф.: . Поскольку , то прямая  —  вертикальная асимптота. 2.   Четность функции, периодичность функции. Функция общего вида и непериодическая. 3.   Корни и знаки функции. Корень функции . Функция неотрицательна при всех значениях . 4.   Монотонность функции. Экстремумы. Вычислим первую производную функции. . Отметим на числовой оси стационарную точку,  и точку разрыва функции. Определим знак первой производной на каждом из полученных интервалов и отметим стрелками характер монотонности функции (рис.26). Рис. 26. Из рисунка ясно, что  — точка минимума. Для построения графика требуется найти значение функции в точке минимума:. В точке разрыва меняется характер монотонности функции. 5.   Выпуклость функции. Точки перегиба. Вычислим вторую производную заданной функции. Вторая производная обращается в ноль в точке  и меняет знак. Это точка перегиба. В точке разрыва  вторая производная знак не меняет. Определим знак второй производной на всей числовой оси и отметим на ней характер выпуклости функции (рис.27). Рис. 27. Значение функции в точке перегиба . 6.   Наклонные (горизонтальные) асимптоты. Выясним, имеет ли функция наклонную асимптоту вида . Для этого вычислим пределы: . . Следовательно, график функции имеет горизонтальную асимптоту . Введем прямоугольную декартову систему координат. Для того, чтобы построить график исследованной функции, нужно: ·   Провести вертикальные и наклонные асимптоты. ·   Отметить все характерные точки (корни, точки экстремума, точки перегиба). ·   Соединить характерные точки кривыми в соответствии с исследованием функции на выпуклость. График заданной функции построен на рисунке 28. Рис. 28.

Решение высшей математики онлайн

‹— Назад

        Упражнение 7.3   Найдите область определения и вертикальные асимптоты графика функции

Подсказка:

Рассмотрите точки , в которых знаменатель обращается в 0. Внимание: в одной из этих точек вертикальной асимптоты нет, так как функция имеет устранимый разрыв.

Решение:

Область определения составляют все точки оси , кроме 0, и 2:

Заметим теперь, что при числитель также обращается в 0:

Значит, многочлен, стоящий в числителе, делится нацело на . Деление столбиком даёт:

Значит, при дробь можно сократить на :

откуда видно, что при функция стремится к а не к .

При , равном двум другим корням знаменателя, 0 и 2, числитель в 0 не обращается, а равен и соответственно. Значит, при и при , и прямые и  — вертикальные асимптоты.

Ответ:

вертикальные асимптоты: и .     

        Упражнение 7.4   Найдите вертикальные асимптоты графиков функций:

а)

б) ;

в) .

Ответы: а) ; б) ; в) вертикальных асимптот нет.     

        Упражнение 7.5   Найдите наклонные или горизонтальные асимптоты графика функции

Подсказка:

Воспользуйтесь общими формулами для и в уравнении асимптоты . Пределы при и при здесь можно искать заодно.

Решение:

Найдём и :

Итак, прямая служит наклонной асимптотой графика

Ответ: наклонная асимптота при имеет уравнение .     

        Упражнение 7.6   Найдите наклонные или горизонтальные асимптоты графиков функций:

а) ;

б) ;

в)

Ответы: а) при ; б) при ; в) при и при .     

        Упражнение 7.7   Найдите наибольшее и наименьшее значения функции на отрезке .

Подсказка:

Найдите стационарные точки функции, попадающие на заданный отрезок, и добавьте к ним концы отрезка. В одной из этих точек функция будет принимать наибольшее, а в другой — наименьшее значение.

Решение:

Поскольку знаменатель дроби положителен при всех , функция непрерывна на всей оси . Поэтому все её критические точки — стационарные. Найдём производную:

Очевидно, что производная обращается в 0 только в одной точке ; эта стационарная точка лежит на заданном отрезке .

Вычисляем значения функции в этой стационарной точке и в концах отрезка:

Выбирая из этих значений наибольшее и наименьшее, получаем ответ:

Ответ:

    

        Упражнение 7.8   Найдите наибольшие и наименьшие значения функций на заданных отрезках:

а) на отрезке ;

б) на отрезке ;

в) на отрезке .

Ответы: а) ;

б) ;

в) .     

        Упражнение 7.9   Найдите интервалы возрастания и убывания, а также точки локального экстремума функции .

Подсказка:

Найдите производную и решите неравенства и .

Решение:

Производная равна . Неравенство имеет решение ; на этих двух интервалах возрастает. Неравенство имеет решение ; на этом интервале убывает. Следовательно, точка  — точка локального максимума, а точка  — точка локального минимума.

Ответ:

Интервалы возрастания: и ; интервал убывания: ; точка локального максимума: , точка локального минимума: .     

        Упражнение 7.10   Найдите интервалы возрастания и убывания и точки локальных экстремумов функций:

а) ;

б) ;

в) .

Ответы: а) интервалы возрастания: и ; интервалы убывания: и ; точка локального максимума ; точки локального минимума ;

б) интервалы возрастания: и ; интервалы убывания: и ; точка локального максимума ; точка локального минимума ;

в) интервал возрастания: ; интервалы убывания: и ; точка локального минимума ; точек локального максимума нет.     

        Упражнение 7.11   Найдите стационарные точки функции

и определите наличие в них локального экстремума.

Подсказка:

Стационарные точки задаются уравнением . Если вторая производная в стационарной точке положительна, то это точка локального минимума, а если отрицательна, то точка локального максимума.

Решение:

Найдём производную: ; стационарные точки задаются уравнением , то есть это точки и . Вторая производная равна . Её значение в стационарных точках: ; . Следовательно, в точке  — локальный максимум, а в точках и  — локальный минимум.

Ответ:

Имеется три стационарные точки: , 0 и 1; и 1 — точки локального минимума, а 0 — точка локального максимума.     

        Упражнение 7. 12   Найти стационарные точки функций и исследовать их на наличие локального экстремума:

а) ;

б) ;

в) .

Ответы: а)  — точка локального максимума;  — точка локального минимума;

б)  — точка локального максимума;  — точка локального минимума;

в)  — точка локального минимума; точек локального максимума нет.     

        Упражнение 7.13   Найдите интервалы выпуклости и вогнутости и точки перегиба функции

Подсказка:

Интервалы выпуклости задаются неравенством , а интервалы вогнутости — неравенством .

Решение:

Найдём вторую производную:

Неравенство имеет решение ; на этом интервале функция выпукла.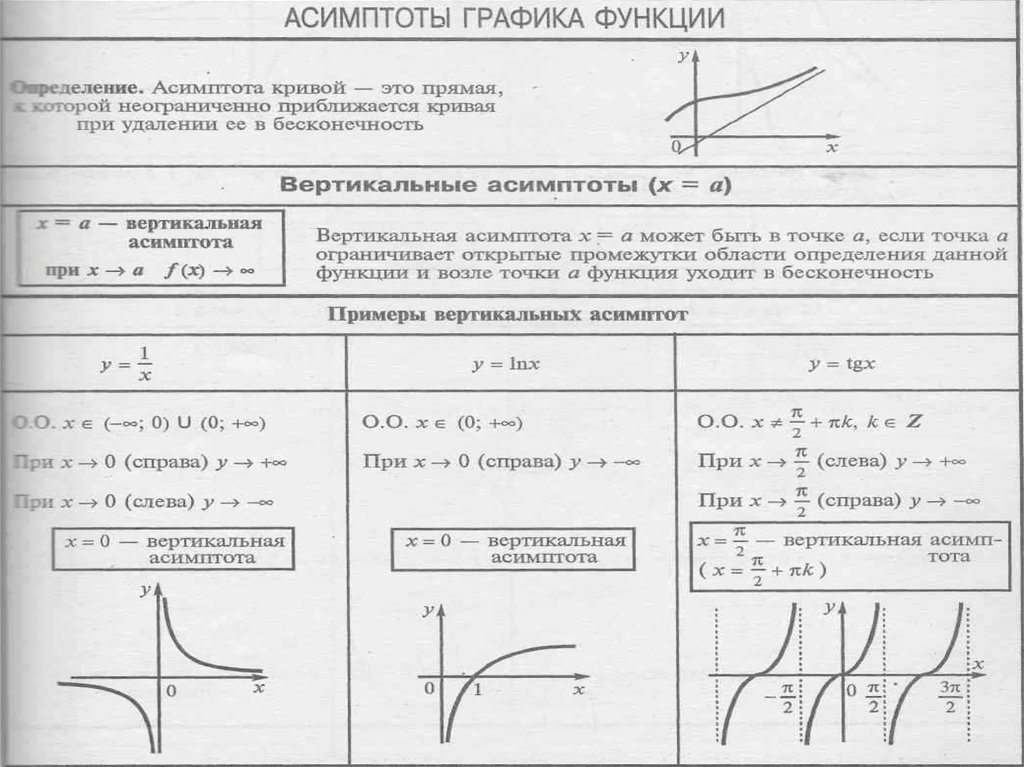 Неравенство имеет решение ; на этих двух интервалах функция вогнута.

В точках и функция меняет направление выпуклости, так что эти точки являются точками перегиба.

Ответ:

Интервал выпуклости: ; интервалы вогнутости: и ; точки перегиба: и .     

        Упражнение 7.14   Найдите интервалы выпуклости и вогнутости и точки перегиба следующих функций:

а) ;

б) ;

в) .

Ответы: а) Интервалы выпуклости: и ; интервал вогнутости: ; точки перегиба: и .

б) Интервалы выпуклости: и ; интервал вогнутости: ; точки перегиба: и .

в) Интервалы выпуклости: и ; интервал вогнутости: ; точек перегиба нет.     

        Упражнение 7.15   Проведите полное исследование функций и постройте их графики (в затруднительных случаях характерные точки можно находить приближённо):

а) ;

б) ;

в) .

Ответы: а) Функция нечётная;

вертикальные асимптоты и , наклонная асимптота . Точка локального максимума , при этом ; точка локального минимума , при этом . Единственная точка перегиба .

Рис.7.52.График функции

б) Функция чётная; ; горизонтальная асимптота . Точки локального максимума ; значение в этих точках ; точка локального минимума . Четыре точки перегиба:

Рис.7.53.График функции

в) Функция нечётная; ; асимптоты при и при . Точка локального максимума , при этом ; точка локального минимума , при этом . Единственная точка перегиба .

Рис.7.54.График функции

    

Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции

2.

4.3.1: Наклонные асимптоты рациональных функций

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

14204

Наклонные асимптоты

Когда степень числителя рациональной функции превышает степень знаменателя на единицу, функция имеет 9{2}}\)

Обратите внимание, что оставшаяся часть будет стремиться к нулю, когда x становится чрезвычайно большим или чрезвычайно малым, поскольку степень числителя меньше степени знаменателя. Это означает, что хотя эта функция может выйти из строя при малых абсолютных значениях x, большие абсолютные значения x очень близки к линии y=x+3.

[Рисунок 1]

Наклонные асимптоты — это наклонные асимптоты, которые точно показывают, как функция неограниченно возрастает или убывает. Наклонные асимптоты также называют наклонными асимптотами. 9{2}+4 x\right)-\frac{12}{10(x-1)}\)

Как видите, это похоже на параболу с остатком. Эта рациональная функция имеет параболическую основу. Основа — это функция, к которой стремится граф. Технически это не наклонная асимптота, потому что это не линия.

[Рисунок 2]

---

Примеры

Пример 1

Ранее вас спрашивали, что происходит, когда степень числителя превышает степень знаменателя более чем на единицу. 9{2}+x-12}=x-2+\frac{13 x-25}{(x-3)(x+4)}\)

Наклонная асимптота равна y=x−2. Вертикальные асимптоты находятся при x=3 и x=-4, которые легче наблюдать в последней форме функции, потому что они явно не сокращаются, чтобы стать дырами.

Пример 4

Создайте функцию с наклонной асимптотой при y=3x−1, вертикальной асимптотой при x=2,−4 и включает отверстие, где x равно 7.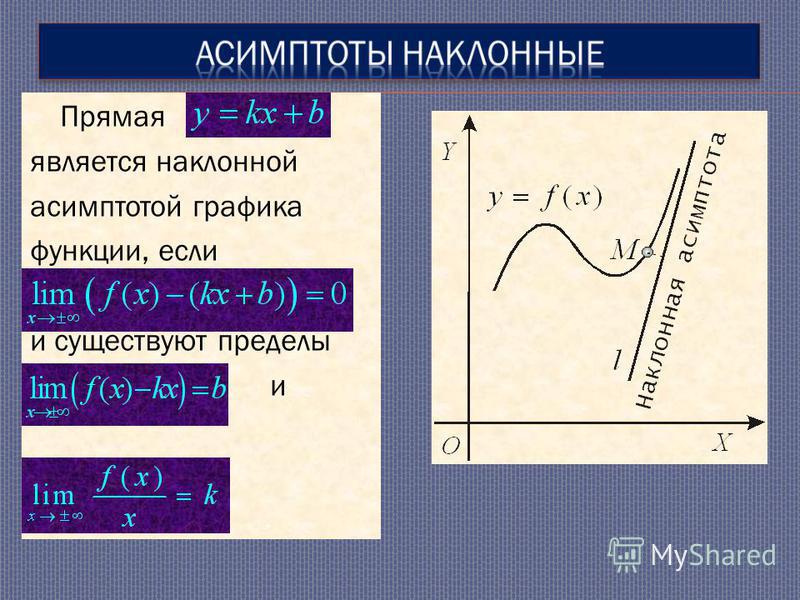

Решение

количество функций, соответствующих этим критериям, один пример: 9{3}}\)

Основой этой функции является парабола y=5x ² . Это не наклонная асимптота, потому что это не прямая.

---

Обзор

1. Что такое наклонная асимптота?

2. Как по уравнению функции определить, будет ли она иметь наклонную асимптоту или нет?

3. Может ли функция иметь как наклонную, так и горизонтальную асимптоту? Объяснять.

Для каждого из следующих графиков нарисуйте график, а затем нарисуйте наклонную асимптоту, если она существует. Если его нет, объясните почему.

4. [Рисунок 3]

5. [Рисунок 4]

6. [Рисунок 5]

7. [Рисунок 6]
8. [Рисунок 7]

Найдите уравнение наклонной асимптоты для каждой из следующих рациональных функций.

Если наклонной асимптоты нет, объясните почему и приведите уравнение основы функции, если она существует. 9{2}+2 х+1}\)

Создайте функцию с наклонной асимптотой при y=2x−1, вертикальной асимптотой при x=3 и отверстием, где x равно 7.

Создайте функцию с наклонной асимптотой при y=x, вертикальной асимптотой при x=1,−3 и без пробелов.

Имеет ли парабола наклонную асимптоту? А как насчет кубической функции?

---

Обзор (ответы)

Чтобы просмотреть ответы на обзор, откройте этот PDF-файл и найдите раздел 2.11.

---

Авторство изображений

1. [Рис. 1]
   Кредит: Фонд CK-12
   Лицензия: CC BY-SA
2. [Рис. 2]
   Кредит: Фонд CK-12
   Лицензия: CC BY-SA
3. [Рис. 3]
   Кредит: Фонд CK-12
   Лицензия: CC BY-SA
4. [Рисунок 4]
   Кредит: Фонд CK-12
   
   Лицензия: CC BY-SA
5. [Рис. 5]
   Кредит: Фонд CK-12
   Лицензия: CC BY-SA
6. [Рис. 6]
   Кредит: Фонд CK-12
   Лицензия: CC BY-SA
7. [Рис. 7]
   Кредит: Фонд CK-12
   Лицензия: CC BY-SA

---

Эта страница под названием 2.4.3.1: Наклонные асимптоты рациональных функций распространяется под лицензией CK-12 и была создана, изменена и/или курирована Фондом CK-12 посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами Платформа LibreTexts; подробная история редактирования доступна по запросу.

ПОД ЛИЦЕНЗИЕЙ

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   СК12

   Лицензия

   СК-12

   Программа OER или Publisher

   СК-12

2. Теги

   92 — 2x — 1) / (x + 4)??

   Во-первых, вы должны убедиться, что понимаете ситуации, в которых появляются различные типы асимптот.

   Вертикальные асимптоты:

   Все рациональные выражения имеют вертикальную асимптоту. Проще говоря, вертикальная асимптота возникает, когда знаменатель равен 0. Асимптота — это просто неопределенная точка функции; деление на 0 в математике не определено.

   Горизонтальные асимптоты:

   96#.

   2) Если степень знаменателя равна степени числителя, то при отношении между коэффициентами старшей степени функции будет горизонтальная асимптота. Возьмем пример рациональной функции #g(x) = (2x + 1)/(x — 7)#. Степени числителя и знаменателя равны (оба степени 1). Соотношение их коэффициентов #2/1 = 2#. Это означает, что будет горизонтальная асимптота при #y = 2#

   92 — 2x — 1)/(x + 4)# и найти там все асимптоты.

   Давайте начнем с самого простого: вертикальную асимптоту. Его можно найти, установив в знаменателе значение #0# и найдя x.

   #x + 4 = 0#

   #x = -4#

   Следовательно, имеется вертикальная асимптота при #x = -4#

   В этой функции не будет горизонтальной асимптоты, так как знаменатель ни равной, ни большей степени, чем числитель.

   No related posts.