Ответов пока нет
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Решено
На рисунке изображены графики функций y = f(x) и y = g(x). Скорость изменения которой из этих функций наибольшая в точке х = 2?
Решено
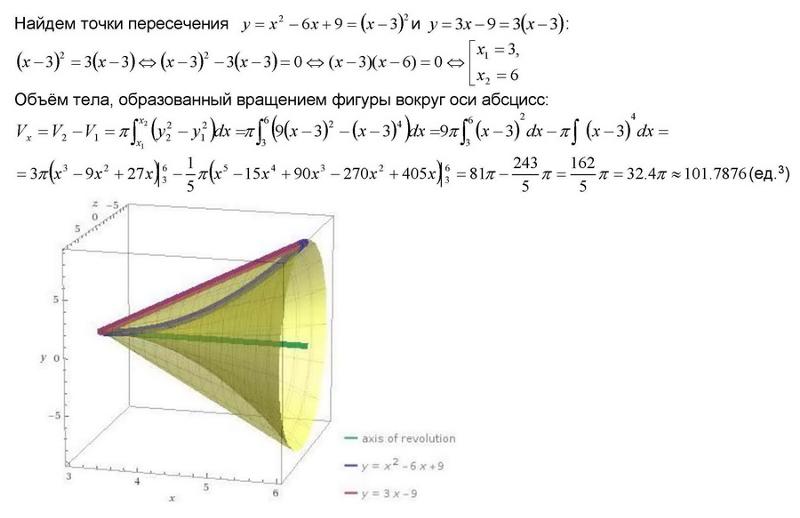
В треугольнике АВС В1-середина АС, точка А1 лежит на стороне ВС так, что ВА1 : А1С = 1 : 2.
2 от точки x=1 до точки x=2 вокруг оси абсцисс
Алгебра, 29.10.2020 09:54, Folknesss14
Показать ответы
Другие вопросы по: Алгебра
После — толстой можно ли сказать, что рассказ толстого открывает нам одну из страниц прошлого россии? мне надо)…
Опубликовано: 02.03.2019 22:50
Ответов: 2
Коллективное хозяйство засеяло пшеницу, хлопчатник и клевер на 12120 га земли. пшеница занимает 30% от всей площади, а хлопчатник занимает на 6244 га больше, чем клевер. сколько ге…
Опубликовано: 03.03.2019 06:10
Ответов: 3
Расположите слова, характеризующий процесс преобразования объектов природы в предметы потребления в правильной последовательности: обмен, ресурсы, технология, распределение, произ…
Опубликовано: 03.03.2019 07:10
Ответов: 2
Всосуд налили воду до высоты 15 см.
2 от точки x=1 до точки x=2 вокруг оси абс…
Популярные вопросы
Шесть одинаковых по длительности сеансов радиосязи продолжались 1 час 12 минут. какова длительность одного сеанса….
Опубликовано: 01.03.2019 00:00
Ответов: 1
Какое наименьшее число точек определяет прямую в пространстве…
Опубликовано: 01.03.2019 19:40
Ответов: 1
21. кран поднимает груз массой 2 тонны. какова совершённая краном работа за первые 5 секунд , если скорость поднятия 30 м/мин. 2.сила тяги сверхзвукового самолета при скорости поле…
Опубликовано: 01.03.2019 23:50
Ответов: 1
Вычислить площадь прямоугольного треугольника стороны имеют длину 9см 12 см 15см…
Опубликовано: 02.03.2019 04:30
Ответов: 2
Определите радиус круга, который может описать мотоциклист, если он едит со скоростью 36км/ч, а предельный угол его наклона к дороге=60градусов.
..
Опубликовано: 02.03.2019 09:20
Ответов: 2
Придумать примеры, отражающие свойства информации…..
Опубликовано: 02.03.2019 14:20
Ответов: 1
Главные требования афинского демоса в7 веке до н. э….
Опубликовано: 02.03.2019 21:20
Ответов: 3
Два автобуса выехали одновременно из двух городов навстречу друг к другу со скоростью 40км/ ч и 48км/ч. расстояние между 132км. через сколько часов автобусы встретятся?…
Опубликовано: 02.03.2019 21:40
Ответов: 1
Катеты прям. треуг. =40 и 42см. на сколько радиус описанной окружности больше радиуса вписанной?…
Опубликовано: 02.03.2019 23:40
Ответов: 2
Методом электронного , определить коэффициенты в следующей схеме реакции: cuo+nh4=n2+cu+h3o.
..
Опубликовано: 03.03.2019 03:00
Ответов: 2
Случайные вопросы
Популярные вопросы
Вопрос Видео: Нахождение объема твердого тела, образованного вращением области, ограниченной параболой вокруг оси 𝑥
Стенограмма видео
Найдите объем твердого тела, образованного вращением области, ограниченной кривой 𝑦, равно отрицательному 𝑥 в квадрате плюс два 𝑥, а ось 𝑥 — полный оборот вокруг оси 𝑥.
Напомним, что формула, которую мы используем для нахождения объема твердого тела, образованного вращением области вокруг оси 𝑥, представляет собой определенный интеграл между 𝑎 и 𝑏 от 𝐴 от 𝑥 относительно 𝑥, где 𝐴 от 𝑥 есть функция который описывает площадь поперечного сечения объема в данной точке. Иногда лучше использовать формулу, представляющую собой определенный интеграл между 𝑎 и 𝑏 от 𝜋, умноженный на 𝑦 в квадрате по отношению к 𝑥, где 𝑥 равно 𝑎, а 𝑥 равно 𝑏 — это вертикальные линии, ограничивающие нашу область.
И это формула, которую мы собираемся применить в этом вопросе.
Теперь, чтобы увидеть, что происходит, давайте начнем с наброска графика 𝑦 равно отрицательному 𝑥 в квадрате плюс два 𝑥. Чтобы найти 𝑥-перехват, мы установим 𝑦 равным нулю и найдем 𝑥. Итак, минус 𝑥 в квадрате плюс два 𝑥 равно нулю. Разложим на множители 𝑥 такое, что 𝑥 умножить на минус 𝑥 плюс два равно нулю. Теперь, конечно, это утверждение может быть истинным только в том случае, если либо 𝑥 равно нулю, либо отрицательное 𝑥 плюс два равно нулю. И если мы решим второе уравнение, добавив 𝑥 к обеим частям, мы обнаружим, что 𝑥 равно двум. Итак, это корни нашего уравнения. Это точки пересечения графика с осью 𝑥.
Само уравнение представляет собой квадратное уравнение с отрицательным коэффициентом 𝑥 в квадрате. Это означает, что он выглядит как перевернутая парабола, как показано на рисунке. И мы собираемся вращать эту область на 360 градусов вокруг оси 𝑥. Поскольку эта область ограничена вертикальными линиями, 𝑥 равно нулю, а 𝑥 равно двум, мы можем сказать, что само 𝑎 должно быть равно нулю, а 𝑏 должно быть равно двум.
Итак, объем — это определенный интеграл между нулем и двумя из 𝜋, умноженных на 𝑦 в квадрате. Теперь 𝑦 — это уравнение отрицательного 𝑥 в квадрате плюс два 𝑥. Мы можем взять постоянный множитель 𝜋 вне нашего интеграла. И потом, лучший способ интегрировать это — просто распределить скобки. Когда мы это сделаем, мы обнаружим, что наше подынтегральное выражение становится 𝑥 в четвертой степени минус четыре 𝑥 в кубе плюс четыре 𝑥 в квадрате. Итак, выполним интегрирование.
Мы знаем, что для интегрирования члена полинома, показатель степени которого не равен отрицательной единице, мы прибавляем единицу к показателю степени, а затем делим на это новое значение. Это означает, что интеграл от 𝑥 в четвертой степени равен 𝑥 в пятой степени, деленному на пять. Когда мы интегрируем отрицательные четыре 𝑥 в кубе, мы получаем отрицательные четыре 𝑥 в четвертой степени, деленные на четыре. Что упрощает отрицательное 𝑥 в четвертой степени. И тогда интеграл от четырех 𝑥 в квадрате равен четырем 𝑥 в кубе на три.
Теперь нам нужно оценить это в пределах от нуля до двух. Таким образом, получается 𝜋, умноженное на два в пятой степени на пять минус два в четвертой степени плюс четыре раза на два в кубе на три, все минус ноль.
Получается 𝜋 умножить на 32 больше пяти минус 16 плюс 32 больше трех. А затем мы создадим общий знаменатель 15. Для этого мы умножим 32 на пять на три на три. Мы записываем минус 16 как минус 16 на единицу, а затем умножаем на 15. И мы умножаем 32 на три на пять на пять. Это 𝜋 умножить на 96 на 15 минус 240 на 15 плюс 160 на 15. Что полностью упрощается до 16𝜋 на 15. Таким образом, мы можем сказать, что объем твердого тела, образованного вращением области, ограниченной кривой 𝑦, равен отрицательному 𝑥 в квадрате. плюс два 𝑥 и ось 𝑥 на 360 градусов вокруг оси 𝑥 составляет 16𝜋 на 15 кубических единиц.
исчисление — Вычисление объема тела вращения, полученного вращением двух парабол
спросил
Изменено 2 года, 10 месяцев назад
Просмотрено 1к раз
$\begingroup$
Я пытаюсь вычислить объем тела вращения, полученного вращением двух парабол, $y=x^2-x-6$ и $y=-x^2+x+6$.
При использовании последней функции в качестве $g(x)$ (поскольку на интервале она имеет более высокие значения) я получаю $0$ в результате интеграла. Не уверен, что делать сейчас.
Спасибо
- исчисление
- интеграция
$\endgroup$
9
$\begingroup$ 9{+3 }_{-2}=\frac{625}{6}\pi.$$ Я включил рис. 2, чтобы показать вам, что также можно найти требуемый объем, рассматривая горизонтальную полосу и выполняя интегрирование в направлении $y$ от $y=0$ до $y=6,25$ и, наконец, умножая результат. интегрирования на 2. В этом случае осью вращения является вертикальная линия, определяемая выражением $x=0,5$.
Я предполагаю, что вы выяснили, почему вы получили тело вращения с нулевым объемом в вашей предыдущей попытке.