Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Коля, Дима и Саша собрали. ..
..
Через точку О,не лежащую между…
Используя в каждом случае 4 раза цифру 7 , знаки арифметических действий и , если надо , скобки , составь 5 выражений со значениями 5,6,7,8,9, например 7-(7+7):7=5
Решено
Задача 4-го класса. через иксы решать нельзя. Подскажите пожалуйста!
Полина старше Аллы на 9 лет. Вместе им 15 лет. Сколько лет будет Алле через 2 года
Пользуйтесь нашим приложением
25 Найдите область определения и множество значений функции. Мордкович 8 класс алгебра – Рамблер/класс
25 Найдите область определения и множество значений функции. Мордкович 8 класс алгебра – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
область определения и множество значений функции;
б) промежутки монотонности функции;
в) координаты центра симметрии гиперболы;
г) асимптоты гиперболы.
ответы
область находится так
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Психология
10 класс
9 класс
похожие вопросы 4
Домашняя контрольная работа № 3 Вариант 2 10. При каких значениях р уравнение… Мордкович 8 класс алгебра
10. При каких значениях р уравнение -х 2 + 6х — 2 = р:
а) не имеет корней;
б) имеет один корень; (Подробнее…)
ГДЗМордкович А.Г.Алгебра8 класс
Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308
Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее. ..)
..)
ГДЗ11 классКолмогоров А.Н.Алгебра
Приготовление раствора сахара и расчёт его массовой доли в растворе. Химия. 8 класс. Габриелян. ГДЗ. Хим. практикум № 1. Практ. работа № 5.
Попробуйте провести следующий опыт. Приготовление раствора
сахара и расчёт его массовой доли в растворе.
Отмерьте мерным (Подробнее…)
ГДЗШкола8 классХимияГабриелян О.С.
ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 13. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…
18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
Как найти домен в интервальной нотации на графике
1. Поиск домена функции может быть трудным, но это необходимый шаг при построении графика функции.
Домены — это набор всех значений x, для которых функция выдает допустимое значение y. Другими словами, домен — это набор всех значений x, для которых функция выдает реальное значение y. Нахождение области определения функции может быть трудным, но это необходимый шаг в построении графика функции. Область определения функции можно найти, просмотрев определение функции и определив набор всех значений x, для которых функция выдает реальное значение y.
Другими словами, домен — это набор всех значений x, для которых функция выдает реальное значение y. Нахождение области определения функции может быть трудным, но это необходимый шаг в построении графика функции. Область определения функции можно найти, просмотрев определение функции и определив набор всех значений x, для которых функция выдает реальное значение y.
2. Есть несколько различных способов найти область определения функции, но запись интервала является одним из наиболее распространенных.
Существует несколько различных способов найти область определения функции, но запись интервала является одним из наиболее распространенных. Область определения функции — это набор всех входных значений, для которых функция выдает результат. В интервальной нотации домен представлен парой чисел, разделенных запятой. Первое число — это нижняя граница, а второе число — верхняя граница. Например, область определения функции f(x) = x2 равна [-�?∞]. Это означает, что функция примет любое входное значение и выдаст результат.
3. Чтобы найти домен в интервальной нотации, начните с нахождения точек пересечения x на графике.
Домен в математике — это набор значений, которые может принимать функция. Другими словами, это набор всех входных значений, для которых функция выдает результат. Область определения функции может быть представлена в виде интервала. Чтобы найти область в интервальной нотации, начните с поиска пересечений графика по оси x.
4. Х-перехваты дадут вам границы домена.
Х-образные пересечения графика дадут вам границы домена. Домен — это набор всех значений x, для которых график дает реальное значение y. Например, если x-отрезки графика равны -1 и 3, то областью определения будут все действительные числа от -1 до 3.
5. Используйте информацию из x-отрезков для записи домена в интервальной нотации. .
Область определения функции — это набор всех входных значений, для которых функция выдает результат. Область определения функции может быть выражена в интервальной записи, которая представляет собой способ записи набора чисел, включающего все числа в заданном диапазоне. Х-пересечения функции — это точки, в которых график функции пересекает ось абсцисс. Х-перехваты можно использовать для нахождения области определения функции в интервальной нотации.
Х-пересечения функции — это точки, в которых график функции пересекает ось абсцисс. Х-перехваты можно использовать для нахождения области определения функции в интервальной нотации.
Пожалуйста, внимательно прочитайте этот отказ от ответственности перед тем, как начать пользоваться сервисом. Используя эту услугу, вы подтверждаете, что вы полностью согласны и принимаете содержание этого заявления об отказе от ответственности. Вы можете отказаться от использования сервиса, если не согласны с данным отказом от ответственности. Этот документ создается автоматически на основе общедоступного контента в Интернете, захваченного Платформой машинного обучения для ИИ. Авторские права на информацию в этом документе, такую как веб-страницы, изображения и данные, принадлежат их соответствующим авторам и издателям. Такой автоматически сгенерированный контент не отражает точку зрения или мнение Alibaba Cloud. Вы несете ответственность за определение законности, точности, подлинности, практичности и полноты содержания. Мы рекомендуем вам проконсультироваться со специалистом, если у вас есть какие-либо сомнения по этому поводу. Alibaba Cloud не несет ответственности за любые последствия использования вами контента без проверки. Если у вас есть отзывы или вы обнаружите, что в этом документе используется некоторый контент, в отношении которого у вас есть права и интересы, свяжитесь с нами по этой ссылке: https://www.alibabacloud.com/campaign/contact-us-feedback. Мы будем решать вопрос в соответствии с соответствующими правилами.
Мы рекомендуем вам проконсультироваться со специалистом, если у вас есть какие-либо сомнения по этому поводу. Alibaba Cloud не несет ответственности за любые последствия использования вами контента без проверки. Если у вас есть отзывы или вы обнаружите, что в этом документе используется некоторый контент, в отношении которого у вас есть права и интересы, свяжитесь с нами по этой ссылке: https://www.alibabacloud.com/campaign/contact-us-feedback. Мы будем решать вопрос в соответствии с соответствующими правилами.
Домен, совместный домен и диапазон функций
Введение Функции составляют один из важнейших строительных блоков математики. Слово «функция» произошло от латинского слова, означающего операцию, и слова «отображение» и «отображение» являются его синонимами. Мы используем множество стандартных определенных функций, таких как модульные функции, логарифмические функции, экспоненциальные функции и т. д.0028 Домен . Co-Domain — Набор всех выходных параметров функции известен как диапазон функции или после замены домена весь набор всех возможных значений в качестве результатов зависимой переменной. Диапазон — Набор всех выходных значений функции называется диапазоном функции или, после замены домена, полным набором всех значений, возможных в качестве результатов зависимой переменной. Математически область определения, сообласть и диапазон функции могут быть определены как – Пусть f : A → B. тогда множество A известно как область определения f, а множество B известно как диапазон содомен f. Набор всех f-изображений элементов A известен как диапазон f или набор изображений A при f и обозначается через f ( A ). Таким образом, f ( A ) = { f (x) : x ∈ A } = Диапазон f Проще говоря, мы можем таким образом определить домен, со-домен и диапазон функции как – Домен относится к тому, что может использоваться в функции. Кодомен, с другой стороны, относится к тому, что может получиться из функции. Диапазон функции относится к тому, что на самом деле получается из функции. Давайте теперь разберемся, домен, совместный домен и ряд некоторых общих функций. Функция f ( x ) определяется как f ( x ) = | х | = {-x, x<0 x} x≥0 называется функцией модуля. Ее также называют функцией абсолютного значения. Мы можем заметить, что область определения функции модуля — это множество R всех действительных чисел, а область значений — это множество всех неотрицательных действительных чисел. R + = { x ∈ R : x ≥ 0 } График функции модуля показан на рисунке ниже. Здесь важно отметить, что при x > 0 график функции модуля совпадает с графиком функции идентичности, т.е. линия y = x, а при x < 0 он совпадает с линией y = -x. Если a > 0 и a ≠ 1, то функция, определяемая выражением f ( x ) = x , x > 0, называется логарифмической функцией. Логарифмическая функция является обратной функцией. Напомним, что в случае обратных функций Пусть f : A → B биекция. Тогда функция g : B → A, которая ставит в соответствие каждому элементу y ∈ B уникальный элемент x ∈ A такой, что f ( x ) = y, называется обратной к f . Теперь, поскольку логарифмическая функция является обратной функцией, это означает, что x = y ⬄ x = a y Давайте теперь проверим область определения и диапазон этой кусочной функции. Мы видим, что область определения и область значений логарифмической функции представляет собой множество всех положительных действительных чисел. Это означает, что ( 0, ∞) — область определения функции, а диапазон — множество R всех действительных чисел. Поскольку a > 0 и a ≠ 1, у нас есть следующие случаи – Случай 1 Когда a > 1 В этом случае мы имеем y = x {<0 для 0 Кроме того, значения y увеличиваются с ростом увеличение х. Теперь рассмотрим второй случай, когда a лежит между 0 и 1 Случай 2 Когда 0 < a < 1 В этом случае имеем y = x { >0 for 0< x<1 =0 для x=1 <0 для x>1 Выше мы узнали определение логарифмической функции. Мы также обсудили два различных случая, зависящих от значений а. Итак, есть два разных графика, основанные на этих разных значениях. Сначала построим график для первого случая, когда b > 1 y = x {<0 для 0 График этой функции будет представить как – Теперь построим график случая 2. Случай 2 Когда 0 < a < 1 В этом случае имеем y = x { >0 для 0 График этой функции будет представлено как – Если a – положительное действительное число, отличное от единицы, то функция, которая связывает каждый x R с x , называется экспоненциальной функцией. Другими словами, экспоненциальная функция — это математическая функция в форме f (x) = a x , где «x» — переменная, а «a» — константа, которая называется основанием функции и должна быть больше 0. Функция f : R → R определяется как f ( x ) = a x , где a > 0 и a ≠ 1 — формула экспоненциальной функции. f ( x ) = a x , где a > 0 и a ≠ 1, а x — действительное число 9.0005 Здесь важно отметить, что если мы имеем отрицательные значения переменной, экспоненциальная функция не определена, когда – 1 < x < 1. Кривая экспоненциального графика зависит от экспоненциальной функции, которая далее зависит при значении х. Следовательно, именно значение x определяет кривую графика экспоненциальной функции. Каковы домен и диапазон экспоненциальной функции? Давайте узнаем. Мы знаем, что область определения функции y = f ( x ) — это множество всех значений x, где ее можно вычислить, а диапазон — это множество всех значений y функции. Область определения экспоненциальной функции — это R множество всех действительных чисел. Областью экспоненциальной функции является множество ( 0 , ∞), поскольку она достигает только положительных значений. Случай 1: Когда a > 1 Рассмотрим значения y = f ( x ) = a x при увеличении значения x. Также мы знаем, что f ( x ) = {<1 при x<0 =1 при x=0 >1 при x>0 Следовательно, график показательной функции f ( x ) = b x для b > 1 будет равно – Например, рассмотрим график y = 2 x . График этой функции будет Мы можем видеть, что указанная выше экспоненциальная функция быстро возрастает. Также мы можем ясно заметить, что – Отсюда графики f ( x ) = 2 x , f ( x 90 ) = 7 x , f ( x ) = 4 x в соответствии с графиком, показанным выше. Случай 2: когда 0 < a < 1 В этом случае значения y = f ( x ) = a x уменьшаются с увеличением x и y > 0 для всех x R. Также мы знаем, что – f ( x ) = { <1 для x<0 = 1 для x=0 >1 для x>0 Таким образом, график f ( x ) = b x для 0 < b < 1, как показано ниже – Функция f : A → B называется вещественной функцией, если B является подмножеством R (множество всех действительных чисел). Если A и B являются подмножествами R, то f называется вещественной функцией. Для математического определения функции for необходимо указать ее область определения, сообласть и образы элементов в ее области определения, либо задав общую формулу, либо перечислив их один за другим. Поскольку область определения и область значений действительных функций являются подмножествами R, поэтому условно вещественные функции описываются путем предоставления общей формулы для нахождения образов элементов в нем. . диапазон реальной функции реальной переменной — это набор всех действительных значений, принимаемых f ( x ) в точках ее области определения. Следующий алгоритм используется для нахождения области значений действительной функции f(x) – Набор всех возможных значений, которые квалифицируются как входные данные для функции, известен как домен функции. Другими словами, область определения функции можно определить как все множество значений, возможных для независимых переменных.
Набор всех возможных значений, которые квалифицируются как входные данные для функции, известен как домен функции. Другими словами, область определения функции можно определить как все множество значений, возможных для независимых переменных.
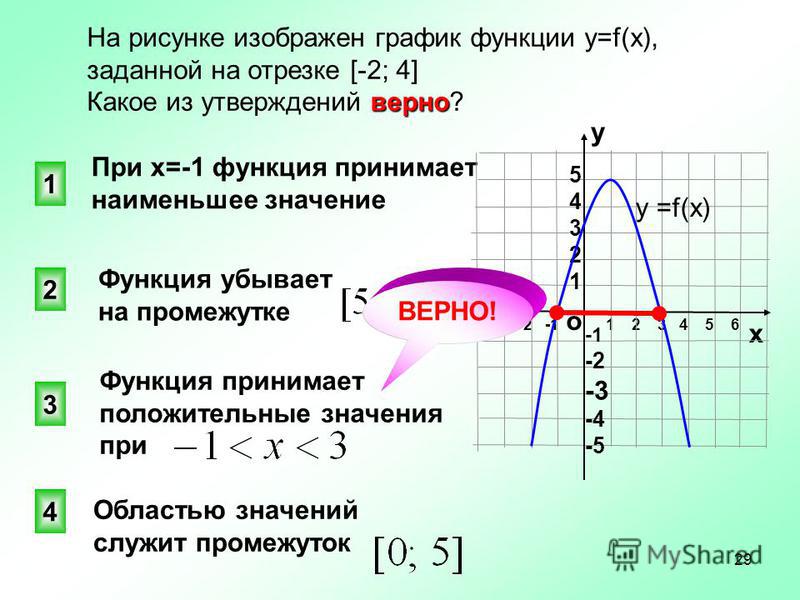 Это означает, что
Это означает, что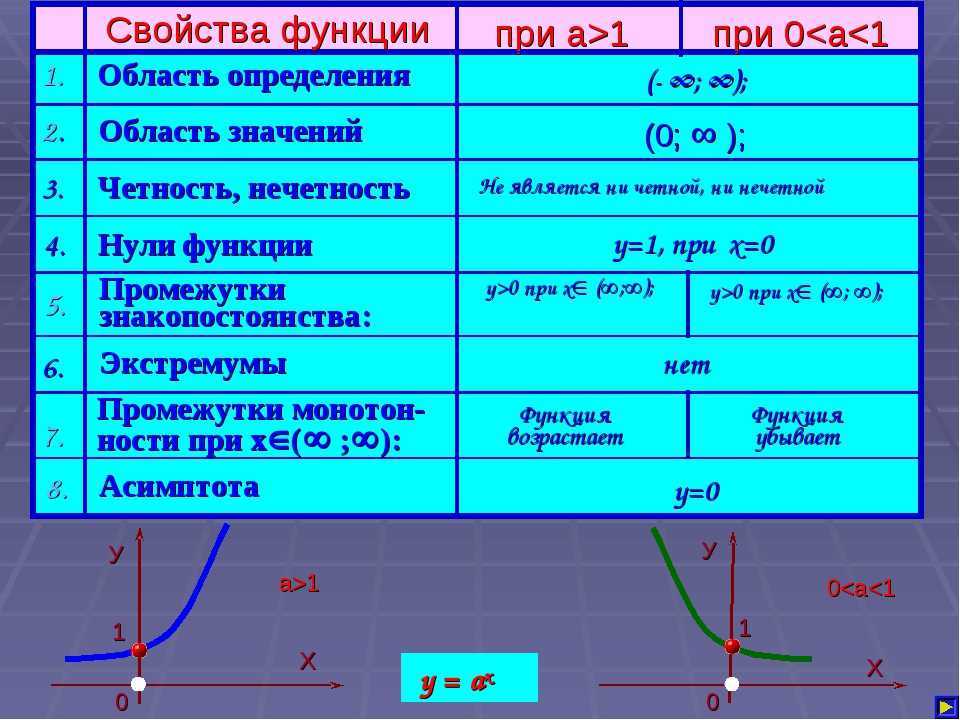

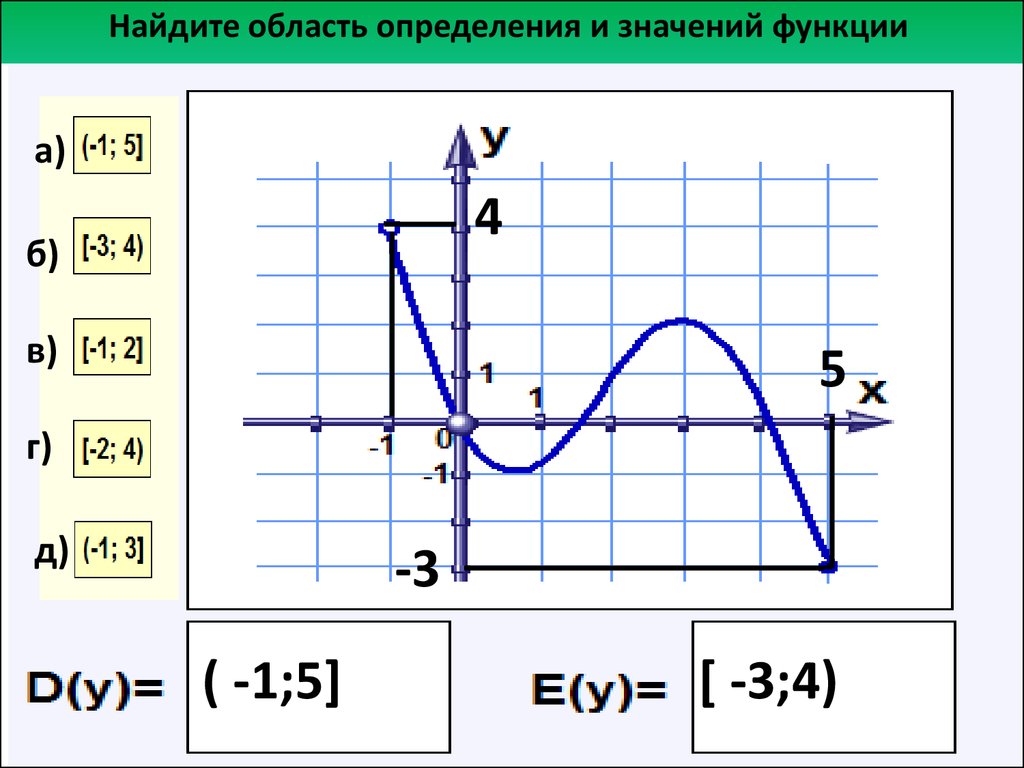 Следовательно, мы имеем
Следовательно, мы имеем 

 В таких случаях область определения действительной функции f ( x ) представляет собой множество всех тех действительных чисел, для которых выражение для f ( x ) или формула для f ( x ) принимает только действительные значения. Другими словами, область определения f(x) — это набор всех тех действительных чисел, для которых f(x) имеет смысл. 92-1}$ становится нулем при x = ∓1. Следовательно, областью определения f(x) будет множество всех действительных чисел, отличных от – 1 и 1, т. е. областью определения будет область определения (f) = R–{- 1,1}
В таких случаях область определения действительной функции f ( x ) представляет собой множество всех тех действительных чисел, для которых выражение для f ( x ) или формула для f ( x ) принимает только действительные значения. Другими словами, область определения f(x) — это набор всех тех действительных чисел, для которых f(x) имеет смысл. 92-1}$ становится нулем при x = ∓1. Следовательно, областью определения f(x) будет множество всех действительных чисел, отличных от – 1 и 1, т. е. областью определения будет область определения (f) = R–{- 1,1}
Область определения f
Мы видим, что f определено для всех x, удовлетворяющих условию 3 – x ≠ 0. Это означает, что x ≠ 3. Следовательно, область определения функции f ( x ) = $\frac{ x-2}{3-x}$ будет Домен ( f ) = R – { 3 }
Диапазон f
Мы будем использовать вышеизложенное, обсужденное выше, чтобы найти диапазон данной функции.
Пусть y = f ( x ). Тогда имеем
y = $\frac{x-2}{3-x}$
⇒ y ( 3 – x ) = x – 2
⇒ 3 y – x y = x – 2
⇒ x ( y + 1 ) = 3 y + 2
⇒ x = $\frac{3 y+2}{y+1}$ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ( 1 )
Из уравнения (1) видно, что x принимает действительные значения всех y, кроме y + 1 = 0. Это означает, что y = – 1
Это означает, что y = – 1
Следовательно, диапазон функции f ( x ) = $\frac{x-2}{3-x}$ будет Range ( f ) = R – { – 1 }
Пример 2 Найдите область определения и область значений функции f ( x ) = $ \frac{1}{2-sin 3 x}$
Решение Нам задана функция f ( x ) = $\frac{1}{2-sin 3 x}$, и нам нужно найти ее область определения и область значений. Давайте найдем их один за другим.
Домен из F
Мы знаем, что — 1 ≤ SIN 3 x ≤ 1 для всех x ∈ R
⇒ — 1 ≤ — sin 3 x ≤ 1 для всех x ∈ R R R Rout
⇒ 1 ≤ 2 – sin 3 x ≤ 3 для всех x ∈ R
⇒ f ( x ) = $\frac{1}{2-sin 3 x}$ определено для всех x ∈ R
Следовательно, областью определения функции f ( x ) = $\frac{1}{2-sin 3 x}$ будет Область определения f( f ) = R
Диапазон f
Выше мы уже обсуждали, что 1 ≤ 2 – sin 3 x ≤ 3 для всех x ∈ R R
⇒ 13 ≤ f ( x ) ≤ 1 для всех x ∈ R
⇒ f ( x ) = [ 1 / 3 , 1 ]
Следовательно, область значений функции f ( x ) = $\frac{1}{2-sin 3 x}$ будет Range (f) = [1/3, 1]
Ключевые факты и сводка- Пусть A и B — два не- пустые наборы.
 Отношение f из A в B, т. е. подмножество A x B, называется функцией или отображением или отображением из A в B,
Отношение f из A в B, т. е. подмножество A x B, называется функцией или отображением или отображением из A в B,- Для каждого a ∈ A существует b ∈ B такое, что ( a, b ) ∈ f
- ( a, b ) ∈ f и ( a , c ) ∈ f ⇒ b = c
- Пусть f : A → B. тогда множество A известно как область определения f, а множество B известный как ко-домен диапазона f. Набор всех f-изображений элементов A известен как диапазон f или набор изображений A при f и обозначается через f ( A ).
- Функция f ( x ) определяется как f ( x ) = | х | = {-x, x<0 x, x≥0 называется функцией модуля. Ее также называют функцией абсолютного значения.
- Если a > 0 и a ≠ 1, то функция, определяемая соотношением f ( x ) = x , x > 0, называется логарифмической функцией.
- Функция f : R → R определяется формулой f ( x ) = a x , где a > 0 и a ≠ 1 — формула экспоненциальной функции. Область определения экспоненциальной функции — это R множество всех действительных чисел.


 12.17
12.17 Отношение f из A в B, т. е. подмножество A x B, называется функцией или отображением или отображением из A в B,
Отношение f из A в B, т. е. подмножество A x B, называется функцией или отображением или отображением из A в B,