10 класс А. Н. Колмогоров №193 – Рамблер/класс
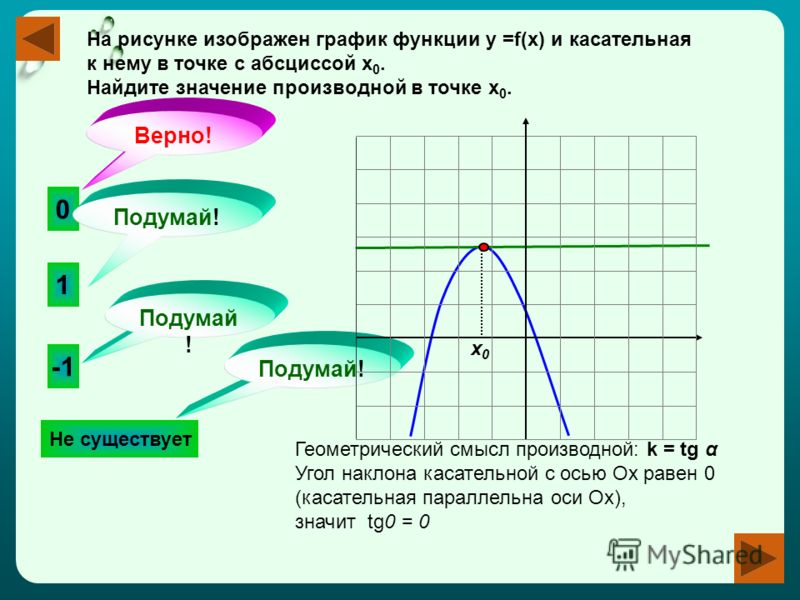
Используя формулы дифференцирования, полученные в п. 13, найдите производную функции f в точке х0, если: 10 класс А. Н. Колмогоров №193 – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Добрый вечер, мучаюсь битый час-помогите с ответами)
п.
13, найдите производную функции f в точке х0, если:
а) f (х) = х3, х0 равно 2; -1,5;
б) f (х) = 4 — 2х, х0 равно 0,5; -3;
a) f (х) = Зх — 2, х0 равно 5; -2;
г) f (х) = х2, х0 равно 2,5; -1.
ответы
Чего тут мучаться?? тут же не сложно..
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
ЕГЭ
9 класс
11 класс
Химия
похожие вопросы 5
В какой момент времени ускорение движения будет наименьшим? Колмогоров Алгебра 10-11 класс Упр 309
Привет! Поможете с решением?)
(скорость измеряется в метрах в секунду). В какой момент времени (Подробнее…)
ГДЗ11 классКолмогоров А.
Н.10 классАлгебра
Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308
Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее…)
ГДЗ11 классКолмогоров А.Н.Алгебра
Почему сейчас школьники такие агрессивные ?
Читали новость про 10 классника который растрелял ? как вы к этому относитесь
Новости10 классБезопасность
16. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)… Цыбулько И. П. Русский язык ЕГЭ-2017 ГДЗ. Вариант 13.
16.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
ГДЗЕГЭРусский языкЦыбулько И.П.
ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 13.
18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…
18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
Производные высших порядков
Определение 3: Производная второго порядка (вторая производная) от функции y=f(x) есть производная от ее первой производной: .
Определение 4: Производная n-ого порядка (n-я производная) от функции y=f(x) есть производная от ее (
n-1)-й производной: .Пример 9: Найти производную функции
Решение:
+
Пример 10: Найти производную функции
Решение:
Применим правило дифференцирования
Пример 11: Найти производную функции
Решение:
Применим правило дифференцирования
Пример 12: Найти дифференциал функции
Решение: По определению дифференциал
Так
как ,
то .
Ответ: Дифференциал функции равен
Пример 13: Найти производную сложной функции
Пример 14: Найти производную функции сложной функции
Решение:
=
+
Пример 15: Найти производную второго порядка для функции .
Решение:
Ответ:
Пример 16: Найти производную второго порядка функции в точке .
Решение:
Найдем при
Ответ:
Основные понятия и формулы
Определение 1: Точка х0 называется точкой локального максимума, если для любого х из окрестности точки х0 выполняется неравенство:
.
Определение 2: Точка х0 называется точкой локального минимума, если для любого х из окрестности точки х0 выполняется неравенство:
.
Точки минимума и максимума функции называются точками экстремума данной функции, а значения функции в этих точках – экстремумами функции.
Правило нахождения экстремумов функции с помощью первой производной
Найти производную функции .
Найти критические точки по первой производной, т.е. точки, в которых производная обращается в нуль или терпит разрыв.
Исследовать знак первой производной в промежутках, на которые найденные критические точки делят область определения функции . Если на промежутке , то на этом промежутке функция убывает; если на промежутке , то на этом промежутке функция возрастает.
Если в окрестности критической точки меняет знак
с «+» на «-», то эта точка является точкой максимума, если с «-» на «+», то точкой минимума.
Вычислить значения функции в точках минимума и максимума.
С помощью приведенного алгоритма можно найти не только экстремумы функции, но и промежутки возрастания и убывания функции.
Направление выпуклости графика функции. Точки перегиба.
Определение 3: Кривая называется выпуклой вниз на промежутке , если она лежит выше касательной в любой точке этого промежутка (рис.1).
О пределение 4: Кривая называется выпуклой вверх на промежутке , если она лежит ниже касательной в любой точке этого промежутка (рис.2).Рис.1 Рис. 2
Определение
5: Точка
графика функции
,
разделяющая промежутки выпуклости
противоположных направлений этого
графика, называется точкой перегиба
(рис.
3).
Рис. 3
Правило нахождения точек перегиба графика функции
a. Найти вторую производную .
b. Найти точки, в которых вторая производная обращается в нуль или терпит разрыв.
c. Исследовать знак второй производной на каждом промежутке, на которые найденные критические точки делят область определения функции . Если при этом критическая точка разделяет промежутки выпуклости противоположных направлений, то является абсциссой точки перегиба графика функции.
d. Вычислить значения функции в точках перегиба.
Общая схема для построения графиков функций
Найти область определения функции.
Исследовать функцию на четность или нечетность.
Найти точки пересечения графика функций с осями координат.
Найти асимптоты функции.
Найти промежутки монотонности и точки экстремума функции.
Найти промежутки выпуклости и точки перегиба функции.
По результатам исследования построить график.
Пример 17: Найти промежутки монотонности и экстремумы функции: .
Решение: Найдем первую производную функции .
Найдем критические точки по первой производной, решив уравнение
Исследуем поведение первой производной в критических точках и на промежутках между ними.
0 | 2 | ||||
+ | 0 | — | 0 | + | |
т. 0 | т. min -4 |
maxОтвет: Функция возрастает при ; функция убывает при ; точка минимума функции ; точка максимума функции .
Пример 18: Найти промежутки выпуклости и точки перегиба функции .
Решение: Находим , .
Найдем критические точки по второй производной, решив уравнение
2 | |||
+ | 0 | — | |
точка перегиба 16 |
Ответ: Функция выпукла вверх при ;
функция выпукла вниз при ;
точка перегиба .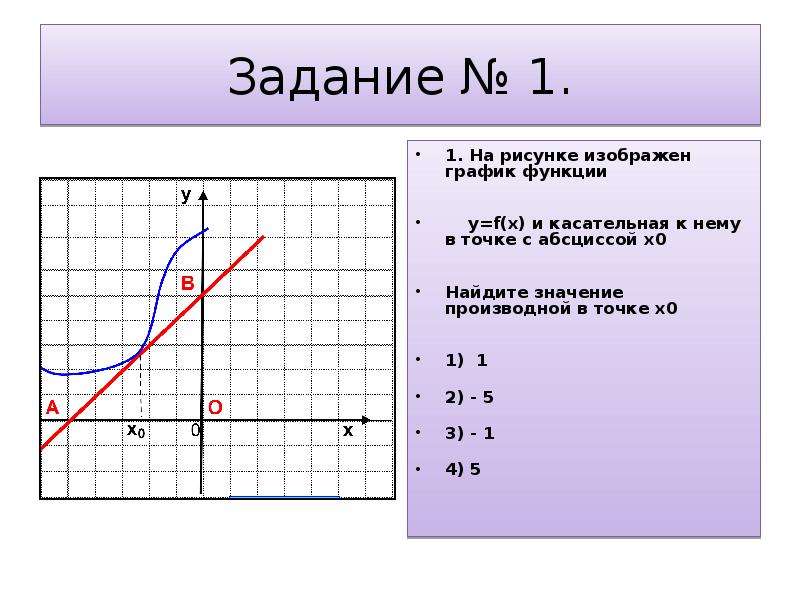
Пример 19: Провести полное исследование функции и построить ее график
Решение:
Функция определена на всей числовой оси, т. е. ее область определения .
Выясним, является ли функция четной или нечетной:
.
Отсюда следует, что функция является нечетной, т.е. график симметричен относительно начала координат.
Найдем точки пересечения с осями координат:
— с осью ОХ: решим уравнение
.
Точки пересечения с осью ОХ
— с осью ОY:
Точка пересечения с осью ОY
Функция непрерывна, асимптот у нее нет.
Найдем промежутки монотонности и точки экстремума функции: .
Критические точки: .
-1 | 1 | ||||
+ | 0 | — | 0 | + | |
т. max 2 | т. min -2 |
Найдем промежутки выпуклости и точки перегиба функции:
Критические точки: .
0 | |||
— | 0 | + | |
точка перегиба 0 |
По результатам исследования построим график функции (рис. 4):
Рис. 4
исчисление — Нахождение $n$-й производной функции при $x=0$ с использованием ряда Маклорена.
спросил
Изменено 3 года, 10 месяцев назад
Просмотрено 832 раза
$\begingroup$
КОНТЕКСТ: Uni вопрос составлен лектором 9{(6)}(0)=360$.
$\endgroup$
3.2: Производная как функция
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 2491
- Гилберт Странг и Эдвин «Джед» Герман
- ОпенСтакс
Цели обучения
- Определить производную функцию заданной функции.
- Постройте производную функцию по графику заданной функции.
- Укажите связь между производными и непрерывностью.
- Опишите три условия, при которых функция не имеет производной.
- Объясните значение производной высшего порядка.
Как мы видели, производная функции в данной точке дает нам скорость изменения или наклон касательной к функции в этой точке. Если мы продифференцируем функцию положения в данный момент времени, мы получим скорость в этот момент. Кажется разумным заключить, что знание производной функции в каждой точке даст ценную информацию о поведении функции. Однако процесс нахождения производной даже при нескольких значениях с использованием методов из предыдущего раздела быстро стал бы довольно утомительным. В этом разделе мы определяем производную функцию и изучаем процесс ее нахождения.
Производные функции
Производная функция дает производную функции в каждой точке области определения исходной функции, для которой определена производная.
Мы можем формально определить производную функцию следующим образом.
Определение: производная функция
Пусть \(f\) — функция. Производная функция , обозначаемая \(f’\), является функцией, область определения которой состоит из таких значений \(x\), что существует следующий предел:
\[f'(x)=\lim_{h→0}\frac{f(x+h)−f(x)}{h}. \label{derdef} \]
Функция \(f(x)\) называется дифференцируемой в \(a\), если \(f'(a)\) существует. В более общем смысле функция называется дифференцируемой на \(S\), если она дифференцируема в каждой точке открытого множества \(S\), а дифференцируемой функцией является функция, в которой \(f'( x)\) существует в своей области определения.
В следующих нескольких примерах мы используем уравнение \ref{derdef} для нахождения производной функции.
Пример \(\PageIndex{1}\): нахождение производной функции квадратного корня
Найдите производную \(f(x)=\sqrt{x}\).
Решение
Начните непосредственно с определения функции производной.
Подставьте \(f(x+h)=\sqrt{x+h}\) и \(f(x)=\sqrt{x}\) в \(f'(x)= \displaystyle \lim_{ h→0}\frac{f(x+h)−f(x)}{h}\).
| \(f'(x)=\displaystyle \lim_{h→0}\frac{\sqrt{x+h}−\sqrt{x}}{h}\) | |
| \(=\displaystyle\lim_{h→0}\frac{\sqrt{x+h}−\sqrt{x}}{h}⋅\frac{\sqrt{x+h}+\sqrt{ х}}{\sqrt{х+ч}+\sqrt{х}}\) | Умножить числитель и знаменатель на \(\sqrt{x+h}+\sqrt{x}\) без распределения в знаменателе. |
| \(=\displaystyle\lim_{h→0}\frac{h}{h\left(\sqrt{x+h}+\sqrt{x}\right)}\) | Умножьте числители и упростите. |
| \(=\displaystyle\lim_{h→0}\frac{1}{\left(\sqrt{x+h}+\sqrt{x}\right)}\) 92}{ч}\) | Упростить |
| \(=\displaystyle\lim_{h→0}\frac{h(2x−2+h)}{h}\) | Вынести \(h\) из числителя |
| \(=\displaystyle\lim_{h→0}(2x−2+h)\) | Отменить общий множитель \(h\) |
| \(=2x−2\) | Оценить предел |
Упражнение \(\PageIndex{1}\)
Найдите производную \(f(x)=x^2\).
92−2x\справа)=2x−2\). Таким образом, для функции \(y=f(x)\) каждое из следующих обозначений представляет собой производную от \(f(x)\):
\(f'(x), \quad \dfrac{dy }{dx}, \quad y′,\quad \dfrac{d}{dx}\big(f(x)\big)\).
Вместо \(f'(a)\) мы также можем использовать \(\dfrac{dy}{dx}\Big|_{x=a}\). Использование нотации \(\dfrac{dy}{dx}\) (называемой нотацией Лейбница) довольно распространено в технике и физике. Чтобы лучше понять эти обозначения, вспомним, что производная функции в точке — это предел наклона секущих по мере приближения секущих к касательной. Наклоны этих секущих часто выражаются в виде \(\dfrac{Δy}{Δx}\), где \(Δy\) — разность значений \(y\), соответствующая разнице в \(x \) значения, которые выражаются как \(Δx\) (рисунок \(\PageIndex{1}\)). Таким образом, производная, которую можно рассматривать как мгновенную скорость изменения \(у\) по отношению к \(х\), выражается как
\(\displaystyle \frac{dy}{dx}= \lim_{Δx→0}\frac{Δy}{Δx}\).
Рисунок \(\PageIndex{1}\): производная выражается как \(\dfrac{dy}{dx}=\displaystyle\lim_{Δx→0}\frac{Δy}{Δx}\).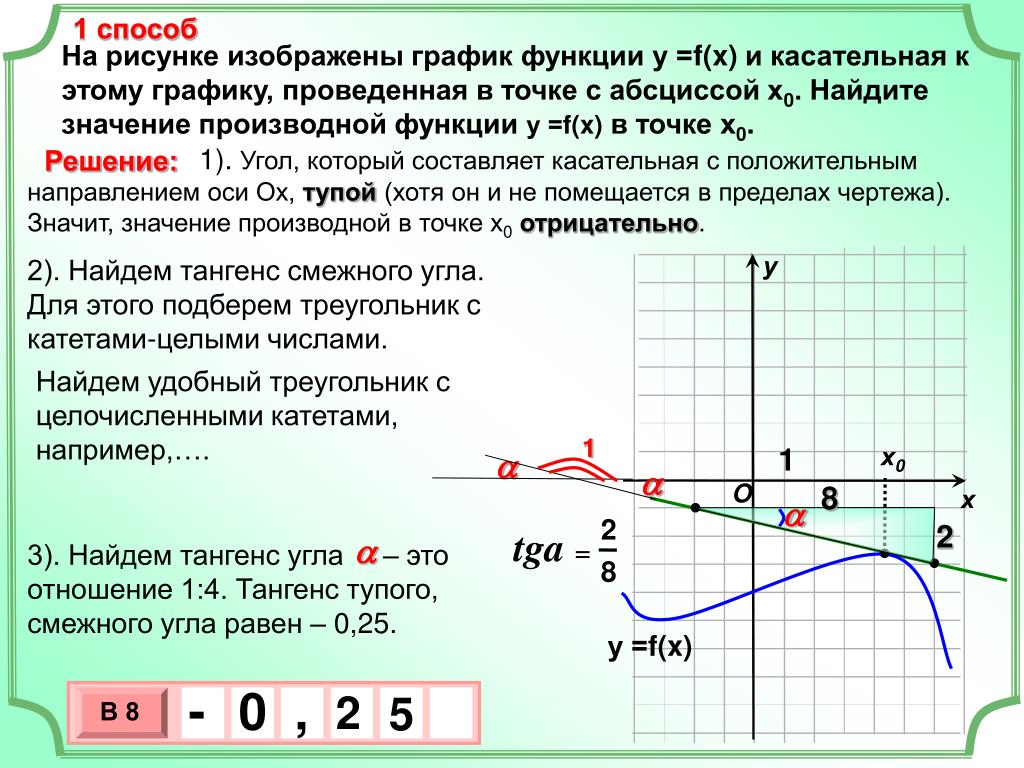
Построение графика производной
Мы уже обсуждали, как построить график функции, поэтому, имея уравнение функции или уравнение функции производной, мы можем построить ее график. Учитывая оба, мы ожидаем увидеть соответствие между графиками этих двух функций, поскольку \(f'(x)\) дает скорость изменения функции \(f(x)\) (или наклон касательной строка к \(f(x)\)).
В примере \(\PageIndex{1}\) мы обнаружили, что для \(f(x)=\sqrt{x}\), \(f'(x)=\frac{1}{2\sqrt {Икс}}\). Если мы изобразим эти функции на тех же осях, как на рисунке \(\PageIndex{2}\), мы сможем использовать графики, чтобы понять связь между этими двумя функциями. Во-первых, мы замечаем, что \(f(x)\) возрастает по всей своей области, а это означает, что наклоны ее касательных во всех точках положительны. Следовательно, мы ожидаем \(f'(x)>0\) для всех значений x в его области определения. Кроме того, по мере увеличения \(x\) наклоны касательных линий к \(f(x)\) уменьшаются, и мы ожидаем увидеть соответствующее уменьшение \(f'(x)\).
+}f'(x)=+∞\), что соответствует вертикальной касательной к \(f( х)\) в \(0\). 92−2x,\; f'(x)=2x−2\). Графики этих функций показаны на рисунке \(\PageIndex{3}\). Обратите внимание, что \(f(x)\) убывает при \(x<1\). Для этих же значений \(x\), \(f'(x)<0\). Для значений \(x>1\) \(f(x)\) возрастает и \(f'(x)>0\). Кроме того, \(f(x)\) имеет горизонтальную касательную в точках \(x=1\) и \(f'(1)=0\).
Пример \(\PageIndex{3}\): набросок производной с помощью функции
Используйте следующий график \(f(x)\) для построения графика \(f'(x)\).
Решение
Решение показано на следующем графике. Заметим, что \(f(x)\) возрастает и \(f'(x)>0\) на \((–2,3)\). Кроме того, \(f(x)\) убывает и \(f'(x)<0\) на \((−∞,−2)\) и на \((3,+∞)\). Также обратите внимание, что \(f(x)\) имеет горизонтальные касательные в точках \(-2\) и \(3\), а \(f'(-2)=0\) и \(f'(3)= 0\).
92−4\). На каком интервале находится график \(f'(x)\) над осью \(x\)?
- Подсказка
График \(f'(x)\) положителен, где \(f(x)\) возрастает.
- Ответить
\((0,+∞)\)
Производные и непрерывность
Теперь, когда мы можем изобразить производную, давайте рассмотрим поведение графиков. Сначала рассмотрим связь между дифференцируемостью и непрерывностью. Мы увидим, что если функция дифференцируема в точке, она должна быть там непрерывной; однако функция, непрерывная в точке, не обязательно должна быть дифференцируемой в этой точке. На самом деле функция может быть непрерывной в точке и не быть дифференцируемой в этой точке по одной из нескольких причин.
Дифференцируемость подразумевает непрерывность
Пусть \(f(x)\) — функция и \(a\) находится в ее области определения. Если \(f(x)\) дифференцируема в \(а\), то \(f\) непрерывна в \(а\).
Доказательство
Если \(f(x)\) дифференцируема в \(a\), то \(f'(a)\) существует и, если положить \(h = x — a\), мы имеют \( x = a + h \), и поскольку \(h=x-a\to 0\), мы можем видеть, что \(x\to a\).
Тогда
\[ f'(a) = \lim_{h\to 0}\frac{f(a+h)-f(a)}{h}\nonumber \]
можно переписать как
\(f'(a)=\displaystyle \lim_{x→a}\frac{f(x)−f(a)}{x−a}\).
Мы хотим показать, что \(f(x)\) непрерывно в \(a\), показав, что \(\displaystyle \lim_{x→a}f(x)=f(a).\) Таким образом ,
\(\begin{align*} \displaystyle \lim_{x→a}f(x) &=\lim_{x→a}\;\big(f(x)−f(a)+f( a)\big)\\[4pt]
&=\lim_{x→a}\left(\frac{f(x)−f(a)}{x−a}⋅(x−a)+f( a)\right) & & \text{Умножить и разделить}(f(x)−f(a))\text{ на }x−a.\\[4pt]
&=\left(\lim_{x→ a}\frac{f(x)−f(a)}{x−a}\right)⋅\left( \lim_{x→a}\;(x−a)\right)+\lim_{x→ а}ж(а)\\[4pt]
&=f'(a)⋅0+f(a)\\[4pt]
&=f(a). \end{align*}\)
Следовательно, поскольку \(f(a)\) определено и \(\displaystyle \lim_{x→a}f(x)=f(a)\), мы заключаем, что \(f\) непрерывна в \(a\).
□
Мы только что доказали, что дифференцируемость влечет непрерывность, но теперь мы рассмотрим, влечет ли непрерывность дифференцируемость. Чтобы определить ответ на этот вопрос, мы исследуем функцию \(f(x)=|x|\). Эта функция всюду непрерывна; однако \(f'(0)\) не определено. Это наблюдение приводит нас к мысли, что непрерывность не влечет дифференцируемости. Давайте исследовать дальше. Для \(f(x)=|x|\), 92}}=+∞\).
Таким образом, \(f'(0)\) не существует. Беглый взгляд на график \(f(x)=\sqrt[3]{x}\) проясняет ситуацию. Функция имеет вертикальную касательную в точке \(0\) (рисунок \(\PageIndex{5}\)).
Рисунок \(\PageIndex{5}\): функция \(f(x)=\sqrt[3]{x}\) имеет вертикальную касательную в точке \(x=0\). Он непрерывен в точке \(0\), но не дифференцируем в точке \(0\). Функция \(f(x)=\begin{cases} x\sin\left(\frac{1}{x}\right), & & \text{ if } x≠0\\0, & & \ text{ if } x=0\end{cases}\) также имеет производную, которая демонстрирует интересное поведение при \(0\).
Мы видим, что
\(f'(0)=\displaystyle \lim_{x→0}\frac{x\sin\left(1/x\right)−0}{x−0}= \lim_ {x→0}\sin\left(\frac{1}{x}\right)\).
Этого предела не существует, в основном потому, что наклоны секущих постоянно меняют направление по мере приближения к нулю (рис. \(\PageIndex{6}\)).
Рисунок \(\PageIndex{6}\): функция \(f(x)=\begin{cases} x\sin\left(\frac{1}{x}\right), & & \text{ если } x≠0\\0, & & \text{ если } x=0\end{cases}\) не дифференцируемо в \(0\).Итого:
- Заметим, что если функция не непрерывна, то она не может быть дифференцируемой, поскольку каждая дифференцируемая функция должна быть непрерывной. Однако, если функция непрерывна, она может не быть дифференцируемой.
- Мы видели, что \(f(x)=|x|\) не может быть дифференцируемым в \(0\), потому что предел наклона касательных линий слева и справа не одинаков. Визуально это привело к острому углу на графике функции в точке \(0.\). Отсюда заключаем, что для того, чтобы быть дифференцируемой в точке, функция должна быть в этой точке «гладкой».
- Как мы видели на примере \(f(x)=\sqrt[3]{x}\), функция не может быть дифференцируемой в точке, где есть вертикальная касательная.
- Как мы видели с \(f(x)=\begin{cases}x\sin\left(\frac{1}{x}\right), & & \text{ if } x≠0\\0, & &\text{ if } x=0\end{cases}\) функция может не быть дифференцируемой в точке и более сложными способами.
Пример \(\PageIndex{4}\): кусочная функция, которая является непрерывной и дифференцируемой 92+bx+c, & & \text{, если }x
<−10\\−\frac{1}{4}x+\frac{5}{2}, & & \text{, если } x≥−10\ end{cases}\), где \(x\) и \(f(x)\) указаны в дюймах. Для плавного движения автомобиля по трассе функция \(f(x)\) должна быть одновременно непрерывной и дифференцируемой в точке \(−10\). Найдите значения \(b\) и \(c\), которые делают \(f(x)\) одновременно непрерывным и дифференцируемым. Рисунок \(\PageIndex{7}\): Чтобы автомобиль двигался плавно по трассе, функция должна быть одновременно непрерывной и дифференцируемой.92−10b+c=10−10b+c\)
и \(f(−10)=5\), мы должны иметь \(10−10b+c=5\).
2+bx+c−5}{x+10}\\[4pt] 92, & & \text{ если } x≥3\end{cases}\) как непрерывны, так и дифференцируемы в \(3\).
- Подсказка
Используйте пример \(\PageIndex{4}\) в качестве руководства.
- Ответить
\(a=6\) и \(b=−9\)
Производные высшего порядка
Производная функции сама по себе является функцией, поэтому мы можем найти производную производной. Например, производная функции положения — это скорость изменения положения или скорость. Производная скорости — это скорость изменения скорости, то есть ускорение. Новая функция, полученная дифференцированием производной, называется второй производной. Кроме того, мы можем продолжать брать производные, чтобы получить третью производную, четвертую производную и так далее. В совокупности они обозначаются как 92−3ч}{ч}\) Упростите числитель. \(=\displaystyle \lim_{h→0}(4x+2h−3)\) Вынесите \(h\) в числителе и сократите с \(h\) в знаменателе.
\(=4x−3\) Возьмите предел.
Затем найдите \(f»(x)\), взяв производную от \(f'(x)=4x−3.\)
93\), найти \(a(t).\)- Подсказка
Используйте пример \(\PageIndex{6}\) в качестве руководства.
- Ответить
\(а(т)=6т\)
Ключевые понятия
- Производной функции \(f(x)\) называется функция, значение которой в точке \(x\) равно \(f'(x)\).
- График производной функции \(f(x)\) связан с графиком функции \(f(x)\). Где \(f(x)\) имеет касательную с положительным наклоном, \(f'(x)>0\). Где \(f(x)\) имеет касательную с отрицательным наклоном, \(f'(x)<0\). Где \(f(x)\) имеет горизонтальную касательную, \(f'(x)=0.\) 9{\text{th}}\) производная.
Ключевые уравнения
- Производная функция
\(f'(x)=\displaystyle \lim_{h→0}\frac{f(x+h)−f(x)}{h}\)
Глоссарий
- производная функция
- дает производную функции в каждой точке области определения исходной функции, для которой определена производная
- дифференцируемый по \(а\)
- функция, для которой \(f'(a)\) существует, дифференцируема в точке \(a\) 9{\text{th}}\) называется производной высшего порядка
Авторы и авторство
Эта страница под названием 3.2: Производная как функция распространяется под лицензией CC BY-NC-SA 4.
| \(f»(x)= \displaystyle \lim_{h→0}\frac{f'(x+h)−f'(x)}{h}\) | Используйте \(f'(x)=\displaystyle \lim_{h→0}\frac{f(x+h)−f(x)}{h}\) с \(f ‘(x)\) в место \(f(x).\) |
| \(=\displaystyle \lim_{h→0}\frac{(4(x+h)−3)−(4x−3)}{h}\) | Замените \(f'(x+h)=4(x+h)−3\) и \(f'(x)=4x−3.\) |
| \(=\displaystyle \lim_{h→0}4\) | Упростить. |
| \(=4\) | Возьмите предел. |