Найдите угол образованный касательной к графику функции: Найти угол, образованный касательной к графику функции y=g(x) с положит. направлением оси абсцисс в точке…

Практическая тетрадь по теме «Касательная к графику функции»

ПРАКТИЧЕСКАЯ ТЕТРАДЬ

по теме «Касательная к графику функции»

Пояснительная записка:

Практическая тетрадь «Касательная к графику функции» предназначена в первую очередь для самоконтроля учащихся усвоения ЗУН по вышеуказанной теме. Учителя могут использовать данный материал при подготовке учащихся средней школы к итоговой аттестации по алгебре и началам анализа.

Тема: КАСАТЕЛЬНАЯ К ГРАФИКУ ФУНКЦИИ

СПРАВОЧНЫЙ МАТЕРИАЛ

 

Пусть функция f дифференцируема в точке х0.Тогда существует касательная к графику функции f в точке (х0,у0),где у0= f(x0),уравнение которой имеет вид:

у=f(x0)+f ‘(x0)(x-x0).

Геометрический смысл производной

Значение производной состоит в том,что значение производной функции в точке равно угловому коэффициенту касательной к графику функции в этой точке.

f‘((x)== tgα

Механический смысл производной скорости движения.

Пусть точка движется по закону .

Тогда ; ,

где s — путь, пройденный точкой; V — скорость точки; а — ускорение точки.

УПРАЖНЕНИЯ С РЕШЕНИЯМИ

Пример 1. Составьте уравнение касательной к графику функции в точке

Решение:

1) — уравнение искомой касательной;

2) ;

3) ;

4) ;

5) Подставляем значения , и в уравнение касательной: или ,

Пример 2. Составьте уравнение касательной к гиперболе в точке с абциссой

Решение:

1) ;

2) ;

3) ;

4) ;

5) ;

Пример 3.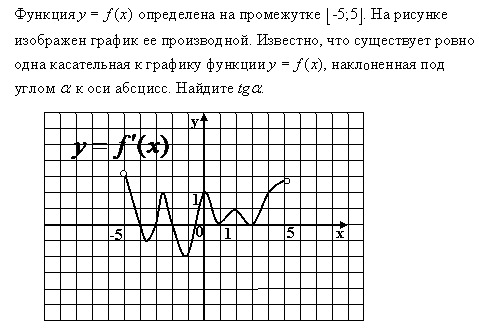 Тело движется прямолинейно по закону , где измеряется в метрах, время — в секундах. Найдите скорость движения тела в момент времени

Решение:

,

Пример 4. Тело движется прямолинейно по закону , где измеряется в метрах, время — в секундах. Найдите ускорение движения тела в момент времени

Решение:

Функция есть закон прямолинейного движения. Мгновенная скорость этого движения равна производной Мгновенная скорость есть функция от времени. Ускорение движения есть скорость изменения скорости, поэтому ускорение движения в момент времени равно производной . Таким образом, ускорение движения в момент времени равно: , т.е. равно производной от производной. Эту производную называют второй производной от функции и обозначают Поэтому ускорение движения равно второй производной

Итак, = ; ; ;

ДИДАКТИЧЕСКИЙ МАТЕРИАЛ

1. Составьте уравнение касательной к графику данной функции f(x) в указанной точке М:

; ,, .

Ответ:.

2. Точка движется по закону . Найдите зависимость скорости движения от времени. Определите мгновенную скорость в момент времени .

Ответ:.

3. Найдите угол между касательной к графику функции в точке и осью . Ответ: .

4. Найдите уравнение касательной к графику функции в точке с абсциссой .

Ответ:.

5. Найдите угол, образованный касательной к кривой в точке с положительным направлением оси абсцисс.

Ответ: 1350.

6. Точка движется прямолинейно по закону

Найдите зависимость ускорения движения от времени, если .

Ответ: .

7. Найдите уравнение касательной к графику функции в точке с абсциссой 2.

Ответ: .

8. Тело массой 10 кг движется прямолинейно по закону . Найдите кинетическую энергию тела через 4с после начала движения.

Ответ: 3125 Дж.

ТЕСТ №1

1. Составьте уравнение касательной к графику функции у=3х2+6х+1 в

точке пересечения этого графика с осью ординат.

А) у=-6х+1; В) у=х+6; С) у=6х+1; D) у=6х; Е) у=6х-1.

2. Найти тангенс угла наклона касательной к графику функции

f(x)=2х3-5х в точке М(2;6)

А) tg α=13; В) tgα=19; С) tgα=17; D) tgα=29; Е) tgα=8.

3. Скорость движения материальной точки по прямой изменяется по закону

V(t)=4t+1/t. Наибольшее значение скорости за время 0,25 ≤ t ≤1 равно

А) 5; В) 4; С) 3; D) 7; Е) 0.

4. Какой угол образует с направлением оси Ох касательная к графику

функции f(x)=(1-х)3, проведенная в точке х=3?

А) острый; В) 300; С) прямой; D) тупой; Е) 00.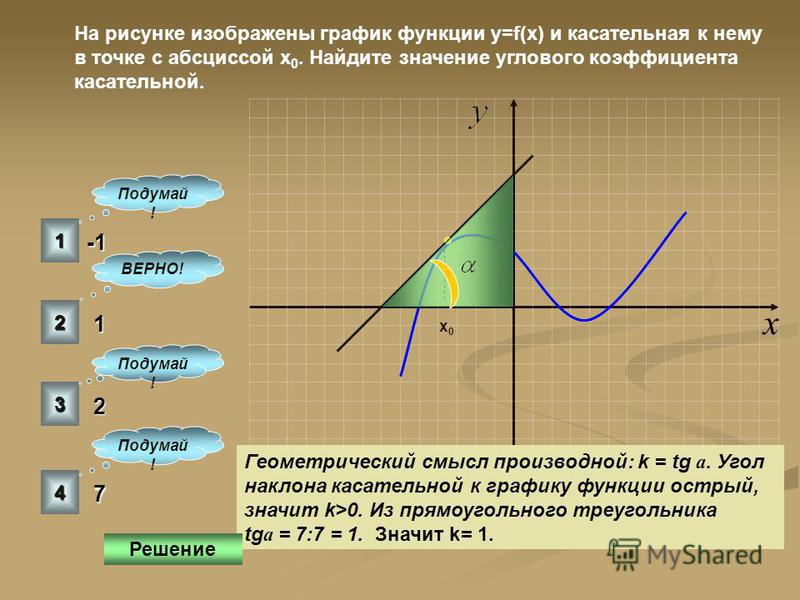

5. Точка движется прямолинейно по закону .Найти значения скорости в момент времени .

А) 202; В) 198; С) 98; D) 104; Е) 128.

6. К графику функции f(x)=5х3+9х-27в точке с абсциссой х=0 проведена

касательная. Найдите абсциссу точки пересечения касательной с осью Ох.

А) 3; В) 1; С) 4; D) 2; Е) -2.

7. Точка движется прямолинейно по закону .В какой момент времени скорость точки окажется равной нулю.

А) 9 В) 4 С) 3 D) 8 Е) 6.

8.Дана функция .Составьте уравнение касательной к графику функции в точке

А) ; В) ; С);

D) Е)

9. Точка движется по координатной прямой по закону S(t)=-t2+10t-7. Найдите S(3).

А) 19; В) 14; С) 4; D) 46; Е) -5.

10. Найти угловой коэффициент прямой, проходящей через точки А(1;-1) и В(2;3).

А) ; В) -; С) -4; D) 1; Е) 4.

ТЕСТ №2

1. Какой угол с осью Ох образует касательная к графику функции в точке с абсциссой ?

А) ; В); С); D); Е).

2. Какой угол с осью Ох образует касательная к графику функции в точке с абсциссой ?

А); В) ; С) ; D) ; Е).

3. Напишите уравнение касательной к графику функции в точке .

А); В) ; С) ; D) ; Е) .

4. Материальная точка движется по прямой линии по закону . Найдите скорость материальной точки в момент времени .

А) В) С) D) Е)

5. Прямолинейное движение точки задано уравнением .Найти скорость движения точки в момент времени .

А)28 В)34 С)25 D)45 Е)18.

6. Точка движется прямолинейно по закону .Найти значения ускорения в момент времени .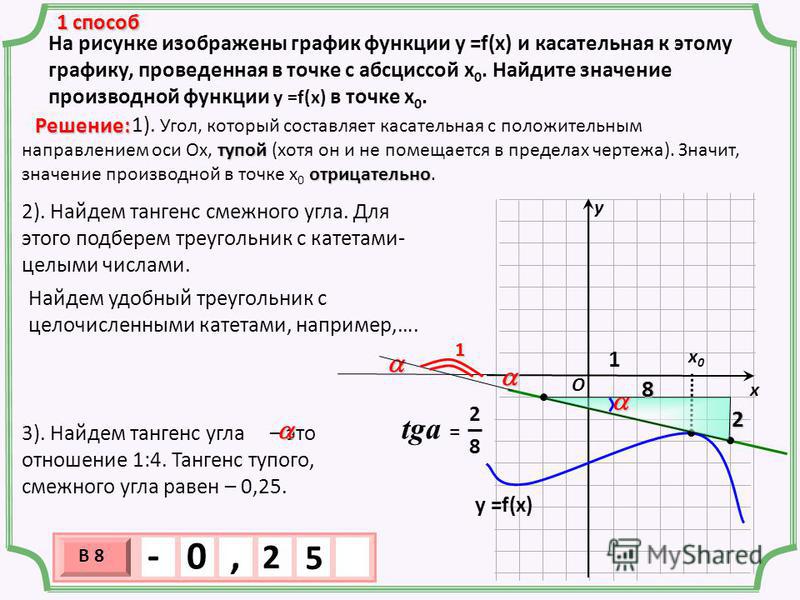

А) 48 В) 50 С)32 D)58 Е)74

7. Напишите уравнение касательной к графику функции в точке пересечения графика с осью ординат.

А) В) С) D) Е)

8. Написать уравнение касательной к графику функции в точке с абсциссой .

А) В) С) D) Е)

9. Найдите уравнение касательной к графику функции , которая параллельна прямой, заданной уравнением .

А) В) С) D) Е)

10. При каком значении прямая является касательной к графику функции

А) В) С) D) Е)

ОТВЕТЫ

Тема: КАСАТЕЛЬНАЯ К ГРАФИКУ ФУНКЦИИ

№	1	2	3	4	5	6	7	8	9	10
Тест№1	С	В	А	D	D	А	С	В	С	Е
Тест№2	D	Е	А	С	А	В	В	В	Е	D

СГА ответы Комбат бесплатно — 9289.

01.01;Т-Т.04;1

График какой функции изображен на рисунке?

Сколько пар решений имеет система уравнений?

Исследуйте функцию на монотонность
Найдите абсциссу точки минимума функции
Найдите абсциссу точки минимума функции
Найдите абсциссу точки минимума функции
Найдите абсциссу точки минимума функции у=х4 — 4lnx
Найдите значение производной функции у= в точке х0=1
Найдите значение производной функции у= х2-lnx в точке х0=0,5
Найдите значение производной функции у=ln(5-2x) в точке х0=2
Найдите значение производной функции у=lnx+x в точке х0=
Найдите значение производной функции у= в точке х0=0
Найдите значение производной функции у=е3х-1 в точке х0=
Найдите значение производной функции у=е4-9х в точке х0=
Найдите значение производной функции у=ех+х2 в точке х0=0
Найдите значение производной функции у=хех в точке х0=1
Найдите наибольшее целое решение неравенства g′(x)<a, если
Найдите наибольшее целое решение неравенства g′(x)<a, если
Найдите наименьшее и наибольшее значения функции у=х-lnx на отрезке [;е]
Найдите наименьшее и наибольшее значения функции у=х-lnx на отрезке [е;e2]
Найдите область определения функции f(x)=log x(37-2x)log7-2×3
Найдите производную функции
Найдите производную функции у=12х3-ех
Найдите производную функции у=
Найдите производную функции у=
Найдите производную функции у=х3ех
Решите уравнение f ′(x)=a, если
Решить уравнение 4х+2-11. 4х=80
Составьте уравнение касательной к графику функции y=x5 – lnх в точке а=1
Составьте уравнение касательной к графику функции в точке а=2
Вычислить
Вычислить
Вычислить
Вычислить
Известно, что lgx=2lgy-lgz+0,5lgt. Выразить x через y, z, t
Известно, что log23=a. Найдите log3
Найдите значение выражения
Найдите наибольшее целочисленное решение неравенства
Найдите наименьшее значение функции у= на промежутке [;]
Найдите сумму корней уравнения
Найдите угол, образованный касательной к графику функции y= с положительным направлением оси абсцисс в точке с абсциссой x0= —
Найдите экстремумы функции
Расположите числа по убыванию:
Решите уравнение
Решить неравенство 16≤2х+3
Решить неравенство 52-3x-1≥0
Решить неравенство 54x+6≤125x
Решить неравенство log(x-21)> log(6x)
Решить неравенство
Решить неравенство log0,5(2-0,5x)≥-1
Решить неравенство log(x+3)>-1
Решить уравнение 7x+1-5 . 7х=98
Составьте уравнение касательной к графику функции y= -2xlnx в точке a = e
Укажите верные утверждения:
Укажите верные утверждения:
Укажите промежуток, которому принадлежит корень уравнения
Упорядочите числа по возрастанию:
Через точку с абсциссой х0=0 проведена касательная к графику функции у=.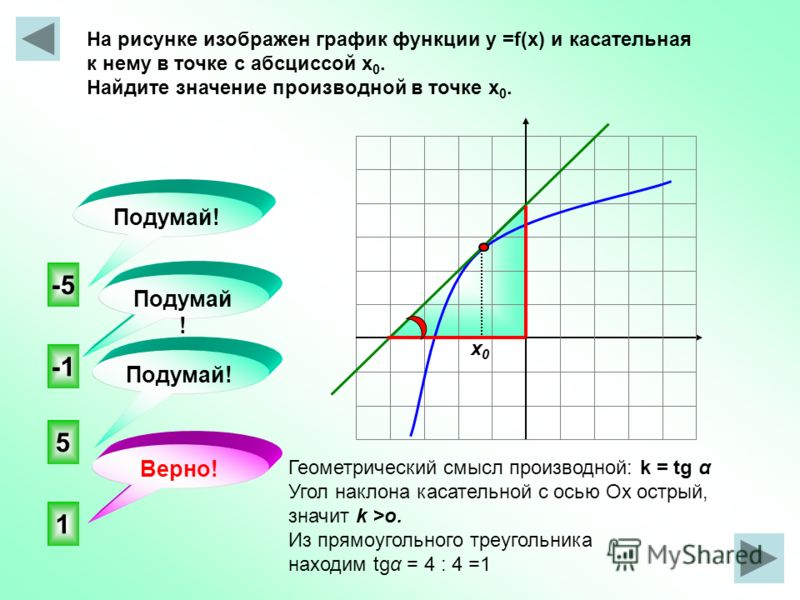 Найдите тангенс угла наклона этой касательной к оси абсцисс
Через точку с абсциссой х0=2 проведена касательная к графику функции у=е-х+2. Найдите тангенс угла наклона этой касательной к оси абсцисс

x {\\ Слева ({2t

Последняя обновленная дата: 23 февраля 2023

•

Общее представление: 273,3K

•

Просмотры сегодня: 4,59K

Ответ

Проверенные

273,3K+ просмотры

93

. Подсказка: Касательная — это линия, которая касается кривой только в одной точке
Решите данный интеграл, чтобы найти функцию кривой
Используйте дифференцирование, чтобы найти наклон касательной к кривой в заданной точке
Попробуйте используйте формулу угла между двумя прямыми через их наклоны, чтобы найти требуемый угол в заданном вопросе.2 — 5x + 6\]
$\потому что y = \left( {x — 3} \right)\left( {x — 2} \right)$ (из шага 1)
Учитывая, что кривая пересекает x- ось:
Координата y по оси x равна 0
$
   \Стрелка вправо y = \left( {x — 3} \right)\left( {x — 2} \right) = 0 \\
   \Стрелка вправо \left( {x — 3} \right) = 0{\text{ и }}\left( {x — 2} \right) = 0 \\
 $
Следовательно, $x = 3,2$
Таким образом, координаты где кривая, пересекающая ось x, равна $\left( {2,0} \right)$, $\left( {3,0} \right)$. 92 — 5x + 6} \right)}}{{dx}} \\
   \Стрелка вправо \dfrac{{dy}}{{dx}} = 2x — 5 \\
 $
Производная функции дает наклон касательная.
Пусть наклон касательной к кривой $y = f\left( x \right)$ в точке $\left( {2,0} \right)$= \[\mathop m\nolimits_1 \]
Таким образом, наклон касательной к кривой $y = f\left( x \right)$ в точке $\left( {2,0} \right)$ определяется выражением:

\[
  {\text{ } }\mathop m\nolimits_1 = \mathop {\dfrac{{dy}}{{dx}}}\nolimits_{\left({2,0} \right)} = 2x — 5 \\
   \Стрелка вправо \mathop m\nolimits_1 = 2\left( 2 \right) — 5 \\
  \because {\text{ }}\mathop m\nolimits_1 = — 1 \\
 \]
Пусть наклон касательной к кривая $y = f\left( x \right)$ в точке $\left( {3,0} \right)$= \[\mathop m\nolimits_2 \]
Таким образом, наклон касательной к кривая $y = f\left( x \right)$ в точке $\left( {3,0} \right)$ определяется как:
\[
  {\text{ }}\mathop m\nolimits_2 = \ mathop {\dfrac{{dy}}{{dx}}}\nolimits_{\left({3,0} \right)} = 2x — 5 \\
   \Стрелка вправо \mathop m\nolimits_2 = 2\left( 3 \right) — 5 \\
  \потому что {\text{ }}\mathop m\nolimits_2 = 1 \\
 \]
Шаг 4. Найдите углы между две касательные.
Тангенс (или тангенс) угла между двумя прямыми в терминах их наклона определяется как:
$\tan \theta = \left| {\dfrac{{\mathop m\nolimits_1 — \mathop m\nolimits_2}}{{1 + \mathop m\nolimits_1 \mathop m\nolimits_2 }}} \right|$
Где $\theta $ — острый угол между две строки. \[\mathop m\nolimits_1 \]и \[\mathop m\nolimits_2 \] — соответствующие наклоны двух линий.
Используя приведенную выше формулу, найдите углы между двумя касательными. (мы знаем, что касательная — это прямая линия)
$\потому что \tan \theta = \left| {\dfrac{{\left( { — 1} \right) — 1}}{{1 + \left( { — 1} \right)1}}} \right|$ (из шага 3: \[\ mathop m\nolimits_1 = — 1\], \[\mathop m\nolimits_2 = 1\])
$
   \Стрелка вправо \tan \theta = \infty \\
  \потому что \theta = \dfrac{\pi }{2} \\
 $ ($\потому что \tan \dfrac{\pi }{2} = \infty $) 9\circ }$. Таким образом, правильный вариант (D).

Примечание: В аналогичном вопросе уравнение касательной можно задать дополнительно. Используйте уравнение прямой линии, проходящей через заданную точку $\left( {\mathop x\nolimits_0 ,\mathop y\nolimits_0} \right)$ с конечным наклоном $m$:
$y — \mathop y\nolimits_0 = m \left( {x — \mathop x\nolimits_0 } \right)$
Другой объект, нормальный, связан с касательной.
Нормальная линия к кривой в данной точке перпендикулярна касательной в этой точке.
Таким образом, наклон нормали $ = — \dfrac{1}{{{\text{наклон касательной}}}}$
Наклон нормали к кривой $y = f\left( x \right )$ определяется как
. Наклон нормальной линии $ = — \dfrac{1}{{\dfrac{{dy}}{{dx}}}}{\text{ или }} — \dfrac{1}{{f ‘\left( x \right)}}$

Недавно обновленные страницы

Если ab и c единичные векторы, то left ab2 right+bc2+ca2 class 12 maths JEE_Main

Стержень AB длиной 4 единицы перемещается горизонтально при выполнении класса 11 математика JEE_Main

Оценить значение intlimits0pi cos 3xdx A 0 B 1 класс 12 математика JEE_Main

Что из следующего верно 1 nleft S cup T right класс 10 математика JEE_Main

Какова площадь треугольника с вершинами Aleft класс 11 математика JEE_Main

KCN легко реагирует с образованием цианида с A. Этиловый спирт класс 12 химический состав JEE_Main

Если ab и c единичные векторы, то левый ab2 правый+bc2+ca2 математический класс 12 JEE_Main

Стержень AB длиной 4 единицы движется горизонтально когда 11 класс математика JEE_Main

Оценить значение intlimits0pi cos 3xdx A 0 B 1 класс 12 математика JEE_Main

Что из следующего верно 1 nleft S cup T right класс 10 математика JEE_Main

Какова площадь треугольника с вершинами Aleft класс 11 математика JEE_Main

KCN легко реагирует с образованием цианида с этиловым спиртом класса 12 по химическому составу JEE_Main

Возникающие сомнения

Объяснение урока: Углы касания

по кругу и найти его меру, используя меру его стягиваемой дуги, вписанного угла или центрального угла, стягиваемого той же дугой.

Начнем с того, что вспомним, что касательная к окружности — это линия, которая пересекает окружность только в одной точке, как показано ниже.

Заметим, что отрезок от точки пересечения 𝐴 к центру круга 𝑀 есть радиус окружности. Кроме того, этот радиус перпендикулярен (т.е. под углом 90 градусов) к касательной линии.

В этом объяснителе мы хотим обсудить углы касания. Рассмотрим касательную к окружность, которая встречается с хордой окружности (т. е. с отрезком внутри окружность) в точке 𝐴.

Угол 𝜃 между хордой и касательной известен как угол касания . Вычислить этот угол можно с помощью несколько теорем и наблюдений, которые мы обсудим в ходе этого объяснитель.

Также важно помнить о некоторых свойствах треугольников. Равнобедренные и равнобедренные треугольники — это треугольники, у которых есть два или три равных сторон соответственно, как показано ниже.

Важно отметить, что, поскольку все радиусы круга имеют одинаковые длина, два радиуса могут образовывать стороны равнобедренного треугольника, как показано на рисунке ниже.

Это может быть полезно знать, так как это говорит нам о том, что меры углов при 𝐴 и 𝐵 равны.

Кроме того, давайте рассмотрим теорему о вписанном угле (также называемую теоремой ). теорема о центральном угле), которая имеет решающее значение для предстоящих расчетов, связанных с углы внутри окружности.

Напомним, что две точки на окружности 𝐴 и 𝐵, делим окружность на две дуги: большую дугу и дуга второстепенная

(когда дуги имеют одинаковую длину, они делят окружность на две полукруглые дуги). Мы также можем образовать вписанный угол с любой точкой 𝐶 на большой дуге, как показано.

Обратите внимание, что иногда главную дугу называют вложенной дугой а меньшая дуга пересекает дугу . Тогда имеем следующее теорема.

Теорема: Теорема о вписанном угле

Пусть 𝐴 и 𝐵 две точки на окружности, 𝑀 быть центром круга, а 𝐶 быть любым точка на большой дуге. Тогда мера центрального угла ∠𝐴𝑀𝐵 вдвое больше меры вписанный угол ∠𝐴𝐶𝐵, как показано.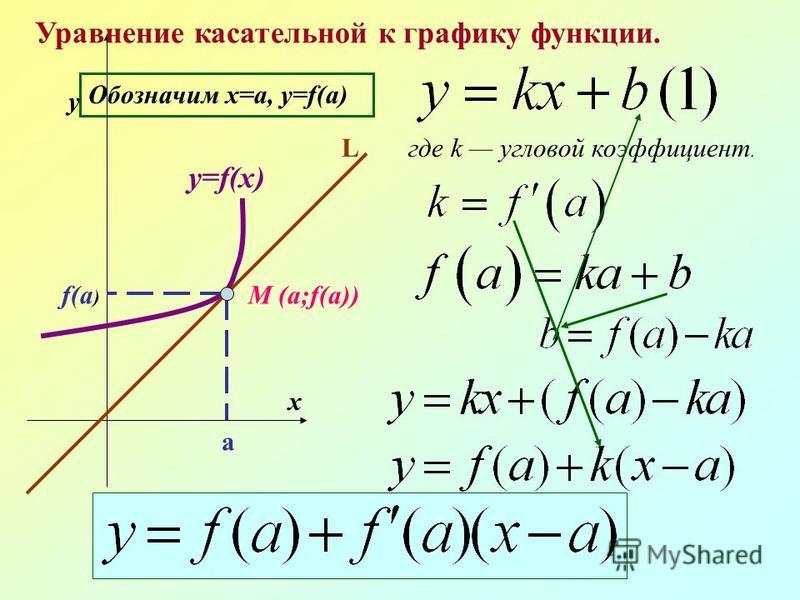

Другой способ сформулировать эту теорему состоит в том, что мера центрального угла , стягиваемое двумя точками на окружности, в два раза больше вписанного угол, образуемый этими точками.

Вспомнив эту теорему, давайте выучим новую теорему об углах касание по кругу.

Теорема: теорема об альтернативном отрезке

Пусть 𝐴 и 𝐵 две точки на окружности и 𝐶 — точка, в которой касательная (проходящая через 𝐸, 𝐶 и 𝐷) пересекает круг. Тогда углы касания ∠𝐴𝐶𝐷 и ∠𝐵𝐶𝐸 равны углам чередующиеся сегменты ∠𝐴𝐵𝐶 и ∠𝐵𝐴𝐶 соответственно. Это показано ниже.

Докажем эту теорему. Для начала вспомним, что касательная окружности в точке точка 𝐶 образует прямой угол с радиусом 𝑀𝐶 в точке пересечения.

Теперь начнем с рассмотрения одного из углов касания ∠𝐴𝐶𝐷, которые мы помечаем как 𝜃 ниже.

Поскольку тангенс и радиус образуют прямой угол, мы знаем, что 𝑚∠𝐴𝐶𝐷+𝑚∠𝐴𝐶𝑀=90∘. Следовательно, 𝑚∠𝐴𝐶𝑀=90−𝜃∘. Мы также знаем, что внутренний треугольник 𝐴𝐶𝑀 является равнобедренным. треугольника, так как две его стороны являются радиусами и, следовательно, равны. Так, 𝑚∠𝐶𝐴𝑀=90−𝜃∘ также.

Поскольку в треугольнике сумма всех углов всегда равна 180∘, мы имеем (90−𝜃)+(90−𝜃)+𝑚∠𝐴𝑀𝐶=180.∘∘∘

Переставляя, мы имеем 𝑚∠𝐴𝑀𝐶=180−(90−𝜃)−(90−𝜃)=2𝜃.∘∘∘

Это дает нам, что мера центрального угла между 𝐴 и 𝐶 равно 2𝜃. Окончательно, используя теорему о вписанном угле, мы можем заключить, что мера ∠𝐴𝐵𝐶 — половина центрального угла 2𝜃, так как это вписанный угол 𝐴 и 𝐶. Таким образом, 𝑚∠𝐴𝐵𝐶=𝜃.

Заметим, что тот же метод применим и к другому углу касания ∠𝐵𝐶𝐸, так как мы можем просто повторить процесс с аккорд 𝐵𝐶. Таким образом, мы доказали альтернативный отрезок теорема.

Давайте посмотрим на пример, где мы можем непосредственно применить эту теорему.

Пример 1. Нахождение меры угла касания по заданной мере Вписанный угол, опирающийся на ту же дугу

Учитывая, что 𝐵𝐶 является касательной к круг, найти 𝑚∠𝐴𝐵𝐶.

Ответ

Прежде всего отметим угол, который мы хотим найти на диаграмме с 𝜃.

Для любого вопроса, где нам нужно найти угол касания, нам нужно спросите себя, можем ли мы использовать теорему об альтернативных сегментах Помочь нам.

Теперь мы знаем, что 𝐵𝐶 является касательной к обведите 𝐵, что 𝐴, 𝐵, и 𝐷 три точки на окружности, и что угол, который мы хотите найти угол касания ∠𝐴𝐵𝐶. Следовательно, мы можем использовать теорему об альтернативных сегментах, чтобы найти этот угол. То есть, 𝑚∠𝐴𝐵𝐶=𝑚∠𝐴𝐷𝐵𝑚∠𝐴𝐵𝐶=78.∘

Поскольку ∠𝐴𝐷𝐵 — это угол в альтернативной сегмент на ∠𝐴𝐵𝐶, мы непосредственно используем теорему чтобы найти, что 𝑚∠𝐴𝐵𝐶=78∘.

Мы видели, как можно напрямую использовать теорему об альтернативных сегментах для нахождения вписанные углы заданы углом касания и наоборот, но мы также можем использовать другие аспекты теоремы, чтобы помочь решить различные проблемы.

Например, давайте рассмотрим, как углы касания связаны с центральными углами.

Следствие: углы касания и центральные углы

Пусть 𝐴 будет точкой на окружности с центром 𝑀 и 𝐵 — точки, в которых касательная (проходя через 𝐵 и 𝐶) пересекает круг. Тогда угол касания ∠𝐴𝐵𝐶 равен половине центрального угла ∠𝐴𝑀𝐵. Это показано ниже.

Другой способ сформулировать это так: угол касания равен половине центрального угла опирается на одну и ту же дугу (т. е. дугу 𝐴𝐵).

Обратите внимание, что поскольку это следствие мы продемонстрировали во время доказательства теорему об альтернативных сегментах, поэтому нам не нужно доказывать ее снова. Давайте рассмотрим пример, в котором мы можем использовать эту теорему непосредственно, чтобы найти угол касание.

Пример 2. Нахождение меры угла касания по заданной мере Центральный угол, опирающийся на ту же дугу

Найдите 𝑚∠𝐵𝐴𝐶.

Ответ

Начнем с того, что отметим угол, который нас попросили найти на диаграмма:

Мы видим, что нас попросили найти меру угла касание ∠𝐵𝐴𝐶.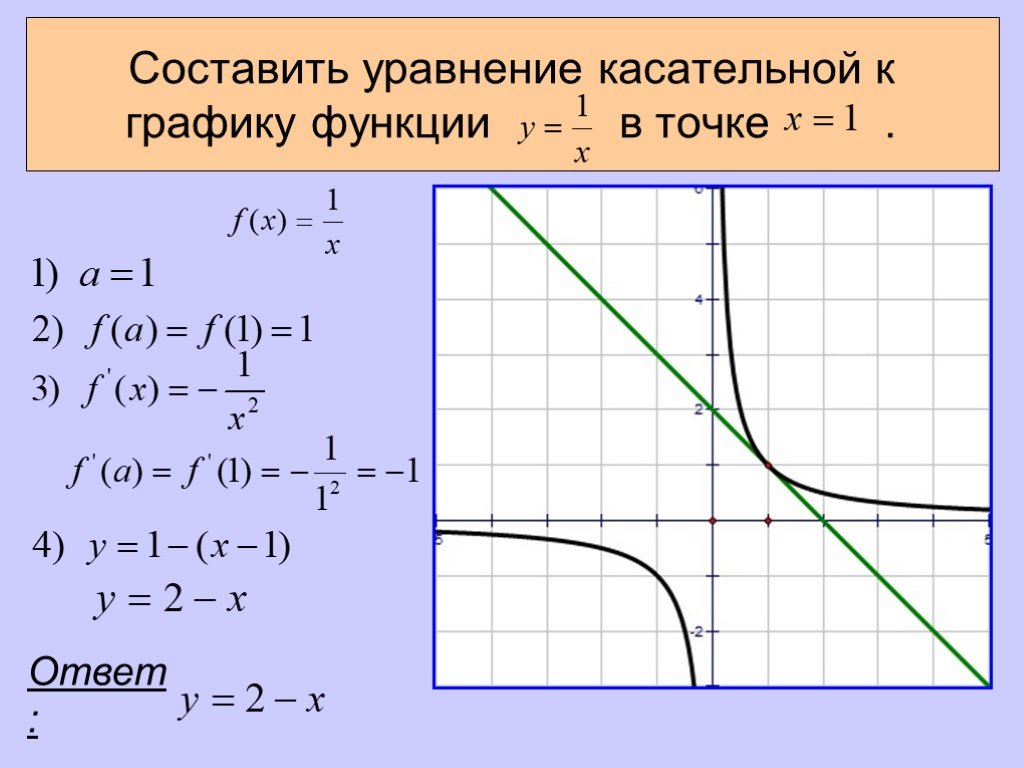 Обратите внимание, что угол ∠𝐴𝑀𝐵 на схеме прямой угол потому что он отмечен квадратом, что говорит нам о том, что его мера 90∘. Мы также отмечаем, что ∠𝐴𝑀𝐵 — центральный угол, опирающийся на той же дуге (т. Е. 𝐴𝐵), что и угол касание.

Напомним, что мера угла касания 𝑚∠𝐵𝐴𝐶 равно половине меры центральный угол опирается на ту же дугу, которая 𝑚∠𝐴𝑀𝐵. Таким образом, у нас есть 𝑚∠𝐵𝐴𝐶=12𝑚∠𝐴𝑀𝐵=12(90)=45.∘∘

До сих пор мы видели, как вычислить угол касания, используя центральный угол и с помощью вписанного угла. Мы также можем вычислить углы касания, используя мера дуги.

Напомним, что мерой дуги является угол, который образует дуга в центре круга. Например, рассмотрим схему ниже.

Здесь мы видим, что мера большой дуги окружности, созданной две точки 𝐴 и 𝐵 (обозначаются 𝜃 снаружи круга) эквивалентна мере угла между радиусами, образованными 𝐴 и 𝐵 внутри круга.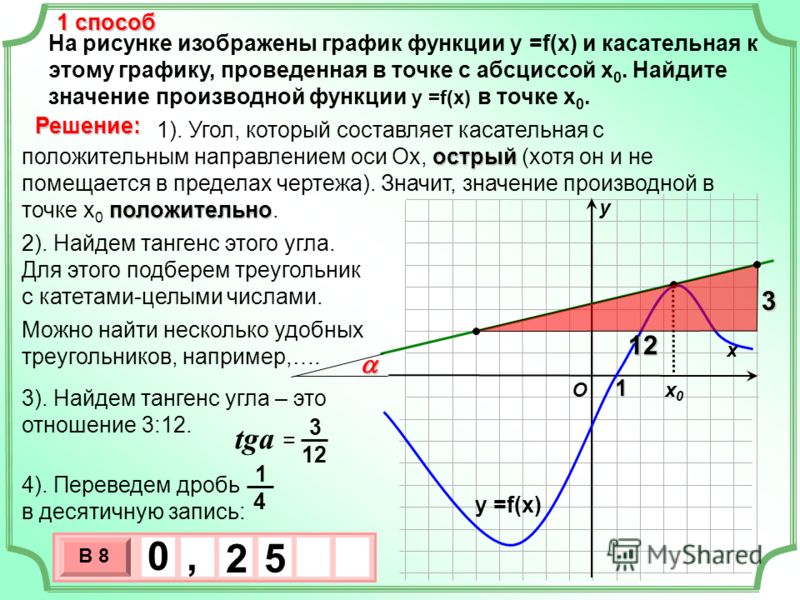

Напомним, что у нас уже есть следствие, связывающее центральный угол окружности к углу касания. Используя равенство между центральным углом и меры дуги, мы можем распространить это следствие на дугу окружности. Этот эквивалентность можно увидеть на следующей диаграмме.

Другими словами, поскольку мера центрального угла и мера дуги равны 2𝜃, они оба в два раза больше угла касания. Таким образом, мы имеют следующее следствие.

Следствие: углы касания и дуговые меры

Пусть 𝐴 — точка на окружности, а 𝐵 быть точкой, где касательная (проходящая через 𝐵 и 𝐶) пересекает окружность. Тогда угол касания ∠𝐴𝐵𝐶 — половина меры дуги 𝐴𝐵 образовались на той же стороне. Это показано ниже.

Важно понимать, к какой дуге относится 𝐴𝐵, так как есть две возможности: большая дуга и малая дуга (также известные как стянутые и перехваченные дуги). На приведенной выше диаграмме минор была использована дуга, так как она находится на той же стороне, что и угол касания.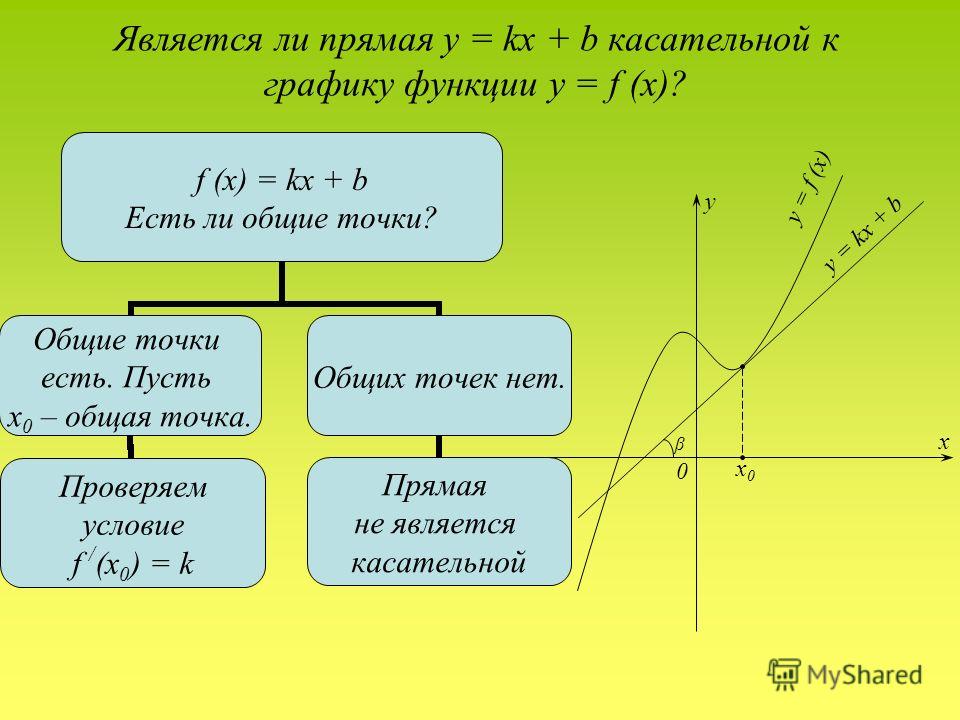 Однако обратное было бы верно, если бы мы рассматривали тупой угол, как показано ниже.

Здесь 𝐴𝐵 теперь является большой дугой окружности. Это также важно отметить, что если нам задана дуга, противоположная той, которая нам нужна, мы можем использовать тот факт, что меры двух дуг окружности в сумме 360∘. Итак, это всегда можно найти большую дугу, если нам дана малая дуга, или наоборот.

Рассмотрим пример, в котором мы можем использовать эту теорему для вычисления угла касание с использованием меры дуги.

Пример 3. Нахождение меры угла касания с помощью дуги

Учитывая, что 𝐵𝐶 является касательной к окружности ниже найдите 𝑚∠𝐴𝐵𝐶.

Ответ

Начнем с того, что отметим угол, который нам нужно найти, на диаграмме.

Напомним, что угол касания ∠𝐴𝐵𝐶 составляет половину меры дуги 𝐴𝐵 формируется на той же стороне. В этом примере мы видим, что мера дуги нам дано (т.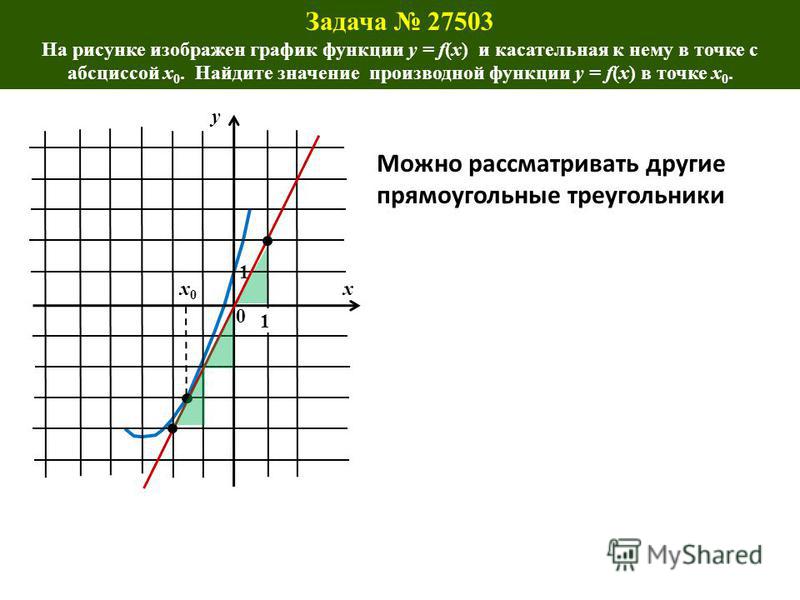 е. 190∘) находится не на одной стороне. Однако мы можем найти правильную меру дуги с помощью используя тот факт, что меры двух дуг окружности должны суммироваться 360∘. Таким образом, правильная мера дуги равна 360−190=170.∘∘∘

Отметим это на диаграмме.

Теперь мы можем использовать тот факт, что угол касания составляет половину меры дуги с той же стороны, чтобы получить ∠𝐴𝐵𝐶=12⋅170=85.∘∘

Еще один тип вопросов, связанных с углами касания, имеет точку вне окружность, проходящая через две различные касательные. Давайте рассмотрим пример этого.

Пример 4. Нахождение мер двух вписанных углов по мерам углов касания, стягиваемого теми же дугами, чтобы найти другие неизвестные углы

Учитывая, что 𝑚∠𝐸𝐶𝐷=54∘ и 𝑚∠𝐹𝐵𝐷=78∘, найти 𝑥 и 𝑦.

Ответ

Начнем с того, что поместим полученную информацию. 𝑚∠𝐸𝐶𝐷=54∘ и 𝑚∠𝐹𝐵𝐷=78∘, в диаграмма.

Для начала попробуем найти 𝑥. Так как это вопрос об углах касания, мы спрашиваем себя, Нам может помочь теорема об альтернативных сегментах. Мы можем видеть, что там два угла касания и три точки на окружности, мы можем использовать теорема дважды во внутреннем треугольнике, чтобы найти недостающие углы. Это показано ниже.

Теперь мы замечаем, что у нас есть два из трех углов внутреннего треугольника. Так как сумма углов треугольника равна 180∘, мы имеем 𝑥+78+54=180𝑥=48.∘∘∘∘

Найдя 𝑥, мы теперь хотим найти 𝑦, что означает нахождение углов треугольника, в котором находится 𝑦. Чтобы найти другие углы, мы можем использовать тот факт, что углы треугольника прямая линия должна составить 180∘. Таким образом, используя точный расчет, как и раньше, находим, что остальные углы должны быть 48∘, что дает нам следующее.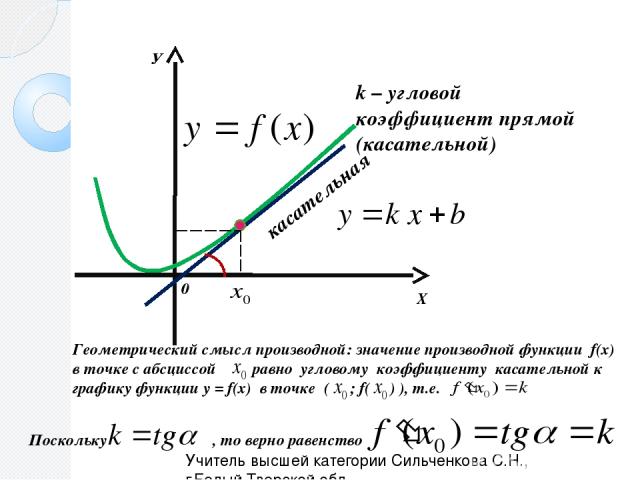

Вспоминая, что два касательных отрезка, пересекающихся в одной точке, имеют одинаковые длины и, таким образом, образуют равнобедренный треугольник при соединении хордой, мы можем подтвердить, что равенство этих двух углов согласуется с этим правило. Наконец, мы можем вычислить 𝑦, используя сумму углы в треугольнике. 48+48+𝑦=180𝑦=84.∘∘∘∘

Итак, в сумме имеем 𝑥=48∘ и 𝑦=84∘.

До сих пор мы использовали теорему об альтернативных сегментах и ​​ее варианты для найти угол, который образует касательная с хордой окружности. Как есть можно использовать теорему для нахождения углов таким образом, мы также можем использовать обратное, чтобы доказать, что данный луч или отрезок касаются окружности, если соответствующие углы совпадают. Формально имеем следующее следствие.

Следствие: обращение теоремы об альтернативном отрезке

Если луч или отрезок пересекаются с хордой окружности снаружи окружность и угол, который она образует с хордой, равны угол в альтернативном сегменте окружности, затем этот луч или сегмент линии должна быть касательной к окружности.

Если углы не равны, то этот луч или отрезок не касаются круг.

Поясним, что это конкретно означает. Предположим, у нас есть луч 𝐶𝐷 и нам дан угол, который он составляет с аккорд 𝐴𝐶. Тогда у нас есть две возможности, как показано ниже.

В первом случае мера ∠𝐴𝐶𝐷 равна мере угла в чередующемся отрезке ∠𝐴𝐵𝐶; следовательно, 𝐶𝐷 должна быть касательной. Во втором случае углы не равны, так как 𝑚∠𝐴𝐶𝐷>𝑚∠𝐴𝐵𝐶; следовательно, 𝐶𝐷 не может быть касательной.

Одна конкретная ситуация, в которой нам может понадобиться использовать это следствие, — описанные окружности. Напомним, что если нам дан треугольник, то существует ровно одна окружность, проходящая через через все вершины треугольника. Мы называем этот круг описанная окружность .

Иногда нам могут задавать вопросы о касательных к описанной окружности. треугольник. Например, нам может понадобиться проверить, является ли луч касательной к описанную окружность, измерив ее угол хордой и убедившись, что она удовлетворяет свойства угла касания. Давайте рассмотрим эту идею в следующем пример.

Пример 5. Нахождение угла касания при условии, что прямая касается Окружность треугольника

На данном рисунке, если 𝐶𝐷≠𝐷𝐴, какой из Ниже приведена касательная к окружности, проходящей через вершины треугольник 𝐴𝐵𝐸?

1. 𝐸𝐷
2. 𝐸𝐶
3. 𝐴𝐷
4. 𝐵𝑌
5. 𝐵𝐶

Ответ

. информацию, которую нас просят найти. В частности, нам необходимо рассмотреть окружность, проходящая через вершины треугольника 𝐴𝐵𝐸 (т. е. описанная окружность). Выделим это треугольник.

Хотя мы еще не нарисовали описанную окружность вокруг 𝐴𝐵𝐸, мы можем сразу увидеть, что 𝐸𝐷 и 𝐸𝐶 не может касаться круг, так как они являются продолжением сторон треугольника (другими словами, они являются секущими). Остается выяснить, будет ли 𝐴𝐷, 𝐵𝑌, или 𝐵𝐶 касается окружности.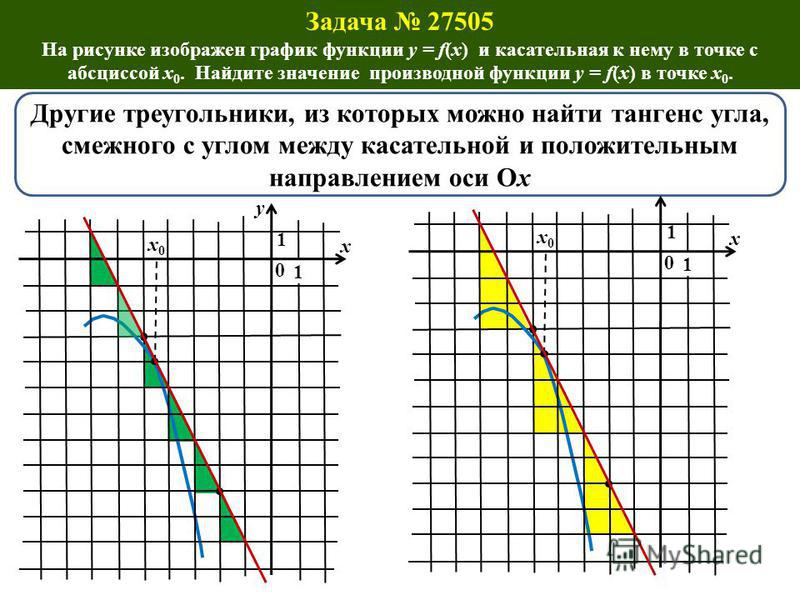

Чтобы проверить эти другие варианты, нам нужно исследовать окружающие углы и выясните, имеет ли смысл, чтобы они были касательными. В частности, мы можем использовать обратную теорему об альтернативных сегментах для докажите в каждом случае, являются ли они касательной или нет.

Начнем с рассмотрения 𝐴𝐷. Напомним, что в задаче описание, нам было дано, что 𝐶𝐷≠𝐷𝐴. В частности, это означает, что соответствующие дуги не равны в длина. Рассмотрим дуги 𝐷𝐴 и 𝐶𝐷. Заметим, что угол ∠𝐴𝐵𝐸 — вписанный угол 𝐷𝐴 и ∠𝐷𝐴𝐸 — вписанный угол 𝐶𝐷. Выделим эти дуги и соответствующие вписанные углы ниже.

Напомним, что мера вписанного угла, опирающегося на дугу, равна половине мера дуги. Поскольку дуги 𝐷𝐴 и 𝐶𝐷 имеют разную длину, это означает 𝑚∠𝐴𝐵𝐸 и 𝑚∠𝐷𝐴𝐸 не равны.

Теперь давайте вспомним обратную теорему об альтернативном отрезке: если угол между 𝐴𝐷 и 𝐴𝐸 (это аккорд описанная окружность) не равна углу в альтернативном сегменте (т. е. ∠𝐴𝐵𝐸), то 𝐴𝐷 не может быть касательной к этой окружности. Таким образом, 𝐴𝐷 не является касательной.

Далее давайте посмотрим на 𝐵𝑌. Рассмотрим треугольник 𝐸𝐵𝐶. Мы видим, что ∠𝐴𝐸𝐵 — внешний угол этого треугольника, что означает, что он равен сумме удаленных внутренних углов (по теореме о внешнем угле). Другими словами,

(1)

Мы выделяем это ниже.

Теперь, поскольку 𝐵𝑌 является касательной к большему круг, мы можем применить к нему теорему об альтернативных сегментах. В частности, если мы рассмотрим треугольник 𝐴𝐵𝐶, мы можем видеть, что

𝑚∠𝐴𝐶𝐵=𝑚∠𝐴𝐵𝑌.

(2)

Это также указано на схеме.

Однако теперь мы можем использовать обратную теорему об альтернативных сегментах в треугольник 𝐴𝐵𝐸: подставляя уравнение (2) в (1), имеем 𝑚∠𝐴𝐸𝐵=𝑚∠𝐴𝐵𝑌+𝑚∠𝐶𝐵𝐸.

Поскольку 𝑚∠𝐶𝐵𝐸>0, это означает, что 𝑚∠𝐴𝐸𝐵>𝑚∠𝐴𝐵𝑌.

Итак, два угла не могут быть равны, а значит 𝐵𝑌 не может касаться окружности, проходящей через треугольник 𝐴𝐸𝐵.

Наконец, давайте рассмотрим 𝐵𝐶. Для начала воспользуемся информацией, указанной в вопросе. Мы можем видеть что 𝑋𝐶 и 𝐵𝐸 — параллельные прямые, так как они имеют были отмечены двойными стрелками. Это означает, что противоположные углы ∠𝑋𝐶𝐵 и ∠𝐶𝐵𝐸 должны быть равны. Мы выделяем это ниже.

Теперь мы видим, что 𝑋𝐶 является касательной к больший круг и что внутри этого круга есть несколько треугольников, поэтому мы можем использовать здесь теорему об альтернативных сегментах. В частности, рассмотрим треугольник 𝐴𝐵𝐶. Мы видим, что угол касания ∠𝐵𝐶𝑋 равно углу в альтернативной сегмент, ∠𝐵𝐴𝐸, как показано.

Теперь, возвращаясь к треугольнику 𝐴𝐵𝐸, рисуем обведите окружность вокруг нее и выделите углы ∠𝐶𝐵𝐸 и ∠𝐵𝐴𝐸:

Применим еще раз обратную теорему об альтернативном отрезке.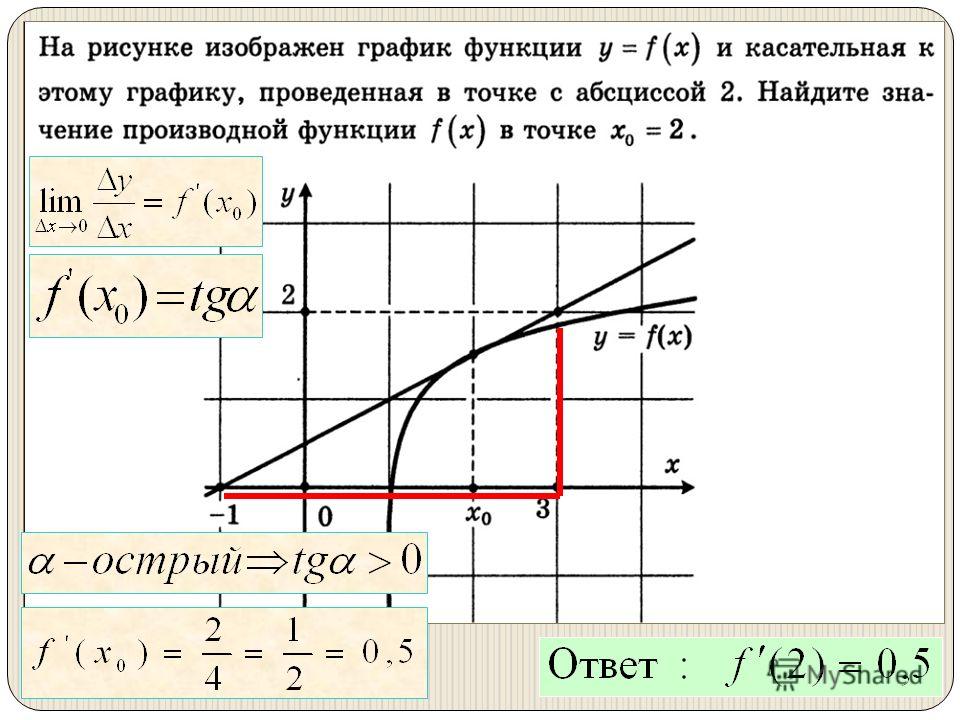 В частности, поскольку углы ∠𝐶𝐵𝐸 и ∠𝐵𝐴𝐸 равны, он должен поэтому будет так, что 𝐵𝐶 является касательной к окружности.

Таким образом, ответ E: 𝐵𝐶.

Давайте закончим повторением теоремы об альтернативных сегментах и ​​местами, которые мы можем используй это.

Ключевые точки

• Пусть 𝐴 и 𝐵 две точки на окружности и 𝐶 — точка, в которой касательная (проходящая через 𝐸, 𝐶 и 𝐷) пересекается круг. Тогда углы касания ∠𝐴𝐶𝐷 и ∠𝐵𝐶𝐸 равны углам в альтернативной сегменты ∠𝐴𝐵𝐶 и ∠𝐵𝐴𝐶 соответственно.
• В качестве расширения вышеизложенного для круга с центром 𝑀, угол касания ∠𝐴𝐵𝐶 составляет половину центральный угол ∠𝐴𝑀𝐵.
• Кроме того, угол касания ∠𝐴𝐵𝐶 составляет половину меры дуги 𝐴𝐵 формируется на той же стороне.
• И наоборот, если луч или отрезок пересекаются с хордой окружности на вне круга и угол, который он образует с хордой, равен по величине к углу в альтернативном сегменте окружности, то этот луч или сегмент линии должна быть касательной к окружности.

  No related posts.