Error
Sorry, the requested file could not be found
More information about this error
Jump to…
Jump to…Согласие на обработку персональных данных Учебно-тематический планАвторы и разработчики курсаИнформация для студентов и преподавателейВводная лекцияIntroductory lectureЛекция о системе обозначений Lecture on the notation systemВидеолекция (часть 1)Lecture (Part 1)Видеолекция 2. Операции над функциями. Свойства функции.Lecture 2. Operations on functions. The properties of the functionТеоретический материал Практическое занятие. Исследование свойств функций по определениюPractical lesson. Investigation of the properties of functions by definitionЗадачи для самостоятельной работыРешения задачТест 1.1.1(Часть 1). Числовые функцииQuiz 1.1.1 (part 1)Тест 1.1.1(Часть 2). Числовые функцииQuiz 1.1.1 (part 2)Видеолекция 1. Числовая последовательность Lecture 1. Numeric sequenceВидеолекция 2. Предел числовой последовательностиLecture 2.
 4. Непрерывность функции в точкеВидеолекция (часть 1)Lecture 1. Differential calculus of functions of a single variableВидеолекция (часть 2)Lecture 2. Differentiation of a function given parametricallyПрактическое занятие 1. Правила дифференцированияПрактическое занятие 2. Логарифмическое дифференцирование. Дифференцирование функции, заданной параметрическиPractical lesson 1. Logarithmic differentiation. Differentiating a function defined parametricallyPractical lesson 2. Rules of differentiationЗадачи для самостоятельной работыРешения задачТаблица производныхТест 1.1.5 Производная функцииВидеолекция 1. Геометрический и физический смысл производнойLecture 1. Geometric and physical meaning of the derivativeВидеолекция 2. Дифференциал функцииLecture 2. Differential of a functionПрактическое занятие 1. Геометрический смысл производнойPractical lesson 1. The geometric meaning of the derivativeПрактическое занятие 2. Производные и дифференциалы высших порядковPractical lesson 2. Higher-order derivatives and differentialsЗадачи для самостоятельной работыРешения задачТест 1.
4. Непрерывность функции в точкеВидеолекция (часть 1)Lecture 1. Differential calculus of functions of a single variableВидеолекция (часть 2)Lecture 2. Differentiation of a function given parametricallyПрактическое занятие 1. Правила дифференцированияПрактическое занятие 2. Логарифмическое дифференцирование. Дифференцирование функции, заданной параметрическиPractical lesson 1. Logarithmic differentiation. Differentiating a function defined parametricallyPractical lesson 2. Rules of differentiationЗадачи для самостоятельной работыРешения задачТаблица производныхТест 1.1.5 Производная функцииВидеолекция 1. Геометрический и физический смысл производнойLecture 1. Geometric and physical meaning of the derivativeВидеолекция 2. Дифференциал функцииLecture 2. Differential of a functionПрактическое занятие 1. Геометрический смысл производнойPractical lesson 1. The geometric meaning of the derivativeПрактическое занятие 2. Производные и дифференциалы высших порядковPractical lesson 2. Higher-order derivatives and differentialsЗадачи для самостоятельной работыРешения задачТест 1.
 1.8. Асимптоты графика функцииВидеолекция. Дифференциальное и интегральное исчислениеLecture. Differential and Integral CalculationЗадачи для самостоятельной работыРешения задачТаблица интеграловТест 1.2.1. Неопределенный интегралВидеолекция. Неопределенный интеграл: методы интегрирования.Lecture. Indefinite integral: methods of integration.Практическое занятие. Внесение функции под знак дифференциалаPractical lesson. Adding a function under the sign of the differentialЗадачи для самостоятельной работыРешения задачТест 1.2.2. Методы интегрированияВидеолекция 1. Интегрирование дробно-рациональных функций (часть1)Lecture 1. Integration of fractional-rational functions (part 1)Видеолекция 2. Интегрирование дробно-рациональных функций (часть 2)Lecture 2. Integration of fractionally rational functions (part 2)Практическое занятие 1. Интегрирование иррациональных выражений (часть 1)Practical lesson 1. Integration of irrational expressions (part 1)Практическое занятие 2. Интегрирование тригонометрических функцийPractical lesson 2.
1.8. Асимптоты графика функцииВидеолекция. Дифференциальное и интегральное исчислениеLecture. Differential and Integral CalculationЗадачи для самостоятельной работыРешения задачТаблица интеграловТест 1.2.1. Неопределенный интегралВидеолекция. Неопределенный интеграл: методы интегрирования.Lecture. Indefinite integral: methods of integration.Практическое занятие. Внесение функции под знак дифференциалаPractical lesson. Adding a function under the sign of the differentialЗадачи для самостоятельной работыРешения задачТест 1.2.2. Методы интегрированияВидеолекция 1. Интегрирование дробно-рациональных функций (часть1)Lecture 1. Integration of fractional-rational functions (part 1)Видеолекция 2. Интегрирование дробно-рациональных функций (часть 2)Lecture 2. Integration of fractionally rational functions (part 2)Практическое занятие 1. Интегрирование иррациональных выражений (часть 1)Practical lesson 1. Integration of irrational expressions (part 1)Практическое занятие 2. Интегрирование тригонометрических функцийPractical lesson 2.
 3.1. Функции нескольких переменных (основные понятия)Quiz 1.3.1Видеолекция Дифференцируемость функции двух переменныхLecture. Differentiable functions of two variablesПрактическое занятие 1. Производные и дифференциалы высших порядковПрактическое занятие 2. Понятие дифференциала первого и второго порядкаPractical lesson 2. The concept of the first- and second-order differentialЗадачи для самостоятельной работыРешения задач Тест 1.3.2. Дифференцирование функции нескольких переменныхQuiz 1.3.2Видеолекция 1. Дифференцирование сложной функции, заданной неявноLecture 1. Differentiation of a complex function and a function given implicitlyВидеолекция 2. Производная по направлению. ГрадиентLecture 2. The directional derivative and the gradientПрактическое занятие 1. Производная по направлению, градиентPractical lesson 1. The directional derivative, the gradientПрактическое занятие 2. Исследование свойств функций по определениюPractical lesson 2. Investigating function properties by defenition Практическое занятие 3.
3.1. Функции нескольких переменных (основные понятия)Quiz 1.3.1Видеолекция Дифференцируемость функции двух переменныхLecture. Differentiable functions of two variablesПрактическое занятие 1. Производные и дифференциалы высших порядковПрактическое занятие 2. Понятие дифференциала первого и второго порядкаPractical lesson 2. The concept of the first- and second-order differentialЗадачи для самостоятельной работыРешения задач Тест 1.3.2. Дифференцирование функции нескольких переменныхQuiz 1.3.2Видеолекция 1. Дифференцирование сложной функции, заданной неявноLecture 1. Differentiation of a complex function and a function given implicitlyВидеолекция 2. Производная по направлению. ГрадиентLecture 2. The directional derivative and the gradientПрактическое занятие 1. Производная по направлению, градиентPractical lesson 1. The directional derivative, the gradientПрактическое занятие 2. Исследование свойств функций по определениюPractical lesson 2. Investigating function properties by defenition Практическое занятие 3.

 The system of linear equationsПрактическое занятие 3. Исследование систем линейных уравненийТеоретический материал (лекция 3)Задачи для самостоятельной работы 3Решения задач 3Тест 2.1.1. Системы линейных уравненийСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Векторное пространствоLecture 1. Vector spaceВидеолекция 2. линейная зависимость векторов. Базис векторного пространстваLecture 2. Linear dependence of vectors and the concept of the basis of the vector systemПрактическое занятие 1. Арифметическое векторное пространствоPractical lesson 1. Arithmetic vector spaceПрактическое занятие 2. Линейная зависимость векторов. Базис векторного пространстваPractical lesson 2. Linear dependence of vectors and the concept of the basis of the vector systemТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Тест 2.1.2. Арифметическое n-мерное векторное пространствоСправочник (часть 1)Справочник (часть 2)Видеолекция 1.
The system of linear equationsПрактическое занятие 3. Исследование систем линейных уравненийТеоретический материал (лекция 3)Задачи для самостоятельной работы 3Решения задач 3Тест 2.1.1. Системы линейных уравненийСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Векторное пространствоLecture 1. Vector spaceВидеолекция 2. линейная зависимость векторов. Базис векторного пространстваLecture 2. Linear dependence of vectors and the concept of the basis of the vector systemПрактическое занятие 1. Арифметическое векторное пространствоPractical lesson 1. Arithmetic vector spaceПрактическое занятие 2. Линейная зависимость векторов. Базис векторного пространстваPractical lesson 2. Linear dependence of vectors and the concept of the basis of the vector systemТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Тест 2.1.2. Арифметическое n-мерное векторное пространствоСправочник (часть 1)Справочник (часть 2)Видеолекция 1.
 1.4. МатрицыQuiz 2.1.4. MatricesСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Прямоугольная декартова система координатLecture 1. Rectangular Cartesian coordinate systemТеоретический материалПрактическое занятие. Решение задач в координатахPractical lesson. Solution of problems in coordinatesЗадачи для самостоятельной работыРешения задачТест 2.2.1. Декартова система координатСправочникВидеолекция 1. Скалярное произведение векторовLecture 1. Scalar product of vectorsТеоретический материал (Часть 1)Видеолекция 2. Векторное и смешанное произведения векторовLecture 2. Vector and mixed products of vectorsПрактическое занятие 1. Скалярное произведение векторовPractical lesson 1. Scalar product of vectorsПрактическое занятие 2. Применение произведений векторов при решении задачPractical lesson 2. vector and mixed product of vectors to solve themТеоретический материал (Часть 2)Задачи для самостоятельной работы 1Решения задач 1Тест 2.2.2.(часть 1). Скалярное произведение векторов.
1.4. МатрицыQuiz 2.1.4. MatricesСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Прямоугольная декартова система координатLecture 1. Rectangular Cartesian coordinate systemТеоретический материалПрактическое занятие. Решение задач в координатахPractical lesson. Solution of problems in coordinatesЗадачи для самостоятельной работыРешения задачТест 2.2.1. Декартова система координатСправочникВидеолекция 1. Скалярное произведение векторовLecture 1. Scalar product of vectorsТеоретический материал (Часть 1)Видеолекция 2. Векторное и смешанное произведения векторовLecture 2. Vector and mixed products of vectorsПрактическое занятие 1. Скалярное произведение векторовPractical lesson 1. Scalar product of vectorsПрактическое занятие 2. Применение произведений векторов при решении задачPractical lesson 2. vector and mixed product of vectors to solve themТеоретический материал (Часть 2)Задачи для самостоятельной работы 1Решения задач 1Тест 2.2.2.(часть 1). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовЗадачи для самостоятельной работы 2Решения задач 2Тест 2.2.2. (часть2). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовСправочник (Часть 1)Справочник (Часть 2)Видеолекция. Уравнения прямой на плоскости и в пространствеLecture. Equation of a straight line on a plane and in spaceТеоретический материалПрактическое занятие 1. Уравнения прямой на плоскостиPractical lesson 1. Related to the equation of a straight line on a planeЗадачи для самостоятельной работы 1Решение задач 1Практическое занятие 2. Взаимное расположение прямыхPractical lesson 2. The relative position of straight lines.Задачи для самостоятельной работы 2Решение задач 2Тест 2.2.3. Уравнения прямойСправочникВидеолекция. Уравнение плоскости. Взаимное расположение прямой и плоскостиТеоретический материалПрактическое занятие. Уравнение плоскости. Взаимное расположение прямой и плоскости Practical lesson.
Длина вектора. Векторное произведение векторов. Смешанное произведение векторовЗадачи для самостоятельной работы 2Решения задач 2Тест 2.2.2. (часть2). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовСправочник (Часть 1)Справочник (Часть 2)Видеолекция. Уравнения прямой на плоскости и в пространствеLecture. Equation of a straight line on a plane and in spaceТеоретический материалПрактическое занятие 1. Уравнения прямой на плоскостиPractical lesson 1. Related to the equation of a straight line on a planeЗадачи для самостоятельной работы 1Решение задач 1Практическое занятие 2. Взаимное расположение прямыхPractical lesson 2. The relative position of straight lines.Задачи для самостоятельной работы 2Решение задач 2Тест 2.2.3. Уравнения прямойСправочникВидеолекция. Уравнение плоскости. Взаимное расположение прямой и плоскостиТеоретический материалПрактическое занятие. Уравнение плоскости. Взаимное расположение прямой и плоскости Practical lesson. Equation of a plane Задачи для самостоятельной работы 1Решение задач 1Задачи для самостоятельной работы 2Практическое занятие 2. Взаимное расположение плоскостейPractical lesson 2. Relative position of planesРешение задач 2Тест 2.2.4. Уравнения плоскостиСправочникВидеолекция 1. ЭллипсLecture 1. EllipseТеоретический материал Часть 1Практическое занятие 1. ЭллипсPractical lesson 1. EllipseЗадачи для самостоятельной работы 1Решение задач 1Видеолекция 2. Гипербола и параболаLecture 2. Hyperbola and parabolaТеоретический материал (Часть 2)Практическое занятие 2. Гипербола и параболаЗадачи для самостоятельной работы 2Решение задач 2Тест 2.2.5. Кривые второго порядкаСправочник (Часть 1)Справочник (Часть 2)Аттестация по модулю 2Анкета обратной связиИтоговое тестирование по курсу (1-2)Итоговое тестирование по курсу (2)Видеолекция 1. Основные понятия теории вероятностей Lecture 1. Basic concepts of probability theoryВидеолекция 2. Вероятность случайного событияLecture 2. Probability of a random eventПрактическое занятие 1.
Equation of a plane Задачи для самостоятельной работы 1Решение задач 1Задачи для самостоятельной работы 2Практическое занятие 2. Взаимное расположение плоскостейPractical lesson 2. Relative position of planesРешение задач 2Тест 2.2.4. Уравнения плоскостиСправочникВидеолекция 1. ЭллипсLecture 1. EllipseТеоретический материал Часть 1Практическое занятие 1. ЭллипсPractical lesson 1. EllipseЗадачи для самостоятельной работы 1Решение задач 1Видеолекция 2. Гипербола и параболаLecture 2. Hyperbola and parabolaТеоретический материал (Часть 2)Практическое занятие 2. Гипербола и параболаЗадачи для самостоятельной работы 2Решение задач 2Тест 2.2.5. Кривые второго порядкаСправочник (Часть 1)Справочник (Часть 2)Аттестация по модулю 2Анкета обратной связиИтоговое тестирование по курсу (1-2)Итоговое тестирование по курсу (2)Видеолекция 1. Основные понятия теории вероятностей Lecture 1. Basic concepts of probability theoryВидеолекция 2. Вероятность случайного событияLecture 2. Probability of a random eventПрактическое занятие 1. Классическая вероятностьPractical lesson 1. Classical probabilityЗадачи для самостоятельной работы (часть 1)Решения задач (часть 1)Практическое занятие 2. Операции над событиями. Practical lesson (part 2). Algebra of events. Properties of probabilitiesЗадачи для самостоятельно работы (часть 2)Решения задач (часть 2)Теоретический материалТест 3.1.1. Классическая вероятностьВидеолекция 1. Условная вероятностьLecture 1. Conditional probabilityПрактическое занятие 1. Условная вероятность. Формула полной вероятности. Формула БайесаPractical lesson 1. Conditional probability. The formula of total probability, Bayes ‘ formulaЗадачи для самостоятельной работы. Условная вероятностьРешения задач. Условная вероятностьВидеолекция 2. Повторные независимые опыты и формула БернуллиLecture 2. Repeated Independent Experiments and the Bernoulli FormulПрактическое занятие 2. Схема БернуллиPractical lesson 2. Bernoulli’s formulaЗадачи для самостоятельной работы. Схема БернуллиРешения задач. Схема БернуллиТеоретический материалТест 3.
Классическая вероятностьPractical lesson 1. Classical probabilityЗадачи для самостоятельной работы (часть 1)Решения задач (часть 1)Практическое занятие 2. Операции над событиями. Practical lesson (part 2). Algebra of events. Properties of probabilitiesЗадачи для самостоятельно работы (часть 2)Решения задач (часть 2)Теоретический материалТест 3.1.1. Классическая вероятностьВидеолекция 1. Условная вероятностьLecture 1. Conditional probabilityПрактическое занятие 1. Условная вероятность. Формула полной вероятности. Формула БайесаPractical lesson 1. Conditional probability. The formula of total probability, Bayes ‘ formulaЗадачи для самостоятельной работы. Условная вероятностьРешения задач. Условная вероятностьВидеолекция 2. Повторные независимые опыты и формула БернуллиLecture 2. Repeated Independent Experiments and the Bernoulli FormulПрактическое занятие 2. Схема БернуллиPractical lesson 2. Bernoulli’s formulaЗадачи для самостоятельной работы. Схема БернуллиРешения задач. Схема БернуллиТеоретический материалТест 3. 1.2. Условная вероятностьВидеолекция 1. Дискретные лучайные величиныLecture 1. Discrete random variablesВидеолекция 2. Числовые характеристики дискретных случайных величинПрактическое занятие. Дискретные случайные величиныPractical lesson. Discrete random variablesЗадачи для самостоятельного решенияРешения задачЛабораторная работа. Законы распределения дискретных случайных величинLaboratory work 1. Distribution Laws of Discrete Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.1. Дискретные случайные величиныВидеолекция 1. Непрерывные случайные величиныВидеолекция 2. Частные случаи распределений случайных величинLecture 2. Special cases of distributions of random variablesПрактическое занятие. Непрерывные случайные величиныPractical lesson. Continuous random variableЗадачи для самостоятельного решенияРешения задачЛабораторная работа (видео). Законы распределения непрерывных случайных величинLaboratory work (video). Distribution Laws of Continuous Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.
1.2. Условная вероятностьВидеолекция 1. Дискретные лучайные величиныLecture 1. Discrete random variablesВидеолекция 2. Числовые характеристики дискретных случайных величинПрактическое занятие. Дискретные случайные величиныPractical lesson. Discrete random variablesЗадачи для самостоятельного решенияРешения задачЛабораторная работа. Законы распределения дискретных случайных величинLaboratory work 1. Distribution Laws of Discrete Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.1. Дискретные случайные величиныВидеолекция 1. Непрерывные случайные величиныВидеолекция 2. Частные случаи распределений случайных величинLecture 2. Special cases of distributions of random variablesПрактическое занятие. Непрерывные случайные величиныPractical lesson. Continuous random variableЗадачи для самостоятельного решенияРешения задачЛабораторная работа (видео). Законы распределения непрерывных случайных величинLaboratory work (video). Distribution Laws of Continuous Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3. 2.2. Непрерывные случайные величиныТеоретический материалТест 3.3.1. Законы больших чиселВидеолекция 1. Система случайных величин (часть 1)Видеолекция 2. Система случайных величин (часть 2)Lecture 2. Systems of random variables (part 2)Практическое занятие. Система случайных величинЗадачи для самостоятельной работыРешения задачЛабораторная работаРешение задачи (лабораторная работа)Теоретический материалТест 3.4.1. Совместный закон распределенияВидеолекция 1. Характеристическая функция случайной величиныLecture 1. Characteristic function of a random variableВидеолекция 2. Свойства характеристической функции случайной величиныLecture 2. Properties of characteristic functions random variable Практическое занятие 1. Вычисление характеристической функции случайной величиныPractical lesson 1. Calculation of Characteristic Functions Практическое занятие 2. Проверка устойчивости для стандартных распределенийPractical lesson 2. Testing the robustness for standard distributions.Задачи для самостоятельного решения (часть 1)Задачи для самостоятельного решения (часть 2)Решения задач (часть 1)Решения задач (часть 2)Тест 3.
2.2. Непрерывные случайные величиныТеоретический материалТест 3.3.1. Законы больших чиселВидеолекция 1. Система случайных величин (часть 1)Видеолекция 2. Система случайных величин (часть 2)Lecture 2. Systems of random variables (part 2)Практическое занятие. Система случайных величинЗадачи для самостоятельной работыРешения задачЛабораторная работаРешение задачи (лабораторная работа)Теоретический материалТест 3.4.1. Совместный закон распределенияВидеолекция 1. Характеристическая функция случайной величиныLecture 1. Characteristic function of a random variableВидеолекция 2. Свойства характеристической функции случайной величиныLecture 2. Properties of characteristic functions random variable Практическое занятие 1. Вычисление характеристической функции случайной величиныPractical lesson 1. Calculation of Characteristic Functions Практическое занятие 2. Проверка устойчивости для стандартных распределенийPractical lesson 2. Testing the robustness for standard distributions.Задачи для самостоятельного решения (часть 1)Задачи для самостоятельного решения (часть 2)Решения задач (часть 1)Решения задач (часть 2)Тест 3. 4.2. (данное тестирование по теме 1)Видеолекция. Основные понятия математической статистикиLecture. The basic concepts of mathematical statisticsЛабораторная работа (видео). Основные понятия математической статистикиLaboratory work (video). Basic concepts of mathematical statisticsТеоретический материалЛабораторная работа. Основные понятия математической статистикиРешения задач (лабораторная работа)Тест 3.5.1. Основные понятия математической статистикиQuiz 3.5.1.Видеолекция. Статистические оценки параметров генеральной совокупности. Lecture. Statistical estimates of general population parametersЛабораторная работа 1 (видео). Статистические оценки параметров генеральной совокупностиLaboratory work 1 (video). Statistical estimators of the parameters of the populationЛабораторная работа 1. Статистические оценки параметров генеральной совокупностиРешения задач 1Лабораторная работа 2 (видео). Минимальный или оптимальный объем выборочной совокупностиLaboratory work 2(video). Minimum or optimal sample sizeЛабораторная работа 2.
4.2. (данное тестирование по теме 1)Видеолекция. Основные понятия математической статистикиLecture. The basic concepts of mathematical statisticsЛабораторная работа (видео). Основные понятия математической статистикиLaboratory work (video). Basic concepts of mathematical statisticsТеоретический материалЛабораторная работа. Основные понятия математической статистикиРешения задач (лабораторная работа)Тест 3.5.1. Основные понятия математической статистикиQuiz 3.5.1.Видеолекция. Статистические оценки параметров генеральной совокупности. Lecture. Statistical estimates of general population parametersЛабораторная работа 1 (видео). Статистические оценки параметров генеральной совокупностиLaboratory work 1 (video). Statistical estimators of the parameters of the populationЛабораторная работа 1. Статистические оценки параметров генеральной совокупностиРешения задач 1Лабораторная работа 2 (видео). Минимальный или оптимальный объем выборочной совокупностиLaboratory work 2(video). Minimum or optimal sample sizeЛабораторная работа 2. Минимальный или оптимальный объем выборочной совокупностиРешения задач 2Теоретический материалТест 3.5.2. Статистические оценкиQuiz 3.5.2Видеолекция. Зависимость между величинами. Виды зависимостейLecture. Dependence between quantities. Types of dependenciesТеоретический материал 1Лабораторная работа 1 (видео, часть 1). Парный корреляционный анализLaboratory work 1 (video, part 1). Pair correlation analysisЛабораторная работа 1. Парный корреляционный анализЛабораторная работа 1 (видео, часть 2). Множественный корреляционный анализРешение задач 1Лабораторная работа 2 (видео, часть 2). Парный регрессионный анализLaboratory work 2 (video, part 2). Paired Regression AnalysisЛабораторная работа 2. Парный регрессионный анализРешения задач 2Теоретический материал 2Тест 3.5.3. Зависимость между величинамиQuiz 3.5.3Лекция. Статистические гипотезы Теоретический материалЛабораторная работа (видео). Статистический критерий хи-квадратLaboratory work. The Chi-Square StatisticЛабораторная работа 1. Критерий хи-квадратРешения задач (Критерий хи-квадрат)Лабораторная работа 2.
Минимальный или оптимальный объем выборочной совокупностиРешения задач 2Теоретический материалТест 3.5.2. Статистические оценкиQuiz 3.5.2Видеолекция. Зависимость между величинами. Виды зависимостейLecture. Dependence between quantities. Types of dependenciesТеоретический материал 1Лабораторная работа 1 (видео, часть 1). Парный корреляционный анализLaboratory work 1 (video, part 1). Pair correlation analysisЛабораторная работа 1. Парный корреляционный анализЛабораторная работа 1 (видео, часть 2). Множественный корреляционный анализРешение задач 1Лабораторная работа 2 (видео, часть 2). Парный регрессионный анализLaboratory work 2 (video, part 2). Paired Regression AnalysisЛабораторная работа 2. Парный регрессионный анализРешения задач 2Теоретический материал 2Тест 3.5.3. Зависимость между величинамиQuiz 3.5.3Лекция. Статистические гипотезы Теоретический материалЛабораторная работа (видео). Статистический критерий хи-квадратLaboratory work. The Chi-Square StatisticЛабораторная работа 1. Критерий хи-квадратРешения задач (Критерий хи-квадрат)Лабораторная работа 2. Критерий ПирсонаЛабораторная работа (расчетная таблица)Решения задач (Критерий Пирсона)Тест 3.6.1. Проверка статистических гипотез: основные понятияQuiz 3.6.1Видеолекция. Проверка статистических гипотезLecture. Testing statistical hypothesesЛабораторная работа 1 (видео). Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейLaboratory work 1. Comparison of Sampled Population Means with Known Population VariancesЛабораторная работа 1. Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейРешения задач (лабораторная работа 1)Лабораторная работа 2 (часть 1). Сравнение средних независимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 1). Comparison of means of independent sample populations with unknown variances of general populationsЛабораторная работа 2 (часть 2). Сравнение средних зависимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 2).
Критерий ПирсонаЛабораторная работа (расчетная таблица)Решения задач (Критерий Пирсона)Тест 3.6.1. Проверка статистических гипотез: основные понятияQuiz 3.6.1Видеолекция. Проверка статистических гипотезLecture. Testing statistical hypothesesЛабораторная работа 1 (видео). Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейLaboratory work 1. Comparison of Sampled Population Means with Known Population VariancesЛабораторная работа 1. Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейРешения задач (лабораторная работа 1)Лабораторная работа 2 (часть 1). Сравнение средних независимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 1). Comparison of means of independent sample populations with unknown variances of general populationsЛабораторная работа 2 (часть 2). Сравнение средних зависимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 2). Comparison of mean dependent sample populations with unknown variances of general populationsЛабораторная работа 2. Проверка статистических гипотез о сравнении средних выборочных совокупностей, если не известны дисперсии генеральных совокупностейРешения задач (лабораторная работа 2)Теоретический материалТест 3.6.2. Проверка гипотезQuiz 3.6.2Аттестация по модулю 3Итоговое тестирование по курсу 1-2-3Итоговое тестирование по курсу для математических специальностейИтоговое тестирование по курсу (3)
Comparison of mean dependent sample populations with unknown variances of general populationsЛабораторная работа 2. Проверка статистических гипотез о сравнении средних выборочных совокупностей, если не известны дисперсии генеральных совокупностейРешения задач (лабораторная работа 2)Теоретический материалТест 3.6.2. Проверка гипотезQuiz 3.6.2Аттестация по модулю 3Итоговое тестирование по курсу 1-2-3Итоговое тестирование по курсу для математических специальностейИтоговое тестирование по курсу (3)линейная алгебра : Чулан (М)
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
| Матика |
| ||
04/11/07 |
| ||
| |||
| Brukvalub |
| |||
01/03/06 |
| |||
| ||||
| Матика |
| ||
04/11/07 |
| ||
| |||
| Brukvalub |
| |||
01/03/06 |
| |||
| ||||
| Матика |
| ||
04/11/07 |
| ||
| |||
| Brukvalub |
| |||
01/03/06 |
| |||
| ||||
| Матика |
| ||
04/11/07 |
| ||
| |||
| Матика |
| ||
04/11/07 |
| ||
| |||
| Brukvalub |
| |||
01/03/06 |
| |||
| ||||
| Матика |
| ||
04/11/07 |
| ||
| |||
| Brukvalub |
| |||
01/03/06 |
| |||
| ||||
| Матика |
| ||
04/11/07 |
| ||
| |||
| Brukvalub |
| |||
01/03/06 |
| |||
| ||||
| Матика |
| ||
04/11/07 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 14 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
10.
 3: Базовая теория однородных линейных систем
3: Базовая теория однородных линейных систем- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 9455
- Уильям Ф. Тренч
- Университет Тринити
В этом разделе мы рассматриваем однородные линейные системы \({\bf y}’= A(t){\bf y}\), где \(A=A(t)\) — непрерывная \(n\times n \) матричная функция на отрезке \((a,b)\). Теория линейных однородных систем имеет много общего с теорией линейных однородных скалярных уравнений, которую мы рассмотрели в разделах 2.1, 5.1 и 9.1.
Всякий раз, когда мы говорим о решениях \({\bf y}’=A(t){\bf y}\), мы будем иметь в виду решения на \((a,b)\). Поскольку \({\bf y}\equiv{\bf 0}\) очевидно является решением \({\bf y}’=A(t){\bf y}\), мы называем его тривиальное решение. Любое другое решение нетривиально .
Любое другое решение нетривиально .
Если \({\bf y}_1\), \({\bf y}_2\), …, \({\bf y}_n\) вектор-функции, определенные на интервале \((a,b) \) и \(c_1\), \(c_2\), …, \(c_n\) являются константами, то
\[\label{eq:10.3.1} {\bf y}=c_1{\bf y}_1+c_2{\bf y}_2+\cdots+c_n{\bf y}_n\]
представляет собой линейную комбинацию \({\bf y}_1\), \({\bf y}_2\), …,\({\bf y}_n\). Легко показать, что если \({\bf y}_1\), \({\bf y}_2\), …,\({\bf y}_n\) являются решениями \({\bf y}’ =A(t){\bf y}\) на \((a,b)\), то такова любая линейная комбинация \({\bf y}_1\), \({\bf y}_2\ ), …, \({\bf y}_n\) ( Упражнение 10.3.1 ). Мы говорим, что \(\{{\bf y}_1,{\bf y}_2,\dots,{\bf y}_n\}\) есть фундаментальных множества решений \({\bf y}’ =A(t){\bf y}\) на \((a,b)\) на, если каждое решение \({\bf y}’=A(t){\bf y}\) на \ ((a,b)\) можно записать в виде линейной комбинации \({\bf y}_1\), \({\bf y}_2\), …, \({\bf y}_n\) , как в уравнении \ref{eq:10.3.1}. В этом случае мы говорим, что уравнение \ref{eq:10. 3.1} является общим решением \({\bf y}’=A(t){\bf y}\) на \((a,b )\).
3.1} является общим решением \({\bf y}’=A(t){\bf y}\) на \((a,b )\).
Можно показать, что если \(A\) непрерывно на \((a,b)\), то \({\bf y}’=A(t){\bf y}\) имеет бесконечно много фундаментальных множеств решений на \((a,b)\) ( Упражнения 10.3.15 и 10.3.16 ). Следующее определение поможет охарактеризовать фундаментальные множества решений \({\bf y}’=A(t){\bf y}\).
Мы говорим, что множество \(\{{\bf y}_1,{\bf y}_2,\dots,{\bf y}_n\}\) \(n\)-векторных функций является линейно независимым на \((a,b)\), если единственные константы \(c_1\), \(c_2\), …, \(c_n\) такие, что
\[\label{eq:10.3.2} c_{1}y_{1}(t)+c_{2}y_{2}(t)+\cdots +c_{n}y_{n}(t) =0,\quad a являются \(c_1=c_2=\cdots=c_n=0\). Если уравнение \ref{eq:10.3.2} верно для некоторого набора констант \(c_1\), \(c_2\), …, \(c_n\), которые не все равны нулю, то \(\{{\bf y}_1,{\bf y}_2,\dots,{\bf y}_n\}\) равно линейно зависит от \((a,b)\) Следующая теорема аналогична теоремам 5. 1.3 и 9.1.2.
1.3 и 9.1.2. Теорема 10.3.1
Предположим, что матрица \(n\times n\) \(A=A(t)\) непрерывна на \((a,b)\). Тогда множество \(\{{\bf y}_1,{\bf y}_2,\dots,{\bf y}_n\}\) из \(n\) решений \({\bf y}’ =A(t){\bf y}\) на \((a,b)\) является фундаментальным множеством тогда и только тогда, когда оно линейно независимо от \((a,b)\).
Пример 10.3.1
Показать, что векторные функции 9{4t}.\end{align*}\]
Поскольку этот определитель никогда не равен нулю, \(c_1=c_2=c_3=0\).
Мы можем использовать метод из примера 10.3.1. для проверки \(n\) решений \(\{{\bf y}_1,{\bf y}_2,\dots,{\bf y}_n\}\) любой \(n\times n\) системы \({\bf y}’=A(t){\bf y}\) для линейной независимости на интервале \((a,b)\), на котором \(A\) непрерывен. Чтобы объяснить это (и для других целей позже), полезно написать линейную комбинацию \({\bf y}_1\), \({\bf y}_2\), …, \({\bf y }_n\) по-другому. Сначала запишем вектор-функции через их компоненты в виде
\[{\bf y}_1=\left[\begin{array}{c} y_{11}\\y_{21}\\ \vdots\\ y_{n1}\end{массив}\right], \quad {\bf y}_2=\left[\begin{array}{c} y_{12}\\y_{22}\\ \vdots\\ y_{n2}\end{массив}\right],\ точки,\quad {\bf y}_n=\left[\begin{array}{c} y_{1n}\\y_{2n}\\ \vdots\\ y_{nn}\end{массив}\right] . \номер\]
\номер\]
Если
\[{\bf y}=c_1{\bf y}_1+c_2{\bf y}_2+\cdots+c_n{\bf y}_n\nonumber \]
, затем
\[\begin{align*} {\bf y}&= c_1\left[\begin{array}{c} y_{11}\\y_{21}\\ \vdots\\ y_{n1}\end {массив}\right]+ c_2\left[\begin{массив}{c} y_{12}\\y_{22}\\ \vdots\\ y_{n2}\end{массив}\right]+\cdots +c_n\left[\begin{массив}{c} y_{1n}\\y_{2n}\\ \vdots\\ y_{nn}\end{массив}\right]\\[4pt] &=\left [\begin{array}{cccc} y_{11}&y_{12}&\cdots&y_{1n} \\ y_{21}&y_{22}&\cdots&y_{2n}\\ \vdots&\vdots&\ddots&\vdots \ \ y_{n1}&y_{n2}&\cdots&y_{nn} \\ \end{массив}\right]\col cn.\end{align*}\]
Это показывает, что
\[\label{eq:10.3.3} c_1{\bf y}_1+c_2{\bf y}_2+\cdots+c_n{\bf y}_n=Y{\bf c},\]
где
\[{\bf c}=\col cn\nonumber \]
и
\[\label{eq:10.3.4} Y=[{\bf y}_1\; {\bf у}_2\; \cdots\; {\bf y}_n]= \left[\begin{array}{cccc} y_{11}&y_{12}&\cdots&y_{1n} \\ y_{21}&y_{22}&\cdots&y_{2n}\ \ \vdots&\vdots&\ddots&\vdots \\ y_{n1}&y_{n2}&\cdots&y_{nn} \\ \end{массив}\right];\]
, то есть столбцы \(Y\) являются векторными функциями \({\bf y}_1,{\bf y}_2,\dots,{\bf y}_n\).
Для справки ниже обратите внимание, что
\[\begin{align} Y’&=[{\bf y}_1’\; {\bf у}_2’\; \cdots\; {\bf y}_n’]\\ &=[A{\bf y}_1\; А {\ bf у} _ 2 \; \cdots\; A{\bf y}_n]\\ &=A[{\bf y}_1\; {\bf у}_2\; \cdots\; {\bf y}_n]=AY;\end{выровнено}\]
, то есть \(Y\) удовлетворяет матричному дифференциальному уравнению
\[Y’=AY.\номер \]
Определитель \(Y\),
\[\label{eq:10.3.5} W=\left|\begin{array}{cccc} y_{11}&y_{12}&\cdots&y_{1n} \\ y_{21}&y_{22}& \cdots&y_{2n}\\ \vdots&\vdots&\ddots&\vdots \\ y_{n1}&y_{n2}&\cdots&y_{nn} \\ \end{массив}\right|\]
называется вронскианским из \(\{{\bf y}_1,{\bf y}_2,\dots,{\bf y}_n\}\). Можно показать (, упражнения 10.3.2, и , 10.3.3, ), что это определение аналогично определениям вронскиана скалярных функций, данным в разделах 5.1 и 9..1. Следующая теорема аналогична теоремам 5.1.4 и 9.1.3. Доказательство набросано в Упражнении 10.3.4 для \(n=2\) и в Упражнении 10. 3.5 для общего \(n\).
3.5 для общего \(n\).
Теорема 10.3.2 : Формула Абеля
Предположим, что \(n\times n\) матрица \(A=A(t)\) непрерывна на \((a,b),\), пусть \({\bf y}_1\ ), \({\bf y}_2\), …, \({\bf y}_n\) — решения \({\bf y}’=A(t){\bf y}\) на \ ((a,b),\) и пусть \(t_0\) находится в \((a,b)\). Тогда вронскиан функции \(\{{\bf y}_1,{\bf y}_2,\dots,{\bf y}_n\}\) равен 9t_{t_0}\big[a_{11}(s)+a_{22}(s)+\cdots+a_{nn}(s)]\, ds\right), \quad a < t < b.\ ]
Следовательно, либо \(W\) не имеет нулей в \((a,b)\), либо \(W\equiv0\) на \((a,b).\)
Примечание
Сумма диагональных элементов квадратной матрицы \(A\) называется следом матрицы \(A\) и обозначается \(\text{tr}(A)\). Таким образом, для матрицы \(n\times n\) \(A\)
\[\text{tr}(A)=a_{11}+a_{22}+\cdots a_{nn},\номер\]
и уравнение \ref{eq:10.3.6} можно записать как 9{t}\text{tr}(A(s))ds \right),\quad a Следующая теорема аналогична теоремам 5. 1.6 и 9.1.4.
1.6 и 9.1.4. Теорема 10.3.3
Предположим, что матрица \(n\times n\) \(A=A(t)\) непрерывна на \((a,b)\) и пусть \({\bf y}_1\), \ ({\bf y}_2\), …,\({\bf y}_n\) — решения \({\bf y}’=A(t){\bf y}\) на \((a ,б)\). Тогда следующие утверждения эквивалентны; то есть они либо все истинны, либо все ложны:
- Общее решение \({\bf y}’=A(t){\bf y}\) на \((a,b)\) равно \({\bf y}=c_1{\bf y }_1+c_2{\bf y}_2+\cdots+c_n{\bf y}_n\), где \(c_1\), \(c_2\), …, \(c_n\) — произвольные константы.
- \(\{{\bf y}_1,{\bf y}_2,\dots,{\bf y}_n\}\) является фундаментальным набором решений \({\bf y}’=A( t){\bf y}\) на \((a,b)\).
- \(\{{\bf y}_1,{\bf y}_2,\dots,{\bf y}_n\}\) линейно не зависит от \((a,b)\).
- Вронскиан функции \(\{{\bf y}_1,{\bf y}_2,\dots,{\bf y}_n\}\) отличен от нуля в некоторой точке \((a,b)\) .
- Вронскиан функции \(\{{\bf y}_1,{\bf y}_2,\dots,{\bf y}_n\}\) отличен от нуля во всех точках \((a,b)\) .
 {-t}}\номер\]
{-t}}\номер\]являются решениями системы постоянных коэффициентов
\[\label{eq:10.3.7} {\bf y}’ = \left[\begin{array}{cc}{-4}&{-3}\\{6}&{5}\end {массив} \справа] {\bf у}\]
на \((-\infty,\infty)\). (Подтвердить.)
- Вычисление вронскиана для \(\{{\bf y}_1,{\bf y}_2\}\) непосредственно из уравнения определения \ref{eq:10.3.5}
- Проверка формулы Абеля Уравнение \ref{eq:10.3.6} для вронскиана \(\{{\bf y}_1,{\bf y}_2\}\). 9{-t}\end{массив}\right] \left[\begin{array}{c}c_1\\c_2\end{массив}\right].\]
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Уильям Ф. Тренч
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 3,0
- Показать страницу TOC
- нет
- Теги
- Теорема Абеля
- источник@https://digitalcommons.
 trinity.edu/mono/9
trinity.edu/mono/9 - Вронскиан
- Чтобы найти общее решение однородное линейное уравнение второго порядка, нужно найти два линейно независимые решения и . Все решения линейные комбинации из них: .
- Чтобы найти общее решение
неоднородного линейного уравнения второго порядка, необходимо найти
одно его решение и два линейно независимых
решений и соответствующего однородного уравнения.
 Все решения имеют вид
.
Все решения имеют вид
.
Раствор d
Установка \(t=0\) в уравнении \ref{eq:10.3.10} и наложение начального условия в уравнении \ref{eq:10.3.8} дает
\[c_1\left[\begin{array}{r}-1 \\2\end{массив}\right]+c_2 \left[\begin{array}{r}-1 \\1\end{массив }\right]= \left[\begin{array}{r} 4 \\-5\end{массив}\right].\nonumber \]
Итак,
\[\begin{aligned} -c_1-c_2&=\phantom{-}4 \\ 2c_1+c_2&=-5.
 \end{aligned}\nonumber \] 9{-t} \конец{массив}\справа]\номер\]
\end{aligned}\nonumber \] 9{-t} \конец{массив}\справа]\номер\]как решение уравнения \ref{eq:10.3.8}.
Эта страница под названием 10.3: Базовая теория однородных линейных систем распространяется под лицензией CC BY-NC-SA 3.0 и была создана, изменена и/или курирована Уильямом Ф. Тренчем посредством исходного контента, который был отредактирован в соответствии со стилем и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.
Линейные уравнения второго порядка
Линейные уравнения второго порядка Линейное дифференциальное уравнение второго порядка можно записать в виде
где , и – произвольные функции, а – независимая переменная. Особенно важно являются уравнениями с постоянными коэффициентами, где и (но не обязательно ) – константы, а однородные уравнения, где – .Теория линейных дифференциальных уравнений тесно связана с теория систем линейных уравнений в линейной алгебре. Как результат этого теории, мы сможем многое сказать о структуре растворов. В частности, наши основные результаты будут следующими:
Пример: Одно решение неоднородного дифференциала уравнение. Два линейно независимых решения уравнения однородное уравнение и . Были сейчас не беспокоюсь о том, как получить эти решения, но это легко чтобы убедиться, что они являются решениями. Вывод будет заключаться в том, что общее решение является .
Чтобы дифференциальное уравнение выглядело больше похоже на линейную алгебру, мы определяем линейный оператор:
Это линейное преобразование в смысле линейной алгебры, но «векторы», с которыми он работает, являются функциями. То есть, если есть дважды дифференцируемая функция, то есть функция
Тот факт, что это линейный оператор, означает, что для любого дважды дифференцируемые функции и и константы и ,
Используя линейный оператор , линейное дифференциальное уравнение второго порядка написано . Это разделяет следующие свойства с матрицей уравнение:
Теорема: Предположим, есть одно решение уравнения . затем
решения состоят из всех функций вида
где
решение однородного уравнения .
Решения однородного уравнения образуют векторное пространство. Доказательство: Если есть любое решение однородного уравнения, то
. Обратно, если есть любое решение
, тогда
так с решением однородного уравнения.
затем
решения состоят из всех функций вида
где
решение однородного уравнения .
Решения однородного уравнения образуют векторное пространство. Доказательство: Если есть любое решение однородного уравнения, то
. Обратно, если есть любое решение
, тогда
так с решением однородного уравнения.Чтобы показать, что решения однородного уравнения образуют векторное пространство, нам нужно показать, что если и любые решения и и константы, то также является решением. Но это легко с
В качестве начальных условий для уравнения второго порядка необходимо задать как значение, так и его производная в какой-то момент. Мы тогда иметь следующее Теорема существования и единственности для линейных уравнений второго порядка:
Теорема: Предположим , и непрерывны на некотором интервале . Учитывая любой с и любые действительные числа и , существует ровно одно решение дифференциального уравнения с начальными условиями , , определено для .
(Мы не будем это доказывать)
Пример: Рассмотрим еще раз. Мы знаем это является решением для любых констант и . Мы можем удовлетворить любые начальные условия при используя функцию этой формы: и так что мы взял бы и . По части уникальности теоремы существования и единственности, это дает нам единственное решение удовлетворяющие этим начальным условиям. Поскольку каждое решение должно удовлетворять некоторых начальных условиях при можно заключить, что все решения имеют форму .
В нашем примере решения однородного уравнения все функции вида . Они образуют векторное пространство. Это на самом деле двумерное векторное пространство: каждая из этих функций записывается ровно одним способом как линейная комбинация двух функций и которые составляют основу пространства. Они известны как фундаментальный набор решений. Напомним из линейной алгебры:
Определение: Набор векторов линейно независим если единственный способ написать линейную комбинацию со всеми скалярами .
Обратите внимание, что в нашем случае векторы являются функциями, а скаляры константы; «’ означает для всех . Для набора из двух функций легко получить линейную независимость. проверить: они линейно независимы, если только один из них не является константой кратно другому.
Определение: Базис векторного пространства решений второго порядка однородное линейное уравнение называется фундаментальный набор решений уравнение.
Теорема: Векторное пространство решений однородного линейного уравнения второго порядка имеет вид двумерный. Таким образом, фундаментальный набор решений уравнения состоит из двух линейно независимых решений.Доказательство: Это следствие теоремы существования и единственности. Возьмем любой в интервале, где и определены. Пусть – решение уравнения с начальными условиями , . Пусть решение с начальное состояние , . Эти линейно независимы (любая постоянная кратное has и любое постоянное кратное из имеет).


 05.2008, 20:18
05.2008, 20:18  05.2008, 21:16
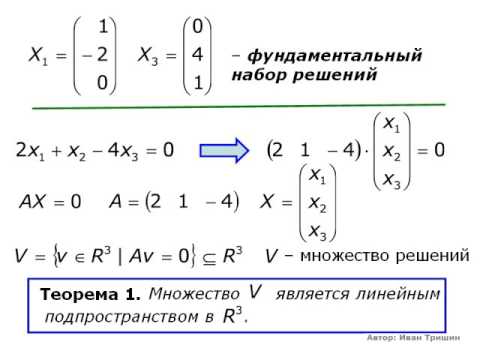
05.2008, 21:16  с.р. неизвестно какой системы
с.р. неизвестно какой системы  — базисные неизвестные, — свободный
— базисные неизвестные, — свободный  Исключив параметры, Вы и получите требуемую систему уравнений.
Исключив параметры, Вы и получите требуемую систему уравнений.

 е. мне нужно решить систему уравнений?
е. мне нужно решить систему уравнений?  линейной комбинацией одного решения, поэтому столбцы матрицы должны быть ЛЗ, т.е. ранг должен равен 1.
линейной комбинацией одного решения, поэтому столбцы матрицы должны быть ЛЗ, т.е. ранг должен равен 1.  Значит, линейная оболочка трехмерна. Поэтому должно быть одно
Значит, линейная оболочка трехмерна. Поэтому должно быть одно Но Вы молчали, я подумал, что Вы его не приняли за правильное.
Но Вы молчали, я подумал, что Вы его не приняли за правильное. к у меня фундаментальная система состоит из одной строки , то однородная система уравнений равна
к у меня фундаментальная система состоит из одной строки , то однородная система уравнений равна Спасибо Вам. Я понял, но показалось слишком просто. Осталось разобраться с базисом подпространства
Спасибо Вам. Я понял, но показалось слишком просто. Осталось разобраться с базисом подпространства 05.2008, 21:37
05.2008, 21:37  {-t}}\номер\]
{-t}}\номер\] \end{aligned}\nonumber \] 9{-t} \конец{массив}\справа]\номер\]
\end{aligned}\nonumber \] 9{-t} \конец{массив}\справа]\номер\] trinity.edu/mono/9
trinity.edu/mono/9 Все решения имеют вид
.
Все решения имеют вид
.  затем
решения состоят из всех функций вида
где
решение однородного уравнения .
Решения однородного уравнения образуют векторное пространство. Доказательство: Если есть любое решение однородного уравнения, то
. Обратно, если есть любое решение
, тогда
так с решением однородного уравнения.
затем
решения состоят из всех функций вида
где
решение однородного уравнения .
Решения однородного уравнения образуют векторное пространство. Доказательство: Если есть любое решение однородного уравнения, то
. Обратно, если есть любое решение
, тогда
так с решением однородного уравнения.

