Найти каноническую систему координат и каноническое уравнение: Общее уравнение кривой второго порядка. Приведение общего уравнения кривой второго порядка к каноническому виду.

alexxlab / / Разное

Содержание

Поверхности второго порядка. Канонические уравнения поверхностей второго порядка

      б) ;

      в) ;

      г) ;

      д) ;

      е) .

§ 8.5. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА

      Геометрическое место точек 3 – мерного пространства, координаты которых в некоторой прямоугольной системе координат  удовлетворяют уравнению

                                         (8.5.1)

где хотя бы один из коэффициентов  не равен нулю, называется поверхностью второго порядка.

      Для любой поверхности второго порядка существует прямоугольная система координат , в которой уравнение этой поверхности имеет один из следующих 17 видов:

      1) эллипсоид (рис. 8.4);

      2) мнимый эллипсоид ;

      3) однополостный гиперболоид (рис. 8.5);

      4) двуполостный гиперболоид (рис. 8.6);

      5) конус (рис. 8.7);

      6) мнимый конус

;

      7) эллиптический параболоид (рис. 8.8);

      8) гиперболический параболоид (рис. 8.9);

      9) эллиптический цилиндр (рис. 8.10);

      10) мнимый эллиптический цилиндр ;

      11) гиперболический цилиндр (рис. 8.11);

      12) параболический цилиндр (рис. 8.12);

      13) пара пересекающихся плоскостей ;

      14) пара мнимых пересекающихся плоскостей ;

      15) пара параллельных плоскостей ;

      16) пара мнимых параллельных плоскостей ;

      17) пара совпадающих плоскостей .

      Уравнения 1) – 17) называются каноническими уравнениями поверхностей второго порядка.

 

                              Рис. 8.4                                                    Рис. 8.5


                       Рис. 8.6                                                       Рис. 8.7

 

 

                              Рис. 8.8                                                 Рис. 8.10 

                                                          Рис. 8.9

 

                   Рис. 8.11                                                          Рис. 8.12

      При преобразовании уравнения поверхности второго порядка (8.5.1) можно, как и в случае кривой второго порядка, использовать инварианты.

Инвариантами поверхностей второго порядка являются

          ,

          ,

          ,

          .

Их значения не меняются при повороте и параллельном переносе осей координат.

      Пример 1. Поверхность задана уравнением в прямоугольной системе координат

      .

Найдите каноническую систему координат и каноническое уравнение этой поверхности. Определите тип поверхности.

      Решение. Найдем сначала ортогональное преобразование переменных, приводящее матрицу А квадратичной формы  к диагональному виду.

      .

      Ее характеристический многочлен

.

Следовательно, матрица А имеет собственные значения   .

      Для нахождения собственных векторов матрицы А решаем однородные системы линейных уравнений с матрицами  соответственно и выделяем по одному ненулевому решению:

, 

                    ;

,     

              ;

,    

                    .

Векторы  ортогональны друг другу как собственные векторы симметричной матрицы, соответствующие различным собственным значениям. Нормируя их, получаем

      ,

      ,

     

и матрицу перехода Р к новому ортонормированному базису

      .

      Проверим правильность нахождения матрицы Р:

Матрица Р найдена верно.

      Применяя к исходному уравнению ортогональное преобразование координат

      ,

получаем новое уравнение поверхности в прямоугольной системе координат со старым центром О и направляющими векторами :

     

     

     

        

         .

      Выполняя параллельный перенос системы координат  по формулам

     

приходим к уравнению

     

или

      .

Это – каноническое уравнение двуполостного гиперболоида в прямоугольной системе координат .

      Вычислим координаты начала  канонической системы координат в старой прямоугольной системе координат. Поскольку

      ,

      .

     

Пример 2. Исследуйте поверхность второго порядка, заданную в прямоугольной системе координат уравнением

      .

      Решение. Начнем с приведения квадратичной формы  к каноническому виду. Матрицей этой квадратичной формы является матрица

Приведение нецентральной линии к каноническому виду



И сейчас мы, по сути, разберём частный случай универсального метода решения, который вкратце состоит в следующем:

На первом шаге выясняется угол поворота системы  – угол ТАКОЙ, чтобы в новой прямоугольной системе координат  исходное уравнение исследуемой линии  приняло вид:

На втором шаге выделяются полные квадраты (при необходимости) и проводится параллельный перенос системы  началом в точку  –  такую, чтобы в итоговой системе координат  получилось уравнение , от которого до канонической формы рукой подать.

Должен отметить неудачные обозначения со штрихами, но так принято практически во всех учебниках, и поэтому я не буду отклоняться от стандарта. Штрихи, как вы поняли, к производным никакого отношения не имеют. В предыдущем параграфе, к слову, я намеренно использовал обозначения   вместо  и  чтобы не привить «чайникам» отвращение к теме.

Таким образом, универсальный способ приведения к линии 2-го порядка к каноническому виду предполагает два последовательных преобразования прямоугольной системы координат – поворот и параллельный перенос:
 

Как, наверное, вы уже догадались и горестно вздохнули, удобный метод инвариантов позволял получить то же самое «одним махом»:

Но в параболическом случае мы вынуждены выехать с тихой просёлочной дороги метода инвариантов на оживлённую автостраду общего способа решения:

Задача 113

Привести уравнение линии второго порядка к каноническому виду

Выполнить чертёж.

Решение: в первую очередь выясним тип линии. Вычислим определитель, составленный из коэффициентов :
, значит, у нас нецентральная линия и это может быть или парабола, или пара параллельных прямых (действительных либо мнимых), или пара совпавших прямых.

1) Осуществим поворот исходной системы координат  ТАК – чтобы в новой системе   получить уравнение вида  (без слагаемого, «отвечающего» за поворот).
Искомый угол поворота найдём по формуле:
 или

Внимание! Данная формула справедлива только для параболического случая!

В нашем примере: .

Очевидно, что , но здесь не всё так просто. Наверняка многие обратили внимание на тот факт, что если линию 2-го порядка (например, гиперболу) повернуть на 180 градусов, то она совпадёт сама с собой. Исключение составляет капризная парабола, ветви которой развернутся в противоположную сторону. А парабола у нас вполне может нарисоваться, поэтому, необходимо взять на заметку ещё один угол: , или, что то же самое: .

Продолжаем:

Если осуществляется поворот прямоугольной системы координат  на произвольный угол  и переход к новой системе координат , то формулы перехода от старых координат к новым координатам выражается следующей системой:
, где «альфа» – угол данного поворота.
Из тригонометрических формул  нетрудно выразить синус и косинус через известный нам тангенс, однако выражения получатся

не однозначными:

И сложившейся ситуации вполне прагматичным решением будет привлечь на помощь метод научного практического тыка. Не теряя времени, начинаем работать с углом  и используем формулы . В результате дальнейших действий может получиться неканоническое уравнение (а это возможно в единственном случае – когда исследуемое уравнение задаёт параболу и она оказывается развёрнутой в другую сторону).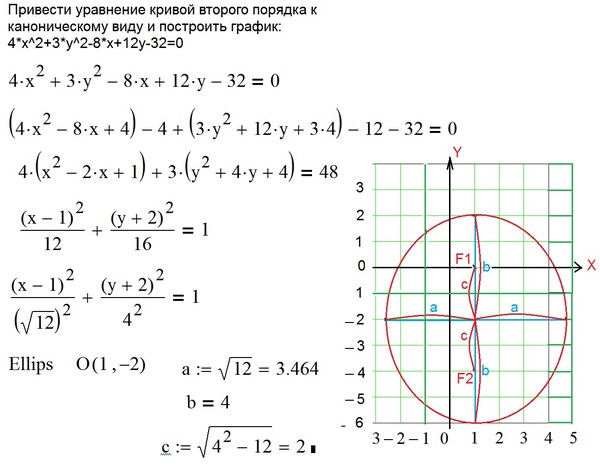 Тогда следует рассмотреть противоположный угол поворота  системы координат, при этом значение тангенса угла останется тем же самым: , но формулы сменят знаки: .

Итак, для угла  выбираем первый комплект формул и находим:

Подставим найденные значения  в аналитические выражения поворота :

Подставляем  и  (не пугаемся) в исходное уравнение :
 

Теперь нужно возвести в квадраты, раскрыть все скобки,… но что-то не хочется. Для нецентральной линии существует эксклюзивная «фишка»: в результате рассматриваемой подстановки сумма  упрощается до , где  – старый знакомый инвариант. Таким образом, громоздкая сумма первых трёх слагаемых превращается в :

Внимательно раскрываем скобки и приводим подобные слагаемые. И НЕ ТЕРЯЕМ ШТРИХИ:

И по всем признакам получается как раз парабола. Сократим каждое слагаемое на 2 и перебросим некоторые из них в правую часть:

Перед слагаемым, содержащим «икс штрих», нарисовался знак минус, и это плохо. Для лучшего понимания проиллюстрирую выполненное действие готовым чертежом:
В результате поворота исходной системы координат  вокруг точки  на 45 градусов, мы перешли от уравнения  к уравнению  в новой системе координат . Но загвоздка состоит в том, что ветви параболы направлены «в противоход» оси  (наклоните головы влево на 45 градусов), о чём нам и сообщил знак «минус» при переменной  нового уравнения.

С углом не повезло…, что делать?

Если вы уже оформили решение на чистовик (что очень вероятно), то поступаем хитро. Невозмутимо выделяем в полученном уравнении полный квадрат и представляем его в виде :

Теперь осуществляем поворот системы  ещё на  радиан (180 градусов) против часовой стрелки:
 При таком «довороте» меняется знак у «иксовой» части уравнения, а также знаки внутри скобок:

Проведём физкульт-разминку и заодно спасём от онемения некоторые части тела 🙂 Пожалуйста, встаньте лицом к монитору и наклонитесь вправо на 90 градусов. Теперь поверните голову ещё на 45 градусов в том же направлении и полюбуйтесь почти канонической параболой.

Если же решение ещё не оформлено на чистовик, то можно сразу выбрать угол , тангенс которого тоже равен единице: , и подставить это значение во второй комплект формул:
, после чего «проворачиваем» тот же алгоритм и получаем уравнение .

2) Шаг второй, параллельный перенос системы . Полный квадрат у нас уже выделен:  и из этого уравнения следует, что в новой системе  вершина параболы имеет координаты  (смотрим на чертёж под углом ):
Осуществим параллельный перенос системы  в точку , то есть  перейдём к новой системе координат .

Аналитически это действие выражается заменами , в результате которых получается долгожданное каноническое уравнение:

Вновь наклонитесь вправо на  и в «позе страуса» хорошенько осмыслите выполненные действия 🙂

Ответ: данная линия представляет собой параболу  – в системе координат , которая получена  поворотом системы  вокруг своего начала на угол   и её параллельным переносом в точку .

Интересно отметить, что для параболы метод инвариантов, хоть и не работает, но тоже позволяет найти её  каноническое уравнение. Во-первых, полезно иметь в виду следующий характеристический признак: уравнение линии 2-го порядка, инварианты которого удовлетворяют условиям , задаёт параболу и только её.

Представьте, что вы видите уравнение  в первый раз. Да… с оттенком черного юмора получилась фраза =) Выпишем  коэффициенты  и вычислим инварианты:

, следовательно, данное уравнение определяет именно параболу, а не какую-то другую линию.

И, во-вторых, найденные инварианты позволяют найти фокальный параметр  параболы  по формуле:

Таким образом:

Желающие могут использовать данный путь для самопроверки или даже в качестве основного решения в критической ситуации – когда не получается найти уравнение параболы стандартным способом, но жизненно важно «родить» хоть что-то.

Следующий пример для самостоятельной разработки:

Задача 114

Привести уравнение линии второго порядка к каноническому виду
, выполнить чертёж, на котором отразить все преобразования системы координат.

Примерный образец чистового оформления задачи в конце книги. 

Следует отметить, что на практике достаточно популярна урезанная версия задачи. Случай, когда нужно выполнять только параллельный перенос, досконально изучен в предыдущих параграфах, но бывает и так, что необходимо осуществить только поворот системы координат. Так, например, в уравнении  отсутствуют слагаемые, «отвечающие» за параллельный перенос. Угол поворота системы координат находится элементарно: , и, более того, с помощью магической плюшки  легко узнать итоговое уравнение:

  – две параллельные прямые в системе , которая получена поворотом системы  на угол .

Также полезно знать, что вырожденное уравнение параболического типа несложно выразить в явном виде и в исходной системе координат, поскольку проходят тривиальные алгебраические преобразования. Так, для того же уравнения :

Полученный результат удобно использовать для проверки и выполнения чертежа.

Что касается инвариантов, то дела тут обстоят хуже. Если для параболы мы ещё смогли «вытянуть» некоторую информацию из инвариантов, то здесь будем созерцать малополезный набор .

Итак, систематизируем порядок действий в параболическом случае:

1) Из формулы  либо  находим угол поворота исходной системы координат :

2) Для данного угла «альфа» рассчитываем . При этом проводим максимальные упрощения: выносим из-под корней всё, что можно вынести, и избавляемся от многоэтажных дробей, если таковые образовались.

3) Подставляем найденные значения  в формулы поворота .

4) Подставляем найденные выражения   в исходное уравнение , внимательно раскрываем все скобки и приводим подобные слагаемые, в результате чего в новой системе координат  должно получиться уравнение вида , где .

4*) Примерно в 15% случаев может получиться уравнение, которое определяет параболу, развёрнутую относительно своего канонического положения (положительного направления оси ) на 180 градусов. Тогда следует использовать хитрый план или  вернуться к Пункту 2 алгоритма: рассмотреть противоположный угол поворота  и использовать формулы , не забывая, что само значение тангенса осталось таким же: .

5) В полученном уравнении  выделяем полный квадрат (если необходимо), в результате чего должно получиться уравнение вида , где  – некоторые константы. И, наконец, после параллельного переноса системы координат  началом в точку  (замен  и перехода к окончательной системе координат ) наша цель достигнута:  – «допиливаем» уравнение до канонического вида.

6) Чертёж. Если совсем тяжко, пойдёт схематический, но проявите аккуратность.
И в заключение главы коротко об общем алгоритме решения, который годится для всех случаев, и из которого, собственно, следуют все рассмотренные выше схемы:

3.8.3. Универсальный метод приведения

3.8.1. Приведение уравнения центральной линии. Метод инвариантов

| Оглавление |



Автор: Aлeксaндр Eмeлин


15.3: Канонические преобразования в гамильтоновой механике

  1. Последнее обновление
  2. Сохранить как PDF
  • Идентификатор страницы
    9651
    • Дуглас Клайн
    • Университет Рочестера

    Гамильтонова механика — это особенно элегантный и мощный способ вывода уравнений движения для сложных систем. К сожалению, интегрирование уравнений движения для получения решения может оказаться сложной задачей. Гамильтон осознавал эту трудность, поэтому он предложил использовать производящие функции для выполнения канонических преобразований, которые переводят уравнения в известную разрешимую форму. Якоби, современный математик, признал важность новаторских разработок Гамильтона в гамильтоновой механике, и поэтому он разработал сложную математическую основу для использования формализма производящей функции для выполнения канонических преобразований, необходимых для решения уравнений движения Гамильтона.

    В формулировке Лагранжа преобразование координат \((q_i, \dot{q}_i)\) в циклические обобщенные координаты \((Q_i, \dot{Q}_i)\) упрощает нахождение уравнений движения Эйлера-Лагранжа . Для гамильтоновой формулировки понятие преобразования координат расширено и включает одновременное каноническое преобразование как пространственных координат \(q_i\), так и сопряженных импульсов \(p_i\) от \((q_i, p_i)\) до \(( Q_i, P_i)\), где обе канонические переменные обрабатываются одинаково при преобразовании. По сравнению с лагранжевой механикой, в гамильтоновой механике вдвое больше переменных, что является преимуществом, а не недостатком, поскольку расширяет область возможных канонических преобразований.

    Преимущество гамильтоновой механики состоит в том, что производящие функции можно использовать для выполнения канонических преобразований для поиска решений, что позволяет избежать прямого интегрирования. Канонические преобразования являются основой гамильтоновой механики; они лежат в основе теории Гамильтона-Якоби и теории переменных угла действия, которые являются мощным средством использования гамильтоновой механики для решения проблем в физике и технике. Концепция, лежащая в основе канонических преобразований, заключается в том, что если уравнения движения упрощаются за счет использования нового набора обобщенных переменных \((\mathbf{Q},\mathbf{P})\), по сравнению с использованием исходного набора переменных \ ((\mathbf{q},\mathbf{p})\), то преимущество получено. Решение, выраженное через обобщенные переменные \((\mathbf{Q},\mathbf{P})\), может быть преобразовано обратно, чтобы выразить решение через исходные координаты, \((\mathbf{q },\mathbf{p})\).

    Будет рассмотрено только специализированное подмножество преобразований, а именно канонических преобразований , сохраняющих каноническую форму уравнений движения Гамильтона. То есть, учитывая, что исходный набор переменных \((q_i, p_i)\) удовлетворяет уравнениям Гамильтона

    \[\mathbf{\dot{q}} = \frac{\partial H (\mathbf{q},\mathbf{p}, t)}{\partial \mathbf{p}} \quad — \mathbf{ \dot{p}} = \frac{\partial H (\mathbf{q},\mathbf{p}, t)}{\partial \mathbf{q}} \label{15.71}\]

    для некоторого гамильтониана \(H(\mathbf{q},\mathbf{p}, t)\), то преобразование к координатам \(Q_i(q_k,p_k, t), P_i (q_k, p_k, t)\ ) является каноническим тогда и только тогда, когда существует функция \(\mathcal{H}(\mathbf{Q},\mathbf{P}, t)\) такая, что \(\mathbf{P}\) и \( \mathbf{Q}\) по-прежнему подчиняются уравнениям Гамильтона. То есть

    \[\mathbf{\dot{Q}} = \frac{\partial\mathcal{H}(\mathbf{Q},\mathbf{P}, t)}{\partial \mathbf{P}} \quad − \ mathbf {\ dot {P}} = \ frac {\ partial \ mathcal {H} (\ mathbf {Q}, \ mathbf {P}, t)} {\ partial \ mathbf {Q}} \ label {15,72 }\]

    , где \(\mathcal{H}(\mathbf{Q},\mathbf{P}, t)\) играет роль гамильтониана для новых переменных. {t_2}_ {t_1} [\mathbf{p} \cdot \mathbf{\dot{q}} — H(\mathbf{q},\mathbf{p}, t)] dt = 0 \label{15,73}\] 9{t_2}_{t_1} \left[ \mathbf{P} \cdot \mathbf{\dot{Q}} — \mathcal{H}(\mathbf{Q},\mathbf{P}, t) \right] дт = 0 \метка{15.74}\]

    Обсуждение калибровочно-инвариантных лагранжианов, глава \(9.3\), показало, что \(L\) и \(\mathcal{L}\) могут быть связаны полной производной по времени производящей функции \(F\) где

    \[\frac{dF}{ dt} = \mathcal{L} — L \label{15,75}\]

    Производящая функция \(F\) может быть любой корректной функцией с непрерывными вторыми производными как от старой, так и от новой канонических переменных \(\mathbf{p}\), \(\mathbf{q}\), \( \mathbf{P}\), \(\mathbf{Q}\) и \(t\). Таким образом, подынтегральные выражения \ref{15.73} и \ref{15.74} связаны соотношением

    \[\mathbf{p} \cdot \mathbf{\dot{q}} — H(\mathbf{q},\mathbf{p}, t) = \lambda \left[ \mathbf{P} \cdot \ mathbf{\dot{Q}} — \mathcal{H}(\mathbf{Q},\mathbf{P}, t) \right] + \frac{dF}{dt} \label{15,76}\]

    , где \(\lambda\) — возможное масштабное преобразование. Преобразование масштаба, такое как изменение единиц измерения, тривиально и предполагается, что оно поглощается координатами, что дает \(\lambda = 1\). Предположим, что \(\lambda \neq 1\) называется расширенным каноническим преобразованием.

    Производящие функции

    Производящая функция \(F\) должна быть выбрана таким образом, чтобы преобразование от начальных переменных \(( \mathbf{q},\mathbf{p})\) к конечным переменным \((\ mathbf{Q},\mathbf{P})\) является каноническим преобразованием. Выбранная производящая функция вносит вклад в \ref{15.76} только в том случае, если она является функцией старых и новых переменных. Четыре возможных типа производящих функций первого рода: \(F_1(\mathbf{q}, \mathbf{Q}, t)\), \(F_2(\mathbf{q},\mathbf{P}, t)\), \(F_3(\mathbf{p}, \mathbf{Q}, t)\) и \(F_4(\mathbf{p}, \mathbf{P}, t)\). Эти четыре производящие функции приводят к относительно простым каноническим преобразованиям, показанным ниже.

    Тип 1: \(F = F_1(\mathbf{q}, \mathbf{Q},t)\):

    Полная производная производящей функции по времени \(F = F_1(\mathbf{q}, \mathbf{Q},t)\) определяется как

    \[\frac{dF(\mathbf{q}, \mathbf{Q},t)}{dt} = \left[ \frac{\partial F_1 (\mathbf{q}, \mathbf{Q},t)}{\partial \mathbf{q}} \cdot \mathbf{\dot{q}} + \frac{\partial F_1(\mathbf{q}, \mathbf{Q},t)}{\partial \mathbf{Q}} \cdot \mathbf{\dot{Q}} \right] + \frac{\partial F_1(\mathbf{q}, \mathbf{Q },t) }{\partial t} \label{15. 77}\]

    Вставить уравнение \ref{15.77} в уравнение \ref{15.76} и предположить, что тривиальный масштабный коэффициент \(\lambda = 1\), тогда

    \[\left[ \mathbf{p} − \frac{ \partial F_1(\mathbf{q}, \mathbf{Q},t)}{\partial \mathbf{q}} \right] \cdot \mathbf{\dot{q}} — H(\mathbf{q} ,\mathbf{p}, t) = \left[\mathbf{P} + \frac{\partial F_1(\mathbf{q}, \mathbf{Q},t)}{\partial \mathbf{Q}} \right] \cdot \mathbf{\dot{Q}} — \mathcal{H}(\mathbf{Q},\mathbf{P}, t) + \frac{\partial F_1(\mathbf{q}, \ mathbf{Q},t) }{\partial t} \nonumber\]

    Предположим, что производящая функция \(F_1\) определяет канонические переменные \(\mathbf{p}\) и \(\mathbf{P}\) равными

    \[\mathbf{p} = \frac{ \partial F_1(\mathbf{q}, \mathbf{Q},t)}{\partial \mathbf{q}} \qquad \mathbf{P} = -\frac{\partial F_1(\mathbf{q}, \mathbf{Q},t)}{ \partial \mathbf{Q}} \label{15.78}\]

    , то члены в каждой квадратной скобке сокращаются, что приводит к требуемому каноническому преобразованию

    \[\mathcal{H }(\mathbf{Q},\mathbf{P}, t) = H(\mathbf{q},\mathbf{p}, t) + \frac{\partial F_1(\mathbf{q}, \mathbf{ Q},t)}{ \partial t} \label{15. 79}\]

    Тип 2: \(F = F_2(\mathbf{q},\mathbf{P},t) − \mathbf{Q} \cdot \mathbf{P}\):

    Полная производная по времени производящей функции \(F = F_2(\mathbf{q},\mathbf{P},t)−\mathbf{Q} \cdot \mathbf{P}\) задается как

    \[\frac{dF }{ dt} = \ left [ \ frac {\ partial F_2 (\ mathbf {q}, \ mathbf {P}, t)} {\ partial \ mathbf {q}} \ cdot \ mathbf {\ dot {q}} + \frac{\partial F_2(\mathbf{q},\mathbf{P},t)}{\partial \mathbf{P}} \cdot \mathbf{\dot{p}} — \mathbf{P} \ cdot \mathbf{\dot{Q}} — \mathbf{\dot{P}} \cdot \mathbf{Q} \right] + \frac{\partial F_2(\mathbf{q},\mathbf{P}, t)}{ \partial t} \label{15.80}\]

    Вставьте это в уравнение \ref{15.76} и предположите, что тривиальный масштабный коэффициент \(\lambda = 1\), тогда

    \[\left( \mathbf{p} — \frac{\partial F_2(\ mathbf{q},\mathbf{P},t)}{\partial \mathbf{q}} \right) \cdot \mathbf{\dot{q}} — H(\mathbf{q},\mathbf{p }, t) = \mathbf{P} \cdot \mathbf{\dot{Q}} — \mathbf{P} \cdot \mathbf{\dot{Q}} + \left[\frac{\partial F_2(\ mathbf{q},\mathbf{P},t)}{\partial \mathbf{P}} — \mathbf{Q} \right] \cdot \mathbf{\dot{P}} — \mathcal{H}( \mathbf{Q},\mathbf{P}, t) + \frac{\partial F_2(\mathbf{q},\mathbf{P},t)}{\partial t} \nonumber\]

    Предположим, что производящая функция \(F_2\) определяет канонические переменные \(\mathbf{p}\) и \(\mathbf{Q}\) равными

    \[\mathbf{p} = \frac{ \partial F_2(\mathbf{q},\mathbf{P},t)}{\partial \mathbf{q}} \qquad \mathbf{Q} = \frac{\partial F_2(\mathbf{q},\ mathbf{P},t) }{\partial \mathbf{P}} \label{15. 81}\]

    , то члены в скобках сокращаются, что приводит к требуемому преобразованию

    \[\mathcal{H}(\mathbf {Q},\mathbf{P}, t) = H(\mathbf{q},\mathbf{p}, t) + \frac{\partial F_2(\mathbf{q},\mathbf{P},t) )}{ \partial t} \label{15.82}\]

    Тип 3: \(F = F_3(\mathbf{p}, \mathbf{Q},t) + \mathbf{q} \cdot \mathbf{p}\):

    Полная производная по времени производящей функция \(F = F_3(\mathbf{p}, \mathbf{Q},t) + \mathbf{q} \cdot \mathbf{p}\) задается как

    \[\frac{dF }{dt } = \left[ \frac{\partial F_3(\mathbf{p}, \mathbf{Q},t)}{\partial \mathbf{p}} \cdot \mathbf{\dot{p}} + \frac {\ partial F_3 (\ mathbf {p}, \ mathbf {Q}, t)} {\ partial \ mathbf {Q}} \ cdot \ mathbf {\ dot {Q}} + \ mathbf {\ dot {q}} \cdot \mathbf{p} + \mathbf{q} \cdot \mathbf{\dot{p}} \right] + \frac{\partial F_3(\mathbf{p}, \mathbf{Q},t)} { \partial t} \label{15.83}\]

    Вставьте это в уравнение \ref{15.76} и предположите, что тривиальный масштабный коэффициент \(\lambda = 1\), тогда

    \[− \left[ \mathbf{q}+ \frac{\partial F_3( \mathbf{p}, \mathbf{Q},t)}{\partial \mathbf{p}} \right] \cdot \mathbf{\dot{p}} — H(\mathbf{q},\mathbf{ p}, t) = \left[ \mathbf{P}+ \frac{\partial F_3(\mathbf{p}, \mathbf{Q},t)}{\partial \mathbf{Q}} \right] \ cdot \mathbf{\dot{Q}} — \mathcal{H}(\mathbf{Q},\mathbf{P}, t) + \frac{\partial F_3(\mathbf{p}, \mathbf{Q} ,t)}{ \partial t} \nonumber\]

    Предположим, что производящая функция \(F_3\) определяет канонические переменные \(\mathbf{q}\) и \(\mathbf{P}\) равными

    \[\mathbf{q} = −\frac {\ partial F_3 (\ mathbf {p}, \ mathbf {Q}, t)} {\ partial \ mathbf {p}} \ qquad \ mathbf {P} = — \ frac {\ partial F_3 (\ mathbf {p} , \mathbf{Q},t)}{ \partial \mathbf{Q}} \label{15. 84}\]

    то члены в скобках сокращаются, что приводит к требуемому преобразованию

    \[\mathcal{H}( \mathbf{Q},\mathbf{P}, t) = H(\mathbf{q},\mathbf{p}, t) + \frac{\partial F_3(\mathbf{p}, \mathbf{Q} ,t)}{ \partial t} \label{15.85}\]

    Тип 4: \(F = F_4(\mathbf{p}, \mathbf{P},t) + \mathbf{q} \cdot \mathbf{p} — \mathbf{Q} \cdot \mathbf{P }\):

    Полная производная по времени производящей функции \(F = F_4(\mathbf{p}, \mathbf{P},t) + \mathbf{q} \cdot \mathbf{p} − \mathbf {Q} \cdot \mathbf{P}\) задается как

    \[\frac{dF }{dt} = \left[ \frac{\partial F_4(\mathbf{p}, \mathbf{P}, t)}{\partial \mathbf{p}} \cdot \mathbf{\dot{p}} + \frac{\partial F_4(\mathbf{p}, \mathbf{P},t)}{\partial \ mathbf{P}} \cdot \mathbf{\dot{p}} + \mathbf{\dot{q}} \cdot \mathbf{p} + \mathbf{q} \cdot \mathbf{\dot{p}} — \mathbf{\dot{Q}} \cdot \mathbf{P} — \mathbf{Q} \cdot \mathbf{\dot{P}} \right] + \frac{\partial F_4(\mathbf{p} , \mathbf{P},t)}{ \partial t}\label{15.86}\]

    Вставьте это в уравнение \ref{15. 76} и предположите, что тривиальный масштабный коэффициент \(\lambda = 1\), тогда

    \[− \left[ \mathbf{q}+ \frac{\partial F_4( \mathbf{p}, \mathbf{P},t)}{\partial \mathbf{p}} \right] \cdot \mathbf{\dot{p}} — H(\mathbf{q},\mathbf{ p}, t) = \left[ \frac{\partial F_4(\mathbf{p}, \mathbf{P},t)}{\partial \mathbf{P} } — \mathbf{Q} \right] \ cdot \mathbf{\dot{P}} — \mathcal{H}(\mathbf{Q},\mathbf{P}, t) + \frac{\partial F_4(\mathbf{p}, \mathbf{P} ,t) }{\partial t} \nonumber\]

    Предположим, что производящая функция \(F_4\) определяет канонические переменные \(\mathbf{q}\) и \(\mathbf{Q}\) равными

    \[\mathbf{q} = −\frac {\ partial F_4 (\ mathbf {p}, \ mathbf {P}, t)} {\ partial \ mathbf {p}} \ qquad \ mathbf {Q} = \ frac {\ partial F_4 (\ mathbf {p}, \mathbf{P},t)}{ \partial \mathbf{P}} \label{15.87}\]

    , то члены в скобках сокращаются, что приводит к требуемому преобразованию

    \[\mathcal{H}(\ mathbf{Q},\mathbf{P}, t) = H(\mathbf{q},\mathbf{p}, t) + \frac{\partial F_4(\mathbf{p}, \mathbf{P}, t)}{ \partial t} \label{15. 88}\]

    Обратите внимание, что последние три производящие функции требуют включения дополнительных билинейных произведений \(q\), \(p\), \(Q\), \(P\), чтобы члены сокращались, чтобы дать требуемый результат. Добавление билинейных членов гарантирует, что результирующая производящая функция \(F\) будет одинаковой при использовании любой из четырех производящих функций \(F_1\), \(F_2\), \(F_3\), \(F_4\ ). Часто производящая функция \(F_2(\mathbf{q},\mathbf{P}, t)\) является наиболее удобной. Четыре возможные производящие функции первого рода, приведенные выше, связаны преобразованиями Лежандра. Каноническое преобразование не обязательно должно соответствовать только одной из четырех производящих функций \(F_k\) для всех степеней свободы, они могут быть смесью разных ароматов для разных степеней свободы. Свойства генерирующих функций сведены в таблицу \(\PageIndex{1}\).

    Таблица \(\PageIndex{1}\): Генерирующие функции канонического преобразования
    Генерирующая функция Производные производные функции Тривиальные специальные примеры
    \(F = F_1(\mathbf{q}, \mathbf{Q}, t)\) \(p_i = \frac{\partial F_1}{\partial q_i } \quad P_i = -\frac{\partial F_1}{\partial Q_i}\) \(F_1 = q_iQ_i \quad Q_i = p_i \quad P_i = −q_i\)
    \(F = F_2(\mathbf{q},\mathbf{P}, t) — \mathbf{Q} \cdot \mathbf{P}\) \(p_i = \frac{\partial F_2}{\partial q_i} \quad Q_i = \frac{\partial F_2}{\partial P_i}\) \(F_2 = q_iP_i \quad Q_i = q_i \quad P_i = p_i\)
    \(F = F_3(\mathbf{p}, \mathbf{Q},t) + \mathbf{q} \cdot \mathbf{p}\) \(q_i = -\frac{\partial F_3}{\partial p_i} \quad P_i = -\frac{\partial F_3}{\partial Q_i}\) \(F_3 = p_iQ_i \quad Q_i = −q_i \quad P_i = −p_i\)
    \(F = F_4(\mathbf{p},\mathbf{P},t) + \mathbf{q} \cdot \mathbf{p} — \mathbf{Q} \cdot \mathbf{P}\ ) \(q_i = -\frac{\partial F_4}{\partial p_i } \quad Q_i = \frac{\partial F_4}{\partial P_i}\) \(F_4 = p_iP_i \quad Q_i = p_i \quad P_i = −q_i\)

    Частные производные производящих функций \(F_i\) определяют соответствующие сопряженные переменные, не включенные явно в производящую функцию \(F_i\). Обратите внимание, что для первого тривиального примера \(F_1 = q_iQ_i\) старые импульсы становятся новыми координатами, \(Q_i = p_i\), и наоборот, \(P_i = −q_i\). Это показывает, что лучше называть их «сопряженными переменными», а не «импульсами» и «координатами».

    Таким образом, Якоби разработал математическую основу для нахождения производящей функции \(F\), необходимой для выполнения канонического преобразования в новый гамильтониан \(\mathcal{H}(\mathbf{Q},\mathbf{P} , t)\), имеющее известное решение. То есть

    \[\mathcal{H}(\mathbf{Q},\mathbf{P}, t) = H(\mathbf{q},\mathbf{p}, t) + \frac{\partial F}{ \partial t} \label{15.89}\]

    Если \(\mathcal{H}(\mathbf{Q},\mathbf{P}, t)\) является константой, то решение было полученный. Теперь можно использовать обратное преобразование для этого решения \(\mathbf{Q}(t), \mathbf{P}(t) \rightarrow \mathbf{q}(t), \mathbf{p}(t)\) выразить окончательное решение через исходные переменные системы.

    Обратите внимание на особый случай, когда \(\mathcal{H}(\mathbf{Q},\mathbf{P}, t)=0\), тогда уравнение \ref{15. 89} сводится к соотношению Гамильтона-Якоби \ref{15.11}

    \[H(\mathbf{q},\mathbf{p}, t) + \frac{\partial S}{\partial t} = 0 \label{15.11}\]

    In в этом случае производящая функция \(F\) определяет функционал действия \(S\), необходимый для решения уравнения Гамильтона-Якоби \((15.4.23)\)). Поскольку уравнение \ref{15.89} преобразовало гамильтониан \(H(\mathbf{q},\mathbf{p}, t) \rightarrow \mathcal{H}(\mathbf{Q},\mathbf{P}, t )\), для которого \(\mathcal{H}(\mathbf{Q},\mathbf{P}, t)=0\), то решение \(\mathbf{Q}(t), \mathbf{ P}(t)\) для гамильтониана \(\mathcal{H}(\mathbf{Q},\mathbf{P}, t)=0\) получается легко. Этот подход лежит в основе теории Гамильтона-Якоби, представленной в главе \(15.4\).

    Применение канонических преобразований

    Процедура канонического преобразования может показаться излишне сложной для решения примеров, приведенных в этой книге, но она необходима для решения сложных систем, встречающихся в природе. Например, канонические преобразования можно использовать для преобразования зависящих от времени (неавтономных) гамильтонианов в независимые от времени (автономные) гамильтонианы, для которых известны решения. Пример \(15.6.2\) описывает такую ​​систему. Канонические преобразования обеспечивают чрезвычайно мощный подход к решению уравнений движения в гамильтоновой механике, особенно при использовании подхода Гамильтона-Якоби, обсуждавшегося в главе \(15.4\).

    Пример \(\PageIndex{1}\): Каноническое преобразование тождества

    Преобразование тождества \(F_2(\mathbf{q},\mathbf{P}) = \mathbf{q} \cdot \mathbf{P }\) удовлетворяет \ref{15.89}, если выполняются следующие соотношения P_i } = q_i\), \(\mathcal{H}=H\). Обратите внимание, что новые и старые координаты идентичны, поэтому \(F_2 = q_iP_i \) генерирует тождественное преобразование \(q_i = Q_i , p_i = P_i\).

    Пример \(\PageIndex{2}\): точечное каноническое преобразование

    Рассмотрим точечное преобразование \(F_2(\mathbf{q} \cdot \mathbf{P}) = f(\mathbf{q},t )\cdot \mathbf{P}\), где \(f(\mathbf{q},t)\) — некоторая функция \(\mathbf{q}\). Это преобразование удовлетворяет \ref{15.89}, если выполняются следующие соотношения \partial q_i} = \frac{\partial f_i(q_i,t)}{\partial q_i}\), \(\mathcal{H}=H\). Точечные преобразования соответствуют точечным преобразованиям координат.

    Пример \(\PageIndex{3}\): обменное каноническое преобразование

    Тождественное преобразование \(F_1(\mathbf{q}, \mathbf{Q}) = \mathbf{q} \cdot \mathbf{Q }\) удовлетворяет \ref{15.89}, если выполняются следующие соотношения частичное Q_i} = −q_i\), \(\mathcal{H}=H\) То есть координаты и импульсы поменялись местами.

    Пример \(\PageIndex{4}\): каноническое преобразование бесконечно малой точки

    Рассмотрим бесконечно малое точечное каноническое преобразование, бесконечно близкое к точечному тождеству.

    \[F_2(\mathbf{q} \cdot \mathbf{P},t) = \mathbf{q} \cdot \mathbf{P}+\epsilon G (\mathbf{q},\mathbf{P} ,t) \nonumber\]

    удовлетворяет \ref{15.89}, если выполняются следующие соотношения

    \[Q_i = \frac{\partial F_2}{ \partial P_i} = q_i + \epsilon \frac{\partial G (\mathbf{q},\mathbf{P}, t) }{\partial P_i} \nonumber\]

    \[p_i = \frac{\partial F_2 }{\partial q_i} = P_i + \epsilon \frac {\ парциальное G (\ mathbf {q}, \ mathbf {P}, t)} {\ парциальное q_i} \ nonumber \] 92 Q) = \omega P \nonumber\]

    откуда следует, что \(Q\) является циклической координатой.

    Гамильтониан консервативен, так как не зависит явно от времени, и равен полной энергии, так как преобразование в обобщенные координаты не зависит от времени. Таким образом,

    \[\mathcal{H} =E = \omega P \nonumber\]

    Поскольку

    \[\dot{Q} = \frac{\partial \mathcal{H}}{\partial P} = \omega \nonumber\]

    затем

    \[Q = \omega t + \phi \nonumber\] 92}} \sin (\omega t + \phi ) \номер\]

    Эта страница под названием 15.3: Канонические преобразования в гамильтоновой механике распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Дугласом Клайном посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами Платформа LibreTexts; подробная история редактирования доступна по запросу.

    1. Наверх
    • Была ли эта статья полезной?
    1. Тип изделия
      Раздел или Страница
      Автор
      Дуглас Клайн
      Лицензия
      CC BY-NC-SA
      Версия лицензии
      4,0
      Показать оглавление
      нет
    2. Теги
      1. канонические преобразования
      2. источник@http://classicalmechanics. lib.rochester.edu

    Университет Пешавара

    • Вице-канцлер профессор доктор Мухаммад Идрис вручает сувенир главному министру Хайбер-Пахтунхва Махмуду Хану после его визита в университет.

    • Меморандум о взаимопонимании между Национальным университетом Таджикистана и Пешаварским университетом Исламской Республики Пакистан, подписанный вице-канцлером профессором Мухаммадом Идрис и послом Таджикистана в Пакистане.

    • Секретарь HED, KP г-н Давуд Хан в сопровождении вице-канцлера профессора доктора Мухаммада Идриса и доктора Аднана Сарвара Хана (бывший декан), доктора Захида Анвара (декан) и доктора Хуссейна Шахида Сохарворди открывает Ярмарку мира 2022 года. организован Департаментом международных отношений.

    • Проф. д-р Мухаммад Идрис, вице-канцлер Пешаварского университета, и г-н Ясин Хан, генеральный директор по охране почв и водных ресурсов, подписали меморандум о взаимопонимании

      • Выставка моделей и плакатов

      Профессор д-р Мухаммад Идрис, вице-канцлер Пешаварского университета, и г-н Ясин Хан, Генеральный директор по охране почв и водных ресурсов, открыли выставку моделей и плакатов, организованную кафедрой географии и геоматики UoP.

    • Вице-канцлер профессор д-р Мухаммад Идрис вручает сувенир профессору д-ру Рубине Фарук, вице-канцлеру государственного колледжа Женского университета Фейсалабада, после ее визита в Пешаварский университет.

      • Созыв 2022

    • Университет Пешавара повторно подписал меморандум о взаимопонимании с Foster Learning Organization в комнате комитета вице-канцлера. На фотографии вице-канцлер профессор д-р Мухаммад Идрис и генеральный директор Foster Learning г-н М. Саннан Хан обмениваются документами меморандума о взаимопонимании.

    • Департамент здравоохранения и физического воспитания (HPE) UoP был открыт вице-канцлером профессором доктором Мухаммадом Идрисом в Институте образования и исследований Университета Пешавара.

    • Известный буддийский монах Таиланда Араявангсо преподносит сувенир вице-канцлеру профессору доктору Мухаммаду Идрису в музее сэра Сабизады Абдул Кайюма (SSAQ) Университета Пешавара.

    • Вице-канцлер профессор д-р Мухаммад Идрис открывает обновленную и реабилитированную Центральную библиотеку Пешаварского университета.

    • Вице-канцлер профессор д-р Мухаммад Идрис вручает сувенир послу Азербайджана в Пакистане Х.Е. Хазару Фархадову после его визита в Пешаварский университет.

    • Вице-канцлер профессор д-р Мухаммад Идрис получает награду за академические успехи 2022 года от губернатора Пенджаба Мухаммада Балиг Ур Рехмана на церемонии, организованной Ассоциацией университетов частного сектора Пакистана (APSUP) в отеле PC Hotel Lahore.

    • Накануне празднования 75-летия независимости студенты и сотрудники Университетской модельной школы, Университетской государственной школы, Университетского колледжа для мальчиков и Колледжа домоводства сфотографировались с вице-канцлером профессором доктором Мухаммадом Идрисом в конференц-зале.

    • Китайский учебный центр Пешаварского университета в сотрудничестве с пакистанско-китайской ассоциацией дружбы КП отпраздновал 75-й день независимости Исламской Республики Пакистан в Китайском учебном центре.

    • Исламский центр шейха Зайда в сотрудничестве с Пакистанским советом друзей мировых религий-веры отпраздновал 75-й День независимости Исламской Республики Пакистан в Общественном центре учителей Университета Пешавара.

    • Вице-канцлер UoP профессор д-р Мухаммад Идрис встретился с профессором д-ром Мухтаром Ахмедом, недавно назначенным председателем Комиссии по высшему образованию в Исламабаде, и обсудил вопросы университета.

    • Г-н Тахир Мунир, доктор наук, научный сотрудник исторического факультета Пешаварского университета, Пешавар, успешно защитил диссертацию на тему «Национальная партия Авами и политическое развитие в Пакистане (1972–1975)» под руководством профессора. Доктор Салман Бангаш. Его внешними экзаменаторами были профессор доктор Сайед Викар Али Шах, бывший исполняющий обязанности вице-канцлера, декан и председатель Университета Куэйд Азам, Исламабад, и профессор доктор Джеханзеб Халил, бывший профессиональный вице-канцлер Абдул Вал.

    • Г-жа Сафина Джехан, магистр философии, Колледж домоводства, UoP, успешно защитила магистерскую диссертацию на тему «Сравнительное исследование самооценки пользователей Facebook и не пользователей Facebook» под руководством профессора доктора Каниза. Фатима Хайдер. Ее экзаменатором был профессор, доктор Эрум Иршад, заведующий кафедрой психологии Пешаварского университета. Поздравляем ученого и ее научного руководителя.

    • Государственная защита научного сотрудника

      Г-жа Узма Мунши, доктор философии. Научный сотрудник Центра краеведения, успешно защитила кандидатскую диссертацию. Диссертация на тему «СТРАТЕГИЧЕСКАЯ ПЕРЕСТРОЙКА МЕЖДУ РОССИИ, КИТАЕМ И ПАКИСТАНОМ: ВЫЗОВЫ И ВОЗМОЖНОСТИ ДЛЯ ПАКИСТАНА» под руководством проф. Хуссейна Шахида Сохерворди. Ее внешними экзаменаторами были бригадный (в отставке) доктор Саиф Ур Рехман и профессор Мухаммад Хан, тогда как внутренним экзаменатором был профессор Шабир Ахмад Хан.

    • Саеда Кокаб Шах из Департамента наук об окружающей среде Пешаварского университета успешно защитила диссертацию на степень магистра философии по агротоксикантам, связанным с распылением гуавы в различных районах Хайбер-Пахтунхвы. Фарьял завершил свою диссертацию под руководством доктора Асифа Хана Хаттака. Внешним экспертом был доктор Мухаммад Науман Ахмед из Сельскохозяйственного университета Пешавара.

    • Заседание Исследовательского совета Департамента наук об окружающей среде, состоявшееся 29 сентября 2022 г. под председательством профессора, доктора Мохаммада Нафиса. Новые курсы MS, M.Phil и Ph.D. рекомендованы на утверждение Ученому совету.

    • Г-н Асим Саджад, магистр философии. ученый успешно защитил степень магистра философии. диссертация под руководством доктора Шаха Хайдера Хана, доцента кафедры физики UoP, и под руководством доктора Гулама Муртазы, доцента кафедры физики Исламийского колледжа в Пешаваре. Его внешним экзаменатором был доктор Абдул Вахид, доцент кафедры физики Исламского колледжа в Пешаваре. Работа проводилась совместно на кафедре физики УОП и колледжа Исламия в Пешаваре.

    • Г-н Асим Саджад, магистр философии. ученый успешно защитил степень магистра философии. защитил диссертацию под названием «Исследование основных принципов неорганических двойных перовскитов, не содержащих свинца, Cs2AgSbX6 (X=Cl, Br, I) для оптических и термоэлектрических применений» под руководством доктора Шаха Хайдера Хана, доцента физического факультета Пешаварского университета, под совместным руководством доктора Гулама Муртазы, доцента кафедры физики Исламийского колледжа в Пешаваре. Его внешним экзаменатором был доктор Абдул Вахид, ассистент специалиста.

    • Халима Якуб из Департамента наук об окружающей среде Пешаварского университета защитила диссертацию о грунтовых водах, воздействии на них твердых отходов и их рекультивации. Она предложила комплексную и эффективную систему управления сбросом бытового мусора в пригороде Пешавара и оценку его негативных последствий. Халима успешно защитила кандидатскую диссертацию. Она завершила свою диссертацию под руководством доктора Саиды Юсуф.

    • Государственная защита научного сотрудника

      Г-жа Суфия Ифтихар, доктор философии. ученый кафедры статистики успешно защитила кандидатскую диссертацию. Работала под руководством доктора Аламгира, доцента кафедры статистики. Ее внешними экспертами были д-р Саджад Ахмад Хан, адъюнкт-профессор Колледжа Исламия в Пешаваре, и д-р Дост Мухаммад Хан, заведующий кафедрой статистики Марданского университета имени Абдула Вали Хана.

    • Государственная защита научного сотрудника

      Департамент компьютерных наук: Канвал Эджаз успешно защитила докторскую диссертацию под руководством профессора доктора Саида Махфуза и под руководством доктора М. Зубаира, KKKUK. Экзаменаторами были профессор д-р Кашиф Кифаят, Университет Эйр, Исламабад, и профессор д-р Джамиль Ахмед, Университет Малаканда.

    • Государственная защита научного сотрудника

      Департамент компьютерных наук: Г-н Фазал Аман успешно защитил докторскую диссертацию под руководством профессора доктора Ажара Рауфа и под руководством доктора Рехмана Али. Экзаменаторами были д-р Фахре Алам, Малакандский университет, и д-р Саджид Анвар, IMSciences.

    • Магистр философии. Защита ученого-исследователя

      Г-жа Нимра Нур защитила диссертацию о сточных водах и их очистке в топленом масле. Для этого была предложена комплексная и эффективная система управления путем оценки отходов, образующихся ежедневно в производстве топленого масла. Нимра Нур успешно защитила диссертацию. Она завершила свою диссертацию под руководством профессора доктора Мухаммада Нафиса.

    • Государственная защита научного сотрудника

      Г-н Асим Саджад, магистр философии. ученый кафедры физики успешно защитил кандидатскую диссертацию. Он работал под руководством доктора Шаха Хайдера Хана, доцента кафедры физики. Его соруководителем был доктор Гулам Муртаза, доцент кафедры физики Исламского колледжа в Пешаваре. Его внешним экзаменатором был доктор Абдул Вахид, доцент кафедры физики Исламского колледжа в Пешаваре.

    • Г-н Аджмал Хан с кафедры зоологии успешно защитил докторскую диссертацию под руководством доцента доктора Мухаммада Хисруна. Его экзаменаторами были д-р Мухаммад Шахид, адъюнкт-профессор Сельскохозяйственного университета Фейсалабада, д-р Гаухар Рахман, адъюнкт-профессор, Университет Абдул Вали Хана в Мардане, и д-р Фарра Заиди, адъюнкт-профессор, UoP.

      No related posts.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *