Найти корни кубического уравнения онлайн: Онлайн калькулятор: Кубическое уравнение

Формула Кардано для решения кубических уравнений

Как известно, корень n-ой степени из комплексного числа z,

z = r *(cosφ + isinφ)

имеет n комплексных значений

где

Следовательно, имеет три значения z₁, z₂, z₃, где

В формуле Кардано два кубических корня, и их значения нужно сочетать по следующему правилу: для каждого из трех значений первого кубического корня , берется такое значение второго кубического корня, , чтобы выполнялось соотношение z_i*z_j = —

.

Чтобы избежать такого сочетания значений разных кубических корней, можно использовать формулу

или, что то же самое,

Каждому найденному по формуле Кардано значению y соответствует решение исходного уравнения x = y — 

.

В зависимости от значения дискриминанта Δ кубическое уравнение может иметь либо 3 действительных корня (Δ <0), либо 1 действительный корень и два комплексно сопряженных (Δ > 0), либо 2 действительных корня (Δ=0) или один действительный корень (Δ=0, p=q=0).

Рассмотрим все эти случаи.

1) Δ <0   =>   3 действительных корня:

Если опустить промежуточные вычисления, то окончательные формулы для трех действительных корней канонического уравнения можно представить в виде

Тогда формулы для корней исходного уравнения будут иметь вид:

x₁ = y₁ — 

,   x₂ = y₂ — 

,   x₃ = y₃ — 

.   

2 ) Δ > 0   =>   1 действительный корень и два комплексно сопряженных:

Формулы для корней исходного уравнения такие же, как в предыдущем случае

x₁ = y₁ — 

,   x₂ = y₂ — 

,   x₃ = y₃ — 

.   

3 ) Δ=0   =>   2 действительных корня:

Следовательно, x₁ = y₁ — 

,   x₂ = y₂ — 

.    

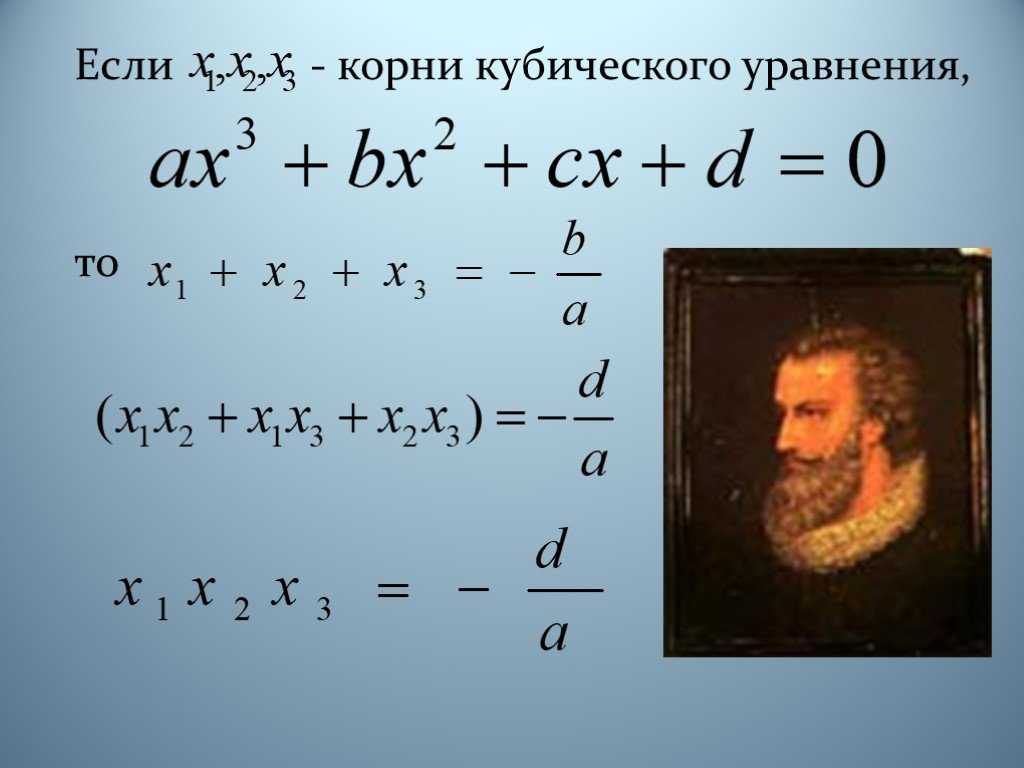
Если Δ=0 и p=q=0, то у канонического уравнения только один корень y₁=0. Соответственно, исходное уравнение будет иметь единственный корень x = —

.

Если кубическое уравнение имеет целый или рациональный корень, то, конечно, проще всего найти этот корень подбором, затем делением свести исходное уравнение к квадратному. Если же рациональных корней нет, то только формула Кардано может помочь найти решение.

Практическое использование формулы Кардано для решения кубических уравнений крайне затруднительно из-за громоздких вычислений. Но в особых случаях, это сделать довольно просто, например, для первого случая (Δ < 0) при q = 0 для нахождения трех действительных корней, или для третьего случая (Δ = 0). Для второго случая, когда Δ > 0 , формулы для корней кубического уравнения можно выписать всегда. Таким образом, применение формулы Кардано оправдано, если уравнение не имеет рациональных корней.

Рассмотрим применение формулы Кардано для решения кубических уравнений на примерах.

Примеры.

Пример 1. Решить уравнение x³ + 6x² + 3x — 10 = 0.

Решение.

Данное уравнение легко решается и без применения формулы Кардано. Легко подобрать корень x = 1. Делением на x — 1 левой части уравнения по схеме Горнера получаем

Следовательно, x² + 7x + 10 = 0. Решая это квадратное уравнение, получаем

А теперь найдем корни исходного уравнения по формуле Кардано. Для данного уравнения a = 1, b = 6, c =3, d = -10. Замена переменной x = y — 

b/3a

 = y — 

6/3

 = y — 2

приводит исходное уравнение к виду y³ + py + q = 0, где

Вычислим дискриминант этого уравнения

Так как Δ <0   =>   каноническое уравнение имеет 3 действительных корня. Поскольку q = 0   =>   φ = 

   =>   

Тогда для корней исходного уравнения получаем:

x₁ = y₁ — 2 = 3 — 2 = 1,
x₂ = y₂ — 2 = -3 — 2 = -5,
x₃ = y₃ — 2 = 0 — 2 = -2.

Ответ: -5, -2, 1.

Пример 2. Решить уравнение x

3 + 3x² + 4x + 2 = 0.

Решение.

Для данного уравнения a = 1, b = 3, c =4, d = 2. Замена переменной x = y — 

b/3a

 = y — 

3/3

 = y — 1

приводит исходное уравнение к виду y³ + py + q = 0, где

Вычислим дискриминант этого уравнения

Так как Δ >0   =>   каноническое уравнение имеет 1 действительный корень и два комплексно сопряженных:

Тогда для корней исходного уравнения получаем:

x₁ = y₁ — 1 = 0 — 2 = -1,
x₂ = y₂ — 1 = i — 1 = i — 1,
x₃ = y₃ — 1 = -i — 1 = -i — 1.

Ответ: -1, -1+i, -1-i.

Пример 3. Решить уравнение x³ + 12x² + 36x + 32 = 0.

Решение.

Для данного уравнения a = 1, b = 12, c =36, d = 32. Замена переменной x = y — 

b/3a

 = y — 

12/3

 = y — 4

приводит исходное уравнение к виду y³ + py + q = 0, где

Вычислим дискриминант этого уравнения

Так как Δ = 0   =>   уравнение имеет 2 действительных корня:

Тогда для корней исходного уравнения получаем:

x₁ = y₁ — 4 = -4 — 4 = -8,
x₂ = y₂ — 4 = 2 — 4 = -2.

Ответ: -8, -2.

Пример 4. Решить уравнение x³ + 9x² + 9x — 137 = 0.

Решение.

Для данного уравнения a = 1, b = 9, c =9, d = -137. Замена переменной x = y — 

b/3a

 = y — 

9/3

 = y — 3

приводит исходное уравнение к виду y³ + py + q = 0, где

Вычислим дискриминант этого уравнения

Так как Δ >0   =>   каноническое уравнение имеет 1 действительный корень и два комплексно сопряженных:

Тогда для корней исходного уравнения получаем:

Ответ:

Пример 5. Решить уравнение x³ + 18x² + 90x + 50 = 0.

Решение.

Для данного уравнения a = 1, b = 18, c =90, d = 50. Замена переменной x = y — 

b/3a

 = y — 

18/3

 = y — 6

приводит исходное уравнение к виду y³ + py + q = 0, где

Вычислим дискриминант этого уравнения

Так как Δ > 0   =>   каноническое уравнение имеет 1 действительный корень и два комплексно сопряженных:

Тогда для корней исходного уравнения получаем:

Ответ:

Так как запомнить промежуточные формулы для нахождения корней кубического уравнения с помощью формулы Кардано довольно сложно, то можно просто повторить вывод формулы Кардано для данного уравнения.

Рассмотрим соответствующий пример.

Пример. Найти действительные корни уравнения x³ + 12x² + 3x + 4 = 0.

Решение.

Для данного уравнения a = 1, b = 12, c = 3, d = 4. Сделаем замену переменной x = y — 

b/3a

 = y — 

12/3

 = y — 4

:

(y — 4)³ + 12(y — 4)² + 3(y — 4) + 4 = 0      

      y³ — 12y² + 48y — 64 + 12y² — 96y + 192 + 3y — 8 = 0      

      y³ — 45y + 120 = 0.

Следовательно, p = -45, q = 120, Δ = (60)² — (15)³ = 225 >0. Значит, исходное уравнение имеет один действительный корень.

Теперь сделаем следующую замену переменной y = t — 

p/3t

 = t +&nbsp

45/3t

 = t + 

15/t

. Получим

Это уравнение домножим на t³ и получим квадратное уравнение относительно t³:

t⁶ + 120t³ + 3375 = 0.

Следовательно,

Тогда Теперь можно найти y по формуле y = t + 

.

Вместо t можно подставить или , или , результат будет один и тот же:

Или

Таким образом, действительный корень исходного уравнения равен

Ответ: .

Теорема Виета для кубического уравнения

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Теорема Виета для кубического уравнения.

Муниципальное образовательное учреждение
«Средняя общеобразовательная школа №44»
Теорема Виета для
кубического
уравнения.
Работа выполнена учениками 11 «А» класса
Емельяновым Тимофеем и
Вдовенковой Алёной
Крамаренко Елена Андреевна,
учитель математики
высшей категории
г. Саратов
2016 год

2. Историческая справка

Виет Франсуа родился в
1540 году в Фонте-ле-Конт
французской провинции
Пуату – Шарант. Отец
Виета был юристом
(прокурором), а мать
(Маргарита Дюпон)
происходила из знатной
семьи, что облегчило
дальнейшую карьеру её
сына.
Получив юридическое образование, он с
девятнадцати лет успешно занимался
адвокатской практикой в родном городе. Он был
широко образованным человеком. Знал
астрономию и математику и все свободное
время отдавал этим наукам.
Но главной страстью Виета была математика.
Виет сделал принципиально новое открытие, поставив
перед собой цель изучать не числа, а действия над
ними. Виета называют «отцом» алгебры,
основоположником буквенной символики. Особенно
гордился Франсуа всем известной теперь теоремой о
выражении коэффициентов уравнения через его корни.
Виет первый обозначил буквами не только неизвестные, но
и данные величины, т.е. коэффициенты
соответствующих уравнений
Виет сначала решает задачи в общем виде, и
только потом приводит числовые
параметры. В общей части он обозначает
буквами не только неизвестные, что уже
встречалось ранее, но и все прочие
параметры, для которых он придумал
термин «коэффициенты». Виет использовал
для этого только заглавные буквы – гласные
для неизвестных, согласные для
коэффициентов.

6. Теорема Виета

Сумма корней приведённого квадратного уравнения x2 + px + q = 0
равна коэффициенту p, взятому с противоположным знаком, а
произведение корней равно свободному члену q:
х1 х2 p
х1 х2 q
В общем случае (для неприведенного квадратного уравнения):
в
х1 х 2
а
с
х1 х2
а
Особый интерес
представляет
исследование Виета
по составлению
уравнений из
линейных
множителей и по
установлению связей
между корнями
уравнения и его
коэффициентами.
Пусть x1 и x2 – корни приведенного квадратного
уравнения x2 + px + q = 0
Перемножим двучлены (х — x1) и (х — x2) :
(х — x1)(х — x2) = x2 — (x1+ x2)х + x1x2 ,
Тогда, сравнивая с исходным уравнением
можно записать систему :
p ( x1 x2 )
q x1 x2
Выполняя аналогичные действия для приведенного
кубического уравнения x3+ax2+bx+c=0, считая x1,x2,x3
корнями исходного кубического уравнения, получаем:
(х-x1)(х-x2)(х-x3) = x3 – (x1+x2+x3 ) x2+(x1x2+ x1x3 + x2,x3)х
— x1x2x3
следовательно, имеет место следующая система
равенств:
а ( х1 х2 х3 ),
в х1 х2 х1 х3 х2 х3 ,
с х х х
1 2 3
Если
x1,x2,x3,- корни
неприведённого кубического уравнения
ax3 + bx2 + cx + d = 0, то
x1+x2+x3=- b/a
(х1*х2+х1*х3+х2*х3)= с/а
х1*х2*х3=-d/a
есть суть теоремы Виета для кубического
уравнения.

11. Решить уравнение x3-4×2+x+6=0.

1 способ: при а=1 свободный член этого уравнения раскладывают на
простые множители, затем поочередно выбирают значения «x»,
равные одному из этих множителей с различными знаками. Эти
значения х проверяют, подставляя их в исходное равенство. Таким
способом иногда удается найти первый корень кубического уравнения
х1. Для нахождения остальных корней кубического уравнения надо
соответствующий многочлен разделить на выражение (х-х1), при этом
в частном получается квадратный трехчлен. Корни получившегося
квадратного трехчлена также являются корнями кубического
уравнения. Таким образом 6=1*2*3, т.е.корни уравнения могут быть
числа 1 или -1,2 или-2,3 или-3. Способом подстановки выясняем, что
х1=-1.Разделим многочлен х3-4х2+х+6 на (х+1) и получим трехчлен
х2-5х+6, т.е.х3-4х2+х+6=(х+1)*(х2-5х+6)=0.
Найдем корни квадратного уравнения х2-5х+6=0 по теореме Виета:
х1=2 и х2=3.
Таким образом исходное кубическое уравнение имеет три
действительных корня:
х1=-1, х2=2, х3=3.
2 способ: применение теоремы Виета для решения
кубического уравнения
Итак, если х3-4х2+х+6=0,
то х1+х2+х3=4
Х1*х2+х1*х3+х2*х3=1,
Х1*х2*х3=-6
Методом подбора находим: (-1)*2*3=-6
(-1)+2+3=4
(-1)*2+(-1)*3+2*3=1,
т. е корни уравнения
х1=-1,х2=2, х3=3.

13. Задача: вычислить, используя теорему Виета, сумму квадратов корней уравнения х3-6х2+11х-6=0

Согласно теореме Виета имеем:
х1+х2+х3=6
х1*х2+х1*х3+х2*х3=11
х1*х2*х3=6
Т.к. (х1+х2+х3)2=х12+х22+х32+2(х1*х2+х1*х3+х2*х3)
то получим 62=х12+х22+х32+2*11
36-22= х12+х22+х32
х12+х22+х32=14
Ответ: 14

14. Задача: Составить кубическое уравнение, корнями которого являются числа -5;3;4

Решение:
Пусть х1=-5, х2=3,х3=4, тогда
а ( 5 3 4),
в 5 * 3 ( 5) * 4 3 * 4,
с ( 5) * 3 * 4
а 2,
в 23,
с 60;
А теперь составим приведенное кубическое уравнение
вида x3+ax2+bx+c=0, корнями которого являются -5,
3, 4. Им будет x3-2×2-23x+60=0

15. Посвящение теореме Виета:

По праву достойна в стихах быть воспета
О свойствах корней теорема Виета.
Что лучше, скажи постоянства такого:
Умножишь ты корни — и дробь уж готова:
В числителе с, в знаменателе а,
А сумма корней тоже дроби равна
Хоть с минусом дробь эта, что за беда
В числителе в, в знаменателе а.

English     Русский Правила

Как решить уравнение с комплексными числами

Как решить уравнение с комплексными числами

Калькулятор на сайте «Контрольная работа Ру» позволяет решать уравнения с комплексными числами и переменными онлайн, в том числе квадратные уравнения с комплексными числами. Итак, пример-инструкция, как воспользоваться калькулятором: Надо решить комплексное уравнение:

, где i — комплексная единица, exp — это экспонента e .. для этого перейдите по ссылке решение уравнений онлайн и введите данное комплексное уравнение, также укажите, что i — это комплексная единица, а то ответа не получится. Получится как здесь Еще один пример с квадратным уравнением с комплексными числами: Надо решить квадратное уравнение

. Вы вводите его по ссылке решение уравнений онлайн , указываете, что i — это комплексная единица (после того как ввели уравнение и нажали кнопку «решить»), нажимаете кнопку под формой «Обновить» и получаете ответ как здесь. Если в ответе присутствуют корни из комплексных чисел, то можно воспользоваться калькулятором по упрощению комлексных чисел по ссылке

Решение уравнений с комплексными числами

Итак, необходимо решить уравнение с комплексными переменными, найти корни этого уравнения. Рассмотрим принцип решения комплексных уравнений, научимся извлекать корень из комплексного числа.

Для того, чтобы решить уравнение n-й степени с комплексными числами, используем общую формулу:

где |z| — модуль числа, φ = arg z — главное значение аргумента, n — степень корня, k — параметр, принимает значения : k = .

Пример 1. Найти все корни уравнения

Выразим z из уравнения:

Все корни заданного уравнения являются значениями корня третьей степени из комплексного числа

Воспользуемся общей формулой для вычисления корней степени n комплексного числа z. Найдем все необходимые значения для формулы:

Подставим найденные значения в формулу:

Последовательно подставляя вместо k значения 0, 1, 2 найдем три корня исходного уравнения.

Пример 2. Найти все корни уравнения

Найдем дискриминант уравнения:

Поскольку дискриминант отрицательный, уравнение имеет два комплексно-сопряженных корня. Вычислим корень из дискриминанта:

Найдем корни уравнения:

Ответ:

Пример 3. Найти все корни уравнения

Выразим z из уравнения:

Все корни заданного уравнения являются значениями корня четвертой степени из комплексного числа

Вновь используем общую формулу для нахождения корней уравнения n степени комплексного числа z.
n = 4 — количество корней данного уравнения. k = . Найдем модуль комплексного числа:

Подставим найденные значения в формулу:

Последовательно подставляя вместо k значения 0, 1, 2, 3 найдем все 4 корня уравнения:

Пример 4. Найти корни уравнения

Решение кубического уравнения комплексными числами:

Воспользуемся общей формулой для вычисления корней степени 3 комплексного числа z.

Найдем все необходимые значения для формулы:

Подставим найденные значения в формулу:

Последовательно подставляя вместо k значения 0, 1, 2 найдем три корня исходного уравнения:

Домашнее задание: Самостоятельно составить и решить уравнение с комплексными числами.

Условия: переменная z должна быть «спрятана» и представлена в качестве аргумента тригонометрической функции косинуса. Чтобы привести данное уравнение к привычной форме, нужно «вытащить» z, а для этого необходимо помнить, как решаются тригонометрические уравнения,а также знать, как применять свойства логарифмической функции от комплексного числа.

После того, как мы решили тригонометрическое уравнение с комплексным числом, получаем «голый» z, который представлен в качестве аргумента обратной тригонометрической функции. Чтобы преобразовать данное выражение, нужно использовать формулу разложения арккосинуса в логарифм.

Вместо z — выражение (3i/4) и дальше все делаем по приведенной выше формуле, преобразовывая выражение под корнем, используя свойства мнимой единицы i.

Как быть далее? Теперь будем использовать формулу для решения выражения с натуральным логарифмом.

Для того чтобы найти корни логарифмического уравнения, нужно найти модуль комплексного числа |z| и его аргумент φ = arg z. По сути, перед нами чисто мнимое число.

Теперь предлагаем ознакомиться с формулами, которые могут пригодиться при решении уравнений или неравенств с комплексными числами. Это формулы, где комплексное число выступает в роли аргумента тригонометрической функции, логарифмической функции или показательной функции.

Примеры решения задач с комплексными числами

Простое объяснение принципов решения задач с комплексными числами и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.

Алгоритм решения задач с комплексными числами

Алгебраическая форма комплексного числа:

Тригонометрическая форма комплексного числа:

Модуль комплексного числа:

Аргумент комплексного числа:

Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

5 Лучший бесплатный факторинговый калькулятор для Windows

Вот список бесплатных факторинговых калькуляторов для Windows . Используя эти бесплатные калькуляторы, вы можете легко найти корни кубического многочлена. Все эти факторинговые кубики калькулятора работают по одному принципу. Вы должны указать значения всех коэффициентов кубического уравнения, чтобы получить все его корни.

Большинство этих бесплатных программ также рассказывают о характере полученных таким образом корней. Я также добавил в этот список калькулятор кубических уравнений, который позволяет создавать собственные макросы для решения различных математических задач.

Мой любимый калькулятор факторинга:

Из всех этих калькуляторов факторинга мне больше всего нравится Microsoft Mathematics . Это полнофункциональный калькулятор, использование которого не ограничивается решением кубических уравнений. Вы можете использовать его для решения как математических, так и научных задач. Он поставляется с рабочим листом. Вы можете написать любой тип проблемы на листе, чтобы получить ее решение. Эта функция делает его очень простым в использовании. Помимо этого, он предлагает множество дополнительных функций. Прочтите статью, чтобы узнать об этом больше.

Вам также могут понравиться лучшие бесплатные программы Math Equation Editor, Geometry Calculator и Matrix Calculator для Windows.

Microsoft Mathematics

Microsoft Mathematics — бесплатный калькулятор кубических вычислений для Windows . Это популярный научный калькулятор, предназначенный для решения как математических, так и научных задач. С помощью этого расширенного калькулятора вы можете решать уравнения, строить графики, преобразовывать единицы измерения и решать многие другие задачи.

Использование Microsoft Mathematics не составляет труда. Просто напишите проблему на рабочем листе, представленном в его интерфейсе, и нажмите кнопку Enter . Вы можете ввести любой тип проблемы на листе. После этого вы получите решение введенной задачи. Помимо этого, вы также можете использовать Equation Solver для решения системы линейных уравнений, квадратных уравнений, кубических уравнений, уравнений четвертой степени и т. д. После решения уравнения вы также можете построить график этого уравнения в Графический раздел .

Ниже приведены некоторые проблемы, которые можно решить с помощью Microsoft Mathematics:

• Интеграция.
• Дифференциация.
• Пределы.
• Перестановки и комбинации.
• Среднее, Медиана, Мода.
• Тригонометрические задачи и др.

Домашняя страница

Страница загрузки

Precise Calculator

Precise Calculator — это бесплатный научный калькулятор с открытым исходным кодом, который можно использовать как Калькулятор корней кубического уравнения .

Как решить кубическое уравнение с помощью точного калькулятора:

Перейдите в меню Macro и выберите Кубическое уравнение . Это напишет код в верхнем пустом поле калькулятора со значениями по умолчанию коэффициентов кубического уравнения. Вам просто нужно изменить значения этих коэффициентов (a, b, c и d) и нажать кнопку Enter . В поле вывода отображаются все три корня кубического уравнения. Время, затраченное на решение проблемы, также отображается в его интерфейсе. Он только решает корни кубического уравнения, но не говорит о природе корней.

Помимо нахождения корней кубического уравнения, он также способен находить корни квадратного уравнения, находить простые числа, решать тригонометрические уравнения, решать гиперболические функции, находить площадь, периметр, объем, и т. д. 2D и трехмерные геометрические фигуры. Некоторые из 2D и 3D геометрических фигур включают круг, воздушный змей, параллелограмм, квадрат, трапецию, куб, конус, трапецию, цилиндр, пирамиду и т. д.

Он имеет четыре режима расчета, а именно: , и англ . Вы можете переключить результат на любой из этих режимов. Кроме того, он также имеет десятичных, шестнадцатеричных, и двоичных преобразований . Для научных расчетов он поставляется с некоторыми предопределенными константами, такими как скорость света , диэлектрическая проницаемость вакуума, масса электрона, масса протона, масса нейтрона, постоянная Больцмана, постоянная Стефана-Больцмана и т. д. Вы можете использовать эти константы непосредственно в своих расчетах. .

Общие характеристики точного калькулятора:

• Поддерживает более 5 языков: английский, каталанский, испанский, французский, итальянский и т. д.
• Вы можете изменить стиль и размер шрифта.
• Позволяет сохранить результат в формате .txt.
• Вы можете создавать свои собственные макросы и сохранять их.
• Автоматически сохраняет историю расчетов. Вы можете очистить его в любое время.

Precise Calculator — это портативный калькулятор кубических факторингов .

Домашняя страница

92+CX+D=0 с пустыми ячейками вместо коэффициентов. Вы должны заполнить значение коэффициентов в необходимых местах и ​​нажать на кнопку Решить это уравнение . Окончательный ответ отображается вместе с характером корней.

Он поставляется с пятью категориями инструментов:

• Алгебра : В этом разделе вы найдете факторинг квадратичный калькулятор, факторинговый калькулятор кубических вычислений, калькулятор решения систем уравнений с 2 ​​и 3 неизвестными, и HCF и Искатель LCM .
• Арифметико-дискретный : Этот раздел включает в себя базовый преобразователь, калькулятор факториала, и генератор случайных чисел .
• Последовательность : Числа Фибоначчи и Калькуляторы чисел Ферма представлены здесь.
• Вероятность : Вы можете узнать вероятность с помощью калькулятора вероятности.
• Викторина : Викторина доступна на трех уровнях (легкий, средний и сложный). Вы также можете установить время для прохождения викторины.

Домашняя страница

Страница загрузки

Cubique — Решатель кубических уравнений

Cubique — Решатель кубических уравнений — еще один бесплатный факторинговый калькулятор для Windows. Калькулятор имеет очень простой интерфейс. Показан общий формат уравнения третьего порядка (кубического). Вы должны ввести значения всех четырех коэффициентов в пустые места. Вы можете вводить коэффициенты в десятичной, дробной или экспоненциальной форме.

Также отображает характер корней. Преимущество программы в том, что она отображает комплексно-сопряженные корни уравнения красным цветом. С другой стороны, все действительные корни отображаются синим цветом. Таким образом, вы можете легко их идентифицировать. 92+CX+D=0) отображается на его интерфейсе. Вы должны заполнить значения коэффициентов в необходимых полях отображаемого кубического уравнения и нажать на кнопку Решить . Корни кубического уравнения отображаются в разделе Solutions вместе с характером корней.

Другие преимущества этого бесплатного программного обеспечения включают интерполяцию, экстраполяцию, калькулятор квадратных корней , калькулятор корней уравнения четвертой степени (только для платных пользователей), и сложное умножение на .

ПРИМЕЧАНИЕ : Бесплатная версия этой программы отображает только реальные корни, а не воображаемые. Если кубическое уравнение имеет мнимые корни, отображается сообщение: Комплексные корни отображаются при обновлении.

Домашняя страница

Страница загрузки

Похожие сообщения

Написать комментарий

Калькулятор кубических уравнений | ax3 + bx2 + cx + d = 0

Вы хотите решить кубическое уравнение онлайн ? Ниже вы найдете калькулятор, чтобы решить их немедленно. Просто введите значение коэффициентов уравнения, нажмите кнопку расчета, и все готово.

Если у вас все еще есть сомнения, в этой статье мы научим вас решать уравнения третьей степени упражнений и много интересных ресурсов.

 

Разделы статьи

• Как решить кубическое уравнение?
• Неполное кубическое уравнение
• Кубическое уравнение решено
• Как решить кубическое уравнение на калькуляторе
• Как работает калькулятор кубического уравнения

Как решить кубическое уравнение?

Для обучения решению кубического уравнения важно знать, что они имеют такую ​​форму:

Ax ³  + Bx ²  + Cx + D = 0

Вот как выглядит полное кубическое уравнение, и это то, что мы научимся решать далее, используя несколько методов. Вам важно знать, что этот тип уравнений всегда имеют три решения или корня . Кроме того, в зависимости от значения независимого члена D решения могут быть следующими:

• D > 0 Одно из решений вещественное, а два других комплексные.
• D = 0 Все решения действительны и по крайней мере два из них равны.
• D < 0 все решения реальны и совершенно разные.

Теперь, когда мы знаем основы уравнений 3-й степени, давайте посмотрим, как их решать. Если вы хотите узнать, как решать неполные уравнения третьей степени, читайте дальше, чтобы узнать, как это сделать.

Руффини

 

Использование правила Руффини является одним из наиболее рекомендуемых методов для пошагового решения кубического уравнения .

Процесс намного легче понять, если мы покажем его вам на видео, чем если запишем его, поэтому мы оставляем вам один из лучших, которые мы нашли на YouTube. Не волнуйтесь, если вместо Руффини вы услышите, как профессор говорит о синтетическом делении, это то же самое.

Без Руффини

В случае, если Руффини не убедит вас в расчете кубических уравнений, вы можете использовать этот другой метод, основанный на вычислении различных формул и значений для этого уравнения третьей степени:

x ³  + a ₁ x ²  + a ₂ x + a ₃ = 0

Первый шаг — найти следующие значения:

С уже рассчитанными значениями Q, R, S1 и S2 теперь подставляем в следующие общие уравнения , чтобы найти три решения кубического уравнения:

Общая формула

Если ни один из вышеперечисленных методов вас не убеждает, вот что вы можете сделать с тремя формулами для каждого решений уравнения , но я предупреждаю вас, что их довольно утомительно решать.

Формула первого раствора Х ₁ :

Формула второго раствора Х ₂ :

Формула третьего решения X ₃ :

Надеемся, что хотя бы один из трех предложенных нами вам способов для решения кубического уравнения окажется для вас полезным. Кроме того, вы всегда можете проверить правильность полученного результата с помощью нашего калькулятора.

Неполное кубическое уравнение

Иногда нам присылают решение неполного кубического уравнения или без самостоятельного члена, который выглядит так:

Ax ³  + Bx ²  + Cx = 0

В этих случаях одно из решений всегда будет X = 0. Два других будут вычисляться путем вычитания общего множителя следующим образом:

х (АХ ² + Вх + С) = 0

Если мы посмотрим на это, два других недостающих решения неполного кубического уравнения находятся в уравнении второй степени между скобками, которые мы должны решить. Если вы не знаете, как это сделать, вы можете воспользоваться нашим калькулятором уравнений второй степени.

Решение кубического уравнения

Вы ищете упражнения решенное кубическое уравнение ? Вот несколько примеров с решениями, чтобы вы могли попробовать решить их самостоятельно:

Первое упражнение : x ³ — 6x ² + 3x + 10 = 0

Решения:

30 7 x

= 5

х ₂ = 2

х ₃ = -1

Второе упражнение : 2x ³ — 5x ² + 3x = 0

Решения:

• x ₁ = 0
• х ₂ =1
• х ₃ = 3/2

Как решить кубическое уравнение на калькуляторе

Если у вас есть относительно современный научный калькулятор, вы можете решить кубическое уравнение с его помощью . Чтобы увидеть, как это делается, мы будем использовать одну из торговых марок Casio, поскольку они наиболее популярны среди старшеклассников, студентов колледжей или университетов.

Чтобы вычислить все решения кубического уравнения с помощью калькулятора, вам нужно buscar el botón «MODE SETUP» o «MENU CONFIG» que suele encontrarse en la esquina superior derecha. Púlsalo у entre todas las opciones Que te salen en pantalla, selecciona aquella que estápresentada como «EQN».

Если все прошло успешно, на экране появятся уравнения разной степени. Мы останемся с одним из степени 3, который выглядит так:

ТОПОР ³  + bX ²  + cX + d = 0

Выбираем его и следующий шаг будет состоять из записываем значения коэффициентов a, b, c и d . После того, как вы ввели их, нажмите клавишу равенства (=), чтобы отобразить решения.

Возможно, вам придется использовать джойстик (на картинке выше вы можете видеть его), чтобы отобразить все решения уравнения, которое вы написали.

Как работает калькулятор кубических уравнений

Если вам непонятно, как работает наш 9Калькулятор кубического уравнения 0003 онлайн , мы собираемся объяснить это более подробно.

Как мы уже видели, кубическое уравнение должно иметь следующий формат:

Ax ³  + Bx ²  + Cx + D = 0

Вам просто нужно ввести в инструмент значения A, B, C и D. Если какое-либо из этих значений равно 0, вы должны ввести его. Например, если кубическое уравнение, которое вы хотите решить онлайн, равно 2X ³ — 4X ² — 22X + 24 = 0, entonces los valores que debes escribir en la calculadora es lo siguiente:

• А = 2
• Б = -4
• С = -22
• Д = 24

Тогда просто нажмите кнопку расчета, и вы сразу же получите результат.

Если у вас есть какие-либо сомнения относительно , как решить кубическое уравнение , оставьте нам комментарий, и мы поможем вам как можно скорее.

Nacho

Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En Esta веб-те Ayudo hacer cálculos у преобразования sencillas дие кон-эль-Пасо-де-лос-Años се-нос-ха olvidado Cómo себе Hace. Si tienes dudas, déjame un commentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, напишите мне сообщение.

• градусов с радианами
• Apothem
• Antilogarithm Calculator
• Calculator
• Exponent Calculator
• Exponential Function Calculator
• Logarithm Calculator
• NEARELENTION FUNCTION
• LOGARITHM CALCUTUTURE
• NEARELENTIO
• Калькулятор кубического корня
• Калькулятор n-го корня числа
• Калькулятор квадратных уравнений
• Онлайн-калькулятор факториала
• Калькулятор гипотенузы
• Калькулятор наибольшего общего делителя
• Калькулятор наименьшего общего кратного
• Калькулятор умножения
• Онлайн-калькулятор

Как решить кубическое уравнение | Решение кубического уравнения

Как решить кубическое уравнение

Вопрос

Задача: Как решить кубическое уравнение

Ответ

Следующая оценка изображает значение кубического уравнения и подходы к решению кубического уравнения . Кубическое уравнение может быть представлено в следующем виде:

ax ³ + bx ² + cx + d = 0.

Основным критерием для кубического уравнения является то, что значение «а» в уравнении не может быть нулем, в то время как любой или все «b», «c» или «d» могут быть связаны с нулевым значением. Коэффициенты a, b, c и d могут быть как действительными, так и комплексными числами. Подобно случаю квадратного уравнения, имеющего два действительных корня, кубическое уравнение может иметь три действительных корня или один корень. Некоторые примеры как решать кубические уравнения предложить следующие форматы кубических уравнений,

• 4x ³ + 2x ² + 5x + 2 = 0
• 9x ³ + 27 = 0
• х ³ + 6х = 0

Чтобы решить кубическое уравнение , важно понимать, что оно отличается от квадратного уравнения, и вместо отсутствия реального решения кубическое уравнение может дать решение в виде минимум одного корня. Обычная стратегия решения кубического уравнения заключалась в его сведении к квадратному уравнению с последующим применением подхода формулы или факторизации для получения решения (Ames, 2014).

Целесообразно следовать общему уравнению для решения кубических уравнений, которое может быть представлено следующим образом: форме и может быть представлено в виде следующего примера:

x ² + 4x – 1= 6/x

Шаг 1
Поскольку представленное уравнение не имеет стандартной формы, его необходимо преобразовать в кубическое уравнение. Чтобы решить кубическое уравнение, необходимо умножить «x» на уравнение с обеих сторон, чтобы избавиться от дроби, чтобы получить

x ³ + 4x ² – x = 6

Шаг 2
Обобщение предоставленного уравнения в кубическое уравнение важно при решении кубических уравнений. Вы можете вычесть 6 из любой части уравнения, полученного на шаге 1, чтобы получить

x ³ + 4x ² – x- 6 = 0

Использование факторной теоремы для решения кубических уравнений:
Факторная теорема предполагает, что остаток многочлена p (x) делится на множитель многочлена, т. Е. (x-a) равен нулю.

p(x) = (x – a)q(x) + r(x)

Учитывая приведенное выше уравнение, если p(x) разделить на (x-a), то остаток равен нулю.

p(x) = (x – a)q (x)

Рассмотрим следующую задачу: решение х = -2.

Согласно теореме о множителях очевидно, что (x+2) можно принять за множитель всего выражения, поскольку решение представлено как x= -2. Следовательно, уравнение:

x ³ – 5x ² – 2x+24 = 0

Можно представить в виде

(x+2)(x ² + ax+b)=0

‘0002 Здесь a’ и ‘b’ обозначают числа, и их значения можно получить путем синтетического деления, выполнив шаги, показанные ниже.

Шаг 1
Определите коэффициенты a, b, c и d в кубическом уравнении, представленном в качестве задачи. Значения обозначены как 1, -5, 2 и 24 соответственно. Постройте коэффициенты следующим образом, отметив известный корень, то есть x = -2 на правой стороне вертикали.

Шаг 2
На этом шаге как решать кубические уравнения , вы должны умножить полученное число, т. е. 1, на известное решение, т.е. x= -2. Результат умножения должен быть представлен в другой строке следующим образом.

Шаг 3
IСложите числа во втором столбце, что даст результат:

Шаг 4
IЧисло, полученное на предыдущем шаге, нужно умножить на результат известного решения, т.е. -2. Полученный результат должен быть представлен во второй строке над линией с левой стороны как

Шаг 5
Чтобы решить кубическое уравнение, этот шаг следует шагу 3 и суммирует числа в столбце, чтобы получить в результате 12. Результат может быть представлен в виде:

Шаг 6
Процесс необходимо повторить, чтобы получить следующее:

Шаг 7
Окончательный нулевой результат в нижней строке предполагает, что x = -2 является проверенным корнем предложенного кубического уравнения. Результаты на этом этапе отражают коэффициенты квадратного уравнения, которое можно записать как

x ² – 7x+12

Это уравнение можно умножить на коэффициент (x+2), чтобы преобразовать кубическое уравнение в следующий формат:

(x+2)(x ² – 7x + 12) =0

Шаг 8
Применение квадратного члена обобщило уравнение в

(x +2) (x – 3) (x – 4) = 0

Этот результат решения кубического уравнения предполагает, что корни кубического уравнения x = -2, 3 или 4.

Другой пример:

Давайте возьмем следующее уравнение, чтобы уточнить решение кубического уравнения:

x ³ – 7x-6=0

Шаг 1
На этом шаге вы должны предположить, что x = -1 является действительным решением, и ввод этого значения в уравнение дает результат как ноль, что предполагает, что (x + 1) является фактором, влияющим на то, как решать кубические уравнения. Уравнение можно записать так:

(x+1)(x ² +ax+b)= 0

Шаг 2
Следуя подходу синтетического деления, как показано в предыдущем примере, коэффициенты кубическое уравнение идентифицировано. Значения 1, 0, -7 и -6 должны быть записаны в верхней части строки слева от вертикали, а справа вы можете написать действительное решение (x = -1) следующим образом:

Шаг 3
Теперь можно умножить полученное число, т.е. 1, на известный корень и представить результат во второй строке следующим образом,

Шаг 4
Сложить числа в первом столбце чтобы получить следующий результат,

Этот шаг необходимо повторить, добавив числа в столбце.