Найти магнитную индукцию в точке а: Как найти магнитную индукцию в точке равноудаленной от…

Методика решения задач

При решении задач на данную тему надо пользоваться общей методикой решения задач, но существуют тонкости, которые необходимо учитывать в этом разделе электромагнетизма. Порядок решения задач на нахождение индукции или напряженности магнитного поля от одного или нескольких источников магнитного поля следующий.

1. Записать условия задачи кратко и перевести все численные данные в единую систему единиц.

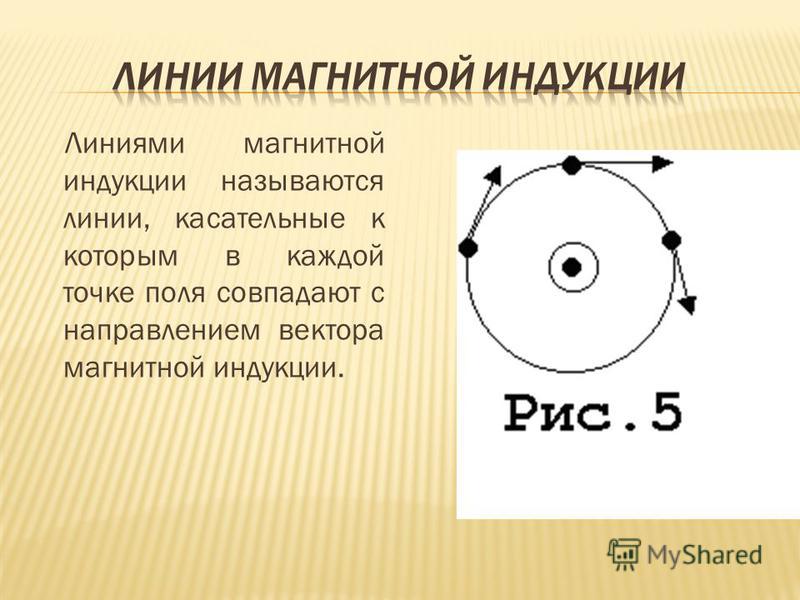
2. Нарисовать рисунок. При этом следует помнить, что индукция или напряженность магнитного поля – величины векторные, которые характеризуются как величиной, так и направлением.

3. Для изображения вектора магнитной индукции или напряженности магнитного поля необходимо нарисовать силовые линии магнитной индукции, проходящие через точку пространства, в которой необходимо определить магнитную индукцию, и изобразить их направление по правилу буравчика.

4. Вектор магнитной индукции, так же как и вектор напряженности поля будет совпадать с касательной к силовым линиям в данной точке.

5. Если поле создается несколькими проводниками с током или несколькими частями проводника с током, имеющим сложную геометрию, то результирующую магнитную индукцию или напряженность следует искать по принципу суперпозиции как векторную сумму всех напряженностей или магнитных индукций поля..

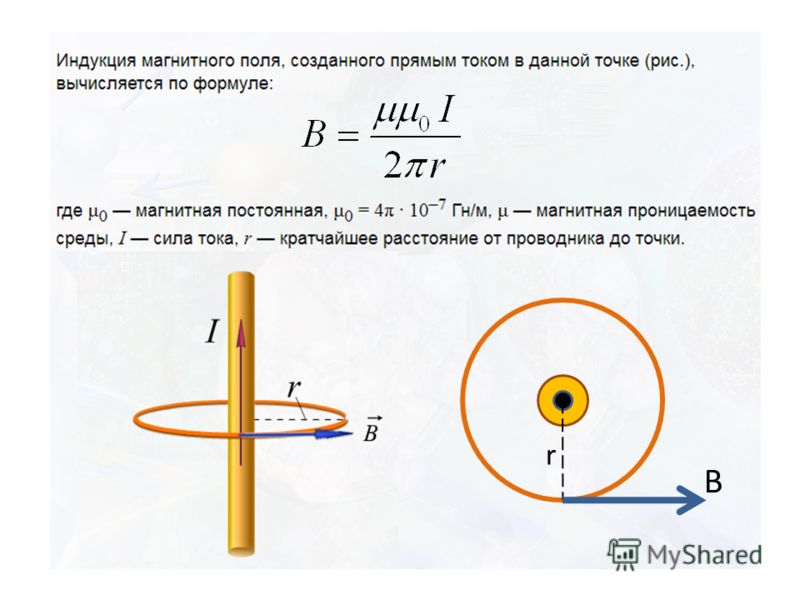
6. Величину каждой магнитной индукции или напряженности определяют апо закону Био-Савара-Лапласа в соответствии с геометрией проводника.

Задача 1. Два параллельных бесконечно длинных провода, по которым текут в одном направлении токи I₁ = 60 А и I₂ = 30 А, расположены на расстоянии d = 10 см друг от друга в воздухе . Определить магнитную индукцию B в точках:

1. А₁, расположенной между проводниками с током на расстоянии

   d/2 от каждого из них;

2. А₂, расположенной на расстоянии d/2 от проводника с током I₁ и на расстоянии 3d/2 от проводника с током I₂;

3. А₃,, расположенной на расстоянии R₁ = 5 см от первого тока и на расстоянии R₂ = 12 см от второго тока.

I₁ = 60 А Найдем магнитную индукция в точке А₁.

I₂ = 30 А Для этого нарисуем рисунок.

R₁ = 5 см = 5^.10^-2 м

R₂ = 12 см = 12^. 10^-2 м

d = 10 см = 10^-1 м

B = ?

Согласно принципу суперпозиции

B = B₁ + B₂

В проекции на выбранную ось y это уравнение примет вид:

B = B₂ – B₁.

прямого бесконечно длинного провода

Подставив численные значения величин, получим значение магнитной индукции в точке А_1..

B = — 120 мкТл

Знак минус означает, что направление результирующей магнитной индукции противоположно выбранной оси y.

Найдем магнитную индукция в точке А₂

I₁

По принципу суперпозиции магнитная индукция в точке А₂ равна

B = B₁ + B_2,

а в проекции на ось y это уравнение примет вид:

B = B₁

+ B₂.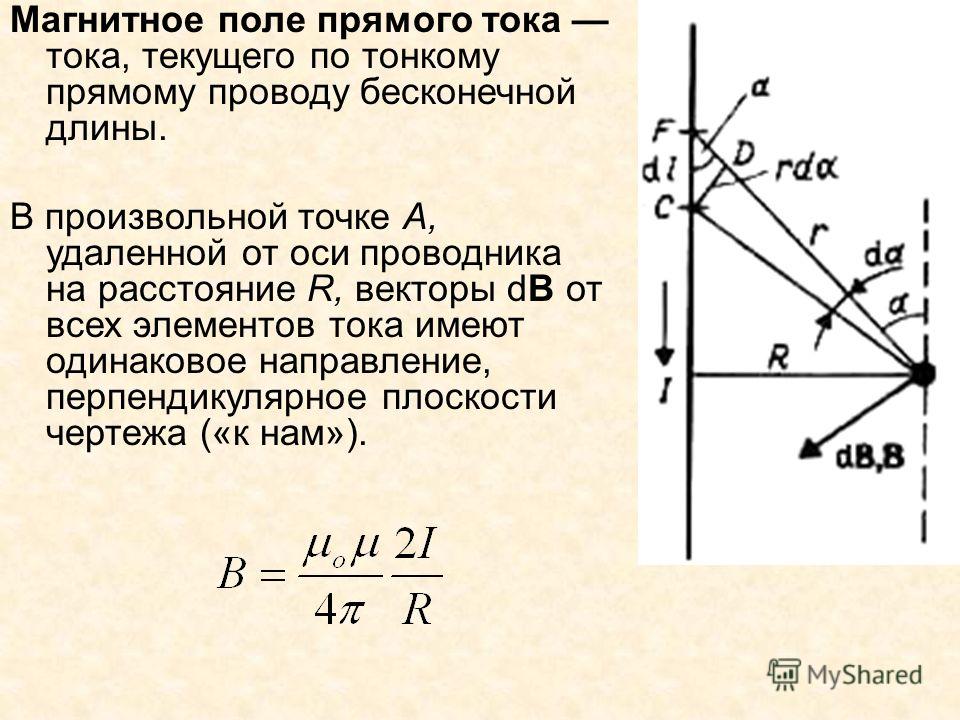

Величина магнитной индукции от первого и второго тока определяется по закону Био-Савара-Лапласа для прямого бесконечно длинного проводника с током:

Подставив численные значения величин, получаем:

B=200 мкТл.

Найдем магнитную индукция в точке А_3.

По принципу суперпозиции результирующая магнитная индукция равна векторной сумме магнитных индукций:

B = B₁ + B₂

Модуль результирующей магнитной индукции можно получить по теореме косинусов:

,

где  — угол между векторами B₁ и B_2. Cos  из геометрического треугольника:

Величины каждой магнитной индукции получим из закона Био-Савара-Лапласа для прямого бесконечно длинного проводника с током:

Подставив численные значения, получим:

B =

Задача 2. Длинный провод с током I = 50 А изогнут под углом =2/3 и находится в воздухе. Определить магнитную индукцию в точке А₁, находящуюся на продолжении одной из сторон угла на расстоянии d = 5 см от его вершины, и в точке А₂,, находящейся на биссектрисе угла на расстоянии d = 5 см от его вершины.

Д ля определения индукции магнитного поля в точке А₁ нужно разбить фигуру на два участка 1 и 2. По принципу суперпозиции результирующая магнитная индукция будет равна векторной сумме магнитных индукция от первого и второго участков провода:

Магнитная индукция В

2 = 0, как следует из закона Био-Савара-Лапласа ,согласно которому в точках, лежащих на оси проводника dВ = 0 ( ).Магнитную индукцию B₂ найдем, воспользовавшись формулой закона Био-Савара-Лапласа для проводника конечной длины с несимметричной точкой, в которой ищем магнитную индукцию,

Для этого надо найти величину r₀ – кратчайшего расстояния от точки до проводника.

,

Для точки А₁ магнитная индукция равна:

B = 17 мТл.

Найдем магнитную индукцию в точке А₂. По принципу суперпозиции В = В₁ + B₂/ По правилу буравчика магнитная индукция будет лежать вдоль прямой, перпендикулярной плоскости чертежа, и направлена на нас.

B = 35 мТл.

Задача3.Бесконечно длинный проводник, находящийся в воздухе, изогнут так, как это показано на рисунке. Радиус дуги R = 10 см. Определить магнитную индукцию поля, создаваемого в точке О током I = 80 А, текущем в этом проводнике.

I = 80 А

R = 0,1 м

B = ?

Рисунок

Для решения задачи разделим проводник на три участка. Тогда по принципу суперпозиции результирующая индукция поля будет равна векторной сумме магнитных индукций от каждого участка. Применив правило буравчика для каждого участка проводника можно увидеть, что все они направлены вдоль прямой, перпендикулярной плоскости чертежа на нас и следователь векторное сложение можно заменить скалярным сложением: B = B₁ + B₂ +

B₃ Причем B₃ = 0 (см. предыдущую задачу).Найдем индукцию магнитного поля для каждого участка

B = 4,14 мкТл.

Задача 4.По тонкому проводящему кольцу, находящемуся в воздухе, радиуса R = 10 см течет ток I = 80 А. Найти магнитную индукцию в точке А, Равноудаленной от всех точек кольца на расстояние, а = 20 см.

R = 0,1 м Для решения задачи воспользуемся законом Био-Савара-Лапласа:

I = 80 А ,

а = 0,2 м где dB – магнитная индукция поля, создаваемого элементом тока Idl в точке, определяемой радиусом-вектором r.

B = ?

Выделим на кольце элемент dI и от

него в точку А проведем радиус-вектор r. Вектор dB направим в

с оответствии с правилом буравчика.

Согласно принципу суперпозиции

Магнитных полей, магнитная

индукция B в точке А определяется

интегралом

,где

Разложим вектор dB на две

составляющие: перпендикулярную

плоскости кольца dB₂ и

параллельную этой плоскости dB₁.

Тогда

Заметив, что из соображений симметрии и что от различных элементов dl сонаправлены, заменим векторное суммирование (интегрирование) скалярным:

(поскольку dl перпендикулярен r и, следовательно ). Таким образом,

; ;

Окончательно получим

Подставив численные значения, получим

B = 6,3 мкТл.

Задача 5.Определить магнитную индукцию поля, созданного соленоидом длиной L=5 см и радиусом витка R

=2 см , в точке, отстоящей от конца соленоида на расстояние а = 0,5 см, если по соленоиду протекает ток I = 50 А.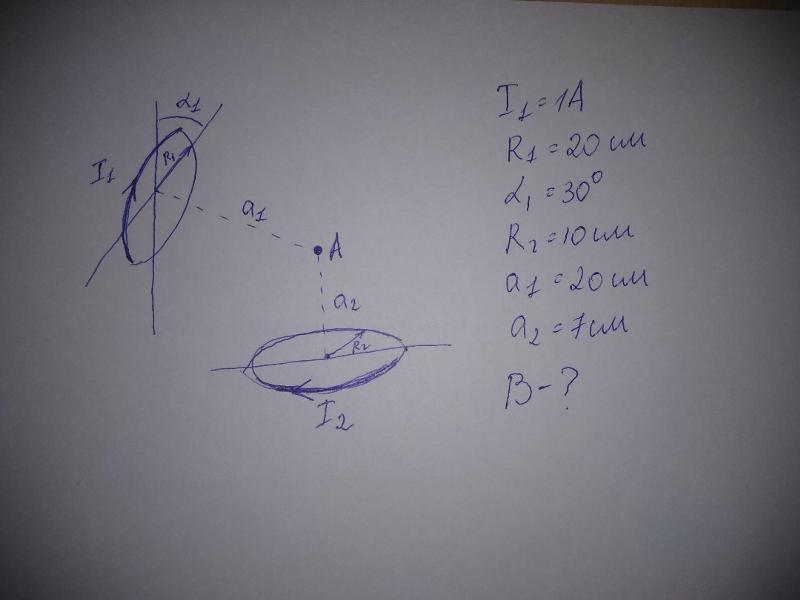 Cоленоид имеет N =20 витков.

R = 0,02 м = 2^.10^-2 м

L = 0,05 м = 5^.10^-2 м

а = 0,005 м = 5^.10^-3 м

I = 50 А

Рассчитаем магнитную индукцию в точке А.Для этого выберем на соленоиде элемент dL, содержащий n = N/L витков на единицу длины. При токе I его можно рассматривать как круговой ток IndL, для которого магнитная индукция равна (см. предыдущую задачу):

,

так как

, и

Окончательно получаем:

,

где и

Подставив численные значения, получим B = 2,5 мТл.

Белорусский государственный университет транспорта — БелГУТ (БИИЖТ)

Регистрация на конференцию ИТЭС

Регистрация на конференцию «Актуальные проблемы теории и практики современной науки»

Регистрация на конференцию «Архитектура и строительство: традиции и инновации»

Как поступить в БелГУТ

Как получить место

в общежитии БелГУТа

Как поступить иностранному гражданину

События

Все события

Пн	Вт	Ср	Чт	Пт	Сб	Вс
	1	2	3	4	5 Дата : 2022-11-05	6 Дата : 2022-11-06
7	8 Дата : 2022-11-08	9	10	11	12 Дата : 2022-11-12	13
14	15	16 Дата : 2022-11-16	17 Дата : 2022-11-17	18	19 Дата : 2022-11-19	20
21 Дата : 2022-11-21	22	23	24 Дата : 2022-11-24	25 Дата : 2022-11-25	26 Дата : 2022-11-26	27
28	29	30

Все анонсы

• ПРОГРАММА. XII Международная научно-практическая к…
• Приглашаем в бассейн
• V Международная научно-практическая конференция ст…
• Олимпиада по высшей математике для студентов…
• Навстречу Дню освобождения г. Гомеля от немецко-…
• Открытая лекция «Конституция как основной закон го…
• А, ну-ка, первокурсник — 2022
• Кубок БелГУТа по гандболу и соревнования по мини-ф…
• С Днем студента поздравляет Студсовет!…
• ЕДИ «Жилищно-коммунальное хозяйство: перспективы р…

Анонсы

Университет

Абитуриентам

Студентам

Конференции

Приглашения

ПРОГРАММА. XII Международная научно-практическая к…

Приглашаем в бассейн

V Международная научно-практическая конференция ст…

Олимпиада по высшей математике для студентов…

Новости

Университет

Международные связи

Спорт

Воспитательная работа

Жизнь студентов

Новости подразделений



• Университет

Встреча ректора БелГУТа с коллективом локомотивного депо Гомель. ..
23 ноября 2022

• Университет

Братские могилы на Лещинском кладбище
23 ноября 2022

• Воспитательная работа

Экскурсия на участок обороны Гомельского народного ополчения…
23 ноября 2022

• Воспитательная работа

Будь в теме!
23 ноября 2022

• Студенческая жизнь

Наши студотрядовцы — лучшие!
23 ноября 2022

• Университет

Лучший молодой специалист года!
23 ноября 2022

• Воспитательная работа

Это — та самая живая история
23 ноября 2022

• Университет

День открытых дверей механического факультета. ..
22 ноября 2022

• Университет

«Полесские зори» на Международном фестивале «ТранспАрт-2022»…
22 ноября 2022

Другие новости

• За содействие в поддержке одаренной и талантливой молодежи…
• «А, ну-ка, первокурсник!» — 2022
• Второй тур осенней серии игр «Что? Где? Когда?»…
• Победа в открытом турнире по аэробике спортивной и танцевальной «Золот…
• Факультет УПП на страже порядка!
• Конкурс «Лучшая комната общежития № 4» от БРСМ БелГУТа…
• Повышение квалификации по вопросам учета, анализа и контроля материаль…
• Победы наших гиревиков!
• Единый день информирования на тему «Жилищно-коммунальное хозяйство: пе…
• Прием ректором университета студентов по личным вопросам…
• Gaudeamus igitur-2022 поет хор БелГУТа

КУДА ПОСТУПАТЬ

Все факультеты

БелГУТ на Доске почета

Достижения университета

Предложения

Все предложения

Видеотека

Все видео

Фотогалерея

Все фото

20.

3 Электромагнитная индукция — физика

Раздел Цели обучения

К концу этого раздела вы сможете делать следующее:

• Объяснять, как изменяющееся магнитное поле создает ток в проводе
• Расчет индуцированной электродвижущей силы и тока

Поддержка учителей

Поддержка учителей

Цели обучения в этом разделе помогут вашим учащимся освоить следующие стандарты:

• (5) Учащийся знает природу сил в физическом мире. Ожидается, что студент:
  • (Г) исследовать и описывать взаимосвязь между электрическими и магнитными полями в таких приложениях, как генераторы, двигатели и трансформаторы.

Кроме того, в Руководстве по физике для старшей школы OSX рассматривается содержание этого раздела лабораторной работы под названием «Магнетизм», а также следующие стандарты:

• (5) Научные концепции. Учащийся знает природу сил в физическом мире. Ожидается, что студент:
  • (ГРАММ) исследовать и описывать взаимосвязь между электрическими и магнитными полями в таких приложениях, как генераторы, двигатели и трансформаторы.

Основные термины раздела

ЭДС

индукция

магнитный поток

Изменение магнитных полей

В предыдущем разделе мы узнали, что ток создает магнитное поле. Если природа симметрична, то, возможно, магнитное поле может создавать ток. В 1831 году, примерно через 12 лет после открытия того, что электрический ток создает магнитное поле, английский ученый Майкл Фарадей (1791–1862) и американский ученый Джозеф Генри (1797–1878) независимо продемонстрировали, что магнитные поля могут создавать токи. Основной процесс генерации токов магнитными полями называется индукцией; этот процесс также называют магнитной индукцией, чтобы отличить его от индукционной зарядки, в которой используется электростатическая кулоновская сила.

Когда Фарадей открыл то, что сейчас называется законом индукции Фарадея, королева Виктория спросила его, как можно использовать электричество. «Мадам, — ответил он, — что хорошего в ребенке?» Сегодня токи, вызванные магнитными полями, необходимы для нашего технологического общества. Электрический генератор, который можно найти во всем, от автомобилей до велосипедов и атомных электростанций, использует магнетизм для выработки электрического тока. К другим устройствам, использующим магнетизм для индукции тока, относятся катушки звукоснимателей в электрогитарах, трансформаторы любого размера, некоторые микрофоны, ворота безопасности в аэропортах и ​​демпфирующие механизмы на чувствительных химических весах.

В одном из экспериментов Фарадея для демонстрации магнитной индукции стержневой магнит перемещался через проволочную катушку и измерялся результирующий электрический ток через провод. Схема этого эксперимента показана на рис. 20.33. Он обнаружил, что ток индуцируется только тогда, когда магнит движется относительно катушки. Когда магнит неподвижен относительно катушки, ток в катушке не индуцируется, как показано на рис. 20.33. Кроме того, перемещение магнита в противоположном направлении (сравните рис. 20.33 с рис. 20.33) или изменение полюсов магнита (сравните рис. 20.33 с рис. 20.33) приводит к возникновению тока в противоположном направлении.

Рисунок 20.33 Движение магнита относительно катушки производит электрические токи, как показано. Такие же токи возникают, если катушку перемещать относительно магнита. Чем больше скорость, тем больше величина тока, а ток равен нулю, когда нет движения. Ток, возникающий при перемещении магнита вверх, имеет направление, противоположное току, возникающему при перемещении магнита вниз.

Виртуальная физика

Закон Фарадея

Попробуйте эту симуляцию, чтобы увидеть, как движение магнита создает ток в цепи. Лампочка загорается, чтобы показать, когда течет ток, а вольтметр показывает падение напряжения на лампочке. Попробуйте провести магнит через катушку с четырьмя витками и через катушку с двумя витками. Какая катушка при той же скорости магнита выдает большее напряжение?

Когда северный полюс находится слева, а магнит перемещается справа налево, возникает положительное напряжение, когда магнит входит в катушку. Напряжение какого знака получится, если повторить опыт с южным полюсом слева?

1. Знак напряжения изменится, потому что направление тока изменится при перемещении южного полюса магнита влево.

2. Знак напряжения останется прежним, потому что направление тока не изменится при перемещении южного полюса магнита влево.

3. Знак напряжения изменится, потому что величина протекающего тока изменится при перемещении южного полюса магнита влево.

4. Знак напряжения останется прежним, поскольку величина протекающего тока не изменится при перемещении южного полюса магнита влево.

Индуцированная электродвижущая сила

Если в катушке индуцируется ток, Фарадей рассудил, что должно существовать то, что он назвал электродвижущей силой , проталкивающей заряды через катушку. Эта интерпретация оказалась неверной; вместо этого внешний источник, выполняющий работу по перемещению магнита, добавляет энергию к зарядам в катушке. Энергия, добавляемая на единицу заряда, имеет единицы вольт, поэтому электродвижущая сила на самом деле представляет собой потенциал. К сожалению, название «электродвижущая сила» прижилось, а вместе с ним и возможность спутать его с реальной силой. По этой причине мы избегаем термина электродвижущая сила и просто используйте аббревиатуру ЭДС , имеющую математический символ ε. ε. ЭДС можно определить как скорость, с которой энергия извлекается из источника на единицу тока, протекающего по цепи. Таким образом, ЭДС представляет собой энергию на единицу заряда , добавляемую источником, что контрастирует с напряжением, которое представляет собой энергию на единицу заряда , высвобождаемую при протекании зарядов по цепи.

Чтобы понять, почему в катушке возникает ЭДС из-за движущегося магнита, рассмотрим рис. 20.34, на котором показан стержневой магнит, движущийся вниз относительно проволочной петли. Первоначально через петлю проходят семь силовых линий магнитного поля (см. изображение слева). Поскольку магнит удаляется от катушки, только пять силовых линий магнитного поля проходят через петлю через короткое время ΔtΔt (см. изображение справа). Таким образом, когда происходит изменение числа силовых линий магнитного поля, проходящих через область, определяемую проволочной петлей, в проволочной петле индуцируется ЭДС. Подобные эксперименты показывают, что ЭДС индукции пропорциональна скорость изменения магнитного поля. Математически мы выражаем это как

ε∝ΔBΔt,ε∝ΔBΔt,

20,24

где ΔBΔB — изменение величины магнитного поля за время ΔtΔt, а A — площадь петли.

Рисунок 20.34 Стержневой магнит движется вниз по отношению к проволочной петле, так что количество силовых линий магнитного поля, проходящих через петлю, со временем уменьшается. Это приводит к тому, что в петле индуцируется ЭДС, создающая электрический ток.

Обратите внимание, что силовые линии магнитного поля, лежащие в плоскости проволочной петли, на самом деле не проходят через петлю, как показано крайней левой петлей на рис. 20.35. На этом рисунке стрелка, выходящая из петли, представляет собой вектор, величина которого равна площади петли и направление которого перпендикулярно плоскости петли. На рис. 20.35 при повороте петли от θ=90°θ=90° до θ=0°, θ=0° вклад силовых линий магнитного поля в ЭДС увеличивается. Таким образом, для создания ЭДС в проволочном контуре важна составляющая магнитного поля, равная перпендикулярно плоскости контура, который равен Bcosθ.Bcosθ.

Это аналог паруса на ветру. Думайте о проводящей петле как о парусе, а о магнитном поле — как о ветре. Чтобы максимизировать силу ветра, действующую на парус, парус ориентируют так, чтобы вектор его поверхности указывал в том же направлении, что и ветер, как в крайней правой петле на рис. 20.35. Когда парус выровнен так, что вектор его поверхности перпендикулярен ветру, как в крайней левой петле на рис. 20.35, тогда ветер не действует на парус.

Таким образом, с учетом угла магнитного поля по отношению к площади пропорциональность E∝ΔB/ΔtE∝ΔB/Δt становится равной

E∝ΔBcosθΔt.E∝ΔBcosθΔt.

20,25

Рисунок 20. 35 Магнитное поле лежит в плоскости крайнего левого контура, поэтому в этом случае оно не может генерировать ЭДС. Когда петлю поворачивают так, что угол магнитного поля с вектором, перпендикулярным площади петли, увеличивается до 90°90° (см. самую правую петлю), магнитное поле вносит максимальный вклад в ЭДС в петле. Точки показывают, где силовые линии магнитного поля пересекают плоскость, определяемую петлей.

Другой способ уменьшить количество силовых линий магнитного поля, проходящих через проводящую петлю на рис. 20.35, — не перемещать магнит, а уменьшить петлю. Эксперименты показывают, что изменение площади проводящего контура в постоянном магнитном поле индуцирует в контуре ЭДС. Таким образом, ЭДС, создаваемая в проводящей петле, пропорциональна скорости изменения произведения перпендикулярного магнитного поля и площади петли

ε∝Δ[(Bcosθ)A]Δt,ε∝Δ[(Bcosθ)A]Δt,

20.26

, где BcosθBcosθ — перпендикулярное магнитное поле, а A — площадь контура. Произведение BAcosθBAcosθ очень важно. Оно пропорционально числу силовых линий магнитного поля, проходящих перпендикулярно через поверхность площадью A . Возвращаясь к нашей аналогии с парусом, это было бы пропорционально силе ветра на парусе. Он называется магнитным потоком и обозначается ΦΦ.

Φ=BAcosθΦ=BAcosθ

20,27

Единицей магнитного потока является вебер (Вб), то есть магнитное поле на единицу площади, или Тл/м ² . Вебер также является вольт-секундой (Vs).

ЭДС индукции фактически пропорциональна скорости изменения магнитного потока через проводящую петлю.

ε∝ΔΦΔtε∝ΔΦΔt

20,28

Наконец, для катушки из Н витков ЭДС в Н раз сильнее, чем для одиночного витка. Таким образом, ЭДС, индуцируемая переменным магнитным полем в катушке N петли это

ε∝NΔBcosθΔtA. ε∝NΔBcosθΔtA.

Последний вопрос, на который нужно ответить, прежде чем мы сможем преобразовать пропорциональность в уравнение: «В каком направлении течет ток?» Русский ученый Генрих Ленц (1804–1865) объяснил, что ток течет в направлении, создающем магнитное поле, которое пытается поддерживать постоянный поток в контуре. Например, снова рассмотрим рис. 20.34. Движение стержневого магнита приводит к уменьшению числа направленных вверх силовых линий магнитного поля, проходящих через петлю. Следовательно, в петле создается ЭДС, которая движет ток в направлении, создающем более направленные вверх силовые линии магнитного поля. Используя правило правой руки, мы видим, что этот ток должен течь в направлении, показанном на рисунке. Чтобы выразить тот факт, что ЭДС индукции действует на противодействие изменению магнитного потока через проволочный контур, в пропорциональность ε∝ΔΦ/Δt.ε∝ΔΦ/Δt., которая дает закон индукции Фарадея, вводится знак минус. 9) внутри катушки, направленной влево. Это будет противодействовать увеличению магнитного потока, направленного вправо. Чтобы увидеть, в каком направлении должен течь ток, укажите большим пальцем правой руки в нужном направлении магнитного поля B→катушка,B→катушка, и ток будет течь в направлении, указанном сгибанием пальцев правой руки. Это показано изображением правой руки в верхнем ряду рис. 20.36. Таким образом, ток должен течь в направлении, показанном на рис. 4(а).

На рис. 4(b) направление движения магнита изменено на противоположное. В катушке направленное вправо магнитное поле B→magB→mag из-за движущегося магнита уменьшается. Закон Ленца гласит, что, чтобы противодействовать этому уменьшению, ЭДС будет управлять током, который создает дополнительное магнитное поле, направленное вправо B → катушка B → катушка в катушке. Снова направьте большой палец правой руки в нужном направлении магнитного поля, и ток потечет в направлении, указанном сгибанием пальцев правой руки (рис. 4(b)).

Наконец, на рис. 4(с) магнит перевернут так, что южный полюс находится ближе всего к катушке. Теперь магнитное поле B→magB→mag указывает на магнит, а не на катушку. Когда магнит приближается к катушке, это вызывает увеличение направленного влево магнитного поля в катушке. Закон Ленца говорит нам, что ЭДС, индуцируемая в катушке, будет направлять ток в направлении, создающем магнитное поле, направленное вправо. Это будет противодействовать увеличивающемуся магнитному потоку, направленному влево из-за магнита. Повторное использование правила правой руки, как показано на рисунке, показывает, что ток должен течь в направлении, показанном на рисунке 4(c).

Рисунок 20.36 Закон Ленца говорит нам, что ЭДС магнитного поля будет вызывать ток, который сопротивляется изменению магнитного потока в цепи. Это показано на панелях (a)–(c) для различных ориентаций и скоростей магнита. Правые руки справа показывают, как применить правило правой руки, чтобы определить, в каком направлении течет индуцированный ток вокруг катушки.

Виртуальная физика

Электромагнитная лаборатория Фарадея

Эта симуляция предлагает несколько действий. Сейчас нажмите на вкладку Pickup Coil, которая представляет собой стержневой магнит, который вы можете перемещать через катушку. При этом вы можете видеть, как электроны движутся в катушке, и загорается лампочка, или вольтметр показывает напряжение на резисторе. Обратите внимание, что вольтметр позволяет вам видеть знак напряжения при перемещении магнита. Вы также можете оставить стержневой магнит в покое и двигать катушку, хотя наблюдать результаты будет труднее.

Исследования PhET: Электромагнитная лаборатория Фарадея Поиграйте со стержневым магнитом и катушками, чтобы узнать о законе Фарадея. Переместите стержневой магнит рядом с одной или двумя катушками, чтобы лампочка загорелась. Посмотрите на линии магнитного поля. Счетчик показывает направление и величину тока. Просмотрите линии магнитного поля или используйте измеритель, чтобы показать направление и величину тока. Вы также можете играть с электромагнитами, генераторами и трансформаторами!

Нажмите, чтобы просмотреть содержимое

Расположите стержневой магнит северным полюсом вправо и поместите приемную катушку справа от стержневого магнита. Теперь переместите стержневой магнит к катушке и посмотрите, как движутся электроны. Это та же самая ситуация, что изображена ниже. Течет ли ток в моделировании в том же направлении, как показано ниже? Объясните, почему да или почему нет.

1. Да, ток в симуляции течет, как показано, потому что направление тока противоположно направлению потока электронов.

2. Нет, ток в моделировании течет в противоположном направлении, потому что направление тока совпадает с направлением потока электронов.

Смотреть физику

Наведенный ток в проводе

В этом видео показано, как можно индуцировать ток в прямом проводе, перемещая его через магнитное поле. через однородное магнитное поле (0,30 Тл) ẑ ? Провод лежит в направлении х . Кроме того, какой конец провода находится под более высоким потенциалом — пусть нижний конец провода будет на y = 0, а верхний конец на y = 0,5 м)?

1. 0,15 В и нижний конец провода будет под более высоким потенциалом
2. 0,15 В и верхний конец провода будет под более высоким потенциалом
3. 0,075 В и нижний конец провода будет под более высоким потенциалом
4. 0,075 В и верхний конец провода будет под более высоким потенциалом

Рабочий пример

ЭДС, индуцированная движущимся магнитом в проводящей катушке

Представьте, что магнитное поле проходит через катушку в направлении, указанном на рис. 20.37. Диаметр катушки 2,0 см. Если магнитное поле изменяется от 0,020 до 0,010 Тл за 34 с, каковы направление и величина индуцированного тока? Предположим, катушка имеет сопротивление 0,1 Ом. Ом.

Рисунок 20.37 Катушка, через которую проходит магнитное поле B .

Стратегия

Используйте уравнение ε=−NΔΦ/Δtε=−NΔΦ/Δt, чтобы найти ЭДС индукции в катушке, где Δt=34sΔt=34s . Подсчитав количество петель в соленоиде, мы находим, что в нем 16 петель, поэтому N=16.N=16. Используйте уравнение Φ=BAcosθΦ=BAcosθ для расчета магнитного потока и мы использовали cos0°=1.cos0°=1. Поскольку площадь соленоида не меняется, изменение магнитного потока через соленоид равно

ΔΦ=ΔBπ(d2)2.ΔΦ=ΔBπ(d2)2.

20,31

Как только мы найдем ЭДС, мы можем использовать закон Ома, ε=IR,ε=IR, чтобы найти ток.

Наконец, закон Ленца говорит нам, что ток должен создавать магнитное поле, которое препятствует уменьшению приложенного магнитного поля. Таким образом, ток должен создавать магнитное поле справа.

Решение

Объединение уравнений ε=−NΔΦ/Δtε=−NΔΦ/Δt и Φ=BAcosθΦ=BAcosθ дает

ε=-NΔΦΔt=-NΔBπd24Δt. ε=-NΔΦΔt=-NΔBπd24Δt.

20,32

Решение закона Ома для тока и использование этого результата дает

εR=-NΔBπd24RΔt=-16(-0,010T)π(0,020м)24(0,10Ом)(34с)=15мкА.

20,33

Закон Ленца говорит нам, что ток должен создавать магнитное поле справа. Таким образом, мы направляем большой палец правой руки вправо и сгибаем правые пальцы вокруг соленоида. Ток должен течь в том направлении, в котором указывают наши пальцы, поэтому он входит в левый конец соленоида и выходит в правый конец.

Обсуждение

Давайте посмотрим, имеет ли смысл знак минус в законе индукции Фарадея. Определите направление магнитного поля как положительное. Это означает, что изменение магнитного поля отрицательно, как мы обнаружили выше. Знак минус в законе индукции Фарадея сводит на нет отрицательное изменение магнитного поля, оставляя нам положительный ток. Следовательно, ток должен течь в направлении магнитного поля, что мы и нашли.

Теперь попробуйте определить положительное направление как направление, противоположное направлению магнитного поля, т. е. положительное направление слева на рис. 20.37. В этом случае вы обнаружите отрицательный ток. Но поскольку положительное направление направлено влево, отрицательный ток должен течь вправо, что опять-таки согласуется с тем, что мы нашли, используя закон Ленца.

Рабочий пример

Магнитная индукция из-за изменения размера цепи

Цепь, показанная на рис. 20.38, состоит из U-образного провода с резистором, концы которого соединены скользящим токопроводящим стержнем. Магнитное поле, заполняющее площадь, ограниченную контуром, постоянно и составляет 0,01 Тл. Если стержень тянут вправо со скоростью v=0,50 м/с, v=0,50 м/с, какой ток индуцируется в контуре и в каком направление течет ток?

Рисунок 20.38 Схема слайдера. Магнитное поле постоянно, и стержень тянется вправо со скоростью против . Изменяющаяся площадь, окруженная цепью, индуцирует ЭДС в цепи.

Стратегия

Мы снова используем закон индукции Фарадея, E=-NΔΦΔt, E=-NΔΦΔt, хотя на этот раз магнитное поле постоянно, а площадь, ограниченная контуром, изменяется. Схема содержит один контур, поэтому N=1.N=1. Скорость изменения площади составляет ΔAΔt=vℓ.ΔAΔt=vℓ. Таким образом, скорость изменения магнитного потока равна

0005

20,34

где мы использовали тот факт, что угол θθ между вектором площади и магнитным полем равен 0°. Зная ЭДС, мы можем найти силу тока, используя закон Ома. Чтобы найти направление тока, применим закон Ленца.

Решение

Закон индукции Фарадея дает

E=-NΔΦΔt=-Bvℓ.E=-NΔΦΔt=-Bvℓ.

20,35

Решая закон Ома для тока и используя предыдущий результат для ЭДС, получаем =-BvℓR=-(0,010T)(0,50м/с)(0,10м)20Ом=25мкА.

20,36

По мере того, как стержень скользит вправо, магнитный поток, проходящий через цепь, увеличивается. Закон Ленца говорит нам, что индуцированный ток создаст магнитное поле, противодействующее этому увеличению. Таким образом, магнитное поле, создаваемое индуцированным током, должно проникать внутрь страницы.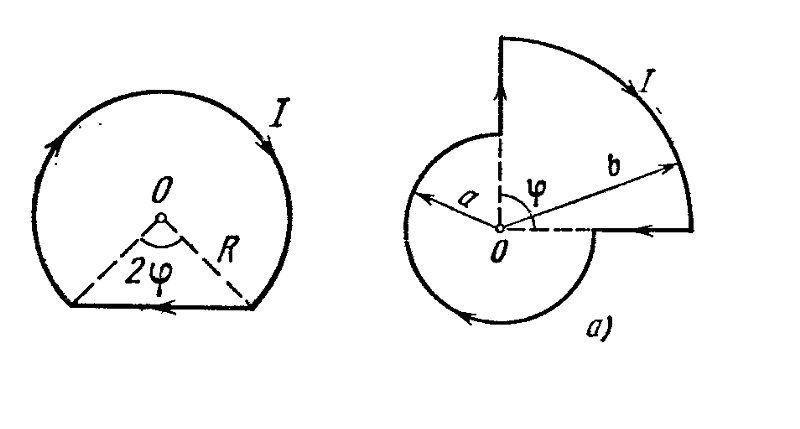 Скручивание пальцев правой руки вокруг петли по часовой стрелке приводит к тому, что большой палец правой руки указывает на страницу, что является желаемым направлением магнитного поля. Таким образом, ток должен течь по часовой стрелке вокруг цепи.

Обсуждение

Сохраняется ли энергия в этой цепи? Внешний агент должен тянуть стержень с достаточной силой, чтобы просто уравновесить силу, действующую на провод с током в магнитном поле — напомним, что F=IℓBsinθ. F=IℓBsinθ. Скорость, с которой эта сила действует на стержень, должна быть уравновешена скоростью, с которой цепь рассеивает мощность. Используя F=IℓBsinθ, F=IℓBsinθ, сила, необходимая для вытягивания проволоки с постоянной скоростью v , равна

Fpull=IℓBsinθ=IℓB,Fpull=IℓBsinθ=IℓB,

20,37

где мы использовали тот факт, что угол θθ между током и магнитным полем составляет 90°.90°. Подстановка приведенного выше выражения для тока в это уравнение дает

Fpull=IℓB=−BvℓR(ℓB)=−B2vℓ2R. Fpull=IℓB=−BvℓR(ℓB)=−B2vℓ2R.

20,38

Мощность, вносимая агентом, тянущим стержень, равна Fpullv, или Fpullv, или

Ppull=Fpullv=−B2v2ℓ2R.Ppull=Fpullv=−B2v2ℓ2R.

20,39

Мощность, рассеиваемая цепью, равна

Pрассеянное=I2R=(-BvℓR)2R=B2v2ℓ2R.Pрассеянное=I2R=(-BvℓR)2R=B2v2ℓ2R.

20.40

Таким образом, мы видим, что Ppull+Pdissipated=0,Ppull+Pdissipated=0, что означает сохранение мощности в системе, состоящей из контура и агента, тянущего за стержень. Таким образом, в этой системе сохраняется энергия.

Практические задачи

11.

Магнитный поток через одну проволочную петлю изменяется с 3,5 Вб до 1,5 Вб за 2,0 с. Какая ЭДС возникает в контуре?

1. –2,0 В
2. –1,0 В
3. +1,0 В
4. +2,0 В

12.

Чему равна ЭДС катушки с 10 витками, через которую изменяется поток со скоростью 10 Вб/с?

1. –100 В
2. –10 В
3. +10 В
4. +100 В

Проверьте свое понимание

13.

Имея стержневой магнит, как можно индуцировать электрический ток в проволочной петле?

1. Электрический ток индуцируется, если рядом с проволочной петлей находится стержневой магнит.

2. Электрический ток индуцируется, если проволочная петля намотана на стержневой магнит.

3. Электрический ток индуцируется, если стержневой магнит перемещается по проволочной петле.

4. Электрический ток индуцируется, если стержневой магнит находится в контакте с проволочной петлей.

14.

Какие факторы могут вызвать индуцированный ток в проволочной петле, через которую проходит магнитное поле?

1. Наведенный ток можно создать, только изменив размер проволочной петли.

2. Наведенный ток можно создать, только изменив ориентацию проволочной петли.

3. Наведенный ток может быть создан только путем изменения силы магнитного поля.

4. Наведенный ток можно создать, изменив силу магнитного поля, изменив размер проволочной петли или изменив ориентацию проволочной петли.

12.3: Магнитное поле, создаваемое тонким прямым проводом

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

4422

• OpenStax
• OpenStax

Цели обучения

К концу этого раздела вы сможете:

• Объясните, как закон Био-Савара используется для определения магнитного поля, создаваемого тонким прямым проводом.
• Определить зависимость магнитного поля от тонкого прямого провода в зависимости от расстояния до него и тока, протекающего в проводе.
• Нарисуйте магнитное поле, создаваемое тонким прямым проводом, используя второе правило правой руки.

Какой ток необходим для создания значительного магнитного поля, возможно такого же сильного, как поле Земли? Геодезисты скажут вам, что воздушные линии электропередач создают магнитные поля, которые мешают показаниям их компаса. Действительно, когда в 1820 году Эрстед обнаружил, что ток в проводе влияет на стрелку компаса, он не имел дело с чрезвычайно большими токами. Как форма проводов, по которым течет ток, влияет на форму создаваемого магнитного поля? В главе 28 мы отмечали, что токовая петля создает магнитное поле, подобное магнитному стержню, но как насчет прямого провода? Мы можем использовать закон Био-Савара, чтобы ответить на все эти вопросы, включая определение магнитного поля длинного прямого провода.

На рисунке \(\PageIndex{1}\) показан участок бесконечно длинного прямого провода, по которому течет ток I . Чему равно магнитное поле в точке P , расположенной на расстоянии R от провода?

Рисунок \(\PageIndex{1}\): Участок тонкого прямого провода с током. Независимая переменная \(\theta\) имеет пределы \(\theta_1\) и \(\theta_2\).

Начнем с рассмотрения магнитного поля элемента тока \(I \, d\vec{x}\), расположенного в позиции х . Используя правило правой руки 1 из предыдущей главы, \(d\vec{x} \times \hat{r}\) указывает за пределы страницы для любого элемента вдоль проводника. Следовательно, в точке \(P\) магнитные поля всех элементов тока имеют одинаковое направление. Это означает, что мы можем вычислить там чистое поле, оценивая скалярную сумму вкладов элементов. С

\[|d\vec{x} \times \hat{r}| = (dx)(1) \, \sin \, \theta \]

имеем из закона Био-Савара 9{\infty}.\]

Подстановка пределов дает нам решение

\[\boxed{B = \dfrac{\mu_0 I}{2\pi R}.}\]

Силовые линии магнитного поля бесконечного провода имеют круглую форму с центром в проводе (рис. \(\PageIndex{2}\)), и они идентичны во всех плоскостях, перпендикулярных проводу. Поскольку поле уменьшается с расстоянием от провода, расстояние между линиями поля должно соответственно увеличиваться с расстоянием. Направление этого магнитного поля можно найти с помощью второй формы правило правой руки (Рисунок \(\PageIndex{2}\)). Если вы держите провод правой рукой так, чтобы большой палец был направлен вдоль тока, то ваши пальцы обхватывают провод в том же смысле, что и \(\vec{B}\).

Рисунок \(\PageIndex{2}\):​​​​​​​. Некоторые линии магнитного поля бесконечной проволоки. Направление \(B\) можно найти с помощью правила правой руки.

Направление силовых линий можно наблюдать экспериментально, поместив несколько маленьких стрелок компаса на окружность рядом с проводом, как показано на рисунке \(\PageIndex{3a}\). Когда в проводе нет тока, иглы выравниваются с магнитным полем Земли. Однако, когда по проводу проходит большой ток, все стрелки компаса касаются окружности. Железные опилки, разбросанные по горизонтальной поверхности, также очерчивают линии поля, как показано на рисунке \(\PageIndex{3b}\).

Рисунок \(\PageIndex{3}\): Форму линий магнитного поля длинного провода можно увидеть с помощью (а) маленькой стрелки компаса и (б) железных опилок.

Пример \(\PageIndex{1}\): расчет магнитного поля, создаваемого тремя проводами

Три провода расположены по углам квадрата, по всем проводам на страницу поступает ток силой 2 ампера, как показано на рисунке \(\PageIndex{4 }\). Вычислите величину магнитного поля в другом углу квадрата, точке P , если длина каждой стороны квадрата равна 1 см.

Рисунок \(\PageIndex{4}\)​​​​​​​: по трем проводам на страницу поступает ток. Магнитное поле определяется в четвертом углу квадрата.

Стратегия

Рассчитывается магнитное поле каждого провода в нужной точке. Диагональное расстояние рассчитывается по теореме Пифагора. Затем направление вклада каждого магнитного поля определяется путем рисования круга с центром в точке провода и в направлении желаемой точки. Направление вклада магнитного поля от этого провода тангенциально к кривой. Наконец, работая с этими векторами, вычисляется результирующая. 9{-5} T. \end{align}\]

Значение

Геометрия в этой задаче приводит к тому, что вклады магнитного поля в направлениях x и y имеют одинаковую величину. Это не обязательно так, если бы токи были разных значений или если бы провода располагались в разных положениях. Независимо от численных результатов, работа с компонентами векторов даст результирующее магнитное поле в нужной точке.

Упражнение \(\PageIndex{1}\)

Используя пример \(\PageIndex{1}\)​​​​​​​, сохраняя одинаковые токи в проводах 1 и 3, какой ток должен быть в проводе 2 противодействовать магнитным полям проводов 1 и 3 так, чтобы в точке \(P\) не было результирующего магнитного поля?

Решение

4 ампера, вытекающие из страницы

Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойолы Мэримаунт) и Билл Моебс с многими соавторами. Эта работа находится под лицензией OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).

---

Эта страница под названием 12.3: Магнитное поле из-за тонкого прямого провода распространяется под лицензией CC BY 4.

No related posts.