Найти наименьшее общее кратное чисел 18 и 45 решение: Как найти наименьшее общее кратное чисел 18 и 45

Содержание

Наибольший общий делитель и наименьшее общее кратное (НОД и НОК)

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Путь к успеху комбинированный урок по теме:

Наибольший общий делитель и
наименьшее общее кратное
(НОД и НОК).
Учитель математики
Маргарита Николаевна Кондратьева
Великие Луки
2017 год
У С Т Н А Я РАБОТА
Работаем устно
Назовите из данных чисел те, которые являются простыми
25, 13, 27, 45, 29, 1, 14, 17,5, 19, 81,7
13, 29,17,19,7
Работаем устно
Найти НОД и НОК чисел:
•5и9
• 6 и 12
•3и8
• 7 и 21
• 11 и 1
• 24 и 18
НОД= 1 ; НОК= 45
НОД=6 ; НОК=12
НОД=1 ; НОК=24
НОД=7 ; НОК=21
НОД= 1 ; НОК=11
НОД=6 ; НОК=72
ПОВТОРЕНИЕ
У С Т Н А Я РАБОТА
ПОВТОРЕНИЕ
№ 1.

Найдите НОД и НОК чисел 8 и 12 методом перебора.
НОД(a ; b)·НОК(a ; b) = a · b
ПОВТОРЕНИЕ
№ 2. Найдите НОД и НОК чисел 252 и 264 методом
разложения на простые множители.
ПОВТОРЕНИЕ
№3. Найдите НОД и НОК чисел наиболее удобным способом :
а) 18 и 45 ; б) 8 и 27 ; в) 12 и 60 .
ПРОВЕРИМ СЕБЯ
№3. Найдите НОД и НОК чисел наиболее удобным способом : а) 18 и 45 ;
б) 8 и 27 ; в) 12 и 60 .
а) Удобнее решать методом разложения на простые множители
18 = 2·3·3
; 45 = 5·3·3
НОД(18;45)=3·3=9 ;
НОК(18;45) = 2·3·3·5 = 90
б) НОД(8;27) = 1 НОК(8;27) = 8*27=216
в) ( 60 делиться на 12 )
НОД(12;60) = 12 ; НОК(12;60) = 60
НОД и НОК
РЯДОМ С НАМИ
ПОВТОРЕНИЕ
У С Т Н А Я РАБОТА
Помогут ли спортсмену на
соревнованиях знания о НОК и НОД?
Задача
Толя и Коля друзья. Толя любит
математику, а Коля физкультуру,
поэтому задачи решает быстрее Толя, а
бегает быстрее Коля. Мальчики
участвуют в забеге на 5 км.

Через каждые 600 м от старта стоит наблюдатель, а через
каждые 800 м от старта можно попить воды. Коля
останавливался два раза, чтобы попить воды, а затем задать
вопрос наблюдателю. Толя тоже останавливался пил воду и
задавал вопрос. Однако к старту первым пришел Толя.
Как такое могло произойти, если Коля бегает чуть быстрее
Толи?
Физкультм ин утка
Два! Нам с места нужно встать!
Три! Пять! Руки вверх поднять!
Семь! Одиннадцать! Переносим вес на пятки!
Тринадцать! Семнадцать! Соединить лопатки!
Вместе говорим: «УРА»!
Число девятнадцать назвать нам пора!
Тело расслабилось, все мы здоровы
И математикой заняться готовы!
СТРАНИЦА ИСТОРИИ
НОД и НОК
РЯДОМ С НАМИ
ПОВТОРЕНИЕ
У С Т Н А Я РАБОТА
1742
Тернарная проблема
Гольдбаха
1937
Бинарная проблема Гольдбаха
(или проблема Эйлера)
Каждое чётное
число, большее
двух, можно
представить в
виде суммы двух
простых чисел.

16. Спустя почти 200 лет …

1937 год
Иван Матвеевич Виноградов доказал, что любое
достаточно большое нечётное число может быть
представлено в виде суммы трёх простых.
Показал, что почти все чётные числа представимы в виде
суммы двух простых чисел.

17. По следам доказательства

П о с л ед а м д о ка з а т ел ь с т в а
1 вариант
Представить
нечётное число 21
в виде суммы трёх
простых чисел.
2 вариант
Представить чётное 34
число в виде суммы двух
простых чисел.
ЭКОЛОГИЯ
СТРАНИЦА ИСТОРИИ
НОД и НОК
РЯДОМ С НАМИ
ПОВТОРЕНИЕ
У С Т Н А Я РАБОТА
Красная Книга Псковской области
ЗАДАНИЕ
Найдите наименьшее общее кратное каждой
пары чисел , затем впишите букву ,
соответствующую этому числу , в таблицу .
1)
2)
3)
4)
5)
6)
7)
НОК(3,12) =
НОК(4;5;8)=
НОК(9;6) =
НОК(16;12)=
НОК(9;15) =
НОК(8;12)=
НОК(10;20)=
12 О
40 П
18 Р
48 Ш
45 Е
24 К
20 Н
24 18 12 20 48 20 45 40
К Р О Н Ш Н Е П
Красная Книга Псковской области
КРОНШНЕП
ПРОВЕРОЧНАЯ РАБОТА
ЭКОЛОГИЯ
СТРАНИЦА ИСТОРИИ
НОД и НОК
РЯДОМ С НАМИ
ПОВТОРЕНИЕ
У С Т Н А Я РАБОТА
проверочн ая работа
Вариант 1.

Вариант 2 .
Найдите НОД и НОК чисел наиболее удобным способом:
а) 12 и 18 ;
б) 13 и 39 ;
в) 11 и 15 ;
а) 10 и 15 ;
б) 19 и 57 ;
в) 7 и 12 .
Проверь се бя

Вариант1.
а) 12 =2·2·3 ; 18=2·3·3 ; НОД=6 НОК=36
б) т.к. 3 9 делится на 13 НОД = 13 НОК=39
в) 11 и 15 взаимно простые НОД=1 ,
НОК = 11 ·15 = 165
Вариант 2.
а) 10 = 2·5 ; 15 = 3·5
НОД =5 , НОК =30
б) т.к. 57 делится на 19
НОД=19 , НОК=57
в) 7 и 12 взаимно простые НОД = 1 ,
НОК=7·12=84
Критерии оценки:
Каждое правильно
решенное задание
оцените в 1 балл.
0 б. – оценка «2»
1 б. – оценка «3»
2 б. – оценка «4»
3 б — оценка «5»
ПРОВЕРОЧНАЯ РАБОТА
ЭКОЛОГИЯ
СТРАНИЦА ИСТОРИИ
НОД и НОК
РЯДОМ С НАМИ
ПОВТОРЕНИЕ
У С Т Н А Я РАБОТА
Домашнее задание
Подготовиться к контрольной работе.
Творческое задание: привести
примеры из жизни, где могут
применяться знания по теме
«Делимость чисел», в чем они
нам помогают.

Можно оформить
в виде рисунков, чертежей,
подобрать текстовые задачи.
http://globuss24.ru/web/userfiles/image/doc/hello_html_m1f
299ef7.png
Продолжите предложение:
Сегодня на уроке я повторил…
Сегодня на уроке я закрепил…
Сегодня на уроке я поставил себе оценку …
Какие виды работ вызвали затруднения и требуют
повторения…
Кому, над, чем следовало бы ещё поработать…
• http://www.pskovkid.ru/2013/04/blog-post_5218.html
• https://pptcloud.ru/matematika/nod-i-nok-chisel
• http://открытыйурок.рф/статьи/632585/
• http://открытыйурок.рф/статьи/656718/
• https://ru.wikipedia.org/wiki/Виноградов,_Иван_Матвеевич

English Русский Правила

Вычисление наименьшего общего кратного

Введите цифры

Три автобуса
Три автобуса общественного транспорта отправляются вместе с автовокзала утром. Первый автобус возвращается на станцию через 18 минут, второй – через 12 минут, а третий – через 24 минуты.
Как долго снова будем вместе на вокзале? Пожалуйста, экспресс
Портниха
Портниха оставила кусок холста короче 5 метров. Она решает, сшить ли ей юбку или платье. Холста было ровно столько, сколько они израсходовали, разрезав юбку до 120 см, или 180 сантиметров. Какой кусок холста оставил ей?
LCM двух чисел
Найдите наименьшее кратное 63 и 147
Различные 6975
Три разных автобусных маршрута, 80, 81 и 82, отправляются с конечной станции в 5 ч 20 мин. Маршрут 80 отправляется каждые 30 минут, маршрут 81 — каждые 20 минут, а маршрут 82 — каждые 40 минут. Во сколько они снова уйдут?
Напоминание и частное
Даны числа A = 135, B = 315. Найдите наименьшее натуральное число R, большее единицы, чтобы отношения R:A, R:B были с остатком 1.
Бакалейная лавка
Сьюзен решила сделать продуктовые наборы для своего магазина. Оптовый торговец, у которого она покупает, продает сахар в упаковках по 20 штук в коробке, муку в упаковках по 12 штук в коробке и 15 мешков риса в коробке. Сколько штук каждого предмета она должна купить, чтобы их было одинаковое количество
Вокруг клумбы
Вокруг прямоугольной клумбы размерами 5,25 м и 3,5 м нужно посадить розы через равные промежутки так, чтобы розы находились в каждом углу клумбы и потреблять как можно меньше. а) На каком расстоянии посажены розы? б) Сколько роз
Автобусы
На остановке в 10 часов встретились автобусы №2 и №9. Автобус №2 ходит с интервалом 4 минуты, а автобус №9 с интервалом 9 минут. Сколько раз автобус встречается в 18:00 по местному времени?
Зубчатая передача
Зубчатая передача состоит из двух колес. У одного 88, а у второго 56 зубов. Сколько раз поверните меньшее колесо, чтобы попасть в те же зубья, что и в начале? Сколько раз мы повернём самое большое колесо?
Автобусы 4
Интервалы: 1-й автобус 40 мин. 2-й автобус 2 часа 3-й бутон 20 минут Через какое время они встретятся — как можно скорее?

Четыре класса
Учащиеся всех 7, 8 и 9 классов одной школы могут занять 4, 5, 6 и 7 ряды, и никого не останется. Сколько в среднем учеников в одном классе, если в каждом классе всегда четыре класса?
Gcd и lcm
Вычислить наибольший общий делитель и наименьшее общее кратное чисел. a) 16 и 18 b) 24 и 22 c) 45 и 60 d) 36 и 30
Вычислить 2976
Вычислить наименьшее общее кратное чисел 120, 660 и 210.
Уточните: 4001
Укажите: a = D (240,320) b = n (40,64)
Pardubická 4651
Йирка решил разделить выигрыш от пари в Velká Pardubická между собой и тремя своими младшими братьями по возрасту в соотношении 2:3:5:7. Каждую сумму они платили целыми кронами. Одна из сумм составила 679 чешских крон. Насколько велик был выигрыш?

Веревка
Пол может разрезать веревку на равные части, не оставив ни одной веревки. Длина может быть 15 см, 18 см или 25 см. Какова наименьшая возможная длина веревки?

Подробнее математические задачи »

LCM 18, 45 и 60

Дом
Математические функции
LCM Калькулятор
LCM 18, 45 и 60

LCM, 45 и 60 180. Всеобъемлющая работа дает более полное представление о том, как найти LCM чисел 18, 45 и 60, используя простые множители и специальные методы деления, а также примеры использования математических и реальных задач.

что такое lcm 18, 45 и 60?
lcm (18 45 60) = (?)
18 => 2 x 3 x 3
45 => 3 x 3 x 5
60 => 2 x 2 x 3 x 5

= 2 x 3 x 3 x 5 x 2
= 180
lcm (18, 45 и 60) = 180
180 lcm 18, 45 и 60.

где
18 — натуральное число, 450004 ,

180 — lcm 18, 45 и 60,
{2, 3, 3, 5} в {2 x 3 x 3, 3 x 3 x 5, 2 x 2 x 3 x 5} — наиболее повторяющиеся факторы из 18, 45 и 60,
{2} в {2 х 3 х 3, 3 х 3 х 5, 2 х 2 х 3 х 5} другие оставшиеся множители 18, 45 и 60.

Использование в математике: НОК 18, 45 и 60
Ниже приведены некоторые математические приложения, где можно использовать МОК 18, 45 и 60:

найти наименьшее число, которое точно делится на 18, 45 и 60.
, чтобы найти общие знаменатели для дробей, имеющих 18, 45 и 60 в качестве знаменателей при сложении или вычитании разнородных дробей.

Использование в реальных задачах: 18, 45 и 60 lcm
В контексте задач реального мира lcm, lcm 18, 45 и 60 помогает найти точное время, когда три одинаковых и повторяющихся с разным графиком времени происходят вместе в одно и то же время. Например, задачи реального мира включают lcm в ситуации, когда нужно определить, в какое время все колокола A, B и C звонят вместе, если колокол A звонит через 18 секунд, B звонит через 45 секунд и C многократно звонит через 60 секунд. Ответ заключается в том, что все колокола A, B и C звонят вместе через 180 секунд в первый раз, через 360 секунд во второй раз, через 540 секунд в третий раз и так далее.

Важные примечания: 18, 45 и 60 lcm
Ниже приведены важные примечания, которые следует помнить при решении lcm из 18, 45 и 60:

Повторяющиеся и неповторяющиеся простые множители 18, 45 и 60 следует умножить, чтобы найти наименьшее общее кратное 18, 45 и 60, при решении lcm методом простых множителей.
Результаты lcm 18, 45 и 60 идентичны, даже если мы изменим порядок заданных чисел в вычислении lcm, это означает, что порядок заданных чисел в вычислении lcm не повлияет на результаты.

Для значений, отличных от 18, 45 и 60, используйте этот инструмент ниже:

Приведенный ниже решенный пример с пошаговой работой показывает, как найти lcm для 18, 45 и 60, используя либо метод простых множителей, либо метод специального деления. .

Пример решения с использованием метода простых множителей:
Чему равно НОК 18, 45 и 60?

шаг 1 Обратитесь к входным параметрам, значениям и посмотрите, что будет найдено:
Входные параметры и значения:
A = 18
B = 45
C = 60

Что нужно найти:
найти lcm числа 18, 45 и 60

шаг 5, 60 4:
Простые множители 18 = 2 x 3 x 3
Простые множители 45 = 3 x 3 x 5
Простые множители 60 = 2 x 2 x 3 x 5

шаг 3 Определите повторяющиеся и неповторяющиеся простые делители числа 18 , 45 и 60:
{2, 3, 3, 5} — наиболее повторяющиеся множители, а {2} — неповторяющиеся множители 18, 45 и 60.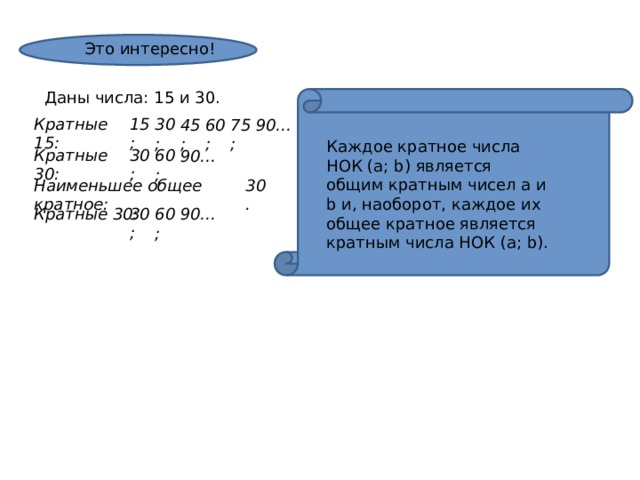

Шаг 4 Найдите произведение повторяющихся и неповторяющихся простых множителей 18, 45 и 60:
= 2 x 3 x 3 x 5 x 2
= 180
lcm(20 и 30) = 180

Следовательно,
lcm 18, 45 и 60 равно 180

Пример решения с использованием специального метода деления:

Этот специальный метод деления является самым простым способом понять весь расчет того, что такое lcm для 18, 45 и 60.

Шаг 1 Адресуйте входные параметры, значения и наблюдайте, что нужно найти:
Входные параметры и значения:
Целые числа: 18, 45 и 60

Что нужно найти:
lcm (18, 45, 60) = ?

шаг 2 Расположите заданные целые числа по горизонтали, разделяя их пробелами или запятыми. Формат:
18, 45 и 60

шаг 3 Выберите делитель, который делит каждое или большинство заданных целых чисел (18, 45 и 60), разделите каждое целое число отдельно и запишите частное в следующей строке прямо под соответствующими целыми числами.