Приведение матрицы к треугольному виду
Ниже два калькулятора для приведения матриц к треугольному, или ступенчатому, виду. Первый использует для этого метод Гаусса, второй — метод Барейса. Описание методов и немного теории — под калькуляторами.
Приведение матрицы к треугольному виду (метод Гаусса)
3 2 3 4 4 4 3 2 1 4 4 3 2 3 1 1
Матрица
Точность вычисления
Знаков после запятой: 4
Треугольная матрица (метод Гаусса)
Треугольная матрица (метод Гаусса с выбором максимума в столбце)
Треугольная матрица (метод Гаусса с выбором максимума по всей матрице)
Приведение матрицы к треугольному виду (метод Барейса)
3 2 3 4 4 4 3 2 1 4 4 3 2 3 1 1
Матрица
Точность вычисления
Знаков после запятой: 4
Треугольная матрица (метод Барейса)
Треугольная матрица (метод Барейса с выбором максимума в столбце)
Треугольная матрица (метод Барейса с выбором максимума по всей матрице)
Итак, для начала определимся с понятием треугольной, или ступенчатой матрицы:
Матрица имеет ступенчатый вид, если:
- Все нулевые строки матрицы стоят последними
- Первый ненулевой элемент строки всегда находится строго правее первого ненулевого элемента предыдущей строки
- Все элементы столбца под первым ненулевым элементом строки равны нулю (это впрочем следует из первых двух пунктов)
Пример ступенчатой матрицы:
1 0 2 5
0 3 0 0
0 0 0 4
Понятие треугольной матрицы более узкое, оно используется только для квадратных матриц (хотя я думаю, что это не строго), и формулируется проще: треугольная матрица — квадратная матрица, в которой все элементы ниже главной диагонали равны нулю. Строго говоря, это даже определение верхнетреугольной матрицы, но мы будем использовать его. Понятно, что такая верхнетреугольная матрица является также и ступенчатой.
Строго говоря, это даже определение верхнетреугольной матрицы, но мы будем использовать его. Понятно, что такая верхнетреугольная матрица является также и ступенчатой.
Пример треугольной (верхнетреугольной) матрицы:
1 0 2 5
0 3 1 3
0 0 4 2
0 0 0 3
Кстати, определитель треугольной матрицы вычисляется простым перемножением ее диагональных элементов.
Чем же так интересны ступенчатые (и треугольные) матрицы, что к ним надо приводить все остальные? — спросите вы.
Что же такое элементарные преобразования? — спросите вы.
Элементарными преобразованиями матрицы называют следующие операции:
- перестановка любых двух строк (столбцов) матрицы
- умножение любой строки (столбца) на призвольное, отличное от нуля, число
- сложение любой строки (столбца) с другой строкой (столбцом), умноженной (умноженным) на произвольное, отличное от нуля, число.

И что? — спросите вы.
А то, что элементарные преобразования матрицы сохраняют эквивалентность матриц. А если вспомнить, что системы линейных алгебраический уравнений (СЛАУ) записывают как раз в матричной форме, то это означает, что элементарные преобразования матрицы не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.
Приведя матрицу системы линейных уравнений AX=B к треугольной форме A’X = B’, то есть, с соответствующими преобразованиями столбца B, можно найти решение этой системы так называемым «обратным ходом».
Чтобы было понятно, используем треугольную матрицу выше и перепишем систему уравнений в более привычной форме (столбец B я придумал сам):
Понятно, что сначала мы найдем , потом, подставив его в предыдущее уравнение, найдем и так далее — двигаясь от последнего уравнения к первому. Это и есть обратный ход.
Алгоритм приведения матрицы к ступенчатой форме с помощью элементарных преобразований называют методом Гаусса. Метод Гаусса — классический метод решения систем линейных алгебраических уравнений. Также его еще называют Гауссовым исключением, так как это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к эквивалентной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Метод Гаусса — классический метод решения систем линейных алгебраических уравнений. Также его еще называют Гауссовым исключением, так как это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к эквивалентной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Теперь про сам метод.
Собственно, как можно занулить переменную во втором уравнении? Вычтя из него первое, домноженное на коэффициент
Поясним на примере:
Зануляем во втором уравнении:
Во втором уравнении больше не содержится
Обобщенно алгоритм метода Гаусса можно представить следующим образом:
где N — число строк,
— i-тая строка,
— элемент, находящийся в i-той строке, j-том столбце
И все бы ничего, да и метод отличный, но. Дело все в делении на , присутствующем в формуле. Во-первых, если диагональный элемент будет равен нулю, то метод работать не будет.
Для уменьшения погрешности используют модификации метода Гаусса, которые основаны на том, что погрешность тем меньше, чем больше знаменатель дроби. Эти модификации — метод Гаусса с выбором максимума в столбце и метод Гаусса с выбором максимума по всей матрице. Как следует из названия, перед каждым шагом исключения переменной по столбцу (всей матрице) ищется элемент с максимальным значением и проводится перестановка строк (строк и столбцов), таким образом, чтобы он оказался на месте .
Но есть еще более радикальная модификация метода Гаусса, которая называется методом Барейса (Bareiss).
Как можно избавиться от деления? Например, умножив перед вычитанием строку на . Тогда вычитать надо будет строку , домноженную только на , без всякого деления.
Уже хорошо, но возникает проблема с ростом значений элементов матрицы в ходе вычисления.
Барейс предложил делить выражение выше на и показал, что если исходные элементы матрицы — целые числа, то результатом вычисления такого выражения тоже будет целое число. При этом принимается, что для нулевой строки .
При этом принимается, что для нулевой строки .
Кстати, то, что в случае целочисленных элементов исходной матрицы алгоритм Барейса приводит к треугольной матрице с целочисленными элементами, то есть без накопления погрешности вычислений — довольно важное свойство с точки зрения машинной арифметики.
Алгоритм Барейса можно представить следующим образом:
Алгоритм, аналогично методу Гаусса, также можно улучшить поиском максимума по столбцу(всей матрице) и перестановкой соответствующих строк (строк и столбцов).
Барейсс линейная алгебра Математика матрица метод Барейса метод Гаусса треугольная матрица
Навигация по странице:
Онлайн калькулятор. Определитель матрицы или детерминант матрицы — это одна из основных численных характеристик квадратной матрицы, применяемая при решении многих задач.Определение. Определителем матрицы n×n будет число:
где (α1,α2,…,αn) — перестановка чисел от 1 до n, N(α1,α2,…,αn) — число инверсий в перестановке, суммирование идёт по всем возможным перестановкам порядка n. Обозначение Определитель матрици A обычно обозначается det(A), |A|, или ∆(A). Свойства определителя матрицы
Методы вычисления определителя матрицыВычисление определителя матрицы 1×1Правило: Для матрицы первого порядка значение определителя равно значению элемента этой матрицы: ∆ = |a11| = a11 Вычисление определителя матрицы 2×2Правило: Для матрицы 2×2 значение определителя равно разности произведений элементов главной и побочной диагоналей:
Пример 1. Найти определитель матрицы A
Решение:
Вычисление определителя матрицы 3×3Правило треугольника для вычисления определителя матрицы 3-тего порядкаПравило: Для матрицы 3×3 значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной побочной диагонали.
= a11·a22·a33 + a12·a23·a31 + a13·a21·a32 — a13·a22·a31 — a11·a23·a32 — a12·a21·a33 Правило Саррюса для вычисления определителя матрицы 3-тего порядкаПравило: Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком «плюс»; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком «минус»:
= a11·a22·a33 + a12·a23·a31 + a13·a21·a32 — a13·a22·a31 — a11·a23·a32 — a12·a21·a33 Пример 2. Найти определитель матрицы A
Решение:
= 15 + 0 + 0 — 2 — 0 + 84 = 97 Вычисление определителя матрицы произвольного размераРазложение определителя по строке или столбцуПравило: Определитель матрицы равен сумме произведений элементов строки определителя на их алгебраические дополнения:
Правило: Определитель матрицы равен сумме произведений элементов столбца определителя на их алгебраические дополнения:
При разложение определителя матрицы обычно выбирают ту строку/столбец, в которой/ом максимальное количество нулевых элементов. Пример 3. Найти определитель матрицы A
Решение: Вычислим определитель матрицы разложив его по первому столбцу:
= 2·(2·1 — 1·1) + 2·(4·1 — 2·1) = 2·(2 — 1) + 2·(4 — 2) = 2·1 + 2·2 = 2 + 4 = 6 Пример 4. Найти определитель матрицы A
Решение: Вычислим определитель матрицы, разложив его по второй строке (в ней больше всего нулей):
= 2·(2·1·3 + 1·3·4 + 1·2·2 — 1·1·4 — 2·3·2 — 1·2·3) = 2·(6 +12 + 4 — 4 — 12 — 6) = 2·0 = 0 Приведение определителя к треугольному видуПравило: Используя свойства определителя для элементарных преобразований над строками и столбцами 8 — 11, определитель приводится к треугольному виду, и тогда его значение будет равно произведению элементов стоящих на главной диагонали. Пример 5. Найти определитель матрицы A приведением его к треугольному виду
Решение:
Сначала получим нули в первом столбце под главной диагональю. Для этого отнимем от 3-тей строки 1-ую строку, а от 4-той строки 1-ую строку помноженную на 2:
Получим нули во втором столбце под главной диагональю.
Получим нули во третьем столбце под главной диагональю. Для этого к 3-ему столбцу добавим 4-тий столбец умноженный на 8:
Теорема ЛапласаТеорема: Пусть ∆ — определитель n-ого порядка. Онлайн калькуляторы с матрицами. Упражнения с матрицами. Матрицы. вступление и оглавлениеМатрицы: определение и основные понятия.Сведение системы линейных уравнений к матрице.Виды матрицУмножение матрицы на число.Сложение и вычитание матриц.Умножение матриц.Транспонирование матрицы.Элементарные преобразования матрицы.Определитель матрицы.Минор и алгебраическое дополнение матрицы.Обратная матрица.Линейно зависимые и независимые строки.Ранг матрицы. Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список! |
Метод приведения матрицы к треугольному виду
При помощи элементарных преобразований любую матрицу можно привести к верхнему (или нижнему) треугольному виду (метод Гаусса). Отсюда следует, что любой определитель, используя перечисленные выше элементарные преобразования, можно привести к треугольному виду, а затем вычислить согласно п.3 замечаний 2.2.
Отсюда следует, что любой определитель, используя перечисленные выше элементарные преобразования, можно привести к треугольному виду, а затем вычислить согласно п.3 замечаний 2.2.
Итак, метод состоит из двух шагов.
1. При помощи элементарных преобразований привести определитель к треугольному виду.
2. Вычислить определитель треугольного вида, перемножая его элементы, стоящие на главной диагонали.
Пример 2.12. Вычислить определитель четвёртого порядка
приводя его к треугольному виду.
Решение. 1. При помощи элементарных преобразований приведем матрицу к треугольному виду. Взяв элемент первой строки в качестве ведущего, все остальные элементы первого столбца сделаем равными нулю. Для этого ко второй строке прибавим первую, умноженную на (-2), к третьей строке прибавим первую, умноженную на (-3), а к четвертой строке прибавим первую, умноженную на (-4):
Заметим, что при использовании этих элементарных преобразований III типа определитель не изменяется.
Умножим элементы второй строки на (-1), а элементы третьей строки — на 0,5, при этом, чтобы не нарушить равенство, надо полученный определитель разделить на , т.е. умножить на (-2):
В полученной матрице нужно сделать равными нулю элементы и второго столбца, стоящие ниже главной диагонали. Для этого берем в качестве ведущего элемента и прибавляем к третьей и четвертой строкам вторую строку, умноженную на 1 и на 7 соответственно:
Осталось сделать равным нулю элемент . К четвертой строке прибавим третью, умноженную на 2 (определитель при этом не изменится):
Получили определитель треугольного вида.
2. Вычислим определитель верхней треугольной матрицы, перемножая элементы, стоящие на главной диагонали:
Не нашли то, что искали? Воспользуйтесь поиском:
Метод сведения определителя к треугольному виду использует те же преобразования, что и метод эффективного понижения порядка. Только при вычислении определителя методом эффективного понижения порядка мы постепенно уменьшаем порядок определителя, а для метода сведения к треугольному виду порядок определителя остаётся неизменным до конца процесса решения. Суть метода сведения к треугольному виду такова: с помощью действий со строками (или столбцами) преобразовать определитель к виду, когда все элементы, лежащие ниже (или выше) главной диагонали равны нулю. Т.е. после преобразований определитель должен принять одну из двух форм (элементы на главной диагонали выделены синим цветом):
Суть метода сведения к треугольному виду такова: с помощью действий со строками (или столбцами) преобразовать определитель к виду, когда все элементы, лежащие ниже (или выше) главной диагонали равны нулю. Т.е. после преобразований определитель должен принять одну из двух форм (элементы на главной диагонали выделены синим цветом):
Хотя разницы и нет, обычно приводят к первому случаю, когда нули расположены под главной диагональю. После преобразований определитель вычисляется простым умножением элементов, расположенных на главной диагонали. Для того, чтобы обнулить требуемые элементы и вычислить определитель, нам пригодятся несколько свойств определителей, которые указаны в теме «Некоторые свойства определителей». Я запишу ниже несколько свойств, которые нам пригодятся при решении. В примечании после каждого свойства будет указан пример его применения.
- Если поменять местами две строки (столбца) определителя, то знак определителя изменится на противоположный.
Пример применения этого свойства: показатьскрыть
Рассмотрим определитель $left| egin 2 & 5 \ 9 & 4 end
ight|$. Найдём его значение, используя формулу №1 из темы вычисления определителей второго и третьего порядков:
Найдём его значение, используя формулу №1 из темы вычисления определителей второго и третьего порядков:
$$left| egin 2 & 5 \ 9 & 4 end
ight|=2cdot 4-5cdot 9=-37.$$
Теперь поменяем местами первую и вторую строки. Получим определитель $left| egin 9 & 4 \ 2 & 5 end
ight|$. Вычислим полученный определитель: $left| egin9 & 4 \ 2 & 5 end
ight|=9cdot 5-4cdot 2=37$. Итак, значение исходного определителя равнялось (-37), а у определителя с изменённым порядком строк значение равно $-(-37)=37$. Знак определителя изменился на противоположный.
Пример применения этого свойства: показатьскрыть
Рассмотрим определитель $left| egin -7 & 10 & 0\ -9 & 21 & 4 \ 2 & -3 & 1 end
ight|$. Прибавим к элементам второй строки соответствующие элементы третьей строки, умноженные на 5. Записывают это действие так: $r_2+5cdot$. Вторая строка будет изменена, остальные строки останутся без изменений.
$$ left| egin -7 & 10 & 0\ -9 & 21 & 4 \ 2 & -3 & 1 end
ight| eginphantom<0>\ r_2+5cdot\ phantom <0>end= left| egin-7 & 10 & 0\ -9+5cdot 2 & 21+5cdot (-3) & 4+5cdot 1 \ 2 & -3 & 1 end
ight|= left| egin-7 & 10 & 0\ 1 & 6 & 9 \ 2 & -3 & 1 end
ight|. $$
$$
Пример применения этого свойства: показатьскрыть
Рассмотрим определитель $left| egin -7 & 10 \ -9 & 21 end
ight|$. Заметьте, что все элементы второй строки делятся на 3:
$$left| egin -7 & 10 \ -9 & 21 end
ight|=left| egin-7 & 10 \ 3cdot(-3) & 3cdot 7 end
ight|$$
Число 3 и есть общий множитель всех элементов второй строки. Вынесем тройку за знак определителя:
$$ left| egin -7 & 10 \ -9 & 21 end
ight|=left| egin-7 & 10 \ 3cdot(-3) & 3cdot 7 end
ight|= 3cdot left| egin-7 & 10 \ -3 & 7 end
ight| $$
Пример применения этого свойства: показатьскрыть
Буквами $r$ (от слова «row») станем обозначать строки: $r_1$ – первая строка, $r_2$ – вторая строка и так далее. Буквами $c$ (от слова «column») станем обозначать столбцы: $c_1$ – первый столбец, $c_2$ – второй столбец и так далее.
Найти определитель $Delta = left|egin -8 & 2 & 9 & 17\ -3 & 1 & 2 & 6\ 13 & -3 & -7 & -26\ 11 & 1 & 23 & 6end
ight|$.
В принципе, начинать решение можно и не преобразовывая определитель. Однако очень удобно, когда первым элементом первой строки является единица (ну, или (-1) на крайний случай). Единицы есть во втором столбце нашего определителя. Сделаем так, чтобы второй столбец стал первым. Для этого просто поменяем местами первый и второй столбцы, используя свойство (1). Не забываем, что при смене мест двух столбцов перед определителем появится знак «минус»:
$$Delta = left|egin -8 & 2 & 9 & 17\ -3 & 1 & 2 & 6\ 13 & -3 & -7 & -26\ 11 & 1 & 23 & 6end
ight|=-left|egin2 & -8 & 9 & 17\ 1 & -3 & 2 & 6\ -3 & 13 & -7 & -26\ 1 & 11 & 23 & 6end
ight|.$$
Итак, столбцы поменяли, однако единица покамест не вышла на первое место в первой строке, – но это дело поправимое. Поменяем местами первую и вторую строки, при этом перед определителем вновь возникнет знак «минус». Ну, а так как «минус» на «минус» даёт «плюс», то получим мы следующее:
$$Delta =-left|egin 2 & -8 & 9 & 17\ 1 & -3 & 2 & 6\ -3 & 13 & -7 & -26\ 1 & 11 & 23 & 6end
ight|=-left( -left|egin1 & -3 & 2 & 6\ 2 & -8 & 9 & 17\ -3 & 13 & -7 & -26\ 1 & 11 & 23 & 6end
ight|
ight)= left|egin1 & -3 & 2 & 6\ 2 & -8 & 9 & 17\ -3 & 13 & -7 & -26\ 1 & 11 & 23 & 6end
ight|. $$
$$
Начнём решение. Нам нужно получить нули под главной диагональю. Для этого придётся осуществить несколько шагов, на которых будем изменять строки нашего определителя. На первом шаге мы должны сделать так, чтобы все элементы первого столбца стали нулями – кроме элемента на главной диагонали, выделенного красным цветом:
$$ left|egin oldred <1>& -3 & 2 & 6\
ormgreen <2>& -8 & 9 & 17\
ormblue <-3>& 13 & -7 & -26\
ormpurple <1>& 11 & 23 & 6end
ight| $$
Преобразования со строками, которые нужно выполнить, чтобы обнулить «серые» элементы, получаются так:
Запись $r_2-2r_1$ означает, что от элементов второй строки вычли соответствующие элементы первой строки, умноженные на два. Полученный результат записали вместо прежней второй строки. Остальные записи расшифровываются аналогично. Согласно свойству (2) значение определителя от таких действий не изменится. Для наглядности я запишу это действие отдельно:
После выполнения всех требуемых операций со строками, мы получим новый определитель. Записывается это так:
Записывается это так:
$$ Delta=left|egin 1 & -3 & 2 & 6\ 2 & -8 & 9 & 17\ -3 & 13 & -7 & -26\ 1 & 11 & 23 & 6end
ight| eginphantom <0>\ r_2-2r_1 \ r_3+3r_1 \ r_4-r_1 end= left|egin1 & -3 & 2 & 6\ 0 & -2 & 5 & 5\ 0 & 4 & -1 & -8 \ 0 & 14 & 21 & 0end
ight|. $$
Перед тем, как мы пойдём дальше, обратим внимание на то, что все элементы четвёртой строки делятся на 7. Согласно свойству (3) число 7 можно вынести за знак определителя:
$$ left|egin 1 & -3 & 2 & 6\ 0 & -2 & 5 & 5\ 0 & 4 & -1 & -8 \ 0 & 14 & 21 & 0end
ight|=7cdot left|egin1 & -3 & 2 & 6\ 0 & -2 & 5 & 5\ 0 & 4 & -1 & -8 \ 0 & 2 & 3 & 0end
ight| $$
Теперь нам нужно обнулить элементы во втором столбце (под главной диагональю). Т.е., обнулению подлежат элементы, выделенные зелёным и синим цветом. Элемент на главной диагонали, который останется без изменений, выделен красным цветом:
$$ left|egin 1 & -3 & 2 & 6\ 0 & oldred <-2>& 5 & 5\ 0 &
ormblue <4>& -1 & -8 \ 0 &
ormblue <2>& 3 & 0end
ight| $$
А если бы вместо числа -2 возник ноль? показатьскрыть
Если бы вместо числа -2 получился ноль, мы бы поменяли местами строки или столбцы. Например, вот так:
Например, вот так:
$$ left|egin 1 & -3 & 2 & 6\ 0 & 0 & 5 & 5\ 0 & 4 & -1 & -8 \ 0 & 2 & 3 & 0end
ight| =[r_2leftrightarrow] =-left|egin1 & -3 & 2 & 6\ 0 & 2 & 3 & 0\ 0 & 4 & -1 & -8 \ 0 & 0 & 5 & 5 end
ight| $$
Или же может возникнуть иная ситуация: когда обнулятся все элементы во втором столбце под первой строкой. Вот так:
$$ left|egin 1 & -3 & 2 & 6\ 0 & 0 & 5 & 5\ 0 & 0 & -1 & -8 \ 0 & 0 & 3 & 0end
ight| $$
В этом случае имеем пропорциональность столбцов, т.е. $c_2=-3c_1$, а это означает, что определитель равен 0.
В принципе, мы можем получить (-1) на месте диагонального «красного элемента». Для этого достаточно поменять местами второй и третий столбцы, а затем поменять местами вторую и третью строки. Однако в нашем случае этого можно и не делать, так как все «синие элементы» нацело делятся на «красный элемент», т. е. на (-2). Следовательно, никакой работы с дробями не предвидится. Впрочем, тут дело вкуса: можете попробовать для тренировки продолжить решение, поменяв местами строки и столбцы, чтобы «красным элементом» стала (-1). Выполним такие операции со строками:
е. на (-2). Следовательно, никакой работы с дробями не предвидится. Впрочем, тут дело вкуса: можете попробовать для тренировки продолжить решение, поменяв местами строки и столбцы, чтобы «красным элементом» стала (-1). Выполним такие операции со строками:
Отдельно выписывать действия со строками не станем, так как они полностью аналогичны рассмотренным ранее. Наш определитель станет таким:
$$ Delta=7cdot left|egin 1 & -3 & 2 & 6\ 0 & -2 & 5 & 5\ 0 & 4 & -1 & -8 \ 0 & 2 & 3 & 0end
ight| eginphantom <0>\ phantom <0>\ r_3+2r_2 \ r_4+r_2end= 7cdot left|egin1 & -3 & 2 & 6\ 0 & -2 & 5 & 5\ 0 & 0 & 9 & 2 \ 0 & 0 & 8 & 5end
ight|. $$
Осталось последнее действие. Нужно обнулить элемент 8 под главной диагональю:
$$ left|egin 1 & -3 & 2 & 6\ 0 & -2 & 5 & 5\ 0 & 0 & 9 & 2 \ 0 & 0 & oldred <8>& 5end
ight| $$
Тут уже придется поработать с дробями. Обычно такой работы стараются избегать – и до этого момента нам это удавалось – но теперь уже деваться некуда:
Обычно такой работы стараются избегать – и до этого момента нам это удавалось – но теперь уже деваться некуда:
$$ Delta = 7cdot left|egin 1 & -3 & 2 & 6\ 0 & -2 & 5 & 5\ 0 & 0 & 9 & 2 \ 0 & 0 & 8 & 5end
ight| eginphantom <0>\ phantom <0>\ phantom <0>\ r_4-frac<8><9>r_3 end= 7cdot left|egin1 & -3 & 2 & 6\ 0 & -2 & 5 & 5\ 0 & 0 & 9 & 2 \ 0 & 0 & 0 & frac<29><9>end
ight|. $$
Преобразования окончены. Осталось лишь использовать свойство (4) и переменожить элементы, расположенные на главной диагонали:
$$ Delta=7cdot 1cdot (-2)cdot 9 cdot frac<29><9>=-406. $$
Ответ получен. Полное решение без пояснений выглядит так:
$$ Delta = left|egin -8 & 2 & 9 & 17\ -3 & 1 & 2 & 6\ 13 & -3 & -7 & -26\ 11 & 1 & 23 & 6end
ight| =[c_1leftrightarrow] =left|egin2 & -8 & 9 & 17\ 1 & -3 & 2 & 6\ -3 & 13 & -7 & -26\ 1 & 11 & 23 & 6end
ight| =[r_1leftrightarrow]=\ =left|egin1 & -3 & 2 & 6\ 2 & -8 & 9 & 17\ -3 & 13 & -7 & -26\ 1 & 11 & 23 & 6end
ight| eginphantom <0>\ r_2-2r_1 \ r_3+3r_1 \ r_4-r_1 end= 7cdot left|egin1 & -3 & 2 & 6\ 0 & -2 & 5 & 5\ 0 & 4 & -1 & -8 \ 0 & 2 & 3 & 0end
ight| eginphantom <0>\ phantom <0>\ r_3+2r_2 \ r_4+r_2 end=\ =7cdot left|egin1 & -3 & 2 & 6\ 0 & -2 & 5 & 5\ 0 & 0 & 9 & 2 \ 0 & 0 & 8 & 5end
ight| eginphantom <0>\ phantom <0>\ phantom <0>\ r_4-frac<8><9>r_3end=7cdot left|egin1 & -3 & 2 & 6\ 0 & -2 & 5 & 5\ 0 & 0 & 9 & 2 \ 0 & 0 & 0 & frac<29><9>end
ight| =7cdot 1cdot (-2)cdot 9 cdot frac<29><9>=-406. $$
$$
В принципе, преобразования метода сведения к треугольному виду просты, однако стоит иметь в виду свойства определителей, изложенные соответствующей теме. Например, на каком-то шаге может обнулиться строка или столбец, или же окажется, что некие строки или столбцы пропорциональны. Это будет означать, что рассматриваемый определитель равен 0.
Для того что бы вычислить определитель матрицы четвертого порядка или выше можно разложить определитель по строке или столбцу или применить метод Гаусса и привести определитель к треугольному виду. Рассмотрим приведение определителя матрицы к треугольному виду.
Для того чтобы привести матрицу к треугольному используйте свойства определителя для элементарных преобразований над строками и столбцами. Для нахождения определителя нужно умножить все элементы на главной диагонали.
Найдем определитель матрицы четвертого порядка.
Сделаем элемент a2,1 равный нулю.
Из строки №2 вычтем строку №1, умноженную на 1 элемент строки №2, т. е. на 3
е. на 3
Сделаем элемент a3,1 равный нулю.
Из строки №3 вычтем строку №1, умноженную на 1 элемент строки №3, т.е. на 8
Сделаем элемент a4,1 равный нулю.
Из строки №4 вычтем строку №1, умноженную на 1 элемент строки №4, т.е. на 6
Сделаем элемент a3,2 равный нулю.
Из строки №3 вычитаем строку №2, умноженную на 5
Сделаем элемент a4,2 равный нулю.
Из строки №4 вычитаем строку №2, умноженную на 2
Сделаем элемент a4,3 равный нулю.
Из строки №4 вычтем строку №3, умноженную на 9/21.
Умножим элементы матрицы находящиеся на диагонали.
теоремы и примеры нахождения определителей
Содержание:
- Вычисления определителей второго порядка
- Методы вычисления определителей третьего порядка
- Приведение определителя к треугольному виду
- Правило треугольника
- Правило Саррюса
- Разложение определителя по строке или столбцу
- Разложение определителя по элементам строки или столбца
- Теорема Лапласа
В общем случае правило вычисления определителей $n$-го порядка является довольно громоздким. Для определителей второго и третьего порядка существуют рациональные способы их вычислений.
Вычисления определителей второго порядка
Чтобы вычислить определитель матрицы второго порядка, надо от произведения элементов главной диагонали отнять произведение элементов побочной диагонали:
$$\left| \begin{array}{ll}{a_{11}} & {a_{12}} \\ {a_{21}} & {a_{22}}\end{array}\right|=a_{11} \cdot a_{22}-a_{12} \cdot a_{21}$$
Пример
Задание. Вычислить определитель второго порядка
$\left| \begin{array}{rr}{11} & {-2} \\ {7} & {5}\end{array}\right|$
Вычислить определитель второго порядка
$\left| \begin{array}{rr}{11} & {-2} \\ {7} & {5}\end{array}\right|$
Решение. $\left| \begin{array}{rr}{11} & {-2} \\ {7} & {5}\end{array}\right|=11 \cdot 5-(-2) \cdot 7=55+14=69$
Ответ. $\left| \begin{array}{rr}{11} & {-2} \\ {7} & {5}\end{array}\right|=69$
Методы вычисления определителей третьего порядка
Для вычисления определителей третьего порядка существует такие правила.
Правило треугольника
Схематически это правило можно изобразить следующим образом:
Произведение элементов в первом определителе, которые соединены прямыми, берется со знаком «плюс»; аналогично, для второго определителя — соответствующие произведения берутся со знаком «минус», т.е.
$$\left| \begin{array}{ccc}{a_{11}} & {a_{12}} & {a_{13}} \\ {a_{21}} & {a_{22}} & {a_{23}} \\ {a_{31}} & {a_{32}} & {a_{33}}\end{array}\right|=a_{11} a_{22} a_{33}+a_{12} a_{23} a_{31}+a_{13} a_{21} a_{32}-$$
$$-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}-a_{13} a_{22} a_{31}$$
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Вычислить определитель $\left| \begin{array}{rrr}{3} & {3} & {-1} \\ {4} & {1} & {3} \\ {1} & {-2} & {-2}\end{array}\right|$ методом треугольников.
Вычислить определитель $\left| \begin{array}{rrr}{3} & {3} & {-1} \\ {4} & {1} & {3} \\ {1} & {-2} & {-2}\end{array}\right|$ методом треугольников.
Решение. $\left| \begin{array}{rrr}{3} & {3} & {-1} \\ {4} & {1} & {3} \\ {1} & {-2} & {-2}\end{array}\right|=3 \cdot 1 \cdot(-2)+4 \cdot(-2) \cdot(-1)+$
$$+3 \cdot 3 \cdot 1-(-1) \cdot 1 \cdot 1-3 \cdot(-2) \cdot 3-4 \cdot 3 \cdot(-2)=54$$
Ответ. $\left| \begin{array}{rrr}{3} & {3} & {-1} \\ {4} & {1} & {3} \\ {1} & {-2} & {-2}\end{array}\right|=54$
Правило Саррюса
Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком «плюс»; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком «минус»:
$$-a_{13} a_{22} a_{31}-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}$$
Пример
Задание. Вычислить определитель $\left| \begin{array}{rrr}{3} & {3} & {-1} \\ {4} & {1} & {3} \\ {1} & {-2} & {-2}\end{array}\right|$ с помощью правила Саррюса.
Вычислить определитель $\left| \begin{array}{rrr}{3} & {3} & {-1} \\ {4} & {1} & {3} \\ {1} & {-2} & {-2}\end{array}\right|$ с помощью правила Саррюса.
Решение.
$$+(-1) \cdot 4 \cdot(-2)-(-1) \cdot 1 \cdot 1-3 \cdot 3 \cdot(-2)-3 \cdot 4 \cdot(-2)=54$$
Ответ. $\left| \begin{array}{rrr}{3} & {3} & {-1} \\ {4} & {1} & {3} \\ {1} & {-2} & {-2}\end{array}\right|=54$
Разложение определителя по строке или столбцу
Определитель равен сумме произведений элементов строки определителя на их алгебраические дополнения. Обычно выбирают ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой.
Пример
Задание. Разложив по первой строке, вычислить определитель $\left| \begin{array}{lll}{1} & {2} & {3} \\ {4} & {5} & {6} \\ {7} & {8} & {9}\end{array}\right|$
Решение. Ответ. $\left| \begin{array}{lll}{1} & {2} & {3} \\ {4} & {5} & {6} \\ {7} & {8} & {9}\end{array}\right|=0$ Этот метод позволяет вычисление определителя свести к вычислению определителя более низкого порядка. Пример Задание. Вычислить определитель $\left| \begin{array}{lll}{1} & {2} & {3} \\ {4} & {5} & {6} \\ {7} & {8} & {9}\end{array}\right|$ Решение. Выполним следующие
преобразования над строками определителя: из второй строки отнимем четыре
первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель,
равный данному. $$\left| \begin{array}{ccc}{1} & {2} & {3} \\ {4} & {5} & {6} \\ {7} & {8} & {9}\end{array}\right|=\left| \begin{array}{ccc}{1} & {2} & {3} \\ {4-4 \cdot 1} & {5-4 \cdot 2} & {6-4 \cdot 3} \\ {7-7 \cdot 1} & {8-7 \cdot 2} & {9-7 \cdot 3}\end{array}\right|=$$ $$=\left| \begin{array}{rrr}{1} & {2} & {3} \\ {0} & {-3} & {-6} \\ {0} & {-6} & {-12}\end{array}\right|=\left| \begin{array}{ccc}{1} & {2} & {3} \\ {0} & {-3} & {-6} \\ {0} & {2 \cdot(-3)} & {2 \cdot(-6)}\end{array}\right|=0$$ Определитель равен нулю, так как вторая и третья строки являются пропорциональными. Ответ. $\left| \begin{array}{lll}{1} & {2} & {3} \\ {4} & {5} & {6} \\ {7} & {8} & {9}\end{array}\right|=0$ Для вычисления определителей четвертого порядка и выше применяется либо разложение по строке/столбцу, либо приведение
к треугольному виду, либо с помощью теоремы Лапласа. Пример Задание. Вычислить определитель
$\left| \begin{array}{llll}{9} & {8} & {7} & {6} \\ {5} & {4} & {3} & {2} \\ {1} & {0} & {1} & {2} \\ {3} & {4} & {5} & {6}\end{array}\right|$ , разложив его по элементам какой-то строки или какого-то столбца. Решение. Предварительно выполним
элементарные преобразования над строками определителя, сделав
как можно больше нулей либо в строке, либо в столбце. Для этого вначале от первой строки отнимем девять третьих,
от второй — пять третьих и от четвертой — три третьих строки, получаем: $$\left| \begin{array}{cccc}{9} & {8} & {7} & {6} \\ {5} & {4} & {3} & {2} \\ {1} & {0} & {1} & {2} \\ {3} & {4} & {5} & {6}\end{array}\right|=\left| \begin{array}{cccc}{9-1} & {8-0} & {7-9} & {6-18} \\ {5-5} & {4-0} & {3-5} & {2-10} \\ {1} & {0} & {1} & {2} \\ {0} & {4} & {2} & {0}\end{array}\right|=\left| \begin{array}{rrrr}{0} & {8} & {-2} & {-12} \\ {0} & {4} & {-2} & {-8} \\ {1} & {0} & {1} & {2} \\ {0} & {4} & {2} & {0}\end{array}\right|$$ Полученный определитель разложим по элементам первого столбца: $$\left| \begin{array}{rrrr}{0} & {8} & {-2} & {-12} \\ {0} & {4} & {-2} & {-8} \\ {1} & {0} & {1} & {2} \\ {0} & {4} & {2} & {0}\end{array}\right|=0+0+1 \cdot(-1)^{3+1} \cdot \left| \begin{array}{rrr}{8} & {-2} & {-12} \\ {4} & {-2} & {-8} \\ {4} & {2} & {0}\end{array}\right|+0$$ Полученный определитель третьего порядка также разложим по элементам строки и столбца, предварительно получив нули,
например, в первом столбце. $$=4 \cdot(2 \cdot 8-4 \cdot 4)=0$$ Ответ. $\left| \begin{array}{cccc}{9} & {8} & {7} & {6} \\ {5} & {4} & {3} & {2} \\ {1} & {0} & {1} & {2} \\ {3} & {4} & {5} & {6}\end{array}\right|=0$ Замечание Последний и предпоследний определители можно было бы и не вычислять,
а сразу сделать вывод о том, что они равны нулю, так как содержат пропорциональные строки. С помощью элементарных преобразований над строками или столбцами определитель приводится к треугольному виду и тогда его
значение, согласно свойствам определителя, равно произведению
элементов стоящих на главной диагонали. Пример Задание. Вычислить определитель
$\Delta=\left| \begin{array}{rrrr}{-2} & {1} & {3} & {2} \\ {3} & {0} & {-1} & {2} \\ {-5} & {2} & {3} & {0} \\ {4} & {-1} & {2} & {-3}\end{array}\right|$ приведением его к треугольному виду. Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования
будет выполнять проще, если элемент $a_{11}$ будет
равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя,
приведет к тому, что он сменит знак на противоположный: $$\Delta=\left| \begin{array}{rrrr}{-2} & {1} & {3} & {2} \\ {3} & {0} & {-1} & {2} \\ {-5} & {2} & {3} & {0} \\ {4} & {-1} & {2} & {-3}\end{array}\right|=-\left| \begin{array}{rrrr}{1} & {-2} & {3} & {2} \\ {0} & {3} & {-1} & {2} \\ {2} & {-5} & {3} & {0} \\ {-1} & {4} & {2} & {-3}\end{array}\right|$$ Далее получим нули в первом столбце, кроме элемента $a_{11}$ ,
для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь: $$\Delta=-\left| \begin{array}{rrrr}{1} & {-2} & {3} & {2} \\ {0} & {3} & {-1} & {2} \\ {0} & {-1} & {-3} & {-4} \\ {0} & {2} & {5} & {-1}\end{array}\right|$$ Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. $$\Delta=\left| \begin{array}{rrrr}{1} & {-2} & {3} & {2} \\ {0} & {-1} & {-3} & {-4} \\ {0} & {3} & {-1} & {2} \\ {0} & {2} & {5} & {-1}\end{array}\right|$$ Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом:
к третьей строке прибавляем три вторых, а к четвертой — две вторых строки, получаем: $$\Delta=\left| \begin{array}{rrrr}{1} & {-2} & {3} & {2} \\ {0} & {-1} & {-3} & {-4} \\ {0} & {0} & {-10} & {-10} \\ {0} & {0} & {-1} & {-9}\end{array}\right|$$ Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под
главной диагональю, а для этого к последней строке прибавляем третью: $$\Delta=-10 \left| \begin{array}{rrrr}{1} & {-2} & {3} & {2} \\ {0} & {-1} & {-3} & {-4} \\ {0} & {0} & {1} & {1} \\ {0} & {0} & {-1} & {-9}\end{array}\right|=$$ $$=-10 \cdot \left| \begin{array}{cccc}{1} & {-2} & {3} & {2} \\ {0} & {-1} & {-3} & {-4} \\ {0} & {0} & {1} & {1} \\ {0} & {0} & {0} & {-8}\end{array}\right|=(-10) \cdot 1 \cdot(-1) \cdot 1 \cdot(-8)=-80$$ Ответ. Теорема Пусть $\Delta$ — определитель
$n$-го порядка. Выберем в нем произвольные
$k$ строк (или столбцов), причем
$k \leq n-1$ . Тогда сумма произведений всех
миноров
$k$-го порядка, которые содержатся в выбранных
$k$ строках (столбцах), на их
алгебраические дополнения равна определителю. Пример Задание. Используя теорему Лапласа, вычислить определитель
$\left| \begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \\ {0} & {1} & {0} & {-1} & {2} \\ {3} & {2} & {1} & {0} & {1} \\ {0} & {4} & {0} & {-5} & {0} \\ {1} & {1} & {2} & {-2} & {1}\end{array}\right|$ Решение. Выберем в данном определителе пятого порядка две строки —
вторую и третью, тогда получаем (слагаемые, которые равны нулю, опускаем): $$\left| \begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \\ {0} & {1} & {0} & {-1} & {2} \\ {3} & {2} & {1} & {0} & {1} \\ {0} & {4} & {0} & {-5} & {0} \\ {1} & {1} & {2} & {-2} & {1}\end{array}\right|=\left| \begin{array}{cc}{1} & {-1} \\ {4} & {-5}\end{array}\right| \cdot(-1)^{2+4+2+4} \cdot \left| \begin{array}{ccc}{2} & {0} & {5} \\ {3} & {1} & {1} \\ {1} & {2} & {1}\end{array}\right|+$$ $$+\left| \begin{array}{ll}{1} & {2} \\ {4} & {0}\end{array}\right| \cdot(-1)^{2+4+2+5} \cdot \left| \begin{array}{rrr}{2} & {0} & {4} \\ {3} & {1} & {0} \\ {1} & {2} & {-2}\end{array}\right|+\left| \begin{array}{cc}{-1} & {2} \\ {-5} & {0}\end{array}\right| \cdot(-1)^{2+4+5} \cdot \left| \begin{array}{ccc}{2} & {3} & {0} \\ {3} & {2} & {1} \\ {1} & {1} & {2}\end{array}\right|=$$ $$=-23+128+90=195$$ Ответ. Читать дальше: обратная матрица. Определители четвертого и старших порядков возможно вычислять по упрощенным схемам, которые заключаются в разложении по элементам строк или столбцов или сведении к треугольному виду. Оба метода для наглядности будут рассмотрены на матрицах 4-го порядка. Первый пример мы рассмотрим с подробными объяснениями всех промежуточных действий. Пример 1. Вычислить определитель методом разложения. Решение. Для упрощения вычислений разложим определитель четвертого порядка по элементам первой строки (содержит нулевой элемент). Они образуются умножением элементов на соответствующие им дополнения (образуются вычеркивания строк и столбцов на пересечении элемента, для которого исчисляются — выделено красным) В результате вычисления сведутся к отысканию трех определителей третьего порядка, которые находим по правилу треугольников Результат легко проверить с помощью матричного калькулятора YukhymCALC . Далее вводим же матрицу и осуществляем вычисления. Результатом расчетов будет следующий вывод данных Результаты совпадают, следовательно вычисления проведены верно. Пример 2. Вычислить определитель матрицы четвертого порядка. Решение. Как и в предыдущем задании осуществим вычисления методом разложения. Для этого выберем элементы первого столбца. Упрощенно определитель можно подать через сумму четырех детерминант третьего порядка в виде Далее переходим к отысканию определителей по правилу треугольников Вычисления не слишком сложные, главное не напутать со знаками и треугольниками. Найденные величины подставляем в главный определитель и суммируем Результат проверяем матричным калькулятором YukhymCALC . Данный метод позволяет ряд определителей вычислить достаточно быстрый способ. Суть его заключается в объединении определителя к треугольному виду, при этом следует учитывать все множители на которые увеличиваем или уменьшаем строки и учете при конечных расчетах. Из данного определения Вы ничего для себя не поймете, поэтому лучше все показать на конкретных примерах. Пример 3. Найти определитель матрицы сведением к треугольному виду Решение. Сначала осуществляем математические манипуляции, чтобы получить все нулевые элементы кроме первого в первом столбце. Для этого от второй строки вычитаем первый, умноженный на два. В результате получим Далее есть два варианта: от третьей строки вычесть первый умноженный на три, или от третьего вычесть сумму первых двух строк. Последний вариант позволит получить сразу два нуля в строке, его и выбираем Дальше целесообразнее от четвертой отнять удвоенную вторую строчку. Осталось превратить в ноль один элемент в третьем столбце. Для этого от четвертой строки вычитаем удвоенную третью в предварительно записанном определителе По свойству, определитель треугольной матрицы равен произведению диагональных элементов. В этом примере никаких умножений строк, в которых зануливали элементы мы не выполняли, поэтому полностью раскрыть метод на этом примере не получилось. Рассмотрим более сложный. Пример 4. Найти определитель матрицы 4-го порядка Решение. Элементарными преобразованиями сводим определитель к треугольного вида. Для этого от каждой строки вычитаем первый. В результате преобразований получим следующий детерминант Для удобства вычислений, меняем третью строчку со вторым местами.. По свойству определителей любая замена строк местами ведет к изменению знака определителя. От третьей строки вычитаем второй, умноженный на минус три. После упрощений получим Превращаем в ноль последний элемент во втором столбце, для этого вычитаем вторую строчку умноженный на 2. Результат будет следующим От удвоенного четвертой строки вычитаем третий. По свойству, умножения строки на постоянную а ведет к изменению определителя в а раз. Данное изменение фиксируем в множителе k=-1*2=-2. Окончательное значение определителя будет равно произведению диагональных элементов разделенных (или нормированных) на множитель k, который отвечает за изменение детерминанта при элементарных преобразованиях. Выполняем вычисления Проверка матричным калькулятором подтверждает правильность производимых вычислений. Метод разложения определителя по элементам строк или столбцов достаточно быстрым при исчислении определителей больших размеров. Метод сведения к треугольного вида эффективен, если элементарные преобразования легко проследить и не приводят к большим произведений. Матрица — это особый объект в математике. Изображается в форме прямоугольной или квадратной таблицы, сложенной из определенного числа строк и столбцов. В математике имеется большое разнообразие видов матриц, различающихся по размерам или содержанию. Числа ее строк и столбцов именуются порядками. Эти объекты употребляются в математике для упорядочивания записи систем линейных уравнений и удобного поиска их результатов. Уравнения с использованием матрицы решаются посредством метода Карла Гаусса, Габриэля Крамера, миноров и алгебраических дополнений, а также многими другими способами. Базовым умением при работе с матрицами является приведение к стандартному виду. Все компоненты этого вида матрицы — нули. Между тем, число ее строк и столбцов абсолютно различно. Количество столбцов и строк этого вида матрицы совпадает. Иначе говоря, она представляет собой таблицу формы «квадрат». Число ее столбцов (или строк) именуются порядком. Частными случаями считается существование матрицы второго порядка (матрица 2×2), четвертого порядка (4×4), десятого (10×10), семнадцатого (17×17) и так далее. Это один из простейших видов матриц, содержащий только один столбец, который включает в себя три численных значения. Она представляет ряд свободных членов (чисел, независимых от переменных) в системах линейных уравнений. Вид, аналогичный предыдущему. Состоит из трех численных элементов, в свою очередь организованных в одну строку. Числовые значения в диагональном виде матрицы принимают только компоненты главной диагонали (выделена зеленым цветом). Подвид диагональной матрицы. Все ее числовые значения являются единицами. Используя единичный тип матричных таблиц, выполняют ее базовые преобразования или находят матрицу, обратную исходной. Канонический вид матрицы считается одним из основных; приведение к нему часто необходимо для работы. Число строк и столбцов в канонической матрице различно, она необязательно принадлежит к квадратному типу. Она несколько похожа на единичную матрицу, однако в ее случае не все компоненты основной диагонали принимают значение, равное единице. Главнодиагональных единиц может быть две, четыре (все зависит от длины и ширины матрицы). Один из важнейших видов матрицы, применяемый при поиске ее детерминанта и при выполнении простейших операций. Треугольный тип происходит от диагонального, поэтому матрица также является квадратной. Треугольный вид матрицы подразделяют на верхнетреугольный и нижнетреугольный. В верхнетреугольной матрице (рис. 1) только элементы, которые находятся над главной диагональю, принимают значение, равное нулю. Компоненты же самой диагонали и части матрицы, располагающейся под ней, содержат числовые значения. В нижнетреугольной (рис. 2), наоборот, элементы, располагающиеся в нижней части матрицы, равны нулю. Вид необходим для нахождения ранга матрицы, а также для элементарных действий над ними (наряду с треугольным типом). Ступенчатая матрица названа так, потому что в ней содержатся характерные «ступени» из нулей (как показано на рисунке). Таким образом, мы рассмотрели важнейшие типы матриц, необходимые для работы с ними. Теперь разберемся с задачей преобразования матрицы в требуемую форму. Как же привести матрицу к треугольному виду? Чаще всего в заданиях нужно преобразовать матрицу в треугольный вид, чтобы найти ее детерминант, по-другому называемый определителем. Выполняя данную процедуру, крайне важно «сохранить» главную диагональ матрицы, потому что детерминант треугольной матрицы равен именно произведению компонентов ее главной диагонали. Напомню также альтернативные методы нахождения определителя. Детерминант квадратного типа находится при помощи специальных формул. Подробно разберем процесс приведения матрицы к треугольному виду на примерах некоторых заданий. Необходимо найти детерминант представленной матрицы, используя метод приведения его к треугольному виду. Данная нам матрица представляет собой квадратную матрицу третьего порядка. Следовательно, для ее преобразования в треугольную форму нам понадобится обратить в нуль два компонента первого столбца и один компонент второго. Чтобы привести ее к треугольному виду, начнем преобразование с левого нижнего угла матрицы — с числа 6. Чтобы обратить его в нуль, умножим первую строку на три и вычтем ее из последней строки. Важно! Верхняя строка не изменяется, а остается такой же, как и в исходной матрице. Записывать строку, в четыре раза большую исходной, не нужно. Далее займемся следующим значением — элементом второй строки первого столбца, числом 8. Умножим первую строку на четыре и вычтем ее из второй строки. Получим нуль. Осталось только последнее значение — элемент третьей строки второго столбца. Это число (-1). Чтобы обратить его в нуль, из первой строки вычтем вторую. Выполним проверку: detA = 2 x (-1) x 11 = -22. Значит, ответ к заданию: -22. Нужно найти детерминант матрицы методом приведения его к треугольному виду. Представленная матрица принадлежит к квадратному типу и является матрицей четвертого порядка. Значит, необходимо обратить в нуль три компонента первого столбца, два компонента второго столбца и один компонент третьего. Начнем приведение ее с элемента, находящегося в нижнем углу слева, — с числа 4. Нам нужно обратить данное число в нуль. Удобнее всего сделать это, умножив на четыре верхнюю строку, а затем вычесть ее из четвертой. Итак, компонент четвертой строки обращен в нуль. Перейдем к первому элементу третьей строки, к числу 3. Выполняем аналогичную операцию. Умножаем на три первую строку, вычитаем ее из третьей строки и записываем результат. Далее видим число 2 во второй строке. Повторяем операцию: умножаем верхнюю строку на два и вычитаем ее из второй. Нам удалось обратить в нуль все компоненты первого столбца данной квадратной матрицы, за исключением числа 1 — элемента главной диагонали, не требующего преобразования. Теперь важно сохранить полученные нули, поэтому будем выполнять преобразования со строками, а не со столбцами. Перейдем ко второму столбцу представленной матрицы. Снова начнем с нижней части — с элемента второго столбца последней строки. Это число (-7). Однако в данном случае удобнее начать с числа (-1) — элемента второго столбца третьей строки. Чтобы обратить его в нуль, вычтем из третьей строки вторую. Затем умножим вторую строку на семь и вычтем ее из четвертой. В данном столбце нам нужно обратить в нуль только одно число — 4. Сделать это несложно: просто прибавляем к последней строке третью и видим необходимый нам нуль. После всех произведенных преобразований мы привели предложенную матрицу к треугольному виду. Теперь, чтобы найти ее детерминант, нужно только произвести умножение получившихся элементов главной диагонали. Получаем: detA = 1 x (-1) x (-4) x 40 = 160. Следовательно, решением является число 160. Итак, теперь вопрос приведения матрицы к треугольному виду вас не затруднит. При элементарных операциях над матрицами ступенчатый вид является менее «востребованным», чем треугольный. Чаще всего он используется для нахождения ранга матрицы (т. е. количества ее ненулевых строк) или для определения линейно зависимых и независимых строк. Однако ступенчатый вид матрицы является более универсальным, так как подходит не только для квадратного типа, но и для всех остальных. Чтобы привести матрицу к ступенчатому виду, сначала нужно найти ее детерминант. Для этого подойдут вышеназванные методы. Цель нахождения детерминанта такова: выяснить, можно ли преобразовать ее в ступенчатый вид матрицы. Если детерминант больше или меньше нуля, то можно спокойно приступать к заданию. Если же он равен нулю, выполнить приведение матрицы к ступенчатому виду не получится. В таком случае нужно проверить, нет ли ошибок в записи или в преобразованиях матрицы. Если подобных неточностей нет, задание решить невозможно. Рассмотрим, как привести матрицу к ступенчатому виду на примерах нескольких заданий. Задание 1. Найти ранг данной матричной таблицы. Перед нами квадратная матрица третьего порядка (3×3). Мы знаем, что для нахождения ранга необходимо привести ее к ступенчатому виду. Поэтому сначала нам необходимо найти детерминант матрицы. Воспользуемся методом треугольника: detA = (1 x 5 x 0) + (2 x 1 x 2) + (6 x 3 x 4) — (1 x 1 x 4) — (2 x 3 x 0) — (6 x 5 x 2) = 12. Детерминант = 12. Он больше нуля, значит, матрицу можно привести к ступенчатому виду. Приступим к ее преобразованиям. Начнем его с элемента левого столбца третьей строки — числа 2. Умножаем верхнюю строку на два и вычитаем ее из третьей. Благодаря этой операции как нужный нам элемент, так и число 4 — элемент второго столбца третьей строки — обратились в нуль. Далее обращаем в нуль элемент второй строки первого столбца — число 3. Для этого умножаем верхнюю строку на три и вычитаем ее из второй. Мы видим, что в результате приведения образовалась треугольная матрица. В нашем случае продолжить преобразование нельзя, так как остальные компоненты не удастся обратить в нуль. Значит, делаем вывод, что количество строк, содержащих числовые значения, в данной матрице (или ее ранг) — 3. Ответ к заданию: 3. Задание 2. Определить количество линейно независимых строк данной матрицы. Нам требуется найти такие строки, которые нельзя какими-либо преобразованиями обратить в нуль. Мы видим матрицу, не принадлежащую к квадратному типу. Она имеет размеры 3×4. Начнем приведение также с элемента левого нижнего угла — числа (-1). Прибавляем первую строку к третьей. Далее вычитаем из нее вторую, чтобы обратить число 5 в нуль. Дальнейшие ее преобразования невозможны. Значит, делаем вывод, что количество линейно независимых строк в ней и ответ к заданию — 3. Теперь приведение матрицы к ступенчатому виду не является для вас невыполнимым заданием. На примерах данных заданий мы разобрали приведение матрицы к треугольному виду и ступенчатому виду. Чтобы обратить в нуль нужные значения матричных таблиц, в отдельных случаях требуется проявить фантазию и правильно преобразовать их столбцы или строки. Успехов вам в математике и в работе с матрицами! Учеба Математика Алгебра линейная алгебра Матричная триангуляция с использованием методов Гаусса. Ниже приведены два калькулятора для матричной триангуляции. 3 2 3 4
4 4 3 2
1 4 4 3
2 3 1 1 Матрица ПРОТИВАЯ ПЕЗИЦИЯ цифры после десятичной точки: 4 ТРИАНГУЛЯЙСКА с максимальным выбором по всей матрице): 3 2 3 4
4 4 3 2
1 4 4 3
2 3 1 1 Матрица Точность вычислений Знаки после запятой: 4 Треугольная матрица (метод Барейса) Треугольная матрица (метод Барейса с максимальным выбором в столбце) Треугольная матрица с максимальным выбором во всем методе Барейса матрица) Сначала дадим понятие треугольной или ступенчатой матрице строк: Пример эшелонированной матрицы строк: Пример верхней треугольной матрицы: Вы спросите, что интересного в этих ступенчатых (и треугольных) матрицах? Что ж, у них есть удивительное свойство — любую прямоугольную матрицу можно свести к ступенчатой матрице с помощью элементарных преобразований. Итак, что же такое элементарные преобразования, спросите вы? Что теперь? Путем триангуляции матрицы линейного уравнения AX=B к A’X = B’, т.е. с соответствующим преобразованием столбца B, вы можете сделать так называемую «обратную подстановку». Для пояснения воспользуемся приведенной выше треугольной матрицей и перепишем систему уравнений в более общем виде (я составил столбец B): Понятно, что сначала найдем , а потом подставим в предыдущее уравнение, найти и так далее – переход от последнего уравнения к первому. Это то, что называется обратной заменой. Теперь немного мыслей об этом методе. Нуль в первом уравнении Во втором уравнении нет где N – размерность строки, – i-я строка, Однако существует радикальная модификация метода Гаусса – метод Барейса. Барейс предложил разделить приведенное выше выражение на и показал, что если исходными элементами матрицы являются целые числа, то результирующее число будет целым. Также предполагается, что для нулевой строки . Кстати, тот факт, что алгоритм Барейса сводит целые элементы исходной матрицы к треугольной матрице с целыми элементами, т.е. без накопления отклонений, является весьма важной особенностью с точки зрения машинной арифметики. Алгоритм Барейса можно представить в виде: Этот алгоритм можно модернизировать, аналогично Гауссу, с максимальной выборкой в столбце (вся матрица) и перестановкой соответствующих строк (строк и столбцов). URL скопирован в буфер обмена 0011 PlanetCalc, Матриц-триангуляционные калькуляторы Timur 2020-12-04 10:52:17 Верхние треугольные матрицы — это матрицы, в которых все элементы ниже главной диагонали равны ???0???. Привет! Я Криста. Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее. Нижние треугольные матрицы — это матрицы, в которых все элементы выше главной диагонали равны ???0???. Вот главные диагонали в этих верхних треугольных матрицах, и в этих нижних треугольных матрицах: Мы обвели главную диагональ в каждой матрице, так что мы можем видеть, что все элементы в верхней треугольной матрице ниже главной диагонали равны ???0???, и что все элементы в нижней треугольной матрице матрицы выше главной диагонали равны ???0???. Определитель треугольных матриц Поскольку мы можем найти определитель матрицы в любой строке или столбце, который нам нужен, для верхних треугольных матриц всегда нужно выбирать первый столбец (или последнюю строку) , так как он включает в себя больше всего ???0??? записи. Например, мы хотим найти определитель верхней треугольной матрицы ???A???: Обратите внимание, что ???A??? включает ???0??? запись в ???a_{(2,3)}???. Это нормально. У нас могут быть нулевые значения на главной диагонали или выше нее. Чтобы считаться верхней треугольной матрицей, единственное, что имеет значение, это то, что все элементы ниже главной диагонали равны ???0???. Определитель ???A??? по первому столбцу Последние три члена обнуляются. Упростим оставшиеся ???3\times3??? определитель снова по первому столбцу. Последние два члена обнуляются. ???|A|=1\влево[-2((5)(-1)-(3)(0))\вправо]??? ???|A|=1\влево[(-2)(5)(-1)\вправо]??? ???|А|=(1)(-2)(5)(-1)??? ???|А|=10??? В этом результате мы хотим отметить две вещи. Во-первых, вычисление было намного проще, чем обычное ???4\times4??? определителя, поэтому работа с первым столбцом является хорошей стратегией, когда мы вычисляем определитель верхней треугольной матрицы. Во-вторых, значением определителя было произведение ???(1)(-2)(5)(-1)???, которое является произведением всех элементов на главной диагонали ???A ???. На самом деле, для всех верхних треугольных матриц это всегда будет верно! Учитывая любую верхнюю треугольную матрицу, вы можете найти значение определителя, просто перемножив вместе все элементы вдоль главной диагонали матрицы. Это также говорит вам, что если у вас есть ???0??? в любом месте на главной диагонали верхней треугольной матрицы определитель будет равен ???0???. Это означает, что если матрица содержит полную строку нулей в любом месте матрицы, то определитель будет равен ???0???. То же верно и для нижних треугольных матриц. Если бы вы сделали это, то обнаружили бы, что определитель нижней треугольной матрицы является произведением элементов вдоль главной диагонали, как мы это сделали для верхних треугольных матриц. Преобразование матрицы в верхний треугольный или нижний треугольный вид — отличный способ быстро найти определитель. {1+3} \cdot \left| \begin{array}{cc}{4} & {5} \\ {7} & {8}\end{array}\right|=-3+12-9=0$
{1+3} \cdot \left| \begin{array}{cc}{4} & {5} \\ {7} & {8}\end{array}\right|=-3+12-9=0$
Разложение определителя по элементам строки или столбца
 {2+2} \cdot \left| \begin{array}{ll}{2} & {4} \\ {4} & {8}\end{array}\right|=$$
{2+2} \cdot \left| \begin{array}{ll}{2} & {4} \\ {4} & {8}\end{array}\right|=$$Приведение определителя к треугольному виду

 И снова, если
диагональный элемент будет равен $\pm 1$ , то
вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на
противоположный знак определителя):
И снова, если
диагональный элемент будет равен $\pm 1$ , то
вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на
противоположный знак определителя): $\Delta=-80$
$\Delta=-80$Теорема Лапласа
 $\left| \begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \\ {0} & {1} & {0} & {-1} & {2} \\ {3} & {2} & {1} & {0} & {1} \\ {0} & {4} & {0} & {-5} & {0} \\ {1} & {1} & {2} & {-2} & {1}\end{array}\right|=195$
$\left| \begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \\ {0} & {1} & {0} & {-1} & {2} \\ {3} & {2} & {1} & {0} & {1} \\ {0} & {4} & {0} & {-5} & {0} \\ {1} & {1} & {2} & {-2} & {1}\end{array}\right|=195$Определитель 4 порядка. Калькулятор
Найденные значения подставляем в выходной детерминант  Для этого в калькуляторе выбираем пункт Матрицы-Определитель матрицы, размер матрицы устанавливаем 4*4.
Для этого в калькуляторе выбираем пункт Матрицы-Определитель матрицы, размер матрицы устанавливаем 4*4. Правильность расчетов подтверждается следующим рисунком
Правильность расчетов подтверждается следующим рисункомМетод возведения определителя к треугольному виду
 В результате элементарных преобразований определитель примет вид
В результате элементарных преобразований определитель примет вид
По желанию можно проверить результат матричным калькулятором. Учитываем это в некотором множителе k=-1.
Учитываем это в некотором множителе k=-1. В других случаях нужно пользоваться комбинацией этих методов, в последнее образовывать как можно больше нулевых элементов, а методом разложения по строкам или столбцам уменьшать количество выполненных операций. Это позволит без проблем вычислять определители третьего, четвертого и даже пятого порядка.
В других случаях нужно пользоваться комбинацией этих методов, в последнее образовывать как можно больше нулевых элементов, а методом разложения по строкам или столбцам уменьшать количество выполненных операций. Это позволит без проблем вычислять определители третьего, четвертого и даже пятого порядка.Виды матриц. Ступенчатый вид матрицы. Приведение матрицы к ступенчатому и треугольному виду
 Однако для начала давайте разберемся, какие виды матриц выделяют математики.
Однако для начала давайте разберемся, какие виды матриц выделяют математики.Нулевой тип
Квадратный тип
Вектор-стобец
Вектор-строка
Диагональный тип
 Основная диагональ начинается с элемента, находящегося в левом верхнем углу, а заканчивается элементом в правом нижнем соответственно. Остальные компоненты равны нулю. Диагональный тип представляет собой только квадратную матрицу какого-либо порядка. Среди матриц диагонального вида можно выделить скалярную. Все ее компоненты принимают одинаковые значения.
Основная диагональ начинается с элемента, находящегося в левом верхнем углу, а заканчивается элементом в правом нижнем соответственно. Остальные компоненты равны нулю. Диагональный тип представляет собой только квадратную матрицу какого-либо порядка. Среди матриц диагонального вида можно выделить скалярную. Все ее компоненты принимают одинаковые значения.Единичная матрица
Канонический тип
 Или единицы могут не иметься вовсе (тогда она считается нулевой). Остальные компоненты канонического типа, как и элементы диагонального и единичного, равны нулю.
Или единицы могут не иметься вовсе (тогда она считается нулевой). Остальные компоненты канонического типа, как и элементы диагонального и единичного, равны нулю.Треугольный тип
Ступенчатая матрица
 В ступенчатом типе образуется диагональ из нулей (необязательно главная), и все элементы под данной диагональю тоже имеют значения, равные нулю. Обязательным условием является следующее: если в ступенчатой матрице присутствует нулевая строка, то остальные строки, находящиеся ниже нее, также не содержат числовых значений.
В ступенчатом типе образуется диагональ из нулей (необязательно главная), и все элементы под данной диагональю тоже имеют значения, равные нулю. Обязательным условием является следующее: если в ступенчатой матрице присутствует нулевая строка, то остальные строки, находящиеся ниже нее, также не содержат числовых значений.Приведение к треугольному виду
 Например, можно воспользоваться методом треугольника. Для других матриц используют метод разложения по строке, столбцу или их элементам. Также можно применять метод миноров и алгебраических дополнений матрицы.
Например, можно воспользоваться методом треугольника. Для других матриц используют метод разложения по строке, столбцу или их элементам. Также можно применять метод миноров и алгебраических дополнений матрицы.Задание 1
 Но значения строк, компоненты которых нужно обратить в нуль, постоянно меняются.
Но значения строк, компоненты которых нужно обратить в нуль, постоянно меняются.Задание 2
 Запишем итог первого этапа преобразования.
Запишем итог первого этапа преобразования. Мы получили нуль вместо элемента, расположенного в четвертой строке второго столбца. Теперь перейдем к третьему столбцу.
Мы получили нуль вместо элемента, расположенного в четвертой строке второго столбца. Теперь перейдем к третьему столбцу.Приведение к ступенчатому виду


 Фактически нам нужно найти количество ненулевых строк, или ранг представленной матрицы. Для этого выполним ее упрощение.
Фактически нам нужно найти количество ненулевых строк, или ранг представленной матрицы. Для этого выполним ее упрощение. Онлайн калькулятор: Калькуляторы матричной триангуляции

Первый использует метод Гаусса, второй метод Барейса. Описание методов и их теории ниже. Матричная триангуляция (метод Гаусса)
Матричная триангуляция (метод Барейса)
Матрица имеет ступенчатую форму строк, если:
1 0 2 5
0 3 0 0
0 0 0 4
Понятие треугольной матрицы является более узким и используется только для квадратных матриц. Это выглядит так: треугольная матрица — это квадратная матрица, в которой все элементы ниже главной диагонали равны нулю.
Это выглядит так: треугольная матрица — это квадратная матрица, в которой все элементы ниже главной диагонали равны нулю.
1 0 2 5
0 3 1 3
0 0 4 2
0 0 0 3
Кстати, определитель треугольной матрицы вычисляется простым перемножением всех ее диагональных элементов.
Элементарными преобразованиями матрицы являются следующие операции:
Элементарные преобразования матриц сохраняют эквивалентность матриц. А, если вспомнить, что системы линейных алгебраических уравнений записываются только в матричной форме, то это означает, что элементарные матричные преобразования не меняют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.
А, если вспомнить, что системы линейных алгебраических уравнений записываются только в матричной форме, то это означает, что элементарные матричные преобразования не меняют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.
Этот алгоритм сокращения строк называется методом Гаусса. Метод Гаусса — классический метод решения систем линейных уравнений. Его также называют методом исключения Гаусса, так как это метод последовательного исключения переменных, когда с помощью элементарных преобразований системы уравнений приводятся к ступенчатой (или треугольной) форме строк, в которую помещаются все остальные переменные (начиная с последний).
Как обнулить переменную во втором уравнении?
Вычитая из него первую единицу, умноженную на коэффициент
Вот пример:
В обобщенном смысле метод Гаусса можно представлена следующим образом:
– элемент в i-й строке, j-й столбец в формуле. Во-первых, если диагональный элемент равен нулю, этот метод не сработает. Во-вторых, при расчете отклонение будет возрастать и чем дальше, тем больше. Так что результат не будет точным.
Для уменьшения отклонения используются модификации метода Гаусса. Они основаны на том, что чем больше знаменатель, тем меньше отклонение. Этими модификациями являются метод Гаусса с максимальным выбором в столбце и метод Гаусса с максимальным выбором во всей матрице. Как следует из названия, перед каждым стеблем исключения переменных в строке (во всей матрице) ищется элемент с максимальным значением и выполняется перестановка строк, поэтому он поменяется местами с .
Как можно избавиться от деления? Умножая строку на перед вычитанием. Затем вам нужно вычесть , умножить на без деления.
.
Вроде хорошо, но возникает проблема увеличения значения элемента при вычислениях Похожие калькуляторы
Верхний и нижний матричный
Что такое верхние треугольные матрицы и нижние треугольные матрицы?
 Главная диагональ — это набор элементов, идущих от верхнего левого угла матрицы вниз к нижнему правому углу матрицы.
Главная диагональ — это набор элементов, идущих от верхнего левого угла матрицы вниз к нижнему правому углу матрицы.

 Если бы вы вычисляли определитель традиционным способом, вам нужно было бы вычислять его по первой строке или последнему столбцу, так как в них больше всего ???0??? записи.
Если бы вы вычисляли определитель традиционным способом, вам нужно было бы вычислять его по первой строке или последнему столбцу, так как в них больше всего ???0??? записи. Определение и построение верхних треугольных матриц и нижних треугольных матриц
Пройти курс
Хотите узнать больше о линейной алгебре? У меня есть пошаговый курс для этого. 🙂
Приведение матрицы к треугольной форме
Пример
Поставить ???A??? в верхний или нижний треугольный вид, чтобы найти определитель.
В ???A??? у нас не больше нулей ниже главной диагонали, чем над ней, или наоборот, так что мы действительно можем работать в любом направлении. Давайте начнем с того, что перепишем матрицу как определитель, который мы пытаемся найти.
Теперь поменяйте местами первую и вторую строки, чтобы у нас была сводная запись в первой строке. Помните, что когда мы меняем строки, определитель умножается на ???-1???.
Главная диагональ — это набор элементов, идущих от верхнего левого угла матрицы вниз к нижнему правому углу матрицы.
Теперь выполним ???2R_1+R_2\to R_2???.
Теперь выполните ???-3R_2+R_3\to R_3???.
Теперь, когда у нас есть ???A??? в верхнетреугольной форме определитель — это просто произведение элементов вдоль главной диагонали. Не забудьте знак минус перед матрицей, которую мы поставили для переключения строк.
Не забудьте знак минус перед матрицей, которую мы поставили для переключения строк.
???|А|=-(1)(2)(-28)???
???|А|=56???
Получите доступ к полному курсу линейной алгебры
Изучение математикиКриста Кинг математика, изучение онлайн, онлайн-курс, онлайн-математика, линейная алгебра, верхние треугольные матрицы, нижние треугольные матрицы, верхние и нижние треугольные матрицы, главная диагональ, главная диагональ матрицы, определитель треугольная матрица
0 лайковНайти определитель с помощью сокращения строк
\( \) \( \) \( \) \( \)
Приведены примеры и вопросы с их решениями о том, как найти определитель квадратной матрицы, используя ступенчатую форму строк. Основная идея состоит в том, чтобы привести заданную матрицу к треугольной форме, а затем вычислить ее определитель. Определитель данной матрицы вычисляется из определителя треугольной с учетом перечисленных ниже свойств.
Основная идея состоит в том, чтобы привести заданную матрицу к треугольной форме, а затем вычислить ее определитель. Определитель данной матрицы вычисляется из определителя треугольной с учетом перечисленных ниже свойств.
Определяющие свойства и сокращение строк
Данную матрицу приведем к ступенчатой форме строк (верхней треугольной или нижней треугольной) с учетом следующих свойств определителей:
Свойство 1: Если линейную комбинацию строк данной квадратной матрицы добавить к другой строке той же квадратной матрицы, то определитель полученной матрицы будет равен определителю исходной матрицы.
Свойство 2: Если две строки данной матрицы поменять местами, то определитель полученной матрицы равен определителю исходной матрицы, умноженному на — 1.
Свойство 3: Если строку данной матрицы умножить на скаляр k, то определитель полученной матрицы равен определителю исходной матрицы, умноженному на k.
Примеры нахождения определителя с использованием редукции строк
Пример 1Объедините строки и используйте вышеуказанные свойства, чтобы переписать приведенную ниже матрицу 3 3 в треугольной форме и вычислить ее определитель. \[ А = \begin{bmatrix} 2 и -1 и 3 \\ -2&5&6\ 4 и 6 и 7 \end{bmatrix} \]
Решение примера 1
Пусть D определитель данной матрицы.
шаг 1: добавить строку (1) к строке (2) — см. свойство (1) выше — определитель не меняется D
\[
\color{красный}{\begin{matrix}
\\
Р_2 = Р_2+Р_1 \\
\\
\конец{матрица} }
\begin{bmatrix}
2 и -1 и 3 \\
0 и 4 и 9\\
4 и 6 и 7
\end{bmatrix} \]
шаг 2: вычесть 2 раза строку (1) из строки (3) — см. свойство (1) выше — определитель не изменится D
\[
\color{красный}{\begin{matrix}
\\
\\
R_3 -2 \крат R_1\\
\конец{матрица} }
\begin{bmatrix}
2 и -1 и 3 \\
0 и 4 и 9\\
0 и 8 и 1
\end{bmatrix} \]
свойство (1) выше — определитель не изменится D
\[
\color{красный}{\begin{matrix}
\\
\\
R_3 -2 \крат R_1\\
\конец{матрица} }
\begin{bmatrix}
2 и -1 и 3 \\
0 и 4 и 9\\
0 и 8 и 1
\end{bmatrix} \]
шаг 3: вычесть 2 раза строку (2) из строки (3) — см. свойство (1) выше — определитель не изменится D
\[
\color{красный}{\begin{matrix}
\\
\\
Р_3 — 2 \раз Р_2\\
\конец{матрица} }
\begin{bmatrix}
2&-1&3 \\
0 и 4 и 9\\
0 и 0 и -17
\end{bmatrix} \]
Теперь, когда матрица имеет треугольную форму, определитель данной матрицы вычисляется как произведение элементов на главной диагонали (слева вверху справа внизу).
Определитель треугольной матрицы = (2)(4)(-17) = — 136 = D = Det(A)
Пример 2
Объедините строки и используйте вышеуказанные свойства, чтобы переписать приведенную ниже матрицу 5 5 в треугольной форме и вычислить ее определитель.
\[ А = \begin{bmatrix}
-1&0&-1&3&6\\
1&1&-1&0&4\\
1&-3&0&-2&2\\
-1&2&2&1&-3\\
0&-1&2&0&2
\end{bmatrix} \] Решение примера 2
Пусть D определитель матрицы A.
Шаг 1: мы добавляем строки к другим строкам, как показано ниже, и согласно свойству (1) определитель не меняет D.
\[ \color{red}{\begin{matrix}
\\
Р_2+Р_1\
R_3 + R_1\\
R_4 + R_2\\
\\
\конец{матрица} }
\begin{bmatrix}
-1&0&-1&3&6\\
0&1&-2&3&10\\
0&-3&-1&1&8\\
0&3&1&1&1\\
0&-1&2&0&2
\end{bmatrix} \]
Шаг 2: мы добавляем кратные строки к другим строкам, как показано ниже, и согласно свойству (1) определитель не меняет D.
\[ \color{red}{\begin{matrix}
\\
\\
R_3 + 3 \раз R_2\\
Р_4- 3 \раз Р_2\\
Р_5 + Р_2
\конец{матрица} }
\begin{bmatrix}
-1&0&-1&3&6\\
0&1&-2&3&10\\
0&0&-7&10&38\\
0&0&7&-8&-29\\
0&0&0&3&12
\end{bmatrix} \]
Шаг 3: мы добавляем строку к другой строке, как показано ниже, и согласно свойству (1) определитель не меняет D.
\[ \color{red}{\begin{matrix}
\\
\\
\\
R_4+R_3\\
\\
\конец{матрица} }
\begin{bmatrix}
-1&0&-1&3&6\\
0&1&-2&3&10\\
0&0&-7&10&38\\
0&0&0&2&9\\
0&0&0&3&12
\end{bmatrix} \]
Шаг 4: мы добавляем кратное строки к другой строке, как показано ниже, и согласно свойству (1) определитель не меняет D.
\[ \color{red}{\begin{matrix}
\\
\\
\\
\\
R_5 — \dfrac{3}{2} R_4
\конец{матрица} }
\begin{bmatrix}
-1&0&-1&3&6\\
0&1&-2&3&10\\
0&0&-7&10&38\\
0&0&0&2&9\\
0&0&0&0&-\dfrac{3}{2}
\end{bmatrix} \]
Теперь матрица имеет треугольную форму, и ее определитель определяется произведением элементов на главной диагонали.
Определитель треугольной матрицы = (-1)(1)(-7)(2)(-3/2) = — 21 = D = Det(A)
Примечание: Сравните этот метод вычисления определителя квадратной матрицы с методом кофакторов в определителе квадратной матрицы. Какой метод эффективнее?
вычислить определитель матрицы \[ А = \begin{bmatrix} -1&2&4&6\\ 0&0&1&7\\ -1&2&4&14\\ 0&2&4&6 \end{bmatrix} \]
Решение примера 3 Пусть D — определитель данной матрицы.
Шаг 1: из строки (3) вычесть строку (1) и согласно свойству (1) определитель не изменится.
\[ \color{red}{\begin{matrix}
\\
\\
Р_3 — Р_1\\
\\
\конец{матрица} }
\begin{bmatrix}
-1&2&4&6\\
0&0&1&7\\
0&0&0&8\\
0&2&4&6
\end{bmatrix} \]
Шаг 2: поменять местами строки (3) и (4) и согласно свойству (2) знак определителя изменить на — D
\[ \color{red}{\begin{matrix}
\\
\\
\текст{от} R_4\\
\текст{от} R_3\\
\конец{матрица} }
\begin{bmatrix}
-1&2&4&6\\
0&0&1&7\\
0&2&4&6\\
0&0&0&8
\end{bmatrix} \]
Шаг 3: поменять местами строки (2) и (3) и согласно свойству (2) знак определителя изменить на -(- D)
\[ \color{red}{\begin{matrix}
\\
\текст{от} R_3\\
\text{от} R_2 \\
\\
\конец{матрица} }
\begin{bmatrix}
-1&2&4&6\\
0&2&4&6\\
0&0&1&7\\
0&0&0&8
\end{bmatrix} \]
Теперь матрица имеет треугольную форму, а ее определитель равен произведению элементов на главной диагонали.
Определитель треугольной матрицы = (-1)(2)(1)(8) = — 16 = -(- D) = D = Det(A)
Вопросы об определителе и сокращении строк
Часть 1 Используйте метод эшелонированной формы строк для вычисления определителя матриц.
\( А = \begin{bmatrix}
1&-1&-3&0&1\\
-1&0&0&1&5\\
1&-1&1&4&5\\
0&0&1&0&-1\\
1&0&1&2&2
\end{bmatrix} \)
Часть 2
Определитель матрицы \( A = \begin{bmatrix}
а&б&в\\
д&е&е\\
г&ч&к
\end{bmatrix} \) равно D.
Найдите определитель в терминах D следующих матриц
а) \( \begin{bmatrix} 2а&2б&2в\\ д&е&е\\ -3г&-3ч&-3к \end{bmatrix} \) , б) \( \begin{bmatrix} д&е&е\\ а&б&в\\ 7г&7ч&7к \end{bmatrix} \)
Ответы на вышеуказанные вопросы
Пусть D — определитель данной матрицы A.
шаг 1: поменять местами строки 4 и 5; согласно свойству (2) определитель меняет знак на: — D.
\[ \begin{bmatrix}
1&-1&-3&0&1\\
-1&0&0&1&5\\
1&-1&1&4&5\\
1&0&1&2&2 \\
0&0&1&0&-1
\end{bmatrix} \]
шаг 2: добавьте несколько строк к другим строкам; определитель не меняется: — D.
\[ \color{red}{\begin{matrix}
\\
R_2+R_1 \\
Р_3-Р_1\
Р_4-Р_1\\
\\
\конец{матрица} }
\begin{bmatrix}
1&-1&-3&0&1\\
0&-1&-3&1&6\\
0&0&4&4&4\\
0&1&4&2&1\\
0&0&1&0&-1
\end{bmatrix} \]
шаг 3: добавить кратное количество строк в другую строку; определитель не меняется: — D.
\[ \color{red}{\begin{matrix}
\\
\\
\\
R_4+R_2\\
\\
\конец{матрица} }
\begin{bmatrix}
1&-1&-3&0&1\\
0&-1&-3&1&6\\
0&0&4&4&4\\
0&0&1&3&7\\
0&0&1&0&-1
\end{bmatrix} \]
шаг 4: добавьте несколько строк к другим строкам; определитель не меняется: — D.
\[ \color{red}{\begin{matrix}
\\
\\
\\
Р_4-(1/4)Р_3\\
R_5 — (1/4)R_3
\end{матрица}}
\begin{bmatrix}
1&-1&-3&0&1\\
0&-1&-3&1&6\\
0&0&4&4&4\\
0&0&0&2&6\\
0&0&0&-1&-2
\end{bmatrix} \]
шаг 5: добавить кратное количество строк в другую строку; определитель не меняется: — D.
\[ \color{red} {\begin{matrix}
\\
\\
\\
\\
R5 + (1/2)R4
\конец{матрица} }
\begin{bmatrix}
1&-1&-3&0&1\\
0&-1&-3&1&6\\
0&0&4&4&4\\
0&0&0&2&6\\
0&0&0&0&1
\end{bmatrix} \]
Теперь матрица имеет треугольную форму, а ее определитель равен произведению элементов на главной диагонали.
Определитель треугольной матрицы = (1)(-1)(4)(2)(1) = — 8 = — D
Определитель D данной матрицы равен D = 8.
Часть 2
а) строка (1) умножается на 2, а строка (3) на -3, следовательно, согласно свойству (3) выше, определитель равен 2 (-3) D = — 6 D.
б) строки (1) и (2) поменять местами, а строку (3) умножить на 7, следовательно, согласно свойствам (2) и (3), определитель
равен (-1) 7 D = — 7 D.
Дополнительные ссылки
Дополнительные ссылки
- определитель квадратной матрицы
- Матрицы с примерами и вопросы с решениями
- Калькулятор формы эшелона строки
- Линейная алгебра
линейная алгебра — Найдите треугольную матрицу и определитель.

Задавать вопрос
спросил
Изменено 4 года, 2 месяца назад
Просмотрено 5к раз
$\begingroup$
У меня есть матрица 4×4, и я хочу найти треугольную матрицу (нижние половины равны нулю).
$$А= \begin{bmatrix} 2 и -8 и 6 и 8\\ 3 и -9 и 5 и 10\\ -3 и 0 и 1 и -2\\ 1 и -4 и 0 и 6 \end{bmatrix} $$
Вот элементарные операции со строками, которые я выполнил, чтобы привести его к треугольной форме.
поменять местами строку 1 и строку 4
$r_2 — 3\cdot r_1$ заменить $r_2$
$r_3 + 3\cdot r_1$ заменить $r_3$
$r_4 — 2\cdot r_1$ заменить $r_4 $
Я получаю эту матрицу
$$A= — \begin{bmatrix} 1 и -4 и 0 и 6\\ 0 и 3 и 5 и -8\\ 0 и -12 и 1 и 16\\ 0 и 0 и 6 и -4 \end{bmatrix} $$
Затем я сделал $4\cdot r_2 + r_3$ для замены $r_3$ и получил
$$A= — \begin{bmatrix} 1 и -4 и 0 и 6\\ 0 и 3 и 5 и -8\\ 0 и 0 и 21 и -16\\ 0 и 0 и 6 и -4 \end{bmatrix} $$
Затем я сделал $-21\cdot r_4 + 6\cdot r_3$ для замены $r_4$ и получил
$$A= — \begin{bmatrix} 1 и -4 и 0 и 6\\ 0 и 3 и 5 и -8\\ 0 и 0 и 21 и -16\\ 0 и 0 и 0 и -12 \end{bmatrix} $$
Я не уверен, что сделал это правильно, но определитель матрицы должен быть -36. Когда я умножаю диагональные записи, это не -36. Я не могу понять, что я делаю неправильно.
Когда я умножаю диагональные записи, это не -36. Я не могу понять, что я делаю неправильно.
- линейная алгебра
- матрицы
- определитель
$\endgroup$
$\begingroup$
«Затем я сделал -21*строку 4 + 6*строку 3, чтобы заменить строку 4, и получил»
Это операция изменения определителя, а не элементарная операция.
Не пишите, что $A$ равно чему-то, что не является $A$.
Подбирая то, где вы ошиблись, и используя ту же идею, что и у вас, получается:
$$\begin{align} \begin{bmatrix}
1 и -4 и 0 и 6\\
0 и 3 и 5 и -8\\
0 и 0 и 21 и -16\\
0 и 0 и 6 и -4
\end{bmatrix}&\leadsto \begin{bmatrix}
1 и -4 и 0 и 6\\
0 и 3 и 5 и -8\\
0 & 0 & 6\cdot 21 & -6\cdot 16\\
0 & 0 & -21\cdot 6 & (-21)\cdot (-4)
\end{bmatrix}\\
&\ ведет к \begin{bmatrix}
1 и -4 и 0 и 6\\
0 и 3 и 5 и -8\\
0 и 0 и 6\cdot 21 и -16\\
0 и 0 и 0 и -12
\end{bmatrix}_. \end{align}$$
\end{align}$$
Получение надлежащей компенсации дает $$\det(A)=-\dfrac{1\cdot 3\cdot (6\cdot 21)\cdot (-12)}{-21\cdot 6}=-36.$$
$\endgroup$
4
$\begingroup$
«Затем я сделал -21⋅r4+6⋅r3, чтобы заменить r4 и получил». взят как делитель со знаком вне определителя. Например, У вас есть матрица A, и ее определитель равен |A|
Если мы выполняем следующую операцию, Р3 -> 3 Р2 — 5Р3 Операционный крик можно выполнить, взяв (-1/5) наружу. Идея заключается в том, что с помощью этой операции мы косвенно умножаем строку 3 на (-5). Нам не нужно беспокоиться о множителе 3 с R2, так как он не повлияет на значение определителя (мы изменяем строку 3, следовательно, оставшиеся коэффициенты строки не повлияют на |A|).
В вашем случае, до последнего шага, операции со строками не имели коэффициентов для конкретных изменений строк. В последнем шаге вы сделали,
В последнем шаге вы сделали,
R4 -> -21 R4 + 6 R3
Итак, вы должны взять (-1/21) снаружи.
После выхода наружу вычисление определителя будет выглядеть так:
|A| = — (-1/21) (1) (3) (21) (-12) = -36
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Верхняя треугольная матрица — обзор
ScienceDirectЗарегистрироватьсяВойти
Сумма верхней треугольной матрицы и нижней треугольной матрицы представляет собой симметричную матрицу.
Из: Элементарная линейная алгебра (четвертое издание), 2010 г.
PlusAdd TO Mendeley Fred E. Szabo PhD, в руководстве по линейной алгебре, 2015
Манипуляции
- ■
(1 (Matrilix
[MATRIALIRENIX [MATRIALER [MATRILIRELERIRELERIRIX (1000111 (1000111 [1000111. 2 а, 3}, {4, 5, 6 б}, {7, 8в, 9}}]], {а, − 2, 2, 1}, {б, − 3, 3, 1}, {в , − 5, 5, 1}]Мы используем Manipulate, MatrixForm, и UpperTriangularize для построения и исследования верхнетреугольных матриц. Если мы позволим a = 1, b = 2 и c = 3, то функция UpperTriangualize преобразует матрицу
MatrixForm[{{1, 2, 3}, {4, 5, 12}, { 7, 24, 9}}]
12345127249
к матрице верхней части триангулярного article/pii/B978012409520550028X
Стивен Андрилли, Дэвид Хекер, Элементарная линейная алгебра (четвертое издание), 2010 г.

Особенности
- ■
Определитель верхней (или нижней) треугольной матрицы представляет собой произведение элементов главной диагонали.
- ■
Строковая операция типа (I), включающая умножение на c , умножает определитель на c .
- ■
Строковая операция типа (II) не влияет на определитель.
- ■
Строковая операция типа (III) инвертирует определитель.
- ■
Если n × n матрица A умножается на c для получения B , то | Б | = с н | А |.
- ■
Определитель матрицы можно найти, приведя матрицу к верхней треугольной форме и отслеживая выполняемые операции над строками и их влияние на определитель.
- ■
Ан n × n матрица A невырожденна тогда и только тогда, когда | А | ≠ 0 тогда и только тогда, когда ранг( A ) = n .

Просмотр книги Глава Черта
Читать полная глава
URL: https://www.sciendirect.com/science/article/pii/B9780123747518000226
747518000226
747518000226
747518000226
747518000226
747518000226
747518000226
7
9.3 Решение верхней и нижней треугольных систем
В этом разделе представлены алгоритмы решения верхне- и нижнетреугольных систем уравнений. В дополнение к предоставлению дополнительных алгоритмов для изучения нам потребуется использовать оба этих алгоритма на протяжении всей книги.
Верхнетреугольная матрица — это матрица n × n , в которой единственные ненулевые элементы находятся ниже главной диагонали; другими словами
aij=0,j
Если U является n × n верхнетреугольной матрицы, мы знаем, как решить линейную систему Ux = b с помощью обратной подстановки. Фактически, это последний шаг в алгоритме исключения Гаусса, который мы обсуждали в главе 2. Вычислите значение x n = b n /u nn , а затем подставьте это значение в уравнение ( n − 1) найти x n — 1 . Продолжайте, пока не найдете x 9.0552 1 . Алгоритм 9.4 представляет обратную замену в псевдокоде.
Алгоритм 9,4
Решение верхней треугольной системы
Функция Backsolve (U, B)
%Найдите решение до UX = B , где U- N , B , где U- UX = B , где U- UX = B . треугольная матрица.
x n = b n /u nn
для i = n-1:-2:1 do0202
sum = 0.
 0
0for j = i+1:n do
sum = sum + u ij x j
end for
x ( i ) = ( b ( i ) − sum ) / u ii
end for
return x
end function
NLALIB : Функция обратного решения реализует алгоритм 9..4.
Нижнетреугольная матрица — это матрица, все элементы которой выше главной диагонали равны 0; другими словами
aij=0,j>i,1≤i,j≤n.
Система нижнего треугольника представляет собой систему с матрицей коэффициентов нижнего треугольника.
a1100…0a21a220…0a31a32a33…0………⋱0an1an2…an,n−1annx1x2x3⋮xn=b1b2b3⋮bn
Решение системы нижнего треугольника является обратным алгоритму решения системы верхнего треугольника — использовать прямую замену .
 Решите первое уравнение для x1=b1a11 и подставьте это значение во второе уравнение, чтобы найти x 2 и так далее. Пример 9.7 : х=1-423/5T.
Решите первое уравнение для x1=b1a11 и подставьте это значение во второе уравнение, чтобы найти x 2 и так далее. Пример 9.7 : х=1-423/5T.Алгоритм 9.5
Решение системы нижнего треугольника
функция FORSOLVE(L,b)
% Найти решение системы Lx = b , где L — нижнетреугольная матрица n × n .
x 1 = b 1 / l 11
for i = 2:n do
sum = 0.0
for j = 1:i -1 DO
Сумма = Сумма + L IJ x J
END для
1. 9052 (
(1. 9052 (
(1
(0551 I ) = ( B ( I ) — Сумма )/ л II
Конец
return x
22020202020 21202020202020 2120202020202020 220202020 220202020 220202020 22020120120 2
 forsolve реализует алгоритм 9.5. Пример 9.8
forsolve реализует алгоритм 9.5. Пример 9.8>> U = [1 -1 3;0 2 9;0 0 1];
>> L = [1 0 0;-1 2 0;3 4 5];
>> b = [1 9 -2]’;
>> x = backsolve(U,b)
x =
20.5000
13.5000
-2.0000
>> U\b
ans =
20.5000
13.5000
-2.0000
>> y = forsolve (l, b)
y =
1
5
-5
>> L \ B
ANS =
1
5
-5
1
5
-5
9.3.1 Анализ эффективности
Алгоритм 9.4 выполняет 1 деление, а затем начинает внешний цикл, содержащий n − 1 итераций. Внутренний цикл выполняется n — ( i + 1) + 1 = n — i раза, и каждая итерация цикла выполняет 1 сложение и 1 умножение, всего 2 ( n 5-1 i 90 ) проваливается. После завершения внутреннего цикла выполняется 1 вычитание и 1 деление. Общее количество необходимых флопов равно
Общее количество необходимых флопов равно
1+∑i=1n−12n−i+2=1+2n−1+2∑i=1n−1n−i=1+2n−1+2n−1+n− 2+⋯+1=1+2n−1+2nn−12=n2+n−1
Таким образом, обратная замена представляет собой O ( n 2 )(квадратичный) алгоритм. В качестве упражнения остается показать, что алгоритм 9.5 имеет точно такое же количество флопов.
Просмотр книги Глава покупки
Читать полная глава
URL: https://www.sciendirect.com/science/article/pii/b9780123944351000090
Biswa Nath Datta Datta, в цифровой цифре. Если A симметрично, то закон инерции Сильвестра обеспечивает недорогой и численно эффективный метод вычисления его инерции. Симметричная матрица A допускает треугольную факторизацию: A=UDUT, , где U — произведение элементарной единичной верхней треугольной матрицы и матрицы перестановки, а D — симметричная блочная диагональ с блоками порядка 1 или 2. . порядок 2, с р + 2 д = н. Предположим, что ни один из блоков 2 × 2 D не является сингулярным. Предположим, что из p блока 1-го порядка, p ′ из них положительных, p ″ отрицательных и p ″ из них нулевых (т.е. p ′ + p ″ + p ″ = р ). Тогда π(A)=p′+q,v(A)=p″+q,δ(A)=p‴. Разложение на диагональные повороты может быть достигнуто численно устойчивым способом. Требуется только n 3 /3 флопа. Подробную информацию о факторизации с диагональным поворотом см. в Bunch (19).71), Банч и Парлетт (1971) и Банч и Кауфман (1977). Реализация LAPACK: Метод диагонального поворота реализован в подпрограмме LAPACK SSYTRF. Просмотреть главуКнига покупок Прочитать всю главу URL: https://www.sciencedirect.com/science/article/pii/B97801220350112 Richard Bronson, издание Метод Коста Б. ), 2009 В разделе 2.3 мы разработали метод преобразования любой матрицы в сокращенную по строкам форму с использованием элементарных операций со строками. Если мы теперь ограничим наше внимание квадратными матрицами, мы можем сказать, что результирующие матрицы с редуцированными строками являются верхними треугольными матрицами, имеющими либо единичный, либо нулевой элемент в каждом элементе на главной диагонали. Это обеспечивает простой тест для определения того, какие матрицы имеют обратные. Теорема 1 Квадратная матрица имеет обратную тогда и только тогда, когда приведение к приведенной по строкам форме с помощью элементарных операций над строками приводит к матрице, имеющей все единичные элементы на главной диагонали . Мы докажем эту теорему в заключительных комментариях к этой главе как Теорема 2 Матрица размера n × n имеет обратную тогда и только тогда, когда она имеет ранг n . Теорема 1 не только дает тест для определения того, является ли матрица обратимой, но также предлагает метод получения обратной, когда она существует. Как только матрица преобразована в редуцированную по строкам матрицу с единичными элементами на главной диагонали, ее несложно еще больше свести к единичной матрице. Это делается путем применения элементарной операции со строками (E3) — добавления к одной строке матрицы скаляра, умноженного на другую строку той же матрицы, — к каждому столбцу матрицы, , начиная с последнего столбца и последовательно продвигаясь к первому столбцу , размещая нули во всех позициях над диагональными элементами. Пример 1 Используйте элементарные операции со строками для преобразования верхней треугольной матрицы A=[121013001] в единичную матрицу. Решение [121013001] → [121010001] {Добавляя вторую строку (−3) раз в третьем ряду → [120010001] {Добавляя первую строку (−1) время третья строка → [100010001] {добавляя к первой строке (−2), умноженное на вторую строку, Итак, теперь мы знаем, что квадратная матрица A имеет обратную тогда и только тогда, когда ее можно преобразовать в единичную матрицу с помощью элементарных операций над строками. Более того, из предыдущего раздела следует, что каждая элементарная операция со строками представлена элементарной матрицей E , которая генерирует операцию со строками при умножении EA. Следовательно, A имеет обратную тогда и только тогда, когда существует последовательность элементарных матриц. E 1 , E 2 ,…, E k такие, что Но если мы обозначим произведение этих элементарных матриц как B, , то мы получим BA = I, , откуда следует, что B = A −1 . EkEk−1⋯E3E2E1A=I. , затем (EkEk−1⋯E3E2E1)I=EkEk−1⋯E3E2E1=A−1. Таким образом, у нас есть следующая процедура для вычисления инверсий, когда они существуют. Пусть A — матрица n × n , которую мы хотим инвертировать. Поместите рядом с ней другую n × n матрицу B которая изначально является тождественной. Если A не может быть преобразовано в матрицу идентичности, что эквивалентно утверждению, что его преобразование по строкам содержит хотя бы одну нулевую строку, то A не имеет обратной. Пример 2 Invert A = [1234] Решение [12103401] → [12100–2–31] {добавив вторую строку (–3) Время от первой строки → [12100132 — 12] {путем умножения второй строки на (−12) A был преобразован в уменьшенную по строкам форму с главной диагональю, состоящей только из единичных элементов; у него есть инверсия. →[10−210132−12] {путем прибавления к первой строке (–2), умноженной на вторую строку Таким образом, A−1=[−2132−12]. Пример 3 Найдите обратное число A=[58102143−1]. Решение [58110002101043–1001] → [11,60,20,20,20002101043 —1001] {путем умножения ряда на (0,2) → [11,60,20,2000210100-3,4–1,8–0,801]. ) умножить на первую строку→[11.60.20.200010.500.500−3.4−1.8−0.801] {путем умножения второй строки на (0.5)→[11.60.20.200010.500.5000−0.1−0.81.71] ) умножить на вторую строку→[11.60.20.200010.500.500018−17−10] {путем умножения третьей строки на (−0,1) A преобразован в сокращенную по строкам форму с главной диагональю, состоящей только из единичных элементов; у него есть инверсия. Продолжая процесс преобразования, мы получаем →[11.60.20.200010−4950018−17−10] {путем прибавления ко второй строке (−0,5), умноженной на третью строку→[11. Таким образом, A-1=[5-11-6-4958−17−10]. Пример 4 Найдите обратное число A=[011111113]. Решение [0111001110113001] → [1110100111100113001] {Благодаря взаимосвязи первой и второй строки → [111010010010020111] {добавив в третью строку (−1) Время от первой строки → [11101111111111111111111111111111111111111111111111. умножая третью строку на (12)→[111010010112−120010−1212] {путем прибавления ко второй строке(−1), умноженной на третью строку→[110032−12010112−120010−1212] {прибавления к первой строке(−1), раз третья строка→[100−110010112−120010−1212] {путем добавления к первой строке (−1), умноженной на вторую строку, Таким образом, A−1=[−110112−120−1212]. Пример 5 Инвертировать A=[1224]. Решение [12102401]→[121000−21]. {путем добавления ко второй строке (−2) tiems первая строка A была преобразована в сокращенную по строкам форму. Поскольку главная диагональ содержит нулевой элемент, здесь в позиции 2−2 матрица A не имеет обратной. Это единственное число. В задачах 1−20 найти обратные заданные матрицы, если они существуют. [1134], [2112], [4444], [4444], [4444], . [8352], [1121213], [110101011], [001100010], [20−1012311], [123456789], [200510411], [21503−1002 ], [321401392], [12–1201–113], Вычисление инерции симметричной матрицы
 Это известно как факторизация с диагональным поворотом . Таким образом, по закону инерции Сильвестра In( A ) = In( D )). Как только получена эта диагональная поворотная факторизация, инерция симметричной матрицы A может быть получена из элементов D следующим образом:
Это известно как факторизация с диагональным поворотом . Таким образом, по закону инерции Сильвестра In( A ) = In( D )). Как только получена эта диагональная поворотная факторизация, инерция симметричной матрицы A может быть получена из элементов D следующим образом:
3.2 Вычисление инверсий


 То есть обратная квадратная матрица A полного ранга есть произведение тех элементарных матриц, которые сводят A к единичной матрице! Таким образом, чтобы вычислить обратное число A, нам нужно только вести учет элементарных операций со строками или, что то же самое, элементарных матриц, которые использовались для сведения A к I. Это достигается путем одновременного применения одних и тех же элементарных операций со строками к обоим A и единичная матрица того же порядка, потому что если
То есть обратная квадратная матрица A полного ранга есть произведение тех элементарных матриц, которые сводят A к единичной матрице! Таким образом, чтобы вычислить обратное число A, нам нужно только вести учет элементарных операций со строками или, что то же самое, элементарных матриц, которые использовались для сведения A к I. Это достигается путем одновременного применения одних и тех же элементарных операций со строками к обоим A и единичная матрица того же порядка, потому что если Используя элементарные операции со строками над A, преобразуют его в тождество. Каждый раз, когда операция выполняется над A, повторяет точно такую же операцию над B. После преобразования A в тождество матрица, полученная в результате преобразования B , будет равна 9.0201 А −1 .
Используя элементарные операции со строками над A, преобразуют его в тождество. Каждый раз, когда операция выполняется над A, повторяет точно такую же операцию над B. После преобразования A в тождество матрица, полученная в результате преобразования B , будет равна 9.0201 А −1 . Продолжая процесс преобразования, мы получаем
Продолжая процесс преобразования, мы получаем 60−1.43.42010−4950018−17−10] {путем прибавления к первой строке (-0,2), умноженной на третью строку→[1005-11-6010-4950018-17-10]. {добавляя к первой строке (-1,6), умноженное на вторую строку
60−1.43.42010−4950018−17−10] {путем прибавления к первой строке (-0,2), умноженной на третью строку→[1005-11-6010-4950018-17-10]. {добавляя к первой строке (-1,6), умноженное на вторую строку
Проблемы 3.2

111111111111111111111111111 гг.
[2433-4-450-1],
[50−12−1223−1],
[31113−123−1],
[111201−110023000−2],
[10002−1004620324−1].
Используя результаты задач 11 и 20, выведите теорему об обратных матрицах нижнего треугольника.
Используя результаты задач 12 и 19, выведите теорему об обратных верхнетреугольных матрицах.
Инверсия матрицы может использоваться для кодирования и декодирования конфиденциальных сообщений для передачи. Первоначально каждой букве в алфавите присваивается уникальное положительное целое число, причем простейшим соответствием является
ABCDEFGHIJKLMNOPQRSTUVWXYZ ↓↓↓мерапоминапоминаристи спутилщенпоминашенияменментня.
Нули используются для разделения слов. Таким образом, сообщение
ОНА ВИДЯЩАЯ
закодировано
1985091
955180
Однако эту схему слишком легко расшифровать, поэтому перед передачей добавляется эффект скремблирования. Одна схема состоит в том, чтобы упаковать закодированную строку в виде набора двойных кортежей, умножить каждую двойку на обратимую матрицу 2 × 2, а затем передать новую строку. Например, используя матрицу
A=[1223],
, приведенное выше закодированное сообщение будет зашифровано в
[1223][198]=[3562],[1223][50]=[510],[1223 ][919]=[4775], и т. д.
и зашифрованное сообщение становится
35625104775…
Обратите внимание на немедленную выгоду от скремблирования: буква S, которая изначально всегда кодировалась как 19 в каждом из трех ее вхождений, теперь кодируется как 35 в первый раз и как 75 во второй раз. Продолжите скремблирование и определите окончательный код для передачи вышеуказанного сообщения.
Зашифруйте сообщение ОНА ВИДЯЩАЯ, используя матрицу
A=[2−345].
Зашифруйте сообщение AARON IS A NAME, используя матрицу и шаги, описанные в задаче 23.
Передаваемые сообщения расшифровываются путем повторной упаковки полученного сообщения в 2-кортежи и умножения каждого вектора на число, обратное A. Для декодирования зашифрованного сообщения В задаче 23 мы сначала вычисляем
A−1=[−322−1]
, а затем
[−322−1][1831]=[85],[−322−1][4472]=[1216 ].
Расшифрованное сообщение:
851216
, что, согласно буквенно-целочисленному соответствию, данному в Задаче 23, переводится как ПОМОЩЬ. Используя ту же процедуру, расшифруйте зашифрованное сообщение
2643406018312851.
Используйте процедуру декодирования, описанную в задаче 26, но с матрицей A , данной в задаче 24, для расшифровки переданного сообщения. −39131−27453876−5112.
−39131−27453876−5112.
Зашифруйте сообщение ОНА ВИДЯЩАЯ, упаковав закодированные буквы в тройки и умножив их на обратимую матрицу 3 × 3
А=[101011110].
Добавьте столько нулей, сколько необходимо в конец сообщения, чтобы сгенерировать полные 3-кортежи.
Просмотр книги Глава Черта
Читать полная глава
URL: https://www.sciendirect.com/science/article/pii/B9780080
6500097 22225600097 22225600097 22225600097 2225600097 2222500097 Поскольку перестановка двух строк матрицы эквивалентна предварительному умножению матрицы на матрицу перестановок, матрица A ( k ) связан с A ( k − 1) следующим соотношением: A(k)=MkPkA(k−1),k=1,2, …, N — 1, , где p K — матрица перестановки, полученная путем взаимозаменяемости строк K и R K 51 9052. U=A(n-1)=Mn-1Pn-1A(n-2)=Mn-1Pn-1Mn-2Pn-2A(n-3) =⋯=Mn−1Pn−1Mn−2pn−2⋯M2P2M1P1A . Setting M = M n -1 P n -1 M n -2 P n -2 … M 2 P 2 M 1 P 1 , мы имеем следующую факторизацию A : Вышеуказанная факторизация может быть записана в форме: PA = LU , где P = P N -1 P 9552 955155155155155155155155155155155151515151515151515151515151515151515151515151515151515151515151515151555552-1 . Для n = 4 приведение A к верхней треугольной матрице U можно схематически описать следующим образом: A(1)⟶P2P2A(1)⟶M1M2P2A(1)=M2P2M1P1A=(××××0×××00×××00××)=A(2). A(2)⟶P3P3A(2)⟶M3M3P3A(2)=M3P3M2P2M1P1A=(××××0×××00××000×)=A(3)=U. Единственная разница между L здесь и матрица L из исключения Гаусса без поворота заключается в том, что множители в k -м столбце теперь переставлены в соответствии с матрицей перестановок P˜k=Pn−1Pn−2⋯Pk+1. Таким образом, чтобы построить L , снова не нужны явные произведения или обращения матриц. Рассмотрим случай n = 4, и предположим, что P 2 меняет местами ряды 2 и 3, а P 3 меняет местами строки 3 и 4. Тогда матрица L определяется как: L=(1000−m31100−m21−m4210−m41−m32−m341). А=(124456789). K = 1 Вход PIVOT составляет 7: R 1 = 3. 9000 2. ),P1A=(789456124). Сформируйте множители: a21≡m21=−47,a31≡m31=−17. A (1) = M1P1A = (100–4710–1701) (789456124) ≡ (78 197) .. 197) .. Поменяйте местами ряды 2 и 3. P2=(100001010),P2A(1)=(789703767). Сформируйте множитель: m32=−12 A(2)=M2P2A(1)=(1000100−121)(789703767)=(789700−12). Форма L=(100−m3110−m21−m321)=(100171047121). P=P2P1=(001100010). Подтвердить. PA=(7856)=LU.. Счетчик флопа. Исключение Гаусса с частичным поворотом требует всего 23n3 флопов. Кроме того, процесс с частичным поворотом требует не более O ( n 2 ) сравнений для определения поворотов. Просмотр главыКнига покупок Полный текст главы URL: https://www.sciencedirect.com/science/article/pii/B97801220350070 БИСВА НАТ ДАТТА, Численные методы для линейных систем управления, 2004 . Алгоритм Шура для e A . Вход. A ∈ ℝ n x n Выход. Преобразовать A в R, верхнюю треугольную матрицу, используя итерационный алгоритм QR (Глава 4): ( Note that when the eigenvalues of A are all real, the RSF is upper triangular. ) Compute e R = G = ( g и ): For i = 1,…, n do g ii = e r ii End For k = 1, 2,…, n − 1 do For i = 1, 2,…, n – k do Set j = i + k gij=1(rii−rjj)[rij(gii−gjj)+∑p=i+1j−1(giprpj−ripgpj)]. END END Compute E A = PE A = PE A = PE A = PE A = PE A . Количество флопов: Вычисление e R на шаге 2 требует примерно (2 n 3 /3) флопов. MATCONTROL примечание: Алгоритм 5.3.2 реализован в функции MATCONTROL экспмшр . Просмотреть главуКнига покупок Прочитать главу полностью URL: https://www.sciencedirect.com/science/article/pii/B97801220350094 George Lindfield, John Penny, in Numerical Editions, 2019, George Lindfield, John Penny, Numerical Methods. Мы видели, как квадратную матрицу можно разложить или разложить на множители в произведение нижней и верхней треугольных матриц с помощью элементарных операций над строками. A=QR , где R — верхняя треугольная матрица, а Q — ортогональная или унитарная матрица. Если Q является ортогональным, Q-1=QT, а если Q является унитарным, Q-1=QH. Предыдущие свойства очень полезны. Существует несколько процедур, обеспечивающих декомпозицию QR; здесь мы представляем метод Хаусхолдера. Чтобы разложить реальную матрицу, метод Хаусхолдера начинается с определения матрицы P таким образом: (2.21)P=I−2wwT , где w — вектор-столбец, а P — симметричная матрица. При условии, что wTw=1, P также является ортогональным. , так как wTw=1. Чтобы разложить A на QR , мы начинаем с формирования вектора w1 из коэффициентов первого столбца A следующим образом: w1T=µ1[(a11−s1)a21a31…an1] где µ1=12s1(s1−a11) и s1=±(∑j=1naj12)1/2 Подставив µ1 и s1 в w1, можно проверить, что необходимое условие ортогональности, w1Tw1=1, выполняется. . Подставив w1 в (2.21), мы получим ортогональную матрицу P(1). Теперь матрица A(1) создается из произведения P(1)A. Легко проверить, что все элементы в первом столбце матрицы A(1) равны нулю, кроме элемента на главной диагонали, который равен s1. Таким образом, A(1)=P(1)A=[s1+⋯+0+⋯+⋮⋮⋮0+⋯+0+⋯+] В матрице A(1) + указывает на не- нулевой элемент. Теперь мы начинаем второй этап процесса ортогонализации, формируя w2 из коэффициентов второго столбца A(1) таким образом: w2T=µ2[0(a22(1)−s2)a32(1)a42( 1)⋯an2(1)] , где aij — коэффициенты A и μ2=12s2(s2−a22(1)) и s2=±(∑j=2n(aj2(1))2)1/2 Тогда ортогональный матрица P(2) создается из P(2)=I−2w2w2T Затем матрица A(2) создается из произведения P(2)A(1) следующим образом: A(2)= P(2)A(1)=P(2)P(1)A=[s1+⋯+0s2⋯+⋮⋮⋮00⋯+00⋯+] Обратите внимание, что A(2) имеет нулевые элементы в первом два столбца, за исключением элементов на главной диагонали и над ней. (2.22)R=P(n−1)…P(2)P(1)A Заметим, что поскольку P(i) ортогонален, произведение P(n−1) … P( 2)P(1) также ортогонален. Мы хотим определить ортогональную матрицу Q такую, что A=QR. Таким образом, R=Q-1A или R=QTA. Отсюда из (2.22) QT=P(n−1)…P(2)P(1) Помимо знаков, связанных со столбцами Q и строками R , разложение уникален. Эти знаки зависят от того, извлекается ли положительный или отрицательный квадратный корень при определении s1, s2 и т. д. Полное разложение матрицы требует 2n3/3 умножений и n квадратных корня. Для иллюстрации этой процедуры рассмотрим разложение матрицы A=[4−2762−3344] Таким образом, s1=42+62+32=7,8102µ1=12×7,8102×(7,8102−4)=0,1296w1T =0,1296[(4−7,8102)63]=[−0,49390,77770,3889] Используя (2.21), мы получаем P(1) и, следовательно, A(1) таким образом: P(1)=[0,51210,76820,38410,7682 −0. A(1)=P(1)A=[7.81022.04862.81680−4.37533.587300.81237.2936] A элементы первого столбца (1) ниже главной диагонали к нулю. Продолжаем второй этап таким образом: с2=-4,37532+0,81232=4,4501μ2=12×4,4501×(4,4501+4,3753)=0,1128w2T=0,1128[0(-4,3753−4,4501)0,8123]=[0−0, R=A(2)=P(2)A(1)=[7.81022.04862.816804.4501−2.1956007.8259] Обратите внимание, что мы сократили первые два столбцы A(2) ниже ведущей диагонали равны нулю. На этом завершается процесс определения верхней треугольной матрицы R . Наконец, мы определяем ортогональную матрицу Q следующим образом: Q=(P(2)P(1))T=[0,5121−0,68520,51790,76820,0958−0,63300,38410,72200,5754] Читателю нет необходимости выполнять предыдущие вычисления, поскольку Matlab предоставляет функция qr для выполнения этого разложения. Например, >> A = [4 -2 7;6 2 -3;3 4 4] A = 4 -2 7 6 2 -3 3 4 4 Q = -0,5121 0,6852 0,5179 -0,7682 -0,0958 -0,6330 -0,3841 -0,7220 0,5754 r = -7,8102 -2,0486 -2,8168 0 -4,4501 2,1956 LU Факторизация методом исключения Гаусса с частичным поворотом
 9052 и идентификатор 9052 и идентификаторов 9052 и идентификаторов 9052 и идентификаторов 9052 и идентификаторов 9052 и идентификаторов 9052 и идентификаторов 9052. 9052. 9052. 9052.. . — элементарная нижняя треугольная матрица, полученная в результате процесса исключения. Итак,
9052 и идентификатор 9052 и идентификаторов 9052 и идентификаторов 9052 и идентификаторов 9052 и идентификаторов 9052 и идентификаторов 9052 и идентификаторов 9052. 9052. 9052. 9052.. . — элементарная нижняя треугольная матрица, полученная в результате процесса исключения. Итак, 2 P 1 , U = A ( n -1) , а матрица L представляет собой единичную нижнюю треугольную матрицу, образованную из множителей. Подробности см. у Голуба и Ван Лоана (1996, стр. 99).
2 P 1 , U = A ( n -1) , а матрица L представляет собой единичную нижнюю треугольную матрицу, образованную из множителей. Подробности см. у Голуба и Ван Лоана (1996, стр. 99). Мы проиллюстрируем это ниже.
Мы проиллюстрируем это ниже. Пример 3.4.1.
7067197) ..197). запись 67,r2=3.

 е А .
е А .
2.9 QR-разложение
 Альтернативное разложение A находится в верхней треугольной матрице и ортогональной матрице, если A действительное число, или в верхней треугольной матрице и унитарной матрице, если A комплексное. Это называется QR-разложением. Таким образом,
Альтернативное разложение A находится в верхней треугольной матрице и ортогональной матрице, если A действительное число, или в верхней треугольной матрице и унитарной матрице, если A комплексное. Это называется QR-разложением. Таким образом, Ортогональность можно легко проверить, разложив произведение PTP=PP следующим образом: я
Ортогональность можно легко проверить, разложив произведение PTP=PP следующим образом: я Мы можем продолжить этот процесс n−1 раз, пока не получим верхнюю треугольную матрицу Р . Таким образом,
Мы можем продолжить этот процесс n−1 раз, пока не получим верхнюю треугольную матрицу Р . Таким образом, 2097−0.60490.3841−0.60490.6976]
2097−0.60490.3841−0.60490.6976]
> > [Q R] = qr(A)
 в выходных данных Matlab являются отрицательными результатами ручных вычислений Q и R выше. Это не имеет значения, так как их произведение равно A , а при умножении знаки сокращаются.
в выходных данных Matlab являются отрицательными результатами ручных вычислений Q и R выше. Это не имеет значения, так как их произведение равно A , а при умножении знаки сокращаются.Одним из преимуществ QR-разложения является то, что его можно применять к неквадратным матрицам, разлагая матрицу размера m×n на ортогональную матрицу размера m×m и верхнюю треугольную матрицу размера m×n. Заметим, что если m>n, то разложение неоднозначно.
Просмотреть главуКнига покупок
Прочитать главу полностью
URL: https://www.sciencedirect.com/science/article/pii/B9780128122563000117
Stephen Andrilli, Stephen Linear Hecker, издание Elementary Firefal Alge Hecker 2016
Вычисление определителя путем редукции строк
Теперь мы проиллюстрируем, как использовать операции со строками для вычисления определителя заданной матрицы A путем нахождения верхней треугольной матрицы B , который эквивалентен строке A .
Пример 4
Пусть
A=0−14−8132−206.
Приводим A по строке к верхнетреугольной форме следующим образом, отслеживая влияние на определитель на каждом шаге: Поскольку последняя матрица B имеет верхнетреугольную форму, мы останавливаемся. (Обратите внимание, что мы не нацеливаемся на элементы выше главной диагонали, как в сокращенной эшелонированной форме строки.) Из теоремы 3.2 B=(1)(1)467=467. Поскольку | B |=+114|A|, мы видим, что |A|=14|B|=14(467)=92.Более удобный метод вычисления A заключается в создании переменной P (для «продукта») с начальным значением 1 и обновлении P соответствующим образом при выполнении каждой операции строки. То есть мы заменяем текущее значение P на
P×c для операций со строками типа (I) P×(−1) для операций со строками типа (III).
Конечно, операции со строками типа (II) не влияют на определитель. Затем, используя окончательное значение P , мы можем решить для | А | используя A=(1/P)B, где B — верхний треугольный результат процесса сокращения строк. Этот метод проиллюстрирован в следующем примере.
Затем, используя окончательное значение P , мы можем решить для | А | используя A=(1/P)B, где B — верхний треугольный результат процесса сокращения строк. Этот метод проиллюстрирован в следующем примере.
Пример 5
Повторим расчет для A в примере 4. Мы создаем переменную P и инициализируем P значением 1. Ниже перечислены операции над строками, используемые в этом примере для преобразования A в верхнюю треугольную форму B , с B=467. После каждой операции мы обновляем значение Р соответственно.
| Row Operation | Effect | P | |
|---|---|---|---|
| (III): 1↔2 | Multiply P by − 1 | − 1 | |
| (II): 3 ← 21+3 | Нет. 3 | Без изменений | 114 |

Просмотреть главуКнига покупок
Прочитать главу полностью
URL: https://www.sciencedirect.com/science/article/pii/B978012800853
37
Stephen Andrilli, издание Fith, David Hecker, in Elementary 2016
Упражнения по разделу 8.10
- 1.
В каждой части этого упражнения дана квадратичная форма Q :Rn→R. Find an upper triangular matrix C and a symmetric matrix A such that, for every x∈Rn, Q ( x ) = x T Cx = x Т Топор .
- ⋆(a)
Q ([ x , y ]) = 8 x 2 5 − 1 9
30 2 + 12 xy
- (b)
Q ([ x , y ]) = 7 x 2 + 11 y 2 − 17 xy
- ⋆(c)
Q([x1,x2,x3])=5×12−2×22+4x1x2−3x1x3+5x2x3
- 2.

In each part of this exercise, use метод квадратичной формы для диагонализации заданной квадратичной формы Q :Rn→R. Ваши ответы должны включать матрицы A , P и D , определенные этим методом, а также ортонормированный базис B . Наконец, вычислите Q ( x ) для заданного вектора x двумя следующими способами: во-первых, используя данную формулу для Q , и во-вторых, вычислив Q=[x]BTD[x]B где [ x ] B = P −1 x и D = P −1
1 AP0202 .
1 AP 9- ⋆ (a)
Q ([ x , Y ] = 43 x 2 + 57 Y 2 + 57 Y 9052 0 2 + 57 Y 9052 2 0 2 + 57 Y 9052 0 2 + 57 Y 2 + 57 9051 Y 2 + 57 9051 Y 2 .
 x = [1,−8]
x = [1,−8]- (б)
Q([x1,x2,x3])=−5×12+37×22+49×32+32x1x2+80x1x3+32x2x3; x = [7,−2,1]
- ⋆(c)
Q([x1,x2,x3])=18×12−68×22+x32+96x1x2−60x1x3+36x2x3; x = [4,−3,6]
- (г)
Q([x1,x2,x3,x4])=x12+5×22+864×32+864×42−24x1x3+24x1x4+120x2x3+120x2x4+1152x3x4; x = [5,9,−3,−2]
- 3.
Пусть Q :Rn→R — квадратичная форма, а A и B симметричные матрицы так что Q ( x ) = x T Ax = x T2 Bx902. Докажите, что A = B (утверждение единственности из теоремы 8.14). (Подсказка: используйте x = e i , чтобы показать, что a ii = b ii 3 ii.
 Then use x = e i + e j to prove that a ij = b ij when i ≠ j .)
Then use x = e i + e j to prove that a ij = b ij when i ≠ j .)- ⋆4.
Пусть Q :Rn→R — квадратичная форма. Верхнее треугольное представление для Q обязательно уникальный? That is, if C 1 and C 2 are upper triangular n × n matrices with Q ( x ) = x T C 1 x = x T C 2 x , для всех x∈RN, должен C 1 = 0202902 0202. . . . 02. 02.
 02. . . . . . . . . . . Докажите свой ответ.
02. . . . . . . . . . . Докажите свой ответ.- 5.
A quadratic form Q ( x ) on Rn is positive definite if and only if both of the following conditions hold:
- (i)
Q ( x ) ≥ 0 для всех x∈Rn.
- (ii)
Q ( x ) = 0 тогда и только тогда, когда x = 0 .
Квадратичная форма, обладающая только свойством (i), называется положительно-полуопределенной .
Пусть Q — квадратичная форма на Rn, а A — симметричная матрица такая, что Q ( x ) = x T
A x 9.- (a)
Докажите, что Q положительно определено тогда и только тогда, когда каждое собственное значение A положительно.

- (b)
Докажите, что Q является положительно полуопределенным тогда и только тогда, когда каждое собственное значение A неотрицательно.
- ⋆6.
Верно или Неверно:
- (A)
IF Q ( x ) = x T CX T CX T 020120120102010201020102010201020201020102020. и CX . ), тогда Q ( x ) = x T Ax .
- (b)
Q ( x , y ) = xy не является квадратичной формой, потому что она не имеет x 2 или y 2 терминов.
- (C)
Если x T AX = x T 202020202020202020202020202020202020202020202020202020202020202020202023.

- (d)
Каждую квадратичную форму можно диагонализовать.
- (e)
Если A является симметричной матрицей и Q ( x ) = x T Ax является квадратичной формой, которая диагонализируется до Q(x)=[x]BTD[x]B, тогда элементы главной диагонали D являются собственными значениями A .
Просмотреть книгу Глава Черта
Читать полную главу
URL: https://www.sciendirect.com/science/article/pii/b978012800853
86
resportser in verians in resporter in in repormant in in resportser in veriviner in verivin in resportser in verivin in resporter in veriviner in veriviner in verivin in resporter in verivin in repormant in repormant in repormanst , мы научимся находить определитель треугольной матрицы.
Начнем с того, что вспомним, как найти определитель обычной матрицы 3×3. Сделать это,
нам нужно знать определения миноров и кофакторов.
Сделать это,
нам нужно знать определения миноров и кофакторов.
Определение: Миноры
Пусть 𝐴=𝑎 — матрица порядка 𝑚×𝑚. Затем младших элемента 𝑎 (обозначается 𝐴) является определителем Полученная матрица (𝑚−1)×(𝑚−1) после удаления строки 𝑖 и столбца 𝑗 из 𝐴.
Определение: Кофакторы
Пусть 𝐴=𝑎 — матрица порядка 𝑚×𝑚. Затем кофактор элемента 𝑎 (обозначается 𝐶) 𝐶=(−1)𝐴, где 𝐴 — минор элемента 𝑎.
Определитель можно записать с помощью расширения кофактора следующим образом.
Определение: определитель матрицы 3 × 3 (кофакторное разложение)
Пусть 𝐴=(𝑎) — матрица 3×3. Тогда для любого
фиксированный 𝑖=1,2 или 3, определитель 𝐴 равен
det(𝐴)=𝑎𝐶+𝑎𝐶+𝑎𝐶,
где каждый 𝐶 является кофактором входа 𝑎. это известно
как 9Расширение кофактора 0003 (или расширение Лапласа) по строке 𝑖. Альтернативно,
для любого фиксированного 𝑗=1,2 или 3 имеем
det(𝐴)=𝑎𝐶+𝑎𝐶+𝑎𝐶.
Это расширение кофактора по столбцу 𝑗.
Мы также отмечаем, что альтернативная, возможно, более удобная формулировка состоит в том, чтобы записать приведенные выше формулы явно в терминах определителей 2 × 2. Итак, для разложения первой строки имеем det(𝐴)=𝑎|||𝑎𝑎𝑎𝑎|||−𝑎|||𝑎𝑎𝑎𝑎|||+𝑎|||𝑎𝑎𝑎𝑎|||.
Важным аспектом расширения кофактора, который следует учитывать, является то, что мы можем выбирать, какую строку или столбец мы хотим расширяться вместе. Насколько это существенно, становится ясно, если мы рассмотрим, например, матрица как 𝐴=413100−3−24.
Если бы мы рассматривали первую строку, то вычисление определителя было бы det(𝐴)=4||00−24||−1||10−34||+3||10−3−2||.
Это выполнимо, но требует написания и вычисления трех определителей 2×2. С другой стороны, если бы мы использовали вместо этого вторую строку, мы бы просто получили
det(𝐴)=1||13−24||,
поскольку 𝑎 и 𝑎 равны 0. Несмотря на то, что это вычисление намного проще, мы все равно получаем
тот же результат в конце, потому что все формы расширения кофактора эквивалентны.
Несмотря на то, что это вычисление намного проще, мы все равно получаем
тот же результат в конце, потому что все формы расширения кофактора эквивалентны.
Давайте помнить о том, что выбор строки или столбца с большим количеством нулей упрощает расчет при рассмотрении нашего первого примера.
Пример 1. Нахождение определителя матрицы, содержащей строку нулей
Найдите значение ||||5−180260000||||.
Ответ
Чтобы вычислить определитель матрицы 3×3, вспомните, что мы можем использовать разложение кофактора по любой строке по формуле det(𝐴)=𝑎𝐶+𝑎𝐶+𝑎𝐶, где 𝑖=1,2 или 3, и по любому столбцу.
Хотя любой выбор строки или столбца даст нам одно и то же значение определителя, это всегда проще выбрать тот, который имеет наибольшее количество нулей. В частности, мы видим, что третий ряд сплошь нули:
Следовательно, если 𝑖=3, определитель
расчет будет
det(𝐴)=𝑎𝐶+𝑎𝐶+𝑎𝐶=0×𝐶+0×𝐶+0×𝐶=0.
Как показано в последнем примере , так как в третьей строке матрицы для каждого элемента были нули, определитель был равен нулю. Естественно, так как расширение кофактора может быть применено к любой строке или столбцу, тот же результат будет верным, если вся строка или столбец матрицы равны нулю, и это можно обобщить. для матриц любого размера.
Свойство: определители с нулевыми строками или столбцами
Если 𝐴 — квадратная матрица, в которой каждый элемент в определенной строке или столбце равен нулю, тогда det(𝐴) равно нулю.
Некоторые примеры этого включают
Всякий раз, когда нас просят найти определитель, мы всегда должны помнить, чтобы проверить, есть ли строки или столбцы нулевые, так как это позволяет нам сразу заключить, что определитель равен нулю, используя это имущество.
В следующем примере мы рассмотрим еще один частный случай вычисления определителя.
Пример 2.
 Нахождение значения определителя верхнетреугольной матрицы
Нахождение значения определителя верхнетреугольной матрицыЗаполните пропуск: Значение определителя ||||30−2057004||||=.
Ответ
Когда вас попросят найти определитель матрицы 3×3, вспомните, что мы можем использовать разложение кофактора по любой строке по формуле det(𝐴)=𝑎𝐶+𝑎𝐶+𝑎𝐶, где 𝑖=1,2 или 3, и по любому столбцу.
Для нас всегда выгодно выбрать для расширения строку или столбец с наибольшим числом нулевых записей, так как это приводит к меньшему количеству необходимых вычислений. Если мы исследуем данную матрицу, мы находим, что первый столбец и третья строка являются лучшими кандидатами, так как они оба содержат две записи, равные нулю:
Если мы выберем третью строку, то 𝑖=3. Итак, мы получаем det(𝐴)=𝑎𝐶+𝑎𝐶+𝑎𝐶=0×𝐶−0×𝐶+4||3005||=4×3×5=60.
Давайте рассмотрим важный аспект этого примера. В итоге вычисление определителя
просто перемножал три записи по главной диагонали вместе. Как оказалось, причиной тому
расчет был настолько простым, потому что матрица была верхней треугольной матрицей. Позволь нам
Вспомните определение этого типа матрицы.
Как оказалось, причиной тому
расчет был настолько простым, потому что матрица была верхней треугольной матрицей. Позволь нам
Вспомните определение этого типа матрицы.
Определение: треугольная матрица
Если элементы под главной диагональю равны нулю, матрица является верхней треугольной матрицей .
Если элементы выше главной диагонали равны нулю, матрица является нижней треугольной матрицей .
Показаны верхняя и нижняя треугольные матрицы:
Матрица является треугольной , если она либо верхняя, либо нижняя треугольная (или обе).
Причина, по которой нахождение определителей треугольных матриц так просто, заключается в том, что нули в одной половине
матрицы удалить большую часть вычислений. Чтобы убедиться в этом, рассмотрим расчет
определитель общей верхней треугольной матрицы с использованием разложения на кофакторы по третьей строке:
||||𝑎𝑏𝑐0𝑑𝑒00𝑓||||=0×𝐶+0×𝐶+𝑓𝐶=𝑓|||𝑎𝑏0𝑑|||=𝑓(𝑎𝑑−0×𝑏)=𝑎𝑑𝑓.
Другими словами, конечный результат — это просто произведение трех элементов на главной диагонали. Точно так же для нижних треугольных матриц расширение кофактора по первой строке дает нам |||| 𝑎00𝑏𝑐0𝑑𝑒𝑓 |||| = 𝑎𝐶+0 × 𝐶+0 × 𝐶 = 𝑎 ||| 𝑐0𝑒𝑓 ||| = 𝑎 (𝑐𝑓 -0 × 𝑒) = 𝑎𝑐𝑓.
Это дает нам следующее свойство.
Свойство: определители треугольных матриц
Определитель треугольной матрицы является произведением элементов на главной диагонали:
В качестве примечания, это свойство также охватывает подкласс треугольных матриц: диагональные матрицы. Напомним, что диагональная матрица — это та, в которой только элементы на главной диагонали отличны от нуля. Поскольку диагональные матрицы являются и верхними, и нижними треугольными матрицами одновременно время, они, естественно, обладают одним и тем же свойством:
Это также относится к единичным матрицам (где произведение диагональных элементов всегда равно 1)
и нулевые матрицы (где произведение всегда равно 0), так как это частные случаи диагонали,
и, следовательно, треугольные матрицы.
Давайте посмотрим, как мы можем использовать это свойство для упрощения наших решений в следующем примере.
Пример 3. Сравнение значений определителей двух треугольных матриц
Верно или неверно: если 𝐴=142036004,𝐵=100530674, тогда detdet(𝐴)=(𝐵).
Ответ
Один из способов ответить на этот вопрос — вычислить каждый определитель с помощью кофактора расширение по строкам или столбцам. Однако мы можем более эффективно ответить на этот вопрос, если обращаем внимание на то, что 𝐴 — верхнетреугольная матрица, а 𝐵 — нижняя треугольная матрица. Мы можем видеть это, потому что в 𝐴 записи ниже главная диагональ равна нулю, а в 𝐵 элементы над главной диагональю равны ноль:
Таким образом, мы можем воспользоваться тем свойством, что определитель треугольной матрицы равен произведению элементов на главной диагонали. Как видим, 𝐴 и 𝐵 имеют одинаковые диагональные элементы. Следовательно,
То есть detdet(𝐴)=(𝐵)=12, так что ответ верный.
Давайте подробнее рассмотрим примеры, в которых нам нужно найти определители треугольных матриц. В некоторых случаях легкой частью будет определение того, что матрица является треугольной, и применение
свойство для определителей, а трудная часть будет включать дальнейшие вычисления для достижения
требуемый ответ.
В некоторых случаях легкой частью будет определение того, что матрица является треугольной, и применение
свойство для определителей, а трудная часть будет включать дальнейшие вычисления для достижения
требуемый ответ.
Пример 4. Решение уравнений путем нахождения определителя диагональной матрицы
Рассмотрим уравнение ||||𝑥−1000𝑥+𝑥+10001||||=2.
Определите значение 𝑥.
Ответ
Первое, что бросается в глаза, когда мы видим эту матрицу, это то, что она диагональная, а это означает, что все элементы не на главной диагонали равны нулю: ||||𝑥−1000𝑥+𝑥+10001||||.
Диагональные матрицы представляют собой особый вид треугольных матриц, и мы можем вспомнить, что определитель такой матрицы находится путем произведения элементов на главной диагонали. Следовательно, определитель ||||𝑥−1000𝑥+𝑥+10001||||=(𝑥−1)×𝑥+𝑥+1×1=𝑥+𝑥+𝑥−𝑥−𝑥−1=𝑥+𝑥−𝑥+ 𝑥−𝑥−1=𝑥−1.
Теперь мы хотим найти 𝑥, используя тот факт, что этот определитель равен 2. То есть,
𝑥−1=2.
Отсюда можно найти 𝑥, используя свойства индексов, в частности что 𝑥=𝑥. Переставляя и возводя в квадрат обе стороны, мы имеем 𝑥=3𝑥=3𝑥=9.
В качестве последнего примера найдем определитель матрицы, заданной тремя переменными, которая нам придется найти, найдя определители меньших матриц.
Пример 5. Нахождение значения определителя, включающего неизвестные, с использованием свойств
Если det𝑥44𝑦=0, det𝑦99𝑧=0, и det𝑥11𝑧=0, найти дет𝑥120𝑦300𝑧.
Ответ
Поскольку нам дано несколько уравнений с определителями и тремя неизвестными переменными, наиболее очевидным было бы найти эти детерминанты и посмотреть, дает ли это нам любую информацию о переменных, поэтому давайте сделаем это.
Прежде всего, для матриц 2×2 мы можем найти их определители по формуле дет𝑎𝑏𝑐𝑑=𝑎𝑑−𝑏𝑐.
Для первого уравнения имеем det𝑥44𝑦=0𝑥𝑦−4×4=0𝑥𝑦=16.
Для второго уравнения имеем det𝑦99𝑧=0𝑦𝑧−9×9=0𝑦𝑧=81.
Наконец, третье уравнение 2×2 дает нам
det𝑥11𝑧=0𝑥𝑧−1×1=0𝑥𝑧=1.
Мы могли бы использовать эти уравнения сами по себе, чтобы найти 𝑥, 𝑦 и 𝑧, но это может быть больше работы, чем необходимо. Сначала найдем Определитель 3×3, чтобы мы могли видеть, какая информация от нас требуется. Мы можем упростить вычисление этой матрицы, заметив, что это верхняя треугольная матрица, так как записи ниже главной диагонали равны нулю:
Следовательно, определитель будет просто произведением элементов на главной диагонали, давая нам
Чтобы найти 𝑥𝑦𝑧, обратите внимание, что мы можем взять произведение 𝑥𝑦, 𝑦𝑧 и 𝑥𝑧 (поскольку мы уже вычислили эти значения) а потом извлеките квадратный корень. То есть у нас есть (𝑥𝑦𝑧)=(𝑥𝑦)(𝑦𝑧)(𝑥𝑧)=16×81×1=1296.
Тогда, извлекая квадратный корень, получаем 𝑥𝑦𝑧=±36.
Мы должны знать, что здесь возможны как положительные, так и отрицательные 36. Эти разные значения возникают из-за различных возможных значений 𝑥, 𝑦 и 𝑧, поэтому значение определителя будет зависеть от значений переменных.
Следовательно, определитель равен либо −36, либо 36.


 Определитель матрицы.
Определитель матрицы.
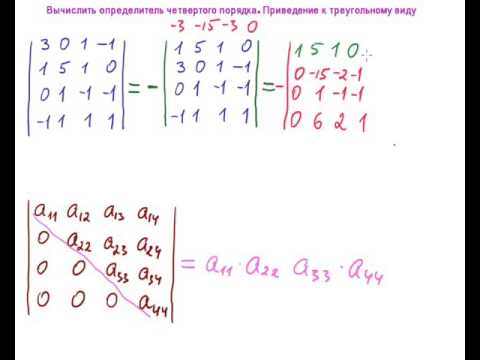 ..
..
 ..
..