Найти седловую точку онлайн: Седловая точка онлайн

Матричные игры. Седловая точка, стратегии, цена игры. Теория игр

Краткая теория

---

В общем случае матричная игра задается прямоугольной матрицей размерности . Номер  строки матрицы соответствует номеру стратегии , применяемой игроком . Номер  столбца соответствует стратегии , применяемой игроком . Описанная игра однозначно определяется матрицей

Каждый элемент  матрицы является действительным числом и представляет собой сумму выигрыша, уплачиваемую игроком  игроку , если  выбирает стратегию, соответствующую -й строке, а  выбирает стратегию, соответствующую -му столбцу.

Матричную игру часто записывают в развернутой форме в виде таблицы, называемой платежной матрицей.

		…		…
		…		…
…	…	…	…	…	…
		…		…
…	…	…	…	…	…
		…		…

Каждый игрок выбирает для себя наиболее выгодную стратегию. При этом первый игрок стремится выбрать такую стратегию, которая доставляет ему максимальный выигрыш, тогда как второй игрок выбирает стратегию, приводящую его к минимальному проигрышу. В этой связи вводят понятия нижней и верхней чистой цены игры.

Нижней чистой ценой игры (максимином) называется число , определяемое по формуле:

Верхней чистой ценой игры (минимаксом) называется число , определяемое по формуле:

Стратегии игроков, соответствующие максимину (минимаксу), называются максиминными (минимаксными).

Различают стратегии чистые и смешанные. Чистая стратегия  первого игрока (чистая стратегия  второго игрока) – это возможный ход первого (второго) игрока, выбранный им с вероятностью, равной 1.

В матричной игре нижняя чистая цена игры не превосходит верхней чистой цены игры, то есть .

Если для чистых стратегий ,  игроков  и  соответственно имеет место равенство , то пару чистых стратегий  называют седловой точкой матричной игры, элемент  матрицы, стоящий на пересечении i-й строки и -го столбца – седловым элементом платежной матрицы, а число  – чистой ценой игры.

Примеры решения задач

.

---

Задача 1

Игра задана платежной матрицей:

Определить нижнюю и верхнюю цену игры и наличие седловой точки.

Решение

Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:

ВКонтакте
WhatsApp
Telegram

Я буду работать с вами, над вашей проблемой, пока она не решится.

Найдем чистые нижнюю и верхнюю цены игры.

 

Цена игры

---

Задача 2

Игра задана платежной матрицей:

Определить нижнюю и верхнюю цену игры и наличие седловой точки.

Решение

Найдем чистые нижнюю и верхнюю цены игры.

 — седловая точка отсутствует

Выпуклое программирование.

Графический метод и функция Лагранжа. Примеры решения задач



Образовательные онлайн сервисы: теория и практика

• Главная
• Примеры
  • Математический анализ
  • Векторная алгебра и аналитическая геометрия
  • Линейная алгебра
  • Теория вероятностей и математическая статистика
  • Математическое программирование
    Методы оптимизации
  • Математика в экономике
    Экономическая статистика
• Видео-уроки
  • Математический анализ
  • Векторная алгебра и Аналитическая геометрия
  • Линейная алгебра
  • Теория вероятностей и математическая статистика
  • Математическое программирование. Методы оптимизации
• Готовые работы
  • Математический анализ
  • Векторная алгебра и аналитическая геометрия
  • Линейная алгебра
  • Теория вероятностей и математическая статистика
  • Математическое программирование
    Методы оптимизации
  • Математика в экономике
    Экономическая статистика
  • Другое
• Контакты

Полезные материалы:

• Учебники
• Справочники
• Онлайн калькуляторы

• Помощь в решении
• Онлайн занятия в Zoom

Выпуклое программирование.

Графический метод и функция Лагранжа

Задача

Дана задача выпуклого программирования. Требуется:

1) найти решение графическим методом

2) написать функцию Лагранжа данной задачи и найти ее седловую точку, используя решение задачи, полученное графически.

Решение.

Графическое решение задачи следующее:

 

 

         Система неравенств определяет область, ограниченную двумя прямыми и координатными осями. График целевой функции представляет собой окружность переменного радиуса с центром в точке (5 , 10). Значение целевой функции графически представляет собой квадрат радиуса этой окружности. Минимальным радиусом, удовлетворяющим системе ограничений, будет  такой радиус, который обеспечивает касание окружности с границей области так, как это показано на рисунке.
Искомая точка определяется как решение системы уравнений

Получаем точку (3 , 8), значение целевой функции в этой точке равно 8.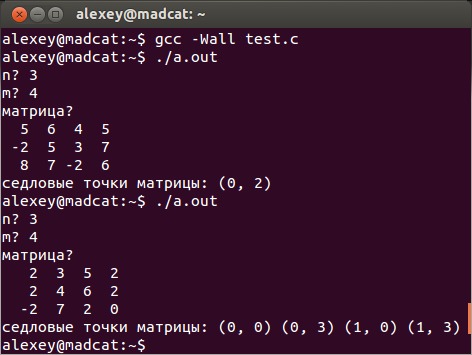

Теперь запишем задачу в традиционном виде:

         Функция  называется функцией Лагранжа,

а переменные  — коэффициентами Лагранжа.
Точка  называется Седловой точкой функции Лагранжа, если для любых  выполняются неравенства:

Если функции  дифференцируемы, то условия определяющие седловую точку (условия Куна-Таккера):
 
 

В нашем случае получаем:

Подставим в эти выражения значения :

Получаем

Седловая точка функции Лагранжа: .

Проверим условия cедловой точки:

Условия выполнены, седловая точка .



Задать вопрос
Заказать помощь

Отзывы

+7-911-7987704

vk.com/id286009794

Написать в Whatsapp

Написать в Viber

@matem96

Skype: matem96. ru



Калькулятор седловой точки — определение седловой точки функции

Онлайн-калькулятор седловой точки поможет вам определить седловую точку функции с несколькими переменными.

Давайте сосредоточимся на концептуальной структуре седловой точки.

Что такое седловая точка в исчислении?

В свете исчисления седловой точки,

« точка, в которой вторые частные производные функции с несколькими переменными становятся равными нулю без минимального или максимального значения». 9{2} + y\right) = -10x + 1 $$

2-я частная производная w.r.t y:

$$ \frac{\partial}{\partial y}\left(- 10 x y + 1\right ) $$ (щелкните калькулятор частных производных для расчетов)

Производная:

$$ \frac{\partial}{\partial y}\left(- 10 x y + 1\right) = -10x $$

Нахождение седловых точек:

Чтобы найти седловые точки, положим f”(x,y) = 0

6x=0

x = 0 / 6 9{2} = 0

x = 0

6y = 0

y = 0

КОНЕ выполненных вами расчетов, вы можете проверить результаты с помощью нашего бесплатного онлайн-калькулятора седловой точки.

Как работает калькулятор седловой точки?

Выполнение расчетов вручную для поиска седловых точек может занять много времени. Кроме того, мы познакомили вас с бесплатным онлайн-калькулятором седловых точек.

Давайте посмотрим, что нам нужно сделать:

Ввод:

• Напишите свои функции в строке меню
• Нажмите «рассчитать»

Вывод:

Калькулятор седловой точки вычисляет:

• Производная первого порядка w.r.t x
• Производная второго порядка относительно x
• Производная первого порядка по y
• Производная второго порядка по y
• Пошаговые расчеты
• Седловая точка для заданной функции

Часто задаваемые вопросы:

Что такое пример седловой точки в реальной жизни?

В реальном мире поверхность носового платка является хорошим примером седловой точки.

Что вы подразумеваете под экстремумом?

Точка, в которой мы можем получить минимальное или максимальное значение функции, называется экстремумом.

Как классифицировать экстремум?

Для каждого значения вы должны протестировать значение x немного меньшее и немного больше, чем это значение x. Если оба меньше f(x), то это максимум. Если оба больше, чем f(x), то это минимум.

Каждая ли поворотная точка является седловой?

Стационарные точки бывают двух типов: седловые точки и точки поворота. В то время как поворотные точки соответствуют локальным экстремумам, седловые точки не соответствуют

Вывод:

В исчислении седловых точек седловая точка или минимаксная точка — это точка на поверхности графика для функции, в которой наклоны в перпендикулярных направлениях становятся равными нулю ( критическая точка), но не являющийся локальным экстремумом функции. Математикам и инженерам всегда приходится находить седловую точку при анализе поверхности. Для этой цели наш бесплатный онлайн-калькулятор седловых точек является полезным инструментом, разработанным до сих пор.

Ссылки:

Из источника Википедии: Седловая поверхность, Максимумы и минимумы, Функции более чем одной переменной.

Из источника академии хана: Тест второй частной производной, Свободная интуиция, Градиентный спуск ценности, множители Лагранжа, оптимизация по нескольким переменным.

в этой функции (если есть); Найдите максимум-минимум и седловые точки.

Математическое исчисление

Актуг Я.

спросил 24.08.20

f(x,y)= 2x ³ +xy ² +5x ² +y ²

Подписаться І 1

Подробнее

Отчет

1 ответ эксперта

Лучший Новейшие Самый старый

Автор: Лучшие новыеСамые старые

Доктор Энди Т. ответил 24.08.20

Репетитор

5 (1)

UT Остин, доктор философии. по физике и сертифицированный учитель математики на Top STEM HS

См. таких репетиторов

Смотрите таких репетиторов

Hi Aktug,

Любые макс/мин/седловые точки должны приходиться на критическую точку, т.е. на точку, где обе частные производные равны 0 (в общем случае нужно также рассматривать точки, где хотя бы одна из частных производных не существует, но поскольку ваша функция является многочленом, частные производные существуют везде).

Частные производные равны f _x = y ² + 6x ² + 10x и f _y = 2y + 2xy. Следовательно, чтобы найти критические точки, нам нужно найти все возможные решения следующей системы уравнений:

y ² + 6x ² + 10x = 0 (1)

2y + 2xy = 0 (2)

Второе уравнение разлагается как 2y(1+x) = 0, так что это верно, если y = 0 или x = -1. Теперь мы по отдельности подставляем их в первое уравнение.

Если y = 0, то первое уравнение принимает вид 6x ² + 10x = 0 или 2x(3x + 5) = 0, что верно, если x = 0 или x = — 5/3. Это означает, что (x,y) = (0,0), (-3/5, 0) являются критическими точками.

Теперь предположим, что x = -1. Тогда первое уравнение принимает вид

y ² + 6 — 10 = 0

y ² — 4 = 0

(y+2)(y-2) = 0

, решение которого y = -2 или y = 2. Это означает, что (x,y) = (-1,-2), (-1,2) также являются критическими точками.

Теперь нам нужно классифицировать каждую из найденных нами критических точек (x,y) = (0,0), (-3/5, 0), (-1,-2), (-1,2) выше.

Это делается с использованием вторых частных производных следующим образом. Сначала вычислите функцию

D = f _xx f _yy — (f _xy ) ²

и оцените ее в каждой критической точке. Тогда

1. Если D > 0 и f _xx > 0, критической точкой является относительная мин.
2. Если D > 0 и f _xx < 0, критической точкой является относительная макс.
3. Если D < 0, то критическая точка является седловой.
4. Если D = 0, тест неопределен, и нам нужно использовать другие методы для классификации критической точки.

Поскольку вторые частные производные равны f _xx = 12x + 10, f _yy = 2x + 2, f _xy = 2y, функция D определяется как

D = (12x + 10)(2x + 2)-(2г) ² .

Теперь исследуем каждую критическую точку:

1. At (x,y) = (0,0), D = 20>0 и f _xx = 10>0, поэтому (0,0) является относительным мин.
2. At (x,y) = (-3/5,0), D = 56/25 >0 и f _xx = 14/5>0, поэтому (-3/5,0) является относительным мин.
3. При (x,y) = (-1,-2), D = -16 < 0, поэтому (-1,-2) является седловой точкой.
4. При (x,y) = (-1,2), D = -16 < 0, поэтому (-1,2) является седловой точкой.

Надеюсь, это поможет!

Голосовать за 1 голосов против

Подробнее

Отчет

Все еще ищете помощи? Получите правильный ответ, быстро.

No related posts.