Найти скалярное произведение векторов онлайн: Онлайн калькулятор. Скалярное произведение векторов

уравнение запишется:

x = x пр =  пр x

(2)

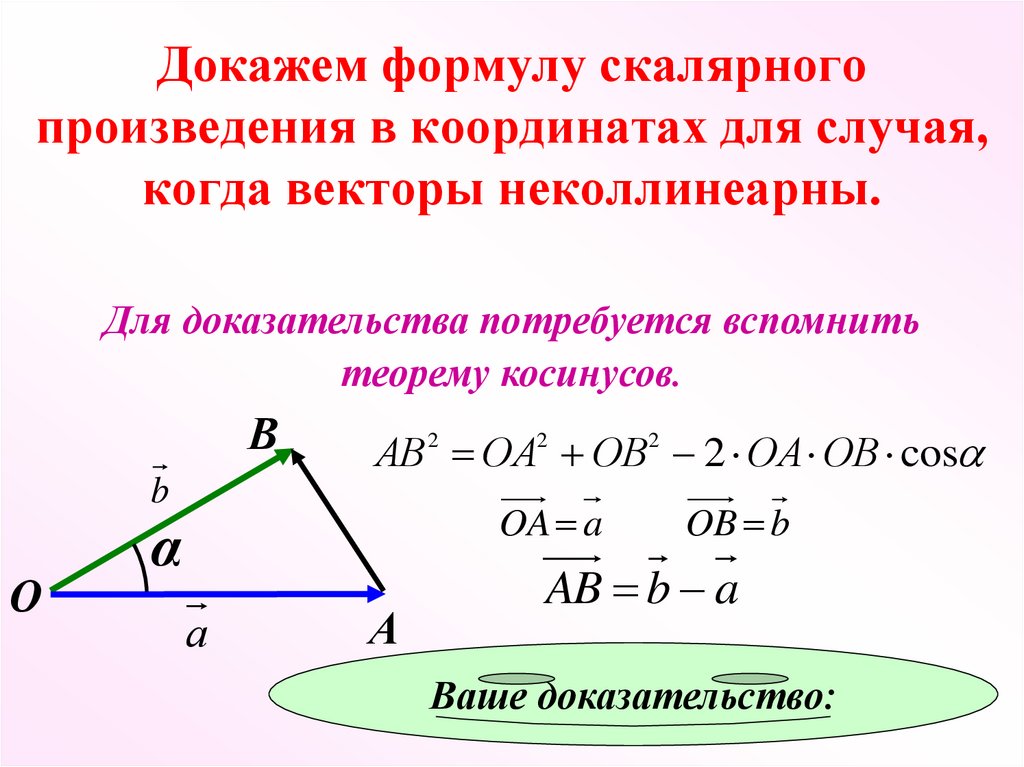
В физике работа постоянной силы при прямолинейном перемещении вдоль вектора пути находится как скалярное произведение этих векторов:

x cos =  x 

Основные свойства скалярного произведения

Скалярное произведение 2 векторов имеет 4 основных свойств. Так как практически в каждом примере, где нужно находить скалярные произведения, необходимо хорошо знать  свойства, рассмотрим их:

1. Скалярное произведение коммутативное (получается из формулы 1):

x  =  x 

2. Числовой множитель можно выносить за знак скалярного произведения:

x  = x  x 

3. Для произвольных векторов  ,  ,  :

x  +  =  x  +  x 

4. Скалярное произведение 2 векторов  и равняется нулю x  тогда, и только тогда, когда один из них нулевой вектор, или когда эти векторы перпендикулярны

Таблица скалярного умножения ортов. Согласно определению 1 x = x x аналогично x = , x , а по свойству (4) x =  x = x =

Скалярное произведение векторов в координатной форме

При помощи основных свойств, которые расписаны выше, можем находить скалярное произведение в координатной форме.

Если  = , тогда  x  =

Действительно, при помощи свойств, у нас получается:

+ +

Как помним, произведение одноимённых ортов равняется 1, а разноимённых = 0, тогда получаем форму скалярного произведения в координатной форме:

x =

(3)

Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Цена работы

Формулы для нахождения скалярного произведения

Чтобы найти скалярное произведение двух векторов, необходимо знать не только свойства, но и несколько важных основных формул, которые подводят к правильному решению.

Длина вектора

Если в формуле (1) , тогда:

.

(4)

Расстояние между двумя точками

Допустим, есть две точки:

1. ;
2. .

Находится как длина вектора = по формуле (4):

(5)

Косинус угла между двумя векторами

Косинус угла между двумя векторами получим из формулы (1) с учётом (3) и (4):

=

(6)

Условия перпендикулярности двух ненулевых векторов

и выходит из свойства 4 и формулы (3):

(7)

Проекция вектора на вектор

Проекция вектора на вектор находится с учётом формул (3) и (4):

пр = = .

(8)

пр = = .

(9)

Декартовые прямоугольные координаты вектора в базисе есть его проекциями на соответствующие оси координат.

Действительно, согласно формуле (9) получается:

пр =  = = , пр = = , пр = = .

Направляющие косинусы вектора

Направляющие косинусы вектора называются косинусы углов , созданные между вектором и координатными осями .

= = = , = = ,  =  

(10)

Примеры нахождения скалярного произведения и направления векторов

Зная все необходимые формулы, легко найти не только скалярное произведение вектора, но и длину сторон, косинус угла, площадь, модуль вектора и т. д. Посмотрите, как решаются задачи при помощи основных формул, которые рассмотрены выше.

Пример 1

Задача

Найти скалярное произведение векторов:

= и = .

Решение

Исходя из формулы (3) у нас получается:

x =

Следующий пример тоже на нахождение скалярного произведения, но решение будет немного другим, хоть и по той же формуле, что и первый пример.

=

Решение

Согласно формуле (4) = . Находим = = = + = , тогда .

Пример 5

Задача

Найти направляющие косинусы вектора и значения выражения .

Решение

=

= = ; = ; = .

= + + = .

Проверим, что для произвольного вектора

= .

Направляющие косинусы вектора полностью определяют направление вектора и они есть координатами единичного вектора , что совпадает за направлением с , то есть:

= = .

Ответ

.

Средняя оценка 5 / 5. Количество оценок: 1

Поставьте вашу оценку

Сожалеем, что вы поставили низкую оценку!

Позвольте нам стать лучше!

Расскажите, как нам стать лучше?

8299

Закажите помощь с работой

Не отобразилась форма расчета стоимости? Переходи по ссылке

Не отобразилась форма расчета стоимости? Переходи по ссылке

Полезно

Вычисление площади параллелограмма построенного на векторах онлайн.

Векторное произведение векторов. Смешанное произведение векторов

Словари. Энциклопедии. История. Литература. Русский язык » Биология » Вычисление площади параллелограмма построенного на векторах онлайн. Векторное произведение векторов. Смешанное произведение векторов

Площадь параллелограмма, построенного на векторах, равняется произведению длин этих векторов на угол угла, который лежит между ними.

Хорошо, когда по условиям даны длины этих самых векторов. Однако бывает и так, что применить формулу площади параллелограмма, построенного на векторах можно только после расчетов по координатам.
Если повезло, и по условиям даны длины векторов, то нужно просто применить формулу, которую мы уже подробно разбирали в статье . Площадь будет равняться произведению модулей на синус угла между ними:

Рассмотрим пример расчета площади параллелограмма построенного на векторах.

Задача: параллелограмм построен на векторах и .

Найдите площадь, если , а угол между ними 30°.
Выразим вектора через их значения:

Возможно, у вас возник вопрос – откуда взялись нули? Стоит вспомнить, что мы работаем с векторами, а для них . также обратите внимание, что если в результате мы получаем выражение ,то оно будет преобразовано в. Теперь проводим итоговые вычисления:

Вернемся к проблеме, когда длины векторов не указаны в условиях. Если ваш параллелограмм лежит в декартовой системе координат, то потребуется сделать следующее.

Расчет длин сторон фигуры, заданной координатами

Для начала находим координаты векторов и отнимаем от координат конца соответствующие координаты начала. Допустим координаты вектора a (x1;y1;z1), а вектора b (x3;y3;z3).
Теперь находим длину каждого вектора. Для этого каждую координату необходимо возвести в квадрат, потом сложить полученные результаты и из конечного числа извлечь корень. По нашим векторам будут следующие расчеты:

Теперь потребуется найти скалярное произведение наших векторов. Для этого их соответствующие координаты множатся и складываются.

Имея длины векторов и их скалярное произведение, мы можем найти косинус угла, лежащего между ними .
Теперь можем найти синус этого же угла:
Теперь у нас есть все необходимые величины, и мы можем запросто найти площадь параллелограмма построенного на векторах по уже известной формуле.

Площадь параллелограмма , построенного на векторах , вычисляется как произведение длин этих векторов на синус угла между ними. Если известны только координаты векторов, то для вычисления нужно применять координатные методы, в том числе и для определения угла между векторами.

Вам понадобится

• — понятие вектора;
• — свойства векторов;
• — декартовы координаты;
• — тригонометрические функции.

Инструкция

• В том случае, если известны длины векторов и угол между ними, то для того, чтобы найти площадь параллелограмма , построенного на векторах , найдите произведение их модулей (длин векторов), на синус угла между ними S=│a│ │ b│ sin(α).
• Если векторы заданы в декартовой системе координат, то для того, чтобы найти площадь параллелограмма , построенного на них, проделайте следующие действия:
• Найдите координаты векторов, если они не даны сразу, отняв от соответствующих координат концов векторов, координаты из начал. Например, если координаты начальной точки вектора (1;-3;2), а конечной (2;-4;-5), то координаты вектора будут (2-1;-4+3;-5-2)=(1;-1;-7). Пусть координаты вектора а(x1;y1;z1), вектора b(x2;y2;z2).
• Найдите длины каждого из векторов. Возведите каждую из координат векторов в квадрат, найдите их сумму x1²+y1²+z1². Из получившегося результата извлеките корень квадратный. Для второго вектора проделайте ту же процедуру. Таким образом, получится │a│и│ b│.
• Найдите скалярное произведение векторов. Для этого перемножьте их соответствующие координаты и сложите произведения │a b│= x1 x2+ y1 y2+ z1 z2.
• Определите косинус угла между ними для чего скалярное произведение векторов, получившееся в п. 3 поделите на произведение длин векторов, которые были рассчитаны в п. 2 (Cos(α)= │a b│/(│a│ │ b│)).
• Синус полученного угла будет равен корню квадратному из разности числа 1, и квадрата косинуса того же угла, рассчитанного в п. 4 (1-Cos²(α)).
• Рассчитайте площадь параллелограмма , построенного на векторах найдя произведение их длин, вычисленное в п. 2, а результат умножьте на число, получившееся после расчетов в п.5.
• В том случае, если координаты векторов заданны на плоскости, при расчетах координата z просто отбрасывается. Данный расчет является числовым выражением векторного произведения двух векторов.

На данном уроке мы рассмотрим ещё две операции с векторами: векторное произведение векторов и смешанное произведение векторов (сразу ссылка, кому нужно именно оно) . Ничего страшного, так иногда бывает, что для полного счастья, помимо скалярного произведения векторов , требуется ещё и ещё. Такая вот векторная наркомания. Может сложиться впечатление, что мы залезаем в дебри аналитической геометрии. Это не так. В данном разделе высшей математики вообще мало дров, разве что на Буратино хватит. На самом деле материал очень распространенный и простой – вряд ли сложнее, чем то же

скалярное произведение , даже типовых задач поменьше будет. Главное в аналитической геометрии, как многие убедятся или уже убедились, НЕ ОШИБАТЬСЯ В ВЫЧИСЛЕНИЯХ. Повторяйте как заклинание, и будет вам счастье =)

Если векторы сверкают где-то далеко, как молнии на горизонте, не беда, начните с урока Векторы для чайников , чтобы восстановить или вновь приобрести базовые знания о векторах. Более подготовленные читатели могут знакомиться с информацией выборочно, я постарался собрать максимально полную коллекцию примеров, которые часто встречаются в практических работах

Чем вас сразу порадовать? Когда я был маленьким, то умел жонглировать двумя и даже тремя шариками. Ловко получалось. Сейчас жонглировать не придётся вообще, поскольку мы будем рассматривать только пространственные векторы , а плоские векторы с двумя координатами останутся за бортом.

Почему? Такими уж родились данные действия – векторное и смешанное произведение векторов определены и работают в трёхмерном пространстве. Уже проще!

В данной операции, точно так же, как и в скалярном произведении, участвуют два вектора . Пусть это будут нетленные буквы .

Само действие обозначается следующим образом: . Существуют и другие варианты, но я привык обозначать векторное произведение векторов именно так, в квадратных скобках с крестиком.

И сразу вопрос : если в скалярном произведении векторов участвуют два вектора, и здесь тоже умножаются два вектора, тогда в чём разница ? Явная разница, прежде всего, в РЕЗУЛЬТАТЕ:

Результатом скалярного произведения векторов является ЧИСЛО:

Результатом векторного произведения векторов является ВЕКТОР : , то есть умножаем векторы и получаем снова вектор. Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву .

Определение векторного произведения

Сначала будет определение с картинкой, затем комментарии.

Определение : Векторным произведением неколлинеарных векторов , взятых в данном порядке , называется ВЕКТОР , длина которого численно равна площади параллелограмма , построенного на данных векторах; вектор ортогонален векторам , и направлен так, что базис имеет правую ориентацию:

Разбираем определение по косточкам, тут много интересного!

Итак, можно выделить следующие существенные моменты:

1) Исходные векторы , обозначенные красными стрелками, по определению не коллинеарны . Случай коллинеарных векторов будет уместно рассмотреть чуть позже.

2) Векторы взяты в строго определённом порядке

: – «а» умножается на «бэ» , а не «бэ» на «а». Результатом умножения векторов является ВЕКТОР , который обозначен синим цветом. Если векторы умножить в обратном порядке, то получим равный по длине и противоположный по направлению вектор (малиновый цвет). То есть, справедливо равенство .

3) Теперь познакомимся с геометрическим смыслом векторного произведения. Это очень важный пункт! ДЛИНА синего вектора (а, значит, и малинового вектора ) численно равна ПЛОЩАДИ параллелограмма, построенного на векторах . На рисунке данный параллелограмм заштрихован чёрным цветом.

Примечание : чертёж является схематическим, и, естественно, номинальная длина векторного произведения не равна площади параллелограмма.

Вспоминаем одну из геометрических формул: площадь параллелограмма равна произведению смежных сторон на синус угла между ними . Поэтому, исходя из вышесказанного, справедлива формула вычисления ДЛИНЫ векторного произведения:

Подчёркиваю, что в формуле речь идёт о ДЛИНЕ вектора, а не о самом векторе . Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма часто находят через понятие векторного произведения:

Получим вторую важную формулу. Диагональ параллелограмма (красный пунктир) делит его на два равных треугольника. Следовательно, площадь треугольника, построенного на векторах (красная штриховка), можно найти по формуле:

4) Не менее важный факт состоит в том, что вектор ортогонален векторам , то есть . Разумеется, противоположно направленный вектор (малиновая стрелка) тоже ортогонален исходным векторам .

5) Вектор направлен так, что базис имеет правую ориентацию. На уроке о переходе к новому базису я достаточно подробно рассказал об ориентации плоскости , и сейчас мы разберёмся, что такое ориентация пространства. Объяснять буду на пальцах вашей правой руки . Мысленно совместите указательный палец с вектором и средний палец с вектором . Безымянный палец и мизинец прижмите к ладони. В результате большой палец – векторное произведение будет смотреть вверх. Это и есть правоориентированный базис (на рисунке именно он). Теперь поменяйте векторы (указательный и средний пальцы ) местами, в результате большой палец развернётся, и векторное произведение уже будет смотреть вниз. Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора) . Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-)

…как всё-таки хорошо, что вы теперь знаете о право- и левоориентированных базисах, ибо страшнЫ высказывания некоторых лекторов о смене ориентации =)

Векторное произведение коллинеарных векторов

Определение подробно разобрано, осталось выяснить, что происходит, когда векторы коллинеарны. Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая

Таким образом, если , то . Строго говоря, само векторное произведение равно нулевому вектору, но на практике этим часто пренебрегают и пишут, что оно просто равно нулю.

Частный случай – векторное произведение вектора на самого себя:

С помощью векторного произведения можно проверять коллинеарность трёхмерных векторов, и данную задачу среди прочих мы тоже разберём.

Для решения практических примеров может потребоваться тригонометрическая таблица , чтобы находить по ней значения синусов.

Ну что же, разжигаем огонь:

Пример 1

а) Найти длину векторного произведения векторов , если

б) Найти площадь параллелограмма, построенного на векторах , если

Решение : Нет, это не опечатка, исходные данные в пунктах условия я намеренно сделал одинаковыми. Потому что оформление решений будет отличаться!

а) По условию требуется найти длину вектора (векторного произведения). По соответствующей формуле:

Ответ :

Коль скоро спрашивалось о длине, то в ответе указываем размерность – единицы.

б) По условию требуется найти площадь параллелограмма, построенного на векторах . Площадь данного параллелограмма численно равна длине векторного произведения:

Ответ :

Обратите внимание, что в ответе о векторном произведении речи не идёт вообще, нас спрашивали о площади фигуры , соответственно, размерность – квадратные единицы.

Всегда смотрим, ЧТО требуется найти по условию, и, исходя из этого, формулируем чёткий ответ. Может показаться буквоедством, но буквоедов среди преподавателей хватает, и задание с хорошими шансами вернётся на доработку. Хотя это не особо натянутая придирка – если ответ некорректен, то складывается впечатление, что человек не разбирается в простых вещах и/или не вник в суть задания. Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже.

Куда подевалась большая буковка «эн»? В принципе, её можно было дополнительно прилепить в решение, но в целях сократить запись, я этого не сделал. Надеюсь, всем понятно, что и – это обозначение одного и того же.

Популярный пример для самостоятельного решения:

Пример 2

Найти площадь треугольника, построенного на векторах , если

Формула нахождения площади треугольника через векторное произведение дана в комментариях к определению. Решение и ответ в конце урока.

На практике задача действительно очень распространена, треугольниками вообще могут замучить.

Для решения других задач нам понадобятся:

Свойства векторного произведения векторов

Некоторые свойства векторного произведения мы уже рассмотрели, тем не менее, я их включу в данный список.

Для произвольных векторов и произвольного числа справедливы следующие свойства:

1) В других источниках информации данный пункт обычно не выделяют в свойствах, но он очень важен в практическом плане. Поэтому пусть будет.

2) – свойство тоже разобрано выше, иногда его называют антикоммутативностью . Иными словами, порядок векторов имеет значение.

3) – сочетательные или ассоциативные законы векторного произведения. Константы безпроблемно выносятся за пределы векторного произведения. Действительно, чего им там делать?

4) – распределительные или дистрибутивные законы векторного произведения. С раскрытием скобок тоже нет проблем.

В качестве демонстрации рассмотрим коротенький пример:

Пример 3

Найти , если

Решение: По условию снова требуется найти длину векторного произведения. Распишем нашу миниатюру:

(1) Согласно ассоциативным законам, выносим константы за переделы векторного произведения.

(2) Выносим константу за пределы модуля, при этом модуль «съедает» знак «минус». Длина же не может быть отрицательной.

(3) Дальнейшее понятно.

Ответ :

Пора подбросить дров в огонь:

Пример 4

Вычислить площадь треугольника, построенного на векторах , если

Решение : Площадь треугольника найдём по формуле . Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов . Решение для ясности разобьём на три этапа:

1) На первом шаге выразим векторное произведение через векторное произведение , по сути, выразим вектор через вектор . О длинах пока ни слова!

(1) Подставляем выражения векторов .

(2) Используя дистрибутивные законы, раскрываем скобки по правилу умножения многочленов.

(3) Используя ассоциативные законы, выносим все константы за пределы векторных произведений. При маломальском опыте действия 2 и 3 можно выполнять одновременно.

(4) Первое и последнее слагаемое равно нулю (нулевому вектору) благодаря приятному свойству . Во втором слагаемом используем свойство антикоммутативности векторного произведения:

(5) Приводим подобные слагаемые.

В результате вектор оказался выражен через вектор, чего и требовалось достичь:

2) На втором шаге найдем длину нужного нам векторного произведения. Данное действие напоминает Пример 3:

3) Найдём площадь искомого треугольника:

Этапы 2-3 решения можно было оформить и одной строкой.

Ответ :

Рассмотренная задача достаточно распространена в контрольных работах, вот пример для самостоятельного решения:

Пример 5

Найти , если

Краткое решение и ответ в конце урока. Посмотрим, насколько вы были внимательны при изучении предыдущих примеров;-)

Векторное произведение векторов в координатах

, заданных в ортонормированном базисе , выражается формулой :

Формула и правда простецкая: в верхнюю строку определителя записываем координатные векторы, во вторую и третью строки «укладываем» координаты векторов , причём укладываем в строгом порядке – сначала координаты вектора «вэ», затем координаты вектора «дубль-вэ». Если векторы нужно умножить в другом порядке, то и строки следует поменять местами:

Пример 10

Проверить, будут ли коллинеарны следующие векторы пространства:
а)
б)

Решение : Проверка основана на одном из утверждений данного урока: если векторы коллинеарны, то их векторное произведение равно нулю (нулевому вектору): .

а) Найдём векторное произведение:

Таким образом, векторы не коллинеарны.

б) Найдём векторное произведение:

Ответ : а) не коллинеарны, б)

Вот, пожалуй, и все основные сведения о векторном произведении векторов.

Данный раздел будет не очень большим, так как задач, где используется смешанное произведение векторов, немного. Фактически всё будет упираться в определение, геометрический смысл и пару рабочих формул.

Смешанное произведение векторов – это произведение трёх векторов :

Вот так вот они выстроились паровозиком и ждут, не дождутся, когда их вычислят.

Сначала опять определение и картинка:

Определение : Смешанным произведением некомпланарных векторов , взятых в данном порядке , называется объём параллелепипеда , построенного на данных векторах, снабжённый знаком «+», если базис правый, и знаком «–», если базис левый.

Выполним рисунок. Невидимые нам линии прочерчены пунктиром:

Погружаемся в определение:

2) Векторы взяты в определённом порядке , то есть перестановка векторов в произведении , как вы догадываетесь, не проходит без последствий.

3) Перед тем, как прокомментировать геометрический смысл, отмечу очевидный факт: смешанное произведение векторов является ЧИСЛОМ : . В учебной литературе оформление может быть несколько другим, я привык обозначать смешанное произведение через , а результат вычислений буквой «пэ».

По определению смешанное произведение – это объем параллелепипеда , построенного на векторах (фигура прочерчена красными векторами и линиями чёрного цвета). То есть, число равно объему данного параллелепипеда.

Примечание : чертёж является схематическим.

4) Не будем заново париться с понятием ориентации базиса и пространства. Смысл заключительной части состоит в том, что к объёму может добавляться знак минус. Простыми словами, смешанное произведение может быть отрицательным: .

Непосредственно из определения следует формула вычисления объема параллелепипеда, построенного на векторах .

Калькулятор скалярного произведения векторов — [100% бесплатно]

Калькулятор скалярного произведения — это удобный инструмент для тех, кому нужно решать задачи на умножение с использованием векторов. Вместо того, чтобы вручную вычислять скалярное произведение, вы можете просто ввести требуемые значения (два или более вектора здесь) в этот калькулятор векторного скалярного произведения, и он вычислит для вас скалярное (внутреннее) произведение.

Загрузка калькулятора…

Содержание

Как пользоваться калькулятором скалярного произведения?

Калькулятор скалярного произведения — очень простой и понятный инструмент. Если у вас есть необходимые значения, вы можете использовать их для автоматических расчетов. Вот шаги, которые нужно выполнить для этого калькулятора скалярного произведения матрицы:

• Сначала введите значения для вектора a: X1 , Y1 и Z1 .
• Затем введите значения для вектора b: X2 , Y2 и Z2 .
• После ввода всех этих значений решатель скалярного произведения автоматически генерирует для вас значения скалярного произведения и угла между векторами.

Что такое скалярное произведение двух векторов?

Несмотря на удобство калькулятора скалярного произведения, который также известен как калькулятор скалярного произведения двух векторов или калькулятор матричного скалярного произведения, вы можете выполнить расчет вручную. Для этого вы должны нарисовать оба вектора и разделить их углом.

Тогда, если вы попытаетесь вычислить образ скалярного произведения, вы обнаружите, что вам нужно умножить две части, а именно проекцию одного из векторов в сторону направления второго вектора вместе с этим вектором. Поскольку эти части параллельны, результат, который вы получите, является произведением длин обеих частей.

Хотя есть два способа выполнить эту операцию, вы получите один и тот же результат. Другими словами, скалярное произведение получается в результате умножения длин векторов, спроецированных в направлении одного из этих векторов.

Как рассчитать скалярный продукт?

Как упоминалось выше, существует два вида умножения векторов, а именно скалярное или скалярное произведение, представленное как «•» , и перекрестное произведение, представленное как «×». Самая большая разница между этими произведениями заключается в том, что произведение операции с точкой всегда является одним числом, а произведение перекрестной операции всегда является вектором.

Чтобы рассчитать скалярное произведение без калькулятора векторного скалярного произведения, давайте предположим, что мы будем выполнять наши вычисления в трехмерном пространстве. В таком случае вы можете записать каждый из векторов, используя 3 компонента:

a = [a₁, a₂, a₃] b = [b₁, b₂, b₃]

Геометрически говоря, скалярное произведение является произведением величин векторов на значение косинуса угла между векторами. Вы можете выразить это с помощью следующего уравнения:

a•b = |a| * |б| * cosα

Если вы не уверены в величине вектора или в том, как выполнять вычисления, вам лучше использовать калькулятор скалярного произведения двух векторов. Но если вы хотите приложить усилия для расчета вручную, давайте продолжим.

Если угол между двумя векторами равен 90˚, то скалярное произведение всегда будет равно нулю независимо от величины векторов. Точно так же, если у вас есть угол 0˚, что означает, что у вас есть коллинеарные векторы, вы можете найти скалярное произведение, просто перемножая множества.

Алгебраически говоря, скалярное произведение относится к сумме произведений компонентов векторов. Следовательно, если у вас есть вектор с 3 компонентами, ваша формула скалярного произведения будет:

a•b = a₁ * b₁ + a₂ * b₂ + a₃ * b₃

В любом пространстве, имеющем более 3-х измерений, добавьте к суммированию дополнительные члены. Но если вы умножаете векторы в двумерном пространстве, удалите третий член в формуле скалярного произведения.

Вы также можете использовать калькулятор скалярного произведения, чтобы найти угол между двумя заданными векторами, где косинус представляет собой отношение величин векторов и скалярных произведений. Для этого вам понадобится следующая формула:

cosα = a•b / (|a| * |b|).

Если вам интересно, как работает этот решатель скалярных произведений, вам нужно выполнить несколько шагов. Чтобы помочь вам лучше понять это, давайте рассмотрим пример:

• Выберите значения для вектора a. Давайте использовать a = [4, 5, -3] .
• Выберите значения для вектора b. Давайте использовать b = [1, -2, -2] .
• Найдите произведение первых компонентов каждого вектора. Для этого примера решение выглядит так: 4 * 1 = 4,
• Найдите произведение средних компонентов каждого вектора. Для этого примера решение выглядит так: 5 * (-2) = -10.
• Найдите произведение третьих компонентов каждого вектора. Для этого примера решение выглядит следующим образом: (-3) * (-2) = 6.
  • Теперь сложите все значения вместе, чтобы найти скалярное произведение: 4 + (-10) + 6 = 0.

Для чего используется скалярное произведение?

Скалярный продукт имеет несколько применений, включая:

• Доказательство закона косинусов с помощью скалярного произведения. Когда вы рисуете треугольник, используя 3 вектора, вы можете записать формулу как c = b – a . Если вам нужно решить для c2 , вы можете расширить это уравнение как c² = (b-a)•(b-a) = b•b – b•a – a•b + a•a = a² + b² – |b| * |а| * коса – |а| * |б| * cosa = a² + b² – 2 * |a| * |б| * cosa . Кстати, именно так можно доказать закон косинусов.
• С его помощью можно узнать, перпендикулярны ли два заданных вектора друг другу.
• Определение различных видов физических величин как скалярных произведений.
• Работа как скалярное произведение смещения и силы.
• Использование мощности как скалярного произведения скорости и силы.
• Использование магнитного или электрического потока как скалярного произведения магнитного или электрического поля на поверхность, через которую оно протекает.
• Использование потенциальной магнитной энергии как скалярного произведения магнитного поля и магнитного момента.

dotproductcalculator.com

Введите значения, чтобы найти скалярное произведение двух векторов с помощью калькулятора скалярного произведения.

Vector a:
i:
j:
k:

Vector b:
i:
j:
k:

Dot product calculator calculates the dot product of two vectors  a  and  b  in Евклидово пространство . Введите i, j, и k для обоих векторов, чтобы получить скалярное число .

а . b

Калькулятор векторного скалярного произведения показывает пошаговое скалярное умножение.

Изображение предоставлено: «Dot Product» от Math is Fun.

Что такое скалярное произведение

?

Скалярное произведение — это алгебраическая операция, которая берет две последовательности чисел одинаковой длины, обычно координатные векторы, и возвращает одно число.

Геометрически это произведение евклидовых величин двух векторов и косинуса угла между ними.

а . b обычно читается как a точка b.

Скалярное произведение формула

Используйте это уравнение для вычисления скалярного произведения двух векторов, если задана величина (длина).

а ∙ б  = | и | × | б | × cos(θ)

Где

| и | длина вектора a

| б | длина вектора b

θ  это угол между a  и b

Направления векторов

Мы также можем найти скалярное произведение, используя направление обоих векторов.

(A _I A _J A _K ) ∙ (B _I B _J B _K ) = (A _I B _K ) = (A _{63636363636262626263626262626262626262626362626262626262626262626362626262626262626262626263. б к  + а к  ∙ б к )}

Где

i, j, и k относятся к x, y, и z в декартовых координатных плоскостях.

Как найти

скалярное произведение двух векторов?

Скалярное произведение двух векторов можно рассчитать с помощью формулы скалярного произведения.

Метод 1 – направление вектора

Вектор a = (2i, 6j, 4k)

Вектор b = (5i, 3j, 7k)

Подставьте значения в формулу.

а ∙ б  = (2, 6, 4) ∙ (5, 3, 7)

(ai aj ak) ∙ (bi bj bk) = (ai ∙ bi + aj ∙ bj + ak ∙ bk )
(2   6   4) ∙ (5   3   7) = (2 ∙ 5 + 6 ∙ 3 + 4 ∙ 7)
(2   6   4) ∙ (5   3   7) = (10 + 18 + 28)

a ∙ b = 56

Метод 2 – Величина вектора

| и | = 15, | б | = 10, θ = 30°

Подставьте значения в формулу.