Найти угол между прямой проходящей через точки и прямой: Угол между прямой и плоскостью

Угол между прямой и плоскостью

Угол между прямой и плоскостью

Навигация по странице:

• Определение угла между прямой и плоскостью
• Формула для вычисления угла между прямой и плоскостью
• Вывод формулы вычисления угла между прямой и плоскостью
• Примеры задач на вычисление угла между прямой и плоскостью

Онлайн калькулятор. Угол между прямой и плоскостью

Определение.

Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость.

Формула вычисления угла между прямой и плоскостью

Если в пространстве заданы направляющий вектор прямой L

s = {l; m; n}

и уравнение плоскости

Ax + By + Cz + D = 0,

то угол между этой прямой и плоскостью можно найти используя формулу

sin φ =	| A · l + B · m + C · n |
	√A2 + B2 + C2 · √l2 + m2 + n2

Вывод формулы для вычисления угла между прямой и плоскостью

Из уравнения прямой можно найти направляющий вектор прямой

s = {l; m; n}

Из уравнения плоскости вектор нормали плоскости имеет вид

q = {A; B; C}

Из формул скалярного произведения векторов найдем косинус угла между нормалью к плоскости и направляющим вектором прямой

cos ψ =	| q · s |
	| s | · |q |

Так как φ = 90° — ψ, то синус угла между прямой и плоскостью sin φ = cos ψ.

Расписав скалярное произведение векторов и модуль векторов через их координаты, получим формулу для вычисления угла между прямой и плоскостью.

Пример вычисления угла между прямой и плоскостью

Пример 1.

Найти угол между прямой

x — 4	=	y + 2	= —	z — 6
2		6		3

и плоскостью x — 2y + 3z + 4 = 0.

Решение.

Из уравнения прямой найдем направляющий вектор прямой

s = {2; 6; -3}

Из уравнения плоскости найдем вектор нормали плоскости

q = {1; -2; 3}

Воспользовавшись формулой, найдем угол между прямой и плоскостью

sin φ =	| 2 · 1 + 6 · (-2) + (-3) · 3 |	=
	√22 + 6 2 + (-3)2 · √12 + (-2)2 + 32

=

| 2 — 12 — 9 |√4 + 36 + 9 · √1 + 4 + 9

=

|-19|√49 · √14

=

197√14

Ответ: sin φ = 197√14.

Онлайн калькуляторы. Аналитическая геометрия. Декартовые координаты

Угол между прямой и плоскостью — что это такое? Как найти?

Поможем понять и полюбить математику

Начать учиться

Представьте: на уроке физкультуры вам нужно кинуть мяч точно в нарисованную на стене мишень. «Целься под углом 45°», — советует физрук. Или вы читаете задачу по физике, где солнечные лучи падают на поверхность под углом α. А может быть, вам надо помочь маме в саду и подпереть дверь старой лопатой. Что общего у этих ситуаций?

Правильный ответ такой: все эти случаи можно озаглавить геометрическим понятием «пересечение плоскости прямой под некоторым углом». Об этом мы сегодня и поговорим, а именно:

• рассмотрим главные определения и примеры;

• изучим свойства и теоремы по теме;

• научимся находить угол между прямой и плоскостью.

Определение угла между прямой и плоскостью

Угол между прямой и плоскостью — это угол между прямой и её проекцией на эту плоскость.

Мы уже знакомы с понятиями «угол», «прямая» и «плоскость» (если подзабыли, то можете повторить по нашим материалам). А сейчас давайте вспомним, что такое проекция.

Проекция — это геометрическое изображение на плоскости, полученное проведением перпендикуляров из всех точек данного тела на плоскость.

То есть под углом между прямой и плоскостью в пространстве мы подразумеваем угол между прямой и её отображением на плоскость.

Важное уточнение

Если прямая перпендикулярна плоскости, то можно считать, что угол между ними равен 90°, что следует из определения перпендикулярности прямой и плоскости. Этот случай — самый простой, его мы рассматривать не будем.

Также стоит заметить, что если прямая параллельна плоскости, то у них нет ни одной общей прямой, а значит, угол между ними не определяется.

Как вы думаете, какой тип имеет угол между прямой и плоскостью? Верно, он может быть только острым. Попробуйте доказать это самостоятельно 😊

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Свойства и теоремы

Свойство угла между прямой и плоскостью

Углом между прямой и плоскостью называется наименьший из углов между прямой и произвольной прямой в плоскости.

Попробуем привести доказательство. Для этого нарисуем плоскость и проведём к ней прямую АВ, являющуюся наклонной. Тогда АВ₁ — проекция прямой на плоскость, АН — произвольная прямая, принадлежащая плоскости, а ВН и ВВ₁ — перпендикуляры к плоскости (ВН ⟂ АН, ВВ₁ ⟂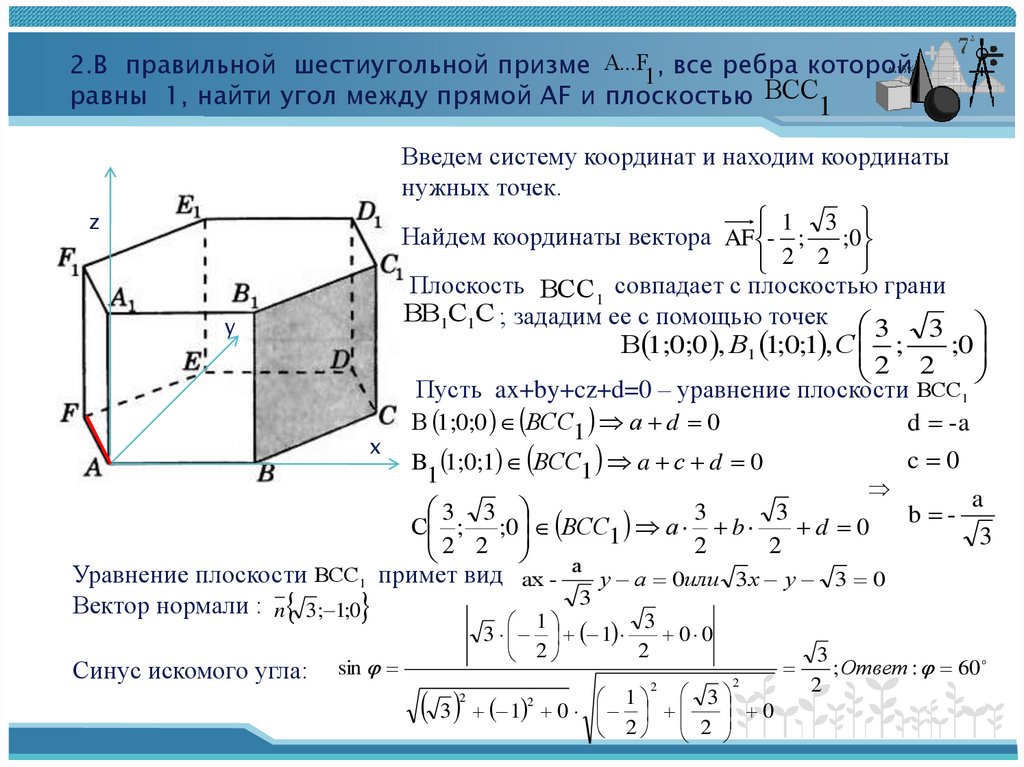

АВ). Чтобы лучше представить себе этот объёмный чертеж, можно сделать небольшой макет из сложенного листа бумаги, прислонив его к поверхности стола или тетради.

Чтобы проверить истинность свойства, нам необходимо доказать, что угол ∠ВАВ₁ намного меньше, чем угол ∠ВАН.

Обозначим проблему: значения этих углов, как и других исходных, нам неизвестны. А значит, на помощь может прийти тригонометрия, ведь сравнить углы можно и через их синусы.

Синус — это отношение противолежащего угла к гипотенузе. В таком случае, .

Оба перпендикуляра ВВ₁ и ВН проведены из точки В, но только один из них является кратчайшим расстоянием от точки по плоскости, и это перпендикуляр ВВ1. Так как значения синусов представляют собой дроби с одинаковыми знаменателями, большей будет та, у которой больше знаменатель.

Следовательно, sin ∠BAB1 < sin ∠BAH, ∠BAB1 < ∠BAH.

Теорема

Из двух наклонных, проведённых из одной точки к плоскости, меньшая образует с плоскостью больший угол, и наоборот: угол, образованный большей наклонной, будет меньшим из двух.

Существует множество разных доказательств этой теоремы, но мы сосредоточимся на одном из них.

Для этого изобразим плоскость и точку . Из точки А проведём две наклонные прямые, причем АВ < АС, а также перпендикуляр к плоскости

АО. Докажем, что ∠АВО > ∠АСО.

Стороны ОВ и ОС являются проекциями АВ и АС соответственно. Меньшая прямая имеет меньшую проекцию, а значит, ОВ < ОС.

Отложим на стороне ОС отрезок ОЕ, равный ОВ. Можно ли доказать равенство треугольников АОВ и АОЕ?

В данных треугольниках:

• ОВ = ОЕ (по построению),

• АО — общий катет.

Следовательно, треугольники АОВ и АОЕ равны по двум катетам (или по первому признаку: две стороны и угол между ними). В таком случае равны и соответственные углы: ∠АВО = ∠АЕО.

Угол АЕО является внешним для треугольника АЕС, и по свойству внешнего угла ∠АЕО = ∠АСЕ + ∠САЕ. Не трудно догадаться: раз угол АЕО равен сумме двух других углов треугольника, не смежных с ним, то он больше любого из этих двух углов.

∠АЕО > ∠АСЕ, и так как ∠АЕО = ∠АВО, то ∠АВО > ∠АСЕ.

Что и требовалось доказать. 😎

Как найти угол между прямой и плоскостью

От теории переходим к практике: а как же можно вычислить угол между прямой и плоскостью? Вопрос лёгкий и сложный одновременно. Дело в том, что задач на нахождение угла очень много, и в каждой из них применяется свой алгоритм решения. Большую роль играет предмет и раздел, в котором эта задача приведена: это может быть стереометрия, векторная алгебра и даже физика. Но все эти алгоритмы сводятся к двум методам: геометрическому и алгебраическому или координатному методу. Давайте подробно рассмотрим каждый из них.

Геометрический метод

Чтобы применить геометрический метод, необходимо опустить перпендикуляр на плоскость из точки, принадлежащей исходной прямой. Выясним, чем в этом задании является перпендикуляр, наклонная и проекция, и решим планиметрическую задачку (чаще всего в таких задачах нам будет необходимо найти один из углов прямоугольного треугольника).

Задача 1

Из точки А на плоскость проведены две наклонные АВ и АС и перпендикуляр АО, причём О, В и С — точки пересечения с плоскостью .

Определите, чему равен АО, если СО = 10, ВО = 26, а угол АСО в два раза больше угла АВО.

Решение:

Отметим на стороне ОВ отрезок, равный ОС. Тогда ОС = ОЕ = 10, а ЕВ = 26 – 10 = 16.

Рассмотрим треугольники АСО и АЕО:

• СО = ОЕ (по построению),

• АО — общий катет.

Следовательно, треугольники равны по двум катетам. А значит, угол АСО равен углу АЕО.

Угол АЕО является внешним для треугольника АЕВ, а значит, ∠АЕО = ∠АВЕ + ∠ВАЕ. Так как ∠ АВЕ = , значит, ∠ ВАЕ = 2-=, и треугольник АЕВ — равнобедренный.

Тогда найдём АО через прямоугольный треугольник АОЕ по теореме Пифагора:

.

Ответ: .

Алгебраический метод

Алгебраический метод или метод координат для нахождения угла между прямой и плоскостью основывается на особой формуле. Чтобы использовать его, необходимо определить координаты двух точек, принадлежащих прямой, описать уравнение плоскости и применить формулу. По сути в этом методе мы находим угол между вектором и плоскостью.

,

где (x₁, y₁, z₁) — это координаты первой точки,

(x₂, y₂, z₂) — координаты второй точки,

А, В и С — это координаты в уравнении плоскости Ax + By + Cz + D = 0.

Иначе эти числа называют координатами вектора нормали плоскости.

Тут может возникнуть вопрос: а что, если в задаче даны не координаты точек, а координаты вектора?

В этом случае вспомним, что координаты вектора находятся через разность координат начала и конца. А значит, мы со спокойно душой подставляем эти координаты в формулу вместо (х₂ – х₁), (y₂ – y₁) и (z₂ – z₁).

В некоторых задачах для нахождения угла между прямой и плоскостью вводят понятие направляющего вектора прямой. Направляющий вектор прямой — это любой вектор, не равный нулю, который размещается на данной прямой или же на прямой, параллельной ей.

Координаты этого вектора можно получить из канонического уравнения прямой:

, где направляющий вектор а имеет координаты (a_x, a_y).

Тогда угол между прямой и плоскостью можно вычислить по формуле:

.

Задача 2

Найдите угол между прямой и плоскостью 3x – y – z + 1 = 0.

Решение:

1. Определим координаты направляющего вектора для прямой: (2; –1; 3).

2. Определим координаты вектора нормали плоскости: (3; –1; –1).

3. Подставим координаты в формулу для расчёта синуса угла между плоскостью и прямой:

   .

Задача 3

Найдите угол между плоскостью, заданной уравнением x + 2y + 2z – 4 = 0, и прямой, которой принадлежат точки А (0, 2, –1) и В (–2, 4, –1).

Решение:

1. Определим координаты вектора нормали плоскости: (1; 2; 2).

2. Подставим координаты вектора нормали и координаты точек прямой в формулу:

   .

За короткий промежуток времени мы изучили понятие угла между прямой и плоскостью, доказали теоремы, разобрали способы нахождения угла и решили практические задания. Мы — молодцы! 💪

Думаем, вы понимаете, что эта тема очень важна — с её помощью решаются сложные стереометрические задачи, которые встречаются на ОГЭ и ЕГЭ. Подготовиться к таким серьёзным заданиям помогут курсы профильной математики в онлайн-школе Skysmart. На уроках мы сможем более подробно разобрать задачи с пирамидами и параллелепипедами, а ещё научимся составлять уравнения для любой плоскости. Узнать свои сильные и слабые стороны, составить план обучения и познакомиться с онлайн-платформой можно на вводном уроке — это бесплатно.

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Дарья Вишнякова

К предыдущей статье

Компланарность векторов

К следующей статье

Теоремы, которые точно пригодятся на ЕГЭ

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

Угол между двумя линиями — Формула, Примеры

Угол между двумя линиями помогает узнать взаимосвязь между двумя линиями. Это мера наклона между двумя линиями. Для двух пересекающихся прямых существует два угла между прямыми: острый угол и тупой угол. Здесь мы рассматриваем острый угол между прямыми, для угла между двумя прямыми .

Угол между двумя линиями полезен для нахождения меры угла между двумя сторонами замкнутого многоугольника. Проверим формулы и примеры для угла между двумя прямыми в координатной плоскости и трехмерном пространстве..

1.	Как найти угол между двумя линиями?
2.	Формулы для угла между двумя линиями
3.	Угол между двумя линиями в трехмерном пространстве
4.	Примеры угла между двумя линиями
5.	Практические вопросы
6.	Часто задаваемые вопросы об угле между двумя линиями

Как найти угол между двумя линиями?

Угол между двумя линиями можно рассчитать, зная наклон двух линий или зная уравнение двух линий. Угол между двумя линиями обычно дает острый угол между двумя линиями.

Угол между двумя линиями можно вычислить по наклону двух линий и с помощью функции тригонометрического тангенса. Рассмотрим две линии с наклонами \(m_1\) и \(m_2\) соответственно. Острый угол θ между прямыми можно вычислить по формуле функции тангенса. Острый угол между двумя прямыми находится по следующей формуле.

Tanθ = \(\dfrac{m_1 — m_2}{1 + m_1.m_2}\)

Далее, мы можем найти угол между двумя линиями, если даны уравнения двух линий. Пусть уравнения двух линий будут \(l_1 = a_1x + b_1y + c_1 = 0\) и \(l_2 = a_2x + b_2y + c_2 = 0\). Угол между двумя прямыми можно вычислить по тангенсу угла между двумя прямыми.

Tanθ =\(\dfrac{a_2b_1 — a_1b_2}{a_1a_2 + b_1b_2}\)

Формулы для угла между двумя линиями

Следующие различные формулы помогают легко найти угол между двумя линиями.

• Угол между двумя линиями, одна из которых представляет собой ax + by + c = 0, а другая линия является осью x, равен θ = Tan ^-1 (-a/b).
• Угол между двумя линиями, одна из которых представляет собой линию y = mx + c, а другая линия является осью x, равен θ = Tan ^-1 м .
• Угол между двумя прямыми, параллельными друг другу и имеющими одинаковый наклон (\(m_1 = m_2\)) равен 0º. 92}{2bc}\)

Угол между двумя линиями в трехмерном пространстве

Угол между двумя линиями в трехмерном пространстве можно вычислить аналогично углу между двумя линиями в координатной плоскости. Для двух линий с уравнениями \(r = a_1 + λb_1\) и \(r = a_2 + λb_2\) угол между линиями определяется следующей формулой.

Cosθ = \(\dfrac{b_1.b_2}{|b_1|.|b_2|}\)

Далее для двух линий, имеющих отношение направлений как \((a_1, b_1, c_1)\), и \( (a_2, b_2, c_2)\), угол между линиями можно вычислить по приведенной ниже формуле. 92}}\)

Также для двух прямых, имеющих направляющие косинусы \(l_1, m_1, n_1\) и \(l_2, m_2, n_2\), угол между двумя прямыми можно вычислить по следующей формуле .

Cosθ = \(|l_1.l_2 + m_1.m_2 + n_1.n_2|\)

Связанные темы

Следующие темы помогут лучше понять понятие угла между двумя линиями.

• Координатная геометрия
• Уравнение прямой
• Параллельные линии
• Типы уголков

Примеры угла между двумя линиями

1. Пример 1: Найдите угол между двумя линиями, имеющими наклон 1 и 1/2 соответственно.

   Решение:

   Наклоны двух прямых равны \(m_1\) = 1 и \(m_2\) = 1/2.

   Формула для нахождения угла между двумя линиями: Tanθ = \(\frac{m_1 — m_2}{1 + m_1.m_2}\).

   Tanθ = \(\frac{1 — 1/2}{1 + 1/2.1}\) 9{-1} \frac{1}{3}\).

2. Пример 2: Найдите угол между двумя прямыми, используя уравнения 3x + 4y — 10 = 0 и 4x -5y + 2 = 0. + 4y — 10 = 0 и 4x -5y + 2 = 0.

   Здесь мы имеем \(a_1 = 3, b_1 = 4, a_2 = 4, b_2 = -5\)

   Угол между двумя линиями может рассчитать по формуле Tanθ =\(\dfrac{a_2b_1 — a_1b_2}{a_1a_2 + b_1b_2}\). 9{-1}-\frac{31}{8}\).

перейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, что стоит за математикой, с нашими сертифицированными экспертами

Запишитесь на бесплатный пробный урок

Практические вопросы по углу между двумя линиями

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы об угле между двумя линиями

Как найти угол между двумя линиями?

Угол между двумя линиями можно рассчитать по наклону линий или по уравнению двух линий. Самая простая формула для нахождения угла между двумя линиями — это наклон двух линий. Угол между двумя линиями с наклоном \(m_1\) и \(m_2\) соответственно равен Tanθ = \(\dfrac{m_1 — m_2}{1 + m_1.m_2}\).

По какой формуле найти угол между двумя прямыми?

Это две важные формулы для нахождения угла между двумя линиями в координатной плоскости. Для двух линий, имеющих наклоны \(m_1\) и \(m_2\) соответственно, угол между двумя линиями равен Tanθ = \(\dfrac{m_1 — m_2}{1 + m_1.m_2}\). И вторая формула для нахождения угла между двумя линиями, имеющими уравнения \(l_1 = a_1x + b_1y + c_1 = 0\) и \(l_2 = a_2x + b_2y + c_2 = 0\), это Tanθ =\(\ dfrac{a_2b_1 — a_1b_2}{a_1a_2 + b_1b_2}\).

Как найти угол между двумя линиями в трехмерной геометрии?

Угол между двумя линиями в трехмерной геометрии, имеющей уравнения линий \(r = a_1 + λb_1\) и \(r = a_2 + λb_2\), равен Cosθ = \(\dfrac{b_1. b_2}{|b_1|.|b_2|}\).

Объяснение урока: Угол между двумя прямыми на координатной плоскости

В этом объяснении мы узнаем, как найти величину острого угла между двумя прямыми на координатной плоскости.

Напомним, что уравнение любой прямой в координатной плоскости можно записать в виде 𝑎𝑥+𝑏𝑦+𝑐=0, где 𝑎, 𝑏 и 𝑐 — константы. Это называется общая форма прямой. В качестве альтернативы, когда мы знаем наклон или градиент линии, 𝑚 и его 𝑦-перехват, 𝑏, мы можем написать уравнение в форме уклон-отрезок : 𝑦=𝑚𝑥+𝑏.

(Обратите внимание, что константа 𝑏 в форме наклона-пересечения и в общей форме не одинакова.)

Учитывая наклон 𝑚 линии и точки, линия, мы также можем записать уравнение линии в форме точка–наклон : 𝑦−𝑦=𝑚(𝑥−𝑥).

Если у нас есть наклон 𝑚 линии, мы знаем, что когда 𝑚 положительно, угол, 𝜃, измеренное против часовой стрелки от положительного направления оси 𝑥 до линии является острым. То есть 0𝜃90∘∘. Мы также знаем из формы точка–наклон, что если у нас есть две различные точки на прямой, скажем 𝑃(𝑥,𝑦) и 𝑄(𝑥,𝑦), то наклон прямой равен отношению разности 𝑦 к разнице в 𝑥: 𝑚=𝑦−𝑦𝑥−𝑥.

Теперь, с геометрической точки зрения, если мы образуем прямоугольный треугольник, используя наши две точки 𝑃 и 𝑄 и третья точка 𝑅 на плоскости, как показано на диаграмме, затем вспоминая, что tanoppositeadjacent𝜃=, имеем загар𝜃=𝑄𝑅𝑃𝑅.

Так как 𝑄𝑅 есть разность 𝑦-координат двух точек на прямой и 𝑃𝑅 — разность соответствующих 𝑥-координат двух точек на прямой, это значит, что загар𝜃=𝑚.

Аналогично, если угол, измеренный против часовой стрелки от положительного направления оси 𝑥 к линия тупая, то есть 90𝜃180∘∘, как показано на диаграмме ниже, то наклон прямой, проходящей через точки 𝑃 и 𝑄, равен 𝑚=−𝑃𝑅𝑄𝑅=−𝛼=𝜃.тантан

Следовательно, независимо от того, измерен ли угол 𝜃 против часовой стрелки от положительного направления 𝑥-ось к линии острая или тупая, наклон линии 𝑚 равен загар𝜃.

Стоит отметить, что, хотя мы можем распространить наш метод на частные случаи вертикальных и горизонтальных линий, мы не рассматриваем их в этом объяснении. Заметим просто, что горизонтальные линии имеют наклон 𝑚=0 и угол 0∘, а вертикальные линии имеют неопределенный наклон и угол 90∘.

Теперь предположим, что у нас есть две линии в координатной плоскости с наклонами 𝑚=𝜃tan и 𝑚=𝜃загар, например, как показано на диаграмме ниже. В этом случае 𝜃>𝜃, и оба угла острые.

Если предположить, что прямые не параллельны, то есть 𝑚≠𝑚, и учитывая, что углы в треугольник должен в сумме давать 180∘, мы имеем 𝜃+𝛼+(180−𝜃)=180𝛼=180−𝜃−(180−𝜃)=𝜃−𝜃. 

Проведение касательной с обеих сторон дает нам тантан𝛼=(𝜃−𝜃) . Теперь, используя тригонометрическое тождество, тантантантантан(𝐴±𝐵)=𝐴±𝐵1∓𝐴𝐵, у нас есть тантантантантан 𝛼=(𝜃−𝜃)=𝜃−𝜃1+𝜃𝜃.

Это верно для любых двух линий, описанных выше. Однако, хотя доказательство немного различается в зависимости от положения линии и положение точки их пересечения при условии, что ни одна из линий не является вертикальной, т. 𝜃 или 𝜃=90∘, это результат справедлив для любых двух непараллельных прямых с углами 𝜃 и 𝜃, измеренными против часовой стрелки от положительного направления оси 𝑥 к каждой строке соответственно.

Следовательно, поскольку 𝑚=𝜃tan и 𝑚=𝜃tan, это приводит нас к следующее определение.

Определение: угол между двумя прямыми линиями в координатной плоскости

Угол 𝛼 между двумя непараллельными линиями в координатной плоскости с уклоном 𝑚 и 𝑚, такое что 𝑚𝑚≠−1, задается формулой tan𝛼=𝑚−𝑚1+𝑚𝑚. 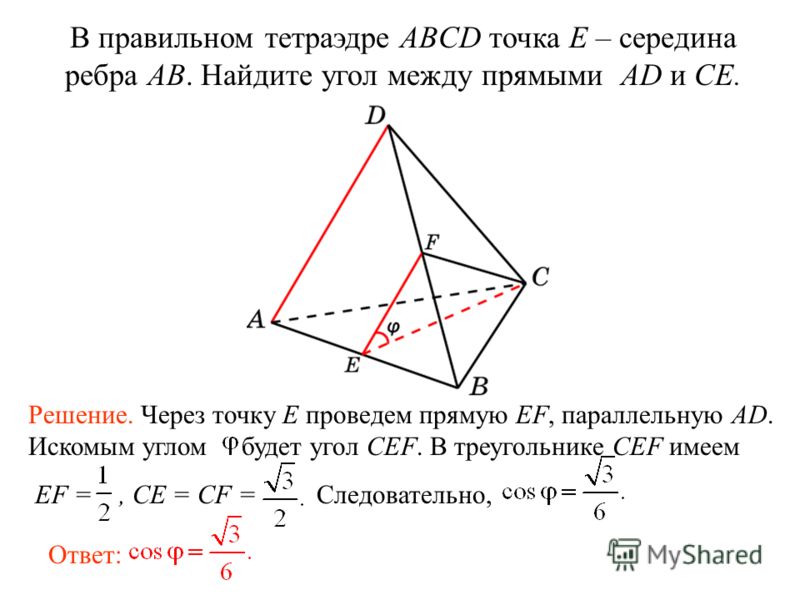

Если прямые параллельны, то 𝑚=𝑚 и между ними нет угла. Если линии не параллельны и не перпендикулярны, то между ними два угла. Мы называем меньший угол «углом». или «острый угол» между линиями.

Отрицательный тангенс соответствует большему тупому углу 𝛼 и гарантирует, что тангенс что острого угла, 𝛼, мы берем абсолютное значение. Следовательно, тангенс острого угла между две линии в координатной плоскости tan𝛼=|||𝑚−𝑚1+𝑚𝑚|||.

Заметим, что если 𝑚𝑚=−1, то знаменатель равен 0, и это выражение не определено. В в этом случае линии перпендикулярны, и 𝛼=90∘.

Давайте посмотрим, как это работает, на примере, где нам заданы наклоны двух линий.

Пример 1. Нахождение меры угла между двумя прямыми по их наклонам

Определить с точностью до секунды мера острого угла между двумя прямыми, имеющими наклоны 5 и 14.

Ответ

Зная наклоны 𝑚 и 𝑚 двух прямых на координатной плоскости, мы можем найдите острый угол 𝛼 между прямыми по формуле tan𝛼=|||𝑚−𝑚1+𝑚𝑚|||. 

Полагая 𝑚=5 и 𝑚=14, имеем загар𝛼=||||5−1+5⋅||||.

Затем оценка правой части приводит к загар𝛼=199, и взятие арктангенса с обеих сторон дает нам 𝛼=199=64,6538….tan∘

Нас просят найти меру угла с точностью до ближайшего во-вторых, и для этого вспомним, что существуют 60 минут в один градус и 60 секунд в одна минута. Поэтому мы умножаем десятичная часть наших градусов на 60: 0,6538…×60=39,2294…. Следовательно, у нас есть 39.2294…’ (минуты), и умножая десятичную часть нашего минут на 60 дает нам 0,2294…×60=13,7666…≈14» (секунды).

Мера острого угла между двумя линиями с точностью до во-вторых, поэтому 6439′14∘.

Наш следующий пример демонстрирует, как найти угол между двумя линиями в координатной плоскости, где линии оба даны в общем виде.

Пример 2. Нахождение угла между двумя прямыми в двух измерениях

Найдите величину острого угла между двумя прямыми, уравнения которых 11𝑥+10𝑦−28=0 и 2𝑥+𝑦+15=0 до ближайшего второй.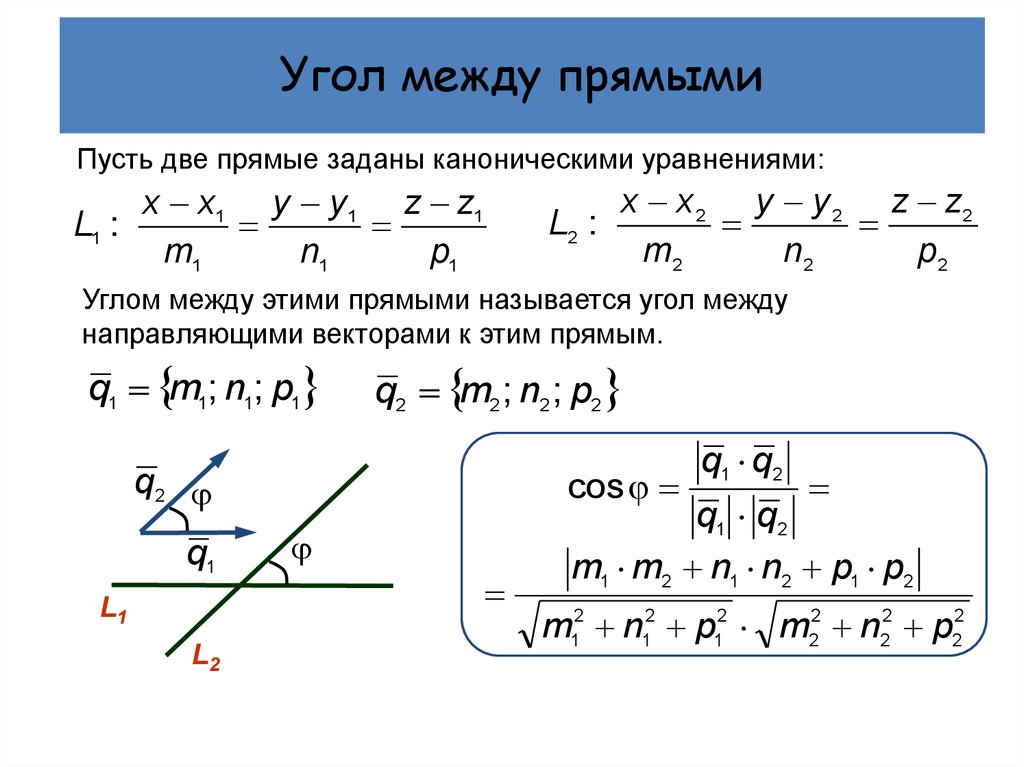

Ответ

Нам даны две прямые, уравнения которых имеют общий вид, то есть в виде 𝑎𝑥+𝑏𝑦+𝑐=0, где 𝑎, 𝑏 и 𝑐 — действительные числа. Чтобы найти острый угол 𝛼 между двумя прямыми, воспользуемся формулой загар𝛼=|||𝑚−𝑚1+𝑚𝑚|||, где 𝑚 и 𝑚 — наклоны данных прямых. Поэтому мы будем, нужно найти эти два наклона, заданные в каждом случае −𝑎𝑏.

Наши линии 𝐿∶11𝑥+10𝑦−28=0,𝐿∶2𝑥+𝑦+15=0, наклоны которого поэтому равны 𝑚=−1110 и 𝑚=−2.

Подставив эти два значения в формулу для tan𝛼, мы получим загар𝛼=||||−(−2)1+(−2)||||=||||+21+||||=932. 

Теперь, взяв арктангенс обеих сторон, находим 𝛼=932=15,7086….tan∘

Нас просят измерить угол до ближайшего второй. Чтобы найти это, вспомним, что есть 60 минут в один градус и 60 секунд в одна минута. Поэтому мы умножаем десятичная часть наших градусов на 60: 0,7086…×60=42,5182…. Отсюда имеем 42,5182…′ (минуты), и умножив десятичная часть наших минут на 60 дает нам 0,5182…×60=31,0961…≈31′′ (секунды).

Мера острого угла между двумя линиями с точностью до во-вторых, следовательно, 1542′31∘.

В следующем примере мы найдем острый угол между одной прямой, уравнение которой задано в общем виде, и второй прямой, проходящей через две известные точки.

Пример 3. Нахождение угла между двумя прямыми в двух измерениях

Определите величину острого угла между прямыми 𝑥−𝑦+4=0 и прямая, проходящая через точки (3,−2) и (−2,4) с точностью до ближайшего второй.

Ответ

Чтобы найти острый угол 𝛼 между двумя заданными прямыми, мы можем использовать формулу загар𝛼=|||𝑚−𝑚1+𝑚𝑚|||, где 𝑚 — наклон нашей первой линии, которую мы будем обозначать 𝐿, и 𝑚 — наклон второй линии, которую мы будем обозначать 𝐿. Чтобы использовать это формуле, нам нужно будет найти наклоны двух линий.

Наша первая строка задается в общем виде: 𝑎𝑥+𝑏𝑦+𝑐=0, где 𝑎, 𝑏 и 𝑐 — действительные числа, и где в нашем случае 𝑎=1, 𝑏=−1 и 𝑐=4. Наклон 𝑚 определяется выражением −𝑎𝑏; следовательно, 𝑚=1.

Чтобы найти второй наклон 𝑚, вспомним, что для двух различных точек на прямой (𝑥,𝑦) и (𝑥,𝑦), наклон линии через точки определяется изменением 𝑦, деленным на изменение 𝑥. То есть, 𝑚=𝑦−𝑦𝑥−𝑥.

Для нашей второй линии 𝐿 нам даны координаты двух точек на линии, (3,−2) и (−2,4). Наклон, 𝑚, 𝐿 поэтому 𝑚=4−(−2)−2−3=−65.

Теперь, когда у нас есть два наклона 𝑚=1 и 𝑚=-65, мы можем использовать заявленная формула тангенса острого угла 𝛼 между двумя прямыми: загар𝛼=||||1−1+1×||||=||||1+1−||||=|−11|=11. 

Теперь, взяв арктангенс, находим 𝛼=(11)=84,8055….tan∘

Нас просят указать угол с точностью до секунды. Чтобы найти это, вспомним, что в один градус и 60 секунд в одна минута. Поэтому мы умножаем десятичную часть наших градусов на 60: 0,8055…×60=48,3342…. Следовательно, у нас есть 48,3342…′ (минуты) и умножение десятичная часть наших минут на 60 дает нам 0,3342…×60=20,0559…≈20′′ (секунды).

Таким образом, угол между двумя линиями с точностью до секунды равен 8448′20∘.

До сих пор наши линии определялись либо в общем виде, либо через известные точки на линии, из которых мы могли найти склоны. Однако есть и другие формы, в которых могут быть выражены прямые линии, как в следующем определении.

Определение: векторная, параметрическая и декартова формы линии на координатной плоскости

Линия, проходящая через точку A с вектором положения ⃑𝑎=(𝑎,𝑎), в направлении вектора ⃑𝑑=(𝑑,𝑑), можно пишется в следующих формах: Векторная форма: параметрическая форма: декартова форма: ⃑𝑟=⃑𝑎+𝑡⃑𝑑(𝑥,𝑦)=(𝑎,𝑎)+𝑡(𝑑,𝑑),𝑥=𝑎+𝑡𝑑𝑦=𝑎+𝑡𝑑,𝑥−𝑎𝑎.  

В векторной форме каждое уникальное значение действительного параметра 𝑡 дает вектор положения ⃑𝑟=(𝑥,𝑦) точки на прямой и в декартовом форме мы предполагаем, что и 𝑑, и 𝑑 отличны от нуля.

Обратите внимание, что, решая каждое из параметрических уравнений для 𝑡 и приравнивая, мы получаем декартову форму, который можно переставить следующим образом: 𝑥−𝑎𝑑=𝑦−𝑎𝑑𝑦=𝑑𝑑(𝑥−𝑎)+𝑎=𝑑𝑑𝑥+𝑎−𝑑𝑑𝑎. 02 Теперь это в форме пересечения наклона, 𝑦 =𝑚𝑥+𝑏, где здесь уклон 𝑚=𝑑𝑑. Следовательно, если дана линия в любой из указанных выше форм и, в частности, ее вектор направления, мы можем найти его наклон, который равен 𝑑𝑑 при условии, что 𝑑 не равно нулю.

В нашем следующем примере мы будем использовать это, чтобы найти угол между двумя линиями, уравнения которых даны в векторной и параметрической формах.

Пример 4. Нахождение угла между двумя прямыми в двух измерениях

Найдите величину острого угла между двумя прямыми 𝐿 и 𝐿 уравнения которого ⃑𝑟=(2,7)+𝐾(−1,8) и 𝑥=3+12𝑑, 𝑦=4𝑑−5, соответственно, по степеням, минут и секунд, с точностью до второй.

Ответ

Чтобы найти острый угол 𝛼 между двумя прямыми на координатной плоскости, мы используем формулу загар𝛼=|||𝑚−𝑚1+𝑚𝑚|||, где 𝑚 и 𝑚 — наклоны двух прямых. Поэтому мы должны найти наклоны двух заданных прямых.

Первая из двух наших строк, 𝐿∶⃑𝑟=(2,7)+𝐾(−1,8), задана в векторной форме, то есть в виде ⃑𝑟=(𝑥,𝑦)=(𝑎,𝑎)+𝑡(𝑑,𝑑), где прямая проходит через точку с вектором положения ⃑𝑎=(𝑎,𝑎), в направлении вектора ⃑𝑑=(𝑑,𝑑). склон, 𝑚, прямой с вектором направления (𝑑,𝑑) является 𝑑𝑑.

Для нашей строки 𝐿 мы видим, что константа 𝐾 соответствует параметру 𝑡 так что наш вектор направления равен ⃑𝑑=(−1,8). Уклон, 𝑚, этой строки поэтому 𝑚=𝑑𝑑=8−1=−8.

Наша вторая строка, 𝐿, 𝑥=3+12𝑑,𝑦=4𝑑−5, задается в параметрическом виде. То есть в виде 𝑥=𝑎+𝑡𝑑,𝑦=𝑎+𝑡𝑑, где снова прямая проходит через точку с вектором положения ⃑𝑎=(𝑎,𝑎), в направлении вектора ⃑𝑑=(𝑑,𝑑). Сравнивая, мы видим, что параметр 𝑑 в 𝐿 ​​соответствует параметру 𝑡 в общих параметрических уравнениях и что поэтому наш вектор направления равен ⃑𝑑=(12,4). Следовательно, наклон линии 𝐿 дается 𝑚=𝑑𝑑=412=13.

Теперь мы можем использовать два наших наклона, 𝑚=−8 и 𝑚=13, в формуле, чтобы найти острый угол между двумя прямыми: tan𝛼=|||𝑚−𝑚1+𝑚𝑚|||=||||−8−1+(−8)||||=5. 

Теперь возьмем арктангенс с обеих сторон, мы имеем 𝛼=(5)=78,6900….tan∘

Нас просят указать угол с точностью до секунды. Чтобы найти это, вспомним, что в один градус и 60 секунд в одна минута. Поэтому мы умножаем десятичную часть наших градусов на 60: 0,6900…×60=41,4040…. Следовательно, у нас есть 41,4040…′ (минуты) и умножение десятичная часть наших минут на 60 дает нам 0,4040…×60=24,2430…≈24» (секунды).

Таким образом, мера острого угла между двумя прямыми 𝐿 и 𝐿, к ближайшая секунда, это 7841′24∘.

Мы будем использовать формулу тангенса угла между двумя прямыми в нашем следующем примере, чтобы найти уравнения прямых.

Пример 5. Нахождение уравнений двух прямых в двух измерениях с использованием тангенса угла между ними

Пусть 𝜃 будет углом между двумя прямыми, которые проходят через (4,−2). Если tan𝜃=121 и наклоны линий равны 𝑚 и 45𝑚, при 𝑚>0, найдите уравнения этих прямых.

Ответ

Вспоминая, что под углом между двумя прямыми мы подразумеваем меньший из двух углов, нам говорят, что две прямые, скажем 𝐿 и 𝐿 проходят через точку (4,−2) и что тангенс угла 𝜃 между ними равен 121.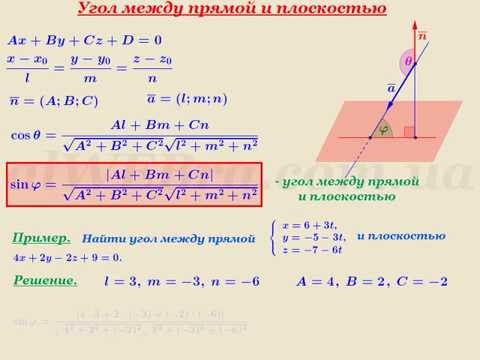 Нам также известно, что наклон 𝐿 равен 𝑚 и что наклон 𝐿 равно 45𝑚, где 𝑚>0.

Чтобы найти уравнения линий 𝐿 и 𝐿, мы сначала используем информацию, которую мы есть в формуле тангенса угла между двумя прямыми, чтобы найти любые возможные значения 𝑚. Затем мы можем использовать данную точку и форму точки и наклона линии, чтобы найти уравнения линий. 𝐿 и 𝐿.

Напомним, что формула тангенса острого угла 𝜃 между двумя прямыми выглядит следующим образом: загар𝜃=|||𝑚−𝑚1+𝑚𝑚|||, где 𝑚 и 𝑚 — наклоны двух прямых. Подставляем наши значения tan𝜃, 𝑚 и 𝑚, имеем 121=||||𝑚−𝑚1+𝑚⋅𝑚||||=𝑚5+4𝑚, отметив, что, поскольку 𝑚 положительно, правая часть положительна. Преобразование этого приводит к квадратичному уравнение 4𝑚−21𝑚+5=0, который мы можем решить для 𝑚. Используя квадратичную формулу или иначе, мы находим, что есть два решения: 𝑚=5 и 𝑚=14.

Точечно-наклонная форма линии 𝑦−𝑦=𝑚(𝑥−𝑥), где 𝑚 — наклон, а прямая проходит через точку (𝑥,𝑦). Используя это с каждым из наших решений для 𝑚 вместе с точкой (4,−2), через которую обе линии проходят, будут получены уравнения для 𝐿 и 𝐿.

Начиная с нашего решения, 𝑚=5, мы помним, что наклон 𝐿 равен 𝑚=5 и наклон 𝐿=45×5=4. Поэтому у нас есть 𝐿∶𝑦−(−2)=5(𝑥−4)𝑦+2=5𝑥−20−5𝑥+𝑦+22=0,𝐿∶𝑦−(−2)=4(𝑥−4)𝑦+2= 4𝑥−164𝑥−𝑦−18=0,

Теперь со вторым решением, 𝑚=14, мы имеем, что наклон 𝐿 равен 𝑚=14 и наклон 𝐿=45⋅14=15.

Следовательно, в данном случае имеем 𝐿∶𝑦-(-2)=14(𝑥-4)𝑦+2=14𝑥-1𝑥-4𝑦-12=0,𝐿∶𝑦-(-2)=15(𝑥-4)𝑦+2=15𝑥- 45𝑥−5𝑦−14=0.

Следовательно, возможны две пары уравнений прямых: −5𝑥+𝑦+22=04𝑥−𝑦−18=0и или 𝑥−4𝑦−12=0𝑥−5𝑦−14=0.and

Мы завершим это объяснение, напомнив себе о некоторых ключевых моментах.

Ключевые моменты

• Чтобы найти острый угол 𝛼 между двумя прямыми с наклонами 𝑚 и 𝑚 в координатной плоскости воспользуемся формулой tan𝛼=|||𝑚−𝑚1+𝑚𝑚|||.
• Если 𝑚𝑚=−1, то знаменатель в формуле для tan𝛼 равен на 0, и выражение не определено.

  No related posts.