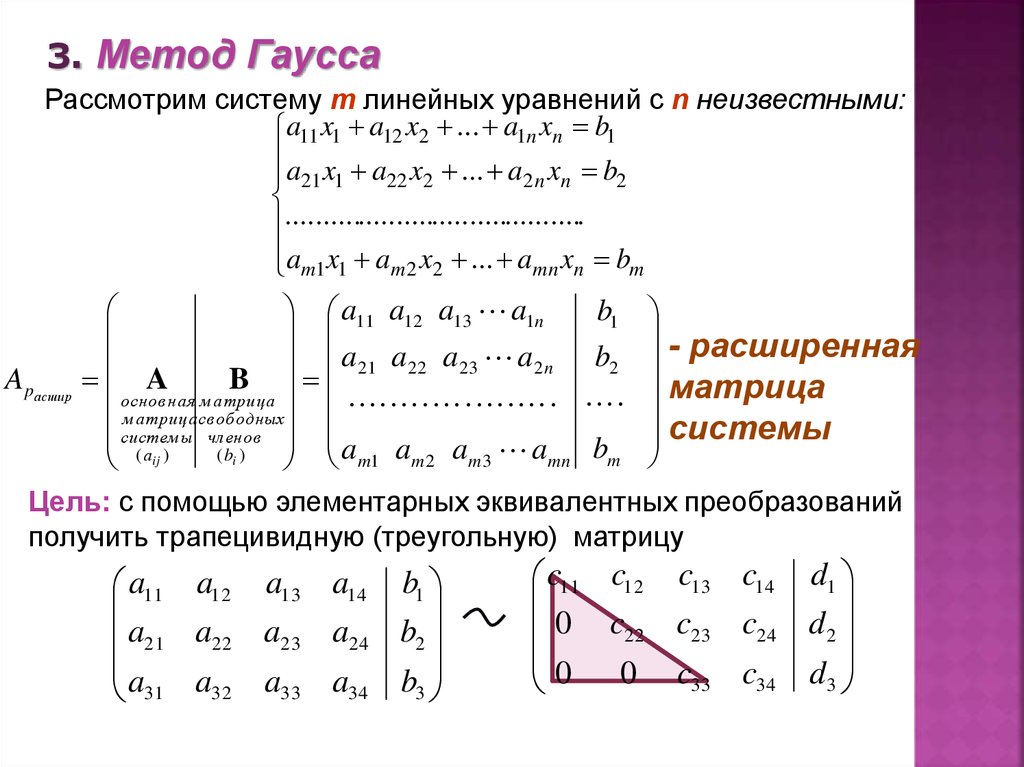
Система m линейных уравнений с n неизвестными
Похожие презентации:
Системы линейных уравнений
Методы и модели линейного программирования. Лекция 4
Системы линейных уравнений. Метод Гаусса. (Тема 9.2)
Методы оптимальных решений
Методы оптимальных решений в линейном программировании
Синтез комбинационных схем. Типовые логические элементы и их обозначения на функциональных схемах
Системы линейных уравнений
Системы логических уравнений. Разбор заданий ЕГЭ (А10, В15)
Системы линейных уравнений
Решение систем логических уравнений
1. Система m линейных уравнений с n неизвестными
Система m линейных уравнений с nпеременными имеет вид
a11 x1 a12 x2 a1n xn b1 ,
a x a x a x b ,
21 1 22 2
2n n
2
,
………………………………………
am1 x1 am 2 x2 amn xn bm
В задачах линейного программирования
представляют интерес системы, в
которых ранг матрицы r системы A=(aij),
i=1,2…m, j=1,2…n, или, что то же самое,
максимальное число независимых
уравнений меньше числа переменных
Любые m переменных системы m
линейных уравнений с n переменными
(m<n) называются основными (или
базисными), если определитель
матрицы коэффициентов при них
отличен от нуля.
Тогда остальные n — m переменных
называются неосновными ( или
свободными)
Базисным решением системы m линейных
уравнений с n переменными называется
решение, в котором все n-m неосновных
переменных равны нулю.
В задачах линейного программирования
особый интерес представляют допустимые
базисные решения (опорные планы).
Число базисных решений является
конечным.
Базисное решение, в котором хотя бы одна
из основных переменных равна нулю,
называется вырожденным.
Основными могут быть разные группы из
n переменных. Максимальное число
групп основных переменных
C
m
n
Пример. Найти все возможные группы
основных переменных в системе
x1 x2 2 x3 x4 0
2 x1 x2 2 x3 x4 2
Решение системы называется
допустимым, если оно содержит только
неотрицательные компоненты, в
противном случае – решение
допустимое.
Базисным решением системы m линейных
уравнений с n переменными называется
решение, в котором все n-m
неосновных переменных равны нулю
Пример.
Найти все базисные решениясистемы
x1 x2 2 x3 x4 0
2 x1 x2 2 x3 x4 2
11. Симплексный метод решения задач линейного программирования
Решение любой задачи линейногопрограммирования можно найти
симплексным методом.
Симплексный метод решения задачи
линейного программирования основан
на переходе от одного опорного плана к
другому, при котором значение целевой
функции возрастает ( убывает) (при
условии, что данная задача имеет
оптимальный план).
Оптимальный план — совокупность
значений переменных, при которых
наименьшее значение целевой
функции, любая другая совокупность
значений, удовлетворяющая
ограничениям, определяет опорный
(базисный) план.
Для реализации симплексного метода
необходимо освоить три основных элемента:
Способ определения какого-либо
первоначального допустимого базисного
решения задачи (опорного плана)
Правило перехода к лучшему (не худшему)
решению
Критерий проверки оптимальности найденного
решения.
Пусть требуется найти максимальное
(минимальное) значение функции
F с1 x1 с2 x2 … сn xn max(min)
при условиях
а11 x1 а12 x2 … а1п хn b1
a x a x … a x b
21 1
22 2
2n n
2
……….
……….
……….
……….
……..
am1 х1 am 2 x2 … amn xn bm
x1 0
……….
x
n 0
Алгоритм решения задачи симплексным
методом:
привести задачу линейного
программирования к стандартному виду.
найти начальное базисное решение
(опорный план). Если базисное решение
отсутствует, задача не имеет решения в виду
несовместности системы ограничений
проверить полученное базисное решение на
оптимальность с помощью критерия
оптимальности
если выполняется критерий оптимальности
решения, то решение задачи заканчивается
если выполняется условие существования
множества оптимальных решений, то путем
простого перебора найти все оптимальные
решения
если имеют место условия неограниченности
целевой функции, то задача не имеет решения
если пункты 4 — 6 алгоритма не выполняются,
найти новое опорное решение и перейти к
пункту 3
Для нахождения первоначального
базисного плана все переменные
разбиваются на две группы:
основные(базисные) и неосновные.
Положив неосновные переменные
равными нулю, получаем базисное
решение.
Критерий оптимальности решения
при отыскании
максимума(минимума) линейной
функции:
Если в выражении линейной функции
через неосновные переменные
отсутствуют положительные
(отрицательные) коэффициенты при
неосновных переменных, то решение
оптимально.
Если система ограничений
непротиворечива, то
выполнение конечного числа
последовательных шагов
симплексного метода приводит
к нахождению оптимального
решения задачи.
Алгоритм решения задачи
линейного
программирования
построением симплексной
таблицы
Алгоритм:
1. Систему линейных неравенств
записываем в каноническом виде. Для
этого в каждое неравенство добавляем
дополнительную переменную со знаком
«+», если неравенство имеет знак
меньше или равно и со знаком «-» в
противном случае
После введения добавочных переменных
систему уравнений и линейную
функцию записываем в виде:
а11 x1 а12 x2 .
.. а1п хn хn 1 b1a x a x … a x x b
21 1
22 2
2n n
n 2
2
…………………………………………
a х a x … a x x
m1 1
m2 2
mn n
n m bm
F c1 x1 c2 x2 … cn xn 0
2.
Исходную расширенную систему
заносим в первую симплексную таблицу.
Базис
Свобо
дный
член
Переменные
х1
х2
…… хn
Оценочные
отношения
3. Проверяем выполнение критерия
оптимальности при решении задач на
максимум- наличие в последней
строке отрицательных коэффициентов.
Если таковых нет, то полученное
решение оптимально.
4 Если критерий оптимальности не
выполнен, то наибольший по модулю
отрицательный элемент в последней
столбец s
Составляем оценочные отношения каждой
строки по правилам:
1) ∞, если bi и ais имеют разные знаки;
2) ∞, если bi=0 и ais <0
3) ∞, если ais =0
4)
, если bi и ais имеют одинаковые
bi
ais
знаки
Определяем
bi
min
i
ais
.
Если конечного минимума нет, то
задача не имеет конечного оптимума
(Fmax=∞)
Если минимум конечен, то выбираем
строку, в которой он достигается и
называем ее разрешающей строкой
q.
На пересечении разрешающей строки
и разрешающего столбца находится
разрешающий элемент аqs
5. Переходим к следующей таблице по
правилам:
в левом столбце записываем новый
базис: вместо основной переменной хqпеременную xs
в столбцах, соответствующим основным
переменным проставляем нули и
единицы: 1 – против «своей» основной
переменной 0- против «чужой»
основной переменной. 0 в последней
строке для всех основных переменных.
новую строку с номером q получаем из
старой строки делением на
разрешающий элемент aqs
все остальные элементы получаем по
правилу прямоугольника:
a aij
/
ij
b bi
/
i
ais aqj
aqs
aisbq
aqs
Пример. Решим задачу об использовании
ресурсов
x1 3 x2 18
2 x x 16
1
2
x2 5
3 x1 21
x 0
1
x2 0
F 2×1 3×2 max
1.
Шагx1 3 x2 х3 18
2 x x х 16
2
4
1
x2 х5 5
3 x х 21
6
1
F 2 x1 3 x2 0
Заполняем первую симплексную таблицу,
в которой переменные х3,х4,х5,х6 основные
Базис
Своб
одны
й
член
х1
х2
х3
х4
х5
х6
х3
18
1
3
1
0
0
0
х4
16
2
1
0
1
0
х5
5
0
1
0
0
1
0
х6
21
3
0
0
0
0
1
F
0
-2
-3
0
0
0
0
Переменные
Оцен
очные
отнош
ения
Базис
Своб
одны
й
член
Переменные
х1
х2
х3
х4
х5
х6
Оцен
очные
отнош
ения
х3
18
1
3
1
0
0
0
18/3
х4
16
2
1
0
1
0
0
16
х5
5
0
1
0
0
1
0
5
х6
21
3
0
0
0
0
1
∞
F
0
-2
-3
0
0
0
0
Базис
х3
х4
х2
х6
F
Своб
одны
й
член
Переменные
х1
х2
х3
х4
х5
х6
Оцен
очные
отнош
ения
Базис
Своб
одны
й
член
Переменные
х1
х2
х3
х4
х5
х6
х3
0
1
0
0
х4
0
0
1
0
х2
1
0
0
0
х6
0
0
0
1
F
0
0
0
0
Оцен
очные
отнош
ения
Базис Своб
одны
й
член
Переменные
х2
х3
х4
х3
0
1
0
0
х4
0
0
1
0
1
0
0
х6
0
0
0
1
F
0
0
0
0
х2
5
х1
0
х5
1
х6
0
Оцен
очны
е
отно
шени
я
Базис
Своб
одны
й
член
Переменные
х2
х3
х4
0
1
0
х4
3 5 1 3 0
18
1
1
16
0
0
1
х2
5
1
0
0
х6
0
0
0
1
F
0
0
0
0
х3
х1
1 5
1 0
2
1
1
0
х5
х6
3 1
1
1 1
0
1
0
1
0
0
0
Оцено
чные
отнош
ения
Базис
Свобо
дный
член
х1
х2
х3
х4
х5
х6
х3
3
1
0
1
0
-3
0
х4
11
2
0
0
-1
0
х2
5
0
1
0
0
1
0
х6
21
3
0
0
0
0
1
F
15
-2
0
0
0
3
0
Переменные
Оцено
чные
отнош
ения
Базис
Свобо
дный
член
х1
х2
х3
х4
х5
х6
х3
3
1
0
1
0
-3
0
3
х4
11
2
0
0
1
-1
0
11/2
х2
5
0
1
0
0
1
0
∞
х6
21
3
0
0
0
0
1
7
F
15
-2
0
0
0
3
0
Переменные
Оцено
чные
отнош
ения
Базис
Свобо
дный
член
х1
х2
х3
х4
х5
х6
х1
3
1
0
1
0
-3
0
х4
5
0
0
-2
1
5
0
х2
5
0
1
0
0
1
0
х6
12
0
0
-3
0
9
1
F
21
0
0
2
0
-3
0
Переменные
Оцено
чные
отнош
ения
Базис
Свобо
дный
член
х1
х2
х3
х4
х5
х6
х1
3
1
0
1
0
-3
0
∞
х4
5
0
0
-2
1
5
0
5/5
х2
5
0
1
0
0
1
0
5/1
х6
12
0
0
-3
0
9
1
12/9
F
21
0
0
2
0
-3
0
Переменные
Оцено
чные
отнош
ения
Базис
Свобо
дный
член
х1
х2
х3
х1
6
1
0
х5
1
0
х2
4
х6
F
Переменные
х4
х5
х6
-0,2 0,6
0
0
0
-0,4 0,2
1
0
0
1
0,4
-0,2
0
0
3
0
0
0,6
-1,8
0
1
24
0
0
0,8
0,6
0
0
Оцено
чные
отнош
ения
English Русский Правила
|
Заглавная страница
Новые добавления Обратная связь КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
⇐ ПредыдущаяСтр 4 из 12Следующая ⇒ Система линейных уравнений Системой m линейных уравнений с n неизвестными называется система m алгебраических уравнений первой степени вида
где – неизвестные, подлежащие определению; – числа, называемые коэффициентами при неизвестных; – числа, называемые свободными членами. Решением системы уравнений (4.1.1) называется совокупность n чисел таких, что если в каждое уравнение системы вместо неизвестных подставить эти числа ( вместо , вместо вместо ), то все уравнения обратятся в тождества. Если система линейных уравнений (4.1.1) имеет хотя бы одно решение, то она называется совместной. В противном случае система называется несовместной. Совместная система, имеющая единственное решение, называется определенной, а система, имеющая более одного решения – неопределенной. Две системы линейных уравнений называются эквивалентными, если любое решение каждой из них является одновременно решением и другой системы. Две произвольные несовместные системы считаются эквивалентными. Системе линейных уравнений (4.1.1) поставим в соответствие матрицу и расширенную матрицу , полученную присоединением к матрице А столбца свободных членов.
Методы решения системы n линейных уравнений с n неизвестными
Рассмотрим систему n линейных уравнений с n неизвестными
Определитель |A| матрицы А называется определителем системы (4.2.1). Теорема Крамера. Если определитель |A| системы (4.2.1) отличен от нуля, то система совместна и имеет единственное решение. Доказательство. Пусть система (4.2.1) совместна и – одно из ее решений. Тогда получим n тождеств:
Умножим обе части первого из равенств (4.2.2) на алгебраическое дополнение , обе части второго равенства умножим на алгебраическое дополнение и т.д. и обе части n-ого равенства – на . Складывая левые и правые части полученных выражений, придем к следующему равенству:
Коэффициент при равен определителю |A| системы (4.2.1), коэффициент при равен нулю, а правая часть равенства (4.2.3) является определителем, полученным из определителя |A| путем замены j-го столбца столбцом свободных членов. Обозначим данный определитель через Тогда равенство (4.2.3) примет вид: , откуда
Из формулы (4. Формулы (4.2.4) называются формулами Крамера. Непосредственной подстановкой значений , во все уравнения системы убедимся в том, что они образуют ее решение: . При , при , . Таким образом, получим . Теорема доказана. Пример. Решить систему линейных уравнений методом Крамера:
Решение. Вычислим определитель : , , , откуда Решение системы линейных уравнений с определителем |A|, отличным от нуля, можно найти с помощью обратной матрицы. Для этого запишем систему (4.2.1) в виде матричного уравнения
где . Решение матричного уравнения (4.2.5) имеет вид
Пример. Решить систему линейных уравнений с помощью обратной матрицы Решение. ее обратную матрицу . Определим неизвестную матрицу-столбец Х: , откуда Формулы Крамера (4.2.4) могут быть получены из выражения (4.2.6). Действительно, запишем матричное равенство в развернутом виде: . Из полученного выражения непосредственно следуют формулы Крамера: . Теорема Кронекера-Карелли Теорема. Система линейных уравнений (4.1.1) совместна тогда и только тогда, когда . Доказательство. Необходимость. Пусть система (4.1.1) совместна и пусть числа – одно из ее решений. Подставляя эти числа вместо неизвестных в систему (4.1.1), получим m тождеств, которые показывают, что последний столбец матрицы является линейной комбинацией всех остальных столбцов, взятых соответственно с коэффициентами . Всякий другой столбец матрицы входит и в матрицу А. Поэтому максимальное число линейно независимых столбцов матриц А и совпадает. Достаточность. Пусть дано, что . Отсюда следует, что максимальное число линейно независимых столбцов матриц А и совпадает и равно r. Для определенности предположим, что первые r столбцов матриц А и линейно независимы, а остальные (n-r) столбцов является их линейными комбинациями. Выражая последний столбец матрицы А как линейную комбинацию первых r столбцов, получим: откуда следует, что числа являются решением системы (4.1.1), т.е. система (4.1.1) совместна. Теорема доказана. На основании теоремы Кронекера-Капелли имеем: 1. Если , то система (4.1.1) несовместна; 2. Если , то система (4.1.1) совместна. Пусть для определенности базисный минор порядка r расположен в верхнем левом углу матрицы А. Тогда первые r строк матрицы А линейно независимы, а остальные ее строки являются линейной комбинацией первых r строк. Но это означает, что первые r уравнений системы (4. При этом возможны два случая: 1. . Тогда систему, состоящую из первых r уравнений системы (4.1.1) можно решить, например, по правилу Крамера. В этом случае система имеет единственное решение, т.е. система совместна и определена; 2. . Рассмотрим первые r уравнений системы (4.1.1). Оставив в левых частях первые r неизвестных, перенесем остальные в правые части. Получим систему: Очевидно, что полученная система и, следовательно, система (4.1.1) являются совместными и неопределенными. Таким образом, если , то система (4.1.1) совместна (определенная или неопределенная), если , то система (4.1.1) несовместна. Если в системе n линейных уравнений с n неизвестными определитель системы равен нулю, то . Теорема Кронекера-Капелли устанавливает необходимое и достаточное условие совместности системы (4.1.1), но не дает способа нахождения решения этой системы. Рассмотрим метод Жордана-Гаусса – метод решения системы m линейных уравнений с n неизвестными.
Метод Жордана-Гаусса
Метод Жордана-Гаусса основан на элементарных преобразованиях (п.3.2) строк расширенной матрицы системы (4.1.1). В результате каждого из элементарных преобразований расширенная матрица изменяется, однако системы линейных уравнений, соответствующие полученным матрицам, эквивалентны исходной системе линейных уравнений. Пусть дана система m линейных уравнений с n неизвестными. Применяя элементарные преобразования, построим эквивалентную систему специального вида. Для этого выберем в качестве первого уравнений одно из тех уравнений системы, где коэффициент при х1 отличен от нуля. . Умножим первое уравнение на . Затем умножим это же уравнение на , и прибавим его почленно к уравнениям системы с номерами i=2,3,…,m. После этого преобразования в уравнениях с номерами i>1 будет исключено неизвестное х1. Первый шаг метода Жордана-Гаусса закончен. . Может случиться, что на первом шаге вместе с неизвестными х1 будут исключены неизвестными , но найдется хотя бы одно уравнение, в котором сохранится неизвестное . Одно из таких уравнений примем в качестве второго уравнения системы. В этом случае расширенная матрица , соответствующая полученной системе, имеет вид: . Используем второе уравнение для исключения неизвестного из всех уравнений, кроме второго. После второго шага метода Жордана-Гаусса получим расширенную матрицу . Продолжая процесс, после r шагов получим матрицу , содержащую r единичных столбцов на месте первых n столбцов матрицы А (r – ранг матрицы А системы). При этом возможны три случая: 1. Если , то матрица преобразуется в матрицу Система имеет единственное решение: . 2. Если и r<n, то Система имеет бесконечное множество решений. Общее решение имеет вид: Неизвестные называются базисными. – свободными неизвестными. Свободным неизвестным можно придавать какие угодно значения, получая при этом соответствующие значения неизвестных . В результате имеем бесконечное множество частных значений. Среди частных решений системы выделим базисные решения, которые получают при равенстве нулю всех свободных неизвестных. Очевидно, что одним из базисных решений является следующее: . В общем случае число базисных решений не превышает . 3. Если , то где хотя бы один из элементов отличен от нуля. В этом случае система (4.1.1) несовместна. Таким образом, метод Жордана-Гаусса состоит из r итераций (r шагов). На каждой S-ой итерации выбирается направляющий элемент соответственно направляющие строка и столбец. Рассмотрим алгоритм произвольной итерации метода Жордана-Гаусса. Положим . Шаг 1. Сформировать множество . Шаг 2. Если , то процесс элементарных преобразований закончить. В противном случае перейти к шагу 3. Шаг 3. Если для , то процесс элементарных преобразований закончить. В противном случае найти направляющий элемент и перейти к шагу 4. Шаг 4. Разделить направляющую строку на . Шаг 5. К i-ой строке, , прибавим строку , умноженную на . Покажем, что столбец преобразуется в единичный с единицей в строке . Пусть . Элементы матрицы выражаются через элементы матрицы следующим образом:
Полагая j=k, из (4.4.1) и (4.4.3) имеем . Пример. Решить систему линейных уравнений методом Жордана-Гаусса.
Решение. Составим из данной системы расширенную матрицу Полагаем . Итерация 1. Шаг 1. . Шаг 2. , переходим к шагу 3. Шаг 3. Находим . Шаг 4. Делим третью строку на . Шаг 5. К первой, второй и четвертой строкам прибавляем третью строку, соответственно умноженную на -2, -2, -3. В результате матрица преобразуется в матрицу . Итерация 2. Шаг 1. . Шаг 2. , переходим к шагу 3. Шаг 3. Находим . Шаг 4. Делим первую строку на . Шаг 5. Ко второй, третьей и четвертой строкам прибавляем первую строку, соответственно умноженную на -4, -3, 1. Получим матрицу . Итерация 3. Шаг 1. . Шаг 2. , переходим к шагу 3. Шаг 3. Находим . Шаг 4. Делим четвертую строку на . Шаг 5. К первой, второй, третьей строкам прибавляем четвертую строку, соответственно умноженную на 0, -5, -2. . Итерация 4. Шаг 1. . Шаг 2. , переходим к шагу 3. Шаг 3. Находим . Шаг 4. Делим четвертую строку на . Шаг 5. К первой, третьей и четвертой строкам прибавляем вторую строку, соответственно умноженную на -1, 2, 0. Получим матрицу . Итерация 5. Шаг 1. . Шаг 2. , поэтому процесс элементарных преобразований закончен. На основании вида матрицы получаем единственное решение исходной системы: .
Решение. Составим расширенную матрицу . В результате итерации 1, полагая , получим матрицу После итерации 2, полагая , получим матрицу Итерация 3. Шаг 1. . Шаг 2. . Шаг 3. Так как , то процесс элементарных преобразований закончен. Матрица определяет общее решение системы: – базисные, – свободные переменные. Получим одно из базисных решений: .
Решение. Матрицы , , имеют вид:
Очевидно, что процесс элементарных преобразований следует закончить, так как . Из первой (или третьей) строки матрицы следует, что исходная система линейных уравнений несовместна. Действительно, первой строке соответствует уравнение , которое не может быть удовлетворено ни при каких значениях неизвестных . Используя метод Жордана-Гаусса, рассмотрим еще один метод вычисления обратной матрицы . Рассмотрим матричное уравнение
где , Е – единичная матрица. Очевидно, что матричное уравнение (4.4.5) имеет единственное решение . Решение матричного уравнения (4.4.5) сводится к решению n систем n линейных уравнений с n неизвестными вида
Системе линейных уравнений (4. Таким образом, чтобы для невырожденной матрицы А вычислить обратную матрицу , необходимо составить матрицу . Методом Жордана-Гаусса в матрице преобразовать матрицу А к виду единичной матрицы Е, тогда на месте единичной матрицы Е получим обратную матрицу . Пример. Вычислить обратную матрицу для матрицы . Решение. Составим матрицу . На итерации 1, полагая , получим . На итерации 2, полагая , получим . На итерации 3, полагая , получим , откуда .
⇐ Предыдущая12345678910Следующая ⇒ Читайте также: Техника прыжка в длину с разбега Тактические действия в защите История Олимпийских игр История развития права интеллектуальной собственности |
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 557; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.005 с.) |
Решение системы линейных уравнений
Все правила по сольфеджио
2.4) следует, что если система (4.2.1) совместна, то она обладает единственным решением.
Вычислим для матрицы
Следовательно, .
1.1) линейно независимы, а остальные (m-r) ее уравнений являются их линейными комбинациями. Поэтому достаточно решить систему r уравнений; решения такой системы будут, очевидно, удовлетворять и остальным (m-r) уравнениям.
Тогда если , то система является совместной и неопределенной. Если , то система несовместна.
Не нарушая общности, предположим, что . Тогда первым уравнением системы будет уравнение
С помощью элементарных преобразований столбец преобразуется в единичный с единицей в строке .
Получим матрицу
4.6) соответствует расширенная матрица . Применяя к матрице алгоритм метода Жордана-Гаусса, получим матрицу . Покажем, что . Расширенной матрице соответствует матричное уравнение , которое имеет единственное решение Х=В. Матрица получена из матрицы методом Жордана-Гаусса. Поэтому системы линейных уравнений, соответствующие матрицам и , равносильны, т.е. имеют одно и то же решение. Отсюда следует, что , следовательно, .
систем линейных уравнений, примеры решений, картинки и практические задачи.
Система просто ..Рабочие листы систем линейных уравнений
Рабочие листы по системам
Интерактивная система линейных уравнений
Что такое система уравнений?
ОтвечатьСистема уравнений просто означает «более 1 уравнения». Система линейных уравнений — это чуть больше 1 строки, см. рисунок:
Итак, что такое
решение системы уравнений? ОтвечатьРешение находится там, где уравнения «встречаются» или пересекаются. Красная точка — решение системы.
Сколько решений может иметь система линейных уравнений?
Отвечать Могут быть нулевые решения, 1 решение или бесконечные решения — каждый случай подробно объясняется ниже.
Примечание. Хотя системы линейных уравнений могут состоять из 3 и более уравнений, мы собираемся обратиться к наиболее распространенному случаю — стеблю, состоящему ровно из 2 строк.
Случай I: 1 Решение
Это наиболее распространенная ситуация, когда линии пересекаются ровно в одной точке.
Вариант 2: Нет решений
Это происходит только тогда, когда прямые параллельны. Как видите, параллельные линии никогда не пересекутся.
Пример стебля, не имеющего решения:
- Строка 1: $$ y = 5x + 13 $$
- Строка 2: $$ y = 5x + 12 $$
Случай III: Бесконечные решения
Это самый редкий случай и возникает только при наличии той же строки
Рассмотрим, например, две строки ниже (y = 2x + 1 и 2y = 4x + 2). Эти два уравнения на самом деле представляют собой одну и ту же прямую.
Пример системы с бесконечными решениями:
- Строка 1: y = 2x + 1
- Строка 2: 2y = 4x + 2
Как мы можем найти решения систем уравнений?
Чтобы найти решение системы линейных уравнений, вы можете использовать любой из следующих методов:
- Решить с помощью графика
- Решить путем исключения
- Решить путем замены
- Интерактивная система линейных уравнений
Видео
по решениям систем уравнений
8 Лучший бесплатный калькулятор системы линейных уравнений для Windows
Вот список лучших бесплатных калькуляторов системы линейных уравнений для Windows .
Эти бесплатные калькуляторы предоставляют вам возможность решать систему линейных уравнений. В то время как некоторые из этих калькуляторов могут решать системы линейных уравнений с тремя переменными, некоторые могут решать линейные уравнения с двумя переменными. Некоторые из этих бесплатных калькуляторов в списке могут вычислять линейные уравнения только с одной переменной.
В этом обзоре вы также найдете программное обеспечение, которое решает линейные уравнения и представляет решение в виде пошагового метода и озвучивает каждый шаг. Это дает вам лучшее понимание каждого шага.
Если вы ищете калькулятор линейных уравнений, который может построить график, то такой тип программного обеспечения также добавлен в список.
Моя любимая система калькулятора линейных уравнений:
Я выберу Universal Algebra Solver . Это единственный калькулятор в этом списке, который дает пошаговое решение введенной задачи. Кроме того, он проговаривает каждый шаг.
Более того, вы можете использовать его для решения как для x, так и для y.
Вам также могут понравиться некоторые из лучших бесплатных калькуляторов геометрии, конвертеров единиц измерения и научных калькуляторов для Windows.
Универсальный алгебраический решатель
Универсальный алгебраический решатель — единственный калькулятор линейных уравнений в этом списке, который показывает пошаговое решение с моделированием введенной алгебраической задачи. С помощью этого расширенного калькулятора вы можете научиться решать математическую задачу, так как он озвучивает каждый шаг, как это делает программа для преобразования текста в речь . Эта функция Universal Algebra Solver выделяет его среди других калькуляторов в этом списке.
Чтобы решить уравнение, просто введите его в исходной форме, например AX + B = C (линейное уравнение с одной переменной) и нажмите Введите кнопку . Вы также можете нажать зеленую кнопку на его интерфейсе, чтобы решить уравнение.
Если вы вводите линейное уравнение с более чем одной переменной, вам будет предложено указать переменную, для которой вы хотите решить уравнение. Например, в уравнении 3x + 4y – 6z = 0 вас просят найти x, y или z. Вы можете выбрать любую из этих или все эти опции.
Он также предоставляет вам возможность сохранить решение в формате PDF.
Доступен как в бесплатной, так и в платной версиях. Его бесплатная версия позволяет решать только алгебраические уравнения. Для более продвинутых функций, таких как Упрощение, Тригонометрия, Промежуточные графы, Комплексные числа, Неравенства, Дифференциация и т. д., вы должны приобрести его полную версию.
Домашняя страница
Страница загрузки
Два уравнения — два неизвестных
Два уравнения — два неизвестных — бесплатная система для калькулятора линейных уравнений для Windows. Это калькулятор линейных уравнений, который позволяет вам решить для x и для y. Он подходит для решения линейного уравнения с двумя переменными.
Два линейных уравнения, отображаемые в интерфейсе, имеют следующий формат: ax + by = c и dx + ey = f. Здесь a, b, c, d, e и f — постоянные члены линейных уравнений с двумя переменными. Чтобы найти x и y, вы должны ввести значение этих констант в предоставленное место. Когда вы закончите, нажмите кнопку Решить , и вы сразу же получите свое решение.
Существует множество методов решения линейных уравнений с двумя переменными. Этот решатель линейных уравнений следует Правило Крамера для решения линейных уравнений.
Самое приятное в этом бесплатном калькуляторе то, что он строит график X и Y двумя разными цветами для каждой введенной задачи.
Домашняя страница
Страница загрузки
Ro3n
Ro3n — еще одна бесплатная система решения линейных уравнений с тремя неизвестными. По умолчанию он настроен на решение линейных уравнений с тремя переменными. Вы также можете использовать его для решения линейных уравнений с 2 переменными.
Вместо коэффициентов переменных предоставляются пустые поля. Вы должны поместить значения коэффициентов в эти пустые поля, чтобы решить линейное уравнение. После ввода значений всех коэффициентов нажмите кнопку Решить и сразу получите решение.
Используется матричный метод для решения системы линейных уравнений. Наряду с отдельными значениями x, y и z он также отображает главный определитель, 1-й определитель, 2-й определитель и 3-й определитель полученной таким образом матрицы.
Отображает значения определителя только для линейных уравнений с тремя переменными. Для системы линейных уравнений с двумя переменными отображается только конечный результат.
Дополнительные возможности этого бесплатного калькулятора линейных уравнений:
- Он предназначен для решения как линейных, так и квадратных уравнений.
- Вы можете экспортировать результат как в формате HTML, так и в формате TXT.
- Поддерживает более 5 языков, в том числе: английский, словацкий, немецкий , французский и т.
д. - Он поставляется с 5 привлекательными оболочками: Windows Style, Windows XP Style, Motif Style, CDE Style, и Plastique Style .
д.Домашняя страница
Страница загрузки
Calculatormatik
Calculatormatik — это еще одна система калькулятора линейных уравнений.
Предназначен для решения линейных уравнений с тремя переменными. Вам просто нужно ввести значения коэффициентов x, y и z, чтобы найти значения всех этих переменных.
Calculatormatik — это расширенный калькулятор в этом списке. Он поставляется с множеством встроенных калькуляторов, которые вам нужны в ваших ежедневных исследованиях. Помимо калькуляторов, вы также найдете в нем несколько конвертеров единиц измерения. Ниже я перечислил названия некоторых из этих калькуляторов и конвертеров единиц измерения:
- Калькуляторы : калькулятор LCM, калькулятор квадратных уравнений, калькулятор дня рождения, калькулятор ИМТ, калькулятор простых множителей, калькулятор сложных процентов, калькулятор простых процентов, прибыль Калькулятор, калькулятор объема, калькулятор расхода воды и т. д.
- Преобразователи единиц измерения : преобразователь байтов, преобразователь плотности, преобразователь электрических конденсаторов, преобразователь энергии в мощность, преобразователь расхода, преобразователь Hex в ASCII, преобразователь температуры и т. д.
д.Домашняя страница
Страница загрузки
Решатель системы линейных уравнений
Решатель системы линейных уравнений — еще одна бесплатная система калькулятора линейных уравнений. Он позволяет вычислять линейные уравнения с тремя переменными. Это программа на основе JAVA, для работы которой на ПК требуется JAVA.
Вам не нужно устанавливать это программное обеспечение на свой компьютер, так как это портативное программное обеспечение. Просто щелкните его исполняемый файл и нажмите кнопку Enter .
На его интерфейсе предусмотрено три пустых места для ввода трех линейных уравнений по отдельности. Вы должны ввести полные линейные уравнения в каждое из этих пустых мест.
Когда вы закончите, нажмите кнопку Решить и получите немедленное решение.
Домашняя страница
Страница загрузки
Math Hub Basic
Math Hub Basic — это бесплатное приложение для Windows 10 для решения линейных уравнений с одной переменной. Следовательно, вы можете решить для X только с помощью этого бесплатного программного обеспечения.
Показывает формат линейного уравнения с одной переменной: AX + B = C. Здесь A, B и C — константы. Вы должны ввести значения этих постоянных членов, и приложение решит линейное уравнение для X. На самом деле это пошаговое решение математических задач. Следовательно, вы можете научиться правильно решать систему линейных уравнений с одной переменной.
Помимо калькулятора линейных уравнений, в нем есть еще три калькулятора, которые будут вам полезны. К этим трем калькуляторам относятся Калькулятор квадратных уравнений, Калькулятор биквадратных уравнений и Калькулятор логарифмов. Все эти три калькулятора также дают пошаговое решение введенной математической задачи.
Домашняя страница
Страница загрузки
Физический калькулятор A-Level
Физический калькулятор A-Level — очень хороший физический калькулятор, предназначенный для выполнения некоторых алгебраических вычислений.
Это приложение для Windows 10 позволяет решить систему линейных уравнений с двумя переменными. Вам просто нужно ввести значения коэффициентов в пустые поля, и он автоматически отобразит результат. Он решает линейное уравнение как для x, так и для y, т. е. вы получите значения обеих переменных линейных уравнений одновременно.
Помимо калькулятора линейных уравнений, в нем есть несколько других калькуляторов, в том числе: Калькулятор квадратных уравнений, Калькулятор движения СУВАТ, Калькулятор движения снаряда и т. д.
Домашняя страница
Страница загрузки
Математические инструменты
Математические инструменты — еще одно бесплатное приложение для расчета линейных уравнений для Windows 10.
Это очень простое приложение, которое позволяет вычислять только линейное уравнение с одной переменной. Другими словами, с помощью этой программы вы можете решить только x.
Чтобы получить решение линейного уравнения с одной переменной, достаточно ввести значения его коэффициентов.
Преимущества этого бесплатного калькулятора линейных уравнений:
- Позволяет вычислять корни квадратного уравнения.
- Он также содержит некоторые математические формулы, такие как тригонометрические отношения, логарифмы, экспоненты и радикалы, геометрические формулы и т. д.
- Он имеет встроенный калькулятор, который имеет некоторые расширенные функции, такие как Тригонометрические вычисления, преобразование радиан в градусы и наоборот, логарифм, факториал, n-я степень числа и т. д.
Единственный недостаток, который я обнаружил в этом калькуляторе, это то, что он не предназначен для решения линейных уравнений с более чем одной переменной.