Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
Поиск по сайту:
| Справочник по математике | Геометрия (Планиметрия) | Параллельность прямых |
При пересечении двух прямых третьей прямой образуются углы, названия которых приведены в следующей таблице.
Углы, образующиеся при пересечении двух прямых третьей прямой
| Рисунок | Определение углов |
| Внутренние накрест лежащие углы | |
| Внешние накрест лежащие углы | |
| Соответственные углы | |
| Внутренние односторонние углы | |
| Внешние односторонние углы | |
| Внутренние накрест лежащие углы |
| Внешние накрест лежащие углы |
| Соответственные углы |
| Внутренние односторонние углы |
| Внешние односторонние углы |
Перечисленные в таблице углы используются в формулировках признаков параллельности двух прямых.
Определение. Две прямые на плоскости называются параллельными, если они не имеют общих точек.
Замечание. Два отрезка называются параллельными, если они лежат на параллельных прямых.
Признаки параллельности двух прямых
| Рисунок | Признак параллельности |
| Прямые параллельны тогда и только тогда, когда внутренние накрест лежащие углы равны | |
| Прямые параллельны тогда и только тогда, когда внешние накрест лежащие углы равны | |
| Прямые параллельны тогда и только тогда, когда соответственные углы равны | |
| Прямые параллельны тогда и только тогда, когда сумма внутренних односторонних углов равна180° | |
| Прямые параллельны тогда и только тогда, когда сумма внешних односторонних углов равна 180° | |
Признак параллельности: Прямые параллельны тогда и только тогда, |
Признак параллельности: Прямые параллельны тогда и только тогда, |
Признак параллельности: Прямые параллельны тогда и только тогда, |
Признак параллельности: Прямые параллельны тогда и только тогда, когда сумма внутренних односторонних углов равна 180° |
Признак параллельности: Прямые параллельны тогда и только тогда, когда сумма внешних односторонних углов равна 180° |
Следствие
| Рисунок | Признак параллельности |
| Две прямые, перпендикулярные к третьей прямой, параллельны |
Признак параллельности: Две прямые, перпендикулярные к третьей прямой, параллельны |
Переход свойства параллельности прямых
| Рисунок | Признак параллельности |
| Если прямая a параллельна прямой b, а прямая b параллельна прямой c, то прямая a параллельна прямой c |
Признак параллельности: Если прямая a параллельна прямой b, |
Задача.
Доказать, что биссектрисы внутренних односторонних углов, полученных при пересечении двух параллельных прямых третьей прямой, перпендикулярны.
Решение. Решение этой задачи почти дословно совпадает с решением задачи из раздела нашего справочника «Углы на плоскости» и предоставляется читателю в качестве несложного самостоятельного упражнения.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
| До ЕГЭ по математике осталось | |||
| дней | часов | минут | секунд |
|
Самаров7 класс. Геометрия. Атанасян. Учебник. Ответы к стр. 66
Параллельные прямые
Аксиома параллельных прямых
Об аксиомах геометрии. Аксиома параллельных прямых. Теоремы об углах, образованных двумя параллельными прямыми и секущей. Углы с соответственно параллельными или перпендикулярным сторонами
Ответы к стр. 66
Задачи
208. Разность двух односторонних углов при пересечении двух параллельных прямых секущей равна 50°. Найдите эти углы.
Д а н о
α||b
c — секущая
∠1 — ∠2 = 50°
Н а й т и
∠1 — ?
∠2 — ?
Р е ш е н и е
Так как ∠1 и ∠2 — односторонние при α||b и секущей с, то ∠1 + ∠2 = 180°. ∠1 — ∠2 = 50° ⇒ ∠1 = 50° + ∠2. Тогда ∠1 + ∠2 = 50° + ∠2 + ∠2 = 180° или 2∠2 = 130° или ∠2 = 65°, а ∠1 = 50° + ∠2 = 50° + 65° = 115°.
О т в е т: ∠1 = 115°, ∠2 = 65°.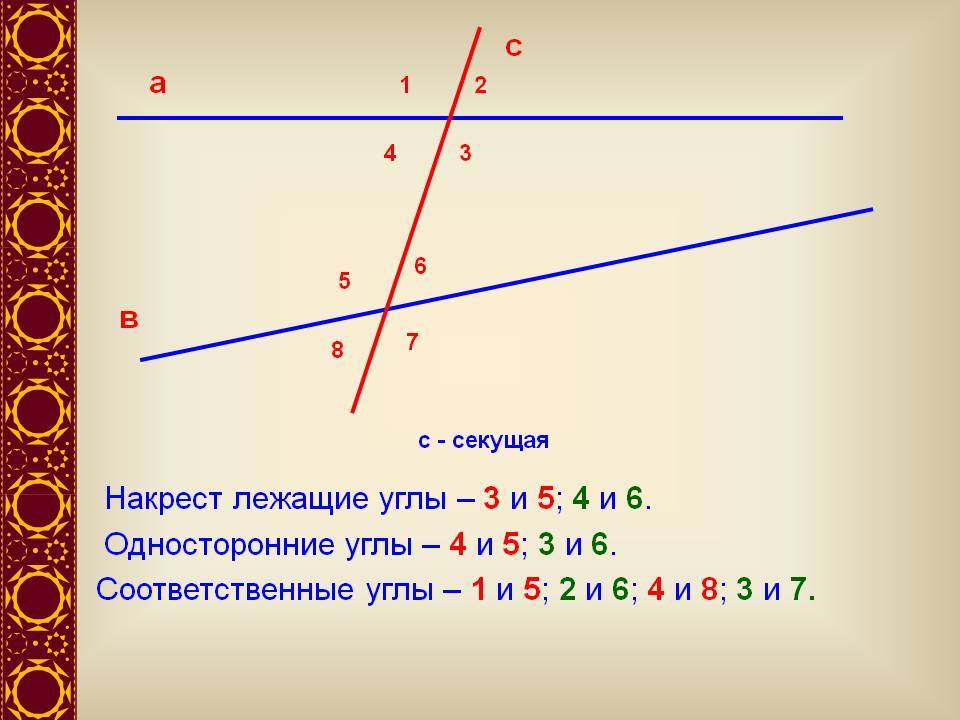
209. На рисунке 120 α||b, c||d, ∠4 = 45°. Найдите углы 1, 2 и 3.
Д а н о
α||b
c||d
∠4 = 45°
Н а й т и
∠1 — ?
∠2 — ?
∠3 — ?
Р е ш е н и е
∠4 и ∠2 — соответственные углы при α||b и секущей d, значит ∠4 = ∠2 = 45°. ∠3 и ∠4 — смежные, значит ∠3 + ∠4 = 180° ⇒ ∠3 = 180° — ∠4 = 180° — 45° = 135°. ∠1 и ∠3 — внутренние накрест лежащие углы при c||d и секущей α, значит ∠1 = ∠3 = 135°.
О т в е т: ∠1 = 135°, ∠2 = 45°, ∠3 = 135°.
210. Два тела Р1 и Р2 подвешены на концах нити, перекинутой через блоки А и В (рис. 121). Третье тело Р3 подвешено на той же нити в точке С и уравновешивает тела Р1 и Р2. (При этом АР1||BР2||СР3.
) Докажите, что ∠ACB = ∠CAP1 + ∠CBP2.
Д а н о
Рисунок
АР1||BР2||СР3
Д о к а з а т ь
∠ACB = ∠CAP1 + ∠CBP2
Д о к а з а т е л ь с и в о
Дополнительное построение: луч СD. ∠ACB = ∠ACD + ∠DCB. ∠CAP1 и ∠ACD — внутренние накрест лежащие углы при АР1||СР3 и секущей АС, значит ∠CAP1 = ∠ACD. ∠CBP2 и ∠DCB — внутренние накрест лежащие углы при СР3||ВР2 и секущей СВ, значит ∠CBP2 = ∠DCB. Тогда ∠ACB = ∠ACD + ∠DCB = ∠CAP1 + ∠CBP2.
О т в е т: ∠ACB = ∠CAP1 + ∠CBP2.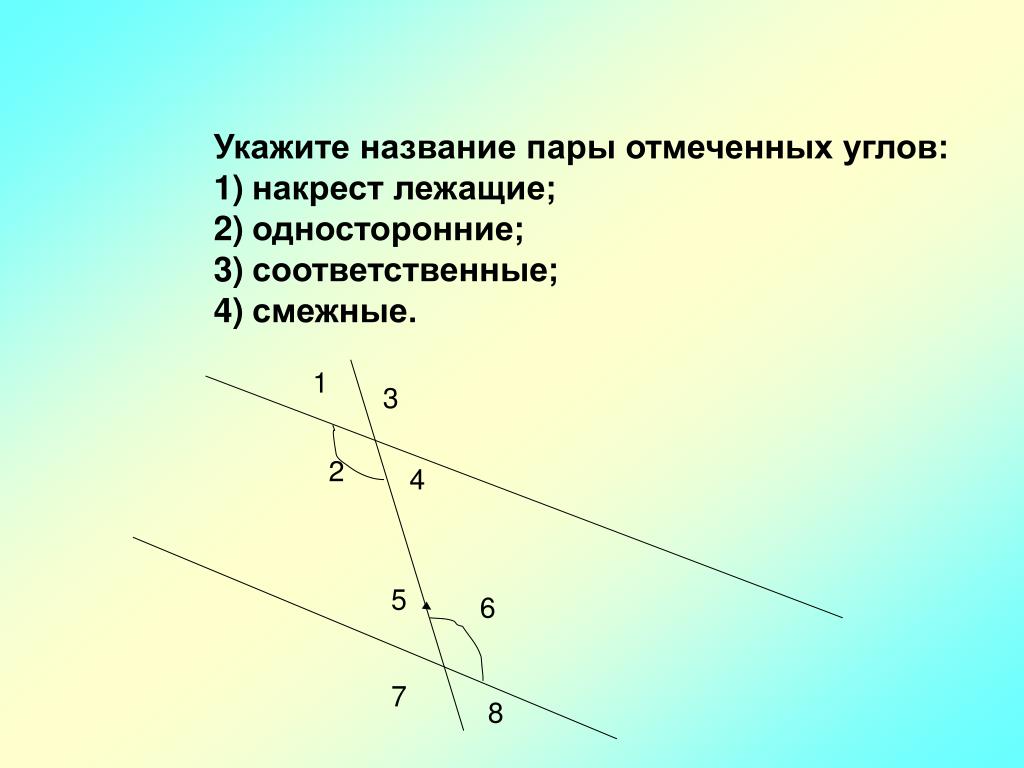
211. Две параллельные прямые пересечены секущей. Докажите, что: а) биссектрисы накрест лежащих углов параллельны; б) биссектрисы односторонних углов перпендикулярны.
Д а н о
α||b
с — секущая
Д о к а з а т ь
а) KF||CL
б) KF⏊CK
Д о к а з а т е л ь с и в о
а) ∠ACF и ∠CFE — внутренние накрест лежащие углы при α||b и секущей c, значит ∠ACF = ∠CFE. ∠ACF = ∠1 + ∠2, ∠1 = ∠2, так как CL — биссектриса ∠ACF. ∠CFE = ∠3 + ∠4, ∠3 = ∠4, так как KF — биссектриса ∠CFE. Следовательно, ∠1 = ∠2 = ∠3 = ∠4. ∠3 и ∠1 — внутренние накрест лежащие углы при KF и CL и секущей CF, ∠3 = ∠1, значит KF||CL.
б) ∠ACF и ∠DFC — внутренние односторонние углы при α||b и секущей c, значит ∠ACF + ∠DFC = 180°.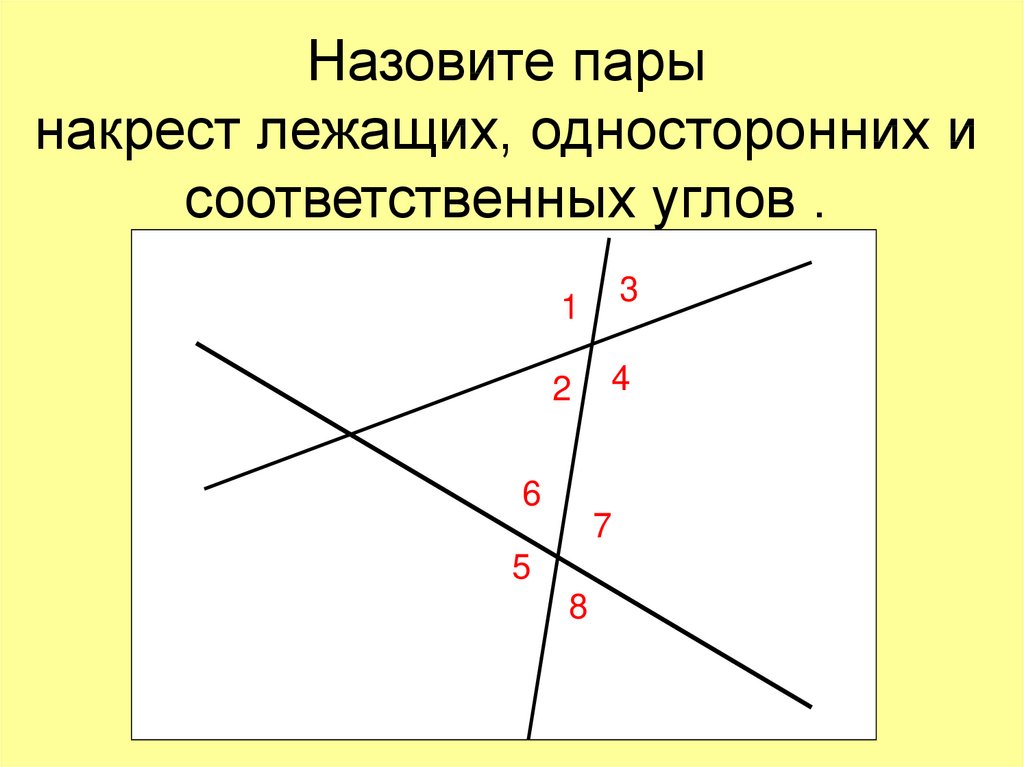
∠ACF = ∠1 + ∠2, ∠1 = ∠2, так как CK — биссектриса ∠ACF. ∠DFC = ∠3 + ∠4, ∠3 = ∠4, так как KF — биссектриса ∠DFC. Рассмотрим ΔCFK: ∠KCF + ∠CFK + ∠FKC = ∠1 + ∠3 + ∠FKC = 180°. ∠1 + ∠3 = 1/2 ∠ACF + 1/2 ∠DFC = 1/2(∠ACF + ∠DFC) = 1/2•180° = 90°. Тогда ∠1 + ∠3 + ∠FKC = 90° + ∠FKC = 180° ⇒ ∠FKC = 180° — 90° = 90°. Так как ∠FKC = 90°, то KF⏊CK.
О т в е т: а) KF||CL, б) KF⏊CK
212. Прямые, содержащие высоты АА1 и ВВ1 треугольника АВС, пересекаются в точке Н, угол В — тупой, ∠С = 20°. Найдите угол АНВ.
Д а н о
ΔAВС
АА1, ВВ1 — высота
АА1 ∩ ВВ1 в т.
Н
∠С = 20°
∠В — тупой
Н а й т и
∠АНВ
Р е ш е н и е
Рассмотри ΔВВ1С: ∠ВВ1С = 90°, так как ВВ1 — высота к АС. Тогда ∠ВВ1С + ∠В1СВ + ∠СВВ1 = 180° ⇒ ∠СВВ1 = 180° — ∠ВВ1С — ∠В1СВ = 180° — 90° — 20° = 70°.
Рассмотрим ΔНВА1: ∠НА1В = 90°, так как АА1 — высота к ВС. ∠НВА1 = ∠СВВ1 = 70° — так как вертикальные. ∠АНВ = А1НВ. Тогда ∠НВА1 + ∠ВА1Н + ∠А1НВ = 180° ⇒ ∠А1НВ = 180° — ∠НВА1 — ∠НА1В = 180° — 70° — 90° = 20°.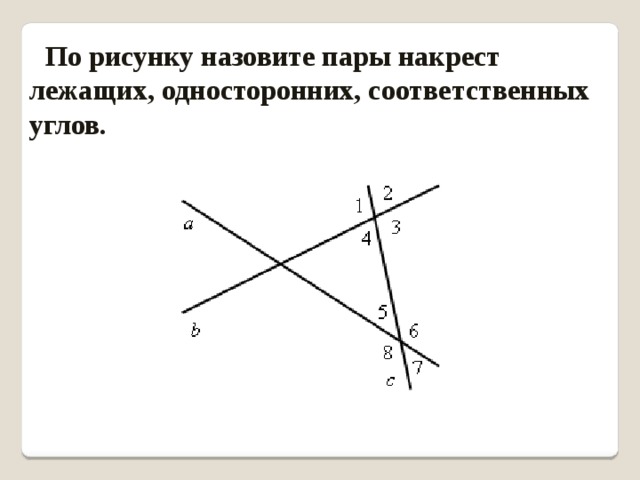
О т в е т: ∠АНВ = 20°.
Вопросы для повторения к главе III
1. Дайте определение параллельных прямых. Какие два отрезка называются параллельными?
Две прямые на плоскости называются параллельными, если они не пересекаются. Два отрезка называются параллельными, если они лежат на параллельных прямых.
2. Что такое секущая по отношению к двум прямым? Назовите пары углов, которые образуются при пересечении двух прямых секущей.
Прямая с называется секущей по отношению к прямым α и b, если она пересекает их в двух точках.
Внутренние накрест лежащие углы: 3 и 6, 4 и 5 — попарно равны.
Внешние накрест лежащие углы: 1 и 8, 2 и 7 — попарно равны.
Внутренние односторонние углы: 4 и 6, 3 и 5 — их сумма 180°.
Внешние односторонние углы: 1 и 7, 2 и 8 — их сумма 180°.
Соответственные углы: 1 и 5, 2 и 6, 3 и 7, 4 и 8 — попарно равны.
3. Докажите, что если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
Д а н о
с ∩ α, с ∩ b
∠1 = ∠2
Д о к а з а т ь
α||b
Д о к а з а т е л ь с и в о
Из середины О отрезка АВ проведём перпендикуляр ОН к прямой α. На прямой b от точки В отложим отрезок ВН1, равный отрезку АН и проведём отрезок ОН1. Треугольники ОНА и ОН1В равны по двум сторонам и углу между ними (АО = ВО, АН = ВН1, ∠1 = ∠2), поэтому ∠3 = ∠4 и ∠5 = ∠6. Из равенства ∠3 = ∠4 следует, что точка Н1 лежит на продолжении луча ОН, то есть точки Н, О и Н1 лежат на одной прямой, а из равенства ∠5 = ∠6 следует, что угол 6 — прямой (так как угол 5 — прямой). Итак, прямые α и b перпендикулярны к прямой НН1, поэтому они параллельны.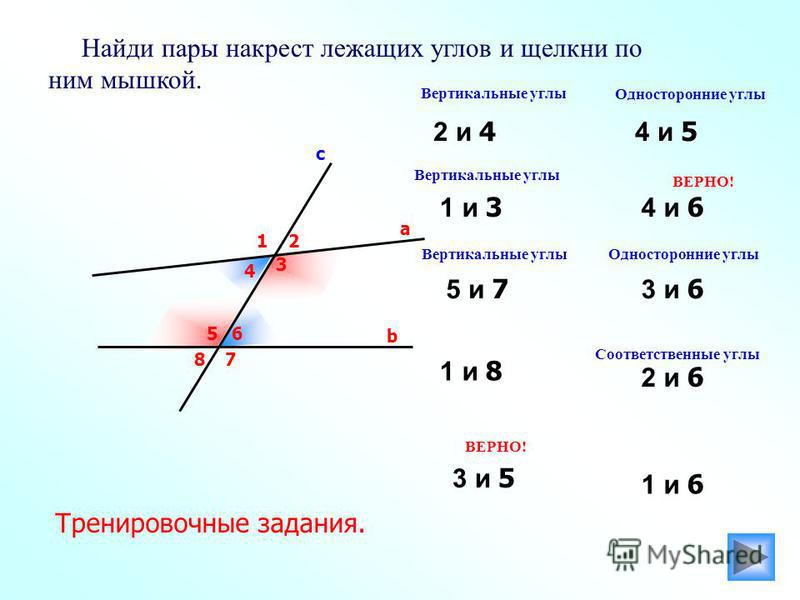
О т в е т: α||b.
4. Докажите, что если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
Д а н о
с ∩ α, с ∩ b
∠1 = ∠2
Д о к а з а т ь
α||b
Д о к а з а т е л ь с и в о
Так как углы 2 и 3 — вертикальные, то ∠2 = ∠3. Из этих двух равенств следует, что ∠1 = ∠3. Но углы 1 и 3 — накрест лежащие, поэтому прямые α и b параллельны.
О т в е т: α||b.
5. Докажите, что если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.
Д а н о
с ∩ α, с ∩ b
∠1 + ∠4 = 180°
Д о к а з а т ь
α||b
Д о к а з а т е л ь с и в о
Так как углы 3 и 4 — смежные, то ∠3 + ∠4 = 180°. Из этих двух равенств следует, что накрест лежащие углы 1 и 3 равны, поэтому прямые α и b параллельны.
О т в е т: α||b.
6. Расскажите о практических способах проведения параллельных прямых.
На практике параллельные прямые проводят с помощью: чертёжного угольника и линейки, рейсшины (в чертёжной практике), малки (две деревянные планки, скреплённые шарниром) при столярных работах.
7. Объясните, какие утверждения называются аксиомами. Приведите примеры аксиом.
Аксиомы — утверждения о свойствах геометрических фигур, принимаемые в качестве исходных положений, на основе которых доказываются далее теоремы и вообще строится вся геометрия.
Через любые две точки проходит прямая, и притом только одна.
На любом луче от его начала можно отложить отрезок, равный данному, и притом только один.
8. Докажите, что через данную точку, не лежащую на данной прямой, проходит прямая, параллельная данной.
Утверждение о единственности прямой, проходящей через данную точку параллельно данной прямой, не может быть доказано на основе остальных аксиом и само является аксиомой.
9. Сформулируйте аксиому параллельных прямых.
Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
10. Какое утверждение называется следствием? Докажите, что прямая, пересекающая одну из двух параллельных прямых, пересекает и другую.
Следствия — утверждения, которые выводятся непосредственно из аксиом или теорем.
Пусть прямые α и b параллельны и прямая с пересекает прямую α в точке М. Если бы прямая с не пересекала прямую b, то через точку М проходили бы две прямые (прямые α и с), параллельные прямой b. Но это противоречит аксиоме параллельных прямых, и, значит, прямая с пересекает прямую b.
ГДЗ. Ответы по геометрии. 7 класс. Учебник. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И.
Геометрия. 7 класс
Соответствующие углы – объяснение и примеры
Прежде чем перейти к теме соответствующих углов, давайте сначала напомним себе об углах, параллельных и непараллельных прямых и поперечных линиях.
В геометрии угол состоит из трех частей: вершины и двух сторон или сторон. Вершина угла находится там, где встречаются две стороны или линии угла, а стороны угла — это просто стороны угла.
Параллельные линии — это две или более линий на двумерной плоскости, которые никогда не встречаются и не пересекаются. С другой стороны, непараллельные прямые — это две или более пересекающихся прямых. Поперечная линия – это линия, пересекающая или проходящая через две другие прямые. Поперечная линия может проходить через две параллельные или непараллельные прямые.
Что такое соответствующий угол?
Углы, образованные при пересечении поперечной линией двух прямых, называются соответственными углами . Соответствующие углы расположены в одном и том же взаимном положении, на пересечении поперечной и двух или более прямых.
Правило соответствующих углов или соответствующих углов постулирует, что соответствующие углы равны, если секущей пересекаются две параллельные прямые.
Соответственные углы равны, если поперечная прямая пересекает не менее двух параллельных прямых.
На приведенной ниже диаграмме показаны соответствующие углы, образованные при пересечении поперечной линией двух параллельных прямых:
На приведенной выше диаграмме пара соответствующих углов:
- < a и < e
- < b и < g
- < d и < f
- < c и < h
1
На рисунке выше две параллельные линии.
Нам нужно это доказать.
Имеем прямые углы:
Из транзитивности,
Из теоремы о альтернативных углах,
Используя подстановку, имеем,
Следовательно,
Соответствующие углы, образованные непараллельными прямыми
9000 образуется при пересечении поперечной линией хотя бы двух непараллельных прямых, которые не равны между собой и фактически не имеют между собой никакого отношения.Иллюстрация:
Соответствующий внутренний угол
Пара соответствующих углов состоит из одного внутреннего и другого внешнего угла. Внутренние углы — это углы, расположенные в углах пересечений.
Соответствующий внешний угол
Углы, образованные вне пересекающихся параллельных прямых. Внешний угол и внутренний угол составляют пару соответствующих углов.
Иллюстрация:
Внутренние уголки включают; b, c, e и f, а внешние углы включают; а, г, г и з.
Следовательно, пары соответствующих углов включают:
- < a и < e.
- < b и < g
- < d и < f
- < c и < h
О соответствующих углах можно сделать следующие выводы:
- Пара соответствующих углов лежит по одну сторону поперечный.
- Соответствующая пара углов состоит из одного внешнего угла и другого внутреннего угла.
- Не все соответствующие углы равны.
Соответственные углы равны, если секущая пересекает две параллельные прямые. Если секущая пересекает непараллельные прямые, то образующиеся соответствующие углы не равны и никак не связаны. - Соответствующие углы образуют дополнительные углы, если секущая перпендикулярно пересекает две параллельные прямые.
- Внешние углы по одну сторону от секущей являются дополнительными, если прямые параллельны. Точно так же внутренние углы являются дополнительными, если две прямые параллельны.
Как найти соответствующие углы?
Один из способов решения соответственных углов — нарисовать букву F на данной диаграмме. Расположите букву лицом в любом направлении и соотнесите углы соответственно.
Пример 1
Учитывая ∠d = 30°, найдите недостающие углы на диаграмме ниже.
Раствор
Указано, что тий D = 30 °
тий D = ♂ B (вертикально противоположные углы)
Следовательно, ♂ B = 30 °
, ▲ B = 30 °
, ♂ B = 30 °
400024. Тий G = 30 ° (соответствующие углы)
Теперь, тий D = ♂ F (Соответствующие углы)
Следовательно, тий F = 30 °
♂ B + ° A = 180 ° (180 ° (180 ° (180 ° (180 ° ( дополнительные углы)
∠ a + 30° = 180°
∠ a = 150°
∠ a = ∠ e = (corresponding angles)
Therefore, ∠e = 150°
∠ d = ∠ h = 30° (соответствующие углы)
Пример 2
Два соответствующих угла фигуры равны 9x + 10 и 55. Найдите значение x.
Решение
Два соответствующих угла всегда равны.
Следовательно,
9x + 10 = 55
9x = 55 — 10
9x = 45
x = 5
Пример 3
Два соответствующих угла показателя показателя рисунка 7y — 12 и 5y + 6. Найдите модуль соответствующего угла.
Решение
Сначала нам нужно определить значение y.
Два соответствующих угла всегда равны.
Следовательно,
7у – 12 = 5у + 6
7у – 5у = 12 + 6
2y = 18
y = 9
Величина соответствующего угла,
5y + 6 = 5 (9) + 6 = 51
Применение соответствующих углов игнорировать. Соблюдайте их, если у вас когда-нибудь будет шанс.
- Обычно окна имеют горизонтальные и вертикальные решетки, образующие несколько квадратов. Каждая вершина квадрата образует соответствующие углы.
- Мост стоит на столбах. Все столбы соединены таким образом, что соответствующие углы равны.
- Железнодорожные пути спроектированы так, что все соответствующие углы на пути равны.
Типы взаимосвязей углов | Соответствующий, альтернативный интерьер и другое
Содержание
[скрыть][показать]- Типы углов
- Имена углов
- Угловые отношения
- Равные углы
- Смежные углы
- Вертикальные углы
- Соответствующие углы
- Наружные углы
- Внутренние уголки
- Примеры соотношения углов
Типы углов
Изучая геометрию, вы узнали, что у вас есть острые, прямые и тупые углы. Возможно, вы даже узнали о прямых и рефлекторных углах, но если вы хотите узнать еще больше, вы можете исследовать многие другие виды углов, такие как внешние и внутренние углы. Вы также можете узнать о конгруэнтных, смежных, вертикальных, соответствующих и переменных углах.
Различные типы углов
Прежде чем углубиться, давайте наметим различные углы, которые мы можем изучать:
- Конгруэнтные углы
- Смежные углы
- Вертикальные уголки
- Соответствующие углы
- Наружные углы
- Последовательные внешние углы
- Альтернативные внешние углы
- Последовательные внутренние углы
- Альтернативные внутренние углы
Отношения углов
Помимо измерения градусов или радиан, вы также можете сравнивать углы и учитывать их отношения к другим углам. Мы говорим об отношениях углов, потому что мы сравниваем положение, измерение и конгруэнтность между двумя или более углами.
Например, при пересечении двух линий или отрезков они образуют две пары вертикальных углов. Когда две параллельные прямые пересекаются секущей, образуются сложные отношения углов, такие как чередующиеся внутренние углы, соответствующие углы и т. Д.
Умение определять взаимосвязь углов и уверенно находить конгруэнтные углы при пересечении линий поможет вам лучше изучить геометрию. Вы будете решать сложные задачи быстрее, когда будете досконально знакомы со всеми типами взаимосвязей углов.
Конгруэнтные углы
Любые два угла, независимо от их ориентации, которые имеют одинаковую меру (в радианах или градусах), конгруэнтны . Они показывают одинаковую «открытость» между двумя лучами, отрезками или линиями, которые их образуют. Таким образом, эти два угла в 35° конгруэнтны, даже если они представлены не одинаково и образованы разными конструкциями:
Смежные углы
Когда две прямые пересекаются, они образуют четыре угла. Любые два угла, имеющие общий луч, отрезок или прямую, являются
- Вы нашли ∠JYO рядом с ∠OYC?
- Как насчет ∠OYC рядом с ∠KYC?
- Вы видели ∠KYC рядом с ∠KYJ, верно?
- И вы наверняка нашли ∠KYJ рядом с ∠JYO!
Вертикальные углы
На том же рисунке выше углы, которые пропускают угол, то есть углы, которые не касаются друг друга, кроме своей вершины, являются вертикальными углами . Здесь слово «вертикальный» означает «относящийся к вершине», а не «вверх и вниз». Вертикальные углы являются противоположными углами; они разделяют только свою точку вершины.
Две пересекающиеся линии образуют две пары вертикальных углов. Посмотрите, сможете ли вы найти их на нашем рисунке.
- Вы нашли пару ∠JYO и ∠KYC? Они соприкасаются только в точке Y .
- Вы обнаружили, что ∠KYJ и ∠OYC составили другую пару? Они также соприкасаются только в точке Y .
Вы можете удивиться, почему смежные углы не являются также и вертикальными углами, ведь они тоже имеют общую вершину. Смежные углы имеют больше общего, чем вершина; они имеют общую сторону с углом.
Соответствующие углы
Каждый раз, когда секущая пересекает две другие прямые, мы получаем соответствующие углы. Чем более ограниченными становятся наши пересекающиеся линии, тем более ограниченными являются их угловые отношения. Когда линия пересекает две параллельные линии (поперечную), открывается совершенно новый уровень угловых отношений:
Мы можем ловко вытянуть из этой фигуры углы, похожие друг на друга. Углы, которые имеют одинаковое положение относительно друг друга в двух наборах из четырех углов (четыре вверху, линия AR; четыре внизу, линия TO), являются соответствующими углами. Когда соответствующие углы лежат на параллельных прямых, они равны.
Наши поперечные и параллельные линии образуют четыре пары соответствующих углов. Можете назвать их всех?
- Вы нашли, что ∠AYD соответствует ∠TLY?
- Как насчет того, чтобы ∠DYR соответствовал &∠YLO?
- Вы нашли, что ∠RYL соответствует ∠OLI, верно?
- И вы не забыли, что ∠AYL соответствует ∠TLI, не так ли?
Во всех случаях, поскольку наши прямые AR и TO параллельны, их соответствующие углы равны.
Внешние углы
Те же самые параллельные линии и их поперечные образуют внешние углы. Внешний угол среди линейных построений (не многоугольников) — это угол, лежащий вне параллельных прямых. Вы можете увидеть два типа взаимосвязей внешних углов:
Последовательные внешние углы
Когда внешние углы находятся на одной стороне поперечной, они являются последовательными внешними углами, и дополнительными (прибавляющими к 180°). На нашем рисунке выше ∠AYD и ∠TLI — последовательные внешние углы. Единственная другая пара последовательных внешних углов — это …
Вы сказали ∠DYR и ∠OLI? Мы надеемся на это, потому что это правильно!
Уголки внешние альтернативные
Уголки внешние альтернативные подобны углам при вершине тем, что они являются противоположными углами (по обе стороны от поперечной). Альтернативные внешние углы находятся на противоположных сторонах поперечной (это альтернативная часть) и вне параллельных прямых (это внешняя часть). Сможете ли вы найти на нашем рисунке две пары альтернативных внешних углов?
Вы записали ∠AYD и ∠OLI, а потом, несомненно, написали ∠DYR в паре с ∠TLI!
Конгруэнтные альтернативные внешние углы используются для доказательства того, что прямые параллельны, с использованием (подходящей) теоремы о альтернативных внешних углах.
Внутренние углы
Углы между границами двух параллельных прямых составляют внутренних углов , опять же созданных секущей. Как и в случае с внешними углами, у нас могут быть последовательные внутренние углы и чередующиеся внутренние углы.
Последовательные внутренние углы
Внутренние углы по одну сторону от секущей составляют последовательных внутренних углов . На нашем рисунке вы можете найти две пары? Вы нашли пару ∠RYL с ∠YLO? Вы видели, что ∠AYL объединился с ∠TLY?
В параллельных прямых последовательные внутренние углы являются дополнительными.
Чередующиеся внутренние углы
Когда внутренние углы находятся на противоположных сторонах секущей, они являются чередующимися внутренними углами . Они поддаются теореме о чередующихся внутренних углах, которая утверждает, что конгруэнтные чередующиеся внутренние углы доказывают параллельность прямых (так же, как это сделала теорема о чередующихся внешних углах).
На нашем рисунке ∠ALY — альтернативный внутренний угол для ∠YLO, делающий их конгруэнтными. И, конечно же, ∠RYL представляет собой альтернативный внутренний угол ∠TLY.
Примеры соотношения углов
Вы можете использовать свои новые знания об отношениях углов для решения алгебраических задач, связанных с геометрическими фигурами. При просмотре любой новой фигуры просмотрите свой список и определите три вещи:
- Относительное положение двух рассматриваемых углов
- Находятся ли углы вне параллельных прямых (внешние) или внутри параллельных прямых (внутренние)
- Находятся ли два исследуемых угла на одной стороне поперечной (последовательные) или на противоположных сторонах поперечной (альтернативные)
Как только вы поймете взаимосвязь между двумя углами, вы сможете предположить некоторые основные факты, такие как их совпадение или то, что они могут быть дополнительными.
Вы можете использовать это знание для решения, казалось бы, сложных алгебраических задач, таких как:
[вставьте параллельные линии MJ и TE и поперечные AS с пересечением точки C на линии MJ и точкой пересечения с точкой I на линии TE, написав по кругу ВЕЛИКИЙ; пусть ∠MCA = 123°]
По фигуре найдите значение x, если ∠MCA = 4x + 3°, а ∠EIS = 5x — 27°.
Сразу видно, что эти два угла, ∠MCA и ∠EIS, являются внешними углами, лежащими по разные стороны от трансверсали. Таким образом, они являются альтернативными внешними углами, что делает их конгруэнтными и позволяет составить простое алгебраическое уравнение:
4x + 3° = 5x — 27°
3° = x — 27° (вычесть 4x с обеих сторон)
30° = x (добавьте 27° к обеим сторонам)
Чтобы найти наши углы, подставьте 30° вместо x:
↑mca = 4x+3 °
↑mca = 4 (30 °)+3 °
↑mca = 120 °+3 °
тнам.
∠EIS = 5x — 27°
∠EIS = 5(30°) — 27°
∠EIS = 150° — 27°
∠EIS 3’s 003’9 Let 003 9 02 попробуйте второе упражнение, используя ту же фигуру. Если вы сможете решить это, вы добились ВЕЛИКИХ математических результатов!
Что вы можете рассказать нам о ∠JCI и ∠TIS?
Что, если мы скажем вам, что ∠JCI = 2y — 7°, а ∠TIS = y — 8°?
Можете ли вы найти у?
Ни один из углов не лежит по одну сторону от поперечной, и оба они не лежат вне параллельных прямых. Они оба не находятся внутри параллельных линий! Кажется, что у них вообще нет отношений!
И все же, путем вывода, вы можете увидеть взаимосвязь:
- ∠JCI является последовательным внутренним угловым партнером ∠EIC
- ∠EIC является партнером по вертикальному углу ∠TIS
Это означает, что наши два проблематичных угла на самом деле являются дополнительными, что является отличным намеком. Вместе их два уравнения должны в сумме давать 180°:
2y — 7° + y — 8° = 180° (теперь упростите)
3y — 15° = 180° (теперь добавьте 15° к обеим сторонам)
3y = 195° (теперь разделите на 3)
y = 65°
Обратно решая задачу, вы обнаружите, что ∠JCI = 123° и ∠TIS = 57°. Успех! Потренируйтесь сами, построив параллельные линии с пересечениями и определяя все отношения углов, которые они создают. Помните также, что отношения остаются в силе, когда линии, пересекаемые секущей, не параллельны; вы просто не можете использовать теоремы, чтобы делать предположения об углах.