найти плоскость проходящую через точку и параллельную плоскости
Вы искали найти плоскость проходящую через точку и параллельную плоскости? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и написать уравнение плоскости проходящей через точку и параллельно плоскости, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «найти плоскость проходящую через точку и параллельную плоскости».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает.
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и найти плоскость проходящую через точку и параллельную плоскости. Просто введите задачу в окошко и нажмите
«решить» здесь (например, написать уравнение плоскости проходящей через точку параллельно векторам).Где можно решить любую задачу по математике, а так же найти плоскость проходящую через точку и параллельную плоскости Онлайн?
Решить задачу найти плоскость проходящую через точку и параллельную плоскости вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.
Уравнение плоскости, проходящей через заданную точку перпендикулярно к заданной прямой, нахождение уравнения плоскости составление уравнения плоскости
Данная статья дает представление о том, как составить уравнение плоскости, проходящей через заданную точку трехмерного пространства перпендикулярно к заданной прямой. Разберем приведенный алгоритм на примере решения типовых задач.
Нахождение уравнения плоскости, проходящей через заданную точку пространства перпендикулярно к заданной прямой
Пусть задано трехмерное пространство и прямоугольная система координат Oxyz в нем. Заданы также точка М1(x1, y1, z1), прямая a и плоскость α, проходящая через точку М1 перпендикулярно прямой a. Необходимо записать уравнение плоскости α.Прежде чем приступить к решению этой задачи, вспомним теорему геометрии из программы 10-11 классов, которая гласит:
Определение 1Через заданную точку трехмерного пространства проходит единственная плоскость, перпендикулярная к заданной прямой.
Теперь рассмотрим, как же найти уравнение этой единственной плоскости, проходящей через исходную точку и перпендикулярной данной прямой.
Возможно записать общее уравнение плоскости, если известны координаты точки, принадлежащей этой плоскости, а также координаты нормального вектора плоскости.
Условием задачи нам заданы координаты x1, y1, z1 точки М1, через которую проходит плоскость α. Если мы определим координаты нормального вектора плоскости α, то получим возможность записать искомое уравнение.
Нормальным вектором плоскости α, так как он ненулевой и лежит на прямой a, перпендикулярной плоскости α, будет являться любой направляющий вектор прямой a. Так, задача нахождения координат нормального вектора плоскости α преобразовывается в задачу определения координат направляющего вектора прямой a.
Определение координат направляющего вектора прямой a может осуществляться разными методами: зависит от варианта задания прямой a в исходных условиях. К примеру, если прямая a в условии задачи задана каноническими уравнениями вида
x-x1ax=y-y1ay=z-z1az
или параметрическими уравнениями вида:
x=x1+ax·λy=y1+ay·λz=z1+az·λ
то направляющий вектор прямой будет иметь координаты аx, аy и аz.
В случае, когда прямая a представлена двумя точками М2(x2, y2, z2) и М3(x3, y3, z3), то координаты направляющего вектора буду определяться как (x3 – x2, y3 – y2, z3 – z2).
Алгоритм для нахождения уравнения плоскости, проходящей через заданную точку перпендикулярно заданной прямой:
— определяем координаты направляющего вектора прямой a: a→ = (аx, аy, аz);
— определяем координаты нормального вектора плоскости α как координаты направляющего вектора прямой a:
n→ = (A, B, C), где A = ax, B = ay, C = az;
— записываем уравнение плоскости, проходящей через точку М1(x1, y1, z1) и имеющей нормальный вектор n→= (A, B, C) в виде A(x – x1) + B(y – y1) + C(z – z1) = 0. Это и будет являться требуемым уравнением плоскости, которая проходит через заданную точку пространства и перпендикулярна к данной прямой.
Полученное общее уравнение плоскости: A(x – x1) + B(y – y1) + C(z – z1) = 0 дает возможность получить уравнение плоскости в отрезках или нормальное уравнение плоскости.
Решим несколько примеров, используя полученный выше алгоритм.
Пример 1Задана точка М1(3, -4, 5), через которую проходит плоскость, и эта плоскость перпендикулярна координатной прямой Оz.
Решение
направляющим вектором координатной прямой Oz будет координатный вектор k⇀= (0, 0, 1). Следовательно, нормальный вектор плоскости имеет координаты (0, 0, 1). Запишем уравнение плоскости, проходящей через заданную точку М1(3, -4, 5), нормальный вектор которой имеет координаты (0, 0, 1):
A(x-x1)+B(y-y1)+C(z-z1)=0⇔⇔0·(x-3)+0·(y-(-4))+1·(z-5)=0⇔z-5=0
Ответ: z – 5 = 0.
Рассмотрим еще один способ решить данную задачу:
Пример 2Плоскость, которая перпендикулярна прямой Oz будет задана неполным общим уравнением плоскости вида Сz+D=0, C≠ 0. Определим значения C и D: такие, при которых плоскость проходит через заданную точку. Подставим координаты этой точки в уравнение Сz + D= 0, получим: С · 5 + D= 0. Т.е. числа, C и D связаны соотношением -DC=5.
Подставим эти значения в уравнение Сz + D= 0 и получим требуемое уравнение плоскости, перпендикулярной к прямой Oz и проходящей через точку М1(3, -4, 5).
Оно будет иметь вид: z – 5 = 0.
Ответ: z – 5 = 0.
Пример 3Составьте уравнение плоскости, проходящей через начало координат и перпендикулярной к прямой x-3=y+1-7=z+52
Решение
Опираясь на условия задачи, можно утверждать, что за нормальный вектор n→ заданной плоскости можно принять направляющий вектор заданной прямой. Таким, образом: n→= (-3, -7, 2). Запишем уравнение плоскости, проходящей через точку О (0, 0, 0) и имеющей нормальный вектор n→= (-3, -7, 2):
Мы получили требуемое уравнение плоскости, проходящей через начало координат перпендикулярно к заданной прямой.
Ответ: -3x-7y+2z=0
Пример 4Задана прямоугольная система координат Oxyz в трехмерном пространстве, в ней – две точки А(2, -1,-2) и B(3, -2, 4).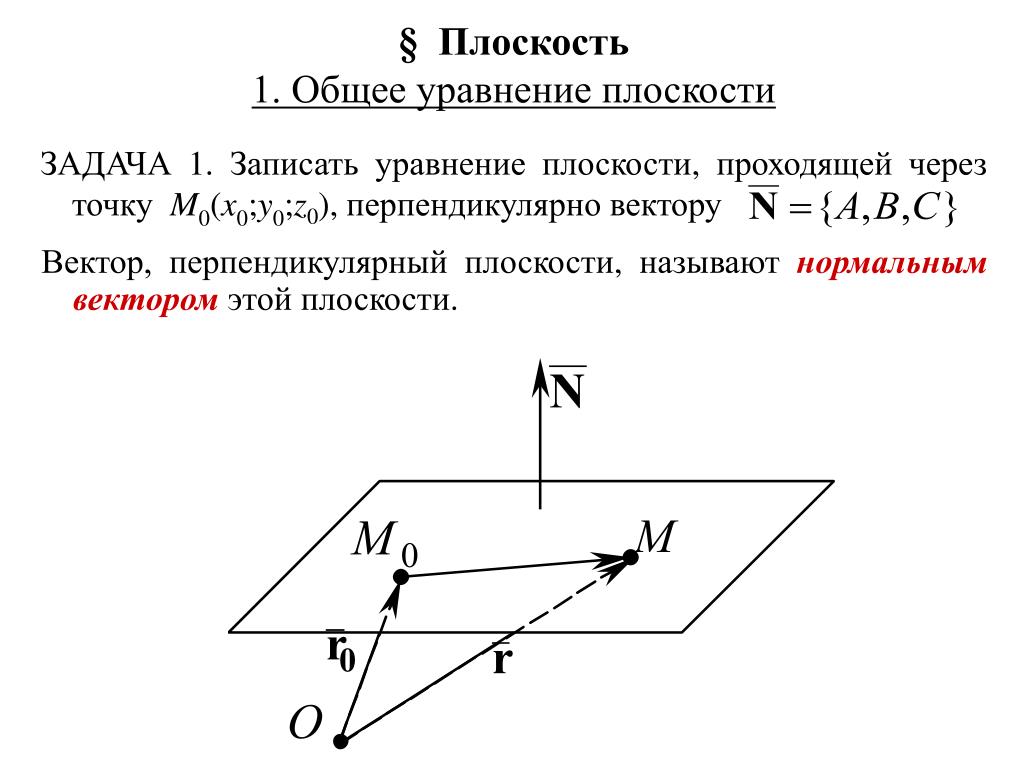
Плоскость α проходит через точку A перпендикулярно прямой АВ. Необходимо составить уравнение плоскости α в отрезках.
Решение
Плоскость α перпендикулярна к прямой АВ, тогда вектор АВ→ будет нормальным вектором плоскости α. Координаты этого вектора определяются как разности соответствующих координат точек В(3, -2, 4) и А(2,-1,-2):
AB→=(3-2, -2-(-1), 4-(-2))⇔AB→=(1, -1, 6)
Общее уравнение плоскости будет записано в следующем виде:
1·x-2-1·y-(-1+6·(z-(-2))=0⇔x-y+6z+9=0
Теперь составим искомое уравнение плоскости в отрезках:
x-y+6z+9=0⇔x-y+6z=-9⇔x-9+y9+z-32=1
Ответ: x-9+y9+z-32=1
Также нужно отметить, что встречаются задачи, требование которых – написать уравнение плоскости, проходящей через заданную точку и перпендикулярной к двум заданным плоскостям. В общем, решение этой задачи в том, чтобы составить уравнение плоскости, проходящей через заданную точку перпендикулярно к заданной прямой, т.
к. две пересекающиеся плоскости задают прямую линию.
Задана прямоугольная система координат Oxyz , в ней – точка М1 (2, 0, -5). Заданы также уравнения двух плоскостей 3x + 2y + 1 = 0 и x + 2z – 1 = 0, которые пересекаются по прямой a. Необходимо составить уравнение плоскости, проходящей через точку М1 перпендикулярно к прямой a.
Решение
Определим координаты направляющего вектора прямой a. Он перпендикулярен как нормальному вектору n1→(3, 2, 0) плоскости n→(1, 0, 2), так и нормальному вектору 3x+2y+1=0 плоскости x+2z-1=0.
Тогда направляющим вектором α→ прямой a возьмем векторное произведение векторов n1→и n2→:
a→=n1→×n2→=i→j→k→320102=4·i→-6·j→-2·k→⇒a→=(4, -6, -2)
Таким образом, вектор n→=(4, -6, -2) будет нормальным вектором плоскости, перпендикулярной к прямой a. Запишем искомое уравнение плоскости:
4·(x-2)-6·(y-0)-2·(z-(-5))=0⇔4x-6y-2z-18=0⇔⇔2x-3y-z-9=0
Ответ: 2x-3y-z-9=0
Объяснитель урока: Уравнения параллельных и перпендикулярных плоскостей
В этом объяснителе мы научимся находить уравнение
плоскость, параллельная или перпендикулярная другой плоскости с учетом ее уравнения или некоторого
характеристики.
Прежде чем начать смотреть на параллельные и перпендикулярные плоскости, вы уже должен быть знаком с нахождением уравнения плоскости. Давайте вспомним различные формы уравнений плоскости:
- Векторная форма ⃑𝑛⋅⃑𝑟=⃑𝑛⋅⃑𝐴, где ⃑𝑛=𝑛,𝑛,𝑛 — ненулевой вектор нормали к плоскости, ⃑𝑟=(𝑥,𝑦,𝑧) — позиция вектор любой точки плоскости, а ⃑𝐴=(𝑥,𝑦,𝑧) — вектор положения точка 𝐴 с координатами (𝑥,𝑦,𝑧) что принадлежит самолету.
- Общая форма: 𝑛𝑥+𝑛𝑦+𝑛𝑧+𝑑=0, где 𝑛, 𝑛 и 𝑛 — компоненты вектора нормали к плоскости и 𝑑 является константой.
- Параметрическая форма представляет собой набор из трех уравнений:
𝑥=𝑥+𝑡𝑢+𝑡𝑣,𝑦=𝑦+𝑡𝑢+𝑡𝑣,𝑧=𝑧+𝑡𝑢+𝑡𝑣,
где точка 𝐴 координат
(𝑥,𝑦,𝑧) принадлежит плоскости,
⃑𝑢=𝑢,𝑢,𝑢
и ⃑𝑣=𝑣,𝑣,𝑣
— два ненулевых и неколлинеарных вектора на плоскости, а 𝑡
и 𝑡 — скаляры.
Тогда нормальный вектор плоскости
дается как ⃑𝑛=⃑𝑢×⃑𝑣. - Форма перехвата: 𝑥𝑎+𝑦𝑏+𝑧𝑐=1, где 𝑎, 𝑏, и 𝑐 — это 𝑥-, 𝑦-, и 𝑧-перехваты самолета, если они все существуют, и 1𝑎, 1𝑏, и 1𝑐 — компоненты нормального вектора самолет.
Тогда нормальный вектор плоскости
дается как ⃑𝑛=⃑𝑢×⃑𝑣.За исключением параметрических уравнений, определяющих плоскость с одной точкой и два ненулевых и неколлинеарных вектора, уравнения основаны на том, что любой вектор на плоскости (например, 𝐴𝑀, с 𝐴 известная точка на плоскости и 𝑀 любая точка на плоскости с координатами (𝑥,𝑦,𝑧)) есть перпендикулярно вектору нормали к плоскости. Таким образом, у нас есть ⃑𝑛⋅𝐴𝑀=0.
При определении плоскости мы видим важность ее вектора нормали
(точнее, одного вектора нормали к плоскости как любого ненулевого вектора, параллельного
вектор нормали также является вектором нормали). Нормальный вектор также
занимает центральное место в определении того, параллельны или перпендикулярны две плоскости.
Определение: параллельные и перпендикулярные плоскости
Две различные плоскости параллельны, если они имеют параллельные ненулевые векторы нормали, а это значит, что у них нет точек пересечения. Две плоскости перпендикулярны если их нормальные векторы перпендикулярны.
Стоит отметить, что две совпадающие плоскости имеют параллельные ненулевые векторы нормали также; тогда уравнение одной из плоскостей кратно уравнению другой.
Это свойство показано на рисунке ниже, где показаны (а) два параллельных (слева) и перпендикулярная (справа) плоскости в трех измерениях и (б) вершина вид обеих плоскостей 𝑃 и 𝑄, показывающий их нормальные векторы.
Воспользуемся этим свойством, чтобы дополнить уравнения двух плоскостей так, чтобы они параллельны.
Пример 1. Нахождение условия параллельности двух плоскостей
Учитывая, что плоскость 𝐾𝑧+2𝑥+3𝑦=−4 параллельна
плоскости 𝐿𝑦−2𝑥−2𝑧=3, найти значения
𝐾 и 𝐿.
Ответ
Назовем сначала 𝑃 плоскость уравнения 𝐾𝑧+2𝑥+3𝑦=−4 и 𝑃 уравнение 𝐿𝑦−2𝑥−2𝑧=3. Если самолеты 𝑃 и 𝑃 параллельны, то их векторы нормалей должны быть параллельны. Назовем вектор нормали 𝑃⃑𝑛 и что из 𝑃⃑𝑛. Компоненты этих векторов нормалей могут быть извлечены из коэффициентов соответствующих переменных в общих уравнениях обеих плоскостей. Осторожно, в обоих уравнениях члены даны не в обычном порядке.
Находим ⃑𝑛=(2,3,𝐾) и ⃑𝑛=(−2,𝐿,−2).
Векторы ⃑𝑛 и ⃑𝑛 параллельны, если существует ненулевой скаляр 𝑚 такой, что ⃑𝑛=𝑚⃑𝑛. Это векторное уравнение дает три скалярных уравнения при приравнивании три компоненты обоих векторов:
| 2=−2𝑚,3=𝑚𝐿,𝐾=−2𝑚. | (1)(2)(3) |
Уравнение (1) дает 𝑚=−1, откуда следует, что 𝐿=−3 и 𝐾=2.
Ответ
Мы находим, что 𝐾=2 и 𝐿=−3.
Теперь найдем уравнение плоскости, проходящей через данную точку и параллельно другой плоскости.
Пример 2. Нахождение общего уравнения плоскости, параллельной другой плоскости и проходит через заданную точку
Найдите уравнение плоскости, проходящей через данную точку (𝑎,𝑏,𝑐) и параллельно плоскости 𝑥+𝑦+𝑧=0.
- 𝑎𝑥+𝑏𝑦+𝑐𝑧=1
- 𝑥+𝑦+𝑧 = 𝑎+𝑏+𝑐
- 𝑥+𝑦+𝑧+𝑎+𝑏+𝑐 = 0
- 𝑎𝑥+𝑏𝑦+𝑐𝑧 = 𝑎+𝑏 𝑐
- 𝑥𝑎 = 𝑦𝑏 = 𝑧𝑐
Ответ
Нам дана точка на плоскости и уравнение другой плоскости параллельна плоскости, уравнение которой мы пытаемся найти. Мы можем написать общее уравнение плоскости, если нам известны координаты одну из его точек и его вектор нормали. Мы можем найти последний, используя факт, что параллельные плоскости имеют параллельные векторы нормали.
Плоскость с общим уравнением 𝑥+𝑦+𝑧=0 имеет
нормальный вектор компонентов (1,1,1). Любой ненулевой вектор, параллельный этому вектору, является вектором нормали к плоскости
мы хотим написать уравнение. Самый простой параллельный вектор, который мы можем найти, это
тот самый вектор, который дает для уравнения плоскости
𝑥+𝑦+𝑧+𝑑=0,
где 𝑑 — константа, которую нужно найти. Для этого мы используем
координаты (𝑎,𝑏,𝑐) точки, которая находится в
самолет. Его координаты должны удовлетворять уравнению плоскости,
и поэтому у нас есть
𝑎+𝑏+𝑐+𝑑=0𝑑=−(𝑎+𝑏+𝑐).
Это дает в качестве окончательного уравнения
𝑥+𝑦+𝑧−(𝑎+𝑏+𝑐)=0,
или, переставляя,
𝑥+𝑦+𝑧=𝑎+𝑏+𝑐.
Ответ
Общее уравнение плоскости 𝑥+𝑦+𝑧−(𝑎+𝑏+𝑐)=0, которое можно записать как 𝑥+𝑦+𝑧=𝑎+𝑏+𝑐.
Обратимся теперь к перпендикулярным плоскостям.
Пример 3. Нахождение условия перпендикулярности двух плоскостей
Учитывая, что плоскость 3𝑥−3𝑦−3𝑧=1
перпендикулярна плоскости 𝑎𝑥−2𝑦−𝑧=4,
найдите значение 𝑎.
Ответ
Если две плоскости перпендикулярны, то их векторы нормали должны быть перпендикуляр. Отсюда следует, что скалярное произведение обоих векторов нормалей равно нулю. Найдем из обоих общих уравнений компоненты обеих нормальных векторы. Для первого находим (3,−3,−3) а для второго находим (𝑎,−2,−1).
Скалярное произведение этих двух векторов равно нулю, что дает (3,−3,−3)⋅(𝑎,−2,−1)=03𝑎+(−3)×(−2)+(−3)×(−1)=03𝑎+9=0𝑎=−3 .
Ответ
Значение 𝑎 равно −3.
В то время как плоскость полностью определена, если мы знаем, что она параллельна другой плоскости и проходит через данную точку, существует бесконечное число плоскостей, перпендикулярно другой плоскости, как показано на рисунке ниже, где все красные плоскости перпендикулярны 𝑃, и каждая из них представляет целое семейство параллельных плоскостей.
Свойство: семейство плоскостей, перпендикулярных заданной плоскости
Векторы нормалей всех плоскостей, перпендикулярных плоскости 𝑃
параллельны 𝑃, а вектор нормали к 𝑃
параллельна всем плоскостям, перпендикулярным 𝑃.
Отсюда следует, что для однозначного определения плоскости с перпендикулярностью плоскость должна быть одной из следующих:
- перпендикулярна двум непараллельным плоскостям и проходит через данную точку,
- перпендикулярна плоскости 𝑃 и проходит через две различные точки 𝐴 и 𝐵 такие, что 𝐴𝐵 и вектор нормали 𝑃 неколлинеарны.
Давайте рассмотрим эти два случая на следующих двух примерах.
Пример 4. Нахождение уравнения плоскости, перпендикулярной двум плоскостям и Проходит через заданную точку
Найдите общее уравнение плоскости, проходящей через данную точку (2,8,1) и перпендикулярна двум плоскостям −6𝑥−4𝑦+6𝑧=−5 и 5𝑥+3𝑦−6𝑧=3.
Ответ
Плоскость, которую мы рассматриваем, перпендикулярна двум плоскостям
уравнений −6𝑥−4𝑦+6𝑧=−5 и
5𝑥+3𝑦−6𝑧=3. Их соответствующие нормальные векторы
равны (−6,−4,6) и
(5,3,−6). Так как мы ищем
плоскость, перпендикулярная обеим этим непараллельным плоскостям, ее нормаль
вектор ⃑𝑛 должен быть перпендикулярен обоим
их непараллельные векторы нормалей. Есть два способа найти вектор
перпендикулярно двум непараллельным векторам.
- Мы говорим, что скалярное произведение между ⃑𝑛 и
любой из этих двух векторов должен быть равен нулю. С
⃑𝑛=𝑛,𝑛,𝑛,
нормальный вектор плоскости, он дает
−6𝑛−4𝑛+6𝑛=05𝑛+3𝑛−6𝑛=0.
Чтобы решить эту систему двух уравнений, нам нужно сократить одно слагаемое. Сложение двух уравнений может отменить член 𝑛
и дает
−𝑛−𝑛=0,𝑛=−𝑛.т.е.
Мы нашли 𝑛 через 𝑛. Заменив 𝑛 на −𝑛 в
второе уравнение и перестановка дают нам 𝑛
с точки зрения 𝑛:
𝑛=𝑛3.
Компоненты вектора нормали теперь могут быть выражены в терминах
из 𝑛:
⃑𝑛=𝑛,−𝑛,𝑛3.
Поскольку 𝑛 может принимать любое ненулевое действительное значение,
отношения направлений компонентов вектора нормали равны
1,−1,13. Умножение отношений на 3 дает ⃑𝑛=(3,−3,1).
- Мы находим векторное произведение этих векторов, которое дает вектор перпендикулярно обоим: ⃑𝑛=(−6,−4,6)×(5,3,−6)=||||⃑𝑖⃑𝑗⃑𝑘−6−4653−6||||=((−4)(−6)−3×6 )⃑𝑖−((−6)(−6)−5×6)⃑𝑗+((−6)×3−5×(−4))⃑𝑘=6⃑𝑖−6⃑𝑗+2⃑𝑘=(6,−6,2) . Этот вектор нормали можно упростить, разделив его компоненты на 2, что дает (3,−3,1), как мы нашли ранее.
Используя ⃑𝑛=(3,−3,1) чтобы написать общее уравнение плоскости 𝑛𝑥+𝑛𝑦+𝑛𝑧+𝑑=0 дает 3𝑥−3𝑦+𝑧+𝑑=0.
Мы знаем, что плоскость проходит через точку (2,8,1). Следовательно, координаты (2,8,1) должны удовлетворять уравнение плоскости. Подставляя их в дает 3×2−3×8+1+𝑑=0𝑑=17.
Ответ
Уравнение плоскости, проходящей через точку
(2,8,1) и перпендикулярна двум
плоскости −6𝑥−4𝑦+6𝑧=−5
и 5𝑥+3𝑦−6𝑧=3 есть
3𝑥−3𝑦+𝑧+17=0.
Повторим метод, использованный в предыдущем примере.
Как найти уравнение плоскости, перпендикулярной двум другим плоскостям
Если плоскость перпендикулярна двум другим непараллельным плоскостям с нормалью векторы ⃑𝑛 и ⃑𝑛, то компоненты его нормального вектор ⃑𝑛 можно найти двумя разными способами. методы:
- решение (в терминах одной из ее составляющих) полученной системы уравнений от ⃑𝑛⋅⃑𝑛=0, и ⃑𝑛⋅⃑𝑛=0, то, разделив компоненты ⃑𝑛 в терминах одного из его компонентов этим компонентом (который был 𝑛 в предыдущем примере), что дает направление соотношение ⃑𝑛,
- найти векторное произведение ⃑𝑛 и ⃑𝑛: ⃑𝑛=⃑𝑛×⃑𝑛.
Наконец, уравнение плоскости завершается с использованием координат одна точка плоскости.
Посмотрим, как найти уравнение плоскости, проходящей через
две точки, и это перпендикулярно другой плоскости в следующем примере.
Пример 5. Нахождение уравнения плоскости, перпендикулярной другой плоскости и проходит через две заданные точки
Найдите общий вид уравнения плоскости, проходящей через две точки 𝐴(2,5,4) и 𝐵(3,−3,5) и перпендикулярно плоскость 2𝑥−𝑦+2𝑧−2=0.
Ответ
Чтобы найти общее уравнение плоскости, нам нужен вектор нормали к плоскости и точку на плоскости. Однако нам не задан вектор нормали к интересующая нас плоскость (назовем эту плоскость 𝑃), но вместо этого нам дано уравнение плоскости, перпендикулярной 𝑃; назовем это 𝑄. 𝑄∶2𝑥−𝑦+2𝑧=0.
Нормальный вектор 𝑄, ⃑𝑛, параллелен 𝑃. Как мы увидим ниже, есть два немного разные способы найти общее уравнение плоскости 𝑃.
Определим сначала вектор нормали к плоскости
𝑄∶2𝑥−𝑦+2𝑧−2=0; это вектор
⃑𝑛 с компонентами
(2,−1,2). Так как плоскость 𝑃 перпендикулярна плоскости
𝑄, ⃑𝑛 это
параллельно плоскости 𝑃. По свойствам
трехмерных векторов можно считать, что плоскость 𝑃 включает
вектор тех же компонент, что и у
⃑𝑛.
Теперь нам нужны два непараллельных вектора, лежащих в плоскости 𝑃 найти вектор нормали ⃑𝑛, заданное их перекрестным произведением.
Далее мы знаем, что самолет проходит через два точки 𝐴(2,5,4) и 𝐵(3,−3,5). Вектор 𝐴𝐵=(1,−8,1) следовательно, входит в плоскость.
Первый способ найти уравнение 𝑃 состоит говоря это как 𝐴𝐵 и ⃑𝑛 неколлинеарны и оба включены в плоскость 𝑃, вектор нормали из 𝑃, ⃑𝑛, дается перекрестным произведением 𝐴𝐵 и ⃑𝑛: ⃑𝑛=𝐴𝐵×⃑𝑛=||||⃑𝑖⃑𝑗⃑𝑘1−812−12||||=(−15,0,15).
Чтобы написать общее уравнение, мы можем взять
115⃑𝑛=(−1,0,1) как вектор нормали,
который дает
−𝑥+𝑧+𝑑=0,
для некоторой постоянной 𝑑.
Как точки 𝐴(2,5,4) и 𝐵(3,−3,5) лежат в плоскости, их координаты удовлетворяют уравнению. Подставляя координаты одного точек, например, точки 𝐵, в уравнение позволяет нам найти значение 𝑑 (мы бы нашли то же значение, используя координаты 𝐴, конечно): −3+5+𝑑=0𝑑=−2.
Таким образом, уравнение плоскости равно −𝑥+𝑧−2=0.
Другой способ состоит в том, чтобы сказать, что для любой точки 𝑀(𝑥,𝑦,𝑧) на плоскости скалярное произведение вектор 𝐴𝑀 (или 𝐵𝑀) с вектором нормали плоскость (которая определяется как 𝐴𝐵 × ⃑𝑛 — см. выше) равна нулю. Если вы знакомы с тройным скалярным произведением, этот метод эквивалентно тому, что векторы 𝐴𝑀 (или 𝐵𝑀), 𝐴𝐵, и ⃑𝑛 компланарны, что означает, что их скалярное тройное произведение равно нулю. У нас есть 𝐴𝑀⋅𝐴𝐵×⃑𝑛=0||||𝑥−2𝑦−5𝑧−41−812−12||||=0(𝑥−2)(−16+1)−(𝑦−5)(2− 2)+(𝑧−4)(−1+16)=0−15𝑥+15𝑧−30=0,
Деление обеих частей этого уравнения на 15 дает
−𝑥+𝑧−2=0.
Ответ
Общее уравнение плоскости, проходящей через две точки 𝐴(2,5,4) и 𝐵(3,−3,5), и это перпендикулярно плоскости 2𝑥−𝑦+2𝑧−2=0 равно −𝑥+𝑧−2=0.
Подытожим два метода, использованных в последнем примере.
Практическое руководство. Нахождение общего уравнения плоскости, перпендикулярной другой плоскости и проходящей через две точки
Если нам говорят, что плоскость перпендикулярна другой плоскости известной нормали вектор и проходит через две различные точки 𝐴 и 𝐵 такое, что 𝐴𝐵 и ⃑𝑛 неколлинеарны, то есть два Методы нахождения уравнения плоскости.
1-й способ: Вектор нормали к плоскости, перпендикулярной другой плоскость вектора нормали ⃑𝑛, которая проходит через две точки 𝐴 и 𝐵 определяется выражением ⃑𝑛=𝐴𝐵×⃑𝑛.
Вектор ⃑𝑛 ненулевой, так как 𝐴𝐵 и ⃑𝑛 неколлинеарны.
Затем можно найти уравнение, используя компоненты
⃑𝑛 и координаты
𝐴 или 𝐵.
2-й способ: Для любой точки 𝑀(𝑥,𝑦,𝑧) в плоскости, перпендикулярной другой плоскости вектора нормали ⃑𝑛 и который проходит через два точки 𝐴 и 𝐵 такие, что 𝐴𝐵 и ⃑𝑛 неколлинеарны, три векторов (или 𝐵𝑀), 𝐴𝐵 и ⃑𝑛 компланарны. Это означает, что 𝐴𝑀⋅𝐴𝐵×⃑𝑛=0𝐵𝑀⋅𝐴𝐵×⃑𝑛=0,и
Запись одного из этих уравнений с тройным скалярным произведением непосредственно дает общее уравнение плоскости.
Обратите внимание, что параметрические уравнения плоскости, перпендикулярной другой плоскости вектора нормали ⃑𝑛, проходящей через два точки 𝐴 и 𝐵 такие, что 𝐴𝐵 и ⃑𝑛 неколлинеарны, можно легко найти, используя два вектора на плоскости, 𝐴𝐵 и ⃑𝑛.
Ключевые точки
- Две параллельные плоскости 𝑃 и 𝑄
характеризуется параллельными векторами нормалей, а это означает, что
⃑𝑛=𝑘⃑𝑛, где
⃑𝑛 и ⃑𝑛
— нормальные векторы 𝑃 и 𝑄,
соответственно, а 𝑘 — ненулевое действительное число. 𝑃 и 𝑄 параллельны, если они
различны, то есть если они не имеют точек пересечения. Два
пересекающиеся плоскости с параллельными векторами нормалей совпадают.
- Любые две перпендикулярные плоскости 𝑃 и 𝑄 имеют перпендикулярные векторы нормали, что означает, что скалярное произведение их нормальные векторы, ⃑𝑛 и ⃑𝑛 соответственно равен нулю: ⃑𝑛⋅⃑𝑛=0.
- Векторы нормалей всех плоскостей, перпендикулярных плоскости 𝑃 параллельны 𝑃.
- Вектор нормали к плоскости 𝑃 параллелен всем плоскости, перпендикулярные 𝑃.
уравнений плоскостей
Уравнения плоскостейЧасть 2:
Уравнение плоскостиДля любой плоскости должен быть хотя бы один ненулевой вектор n = б а , б , в – это перпендикулярно каждому вектор v параллелен плоскости.
В частности, плоскость через точку P 1 ( x 1 , y 1 , z 1 ) с вектором нормали n = б а , б , в – множество точек P ( x , y , z ) такое, что Векторы
|
Однако, n · v = 0 эквивалентно
|
Определение 4.3: Уравнение плоскости с нормалью n = № а , б , в – через точку á x 1 , y 1 , z 1 ñ это
a ( x — x 1 ) + b ( y — y 1 ) + c ( z — z 1 ) = 0 (2)
Если c 0, то мы можем преобразовать (2) в функциональную форму , которая равна
.
|
ПРИМЕР 3 Найти уравнение плоскости с нормалью n = 1,2,7 ñ, который содержит точку P 1 (5,3,4).Решение: Для этого подставим в уравнение (2). В результате получается, что
Затем мы находим z , чтобы получить функциональную форму :
1( x -5) +2( y -3) +7( z -4) = 0
.
z = —
1
7 x —
2
7 г +
39
7
Найти уравнение плоскости через три неколлинеарных точек P 1 , P 2 и P 3 , сначала формируем два вектора
|