Произвольный треугольник по заданным параметрам
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Нарисуйте фигуру в Visio
Вы можете создавать собственные фигуры с помощью прямоугольника, эллипса, дуги, свободной формы и карандаша в Visio.
Если вы хотите применить к новой фигуре цвета заливки, необходимо создать закрытую фигуру. Если вы используете инструмент «Прямоугольник» или «Эллипс», закрытые фигуры становятся автоматически закрытыми. По умолчанию закрытые фигуры заполняются сплошным цветом.
По умолчанию закрытые фигуры заполняются сплошным цветом.
В этом примере прямоугольник — это закрытая фигура, заливка сплошной заливки. Треугольник не закрыт, так как он не заполнен сплошным цветом и фон рисунка можно увидеть в фигуре.
Что необходимо сделать
-
Нарисуйте прямоугольник или круг
-
Рисование произвольной фигуры
-
Изменение фигуры
-
Создание новой фигуры
Нарисуйте прямоугольник или круг
На вкладке Главная в группе Инструменты щелкните стрелку рядом с кнопкой Прямоугольник , а затем сделайте следующее:
-
Чтобы нарисовать прямоугольник, выберите инструмент Прямоугольник.
-
Чтобы нарисовать круг или овал, выберите инструмент Эллипс.
Перетащите фигуру на страницу.
Чтобы вернуться к обычному редактированию, в группе Инструменты щелкните инструмент Указатель .
К началу страницы
Рисование произвольной фигуры
-
На вкладке Главная в группе Инструменты щелкните стрелку рядом с кнопкой Прямоугольник , а затем сделайте следующее:
- org/ListItem»>
Чтобы нарисовать прямую линию, выберите инструмент Линия.
-
Чтобы нарисовать неровную фигуру, выберите инструмент «Freeform».
-
Чтобы нарисовать кривую, выберите инструмент Дуга.
-
Чтобы нарисовать первый сегмент, нарисуйте указатель в том месте, где вы хотите начать фигуру, а затем перетащите указатель, пока сегмент не будет иметь нужный размер.
org/ListItem»>
-
Чтобы нарисовать дополнительные сегменты, нарисуйте вершину в конце последнего добавленного сегмента, а затем перетащите указатель, чтобы нарисовать следующий сегмент.
Примечание: Чтобы отменить сегмент, нажмите CTRL+Z. Сегменты удаляются в обратном порядке, в котором они были нарисованы.
-
Чтобы закрыть фигуру, перетащите конечную точку последнего сегмента, который создается над вершиной в начале первого сегмента. Фигура становится непрозрачной, что означает, что она закрыта.

-
Чтобы вернуться к обычному редактированию, на вкладке Главная в группе Инструменты нажмите кнопку Указатель .
Чтобы нарисовать второй сегмент, нарисуйте вершину первого сегмента и перетащите указатель.
К началу страницы
Изменение фигуры
Большинство фигур в Visio можно изменять, добавляя, удаляя и изумяая их сегменты.
Удаление сегмента из фигуры
-
На вкладке Главная в группе Инструменты щелкните стрелку рядом с кнопкой Прямоугольник и выберите инструмент Карандаш .

-
Выберите фигуру, из которую вы хотите удалить сегмент, щелкните вершину которую нужно удалить, и нажмите кнопку DELETE.
Добавление сегмента к фигуре
-
На вкладке Главная в группе Инструменты щелкните стрелку рядом с кнопкой Прямоугольник и выберите инструмент Карандаш .
org/ListItem»>
Выберите фигуру, к которой вы хотите добавить сегмент, найдите место, куда вы хотите добавить сегмент, а затем, удерживая нажатой клавишу CTRL, щелкните.
В месте щелчка фигуры появляется новая вершина, создав новый сегмент.
Изменить форму фигуры
-
На вкладке Главная в группе Инструменты щелкните стрелку рядом с кнопкой Прямоугольник и выберите инструмент Карандаш .
org/ListItem»>
Вы выберите фигуру, щелкните вершину которую вы хотите переместить, а затем перетащите вершину на новое место.
К началу страницы
Создание новой фигуры
Вы можете повторно использовать настраиваемую фигуру в других рисунках, сделав ее фигурой из вехи. Чтобы превратить пользовательскую фигуру в фигуру», сделайте следующее?
-
В области Фигуры щелкните Дополнительные фигуры ,а затем выберите настраиваемый или создайте новый, выбрав Новый ряд (единицы США) или Новый ряд (метрическая система).

-
На странице рисования выберите пользовательскую фигуру и перетащите ее в новый эскиз в области Фигуры.
-
Чтобы переименовать новую фигуру, щелкните ее правой кнопкой мыши, выберите переименовать и введите имя нового.
-
В области Фигуры в настраиваемом мастере выберите сохранить изменения, внесенные в настраиваемый мастер.
Дополнительные сведения о том, как создать новую фигуру, см. в статью Создание фигуры или Изменение фигуры.
К началу страницы
Как найти среднюю линию треугольника? Свойства, теорема
ф
Понятие треугольника
Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, которые не лежат на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
Виды треугольников:
- Прямоугольный. Один угол прямой, то есть равен 90 градусам, два других меньше 90 градусов.
- Остроугольный. Градусная мера всех углов больше 0, но меньше 90 градусов.
- Тупоугольный. Один угол тупой, два других — острые.
Треугольник считают равнобедренным, если две его стороны равны. Эти стороны называют боковыми сторонами, а третью — основанием.
Треугольник, у которого все стороны равны, называется равносторонним или правильным.
Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, которая лежит напротив прямого угла — гипотенуза, а две другие стороны — катеты.
Правильный (равносторонний или равноугольный) треугольник — это правильный многоугольник, в котором все стороны равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.
Свойства треугольников:
- В треугольнике против большего угла лежит большая сторона — и наоборот.
- Сумма углов треугольника равна 180 градусов.
- Все углы равностороннего треугольника равны 60 градусам.
- В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Запишитесь и участвуйте в розыгрыше 8 уроков
Понятие средней линии треугольника
Определение средней линии треугольника подходит для любого вида этой фигуры.
Средняя линия треугольника — отрезок, который соединяет середины двух сторон. В любом треугольнике можно провести три средних линии.
Основанием считается сторона, которой параллельна средняя линия.
Как найти среднюю линию треугольника — расскажем дальше, а для начала еще немного разберемся со всеми определениями.
Запоминаем
Средняя линия параллельна третьей стороне, а ее длина равна половине длины этой стороны.
Понятие средней линии прямоугольного треугольника
Математики говорят: в любом треугольнике можно провести три средних линии. В прямоугольном треугольнике этот отрезок будет равен половине основания — это и есть формула средней линии прямоугольного треугольника.
Прямой угол помогает нам применить другие признаки равенства и подобия. Для углов в прямоугольном треугольнике можно использовать геометрические тождества без дополнительных построений, а любую из сторон можно найти по теореме Пифагора.
Для углов в прямоугольном треугольнике можно использовать геометрические тождества без дополнительных построений, а любую из сторон можно найти по теореме Пифагора.
В прямоугольном треугольнике две средние линии перпендикулярны катетам, а третья равна медиане, проведенной к гипотенузе. Средние линии острого и разностороннего треугольника не обладают подобными свойствами.
Важное свойство
Средняя линия прямоугольного треугольника делит его на четыре прямоугольных треугольника.
Учёба без слёз (бесплатный гайд для родителей)
Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.
Свойства средней линии треугольника
Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.
Свойства:
- Средняя линия равна половине длины основания и параллельна ему.

- Средняя линия отсекает треугольник, подобный данному с коэффициентом 1/2; его площадь равна четверти площади данного.
- Три средние линии разделяют исходную фигуру на четыре равных треугольника. Центральный из них называют дополнительным.
- Три средние линии разделяют исходный прямоугольный треугольник на четыре равных прямоугольных треугольника.
Теорема о средней линии треугольника
Теорема о средней линии треугольника звучит так:
Средняя линия треугольника параллельна основанию и равна его половине. А так выглядит формула нахождения средней линии треугольника:
Докажем теорему:
По условию нам дано, что MA = MB, NA = NC
Рассмотрим два образовавшихся треугольника ΔAMN и ΔABC.
(по второму признаку подобия треугольников).
Так как △AMN ~ △ABC, то Следовательно, ВС = 2МN.
 Значит, доказано, что средняя линия равна половине основания.
Значит, доказано, что средняя линия равна половине основания.Так как △AMN ~ △ABC, то ∠1 = ∠2 . Так как ∠1 и ∠2 — соответственные углы, то по признаку параллельности прямых MN || BC.
Параллельность средней линии и соответствующего ей основания доказана.
Теорема доказана.
Пример 1. В треугольнике ΔABC AB = 8, BC = 7, CA = 5, точки M, K, N — середины сторон AB, BC, CA соответственно. Найти периметр ΔMNK.
Как найти периметр треугольника:
Соединим середины сторон треугольника ΔABC и получим его средние линии, которые образуют треугольник ΔMNK. Найдем их длины по теореме о средней линии:
Ответ: периметр треугольника ΔMNK равен 10.
Пример 2. В прямоугольном треугольнике АВС есть две средние линии: MN и NP, равные 3 и 4 соответственно. Найти площадь большого прямоугольного треугольника.
Решение:
Площадь треугольника равна половине произведения основания на высоту.
S = ½ × AC × BC Так как треугольник прямоугольный, то его площадь найдем как половину произведения катетов:
Так как треугольник прямоугольный, то его площадь найдем как половину произведения катетов:Так как MN — средняя линия, то по теореме о средней линии она равна половине катета AC:
MN = ½ × AC
Значит, AC = 2MN = 2 × 3 = 6.
Так как NP — средняя линия, то по теореме о средней линии она равна половине катета BC:
NP = ½ × BC
Значит, BC = 2NP = 2 × 4 = 8.
Тогда найдем площадь большого треугольника, используя формулу, указанную выше:
S = ½ × 6 × 8 = ½ × 48 = 24.
Ответ: площадь большого прямоугольного треугольника равна 24.
Вычислить площадь прямоугольного треугольника онлайн
Треугольник – это фигура, имеющая три стороны и три угла. Если один из углов треугольника равен 90°,
то он называется «прямоугольным». При этом две стороны, образующие прямой угол – это катеты.
Гипотенуза – это третья сторона, которая находится напротив прямого угла и соединяет катеты между
собой, образуя замкнутую геометрическую фигуру.
- Площадь прямоугольного треугольника через две стороны
- Площадь прямоугольного треугольника через гипотенузу и острый угол
- Площадь прямоугольного треугольника через гипотенузу и острый угол. Способ 2
- Площадь прямоугольного треугольника через катет и острый угол
- Площадь прямоугольного треугольника через катет и прилегающий острый угол
- Площадь прямоугольного треугольника через гипотенузу и радиус вписанного круга
- Площадь прямоугольного треугольника через гипотенузу и диаметр вписанного круга
- Площадь прямоугольного треугольника через гипотенузу и площадь вписанного круга
- Площадь прямоугольного треугольника через гипотенузу и длину вписанной окружности (периметр)
- Площадь прямоугольного треугольника через касание вписанной окружности которая делит гипотенузу на части
- Площадь прямоугольного треугольника по формуле Герона
- Площадь прямоугольного треугольника через гипотенузу и высоту
Через две стороны
Если в геометрической фигуре известна длина катетов, то можно вычислить площадь фигуры через них. В
некоторых учебниках вертикальный катет называется высотой и обозначается буквой h, но это не
обязательно. При написании формулы можно использовать буквенные обозначения a и b.
В
некоторых учебниках вертикальный катет называется высотой и обозначается буквой h, но это не
обязательно. При написании формулы можно использовать буквенные обозначения a и b.
S = ½ (a · b)
Сторона (a):
ммсмдмм
Сторона (b):
ммсмдмм
Цифр после запятой:
012345678910Результат в: мм²см²дм²м²
Один из самых простых линейных вариантов вычисления — через две стороны, то есть через два катета, прилегающих к прямому углу. В этом случае площадь равна половине произведения катетов.
Через гипотенузу и острый угол
Так как один угол, от которого отходят два катета «а» и «b» равен 90°, два остальных будут острыми.
Эти углы образуются в местах соединения катетов с гипотенузой. Для того, чтобы рассчитать итоговую S
по гипотенузе и острому углу, нужно сначала через длину сторон вычислить sin (синус) и cos
(косинус). Углы в прямоугольном треугольнике обозначаются греческими буквами α (альфа) – угол 90° и
β (бетта) – один из острых углов. Если удается вычислить sin и cos, то через них можно вычислить
площадь по следующей формуле:
Углы в прямоугольном треугольнике обозначаются греческими буквами α (альфа) – угол 90° и
β (бетта) – один из острых углов. Если удается вычислить sin и cos, то через них можно вычислить
площадь по следующей формуле:
S = ¼ · с² · sin(2α)
Гипотенуза (c):
ммсмдмм
Угол (α):
градусырадианыsin
Цифр после запятой:
012345678910Результат в: мм²см²дм²м²
Чтобы вычислить sin α, нужно сторону фигуры «a» (то есть высоту) разделить на гипотенузу: sin α= a / c.
Чтобы вычислить cos α, нужно сторону «b» разделить на гипотенузу: cos α= b / c.
В данных формулах
гипотенуза обозначается буквой «с». Таким образом выглядят формулы sin и cos для угла α. Точно таким
же образом можно сделать расчеты и для угла β, но даже это не обязательно, потому что в
прямоугольном треугольнике cos α = sin β, а sin α = cos β.
Через гипотенузу и острый угол. Способ 2
Для данного расчета также понадобятся синусы всех углов треугольника. Нужно вычислить по уже знакомым
формулам sin α= a / c и sin β= b / c. Также понадобится синус третьего угла, который обозначается
греческой буквой γ (гамма). Синус угла γ рассчитывается из разницы между суммой всех углов (180°)
треугольника и суммы двух других углов, а именно: sin (γ) = 180 – (α + β). Также понадобится длина
гипотенузы, которая будет обозначена буквой «C».
Исходя из всех известных величин, формула
площади треугольника через гипотенузу и острый угол следующая:
S = c²/2 * (sin(γ) * sin(β) / sin(α))
Гипотенуза (c):
ммсмдмм
Угол (β):
градусырадианы
Цифр после запятой:
012345678910Результат в: мм²см²дм²м²
Через катет и острый угол
Зная длину катетов, также можно легко вычислить площадь, но в два этапа. Для этого понадобится
предварительно найти tg (тангенс) одного из углов. Например, tg α можно рассчитать по формуле tg α =
a/b, где «a» – это высота (вертикальный катет), а «b» – второй (горизонтальный) катет. Для того,
чтобы вычислить tg угла β, в формуле нужно поменять местами стороны: tgβ = b/a.
Для этого понадобится
предварительно найти tg (тангенс) одного из углов. Например, tg α можно рассчитать по формуле tg α =
a/b, где «a» – это высота (вертикальный катет), а «b» – второй (горизонтальный) катет. Для того,
чтобы вычислить tg угла β, в формуле нужно поменять местами стороны: tgβ = b/a.
Так, формула вычисления площади прямоугольника через катет и острый угол выглядит следующим образом: если известна сторона «а» —
S = (a² * tgβ) / 2
Если известна сторона «b», то вместо a подставить b.
Катет(a):
ммсмдмм
Угол (α):
градусырадианыsin
Цифр после запятой:
012345678910Результат в: мм²см²дм²м²
Через гипотенузу и радиус вписанного круга
Внутри вписанного круга есть точка (центр круга), которая равноудалена от обоих катетов и гипотенузы. Прямая от этой точки и до катета, проведенная под прямым углом, — это r (радиус) окружности.
Математически его можно рассчитать по формуле r = (a + b – c) / 2. После того, как радиус стал
известен, площадь можно вычислить через него:
Прямая от этой точки и до катета, проведенная под прямым углом, — это r (радиус) окружности.
Математически его можно рассчитать по формуле r = (a + b – c) / 2. После того, как радиус стал
известен, площадь можно вычислить через него:
S = r (r + c)
Радиус (R):
ммсмдмм
Гипотенуза (C):
ммсмдмм
Цифр после запятой:
012345678910Результат в: мм²см²дм²м²
Через гипотенузу и диаметр вписанного круга
Если d (диаметр) вписанного круга неизвестен, его можно рассчитать следующим образом: d = a + b – c. Если в условии задачи известен радиус r вписанной окружности, то для вычисления диаметра его можно умножить на 2, так как d = 2r. Формула площади при известном размере диаметра будет следующая:
S = d/2 * (d/2 + c)
Диаметр (D):
ммсмдмм
Гипотенуза (С):
ммсмдмм
Цифр после запятой:
012345678910Результат в: мм²см²дм²м²
Через гипотенузу и площадь вписанного круга
Для этой формулы понадобится знать площадь вписанного круга. Если в условиях задачи она неизвестна,
но вычисляется она по следующей формуле: S = π · r², где π – это математическая константа, равная в
сокращении 3,14, а r – радиус круга. Таким образом, зная площадь круга, можно рассчитывается площадь
треугольника:
Если в условиях задачи она неизвестна,
но вычисляется она по следующей формуле: S = π · r², где π – это математическая константа, равная в
сокращении 3,14, а r – радиус круга. Таким образом, зная площадь круга, можно рассчитывается площадь
треугольника:
S = √(S/π) * (√(S/π)+C)
Гипотенуза (C):
ммсмдмм
Площадь круга (S):
мм²см²дм²м²
Цифр после запятой:
012345678910Результат в: мм²см²дм²м²
Через гипотенузу и длину вписанной окружности (периметр)
Чтобы найти периметр окружности для главной формулы площади треугольника, нужно знать либо диаметр
окружности, либо радиус. Периметр в данном случае обозначается латинской буквой P. Формулы буду
следующие: если известен диаметр окружности P = d · π, если известен радиус окружности P = 2 · r ·
π.
Зная периметр вписанной окружности, можно рассчитать площадь прямоугольного треугольника по
следующей формуле:
S = P/2π * (P/2π + C)
где C – это гипотенуза треугольника, π – это математическая константа, равная в сокращении 3,14, и периметр окружности P.
Гипотенуза (C):
ммсмдмм
Периметр (P):
ммсмдмм
Цифр после запятой:
012345678910Результат в: мм²см²дм²м²
Через касание вписанной окружности которая делит гипотенузу на части
Если внутри прямоугольного треугольника нарисовать окружность, центр которой будет равноудален от катетов и гипотенузы, она разделит гипотенузу на два отрезка, которые условно обозначаются С1 и С2. С их помощью, не зная других величин, можно вычислить площадь треугольника:
S = C1 · C2
Часть (C1):
ммсмдмм
Часть (C2):
ммсмдмм
Цифр после запятой:
012345678910Результат в: мм²см²дм²м²
Площадь прямоугольного треугольника по формуле Герона
Для вычисления площади по методу Герона понадобится значение полупериметра, который обозначается
маленькой латинской буквой «p» (полный периметр обозначается заглавной Р). Полупериметр – это
половина суммы всех сторон, а именно: p = (a + b + c)/2, где a и b – это катеты, а С –
гипотенуза.
Полупериметр – это
половина суммы всех сторон, а именно: p = (a + b + c)/2, где a и b – это катеты, а С –
гипотенуза.
После того, как полупериметр вычислен, можно переходить к основной формуле площади прямоугольного треугольника. Для того, чтобы ее найти, нужно рассчитать корень квадратный из следующих величин:
S = (P — a) * (P — b)
Катет (a):
ммсмдмм
Катет (b):
ммсмдмм
Гипотенуза (c):
ммсмдмм
Цифр после запятой:
012345678910Результат в: мм²см²дм²м²
Герон Александрийский был математиком во времена Римской империи. Одним из направлений его
деятельности была так называемая «Метрика» и ее подраздел «Геометрика», по которым ученый написал
большую энциклопедию. В содержании этой книги, в том числе, была также формула вычисления площади
прямоугольного треугольника по длинам его сторон. Впервые этот метод определения площади был
установлен еще Архимедом, но конкретную формулу вывел именно Герон, предположительно в I веке до
н.э.
Впервые этот метод определения площади был
установлен еще Архимедом, но конкретную формулу вывел именно Герон, предположительно в I веке до
н.э.
Через гипотенузу и высоту
Высота – это прямая, соединяющая точку пересечения катетов с гипотенузой под углом 90°. При этом высота разделяет прямоугольный угол треугольника на два равных по 45° каждый. Обозначается данная величина латинской буквой h. Формула площадки треугольника через гипотенузу и высоту простая и линейная:
S = ½ch
Гипотенуза (c):
ммсмдмм
Высота (h):
ммсмдмм
Цифр после запятой:
012345678910Результат в: мм²см²дм²м²
Через катет и прилегающий острый угол
Для составления данной формулы нужно определиться с наименованием сторон и углов. Например, нижний
катет треугольника (горизонтально расположенный), будет называться стороной «a». Слева от него
находится прямой угол в 90°, под условным обозначением α, а справа от катета «a» находится
прилегающий острый угол β.
Слева от него
находится прямой угол в 90°, под условным обозначением α, а справа от катета «a» находится
прилегающий острый угол β.
Для итоговой формулы также понадобятся синусы углов. Таким образом, sin α= a / c и соответственно sin β= b / c. После того, как эти величины будут найдены, можно переходить к основной формуле:
S = a²/2 * (sin(α) * sin(β)/sin(180-(α+β))
где 180° — это сумма всех углов треугольника.
Катет (a):
ммсмдмм
Угол (β):
градусырадианы
Цифр после запятой:
012345678910Результат в: мм²см²дм²м²
Когда требуется вычисление площади прямоугольного треугольника
Площадь прямоугольных треугольников напрямую связана с вычислением площади прямоугольников, так как в
них обоих присутствуют углы в 90°. При этом для вычисления нужной величины, можно использовать любой
из вышеперечисленных способов. Выбор зависит только от наличия известных параметров геометрической
фигуры или от выбора самого простого решения. Для того, чтобы уметь пользоваться формулой, нужно
понять логическую цепочку ее вывода и, если не все составляющие уравнения известны, найти способ их
узнать через дополнительные формулы. Зная определенные параметры треугольника, путем различных
вычислений можно рассчитать его площадь.
Выбор зависит только от наличия известных параметров геометрической
фигуры или от выбора самого простого решения. Для того, чтобы уметь пользоваться формулой, нужно
понять логическую цепочку ее вывода и, если не все составляющие уравнения известны, найти способ их
узнать через дополнительные формулы. Зная определенные параметры треугольника, путем различных
вычислений можно рассчитать его площадь.
Как построить высоту треугольника — основные способы » Kupuk.net
Главная » Уроки » Геометрия
Автор Беликова Ирина На чтение 4 мин Просмотров 233
Для решения многих геометрических задач учащемуся нужно уметь быстро построить высоту треугольника. Сделать это можно несколькими простыми для восприятия способами, которые подходят для фигуры разной формы и размера. Весь процесс состоит из определённой последовательности действий, правильно выполнить которые сможет каждый школьник.
С применением циркуля
Если нужно нарисовать высоту (перпендикуляр к противоположной стороне) в произвольном треугольнике и измерить её, то лучше всего воспользоваться классическим методом построения. Он предусматривает использование циркуля в качестве основной рабочей принадлежности. Кроме этого, для работы понадобится лист бумаги, небольшая линейка, ластик и простой карандаш.
Он предусматривает использование циркуля в качестве основной рабочей принадлежности. Кроме этого, для работы понадобится лист бумаги, небольшая линейка, ластик и простой карандаш.
Способ начертить искомый отрезок:
- На листе бумаги чертят треугольник (можно нарисовать заранее, чтобы сэкономить время).
- Рисунок располагают так, чтобы вершина угла, из которого нужно начертить высоту, находилась сверху, а противоположная ему сторона фигуры была расположена горизонтально (по отношению к ученику).
- Иглу циркуля ставят в вершине любого угла у основания.
- Ножку с грифелем ставят в верхнюю точку треугольника, из которой проводится высота.
- Циркулем рисуют окружность и делают пометку в месте её пересечения с основанием фигуры.
- Аналогичным способом чертят круг из другого угла при основании. При этом важно определить новый радиус, который будет равен длине второй стороны треугольника.
- Делают пометку в месте пересечения начерченных окружностей.

- Ластиком стирают лишние линии, оставляя лишь поставленную точку.
- С помощью карандаша и линейки из неё проводят отрезок к вершине, который и будет высотой треугольника.
- Стирают линии, находящиеся под основанием.
Таким же способом можно с помощью циркуля построить высоту треугольника из любого другого угла.
С помощью линейки
Начертить и обозначить высоту можно и без циркуля. Для этого следует воспользоваться чертёжным угольником, 2 стороны которого перпендикулярны друг другу. Альтернативой этой школьной принадлежности могут стать 2 прямые линейки, соединённые между собой под прямым углом.
В остроугольном треугольнике
Провести высоту в треугольнике, где все углы острые (менее 90 градусов), довольно просто.
Чтобы справиться с этой задачей, нужно подготовить все необходимое и заранее начертить на бумаге геометрическую фигуру.
Правильная последовательность действий:
- Находят вершину, из которой хотят провести перпендикуляр.
- Совмещают угольник с противоположной стороной фигуры.
- Перемещают чертёжную принадлежность до тех пор, пока её перпендикулярная сторона не пройдёт через вершину.
- Простым карандашом проводят линию, которая и будет искомым отрезком.
В тупоугольной фигуре
Трёхсторонняя фигура, у которой один из углов тупой (более 90 градусов) имеет только 1 внутреннюю высоту. Для её проведения используют то же, что и в предыдущем случае.
Порядок действий:
- Располагают чертёж так, чтобы тупой угол оказался у основания.
- Угольник прикладывают к наибольшей стороне фигуры.
- Совмещают перпендикулярную сторону линейки с вершиной тупого угла.
- Соединяют 2 точки простым карандашом, получая искомую линию.
В прямоугольном и равнобедренном
В прямоугольном треугольнике нужно находить только 1 высоту. Две другие будут совпадать с катетами.
Пошаговая инструкция:
- Прикладывают одну из перпендикулярных сторон угольника к гипотенузе.
- Вторую сторону линейки совмещают с вершиной прямого угла.
- Проводят линию, которая будет высотой.
Проще всего проводить перпендикуляр из верхней точки равнобедренного треугольника.
Он будет совпадать с биссектрисой и медианой фигуры. Начертить его можно таким же способом, что и для остроугольной фигуры. Более простой метод предусматривает выполнение следующих действий:
- Линейкой замеряют длину основания.
- Эту величину делят на 2.
- Полученное значение откладывают от вершины одного из углов при основании.
- Отмечают середину стороны и соединяют её с верхней точкой фигуры.

Проведение высоты в треугольнике — это простая задача, с которой легко справится каждый ученик.
Для этого достаточно сделать чертёж геометрической фигуры и воспользоваться одним из существующих способов построения. Такая работа потребует минимум времени и не отнимет у школьника много сил.
Оцените автора
Как нарисовать треугольник: этапы выполнения задания
Как нарисовать треугольник? Этому учат в процессе изучения геометрии в школе. Чтобы задание было выполнено правильно, важно точно знать, какой треугольник необходимо изобразить: равносторонний, равнобедренный или же вписанный. Правилам начертания этих фигур будет посвящена данная статья.
Как рисовать треугольник с равными сторонами?
Как нарисовать треугольник, стороны у которого равны? Для этого можно воспользоваться одним из трех методов.
Такая фигура имеет три одинаковые по длине стороны, связанные тремя углами равной ширины. Это может быть сложным для рисования треугольника вручную. Поэтому можно использовать круглый объект для выделения углов.
Варианты создания фигуры
Обязательно используйте линейку и один из представленных ниже способов:
- Применение циркуля: надо начертить ровную линию. Проведите карандаш вдоль прямого края бумаги. Этот сегмент линии образует одну из сторон. А это означает, что нужно будет чертить вторую и третью линии одинаковой длины, каждая из которых достигает точки под углом 60° от первой линии. Удостоверьтесь, что достаточно места для рисования всех трех сторон!
- Разделите сегмент циркулем. Вставьте карандаш и убедитесь, что он острый! Поместите точку циркуля на один конец сегмента и установите карандаш на другую. Опишите дугу. Не изменяйте установленную «ширину» инструмента от точки циркуля до точки карандаша. Нарисуйте вторую дугу, чтобы она пересекала первую дугу, которую уже нарисовали.
 Отметьте точку, в которой пересекаются две дуги. Это вершина (верхняя точка) треугольника. Он должен лежать в точном центре сегмента линии, который нарисовали. Теперь можете сделать две прямые линии, ведущие к этой точке: по одному от каждого конца «нижнего» сегмента линии. Закончите треугольник. Далее с помощью линейки надо нарисовать еще два сегмента прямой линии – это стороны в треугольнике. Подключите каждый конец исходного сегмента линии к точке, в которой пересекаются дуги. Чтобы закончить работу, сотрите дуги, которые нарисовали, так, чтобы остался только треугольник.
Отметьте точку, в которой пересекаются две дуги. Это вершина (верхняя точка) треугольника. Он должен лежать в точном центре сегмента линии, который нарисовали. Теперь можете сделать две прямые линии, ведущие к этой точке: по одному от каждого конца «нижнего» сегмента линии. Закончите треугольник. Далее с помощью линейки надо нарисовать еще два сегмента прямой линии – это стороны в треугольнике. Подключите каждый конец исходного сегмента линии к точке, в которой пересекаются дуги. Чтобы закончить работу, сотрите дуги, которые нарисовали, так, чтобы остался только треугольник. - Использование объекта с круглой базой: этот совет подойдет для построения дуги. Предложенный метод по сути такой же, как с использованием циркуля.
Указанные советы помогут выяснить, как нарисовать равносторонний треугольник.
Рекомендации по построению равнобедренного треугольника
Равнобедренный треугольник представляет собой фигуру с двумя равными сторонами и двумя равными углами. Если знаете длину, основание и высоту стороны, это можно сделать только с линейкой и циркулем (или просто циркулем, если заданы размеры).
Если знаете длину, основание и высоту стороны, это можно сделать только с линейкой и циркулем (или просто циркулем, если заданы размеры).
Как нарисовать равнобедренный треугольник:
- Учитывая все боковые длины. Чтобы использовать этот метод, важно знать длину основания треугольника и длину двух равных сторон.
- Учитывая две равные стороны и угол между ними. Чтобы использовать этот метод, нужно знать длину двух равных сторон и измерение угла между этими двумя сторонами.
- Учитывая базовые и смежные углы – необходимо знать длину базы, градусы двух углов, смежных с основанием. Помните, что два угла, смежные с основанием равнобедренного треугольника, будут равны.
- Основа и высота. Нужно знать длину основания треугольника, а также высоту этой геометрической фигуры.
Вписанный треугольник
Как нарисовать вписанный треугольник? Выберите круглый объект. Используйте предмет с круглым основанием. Выбор компакт-диска станет хорошим вариантом. Но можно взять и другой объект нужного размера. Для этого метода свойственно, что длина каждой стороны равносторонней геометрической фигуры с тремя углами будет равна размерам радиуса (половине диаметра) круга.
Но можно взять и другой объект нужного размера. Для этого метода свойственно, что длина каждой стороны равносторонней геометрической фигуры с тремя углами будет равна размерам радиуса (половине диаметра) круга.
Как нарисовать треугольник, если используете компакт-диск? Представьте себе равносторонний треугольник, который вписывается в верхнюю правую часть компакт-диска. Надо начертить первую из сторон. Радиус круглого объекта – расстояние на полпути до получения желаемого результата. Удостоверьтесь, что линии нарисованы ровно.
С помощью линейки просто выполните измерения диаметра объекта и нарисуйте линию на половину длины. Если ее нет, поместите круглый объект на бумагу, затем тщательно проведите по окружности карандашом. Удалите объект – должен быть идеальный круг. Используйте прямой край, чтобы нарисовать линию через точный центр круга: точку, которая полностью равноудалена от любой точки по окружности круга.
Используйте круглый объект для создания дуги. Поместите объект по отрезку линии, с краем круга, расположенным на одном конце линии. Для обеспечения точности убедитесь, что линия проходит четко через центр круга. Используйте карандаш, чтобы начертить дугу – это четверть пути по окружности.
Для обеспечения точности убедитесь, что линия проходит четко через центр круга. Используйте карандаш, чтобы начертить дугу – это четверть пути по окружности.
Начертите еще одну дугу. Теперь сдвиньте круглый объект так, чтобы край касался другого конца сегмента линии.
Подведем итоги
В статье были предоставлены рекомендации, как нарисовать треугольник равносторонний, равнобедренный и вписанный в окружность.
Нарисуйте треугольник Паскаля — онлайн-инструменты для работы с числами
Скоро Эти числовые инструменты уже в пути
Создание номеров Numberwang
Создание списка номеров Numberwang.
Переписать числа
Учитывая числа и грамматику, рекурсивно переписать их.
Создать число с плавающей запятой
Создать число из мантиссы, основания и экспоненты.
Визуализация числа с плавающей запятой
Показать, как число fp представлено в компьютере. 9б форма.
Преобразование научной записи в число
Преобразование числа в научной записи в обычное число.
Создать символьную нумерацию
Создать список буквенных чисел (a, b, c, …, z, aa, ab, …).
Создать римскую нумерацию
Создать список римских цифр (i, ii, iii, iv, v…).
Создать нумерацию Брайля
Создать список цифр Брайля (⠂, ⠆, ⠒, ⠲, ⠢, …).
Генерация случайных двоичных чисел
Создать список случайных двоичных чисел.
Создание случайных восьмеричных чисел
Создание списка случайных восьмеричных чисел.
Создание случайных десятичных чисел
Создание списка случайных десятичных чисел.
Создание случайных шестнадцатеричных чисел
Создание списка случайных шестнадцатеричных чисел.
Вычислить текущую сумму
Вычислить кумулятивную сумму списка чисел.
Вычисление текущего произведения
Вычисление кумулятивного произведения списка чисел.
Вычислить факториал
Найти факториал числа.
Создание числовых анаграмм
Создание одной или нескольких числовых анаграмм.
Создание числовых биграмм
Создание списка цифровых биграмм из числа.
Создание числовых триграмм
Создание списка цифровых триграмм из числа.
Генерация числовых N-грамм
Создание списка цифровых nграмм из числа.
Создание полиномиальной последовательности
Создать список чисел полиномиальной прогрессии.
Создание префиксов SI
Создание списка префиксов метрик.
Анализ числа
Сообщить, сколько цифр встречается сколько раз.
Преобразование числа в порядковое
Преобразование количественного числительного в порядковое.
Преобразование порядкового числа в число
Преобразование порядкового числа в количественное.
Преобразование числа в римское число
Преобразование арабских цифр в римские.
Преобразование римских чисел в обычные числа
Преобразование римских цифр в арабские.
Создание чисел Негафибоначчи
Вычисление серии расширенных чисел Фибоначчи.
Генерация простых чисел Фибоначчи
Поиск чисел, которые являются одновременно числами Фибоначчи и простыми числами.
Проверка числа Фибоначчи
Проверка, является ли число числом Фибоначчи.
Проверка простых чисел Фибоначчи
Проверяет, является ли число одновременно числом Фибоначчи и простым числом.
Построить слова Фибоначчи
Создать последовательность слов Фибоначчи.
Создать слова Трибоначчи
Создать последовательность слов Трибоначчи.
Генерировать числа Негалука
Вычислить серию расширенных чисел Лукаса.
Генерировать простые числа Лукаса
Вычислить серию расширенных чисел Лукаса.
Lucas Prime Test
Проверить, является ли число одновременно числом Лукаса и простым числом.
Вычисление следа матрицы
Найдите сумму элементов главной диагонали матрицы.
Вычислить собственные значения матрицы
Найти собственные значения матрицы.
Умножение матриц
Вычисление произведения двух матриц.
Добавить матрицы
Вычислить сумму двух матриц.
Вычитание матриц
Вычисление разности двух матриц.
Генерация чисел Мозера де Брюйна
Вычисление последовательности чисел Мозера-Брейна.
Сгенерировать числа Колакоски
Вычислить последовательность чисел Ольденбургера-Колакоски.
Сгенерировать числа Стэнли
Вычислить последовательность чисел Стэнли.
Генерировать числа Гийсвейта
Вычислить последовательность самоописывающих чисел Гийсвейта.
Сгенерировать числа Рудина-Шапиро
Вычислить последовательность чисел Русина-Шапиро.
Генерация чисел Баума-Свита
Вычисление последовательности чисел Баума-Свита.
Генерация последовательности Туэ-Морса
Вычисление членов ряда чисел Туэ-Морса.
Создание идеальных чисел
Создание списка совершенных чисел.
Создание почти идеальных чисел
Создание списка почти идеальных чисел.
Создать последовательность избыточных чисел
Вычислить последовательность избыточных чисел.
Создать последовательность неполных чисел
Вычислить последовательность неполных чисел.
Расчет чисел кривой дракона
Создать список порядковых номеров для складывания бумаги.
Создание составных чисел
Создание списка чисел, которые не являются простыми.
Нарисовать таблицу чисел
Создать таблицу чисел.
Проверить, является ли число совершенным
Проверить, является ли заданное число совершенным числом.
Проверить, является ли число обильным
Проверить, является ли данное число обильным числом.
Проверить, является ли число недостаточным
Проверить, является ли данное число недостаточным.
Вычислить модуль
Найти модуль числа.
Группировка цифр числа
Группировка цифр числа.
Разделить число на цифры
Создать список цифр из числа.
Printf Numbers
Применение функций sprintf или printf к числам.
Создайте номера Zalgo
Позвольте Zalgo уничтожить ваши номера.
Повторить номер
Повторить номер несколько раз.
Зеркальное число
Создать зеркальную копию номера.
Дополнение числа нулями
Добавление нулей к числу.
Обратный порядок цифр
Обратный порядок цифр в числе.
Поворот числа
Циклический поворот цифр числа влево или вправо.
Увеличить число
Добавить единицу к заданному числу.
Увеличить все цифры в числе
Добавить единицу к каждой цифре в числе.
Уменьшить число
Вычесть единицу из заданного числа.
Уменьшить все цифры в числе
Вычесть единицу из каждой цифры в числе.
Находить закономерности в числах
Находить закономерности в последовательностях чисел.
Подсчет числа вхождений
Узнайте, как часто встречаются числовые значения.
Вычисление процентов
Найти x% числа.
Создание больших чисел
Создание списка больших чисел.
Генерация малых чисел
Создать список маленьких чисел.
Создание натуральных чисел
Создание списка натуральных чисел.
Создание рациональных чисел
Создание списка рациональных чисел.
Создать последовательность констант
Создать серию чисел, в которой все термины одинаковы.
Создание действительных чисел
Создание последовательности действительных чисел.
Создание комплексных чисел
Создание списка комплексных чисел.
Создать двоичные числа
Создать последовательность двоичных чисел.
Создание пар чисел
Создание последовательности пар чисел.
Создание троек чисел
Создание последовательности троек чисел.
Создание кортежей чисел
Создание последовательности n-кортежей чисел.
Переплетение чисел
Переплетение двух или более чисел поразрядно.
Найти десятичное представление числа
Переписать число в десятичной форме.
Преобразование дроби в десятичную
Преобразование дроби в десятичное число.
Преобразование десятичного числа в дробь
Преобразование десятичного числа в дробь.
Преобразование двоичного числа в восьмеричное
Преобразование числа с основанием два в число с основанием восемь.
Преобразование двоичного числа в десятичное число
Преобразование числа с основанием два в число с основанием десять.
Преобразование двоичного числа в шестнадцатеричное
Преобразование числа с основанием два в число с основанием шестнадцать.
Преобразование восьмеричного числа в двоичное
Преобразование числа с основанием восемь в число с основанием два.
Преобразование восьмеричного числа в десятичное
Преобразование числа с основанием восемь в число с основанием десять.
Преобразование восьмеричного числа в шестнадцатеричное
Преобразование числа с основанием восемь в число с основанием шестнадцать.
Преобразование десятичного числа в двоичное
Преобразование числа с основанием десять в число с основанием два.
Преобразование десятичного числа в восьмеричное число
Преобразование десятичного числа в восьмеричное.
Преобразование десятичного числа в шестнадцатеричное
Преобразование числа с основанием десять в число с основанием шестнадцать.
Преобразование шестнадцатеричного числа в двоичное число
Преобразование числа с основанием шестнадцать в число с основанием два.
Преобразование шестнадцатеричного числа в восьмеричное
Преобразование числа с основанием шестнадцать в число с основанием восемь.
Преобразование шестнадцатеричного числа в десятичное число
Преобразование числа с основанием шестнадцать в число с основанием десять.
Преобразование любого числа в любое основание
Преобразование любого числа в любом основании в любое другое основание.
Изменение мантиссы числа
Изменение значения числа.
Изменить показатель степени числа
Изменить степень числа.
Замена цифр буквами
Замена цифр в числе буквами алфавита.
Создание спирали чисел
Создание спирали из цифр числа.
Удалить десятичную точку
Удалить десятичный разделитель из десятичного числа.
Проверка числа Numberwang
Проверка, является ли данный номер числом numberwang.
Построение треугольника Паскаля — онлайн математические инструменты
Скоро Эти математические инструменты уже в пути
Функции построения графиков
Рисовать графики математических функций.
Рисование формулы LaTeX
Создание изображения из выражения LaTeX.
Найти n-ю цифру
Вычислить n-ю цифру числа Эйлера.
Найти n-ю цифру золотого сечения
Вычислить n-ю цифру золотого сечения.
Найти n-ю цифру числа пи
Вычислить n-ю цифру числа пи.
Вычислить сумму e цифр
Найти сумму e цифр.
Вычислить сумму цифр золотого сечения
Найти сумму цифр золотого сечения.
Вычислить сумму пи цифр
Найти сумму пи цифр.
Генерировать цифры Чамперноуна
Генерировать цифры константы Чамперноуна.
Найти n-ю цифру Чамперноуна
Вычислить n-ю цифру константы Чамперноуна.
Декодирование последовательности «посмотри и скажи»
Выполните обратную операцию над последовательностью «посмотри и скажи».
Создание P-адических расширений
Вычисление p-адических расширений произвольных чисел.
Создать последовательность панцифровых чисел
Создать список панцифровых чисел.
Создать последовательность номеров Стэнли
Создать список номеров Стэнли.
Создать последовательность номеров звонков
Создать список номеров звонков.
Генерация последовательности номеров Кармайкла
Создание списка номеров Чармичел.
Создать последовательность каталонских номеров
Создать список каталонских номеров.
Создать последовательность треугольных чисел
Создать список треугольных чисел.
Создать последовательность составных чисел
Создать список составных чисел.
Генерация секущей числовой последовательности
Создать список секущих чисел.
Создать последовательность чисел Голомба
Создать список чисел Голомба-Сильвермана.
Создать последовательность чисел Эйлера Тотиент
Создать список фи-чисел Эйлера.
Создать последовательность номеров жонглеров
Создать список номеров жонглеров.
Создать последовательность счастливых номеров
Создать список счастливых номеров.
Создать последовательность номеров Моцкина
Создать список номеров Моцкина.
Создать последовательность номеров Padovan
Создать список номеров Padovan.
Создать последовательность псевдосовершенных чисел
Создать список полусовершенных чисел.
Создать последовательность номеров Ulam
Создать список номеров Ulam.
Создать последовательность странных чисел
Создать список странных чисел.
Создать последовательность суперсовершенных чисел
Создать список суперсовершенных чисел.
Продолжение последовательности цифр
Найти закономерность в числовой последовательности и расширить ее.
Разбить число
Найти все разбиения данного целого числа.
Создать последовательность номеров разделов
Создать список номеров функций разделов.
Создание арифметической прогрессии
Создание арифметической последовательности чисел.
Создание геометрической прогрессии
Создание геометрической последовательности чисел.
Создание полиномиальной прогрессии
Создать полиномиальную последовательность чисел.
Создать последовательность натуральных чисел
Создать список натуральных чисел.
Создание степеней двойки
Создание списка чисел степеней двойки.
Создание степеней десяти
Создание списка чисел в степени десятка.
Создание плотной матрицы
Создание матрицы с очень небольшим количеством нулевых элементов.
Создать разреженную матрицу
Создать матрицу с очень небольшим количеством ненулевых элементов.
Умножить матрицу на скаляр
Умножить все элементы матрицы на число.
Проверить, является ли матрица единственной.
Определить, является ли матрица вырожденной.
Найти матрицу кофакторов
Для заданной матрицы найти ее матрицу кофакторов.
Найдите вспомогательную матрицу
По заданной матрице найдите ее дополнение.
LU Factor a Matrix
Разложить матрицу на LU-факторы.
Найти собственные значения матрицы
Найти собственные значения матрицы.
Украсить матрицу
Украсить матрицу, аккуратно выровняв все ее столбцы.
Переформатировать матрицу
Преобразовать матрицу из одного формата в другой формат.
Рисование архимедовой спирали
Создание архимедовой спирали.
Рисование спирали Эйлера
Создание кривой спирали Корню (полиномиальной спирали).
Рисование спирали Фибоначчи
Создание кривой спирали Фибоначчи.
Нарисуйте спираль Теодора
Создание спирали квадратного корня.
Нарисуйте спираль Ферма
Создайте кривую в виде параболической спирали.
Рисование прямоугольников Фибоначчи
Создание рисунка прямоугольников Фибоначчи.
Нарисуйте головку семени Фибоначчи
Создайте головку цветка Фибоначчи.
Нарисовать фрактал Падована
Создать фрактал равнобуквенных треугольников Падована.
Нарисуйте аполлонову прокладку
Создайте фрактал аполлоновой прокладки.
Нарисовать фрактал Мандельброта
Создать фрактал Мандельброта.
Нарисовать фрактал Юлии
Создать фрактал Джулии.
Нарисовать фрактал Рози
Создать фрактал Рози.
Нарисовать кривую фрактала Бланманже
Создать фрактал Бланманже.
Рисование функции Вейерштрасса
Создание фрактала Вейерштрасса.
Нарисовать кривую Минковского в виде вопросительного знака
Создать фрактал Минковского в виде вопросительного знака.
Нарисуйте функцию Тома
Создайте функцию Тома (также известную как функция попкорна или капли дождя).
Нарисовать функцию Дирихле
Нарисовать функцию Дирихле.
Нарисуйте рог Гавриила
Нарисуйте геометрическую фигуру с бесконечной площадью поверхности и конечным объемом.
Преобразование слов в числа
Преобразование чисел из английского текста в реальные цифры.
Преобразование чисел в слова
Преобразование чисел в письменный текст на английском языке.
Преобразование десятичной записи в научную запись
Преобразование чисел, записанных в десятичной форме, в научную форму.
Преобразование научной записи в десятичную.
Преобразование чисел, записанных в научной форме, в десятичную форму.
Округление чисел вверх
Применение операции ceil к числам.
Округление чисел в меньшую сторону
Применить операцию пола к числам.
Анализ чисел
Подсчитайте, сколько раз встречается каждое число.
Преобразование числа в виде суммы
Создание суммы, которая в сумме составляет заданное число.
Создать таблицу умножения
Нарисовать таблицу умножения n×m.
Нарисовать круговую диаграмму
Нарисовать круговую диаграмму и показать относительные размеры данных.
Визуализация процентов
Нарисуйте диаграмму, показывающую проценты.
Подбрось монетку
Подбрось монетку и выпадет орел или решка.
Бросьте кубик
Бросьте кубик и получите число на его стороне.
Гипотенуза треугольника. Калькулятор
Создано Ханной Памула, кандидатом наук
Отредактировано Bogna Szyk и Jack Bowater
Последнее обновление: 25 августа 2022 г.
Содержание:- Что такое гипотенуза треугольника
- Гипотенуза треугольника
- Как найти гипотенузу прямоугольного треугольника с помощью этого калькулятора гипотенузы?
- Часто задаваемые вопросы
С помощью этого калькулятора гипотенузы вы быстро найдете самую длинную сторону прямоугольного треугольника. Если вы хотите узнать, что такое гипотенуза прямоугольного треугольника, как ее найти и какова формула гипотенузы треугольника, вы найдете ответ ниже с простым примером, чтобы прояснить ситуацию. Не ждите больше, попробуйте этот калькулятор гипотенузы!
Если вы хотите узнать, что такое гипотенуза прямоугольного треугольника, как ее найти и какова формула гипотенузы треугольника, вы найдете ответ ниже с простым примером, чтобы прояснить ситуацию. Не ждите больше, попробуйте этот калькулятор гипотенузы!
Что такое гипотенуза треугольника
Гипотенуза — это самая длинная сторона прямоугольного треугольника . Это сторона, противоположная прямому углу (90°). Длину гипотенузы можно найти, например, из теоремы Пифагора.
Формула гипотенузы треугольника
В этом калькуляторе гипотенузы реализовано несколько формул — таким образом, мы убедились, что он подходит для различных сценариев, с которыми вы можете столкнуться. Вы можете найти гипотенузу:
- Даны две стороны прямоугольного треугольника
Используйте теорему Пифагора для вычисления гипотенузы по сторонам прямоугольного треугольника. Извлеките квадратный корень из суммы квадратов:
-
c = √(a² + b²)
- Данный угол и одна сторона
-
c = a / sin(α) = b / sin(β), по закону синусов
- Заданная площадь и одна ножка
Так как площадь прямоугольного треугольника равна a * b / 2 , затем
-
c = √(a² + b²) = √(a² + (площадь * 2 / a)²) = √((площадь * 2 / b)² + b²)
Как найти гипотенузу прямоугольного треугольника с помощью этого калькулятора гипотенузы?
Давайте посчитаем, какой длины должна быть лестница, если мы хотим спасти котенка с 10-футовой крыши. Калькулятор помогает найти длину лестницы от земли до края крыши, но не забывайте про часть лестницы, которая должна выходить за край!
Калькулятор помогает найти длину лестницы от земли до края крыши, но не забывайте про часть лестницы, которая должна выходить за край!
- Выберите нужный вариант для расчетов . Мы знаем, что наша крыша имеет высоту 10 футов и что самый безопасный угол для лестницы составляет ~75,5°. Из выпадающего списка данного поля выберите вариант: угол ∡ и одна сторона .
- Изменить единицы измерения на футы .
Введите указанные значения . Наша нога a имеет длину 10 футов, а угол α между лестницей и землей равен 75,5°.
- Появляется
Длина лестницы, которая равна гипотенузе прямоугольного треугольника! Равен 10,33 фута.
Также отображаются угол β = 14,5° и катет b = 2,586 фута. Вторая ножка также является важным параметром, так как говорит о том, насколько лестница должна быть удалена от стены (точнее, от края крыши).
 Общий принцип, который следует помнить, — это правило 4:1 : на каждые четыре фута высоты по вертикали ножка лестницы должна отодвигаться от стены на один фут.
Общий принцип, который следует помнить, — это правило 4:1 : на каждые четыре фута высоты по вертикали ножка лестницы должна отодвигаться от стены на один фут.
Часто задаваемые вопросы
Как найти гипотенузу с грехом?
- Выполнить операцию sin над углом (не прямым углом).
- Разделить длину стороны напротив угла из шага 1 на результат шага 1.
- Результатом является гипотенуза .
Всегда ли гипотенуза является самой длинной стороной?
Да, гипотенуза всегда самая длинная сторона , но только для прямоугольных треугольников. В равнобедренных треугольниках две равные стороны называются катетами, а в равнобедренном треугольнике все стороны называются просто сторонами.
Как найти смежную и противоположную гипотенузу?
- Найдите самую длинную сторону и обозначьте ее как гипотенузу .

- Смежное и противоположное можно найти, только если выбрать один из непрямых углов.
- Прилегающая сторона — это сторона, которая вместе с гипотенузой образует выбранный угол .
- Противоположная сторона — это сторона, которая не образует выбранный угол .
Как найти высоту гипотенузы?
- Нарисуйте высоту гипотенузы треугольника. Два новых треугольника, которые вы создали, подобны друг другу и основному треугольнику.
- Разделите длину самой короткой стороны главного треугольника на гипотенузу главного треугольника.
- Умножьте результат на длину оставшейся стороны, чтобы получить длину высоты.
- В качестве альтернативы углы внутри меньших треугольников будут такими же, как углы основного треугольника, так что вы можете выполнить тригонометрию чтобы найти его другим способом.
Что делать, если гипотенуза противоположна?
Если гипотенуза противоположна, то вы считаете неправильный угол — вы не можете использовать тригонометрию с прямым углом треугольника. Рассмотрим один из других углов, и противоположной будет сторона, которая не образует этот угол.
Рассмотрим один из других углов, и противоположной будет сторона, которая не образует этот угол.
Как построить перпендикуляр к гипотенузе?
- Приобретите циркуль, линейку и ручку или карандаш.
- Установите циркуль на длину гипотенузы (или любую длину, если она остается постоянной).
- Нарисуйте окружность с центром на одном из концов гипотенузы.
- Нарисуйте еще один круг с центром на другом конце гипотенузы.
- Нарисуйте линию, соединяющую две точки , где пересекаются эти окружности. Эта линия является гипотенузой.
Как найти гипотенузу равнобедренного прямоугольного треугольника?
- Найдите длину одной из сторон , не лежащих в гипотенузе .
- Квадрат по длине стороны.
- Удвоить результат предыдущего шага.
- Квадратный корень результат шага 3. Это длина гипотенузы .

Что такое теорема об угле гипотенузы?
Теорема об угле гипотенузы — это способ проверки конгруэнтности двух прямоугольных треугольников или нет. Он гласит, что если два прямоугольных треугольника имеют одинаковые гипотенузу и острый угол, то они равны.
Откуда произошло слово гипотенуза?
Слово гипотенуза происходит от древнегреческого hypoteinousa , что означает «растягивающаяся под (прямым углом)». Это, в свою очередь, происходит от гипо- «под» и теинеина «растягиваться». Еще одна вещь, за которую мы должны благодарить древних греков!
Как решить прямоугольный треугольник только с гипотенузой?
Вы не можете построить прямоугольный треугольник, используя только гипотенузу . Это связано с тем, что две другие стороны и углы все еще не определены, и поэтому треугольник может иметь множество форм.
Ханна Памула, кандидат наук
Гипотенуза
Посмотреть 18 подобных калькуляторов треугольников 🔺
30 60 90 треугольник45 45 90 треугольникПлощадь прямоугольного треугольника… еще 15
Как построить (начертить) равносторонний треугольник или линейка
Как построить (начертить) равносторонний треугольник с помощью циркуля и линейки или линейки — Открытый справочник по математикеОткрытая математическая ссылка
Главная Контакт О Тематический указатель
На этой странице показано, как построить
равносторонний треугольник
с циркулем и линейкой или линейкой. Равносторонний треугольник – это треугольник, у которого все три стороны имеют одинаковую длину. Он начинается с заданного
отрезок
что является длиной каждой стороны желаемого равностороннего треугольника.
Равносторонний треугольник – это треугольник, у которого все три стороны имеют одинаковую длину. Он начинается с заданного
отрезок
что является длиной каждой стороны желаемого равностороннего треугольника.
Это работает, потому что ширина компаса не меняется между рисованием каждой стороны, гарантируя, что все они конгруэнтный (одинаковая длина). Это похоже на Конструкция под углом 60 градусов, потому что внутренние углы равностороннего треугольника составляют все 60 градусов.
Печатные пошаговые инструкции
Вышеупомянутая анимация доступна как распечатанная пошаговая инструкция, которую можно использовать для изготовления раздаточных материалов или когда компьютер недоступен.
Доказательство
Изображение ниже является окончательным рисунком выше.
| Аргумент | Причина | |
|---|---|---|
| 1 | PQ, PR и QR все конгруэнтны AB, поэтому все имеют одинаковую длину | Набор ширины компаса от AB, используемый для их рисования |
| 2 | Треугольник RPQ — равносторонний треугольник с заданной длиной стороны AB. | Все три стороны совпадают. См. Определение равностороннего треугольника. |
— Ч.Э.Д.
Попробуйте сами
Нажмите здесь, чтобы распечатать рабочий лист, содержащий две задачи, которые можно попробовать. Когда вы попадете на страницу, используйте команду печати браузера, чтобы распечатать столько, сколько хотите. Распечатанный результат не защищен авторским правом.Другие страницы строительства на этом сайте
- Список рабочих листов для печати конструкций
Линии
- Знакомство с конструкциями
- Скопируйте сегмент линии
- Сумма n отрезков
- Разница двух отрезков
- Биссектриса отрезка
- Перпендикуляр в точке прямой
- Перпендикуляр от прямой через точку
- Перпендикуляр от конечной точки луча
- Разделить отрезок на n равных частей
- Параллельная линия через точку (угловая копия)
- Параллельная линия через точку (ромб)
- Параллельная линия через точку (перемещение)
Уголки
- Разделение угла пополам
- Скопируйте угол
- Построить угол 30°
- Построить угол 45°
- Построение угла 60°
- Построить угол 90° (прямой угол)
- Сумма n углов
- Разность двух углов
- Дополнительный уголок
- Дополнительный уголок
- Построение углов 75° 105° 120° 135° 150° и более
Треугольники
- Скопируйте треугольник
- Равнобедренный треугольник с основанием и стороной
- Равнобедренный треугольник с основанием и высотой
- Равнобедренный треугольник с катетом и углом при вершине
- Равносторонний треугольник
- Треугольник 30-60-90 по гипотенузе
- Треугольник по трем сторонам (sss)
- Треугольник по одной стороне и прилежащим углам (asa)
- Треугольник с двумя углами и не включенной стороной (aas)
- Треугольник по двум сторонам и углу между ними (sas)
- Медианы треугольника
- Средняя часть треугольника
- Высота треугольника
- Высота треугольника (вне корпуса)
Прямоугольные треугольники
- Прямоугольный треугольник с одним катетом и гипотенузой (HL)
- Прямоугольный треугольник с обеими сторонами (LL)
- Прямоугольный треугольник по гипотенузе и одному углу (HA)
- Прямоугольный треугольник по одному катету и одному углу (LA)
Треугольные центры
- Треугольник с центром
- Центр окружности треугольника
- Ортоцентр треугольника
- Центр тяжести треугольника
Окружности, дуги и эллипсы
- Нахождение центра окружности
- За круг дается 3 очка
- Касательная в точке окружности
- Касательные через внешнюю точку
- Касательные к двум окружностям (внешние)
- Касательные к двум окружностям (внутренние)
- Вписанная окружность треугольника
- Точки фокусировки данного эллипса
- Окружность треугольника
Полигоны
- Квадрат с одной стороной
- Квадрат, вписанный в круг
- Шестиугольник с одной стороной
- Шестиугольник, вписанный в данную окружность
- Пятиугольник вписан в заданный круг
Неевклидовы конструкции
- Построить эллипс из нити и булавок
- Найти центр круга с любым прямоугольным объектом
(C) 2011 Copyright Math Open Reference.
Все права защищены
Описанные и вписанные окружности треугольников — Криста Кинг Математика
Описанные и вписанные окружности нарисованы вокруг центра описанной окружности и центра вписанной окружности
В этом уроке мы рассмотрим описанные и вписанные окружности и особые отношения, которые формируются из этих геометрических идей.
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Описанные окружности
Когда окружность описывает треугольник, треугольник находится внутри круга, и треугольник касается окружности каждой вершиной.
Вы используете серединные перпендикуляры каждой стороны треугольника, чтобы найти центр окружности, которая будет описана вокруг треугольника. Так, например, учитывая ???\треугольник GHI???,
найти середину каждой стороны.
Найдите биссектрису, проходящую через каждую середину.
Точка пересечения серединных перпендикуляров является центром окружности.
Центр описанной окружности называется « центром окружности ».
Для остроугольного треугольника центр описанной окружности находится внутри треугольника.
В прямоугольном треугольнике центр описанной окружности находится на стороне, противоположной прямому углу.
В тупоугольном треугольнике центр описанной окружности находится вне треугольника.
Вписанные окружности
Когда окружность вписана в треугольник, треугольник находится вне круга, а окружность касается сторон треугольника в одной точке с каждой стороны. Стороны треугольника касаются окружности.
Чтобы нарисовать вписанную окружность внутри равнобедренного треугольника, используйте биссектрисы каждой стороны, чтобы найти центр окружности, вписанной в треугольник. Например, учитывая ???\треугольник PQR???,
Нарисуйте биссектрисы угла.
Пересечение биссектрисы угла является центром вписанной окружности.
Помните, что каждая сторона треугольника касается окружности, поэтому, если вы проведете радиус от центра окружности до точки, где окружность касается края треугольника, радиус образует прямой угол с краем треугольника. треугольник.
Центр вписанной окружности называется « в центре ». Центр всегда будет внутри треугольника.
Давайте используем то, что мы знаем об этих конструкциях, для решения нескольких задач.
Нахождение и зарисовка описанных и вписанных окружностей
Пройти курс
Хотите узнать больше о геометрии? У меня есть пошаговый курс для этого. 🙂
Учить больше
Нахождение радиуса окружности, описывающей треугольник
Пример
???\overline{GP}???, ???\overline{EP}??? и ???\overline{ ФП}??? являются серединными перпендикулярами треугольника ???\vartriangle ABC???, и ???AC=24??? единицы. Чему равен радиус окружности, описанной вокруг ???\треугольника ABC????
Точка ???P??? является центром описанной окружности, описанной вокруг ???\треугольника ABC??? потому что именно здесь пересекаются серединные перпендикуляры треугольника. Мы можем нарисовать ???\bigcirc P???.
Мы также знаем, что ???AC=24??? единиц, а так как ???\overline{EP}??? является серединным перпендикуляром к ???\overline{AC}???, точка ???E??? является средней точкой. Следовательно,
Следовательно,
???EC=\frac{1}{2}AC=\frac{1}{2}(24)=12??? 9{2}}???
???ПК=13???
Давайте попробуем другую задачу.
Вы используете серединные перпендикуляры каждой стороны треугольника, чтобы найти центр окружности, которая будет описана вокруг треугольника.
Пример
Если ???CQ=2x-7??? и ???CR=x+5???, какова мера ???CS???, учитывая, что ???\overline{XC}???, ???\overline{YC}?? ? и ???\overline{ZC}??? являются биссектрисами треугольника ???\треугольника XYZ???.
Потому что ???\overline{XC}???, ???\overline{YC}??? и ???\overline{ZC}??? являются биссектрисами треугольника ???\треугольника XYZ???, ???C??? является центром треугольника. Окружность с центром ???C??? будет касаться каждой стороны треугольника в точке пересечения.
???\overline{CQ}???, ???\overline{CR}??? и ???\overline{CS}??? все радиусы окружности ???C???, поэтому все они равны по длине.


 1283555449519
1283555449519
 418987695398
418987695398 Настройка.
Настройка. Подробно
Подробно



 Значит, доказано, что средняя линия равна половине основания.
Значит, доказано, что средняя линия равна половине основания.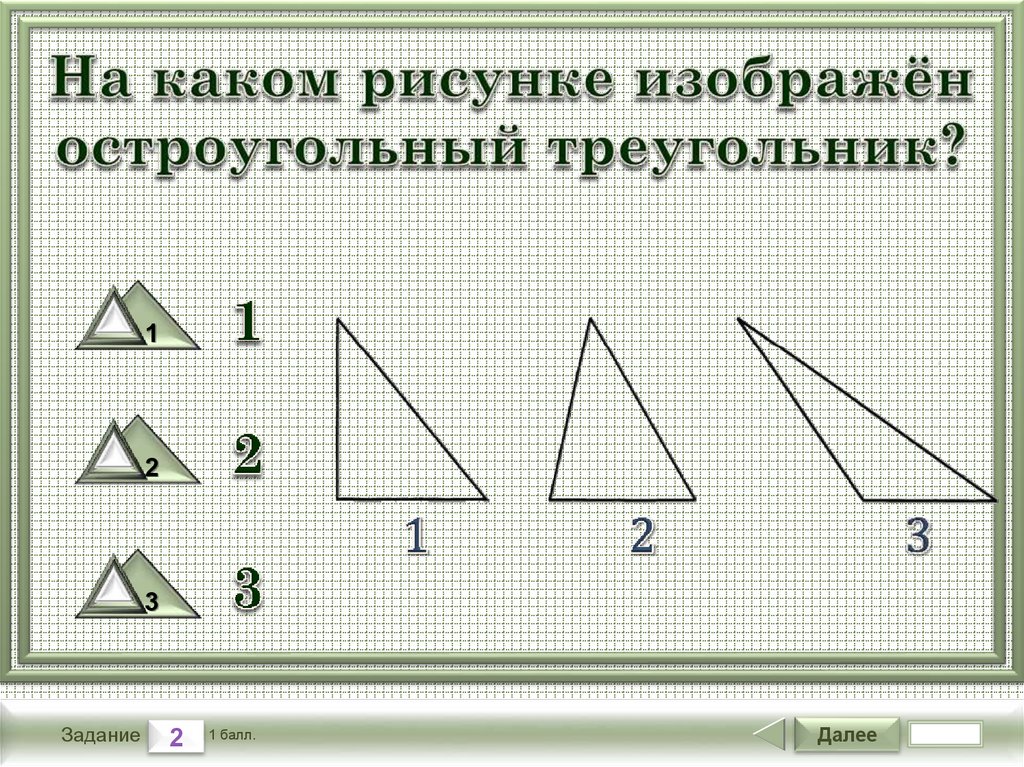 Так как треугольник прямоугольный, то его площадь найдем как половину произведения катетов:
Так как треугольник прямоугольный, то его площадь найдем как половину произведения катетов:


 Отметьте точку, в которой пересекаются две дуги. Это вершина (верхняя точка) треугольника. Он должен лежать в точном центре сегмента линии, который нарисовали. Теперь можете сделать две прямые линии, ведущие к этой точке: по одному от каждого конца «нижнего» сегмента линии. Закончите треугольник. Далее с помощью линейки надо нарисовать еще два сегмента прямой линии – это стороны в треугольнике. Подключите каждый конец исходного сегмента линии к точке, в которой пересекаются дуги. Чтобы закончить работу, сотрите дуги, которые нарисовали, так, чтобы остался только треугольник.
Отметьте точку, в которой пересекаются две дуги. Это вершина (верхняя точка) треугольника. Он должен лежать в точном центре сегмента линии, который нарисовали. Теперь можете сделать две прямые линии, ведущие к этой точке: по одному от каждого конца «нижнего» сегмента линии. Закончите треугольник. Далее с помощью линейки надо нарисовать еще два сегмента прямой линии – это стороны в треугольнике. Подключите каждый конец исходного сегмента линии к точке, в которой пересекаются дуги. Чтобы закончить работу, сотрите дуги, которые нарисовали, так, чтобы остался только треугольник.