Сообщение о том какие бывают числа. Какие бывают виды чисел, понятия и операции
Натуральные числа
Числа, используемые при счете называются натуральными числами. Например, $1,2,3$ и т.д. Натуральные числа образуют множество натуральных чисел, которое обозначают $N$ .Данное обозначение исходит от латинского слова naturalis- естественный.
Противоположные числа
Определение 1
Если два числа отличаются только знаками, их называют в математике противоположными числами.
Например, числа $5$ и $-5$ противоположные числа, т.к. отличаются только знаками.
Замечание 1
Для любого числа есть противоположное число, и притом только одно.
Замечание 2
Число нуль противоположно самому себе.
Целые числа
Определение 2
Целыми числами называют натуральные, противоположные им числа и нуль.
Множество целых чисел включает в себя множество натуральных и противоположных им.
Обозначают целые числа $Z.
$
Дробные числа
Числа вида $\frac{m}{n}$ называют дробями или дробными числами. Так же дробные числа можно записывать десятичной форме записи, т.е. в виде десятичных дробей.
Например:$\ \frac{3}{5}$ , $0,08$ и Т.Д.
Так же, как и целые, дробные числа могут быть как положительными, так и отрицательными.
Рациональные числа
Определение 3
Рациональными числами
Любое рациональное число, как целое, так и дробное можно представить в виде дроби $\frac{a}{b}$, где $a$- целое число, а $b$- натуральное.
Таким образом, одно и то же рациональное число можно записать разными способами.
Например,
Отсюда видно, что любое рациональное число может быт представлено в виде конечной десятичной дроби или бесконечной десятичной периодической дроби.
Множество рациональных чисел обозначается $Q$.
В результате выполнения любого арифметического действия над рациональными числами полученный ответ будет рациональным числом.
2=6$.Корнями этого уравнения будут числа $\surd 6$ и -$\surd 6$. Данные числа не будут являться рациональными.
Так же при нахождении диагонали квадрата со стороной $3$ мы применив теорему Пифагора получим, что диагональ будет равна $\surd 18$. Это число также не является рациональным.
Такие числа называются иррациональными.
Итак, иррациональным числом называют бесконечную десятичную непериодическую дробь.
Одно из часто встречающихся иррациональных чисел- это число $\pi $
При выполнении арифметических действий с иррациональными числами получаемый результат может оказаться и рациональным, так и иррациональным числом.
Докажем это на примере нахождения произведения иррациональным чисел. Найдем:
$\ \sqrt{6}\cdot \sqrt{6}$
$\ \sqrt{2}\cdot \sqrt{3}$
Решениею
$\ \sqrt{6}\cdot \sqrt{6} = 6$
$\sqrt{2}\cdot \sqrt{3}=\sqrt{6}$
На этом примере видно, что результат может оказаться как рациональным, так и иррациональным числом.
Если в арифметических действиях участвуют рациональное и иррациональные числа одновременно, то в результате получится иррациональное число (кроме, конечно, умножения на $0$).
Действительные числа
Множеством действительных чисел называется множество содержащее множество рациональных и иррациональных чисел.
Обозначается множество действительных чисел $R$. Символически множество действительных чисел можно обозначить $(-?;+?).$
Мы говорили ранее о том, что иррациональным числом называют бесконечную десятичную непериодическую дробь, а любое рациональное число может быт представлено в виде конечной десятичной дроби или бесконечной десятичной периодической дроби, поэтому действительным числом будет являться любая конечная и бесконечная десятичная дробь.
При выполнении алгебраических действий будут выполняться следующие правила
- при умножении и делении положительных чисел полученное число будет положительным
- при умножении и делении отрицательных чисел полученное число будет положительным
- при умножении и делении отрицательного и положительного чисел полученное число будет отрицательным
Также действительные числа можно сравнивать друг с другом.
Понятие действительного числа: действительное число — (вещественное число), всякое неотрицательное или отрицательное число либо нуль. С помощью действительных чисел выражают измерения каждой физической величины .
Вещественное , или действительное число возникло из необходимости измерений геометрической и физической величин мира. Кроме того, для проведения операций извлечения корня, вычисления логарифма, решения алгебраических уравнений и т.д.
Натуральные числа образовались с развитием счета, а рациональные с потребностью управлять частями целого, то вещественные числа (действительные) используются для измерений непрерывных величин. Т.о., расширение запаса чисел, которые рассматриваются, привело к множеству вещественных чисел, которое кроме рациональных чисел состоит из других элементов, называемых
Множество действительных чисел (обозначается R ) — это множества рациональных и иррациональных чисел собранные вместе.
Действительные числа делят на рациональные и иррациональные .
Множество вещественных чисел обозначают и зачастую называют вещественной или числовой прямой . Вещественные числа состоят из простых объектов: целых и рациональных чисел .
Число, которое возможно записать как отношение, где m — целое число, а n — натуральное число, является рациональным числом .
Всякое рациональное число легко представить как конечную дробь либо бесконечную периодическую десятичную дробь.
Пример ,
Бесконечная десятичная дробь , это десятичная дробь, у которой после запятой есть бесконечное число цифр.
Числа, которые нельзя представить в виде , являются иррациональными числами .
Пример:
Всякое иррациональное число легко представить как бесконечную непериодическую десятичную дробь.
Пример ,
Рациональные и иррациональные числа создают множество действительных чисел.
Всем действительным числам соответствует одна точка координатной прямой, которая называется числовая прямая .
Для числовых множеств используются обозначения:
- N — множество натуральных чисел;
- Z — множество целых чисел;
- Q — множество рациональных чисел;
- R — множество действительных чисел.
Теория бесконечных десятичных дробей.
Вещественное число определяется как бесконечная десятичная дробь , т.е.:
±a 0 ,a 1 a 2 …a n …
где ± есть один из символов + или −, знак числа,
a 0 — целое положительное число,
a 1 ,a 2 ,…a n ,… — последовательность десятичных знаков, т.е. элементов числового множества {0,1,…9}.
Бесконечную десятичную дробь можно объяснить как число, которое на числовой прямой находится между рациональными точками типа:
±a 0 ,a 1 a 2 …a n и ±(a 0 ,a 1 a 2 …a n +10 −n) для всех n=0,1,2,…
Сравнение вещественных чисел как бесконечных десятичных дробей происходит поразрядно.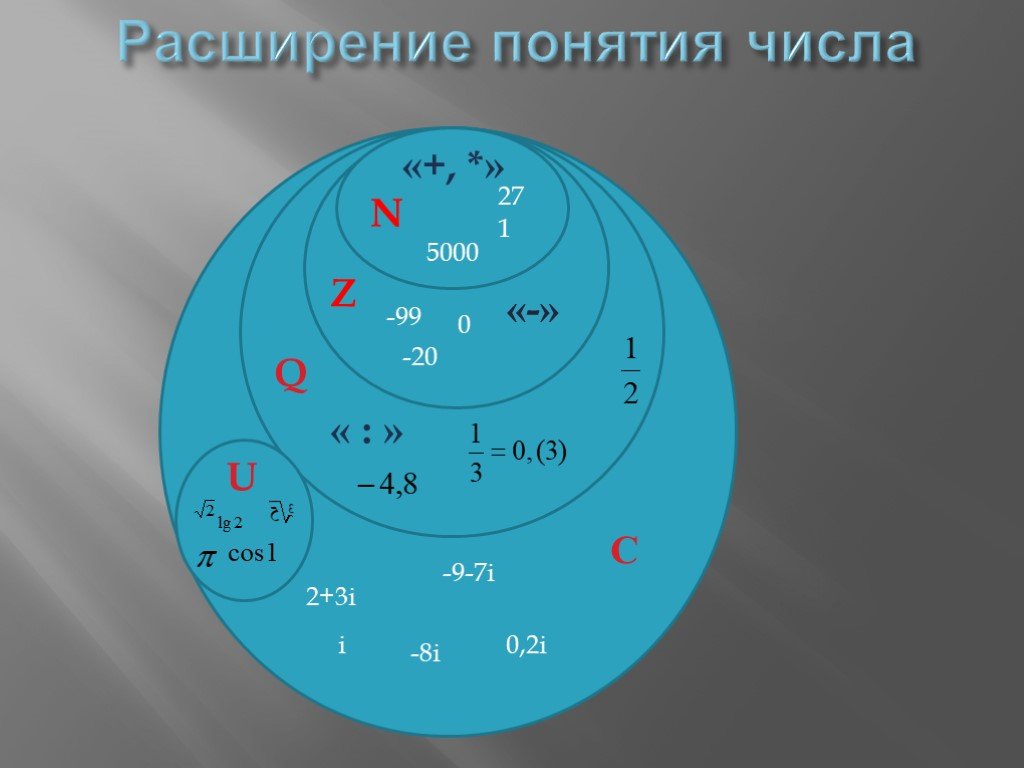
Например , предположим даны 2 положительны числа:
α =+a 0 ,a 1 a 2 …a n …
β =+b 0 ,b 1 b 2 …b n …
Если a 0 0, то α; если a 0 >b 0 то α>β . Когда a 0 =b 0 переходим к сравнению следующего разряда. И т.д. Когда α≠β , значит после конечного количества шагов встретится первый разряд n , такой что a n ≠b n . Если a n n , то α; если a n >b n то α>β .
Но при этом нудно обратить внимание на то, что число a 0 ,a 1 a 2 …a n (9)=a 0 ,a 1 a 2 …a n +10 −n . Поэтому если запись одного из сравниваемых чисел, начиная с некоторого разряда это периодическая десятичная дробь, у которой в периоде стоит 9, то её нужно заменить на эквивалентную запись, с нулем в периоде.
Арифметические операции с бесконечными десятичными дробями это непрерывное продолжение соответствующих операций с рациональными числами. Например , суммой вещественных чисел α и β является вещественное число α+β , которое удовлетворяет таким условиям:
∀ a′,a′′,b′,b′′ ∈ Q(a′ ⩽ α ⩽ a′′) ∧ (b′ ⩽ β ⩽ b′′) ⇒ (a′+b′ ⩽ α + β ⩽ a′′+b′′)
Аналогично определяет операция умножения бесконечных десятичных дробей.
Цифры в записи многозначных чисел разбивают справа налево на группы по три цифры в каждой. Эти группы называют классами . В каждом классе цифры справа налево обозначают единицы, десятки и сотни этого класса:
Первый класс справа называют классом единиц , второй — тысяч , третий — миллионов , четвёртый — миллиардов , пятый — триллионов , шестой — квадриллионов , седьмой — квинтиллионов , восьмой — секстиллионов .
Для удобства чтения записи многозначного числа, между классами оставляется небольшой пробел. Например, чтобы прочитать число 148951784296, выделим в нём классы:
и прочитаем число единиц каждого класса слева направо:
148 миллиардов 951 миллион 784 тысячи 296.
При чтении класса единиц в конце обычно не добавляют слово единиц.
Каждая цифра в записи многозначного числа занимает определённое место — позицию. Место (позицию) в записи числа, на котором стоит цифра, называют разрядом .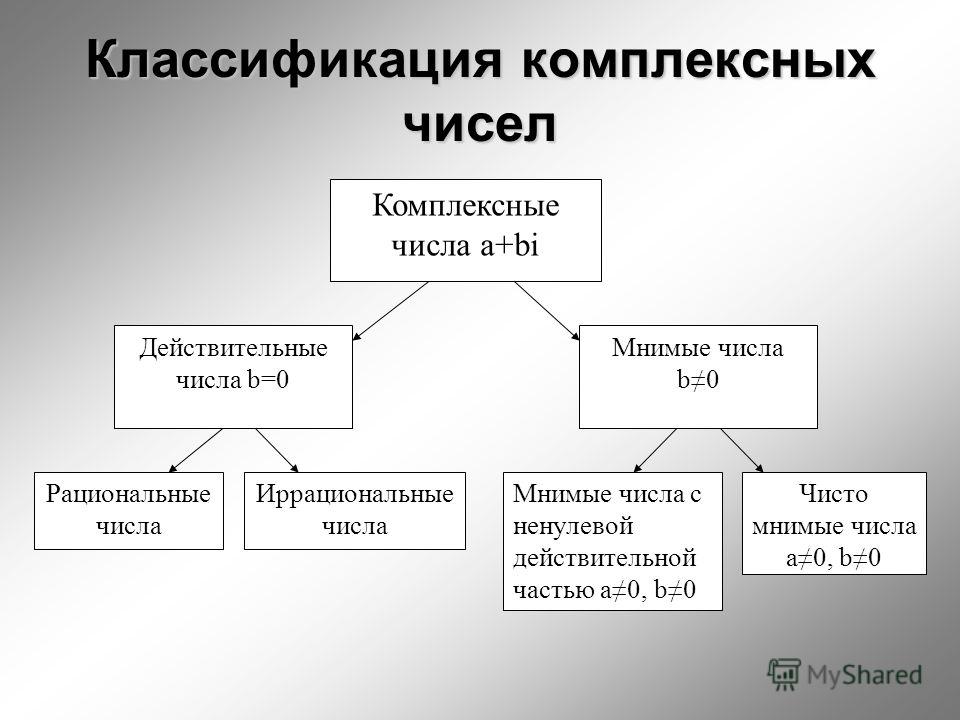
Счёт разрядов идёт справа налево. То есть, первая цифра справа в записи числа называется цифрой первого разряда, вторая цифра справа — цифрой второго разряда и т. д. Например, в первом классе числа 148 951 784 296, цифра 6 является цифрой первого разряда, 9 — цифра второго разряда, 2 — цифра третьего разряда:
Единицы, десятки, сотни, тысячи и т. д. иначе ещё называют разрядными единицами :
единицы называют единицами 1-го разряда (или простыми единицами )
десятки называют единицами 2-го разряда
сотни называют единицами 3-го разряда и т. д.
Все единицы, кроме простых единиц, называются составными единицами . Так, десяток, сотня, тысяча и т. д. — составные единицы. Каждые 10 единиц любого разряда составляют одну единицу следующего (более высокого) разряда. Например, сотня содержит 10 десятков, десяток — 10 простых единиц.
Любая составная единица по сравнению с другой единицей, меньшей её называется единицей высшего разряда , а по сравнению с единицей, большей её, называется единицей низшего разряда .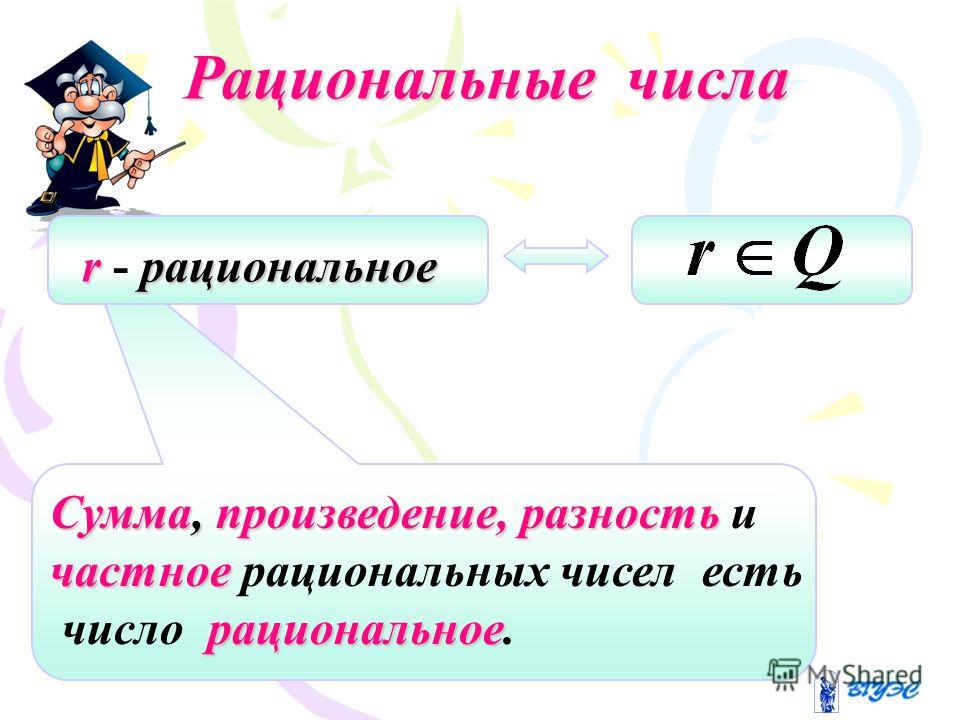
Например, сотня является единицей высшего разряда относительно десятка и единицей низшего разряда относительно тысячи.
Чтобы узнать, сколько в числе заключается всех единиц какого-либо разряда, надо отбросить все цифры, означающие единицы низших разрядов и прочитать число, выражаемое оставшимися цифрами.
Например, требуется узнать, сколько всего сотен содержится в числе 6284, т. е. сколько сотен заключается в тысячах и в сотнях данного числа вместе.
В числе 6284 на третьем месте в классе единиц стоит цифра 2, значит в числе есть две простые сотни. Следующая влево цифра — 6, означает тысячи. Так как в каждой тысяче содержится 10 сотен то, в 6 тысячах их заключается 60. Всего, таким образом, в данном числе содержится 62 сотни.
Цифра 0 в каком-нибудь разряде означает отсутствие единиц в данном разряде. Например, цифра 0 в разряде десятков означает отсутствие десятков, в разряде сотен — отсутствие сотен и т. д. В том разряде, где стоит 0, при чтении числа ничего не произносится:
172 526 — сто семьдесят две тысячи пятьсот двадцать шесть.
102 026 — сто две тысячи двадцать шесть.
Интуитивное представление о числе, по–видимому, так же старо, как и само человечество, хотя с достоверностью проследить все ранние этапы его развития в принципе невозможно. Прежде чем человек научился считать или придумал слова для обозначения чисел, он, несомненно, владел наглядным, интуитивным представлением о числе, позволявшим ему различать одного человека и двух людей или двух и многих людей. То, что первобытные люди сначала знали только “один”, “два” и “много”, подтверждается тем, что в некоторых языках, например в греческом, существуют три грамматические формы: единственного числа, двойственного числа и множественного числа. Позднее человек научился делать различия между двумя и тремя деревьями и между тремя и четырьмя людьми. Счет изначально был связан с вполне конкретным набором объектов, и самые первые названия чисел были прилагательными. Например, слово “три” использовалось только в сочетаниях “три дерева” или “три человека”; представление о том, что эти множества имеют между собой нечто общее – понятие троичности – требует высокой степени абстракции.
О том, что счет возник раньше появления этого уровня абстракции, свидетельствует тот факт, что слова “один” и “первый”, равно как “два” и “второй”, во многих языках не имеют между собой ничего общего, в то время как лежащие за пределами первобытного счета “один”, “два”, “много”, слова “три” и “третий”, “четыре” и “четвертый” ясно указывают на взаимосвязь между количественными и порядковыми числительными.
Названия чисел, выражающие весьма абстрактные идеи, появились, несомненно, позже, чем первые грубые символы для обозначения числа объектов в некоторой совокупности. В глубокой древности примитивные числовые записи делались в виде зарубок на палке, узлов на веревке, выложенных в ряд камешков, причем подразумевалось, что между пересчитываемыми элементами множества и символами числовой записи существует взаимно однозначное соответствие. Но для чтения таких числовых записей названия чисел непосредственно не использовались. Ныне мы с первого взгляда распознаем совокупности из двух, трех и четырех элементов; несколько труднее распознаются на взгляд наборы, состоящие из пяти, шести или семи элементов.
А за этой границей установить на глаз их число практически уже невозможно, и нужен анализ либо в форме счета, либо в определенном структурировании элементов. Счет на бирках, по–видимому, был первым приемом, который использовался в подобных случаях: зарубки на бирках располагались определенными группами подобно тому, как при подсчете избирательных бюллетеней их часто группируют пачками по пять или десять штук. Очень широко был распространен счет на пальцах, и вполне возможно, что названия некоторых чисел берут свое начало именно от этого способа подсчета.
Важная особенность счета заключается в связи названий чисел с определенной схемой счета. Например, слово “двадцать три” – не просто термин, означающий вполне определенную (по числу элементов) группу объектов; это термин составной, означающий “два раза по десять и три”. Здесь отчетливо видна роль числа десять как коллективной единицы или основания; и действительно, многие считают десятками, потому что, как отметил еще Аристотель, у нас по десять пальцев на руках и на ногах.
По той же причине использовались основания пять или двадцать. На очень ранних стадиях развития истории человечества за основания системы счисления принимались числа 2, 3 или 4; иногда для некоторых измерений или вычислений использовались основания 12 и 60.
Считать человек начал задолго до того, как он научился писать, поэтому не сохранилось никаких письменных документов, свидетельствовавших о тех словах, которыми в древности обозначали числа. Для кочевых племен характерны устные названия чисел, что же касается письменных, то необходимость в них появилась лишь с переходом к оседлому образу жизни, образованием земледельческих сообществ. Возникла и необходимость в системе записи чисел, и именно тогда было заложено основание для развития математики.
Основные виды чисел
В отличие от октав, седенионы S не обладают свойством альтернативности, но сохраняют свойство степенной ассоциативности .
Для представления целого положительного числа х в памяти компьютера, оно переводится в двоичную систему счисления.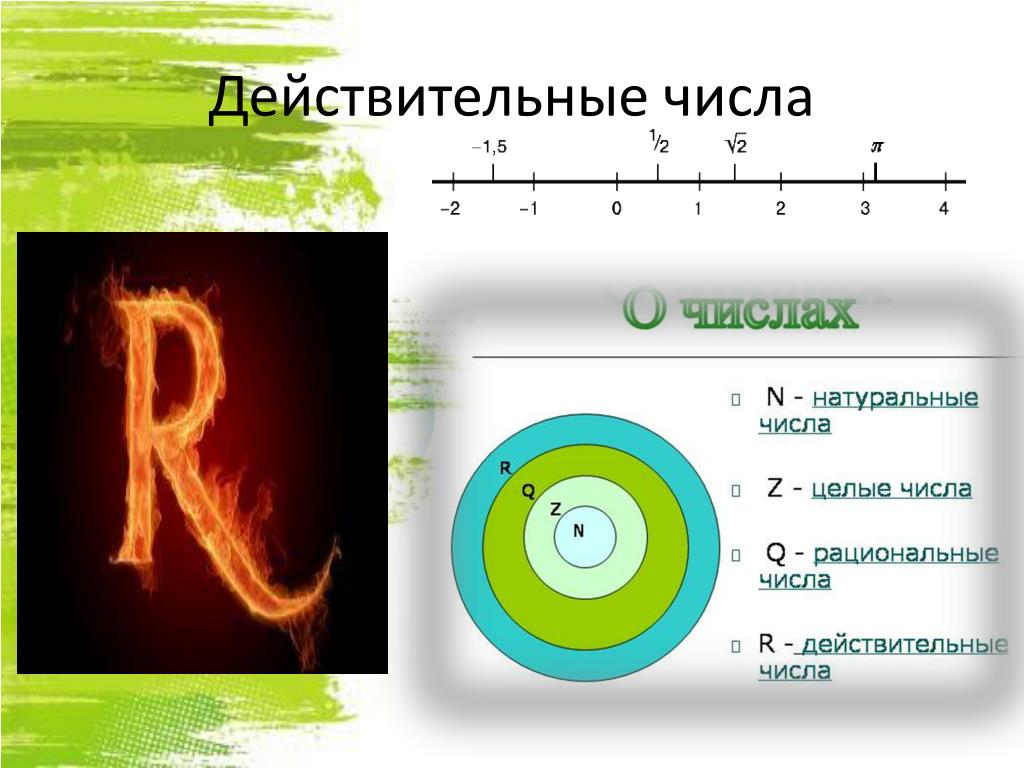
Полученное число в двоичной системе счисления х 2 представляет собой машинную запись соответствующего десятичного числа х 10 . Для записи отрицательных чисел используется т. н. дополнительный код числа, который получается путём прибавления единицы к инвертированному представлению модуля данного отрицательного числа в двоичной системе счисления.
Представление действительных чисел в памяти компьютера (в вычислительной технике для их обозначения используется термин число с плавающей запятой) имеет некоторые ограничения связанные с используемой системой счисления, а также, ограниченностью объёма памяти выделяемого под числа. Так, лишь некоторые из действительных чисел могут быть без потерь в точности представлены в памяти компьютера. В наиболее распространённой схеме число с плавающей запятой записывается в виде блока битов часть из которых представляют собой мантиссу числа, часть — степень, а один бит выделяется для представления знака числа (в случае необходимости знаковый бит может отсутствовать).
Найдите на числовой окружности точки с данной абсциссой. Координаты. Свойство координат точек. Центр числовой окружности. От окружности к тригонометру. Найдите на числовой окружности точки. Точки с абсциссой. Тригонометр. На числовой окружности укажите точку. Числовая окружность на координатной плоскости. Числовая окружность. Точки с ординатой. Назвать координату точки. Назвать линию и координату точки.
««Производные» 10 класс алгебра» — Применение производной для исследования функций. Производная равна нулю. Найдите точки. Обобщаем информацию. Характер монотонности функции. Применение производной к исследованию функций. Теоретическая разминка. Закончите формулировки утверждений. Выберите верное утверждение. Теорема. Сравните. Производная положительна. Сравните формулировки теорем. Функция возрастает. Достаточные условия экстремума.
««Тригонометрические уравнения» 10 класс» — Значения из промежутка. X= tg х. Укажите корни. Верно ли равенство. Серии корней. Уравнение ctg t = a.
Определение. Cos 4x. Найти корни уравнения. Уравнение tg t = a. Sin х. Имеет ли смысл выражение. Sin x =1. Не делай никогда того, чего не знаешь. Продолжите фразу. Сделаем выборку корней. Решите уравнение. Ctg x = 1. Тригонометрические уравнения. Уравнение.
«Алгебра «Производные»» — Уравнение касательной. Происхождение терминов. Решить задачу. Производная. Материальная точка. Формулы дифференцирования. Механический смысл производной. Критерии оценок. Функция производная. Касательная к графику функции. Определение производной. Уравнение касательной к графику функции. Алгоритм отыскания производной. Пример нахождения производной. Структура изучения темы. Точка движется прямолинейно.
«Кратчайший путь» — Путь в орграфе. Пример двух разных графов. Ориентированные графы. Примеры ориентированных графов. Достижимость. Кратчайший путь из вершины A в вершину D. Описание алгоритма. Преимущества иерархического списка. Взвешенные графы. Путь в графе. Программа “ProGraph”. Смежные вершины и рёбра.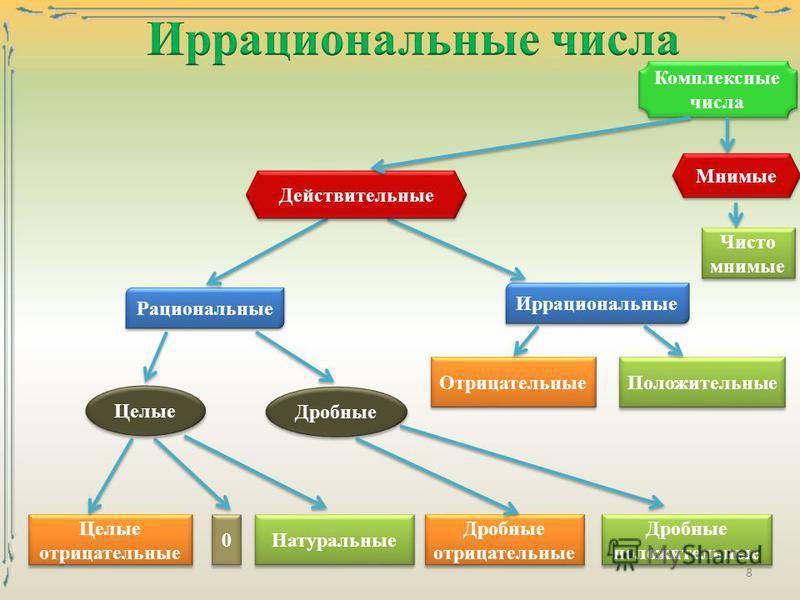
2
Реальная система счисления — другие типы действительных чисел
Домашний
Узнать
Реальный номер
- Натуральные числа
- Целые числа
- Целые числа
- Дроби
- Рациональные числа
- Иррациональные числа
- Другие типы действительных чисел
Помимо основных типов действительных чисел, обсуждавшихся ранее, эти числа также можно классифицировать в соответствии с их свойствами и представлением.
Вот некоторые из них:
Положительные числа — это числа, которые больше нуля.
Примеры положительных чисел: `1/2,98455,1,0,1673.
.., sqrt5`
Отрицательные числа — это числа, которые меньше нуля.
`-3,-sqrt7,-0.45612,-1/5,-19`
Четные числа — это целые числа, которые делятся на 2.
Они заканчиваются цифрами 0, 2, 4, 6 или 8.
Примеры четных чисел:`2, 4, 6, 100, -8, -20`
Нечетные числа — это целые числа, которые не делятся на 2.
Они заканчиваются цифрами 1, 3, 5, 7 или 9.
Примеры нечетных чисел:`1,5,3,99,-7,-41`
В числовом ряду четные и нечетные числа располагаются попеременно друг за другом.
Вот результаты сложения (или вычитания) нечетных или четных чисел:
Тот же результат, если используется операция вычитания (-).
Результатом является четное число, если сложенные числа оба являются четными или оба нечетными числами. В противном случае результатом будет нечетное число.
Вот результаты умножения на нечетное или четное число:
Результатом будет четное число, если одно умноженное число является четным числом. В противном случае результатом будет нечетное число.
Простые числа — натуральные числа, делителями которых являются только само себя и 1.
2 — единственное простое число, являющееся четным. Это также самое маленькое простое число.
Примеры простых чисел:`2,3,5,7,11,13,17,19`
Составные числа – это натуральные числа, имеющие хотя бы один делитель, отличный от самого себя и 1.
4 — наименьшее составное число.
Примеры составных чисел:`4,6,8,9,10,38,250,1700`
В таблице ниже показаны простые и составные числа от 1 до 100.
*Простые числа – синие квадраты
*Составные числа – белые квадраты
*1 не является ни простым, ни составным числом.
Ответ:
- Натуральные числа
- Целые числа
- Целые числа
- Дроби
- Рациональные числа
- Иррациональные числа
- Другие типы действительных чисел
Спиральный
Станьте участником сегодня!
Зарегистрируйтесь (бесплатно)Вы член? Войти!
Войдите в свою учетную записьРациональные, иррациональные и действительные числа
08.05.2018 | 0
Эпизод №2 курса «Основы математики» Джона Робина
it
С возвращением к основам математики.
Теперь, когда мы познакомились с натуральными и целыми числами, пришло время узнать о дополнительных сложностях чисел.
Вы, наверное, знакомы с дробями:
3/4, 5/7, 23/17
Дроби часто являются источником стресса в математике из-за того, насколько сложными могут быть правила их сложения и умножения.
Но давайте по-новому взглянем на дроби в свете того, что мы узнали вчера.
Рациональные числа
Напомним, что целые числа Z — это все отрицательные числа, которые идут до упора влево (до «отрицательной бесконечности»), соединенные со всеми натуральными числами N, которые бесконечно простираются до справа (положительная бесконечность):
…, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, …
Следующий уровень числа состоит из целых чисел. Это так называемые рациональные числа. Мы формируем их, беря целые числа и составляя из них всевозможные дроби, т. е. a/b , где a — целое число, а b — целое число (но b не равно нулю).
Это знакомая дробь, которую мы знаем со школы. Число a называется числителем, а b — знаменателем.
Возможности безграничны. Вы можете выбрать любые два числа из …, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, … и сложить их вместе, чтобы получить рациональное число. Например:
-7/8, 1/5, -4/3, 3, -1, 0
Вам может быть интересно, почему -1, 3 и 0 являются рациональными числами. Разве они не целые? Это просто область, где целые числа перекрываются с рациональными числами (представьте, что это аналогично тому, как натуральные числа 0, 1, 2, 3, 4, 5, … перекрываются с целыми числами …, -5, -4, — 3, -2, -1, 0, 1, 2, 3, 4, 5, …).
В нашем примере мы получаем -1, 3 и 0 всякий раз, когда у нас есть -1/1, 3/1 и 0/1. Знаменатель 1 не влияет на дробь, поэтому мы опускаем его, оставляя нам целое число.
Благодаря этому свойству вы найдете все целых чисел в рациональных числах. Это просто все числа, которые мы образуем из…, -5/1, -4/1, -3/1, -2/1, -1/1, 0/1, 1/1, 2/1, 3/1.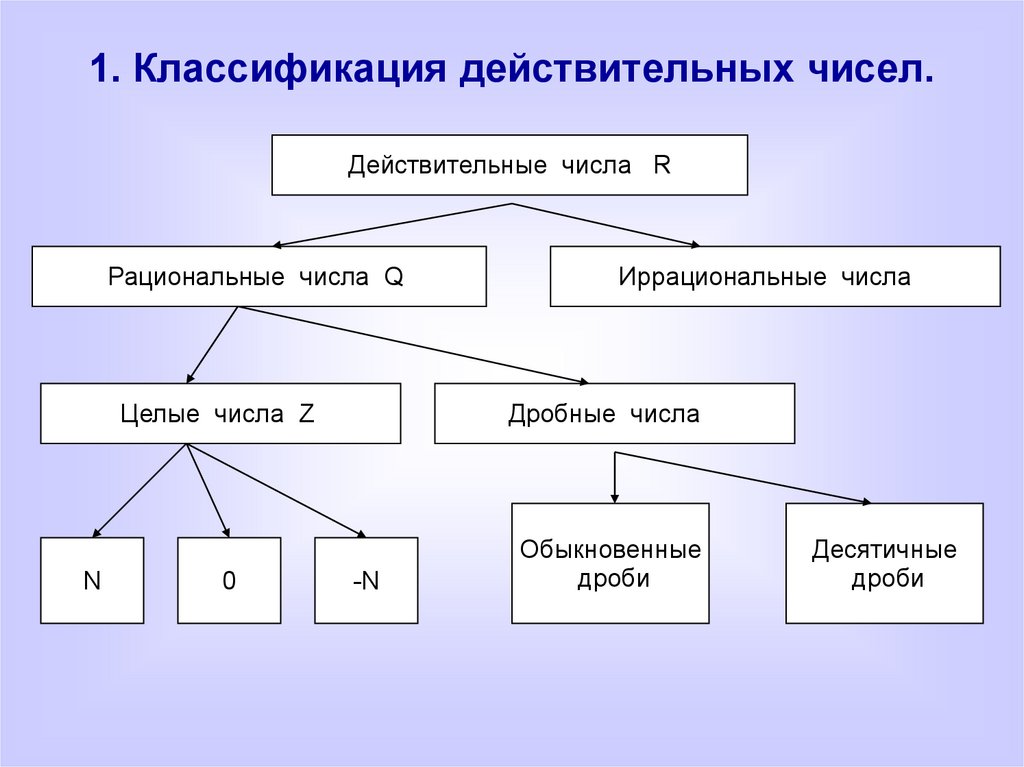
, 4/1, 5/1, ….
Рациональные числа имеют символ Q. Как и Z для целых чисел, Q вошел в употребление, потому что итальянский математик Джузеппе Пеано впервые ввел этот символ в 189 году.5 от слова «quoziente», что означает «частное».
Иррациональные числа
Существует много чисел, которые мы можем составить из рациональных чисел. Мы можем сделать любую дробь. Но все ли это возможные числа? Ответ отрицательный, но позвольте мне показать вам, почему, на примере.
Возможно, вы видели такое обозначение: √2.
Это квадратный корень из 2. Извлечение квадратного корня из числа означает нахождение двух равных чисел и, когда вы их перемножаете, получается исходное число. Например, √4 равно 2, потому что 2×2 = 4, т. е. два одинаковых числа, которые при умножении дают 4, равны 2.
Но √2 не имеет дробного числа. Доказательство этого требует некоторой алгебры. На самом деле, если вы вспомните наши вчерашние простые числа, то также можно доказать, что для любого простого числа не существует рациональных квадратных корней.
Также было доказано, что существует бесконечно много простых чисел. Это означает, что существует бесконечно много чисел, которые не могут быть представлены дробями! Мы называем эти числа иррациональными числами . Это название происходит от греков, потому что они считали, что каждое число должно быть дробью, поэтому для них было просто иррационально говорить о числах так, как будто их нет.
Вещественные числа
Мы называем полный набор чисел (т. е. каждое рациональное, а также иррациональное число) действительными числами. У них есть символ R.
Вы можете думать о действительных числах как о любом возможном десятичном числе. Сюда входят все рациональные числа, т. е. 4, 3/5, 0,6783 и -86 — все десятичные числа. Если мы включим все иррациональные числа, мы сможем представить их десятичными дробями, которые никогда не оканчиваются. Например, 0,5784151727272… — действительное число. (Обратите внимание, что когда мы используем «…» после десятичного числа, это означает, что справа от того места, где мы усекли, есть еще цифры.