Натуральные иррациональные рациональные числа: Какие числа называются действительными?

Числа рациональные и иррациональные

Числа рациональные и иррациональные

Айвен Нивен. Числа рациональные и иррациональные Эта книга посвящена одному из основных понятий математики — понятию действительного числа. Ученики старших классов (именно на них она в первую очередь и рассчитана) узнают из нее некоторые свойства чисел, о которых они раньше и не подозревали, и познакомятся с доказательствами теорем, принимаемых в школьном курсе алгебры на веру. Изложение очень простое и живое. Оно сопровождается рядом вопросов и задач, облегчающих активное усвоение материала. Автор книги — известный американский специалист по теории чисел. Оглавление От редактора Введение ГЛАВА I. Натуральные и целые числа § 1. Простые числа § 2. Единственность разложения на простые множители § 3. Целые числа § 4. Четные и нечетные целые числа § 5. Свойства замкнутости § 6. Замечания о природе доказательства ГЛАВА II. Рациональные числа § 1. Определение рациональных чисел § 2. Конечные и бесконечные десятичные дроби § 3. Различные сгюсобы формулировки и доказательства предложений § 4. Периодические десятичные дроби § 5. Всякую конечную десятичную дробь можно представить в виде периодической десятичной дроби § 6. Краткие выводы ГЛАВА III. Действительные числа § 1. Геометрическая точка зрения § 2. Десятичные представления § 3. Иррациональность числа V2 § 4. Иррациональность числа V3 § 5. Иррациональность чисел V6 и V2+V3 § 6. Слова, которыми мы пользуемся § 7. Приложение к геометрии § 8. Краткие выводы ГЛАВА IV. Иррациональные числа § 1. Свойства замкнутости § 2. Алгебраические уравнения § 3. 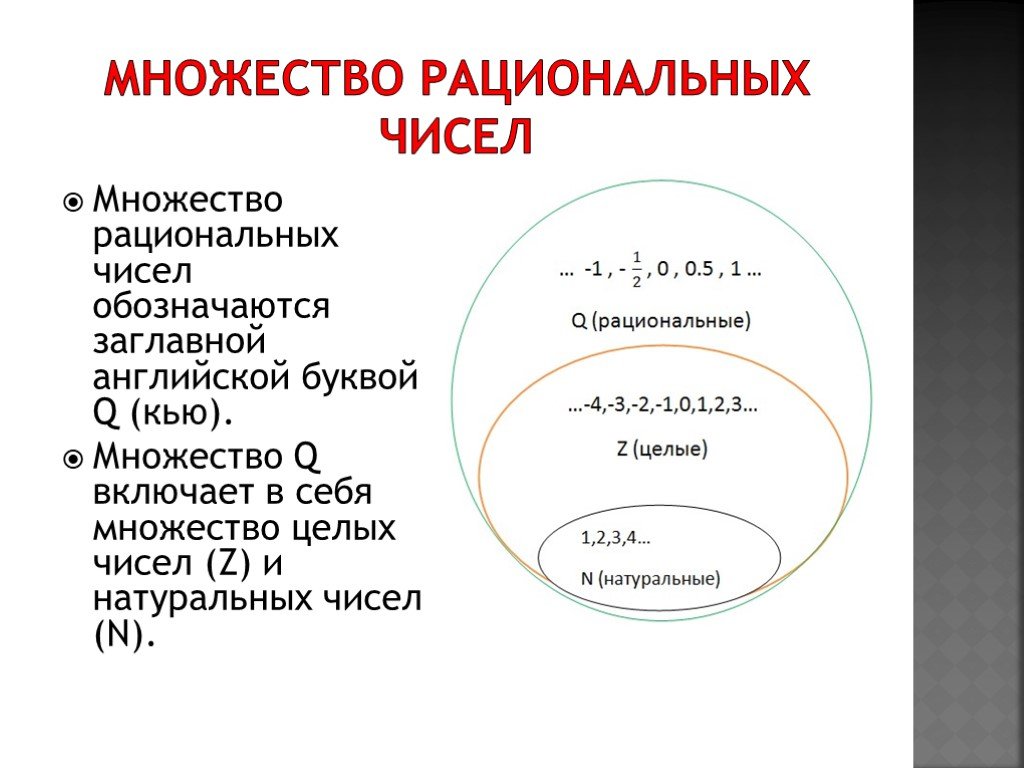Рациональные корни алгебраических уравнений § 4. Дальнейшие примеры § 5. Краткие выводы ГЛАВА V. Значения тригонометрических и логарифмической функций § 1. Иррациональные значения тригонометрических функций § 2. Одно общее правило § 3. Иррациональные значения десятичных логарифмов § 4. Трансцендентные числа § 5. Три знаменитые задачи на построение § 6. Дальнейший анализ числа V2 § 7. Краткие выводы ГЛАВА VI. Приближение иррациональных чисел рациональными § 1. Неравенства § 2. Приближение целыми числами § 3. Приближение рациональными числами § 4. Лучшие приближения § 5. Приближения с точностью до 1/n2 § 6. Ограничения точности приближений § 7. Краткие выводы ГЛАВА VII. Существование трансцендентных чисел § 1. Предварительные сведения из алгебры § 2. Один способ приближения числа а § 3. План доказательства § 4. Свойства многочленов § 5. Трансцендентность числа а § 6. Краткие выводы ПРИЛОЖЕНИЕ А. Доказательство бесконечности числа простых чисел ПРИЛОЖЕНИЕ Б. Доказательство основной теоремы арифметики ПРИЛОЖЕНИЕ В. Доказательство Кантора существования трансцендентных чисел ПРИЛОЖЕНИЕ Г. Доказательство иррациональности значений тригонометрических фуннций И. М. Яглом Ответы и указания к упражнениям ПРИЛОЖЕНИЕ В Литература

Какая классификация настоящих чисел? | Ресурсы самопомощи

вещественные числа является набор рациональных и иррациональных чисел чем существующие, из которых также можно найти различные типы. Они возникли в связи с необходимостью, обнаруженной между XV и XVII веками, когда расчет невозможно было описать логически и точно, поскольку часто использовались ненадежные термины или выражения, такие как «малый» или «предел».

Хотя египтяне уже использовали дроби, это было до тех пор, пока математика греков не изучала «число» более философски, когда последователи Пифагора пришли к выводу, что все вокруг них является числами; и поэтому они применялись в различных областях.

Индекс

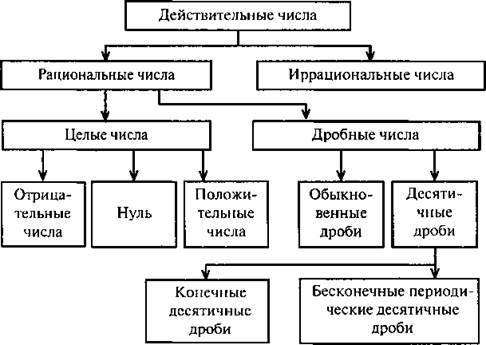
• 1 Классификация действительных чисел по их типу
  • 1.1 1. Рациональные числа
    • 1.1.1 а) Целые числа
    • 1.1.2 б) Дробное
  • 1.2 2. Иррациональные числа

Эти числа можно разделить на два типа, о которых мы упоминали ранее, то есть рациональные числа (положительные, отрицательные и нулевые) и иррациональные (алгебраические и трансцендентные). Точнее можно найти следующую классификацию:

1. Рациональные числа

Это имя, данное числам, которые могут быть представлены как деление целых чисел или, что то же самое, обыкновенная и текущая дробь, в которой числитель и знаменатель не равны нулю и не меньше его.

Они, в свою очередь, также делятся на несколько типов: целые (натуральные, нулевые и отрицательные целые числа) и дробные (правильные и неправильные дроби).

а) Целые числа

Целые числа представляют собой набор натуральных чисел, отрицательных целых чисел и нуля, которые обозначаются буквой «Z». Целые числа также обычно представлены в числовой строке, где положительные или натуральные числа находятся справа, ноль — в середине, а отрицательные — слева.

• Считается «натуральные числа”Для тех, кто привык считать предметы или выполнять некоторые из наиболее распространенных и простых расчетных операций.
• El Cero Это нулевое значение, то есть в нем отсутствует значащая цифра, когда оно не сопровождается. Однако его положение в числе может полностью изменить значение, поскольку, когда оно находится справа от него, значение умножается на десять; а с другой стороны модификации нет.
• отрицательные целые числа они используются противоположно положительным или естественным, то есть вместо того, чтобы считать, их использование состоит в том, чтобы вычитать, иметь, тратить или быть ниже. Чтобы их упомянуть, необходимо перед числом указать термин «минус», например «минус четыре».

б) Дробное

Также среди вещественных чисел можно найти этот тип в рациональных числах, которые возникли с целью решать задачи относительно деления натуральных чисел. Дробное число — это просто выражение, которое указывает деление одной величины на другую.

Дроби характеризуются числителем и знаменателем, которые отделены друг от друга диагональной или горизонтальной чертой. Однако, несмотря на то, что в целых числах мы также можем найти «простую дробь», в этом разделе типы дробей, которые мы находим, правильные и неправильные.

• Правильные состоят из тех, у которых числитель меньше знаменателя.
• Неподходящие будут наоборот, то есть знаменатель больше знаменателя.

2. Иррациональные числа

Иррациональные числа — это числа, которые нельзя записать в виде дроби, поскольку их десятичные дроби продолжают повторяться бесконечно. Например, невозможно записать дробь, включающую число Пи, е, соотношение золота и корней квадратные, кубические и другие.

Иррациональные числа возникли благодаря потребности ученика Пифагора записать корень в виде дроби; понимая, что это невозможно и что сегодня мы знаем это число под термином «иррациональное».

Однако Пифагор не согласился с его открытием, хотя оно приписывается ему не меньше, чем его школе.

Кроме того, их можно разделить на два типа: алгебраические и трансцендентные.

• алгебраический те, которые позволяют решить алгебраическое уравнение.
• трансцендентный Это те, которые не могут быть представлены конечным числом корней (в отличие от алгебраических) и которые не следуют шаблону в своих десятичных дробях. Среди них находим число Пи.

 

Пока что мы подошли к классификации действительных чисел, которую, как мы надеемся, было легко читать и понимать; поскольку многие люди не любят математику, и мы сделали все возможное, чтобы дать подробное и простое объяснение.

Основные операции — типы чисел

Натуральные числа (также известные как счет чисел)

Размышляя о натуральных числах, мы можем перенестись в более простые времена. Старые добрые времена, когда нашей единственной обязанностью было прийти на урок в детский сад и не намочить штаны. Аааа, воспоминания. Именно в этот момент мы укрепили свои навыки счета, а счет — это то, что касается натуральных чисел.

Натуральные числа , также известные как счетные числа , начните с 1 и продолжайте до бесконечности. Числа 1, 2, 3, 4, 5,… все натуральные числа.

Мы используем натуральные числа, такие как 1, 2, 3 и так далее, чтобы считать предметы, дни, людей, лысых кошек, волосатых бегемотов, что угодно. Когда мы используем натуральные числа для счета, мы можем называть их количественными числами. Мы также используем натуральные числа, чтобы упорядочивать вещи, например, упорядочивать одноклассников от самого маленького до самого высокого. В этих случаях мы называем их порядковыми числами и записываем их как 1 ^st , 2 ^nd , 3 ^rd и т. д.

Для получения дополнительной информации о натуральных числах перейдите сюда.

Целые числа

Целые числа очень похожи на счетные числа. Единственное их отличие состоит в том, что целые числа включают в себя ноль. Когда мы перечисляем целые числа от меньшего к большему, мы получаем 0, 1, 2, 3 и так далее, и так далее, и тому подобное.

Целые числа — причудливая связка с довольно сильными чертами характера. Мы любим их за их оптимистичный подход к математике. Они никогда не принимают в свою группу отрицательные числа (или надутые губки) и не принимают никакой чепухи. Целые числа также гордятся своей целостностью, что означает, что дроби и десятичные дроби также не приветствуются. Они такие эксклюзивные.

Для получения более честных примеров целых чисел, проверьте это.

На изображении выше целые числа состоят из каждого числа в большом квадрате, включая содержимое вашего сами знаете чего при -10 градусах. Температура, измеренная в градусах Фаренгейта и Цельсия, может быть положительной или отрицательной, и это то, что отличает целые числа от целых чисел.

Целые числа включают все целые числа, их противоположности и ноль. Нет, не напротив, как в «злом близнеце», а напротив, как в отрицании. Например, противоположность 5 — это (о-о-очень капризный) -5. Противоположность 10 (еще более мрачная) -10.

Получаются целые числа {…, -3, -2, -1, 0, 1, 2, 3, …}.

Хотя целые числа толерантны и включают отрицательные числа, они довольно строго относятся к целостности, что означает, что дроби и десятичные дроби не приветствуются. Эй, они должны где-то провести черту.

Чтобы узнать больше о целых числах, посетите здесь. Просто будьте готовы принять хорошее вместе с плохим.

Теперь есть три ящика. Числа, разрешенные в самом большом поле, также называемые целыми числами, включают также все числа в меньших полях. Таким образом, целые числа включают в себя отрицательные числа, целые числа и натуральные числа.

Рациональные числа

У большинства людей есть два типа друзей: рациональные, уравновешенные друзья, которые отлично подходят для того, чтобы давать советы и копировать домашние задания (э-э, домашние задания), и иррациональные, витающие в облаках друзья, которые отлично подходят для иррациональных советов и поддержки команды.

Рациональные числа дают отличные советы, и они также отлично подходят для раскрашивания лиц. Однако название «рациональный» не имеет никакого отношения к их остроумию. К рациональным числам относятся любые числа, которые можно представить как отношение двух целых чисел. Отсюда они и получают свое название. Ratio -nal числа включают очевидные примеры, такие как или , а также не столь очевидные числа, такие как -10, которые можно записать как .

К рациональным числам также относятся любые десятичные дроби, которые можно превратить в дроби. Вот несколько примеров.

• 0,1 — рациональное число, потому что его можно записать как
• 1,25 — тоже рационально, потому что его можно записать как .
• 0,333333… тоже рационально, хотя это бесконечно повторяющаяся десятичная дробь, потому что ее можно записать как

На самом деле рациональные числа настолько приемлемы, что включают в себя целые числа, целые числа и натуральные числа, поскольку их можно записать в виде дробей со знаменателем 1.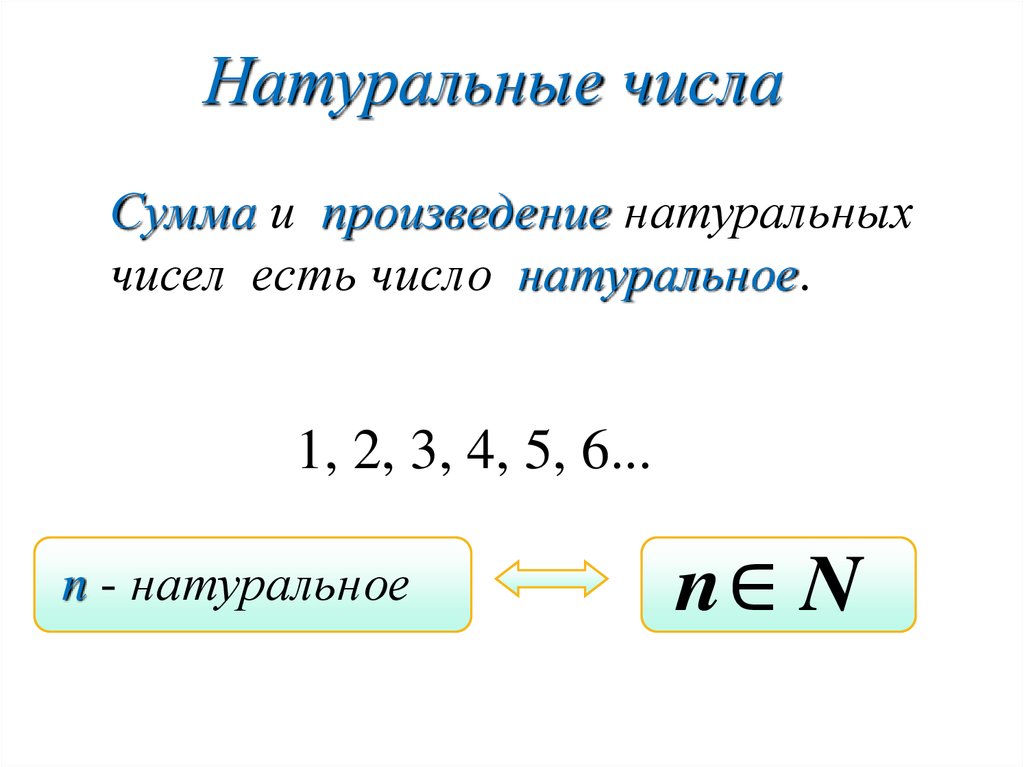

Рациональные числа имеют довольно рациональные правила. Если число можно записать в виде дроби, оно считается рациональным. Если число не может быть записано в виде дроби, то это не так.

Теперь четыре ящика. Числа, разрешенные в самом большом поле, или рациональные числа, также включают в себя все числа в меньших ящиках. К рациональным числам относятся дроби, смешанные числа, десятичные дроби, целые числа, целые числа и натуральные числа. Рационалы — довольно инклюзивная группа.

Подробнее о рациональных числах см. здесь.

Иррациональные числа

Иррациональные числа подобны малышам. Их трудно понять, они создают хаос, куда бы они ни пошли, и у них есть бесконечная, вездесущая энергия.

Иррациональные числа включают несоответствия системы счисления. Иррациональные числа — это числа, которые нельзя записать в виде отношения или дроби, как бы кто ни старался. Когда они записываются в виде десятичных дробей, они продолжают идти вечно без повторяющегося шаблона.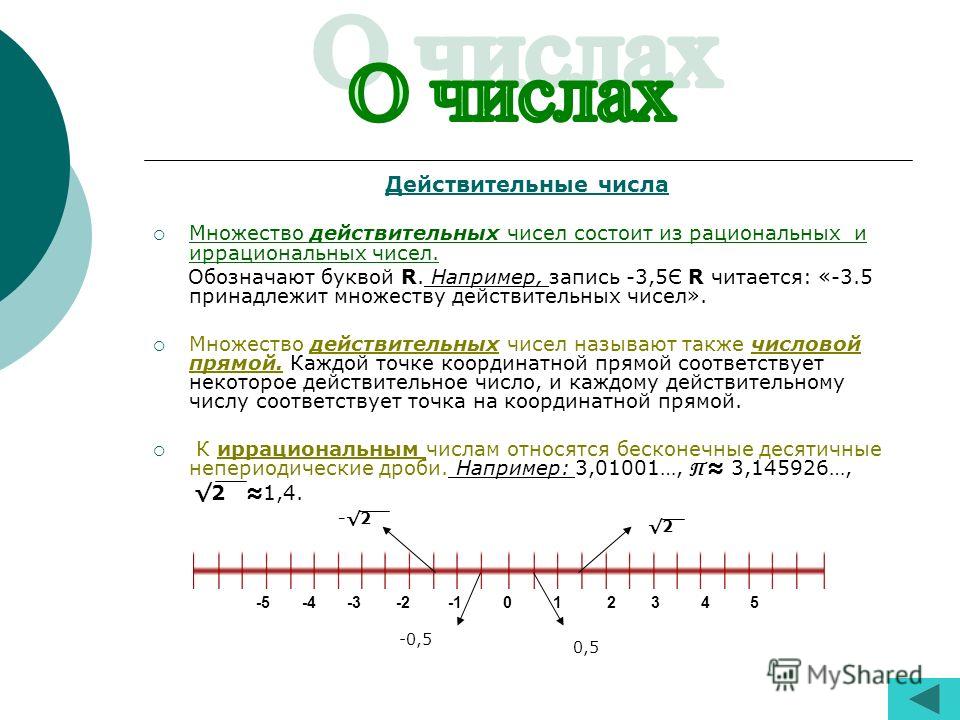

Самое популярное иррациональное число — пи или π. Пи иррационально, потому что его значение — бесконечная, неповторяющаяся десятичная дробь, которую никогда нельзя выразить как отношение к к дроби.

π = 3,1415926535…

Подобно малышу, бьющемуся по земле в продуктовом магазине, число «пи» иррационально.

Квадратный корень из 2, или , является еще одним иррациональным числом, потому что его значение также записывается как бесконечная, постоянно меняющаяся десятичная дробь, которую нельзя выразить в виде отношения или дроби.

Каждый раз, когда мы находим числа, которые нельзя преобразовать в дроби, мы можем списать это на их неразумную природу и назвать их иррациональными. Иррациональные числа не включают никакие другие числа, о которых мы говорили. Они болтаются там сами по себе, будучи неразумными. Только не называй их так в лицо. Они способны на все.

Чтобы продолжить изучение иррациональных чисел с безопасного расстояния, нажмите здесь.

Реальные числа

Реальные числа — самые гостеприимные из всех чисел. Они как наш хороший приятель, Старик Оливер (ОМО, как мы любим его называть). ОМО живет дальше по улице, дает лучшие советы и в этом году приютила двенадцать бездомных кошек. Также известно, что он экономит летние каникулы, но это другой путеводитель. Точно так же, как OMO с трудом отказывается от нужных вещей, реальным числам трудно исключать числа из своей группы.

Действительные числа поддерживает целые числа, отрицательные числа, положительные числа, дроби, иррациональные числа, рациональные числа и . Действительные числа включают всех чисел на числовой прямой.

К ним относятся рациональные числа, такие как -13, и , а также иррациональные числа, такие как π и .

Чтобы узнать больше о действительных числах, нажмите здесь.

Является ли 6/3 рациональным числом?

Числительные — это математические числа, используемые в финансовой, профессиональной, а также в социальной сфере в социальном мире. Цифры и разрядное значение в числе и основание системы счисления определяют значение числа. Числа используются в различных математических операциях, таких как суммирование, вычитание, умножение, деление, процент и т. д., которые используются в нашей повседневной деятельности и торговой деятельности.

Что такое числа?

Числа используются в различных арифметических значениях, применимых для выполнения различных арифметических операций, таких как сложение, вычитание, умножение и т. д., которые применяются в повседневной жизни для целей вычислений. Значение числа определяется цифрой, ее разрядностью в числе и основанием системы счисления.

Числа , также известные как цифры, представляют собой математические значения, используемые для подсчета, измерения, маркировки и измерения основных величин.

Числа — это математические значения или цифры, используемые для измерения или вычисления величин. Он представлен цифрами 2, 4, 7 и т.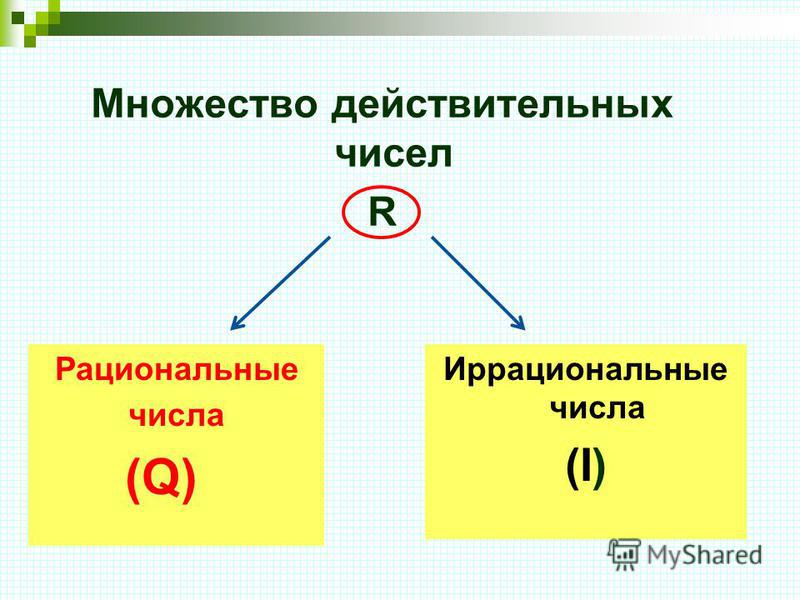 д. Примерами чисел являются целые числа, целые числа, натуральные числа, рациональные и иррациональные числа и т. д.

Типы чисел

Существуют различные типы чисел, разделенные на наборы по системе счисления. Типы описаны ниже:

• Натуральные числа: Натуральные числа — это положительные числа, которые считаются от 1 до бесконечности. Подмножество не включает дробные или десятичные значения. Множество натуральных чисел представлено ‘ N ’. Это числа, которые мы обычно используем для счета. Набор натуральных чисел может быть представлен как N=1,2,3,4,5,6,7,……………
• Целые числа: Целые числа — положительные натуральные числа, включая ноль, который отсчитывается от 0 до бесконечности. Целые числа не включают дроби или десятичные дроби. Набор целых чисел представлен как « W ». Набор может быть представлен как W=0,1,2,3,4,5,………………
• Целые числа: Целые числа представляют собой набор чисел, включающий все положительные счетные числа, ноль, а также все отрицательные числа, которые считают от отрицательной бесконечности до положительной бесконечности. В наборе нет дробей и десятичных знаков. Набор целых чисел обозначается ‘ З ’. Набор целых чисел можно представить в виде Z=………..,-5.-4,-3,-2,-1,0,1,2,3,4,5,………….
• Десятичные числа: Любое числовое значение, состоящее из десятичной точки, является десятичным числом. В некоторых случаях он также может быть выражен в дробной форме. Его можно выразить как 2,5, 0,567 и т. д.
• Действительное число: Действительные числа — это заданные числа, не содержащие мнимых значений. Он включает в себя все положительные целые числа, отрицательные целые числа, дроби и десятичные значения. Обычно обозначается ‘ Р ’.
• Комплексный номер: Комплексные числа — это набор чисел, включающий мнимые числа. Его можно выразить как a+bi, где «a» и «b» — действительные числа. Обозначается ‘ C ’.
• Рациональные числа: Рациональные числа — это числа, которые можно представить как отношение двух целых чисел. Он включает в себя все целые числа и может быть выражен в виде дробей или десятичных знаков. Обозначается ‘ Q ’.
• Иррациональные числа: Иррациональные числа — это числа, которые не могут быть выражены в дробях или отношениях целых чисел. Он может быть записан десятичными знаками и иметь бесконечные неповторяющиеся цифры после запятой. Обозначается ‘ P ’.

Что такое рациональные числа?

Рациональные числа имеют вид p/q, где p и q — целые числа, а q ≠ 0. Из-за лежащей в основе структуры чисел, формы p/q, большинству людей трудно отличить дроби от рациональных чисел. Когда рациональное число делится, вывод находится в десятичной форме, которая может быть как оканчивающейся, так и повторяющейся. 3, 4, 5 и т. д. — некоторые примеры рациональных чисел, поскольку они могут быть выражены дробью как 3/1, 4/1 и 5/1.

Примеры рациональных чисел

3, 4, 5 и т. д. являются некоторыми примерами рациональных чисел, поскольку они могут быть выражены в форме дроби как 3/1, 4/1 и 5/1.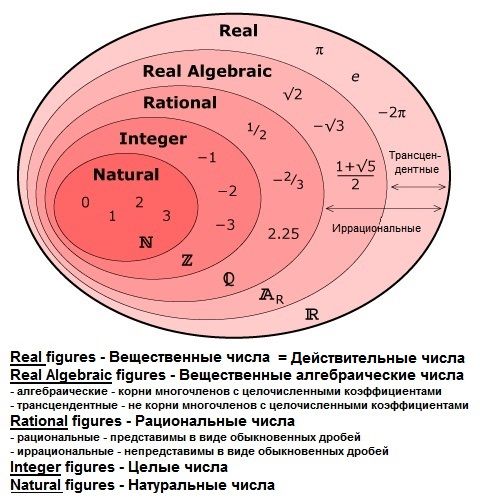 Число «0» также является рациональным, поскольку его можно представить различными способами, включая 0/1, 0/2, 0/3 и так далее.

Является ли 6/3 рациональным числом?

Ответ:

Рациональные числа — один из наиболее распространенных типов чисел, которые мы изучаем в математике после целых чисел. Рациональное число — это своего рода действительное число, имеющее форму p/q, где q≠0. Все целые числа, натуральные числа, дроби целых чисел, целые числа и конечные десятичные дроби являются рациональными числами.

При разделении рационального числа результатом является десятичное число, которое может быть как завершающим, так и повторяющимся десятичным числом. Все рациональные числа можно представить в виде дроби, знаменатель которой не равен нулю. Здесь данное число 6/3 представляет собой дробь двух целых чисел 6 и 3, которая упрощается до 2. Следовательно, это рациональное число.

Похожие вопросы

Вопрос 1.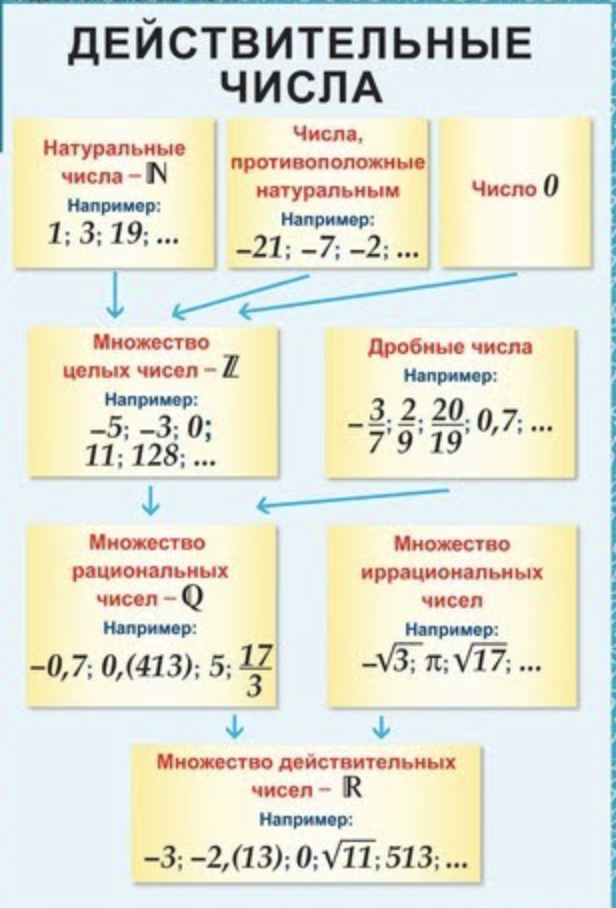

Является ли 1/7 рациональным числом?

Ответ:

Да, 1/7 — рациональное число, поскольку оно представлено в виде p/q с q≠0, где p и q — целые числа.

Вопрос 2: Определите, является ли -0,3333…. является рациональным числом.

Ответ:

Рациональное число — это действительное число, имеющее форму p/q, где q≠0. Когда рациональное число разбивается, результатом является десятичное число, которое может быть как завершающим, так и повторяющимся десятичным числом. Здесь данное число выражается в виде p/q и имеет повторяющееся десятичное число. Следовательно, -0,3333….. является рациональным числом. Да, десятичные значения могут быть рациональными числами, поскольку рациональные числа могут быть записаны как в дробной, так и в десятичной форме. Но десятичное значение должно быть определенным или иметь повторяющиеся цифры после запятой.

Вопрос 3: Является ли √25 рациональным или иррациональным числом?

Ответ:

Рациональное число — это действительное число, имеющее форму p/q, где q≠0.

No related posts.